Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Latinoamericana de Metalurgia y Materiales
Print version ISSN 0255-6952
Rev. LatinAm. Metal. Mater. vol.34 no.1 Caracas June 2014
VARIATION OF MAGNETISM OF Cr1-XGaXN DUE TO THE PRESSURE: A DFT STUDY
122*
Ricardo E. Báez Cruz, Jhon H. Díaz F, Miguel J. Espitia R
1: Department of Physics, National Pedagogical University, Bogotá, Colombia
2: GEFEM Group, Distrital University Francisco José de Caldas, Bogotá Colombia.
* e-mail: mespitiar@udistrital.edu.co
ABSTRACT
We report a firt-principles study of the pressure dependence of electronic and the magnetic properties of Cr1−xGaxN compounds (x= 0,25, 0,50 and 0,75) in wurtzite-derived structures. We use the full-potential linearized augmented plane wave method (FP-LAPW) within of the density functional theory framework. We found that, the lattice constant vary linearly with Ga-concentration. The magnetic moment changes for a critical pressure. At x = 0,75, a rather abrupt onset of the magnetic moment from 0 to 2,2 µB at Pcr = 22,65 GPa is observed. For x = 0,25 and 0,50 Ga concentrations, the magnetic moment increases gradually when the pressure decreases toward the equilibrium value. We study the transition pressure dependence to a ferromagnetic phase near the onset of magnetic moment for each Cr1−xGaxN compounds. The calculation of the density of states with Ga concentration is carried out considering two spin polarizations. The results reveal that for x = 0,75 the compound behaves as a conductor for the spin-up polarization and that the density of states for spin-down polarization is zero at the Fermi level. At this concentration the compound presents a half metallic behavior; therefore this material could be potentially useful as spin injector. At high pressures P > Pcr the compounds exhibit a metallic behavior.
Keywords: FP-LAPW, Magnetic semiconductors, Pressure dependence.
VARIACION DEL MAGNETISMO EN EL COMPUESTO Cr1-XGaXN DEBIDO A LA PRESIÓN: UN ESTUDIO POR DFT
RESUMEN
Reportamos un estudio de primeros principios para estudiar los efectos de la presión sobre las propiedades electrónicas y magnéticas del compuesto Cr1-xGaxN (0,25, 0,50 y 0,75) en la estructura wurtzita. Usamos el método Ondas Plana Aumentadas y Linealizadas Potencial Completo (FP-LAPW) en el marco de la Teoría del Funcional de la Densidad DFT. Hallamos que la constante de red del compuesto aumenta linealmente con la concentración de Ga. El momento magnético cambia para una presión crítica. Para x = 0,75, un cambio bastante abrupto comienza en el momento magnético de 0 a 2,2 µB a la presión Pcr = 22,650 GPa. Para las concentraciones de Ga x = 0,25 y 0,50 el momento magnético aumenta gradualmente cuando la presión disminuye hacia su valor de equilibrio. Estudiamos la dependencia con la presión de transición hacia la fase ferromagnética cerca del inicio del momento magnético para cada compuesto Cr1xGaxN. Calculamos la densidad de estados con la concentración de Ga considerando las dos contribuciones de polarización de espín. Los resultados revelan que a x = 0,75 el compuesto se hace conductor para la polarización de espín arriba y que la densidad de estados de espín abajo es cero en el nivel de Fermi. A esta concentración en el compuesto presenta un comportamiento half-metallic, por consiguiente este material podría ser potencialmente usado como inyector de espín. A presiones P > Pcr el compuesto exhibe un comportamiento metálico.
Palabras Claves: FP-LAPW, Semiconductores magnéticos, dependencia con la presión.
Recibido: 20-12-2012 ; Revisado: 25-02-2013 pISSN: 0255-6952 | eISSN: 2244-7113
142
Aceptado: 08-04-2013 ; Publicado: 14-04-2013 Rev. LatinAm. Metal. Mat. 2014; 34 (1): 142-147
1. INTRODUCTION
At present, various high performance devices fabricated from III-nitride have generated great interest. Amongst the III semiconductor, Gallium nitride (GaN), whose more stable phase is hexagonal (wurtzite) [1]. Due to its wide direct band gap, gallium nitride is a promising candidate in semiconductor technology and has a broad range of potential applications for optoelectronic and high power electronic devices. Intensive activities over the recent years have made of the short wave length blue, violet light emitting diodes (LEDs) a commercial reality [2]. Due to its high chemical stability and high thermal conductivity, is also suitable for the applications in the harsh environments, such as, in high-temperature/highpower electronic devices [3, 4], as metalsemiconductor field effect transistors (MESFETs), high electron mobility transistors (HEMTs) and heterojunction bipolar transistors (HBTs) [5, 6]. Large piezoelectric constants of GaN point out possible applications of GaN-based materials in piezoelectric sensors [1]. Additionally, theoretically [7, 8] and experimentally [9], high Curie temperatures and room-temperature ferromagnetism have been found in GaN-doped with transitionmetal (MT) elements, which in principle opens the door for potentials use of this room-temperature ferromagnetic material for spintronic devices [7 10].
The magnetic properties of transitions metal (MT) in GaN regained prominence due to potential application for Dilute Magnetic Semiconductors (DMS) [11, 12]. In particular, the 3d-MT elements can be expected that substitute Ga-atoms during crystal growth. The knowledge of their associated deep defects is very important to development a new kind of devices such as: electro-optic switches, ultra sensitive magnetic field sensors and quantum– mechanism-based logic for high speed computation [13].
In this paper, we investigate mixed C1−xGaxN compounds. As will be shown, the dilution of CrN with Ga expands the lattice constant according to Vegard’s law as expected. Also Ga incorporation produce the arise of magnetic moment formation. This makes these materials potentially useful as spin injector. In order to model the compounds, simple ordered model structures (Cr3Ga1N4, Cr1Ga1N2, Cr1Ga3N4) based on supercells of the wurtzite structure were investigated.
2. COMPUTATIONAL METHOD
The electronic structure calculations were performed employing the full-potential linearized augmented plane wave method (FPLAPW) as implemented in the WIEN2k package, which includes the LAPW[14], within of the spin density functional theory (DFT) framework [15, 16]. The exchange and correlations electronic energy. were calculated with Generalized Gradient Approximation (GGA) of Perdew et al. [17]. Separation energy between the valence and core states of − 8,0 Ry, and the angular momenta up to lmax = 10, were used. The wave functions in the interstitial region were expanded in plane waves with a cutoff of Kmax = 8,0/RMT (where RMT is the smallest muffin-tin sphere radii inside the cell). For GaxCr1−xN compounds muffintin radii of 1,90, 1,80 and 1,60 bohr for Ga, Cr and N atoms were selected respectively. In calculation of the electronic structure, a 144 k-points mesh were used in Brillouin irreducible zone generated according to the Monkhorst Pack scheme [18]. The iteration for self-consistence was continued until the convergence criterium of 1×10−4 Ry was reached.
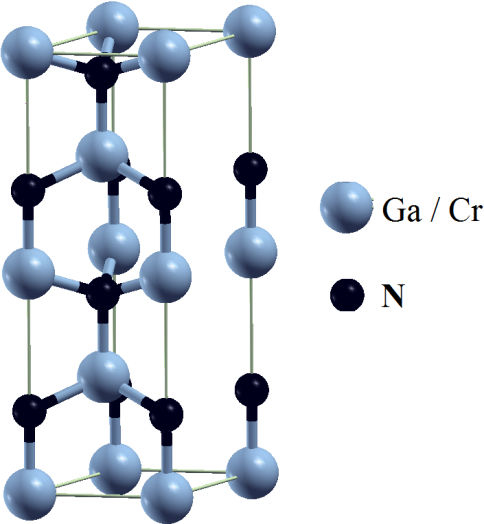
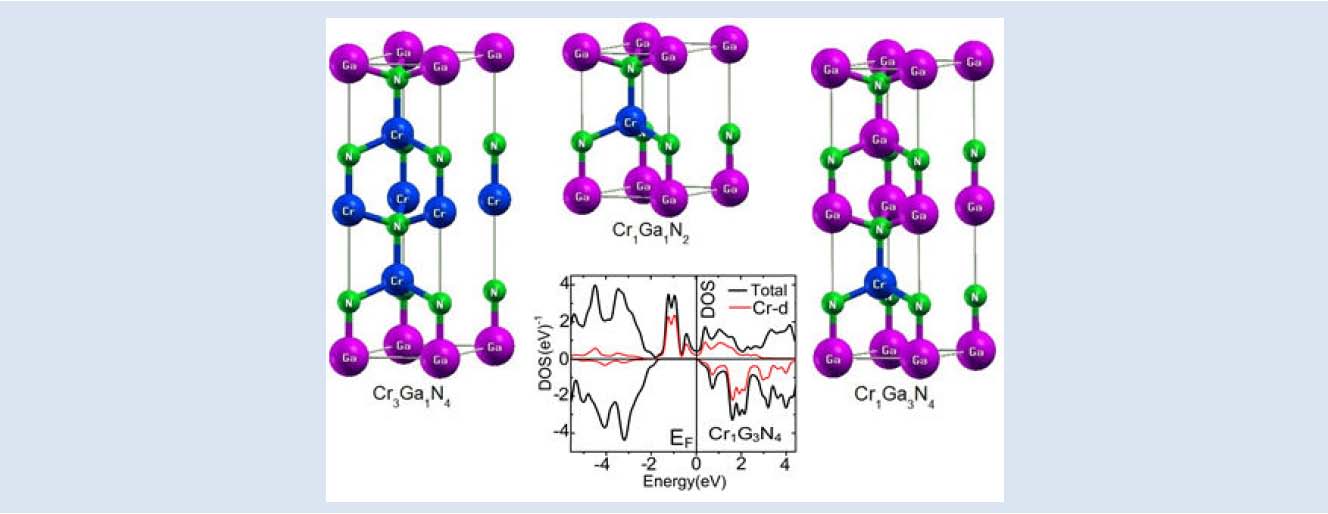
Figure 1. Unit cell used in our calculation for Cr1−xGaxN compounds in wurtzite-like structure.
The C1−xGaxN compounds were modeled for x = 0,25, 0,50 and 0,75 compositions according to special quasirandom structures approach [19] and the disorder aspects were ignored. For Cr1Ga1N2 (x = 0,50) an hexagonal unit cell with alternating [0001] layers of CrN and GaN in conventional wurtzite structure was employed. For Cr3Ga1N4 (x = 0,25) and Cr1Ga3N4 (x = 0,75) an hexagonal unit cell consisting of two wurtzite unit cells piled in the c direction were used [20]. There are eight planes with one Ga (or Cr) or one N atom in a 1× 1configuration, as shown in Figure 1. In this structure, a Cr atom replaces to a Ga atom in the unit cell. This atomic substitution (Cr-Ga) has been experimentally observed by S. E. Park et al. [21] for Cr doped GaN has been successfully grown in the form of bulk single crystals in wurtzite phase using a sodium flux growth method [21] and also used metal organic chemical vapor deposition technique (MOCVD); additionally, Haider et al [22] grown Cr doped GaN by molecular beam epitaxy (MBE) on sapphire (0001) substrate. This has allowed to get, room temperature ferromagnetism of Cr-doped GaN single crystals has stirred further interest in the DMS systems [21].
The lattice parameters and cohesion energy were found by the fitting the total energy versus volume to the Murnaghan’s state equation [23].
3. RESULTS AND DISCUSSION
The cohesion energy per unit cell as function of lattice constant for Cr1−xGaxN compounds are shown in Figure 2. As we showing figure, the minimum for each curve shifts to the right as it increases the concentration of Ga in the Cr1−xGaxN compound.
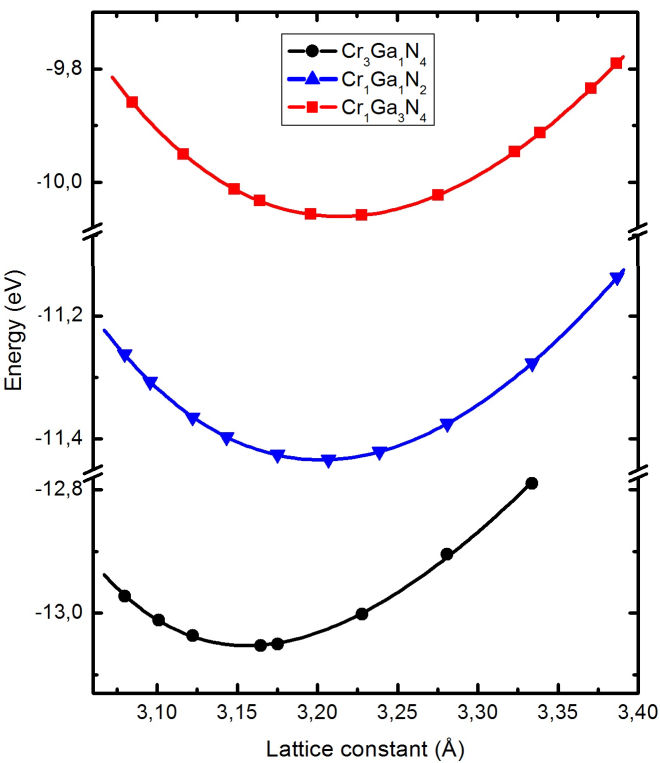
From minimum point energy of Figure 2, the equilibrium lattice constant (square points) and the energy (circular points) per unit cell as a function of Ga concentration are presented in Figure 3. The increase of lattice constant with Ga concentration is due to that Ga-atom is bigger than Cr-atom. We found a linear dependence according to Vegard’s law. Note that the energy also has a linear tendency with the Ga concentration as has been observed in other ternary nitrides [20, 24].
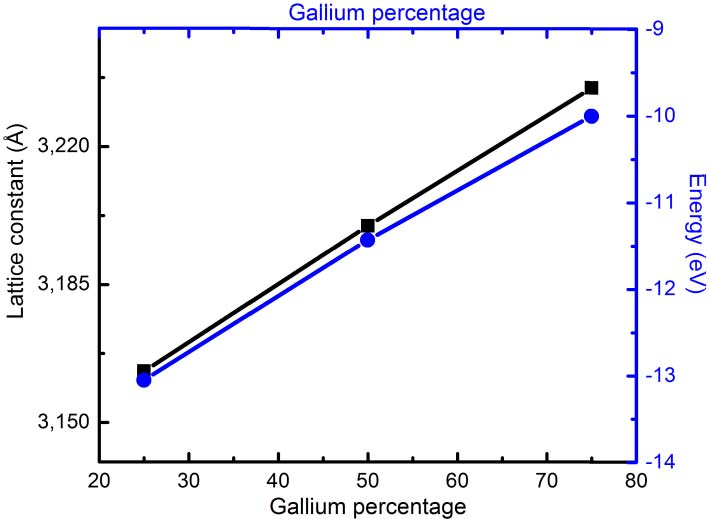
Figure 3. Equilibrium lattice constant and cohesion energy as function of Ga concentration in Cr1−xGaxN.
Magnetic moment for Cr1−xGaxN compounds are shown in Figure 4. As we shown in this figure, for Ga3Cr1N4 (square points) there is a rather abrupt onset of the magnetic moment from 0 to 2,2 µB at ~ 22,65 GPa (3.11 Å). The Cr1Ga1N2 and Cr3Ga1N4 compounds presented the same magnetic moment transition but with a slowly pressure dependence. From this figure, we observe the tendency towards magnetism increases as we further decrease the pressure. A similar behavior has been reported by González et al. GaxV1−xN compounds in wurtzita structures [25].
We found that in the studied cases, Cr1−xGaxN has a nonzero magnetic moment at the zero pressure. Comparing the total energy of the ferromagnetic (FM) and antiferromagnetic (AFM) configurations for x = 0,25 and 0,50 compounds at the equilibrium volume, the FM is found to be lower in energy and is the predicted to be preferred state. Such as has been found experimentally R. K. Singh et al [26] and Sang Eon Park [27] for diluted concentrations of Cr atoms in the GaN semiconductor.
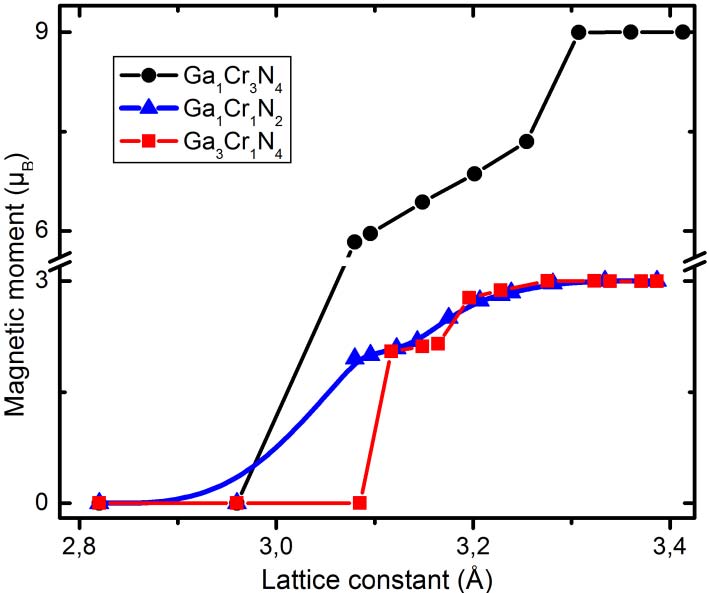
Figure 4. Magnetic moment as a function of the lattice constant for Cr1−xGaxN. The line is guide to the eye.
In Table 1 we show a summary of the structural and magnetic results for Cr1−xGaxN compounds. We give the equilibrium lattice constant (a0), critical pressure at which the magnetic moment appears (Pcr), saturation value of the magnetic moment per unit cell (µ) and the spin polarization PF at the equilibrium lattice constant defined by:
N (E ) − N (E )
↑ F ↓ F
PF = (1)
N (E ) + N (E )
↑ F ↓ F
With NS(EF) being the DOS of spin S (= ↑ or ↓ ) for the Fermi energy EF.
In Table 1, we note that the calculated magnetic moment for each configuration (3 µB/Cr-atom) is due to the Cr3+ electronic configuration, because a Cr-atom provides two net electrons to the Cr1−xGaxN compound [28] and the Cr atoms couple ferromagnetically when doped into GaN whether the host is a cluster or a crystal [10].
Table 1. Structural and magnetic properties of Cr1−xGaxN compounds.
| Compound | a0 (Å) | Pcr (GPa) | µ (µB ) | PF (%) |
|---|---|---|---|---|
| Cr1Ga3N4 | 3,235 | 22,65 | 3,0 | 100 |
| Cr1Ga1N2 | 3,200 | 24,55 | 3,0 | 78,8 |
| Cr3Ga1N4 | 3,160 | 26,60 | 9,0 | 31,8 |
We study the pressure dependence on the electronic
density of states (DOS) for the spin-up and spindown polarization in Cr1−xGaxN compounds. In Figure 5, we show the partial (PDOS) of d states of chromium calculated per atom, and the total DOS estimated per unit cell of the Cr1Ga3N4 compound at the equilibrium lattice constant (P = 0).
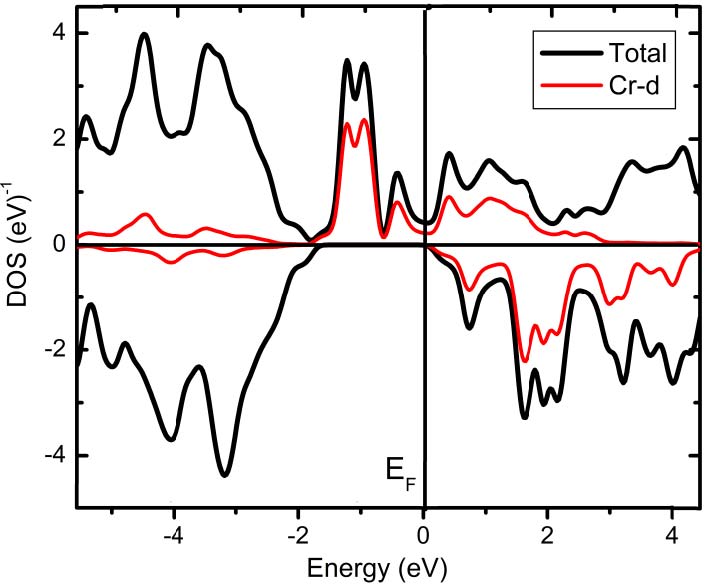
Figure 5. Partial DOS of d-states of Chromium calculated per atom and total DOS estimated per unit cell of the Cr1 Ga3N4 compound at equilibrium pressure P = 0.
Near the Fermi level, the dispersion in the chromium impurity bands show that there is considerable interaction between neighboring Cr atoms in the unit cell. This compound behaves as conductor for spin-up polarization and as semiconductor for spin-down polarization. We found 100% spin polarization at the Fermi level which indicates that Cr1Ga3N4 compound presents a half metallic behavior at P= 0. The figure 6 shows the density of states calculated at the high pressure P = 32 GPa over to the transition pressure P > Pcr . The Fermi level passes through the impurity and conduction bands in both spin polarization. The compound exhibits a metallic behavior. We can observe that the spin polarization splitting is dependent on the pressure and may be manipulated experimentally. Similar results we found for the other concentrations Cr1Ga1N2 and Cr3Ga1N4. On the basis of our present study, we believe that Cr1−xGaxN compounds may be candidates for being ferromagnetic or half-metallic materials in semiconductor-based spintronic applications.
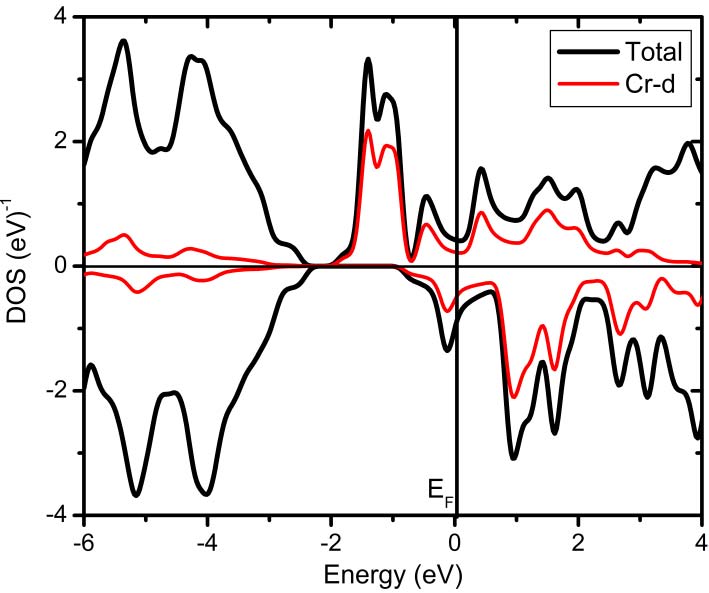
Figure 6. Partial DOS of d-states of Chromium calculated per atom and total DOS estimated per unit cell of the Cr1Ga3N4 compound at over the transition pressure P > Pcr (P = 32 GPa). Energy is relative to Fermi energy.
4. CONCLUSIONS
An ab-initio study of pressure effects on the electronic and magnetic properties of Cr1−xGaxN compounds (x = 0,25, 0,50 and 0,75) in wurtzita derived structures were presented. We used the fullpotential linearized augmented plane wave LAPW within of the spin density functional theory framework. The lattice constant is found to vary linearly with Ga-concentration. The magnetic moment changes for a critical pressure. At x = 0,75, a rather abrupt onset of the magnetic moment from to 2,2 µB at ~ 22,65 GPa, is observed. For x = 0,25 and 0.50 Ga concentrations the magnetic moment increased gradually when pressure is decreased toward the equilibrium volume. Also, we study the pressure dependence of transition to a ferromagnetic phase near the onset of magnetic moment for each Cr1−xGaxN compounds. Calculation of the density of states with Ga concentration was carried out considering two spin polarizations. Results reveal that when x = 0,75 the compound behaves as conductor for spin-up polarization and as semiconductor for spin-down polarization is zero at the Fermi level. At this concentration compound has a possible half metallic behavior; therefore this material could be potentially useful as spin injector. At high pressures P > Pcr the compounds exhibit a metallic behavior.
5. ACKNOWLEDGMENTS
The authors acknowledge the Research Center of the University District CUID for their financial support.
6. REFERENCIAS
[1]. O. Arbouche, B. Belgoumène, B. Soudini, M. Driz. Computational Materials Science. 2009; 47: 432–438.
[2]. S. Nakamura. Solid State Communications. 1997; 102 (2): 237-243
[3]. S. Nakamura, M. Senoh, N. Iwasa, S.-i. Nagahama. Applied Physics Letters. 1995; 67: 1868.
[4]. H. Bar-llan, S. Zamir, O. Katz, B. Meyler, J. Salzman. Materials Science and Engineering A. 2001; 302: 14-17
[5]. R. J. Trew, M. W. Shin, V. Gatto. Solid State Electronics. 1997; 41 (10): 1561-1567.
[6]. S. J. Pearton, F. Ren, A.P. Zhang, K. P. Lee. Materials Science and Engineering R: Reports. 2000; 30 (3–6): 55-212
[7]. T. Dietl, H. Ohno, F. Matsukura, J. Cibert, D. Ferrand. Science. 2000; 287 (5455): 1019-1022
[8]. X. M. Cai, A. B. Djurisic, M. H. Xie, H. Liu, X.
X. Zhang, J. J. Zhu, H. Yang. Materials Science and Engineering B. 2005; 117 (3): 292-295 [9]. Joongoo Kang, K. J. Chang. Physica B. 2006; 376–377: 635–638.
[10]. Yanlu Li, WeiliuFan, Honggang Sun, Xiufeng Cheng PanLi, Xian Zhao, Minhua Jiang. Journal of Solid State Chemistry. 2010; 183 (11): 2662– 2668.
[11]. K. Sato, P. H. Dederics, H. Katayama Yoshida. Europhysics Letters. 2003; 61 (3): 403-408.
[12]. S. J. Pearton, Y. D. Park, C. R. Abernathy, M. E. Overberg, G. T. Thaler, J. Kim, F. Ren, J. M. Zavada, R. G. Wilson. Thin Solid Films. 2004; 447 (447): 493-501.
[13]. M. Souissi, A. Bchetnia, B. El Jani. Journal of Crystal Growth. 2005; 277 (4): 57-63.
[14]. Schwarz Karlheins. Journal of Solid State Chemistry. 2003, 176: 319-328
[15]. P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka. Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties,Vienna University of Technology, 2001, ISBN 3-9501031-1-2.
[16]. P. Hohenberg,W. Kohn. Physical Review. 1964; 136 (3B): 864-871. [17]. W. Kohn, L. J. Sham. Physical Review. 1065; 140