Interciencia
versión impresa ISSN 0378-1844
INCI v.27 n.8 Caracas ago. 2002
SOBRE LA ESTRUCTURA DE LAS ANALOGÍAS EN CIENCIAS
Luis A. Godoy
Luis A. Godoy. Ph.D. en Ingeniería, Universidad de Londres, Inglaterra. Catedrático de Ingeniería Civil, Universidad de Puerto Rico en Mayagüez. Editor de la Revista Internacional de Desastres Naturales, Accidentes e Infraestructura Civil. Dirección: Departamento de Ingeniería Civil, Universidad de Puerto Rico, Mayagüez, Puerto Rico, PR 00681-9041. e-mail: lgodoy@ce.uprm.edu
Resumen
En este trabajo se presenta un análisis acerca de la identidad que tienen las analogías en la práctica científica. Para ello se consideran las perspectivas de estudio, las funciones y estructuras que tienen las analogías en ciencias. Se propone un esquema de estructura que incluye las limitaciones de la relación analógica y de las consecuencias que se derivan de la analogía. Adicionalmente, se propone un esquema de clasificación que permite distinguir analogías de acuerdo a las limitaciones de la relación establecida.
Summary
This work presents an analysis about the nature of analogies in scientific practice. Several perspectives of study are considered, together with functions and the structures of the analogies in science. A structure of analysis is proposed that includes the limitations of the analogical relation and the consequences that result from the analogy. Furthermore, a classification is proposed to identify analogies according to the structure and the limitations found.
Resumo
Neste trabalho apresenta-se uma análise sobre a identidade que têm as analogias na prática científica. Para isto consideram-se as perspectivas de estudo, as funções e estruturas que têm as analogias em ciências. Se propõe um esquema de estrutura que inclui as limitações da relação analógica e das consequências que se derivam da analogia. Adicionalmente, se propõe um esquema de classificação que permite distinguir analogias de acordo às limitações da relação estabelecida.
PALABRAS CLAVE / Analogías / Clasificación de Analogías / Epistemología / Estructura de Analogías /
Recibido: 05/02/2002. Aceptado: 26/06/2002
Analogías
Una analogía es una habilidad que reconoce que una cosa es como otra. Por ejemplo, Rutherford desarrolló la analogía que el átomo es como el sistema solar. Para realizar ese reconocimiento se requiere de una comprensión de ambas partes involucradas en la relación y de los variados aspectos que cada una presenta, para luego identificar el o los aspectos en que se centra la relación. Decimos que es una habilidad, porque siempre hay un acto creativo y original involucrado en la construcción de la analogía.
Esencialmente, una analogía en ciencias establece relaciones entre un problema que denominaremos "alfa" y otro problema, que denominaremos "beta", de modo que se dice que beta es como alfa, y esa relación se establece con un propósito determinado.
En muchos casos la referencia entre alfa y beta se identifica con problema viejo y nuevo y es efectivamente temporal, en el sentido que los aspectos sobre los que se establece la analogía se desarrollaron primero en alfa y posteriormente, mediante el uso de analogías, se exportan a beta o se los identifica en beta. En lo sucesivo abandonaremos la designación de viejo y nuevo y preferiremos las formas más genéricas de alfa y beta con el fin de cubrir casos en los que no hay una secuencia temporal. Otros autores usan los términos dominio de base y dominio de meta (del inglés base domain y target domain).
Las analogías requieren que se establezcan relaciones de correspondencia entre aspectos de alfa y de beta. El proceso de comparación de los aspectos que se relacionan se denomina mapeado (del inglés mapping). Específicamente, la correspondencia es una identificación entre lo que se toma de alfa y lo que se toma de beta para llevar adelante la analogía, de modo que es algo que el investigador construye.
Específicamente, el presente trabajo discute los siguientes postulados: 1) Las analogías cumplen funciones muy diversas, pueden ser consideradas desde perspectivas muy distintas y abarcan aspectos tan diferentes que sólo constituyen un único objeto de estudio a partir de su estructura; y 2) Sólo es posible conceptualizar las analogías mediante la identificación de las estructuras de la propia analogía y de los dominios que se relacionan.
En la segunda sección se presentan las analogías según la concepción de Maxwell en el Siglo XIX. La tercera sección trata de la perspectiva de estudio, que puede ser epistemológica, cognitiva, educativa, computacional, etc. En la sección cuarta consideramos la función que desempeñan las analogías, vale decir los propósitos que satisfacen en un caso determinado, lo que las hace importantes o necesarias en ese caso. Adicionalmente se estudia la estructura de la analogía en la sección quinta, incluyendo las entidades que se relacionan y de qué manera. La última sección presenta un posible esquema de clasificación basado en la estructura de las analogías.
Analogías Sustantivas y Formales según Maxwell
En un trabajo clásico del siglo XIX, James C. Maxwell sostenía que no todas las analogías responden al mismo esquema, y clasificó las analogías en sustantivas y formales. Nagel (1961) y otros filósofos de la ciencia han recogido esa clasificación. En las analogías sustantivas se toma como modelo un sistema con elementos que poseen propiedades conocidas y relacionadas mediante leyes del sistema. Ese modelo se usa para la construcción de un segundo modelo para el nuevo sistema. Por ejemplo, las leyes mecánicas de movimiento de esferas macroscópicas han sido tomadas como analogía para desarrollar la teoría cinética de los gases. En las analogías formales el sistema que sirve de modelo es una estructura de relaciones abstractas que nos resulta conocido. Por ejemplo, en la mecánica de medios continuos se usa el mismo formalismo para expresar diversas teorías (Tonti 1977). En la conceptualización de Maxwell, el énfasis está puesto en qué se relaciona para establecer la analogía y se dan dos alternativas: un formalismo abstracto, o propiedades y comportamientos.
Las analogías formales de Maxwell se refieren a correspondencias entre las relaciones internas que se establecen en cada uno de los sistemas o problemas alfa y beta. Pero aquí intentamos resaltar que hay muchas dimensiones sobre las que pueden establecerse analogías entre alfa y beta, además de las identificadas por Maxwell. Por ejemplo, podemos relacionar los fenómenos que ocurren en alfa y beta, o las variables de ambos problemas, o las metodologías.
Perspectivas en el Estudio de Analogías
En 1998 se celebró en la ciudad de Sofía un seminario sobre "Avances en investigaciones de analogías: Integración de la teoría y datos de las ciencias cognitivas, computacionales y neuronales" (Gentner et al., 2001a). Esta reunión puso en evidencia las diversas facetas que tienen las analogías. Veremos a continuación algunas de las posibles perspectivas que se emplean en la actualidad.
Perspectiva epistemológica. El estudio de analogías es de gran interés en la filosofía de las ciencias, y ha atraído la atención de Nagel (1961), Hesse (1966) y muchos otros. La mayor parte del presente trabajo está dedicado a problemas epistemológicos, de modo que pasaremos ahora a considerar otras perspectivas.
Perspectiva de comunicación interdisciplinaria. La tendencia actual en muchos proyectos de investigación está encaminada hacia el trabajo interdisciplinario, de manera que es de esperar que se empleen analogías frecuentemente como vehículo de comunicación entre personas con formaciones académicas diferentes. Sin embargo, no pueden transplantarse conceptos como simple jerga científica. Cuando se invoca un concepto de otra disciplina es necesario considerar: ¿Qué relaciones existen entre los conceptos de la nueva disciplina beta y los de alfa? ¿Qué propiedades, características y estructuras van a definirse en beta? ¿Cuáles de las relaciones originales en alfa pueden ser mantenidas? ¿Qué mecanismos se prevén para el abandono de la analogía?
Perspectiva del aprendizaje. El empleo de analogías como forma de construir nuevos conocimientos en un campo (epistemológico) no es igual al empleo de analogías como se las usa en la enseñanza de las ciencias. Las funciones de analogías en enseñanza son generalmente de tipo explicativas; se formulan porque nos ayudan a comprender mejor un fenómeno o problema (Duit, 1991; Glynn, 1996; García Monteiro y Justi, 2000; Baker y Lawson, 2001). Un desarrollo más extenso de la perspectiva del aprendizaje mediante analogías fue presentado anteriormente (Godoy, 2002a). Preguntas típicas que aparecen en esta perspectiva son: ¿Cómo puede mapearse una analogía para romper con preconceptos (o ideas preconcebidas) de los estudiantes? ¿Qué conocimientos en alfa son necesarios para sustentar una analogía en beta? ¿Qué analogías son efectivas y en qué contexto de aprendizaje? ¿Qué tipo de soporte computacional puede ser efectivo para que los estudiantes puedan aprovechar mejor las formas de razonamiento por analogía? ¿Cómo hacer que los estudiantes desarrollen ellos mismos nuevas analogías para los problemas que tienen que analizar?
Perspectiva de la cognición. Esta es una dimensión de gran actualidad en la problemática y trata de comprender cuáles son los mecanismos de cognición que entran en juego cuando se hacen analogías. Aquí se consideran problemas como los siguientes: ¿Cómo se perciben las analogías? ¿Cómo se recuperan las analogías de la memoria y cómo se construyen? ¿Cómo se mapean o transfieren conocimientos de un dominio a otro? ¿Cómo se combinan los conocimientos provenientes de múltiples analogías? ¿Cómo se utilizan las analogías para la solución de problemas, para construir explicaciones y argumentaciones? ¿Qué lugar ocupan las analogías con respecto a otros procesos cognitivos, como la percepción, el pensamiento, la memoria, el aprendizaje?
Los aspectos cognitivos de las analogías exceden el alcance de este trabajo. En el ámbito cognitivo parece haber dos grandes problemas: 1) ¿Cómo se generan las analogías? 2) ¿Cómo se comprende una analogía ya existente? El primer problema ha sido abordado por Hofstadter y otros, quienes suponen una función cognitiva de más alto nivel que denominan "percepción de alto nivel" (High Level Perception, o HLP). HLP es un proceso por el cual la representación de una situación en un nivel conceptual se construye a base de una interacción entre conceptos de alto nivel y procesos de percepción de bajo nivel. Los conceptos de alto nivel influyen en los procesos de percepción de bajo nivel, mientras que lo que se percibe en un nivel bajo afecta la activación de conceptos de alto nivel en la medida que se construye la representación de la situación (Chalmers et al., 1992; Hofstadter, 1996). Cuando estas ideas se aplican a la construcción de analogías, Hofstadter señala que "el sujeto percibe algunos aspectos de las estructuras en dos situaciones, y la esencia de ambas situaciones son idénticas en algún sentido" (Hofstadter, 2000). En resumen, este autor considera que hay interacción entre lo que percibimos y lo que conceptualizamos en la construcción de una analogía.
Para la comprensión de una analogía que ya ha sido creada, Gentner considera la hipótesis central que nuestros conceptos psicológicos tienen una estructura propia: estas estructuras son las representaciones psicológicas de las relaciones entre objetos perceptuales y conceptuales. Entonces una analogía es el producto del mapeado de estructuras asociadas a los dos conceptos alfa y beta entre los que se establece la relación (Gentner, 1983). Al centrarse en el estudio del mapeado de estructuras, la autora permite diferenciar claramente entre una analogía y otros procesos cognitivos que involucran similitud.
Perspectiva computacional. Lenguajes de la inteligencia artificial se emplean cada vez más para dar precisiones a las representaciones en analogías, y al mismo tiempo esto facilita que se puedan desarrollar modelos computacionales que permitan revisar teorías cognitivas de analogías. Pero por otra parte el propio desarrollo de la inteligencia artificial utiliza el razonamiento por analogía como una técnica de inferencia (Long, Garigliano y Garigliano, 1994; Nehaniv et al., 1999). Cuestiones típicas de estas perspectivas son: ¿Cómo se combinan las analogías con conocimientos basados en reglas? ¿Cómo podemos utilizar analogías para la prueba automática de teoremas matemáticos? ¿Qué papel juegan las analogías biológicas en algoritmos genéticos y estrategias evolutivas para resolver problemas de ingeniería? ¿Qué analogías pueden emplearse para el desarrollo de nuevos algoritmos de optimización?
Perspectiva neurológica. Aquí se atiende la base biológica del cerebro con relación a la formulación de analogías. Los procesos cognitivos son expresión de procesos neuronales muy complejos, pero sobre los que cada vez se conoce más. Ejemplos de preguntas que se formulan desde esta perspectiva son: ¿Cuáles son las estructuras del cerebro que están involucradas en el proceso de hacer analogías? ¿Hay una base biológica que haga posible generar analogías? ¿Son innatas las capacidades de construir analogías? El enorme avance en la comprensión de la biología del cerebro y la conexión con las facultades mentales permitirá en un futuro próximo responder a muchos de estos interrogantes.
Perspectiva histórica y cultural. Las formas de argumentación por analogía son muy populares en la tradición china, de manera que una explicación no es lo suficientemente buena hasta que no se haya encontrado una analogía para lo que se afirma. También son allí valoradas las argumentaciones por ejemplos y por referencia a una autoridad. Pero lo que es argumentación válida en China quizás no lo sea en Camerún o en Holanda. El lugar de las analogías tampoco ha permanecido fijo en una cultura (Leary, 1990), sino que ha cambiado a través del tiempo. Por ejemplo, un análisis de las teorías medievales de analogías puede encontrarse en Ashworth (1999), y se observa que la conceptualización ha cambiado mucho desde esa época. Preguntas típicas en esta perspectiva son: ¿De qué manera depende la función de una analogía del contexto cultural en el cual se desarrolla? ¿Cómo han evolucionado los usos de analogías en diferentes períodos históricos?
Perspectiva retórica. Las metáforas son figuras literarias en las que se provoca una idea intuitiva de lo que se está refiriendo, sin utilizar su nombre y la comparación no es explícita sino implícita. En las metáforas hay una transferencia1 y se transfieren todos los significados de alfa hacia beta. En una metáfora decimos que "alfa es beta", de manera que alfa se usa para enriquecer el significado asociado con beta. En la analogía decimos que "alfa es como beta", la correspondencia entre alfa y beta es sólo parcial, se restringe a algún aspecto. ¿Qué relaciones hay entre metáforas y analogías? ¿Qué estructuras lingüísticas se emplean en el desarrollo de metáforas? ¿En qué se diferencian las analogías de otras figuras retóricas? ¿Qué beneficios puede traer la separación más detallada entre analogías y otras figuras retóricas en el análisis de la forma en que esas figuras dan soporte a la teoría y práctica del conocimiento?
1 La palabra Metáfora proviene del griego metapherein, que quiere decir "transferir". La palabra griega analogia significa proporción; se trata de una comparación de proporciones, aunque en la actualidad se ha extendido a la comparación de otros aspectos.
Funciones de las Analogías
Consideremos las funciones de las analogías desde la perspectiva epistemológica. Podemos identificar funciones de analogías como explicación, como base para realizar inducción, como modelo tentativo, como forma de validación, como forma de predicción. Seguramente hay otras funciones que se nos escapan en esta breve lista. Veamos cada una de ellas.
Explicar. Una función importante de las analogías es ayudar a explicar algo. Según algunos pensadores, una explicación es aceptada cuando sus premisas están basadas en evidencia aceptada por la comunidad científica o por parte de ésta. En muchos casos las premisas usan ideas con las que la comunidad científica no está familiarizada, y eso dificulta la aceptación. Sin embargo, si fuera posible generar relaciones de analogía entre esas nuevas ideas y nociones ya establecidas empleadas en otros problemas, se facilitaría la aceptación de una explicación. La analogía cumple aquí la función de asimilar lo nuevo en términos de cosas conocidas, y evita que las premisas explicatorias nuevas resulten demasiado extrañas. Las analogías también se han identificado al nivel de hacer más aceptable la respuesta investigada en el sistema beta.
Popularizar. Esta puede considerarse como una función de explicar, pero en los últimos años ha adquirido una importancia muy grande y merece su consideración independiente. Revistas de divulgación científica, como Scientific American, American Scientist, The New Scientist, Ciencia Hoy, Ciencia Hoje, abundan en analogías, algunas de ellas muy ingeniosas. Un anterior director de la National Science Fundation, refiriéndose a la importancia que el público en general comprenda los avances de la ciencia y lo que significan esos avances para la población, escribe:
"Nuestro desafío es aprender que la terminología obscura y detallada de nuestros campos científicos no es el camino para que el público comprenda nuestro trabajo. Necesitamos incorporar analogías y metáforas como herramientas para ayudar a otros a comprender." (Lane, 1997).
Generalizar. Otra función de las analogías es relacionar cosas diferentes, de manera de servir de base a un proceso de generalización. Si uno establece que varios problemas son análogos, podemos usar el proceso de inducción para extraer conclusiones a partir de esos casos análogos. Según Gentner, las analogías y similitudes son factores primarios en la categorización y organización de estructuras conceptuales. Por ejemplo, en la mecánica de medios continuos, Tonti (1977) ha identificado un gran número de campos de la mecánica que presentan analogías en su estructura matemática, aunque las variables que se relacionan en cada caso son diferentes. En este caso puede no ser relevante estudiar cuál de los problemas o campos se originó antes que otro (quién es alfa y quién es beta), porque la función no es justificar una estructura en un campo mediante la analogía con otro campo, sino ilustrar que las relaciones de estructura interna que ya fueron postuladas (quizás independientemente) en varios campos han resultado con la misma estructura matemática.
Formular hipótesis. Una función importante es generar nuevas hipótesis de trabajo para ser investigadas. Esta función es crucial en el contexto de descubrimiento. Las analogías pueden servir también para hacerse preguntas que de otra manera no habrían surgido independientemente. Hay ejemplos en los cuales una analogía ayuda a formar ideas teóricas en otro campo.
Modelar. En algunos casos, una analogía provee un modelo tentativo para un problema beta. Es una manera de solucionar un problema beta a la espera de que surja una mejor solución en el futuro, o una con mayor justificación. Ilumina al investigador acerca de las metodologías que han sido exitosas en problemas análogos.
Validar. Una función diferente es la de validar conceptos en un campo beta utilizando una transferencia desde el campo alfa mediante el uso de analogías. En general, aquí se transfieren los valores reconocidos de una teoría alfa hacia una teoría beta incipiente. Por ejemplo, filósofos como Feyerabend (1975) emplean analogías entre la forma en que los niños aprenden y la forma en que los científicos construyen conocimientos, aunque no se presente justificación formal para hacerlo. Podemos interpretar que los estudios de Sokal y Bricmont (1998) intentan denunciar esta función de las analogías.
Predecir. Se usan analogías para realizar predicciones sobre el problema beta utilizando predicciones realizadas sobre el problema alfa. En las analogías entre dos campos de la física, si las ecuaciones que gobiernan ambos fenómenos son las mismas (por ejemplo, las ecuaciones de Laplace) entonces las soluciones son las mismas funciones (por ejemplo, funciones armónicas). Si las ecuaciones son sólo similares, se pueden transferir métodos matemáticos, técnicas numéricas o experimentos de un campo a otro.
Estructurar. Esta función permite dar una estructura al problema beta a base de la estructura del problema alfa. Del Re menciona la analogía entre moléculas en química y un sistema macroscópico formado por esferas y resortes. Ante la pregunta: ¿tiene estructura una molécula?, la respuesta es que
"...una molécula tiene una estructura en el sentido que tiene propiedades análogas a la estructura de un modelo de resortes y esferas Esta analogía es el origen y la justificación de la estructura y forma que caracterizan las propiedades moleculares... Las propiedades geométricas y mecánicas del modelo macroscópico se supone que se corresponden muy bien (aunque no completamente) con las propiedades de la molécula real." (Del Re, 2000).
Las analogías empleadas en la prueba automática de teoremas en matemática también cumplen esta función. Existen pruebas bastante complejas de teoremas matemáticos. En ellas es de gran beneficio tener un plan sobre cómo realizar la prueba. La construcción de este plan puede ahora hacerse por analogía. Aquí lo que se transfieren son planos de pruebas que son abstractos, representaciones estructuradas de pruebas que consisten en métodos que corresponden a tácticas. El uso de analogías es una estrategia que puede emplearse junto con otras estrategias para la prueba automática de teoremas. Algunos ejemplos interesantes en esta área pueden encontrarse en Melis (1996) y Melis y Whittle (1999).
Estructuras de las Analogías
Vimos en la sección anterior que lo que identifica a una analogía no es su función ni su uso, dada la diversidad de situaciones en las que forma parte. Tampoco hay una única perspectiva que las identifique, sino que hay una gran pluralidad de enfoques de estudios que pueden concentrar su mirada en las analogías. En el resto del trabajo ilustraremos que las analogías toman su identidad de las estructuras que tienen, que en su mínima expresión se reducen a "alfa es como beta". Sin embargo, veremos que es necesario considerar una estructura más compleja a fin de incluir de manera realista las limitaciones de una analogía.
De la misma forma que la estructura de las argumentaciones ha sido estudiada por muchos autores, incluyendo Toulmin (1958), interesa comprender la estructura que puede haber en analogías. Para estudiar las estructuras de analogías consideremos los distintos elementos que la constituyen:
Dominios alfa y beta. Para poder establecer una analogía es necesario comprender las estructuras de lo que se toma como dominios. Consideremos una de las formas de estructurar problemas, la dinámica de sistemas (ver Forrester et al., 1995; Godoy y Bartó, 2001, y las referencias citadas allí), en la que existe el concepto clave de la transferibilidad de estructuras. La disciplina estudia las estructuras genéricas que pueden identificarse en sistemas de naturaleza muy diferente.
"La idea de estructura transferible es importante en dinámica de sistemas, porque le permite estimar el comportamiento de sistemas de disciplinas diferentes a través de entender el comportamiento de sus estructuras genéricas subyacentes." (Forrester et al., 1995).
Típicamente, una estructura está formada por entidades y relaciones entre entidades que permiten realizar operaciones. Las entidades pueden ser conceptos, términos, variables, datos, etc. Por ejemplo, en la teoría de elasticidad las entidades que intervienen son las tensiones, deformaciones, desplazamientos, fuerzas y algunas otras. Esas entidades no son todas de la misma naturaleza: algunas son de naturaleza tensorial (tensiones, deformaciones); otras son de naturaleza vectorial (fuerzas, desplazamientos). Hay relaciones entre esas entidades, como las relaciones de equilibrio que vinculan fuerzas con tensiones; las cinemáticas, que vinculan desplazamientos con deformaciones, y otras. Nuevamente, las relaciones no son todas iguales, e involucran diferentes operadores matemáticos.
Nótese que no decimos que en la ciencia sea imprescindible tener teorías estructuradas, sino que sólo tiene sentido construir analogías si se pueden estructurar los problemas que se relacionan.
Las analogías en ciencias no tienen porqué limitarse a relacionar problemas, y pueden establecerse sobre otros dominios, como conceptos, comportamientos, fenómenos, experimentos, métodos, teorías. Mayntz invita a distinguir entre la transferencia de métodos, de conceptos y de teorías completas.
"La transferencia de teorías, en sentido estricto, presupone isomorfismos entre los fenómenos empíricos en dos áreas diferentes, una relación de uno a uno entre los elementos, las propiedades de los elementos y las relaciones que gobiernan la dinámica en los dos campos diferentes de fenómenos". (Mayntz, 1997)
No es fácil encontrar analogías tan abarcadoras que permitan pasar fluidamente de alfa a beta mediante isomorfismos, sin embargo existen en algunas disciplinas como la física, y posiblemente en otras que el autor desconoce.
Aspectos de alfa y beta relacionados. En las últimas décadas los autores que trabajan en perspectivas epistemológicas y cognitivas coinciden que en una analogía decimos que algunos aspectos de beta se asemejan a algunos aspectos de alfa, pero sólo algunos. De este modo se flexibiliza la relación de analogía con respecto al caso de isomorfismo. Esta conceptualización de la analogía es menos estricta; así ya son viables las analogías entre disciplinas diferentes.
Los aspectos son parte del dominio: por ejemplo, si se toma como dominio un problema, entonces un aspecto puede ser la metodología de solución de ese problema. Si se toma como dominio un concepto, un aspecto puede ser la caracterización de ese concepto, su identificación experimental, etc.
Los aspectos que pueden intervenir en una analogía son muy variados, e incluyen el contexto, el marco de análisis, términos y variables, relaciones internas, suposiciones, modelos, teorías y desarrollo histórico. También podríamos incluir fenómenos, mecanismos, evidencia, etc., pero aun esta versión simplificada puede servir para expresar la diversidad de opciones al construir una analogía.
En lugar de aspectos, si los dominios relacionados pueden visualizarse mediante estructuras internas, entonces también podemos hablar de entidades y de relaciones entre entidades.
Medidas de similitud entre los aspectos relacionados. No basta con enunciar relaciones, también es necesario establecer de qué manera se van a evaluar esas relaciones, de modo de visualizar la credibilidad de la analogía. Por ejemplo, podemos enunciar que "la microgravedad es como el ADN, donde la unidad fundamental de una carga eléctrica se corresponde con las letras del código genético". Sin embargo, ¿tiene sentido esa analogía?
Cuando se abandona la posibilidad de establecer un isomorfismo entre alfa y beta entonces surge la necesidad de establecer medidas que permitan ver cuán similares son dos sistemas o conceptos. La similitud no es una decisión arbitraria de quien la construye y para precisar las analogías necesitamos tener medidas de la similitud entre cosas.
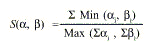
Trillas (1998) menciona que en el razonamiento por analogía se emplea el índice de similitud, S. Para construir el índice es necesario considerar diferentes aspectos que forman alfa y beta, y otorgar puntuaciones a cada uno de ellos, que denominaremos ai y bi. El índice S se define como
donde S toma valores entre 0 y 1, y se acepta que alfa y beta son similares cuando S > 0,7. En realidad, el índice permite establecer cuando alfa y beta tienen un parecido fuerte, pero no es útil cuando se trata de establecer una estructura jerárquica o una clasificación de conceptos porque S no tiene propiedad transitiva.
Mapeado de relaciones. Gentner (1983) señala que la simple medida de un grado de similitud no es una manera adecuada de establecer una correspondencia para la determinación de una analogía. Según esta autora, el centro de la analogía es el mapeado de relaciones. Mas aún, indica que la clave de la analogía no está en las relaciones solamente, sino en sistemas de relaciones interconectadas.
"De acuerdo con la teoría del mapeado de estructuras... el mapeado analógico es un proceso de establecer un alineamiento estructural entre dos situaciones representadas y entonces producir inferencias. La teoría...supone la existencia de representaciones estructuradas hechas con objetos y sus propiedades, relaciones entre objetos y relaciones de orden superior entre relaciones." (Gentner et al., 2001b).
Esta formulación de la analogía sería independiente del contexto en el cual se establezca. La conjetura de Gentner es que el razonamiento de la experiencia comienza con un mapeo de similitudes, continúa con analogías y finalmente evoluciona a la abstracción de los principios generales.
La teoría de mapeado de analogías (Gentner, 1983) no es otra cosa que elementos del álgebra lineal aplicados a la formalización de relaciones; en ese contexto, la analogía es vista como una transformación que toma elementos de un dominio de base y los asigna a un dominio de meta. La teoría de Gentner se construye como una analogía con algunas estructuras del álgebra lineal. Si bien este tipo de marco de análisis es atractivo, porque da un formalismo familiar a los matemáticos, sin embargo no contempla aspectos cruciales de la relación por analogía: que la analogía es una relación parcial que puede conducir a inferencias totalmente equivocadas.
En otro trabajo (Godoy, 2002b) argumentamos sobre los conflictos que han generado diversas analogías en la construcción de conocimientos; esos argumentos no serán repetidos aquí, pero desde esa posición es necesario poner en evidencia cuales son las limitaciones que hay en una analogía, a fin de poder salir de ella en caso que sea un obstáculo para el avance en un tema. Para evitar ese problema es necesario, por lo menos, incluir de manera explícita las limitaciones de la analogía dentro de la estructura.
Limitaciones de las relaciones. Como consecuencia de que una analogía sólo se refiere a algunos aspectos de los dominios relacionados, surge la limitación que por más que se establezca una analogía entre aspectos del problema alfa y del beta, eso no nos autoriza a reclamar que otros aspectos de ambos problemas también deban ser necesariamente análogos. Concretamente, el contexto de los problemas puede ser muy diferente, o su desarrollo histórico, de modo de hacer que los problemas desarrollen fenómenos diferentes a pesar de poder establecerse relaciones entre variables.
Las consecuencias que se extraen de la analogía. Vimos que las analogías se construyen para cumplir alguna función determinada. Trillas toma una de las posibles funciones y establece una versión operativa de las analogías en la siguiente forma:
"Un concepto A es bastante bien conocido ya que del mismo se tiene una experiencia considerable, y otro concepto B es nuevo para el agente que conoce A. El concepto mal conocido B presenta propiedades B1, B2...Bn que lo definen parcialmente y que llegan a ser bien conocidas por el agente en cuestión; pero existen propiedades adicionales Bn+1,..., Bp que no llega a conocer bien. Las correspondientes propiedades A1,..., An, An+1,..., Ap de A son bien conocidas y la analogía entre las A1, B1;...; An, Bn es verificada por el agente quien, entonces, hace la hipótesis de que también son análogos los pares An+1, Bn+1;...; Ap, Bp, y de ello induce que A y B son conceptos análogos. El error de un razonamiento tan habitual puede ser flagrante: especialmente si se confunde análogo con lo mismo en sentido estricto." (Trillas, 1998).
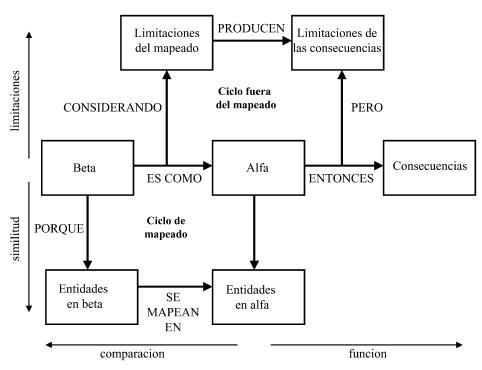
Figura 1. Estructura de las analogías propuesta.
El tema en el que Trillas desarrolla su discusión es el parecido racional entre personas y máquinas (el libro del cual se toman estas citas es sobre inteligencia artificial), pero los ejemplos que propone están limitados al álgebra.
Una Estructuración de las Analogías y sus Limitaciones
Los elementos que forman una analogía y que hemos discutido pueden también organizarse en forma similar a la presentada por Toulmin (1958), de manera de identificar las relaciones y limitaciones. Los elementos que entran en este esquema (Figura 1) son un problema alfa, un problema beta, los aspectos de cada uno que se mapean, el rango en el que cada uno se supone que puede entrar en la analogía, y las limitaciones de la analogía.
La línea central de la estructura es la analogía misma, "<beta> ES COMO <alfa>" (las mayúsculas se usan para los conectores, y < > para las entidades o enunciados específicos), y a continuación le sigue la consecuencia que se extrae de la analogía: "ENTONCES <consecuencias>". Ejemplos de consecuencias son "alfa y beta pertenecen a la misma categoría", "beta se comporta como alfa", "alfa explica el comportamiento de beta", "otras entidades de beta son como otras entidades de alfa", "beta es creíble", etc.
Hay dos ciclos en el esquema: hacia un lado, que enfatiza las similitudes, se encuentra el "ciclo de mapeado", mientras que hacia el otro, que enfatiza las limitaciones, esta el "ciclo fuera del mapeado". El primer ciclo se lee así: "<beta> ES COMO <alfa> PORQUE HAY <entidades en beta> QUE SE MAPEAN EN <entidades de alfa>". Este ciclo establece la base sobre la que se fundamenta la analogía. El segundo ciclo se lee: "<beta> ES COMO <alfa> CONSIDERANDO <limitaciones del mapeado> QUE PRODUCEN <limitaciones en las consecuencias>". Este ciclo advierte que establecida la analogía, "ENTONCES <consecuencias> PERO HAY <limitaciones en esas consecuencias> QUE SON PRODUCIDAS POR <limitaciones en el mapeado>".
Entendemos que tanto las similitudes como las limitaciones son parte estructural de la analogía y que también lo son las consecuencias. Esta estructuración esquemática es simplificada porque no distingue entre las entidades del dominio y las relaciones entre esas entidades; sin embargo, eso forma parte de la estructura de los problemas alfa y beta y entendemos que debe estudiarse en un esquema aparte, como lo hace Tonti (1977).
Identificación de las Analogías con Base en su Estructura
Los conceptos presentados en este trabajo permiten avanzar hacia una mayor precisión de la conceptualización de las estructuras de analogías. Consideraremos que lo que se relacionan pueden ser aspectos (sin discriminación) o bien especificando si se mapean entidades, relaciones entre entidades o comportamientos de la respuesta. Esta no es una clasificación exhaustiva sino restringida, pero permite interpretar los ejemplos propuestos en las secciones anteriores. Proponemos distinguir entre:
Analogía informal
a) Alfa y beta tienen aspectos que se corresponden en la analogía,
b) no se logra establecer que esos aspectos correspondientes tengan similitud entre ellos.
Generalmente las analogías informales son expresiones de deseo, pero sin una justificación; también se denominan analogías verbales o metáforas. También se encuentran en este grupo casos de similitudes muy superficiales. Finalmente ocurren en situaciones en las que se adopta una terminología de alfa para designar las propiedades en beta. "El resultado es entonces una mera innovación semántica que no agrega nada al conocimiento sustantivo" (Mayntz, 1997). Eso no las descarta totalmente, porque pueden ser útiles como planteo de una estrategia de búsqueda, una hipótesis por explorarse, pero en sí mismas son incompletas.
Claramente no se busca aquí lograr un mapeado completo, sino identificar las propiedades y relaciones que están presentes en alfa con el fin de establecer nuevas propiedades y relaciones en beta que sean factibles y realizables. Sokal y Bricmont (1998) protestan contra el empleo de esta clase de analogías para validación de conocimientos en beta.
Analogía en sentido débil
a) Alfa y beta tienen entidades que se corresponden en la analogía,
b) se establece que esas entidades correspondientes tienen similitud,
c) alfa y beta tienen además otras entidades que no entran en la analogía.
En las analogías en sentido débil no se mencionan correspondencias entre relaciones internas establecidas tanto en alfa como en beta, ni respuestas que puedan tener alfa y beta como parte de una evolución en el tiempo. La definición de Trillas reproducida arriba es un enunciado de este caso. No es posible inferir que también las relaciones que entran en alfa y beta sean análogas. Tampoco sabemos si los comportamientos en alfa y beta están gobernados por variables que quedaron fuera de la analogía. Nuevamente, este tipo de analogía puede ser relevante como forma exploratoria, a fin de investigar el tipo de relaciones que podrían existir en beta.
Analogía en sentido fuerte
a) Alfa y beta tienen entidades que se corresponden en la analogía,
b) alfa y beta tienen relaciones que se corresponden en la analogía,
c) se establece que esas entidades y relaciones correspondientes tienen similitud,
d) alfa y beta tienen otras entidades y relaciones que no entran en la analogía.
La analogía establecida por Priestley (la fuerza eléctrica es como la fuerza gravitatoria) es en sentido fuerte, siendo que se mapean tanto algunas variables como también relaciones. En este caso la analogía misma fue originalmente una especulación, pero abrió la posibilidad de búsqueda empírica de la relación en beta.
Analogía fenomenológica
a) Alfa y beta tienen algunos comportamientos como respuesta que se corresponden por analogía,
b) alfa y beta tienen entidades que no se mapean por analogía,
c) alfa y beta presentan relaciones internas que no se mapean por analogía.
Aquí la similitud de las respuestas no garantiza que haya correspondencia entre las estructuras de los sistemas mismos, o sea que tengan propiedades y relaciones internas que sean la causa del comportamiento. Sin embargo, éste puede ser un buen indicador de búsqueda que lleve al investigador a tratar de identificar si las causas de esa analogía se encuentran en un nivel más profundo. La respuesta puede ser positiva o negativa, pero no puede anticiparse antes de investigarla.
Analogía completa
a) Se verifican las condiciones para analogía en sentido fuerte,
b) todas las entidades de beta se corresponden con entidades de alfa,
c) las relaciones en beta son las mismas relaciones que hay en alfa.
Trillas (1998) argumenta la imposibilidad de lograr analogías completas; sin embargo éstas se obtienen en algunos casos de teorías con un alto grado de formalización, como ocurre en las de mecánica del continuo o en sistemas formales. La analogía de propiedades y relaciones permiten anticipar una analogía entre comportamientos en sistemas formales o formalizados. Lo interesante de esta posibilidad es que no aparecerán sorpresas en el comportamiento de beta por encima de las que ya están en alfa. Sin embargo hay casos en los que una analogía falló a pesar de ser completa porque el sistema formal planteado en beta no representaba adecuadamente la evidencia empírica.
En las analogías formales, que se expresan entre sistemas que han sido modelados matemáticamente, las propiedades son las cantidades físicas que se usan en la teoría, mientras que las relaciones son las ecuaciones que gobiernan el problema. En una analogía en sentido fuerte las variables de alfa no precisan ser de la misma naturaleza que las variables correspondientes en beta. Por ejemplo, una variable en alfa puede ser un vector, mientras que su correspondiente en beta puede ser un escalar. Pero si todas las variables en alfa son de la misma naturaleza que las variables correspondientes en beta y las teorías son análogas, entonces las ecuaciones en alfa son las mismas ecuaciones que hay en beta y se trata de un isomorfismo. Muchos problemas de la física que se usan en ingeniería son de este tipo, como discute Tonti (1977).
Conclusiones
Hay una diversidad de funciones que pueden desempeñar las analogías en ciencias, de modo que un análisis específico del enfoque funcionalista no permitiría abarcar a las analogías como unidad. Igualmente, las perspectivas de estudio asociadas a los campos de aplicación son diversas y no permiten concentrar la atención en lo que es específico de las analogías. Se argumenta, en concordancia con los estudios de Gentner, que los aspectos que hacen que hablemos de analogías como un término genérico hay que buscarlos en la estructura de las analogías.
Se presenta una forma de estructura de las analogías que incluye las inferencias y limitaciones como parte explícita del modelo y está basado en los estudios de Toulmin para argumentaciones. El modelo en sí mismo es muy sencillo y tiene seis componentes. Adicionalmente, se presenta una posible clasificación de analogías atendiendo a los aspectos que se relacionan entre los dos campos y las limitaciones de esas relaciones.
La expectativa de este estudio es contribuir a la toma de conciencia por parte de los investigadores de las limitaciones que presentan las relaciones por analogía, de manera de no usar como única guía de dirección a seguir el haber encontrado otro problema con algunas características similares al estudiado.
REFERENCIAS
1. Ashworth EJ (1999) Medieval theories of analogy. En Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/analogy-medieval/. [ Links ]
2. Baker WP, Lawson AE (2001) Complex instructional analogies and theoretical concept acquisition in college genetics. Science Education 85: 666-683. [ Links ]
3. Chalmers DJ, French RM, Hofstadter DR (1992) High-level perception, representation, and analogy: A critique of artificial intelligence methodology, J. Exp. Theor. Artificial Intelligence 4: 185-211. [ Links ]
4. Del Re G (2000) Models and analogies in science. HYLE - Internat. J. Phil. of Chemistry 6: 5-15. [ Links ]
5. Duit R (1991) On the role of analysis and metaphors in learning science. Science Education 75: 49-672. [ Links ]
6. Feyerabend PK (1975) Against Method. NLR. London. 279 pp. [ Links ]
7. Forrester JW, Systems Dynamics Group (1995) Road Maps, 6, System Dynamics in Education Project. Sloan School of Management, Massachusetts Institute of Technology, Cambridge, MA. http://sysdyn.mit.edu/road-maps/rm-toc.html. [ Links ]
8. Garcia Monteiro I, Justi RS (2000) Analogias en livros didaticos de Quimica brasileiros destinados ao ensino medio. Investigações em Ensino de Ciências 5(2): 1-26. [ Links ]
9. Gentner D (1983) Structures mapping: A theoretical framework for analogy. Cognitive Sciences 7: 155-170. [ Links ]
10. Gentner D, Holyoak KJ, Kokinov BN (Eds.) (2001a). The Analogical Mind: Perspectives from the cognitive sciences, The MIT Press. Cambridge, MA. 520 pp. [ Links ]
11. Gentner D, Bowdle B, Wolff P, Boronar C (2001b). Metaphor is like analogy. En Gentner D, Holyoak KJ, Kokinov BN (Eds.) The Analogical Mind: Perspectives from the cognitive sciences. The MIT Press. Cambridge, MA. pp. 199-253. [ Links ]
12. Glynn SM (1996) Teaching with analogies: Building on the science textbook. The Reading Teacher 49: 490-492. [ Links ]
13. Godoy LA (2002a) Exitos y problemas de las analogías en la enseñanza de la mecánica. Revista de Educación en Ciencias 3: 11-15. [ Links ]
14. Godoy LA (2002b) Analogías en ciencias: ¿Facilitadoras u obstaculizadoras en la construcción de conocimientos? Sometido para publicación. [ Links ]
15. Godoy LA, Bartó CA (2001) La dinámica de sistemas como instrumento para la organización de conocimientos. II Encuentro Internacional de Educación y Pensamiento. Mayagüez, Puerto Rico. Pp. 1-18. [ Links ]
16. Hesse MB (1966) Models and Analogies in Science. University of Notre Dame Press. Notre Dame, IL. 148 pp. [ Links ]
17. Hofstadter DR (1996) Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought. Basic Books. New York. 528 pp. [ Links ]
18. Hofstadter DR (2000) Analogy as the core of cognition. En Gleick J (Ed.) The Best American Science Writing. Harper Collins. New York. pp. 116-144. [ Links ]
19. Lane N (1997) NSF is still making key investments in science and technology. American Physical Society News. Noviembre. [ Links ]
20. Leary D (Ed) (1990) Metaphors in the History of Psychology. Cambridge University Press. Cambridge, Inglaterra. 400 pp. [ Links ]
21. Long, Garigliano R, Garigliano R. (1994) Reasoning by Analogy and Causality: A Model and Application. Prentice Hall. Englewood Cliffs, NJ. 206 pp. [ Links ]
22. Mayntz R (1997) Chaos in society: Reflections on the impact of chaos theory on sociology. En Grebory C, York J (Eds.) The Impact of Chaos on Science and Society. United Nations University Press. New York. pp. 298-323. [ Links ]
23. Melis E (1996) When to prove a theorem by analogy? German Annual Conference on Artificial Intelligence. pp. 259-271. [ Links ]
24. Melis E, Whittle J (1999) Analogy in inductive theorem proving. J. Automated Reasoning 22: 117-147. [ Links ]
25. Nagel E (1961) The Structure of Science. Harcourt, Brace and World, New York. 618 pp. [ Links ]
26. Nehaniv CL, Siekmann J, Carbonell JG. (Eds.) (1999) Computation for Metaphors, Analogy and Agents. Springer-Verlag, Berlin. 399 pp. [ Links ]
27. Sokal A, Bricmont J (1998) Fashionable Nonsense: Postmodern intellectuals abuse of science. Picador. New York. 320 pp. [ Links ]
28. Tonti G (1977) The reasons for the analogies in physics. En Branin FH, Huseyin K (Eds.) Problem Analysis in Science and Engineering. Academic Press. New York. pp. 463-514. [ Links ]
29. Trillas E (1998) La Inteligencia Artificial. Editorial Debate. Madrid. 220 pp. [ Links ]
30. Toulmin S (1958) The Uses of Argument. Cambridge University Press. Cambridge. 272 pp. [ Links ]












 uBio
uBio 
