Interciencia
versión impresa ISSN 0378-1844
INCI v.31 n.3 Caracas mar. 2006
modelos del tamaño de copa de pinus sylvestris l. en bosques del centro de españa
Marivel Domínguez Domínguez1, Felipe Bravo2 y Miren del Río3
1Marivel Domínguez Domínguez. Maestra en Ciencias, Colegio de Posgraduados, México. Doctora en Ciencia y Tecnología Agroforestal y Medio Ambiental, Universidad de Valladolid, España. Profesora Investigadora, Colegio de Postgraduados, Campus Tabasco, México. Dirección: C.P. 86500 A.P. 24, H. Cárdenas, Tabasco, México. e-mail: mdguez@colpos.mx
2Felipe Bravo Oviedo. Doctor Ingeniero de Montes, Universidad de Valladolid (UVA), España. Profesor, UVA, España. e-mail: fbravo@pvs.uva.es
3Miren del Río Gaztelurrutia. Doctor Ingeniero de Montes, Universidad Politécnica de Madrid, España. Investigadora, INIA, España. e-mail: delrio@inia.es
Resumen
Las ecuaciones de perfil de copa pueden ser usadas para caracterizar la apertura de la copa, el perfil del área de la copa, el volumen de la copa y la porosidad de la copa de un rodal, para predecir el crecimiento en altura de los árboles individuales, el crecimiento en área basal y la probabilidad de mortalidad en modelos de desarrollo del rodal, lo cual es importante para tomar decisiones de manejo. El objetivo de este estudio es construir ecuaciones para predecir los parámetros de la copa de pino silvestre en un bosque de montaña. Han sido ensayados diferentes modelos para estimar la relación de copa, la máxima anchura de copa, la altura a la base de la copa y la altura al punto de máxima anchura de copa usando regresión no lineal. La validación de los modelos da como resultado que son adecuados para estimar el tamaño de copa de pino silvestre y la importancia que tiene su estudio en los bosques de montaña.
models of crown size in the scots pine pinus sylvestris l. in forests of central spain
Summary
Crown profile equations can be used to characterize the crown closure, crown-area profile, crown volume and crown porosity of a stand to predict individual-tree height growth, basal area growth and the probability of mortality in stands-development models, which is important to decide about the stand management. The purpose of this study was to build equations to predict the crown parameters of Scots pine in mountain forest. Different models to estimate crown ratio, largest crown width, height of crown base and height above the ground to the largest crown width have been studied using nonlinear regression. Results obtained in the validation models are adequate to estimate the crown size of Scots pine.
modelos do tamanho da copa de pinus sylvestris l. nos bosques do centro da espanha
Resumo
As equaçðes de perfil de copa podem ser usadas para caracterizar a abertura da copa, o perfil da área da copa, o volume da copa e a porosidade da copa de um rodal, para predizer o crescimento em altura das árvores individuais, o crescimento em área basal e a probabilidade de mortalidade em modelos de desenvolvimento do rodal, o qual é importante para tomar decisðes de manipulação. O objetivo de este estudo é construir equaçðes para predizer os parâmetros da copa do pinheiro silvestre em um bosque de montanha. Foram ensaiados diferentes modelos para estimar a relação de copa, a máxima largura da copa, a altura até a base da copa e a altura ao ponto de máxima largura da copa usando regressão não linear. A validação dos modelos determina que são adequados para estimar o tamanho da copa do pinheiro silvestre e a importância que tem seu estudo nos bosques de montanh
Palabras claves: Bosques de Montaña, Forma de los Árboles, Modelos de Copa, Pino Silvestre.
Recibido: 11/05/2005. Modificado: 12/01/2006. Aceptado: 26/01/2006.
Introducción
El tamaño y la forma de la copa tienen una importancia relevante en la dinámica del rodal, ya que las copas de los árboles cambian a través del desarrollo del rodal, así como también con las condiciones de competencia entre los árboles. La copa no representa únicamente el estatus social y el nivel de competencia de un árbol en el presente, sino también su situación en el pasado (Mitchell, 1975; Kramer, 1988). A su vez, el crecimiento de los árboles es controlado por los productos de la fotosíntesis y por las hormonas producidas en la copa, por lo que ésta también refleja el potencial de crecimiento de un árbol.
Además del efecto de la copa sobre el crecimiento, existen otros aspectos que son muy importantes para el manejo sostenible de un bosque como los hábitats de aves, la calidad de la madera y la estabilidad de la masa, en donde la forma y tamaño de la copa de los árboles juegan un papel importante (Hedman y Binkley, 1988; Hann, 1999). La relación entre las características del dosel de copa y el hábitat para la vida silvestre ha sido constatada en numerosos trabajos, especialmente con el hábitat de la avifauna (Moeur, 1981; Morrison et al., 1987; Hunter, 1999). Junto con la relación altura/diámetro, el porcentaje de la copa viva o relación de copa es una de las características individuales que más influencia ejerce en la estabilidad de un árbol, incrementando el riesgo a ser dañados por el viento o la nieve con la menor relación de copa, especialmente en masas jóvenes (Rottmann, 1985). La conformación de la copa está siempre influida por pequeñas diferencias de exposición al sol, a los vientos y por la pendiente que establece variaciones de anclaje y humedad alrededor del tronco (Ruiz de la Torre, 1979; Blanco et al., 1997). Por otro lado, la calidad de los productos maderables depende en parte de la copa, ya que ésta determina la ramificación y forma del fuste de un árbol (Kramer y Kolowski, 1979; Oker-Blom et al., 1988).
Como consecuencia del papel importante que desempeña la copa y del interés por estimar las variables que la representan, han sido ensayadas diferentes aproximaciones de modelaje de la copa. Según Hasenauer y Monserud (1996), dependiendo del objetivo de la elaboración de los modelos de copa se pueden presentar: a) Relaciones alométricas para estimar el tamaño de copa usando las características del árbol y del rodal (diámetro del árbol, altura total y a la base de la copa, edad, área basimétrica, altura dominante, etc.); b) relaciones alométricas para estimar el incremento de copa usando las características del árbol y del rodal, cuando existen mediciones repetidas, este tipo de modelización refleja mejor el efecto de las claras; y c) estimaciones del tamaño de copa usando consideraciones fisiológicas, requiriendo de datos raramente medidos en los inventarios forestales. A estos tres grupos habría que añadir la aproximación estructural modelando la arquitectura de la copa (cf. Kurth, 1994).
Entre los atributos de tamaño de la copa que frecuentemente se estiman mediante los modelos destacan la relación de copa (CR), la altura de la base de la copa (HCB), la amplitud de la copa (KCW) y la altura de máxima amplitud de la copa (HLCW). La relación de copa está muy relacionada con el vigor del árbol y por ello es una de las variables frecuentemente utilizadas para predecir el crecimiento de los árboles (Wikoff, 1990; Biging y Dobbertin, 1992; Hasenauer y Monserud, 1996; Bravo et al., 2001). La predicción de la altura de la base de la copa (HCB) permite, junto con la medición de la altura total del árbol, estimar la relación de copa, por ello también ha sido modelada.
El índice de competencia de copas ha sido utilizado para predecir el crecimiento en altura del árbol individual, el crecimiento en área basimétrica y la probabilidad de mortalidad en modelos de desarrollo del rodal (Hann y Ritchie, 1988; Biging y Dobbertin, 1995; Bravo et al., 2001). Para poder calcular adecuadamente este índice es preciso disponer de ecuaciones que estimen la amplitud de copa y la altura de máxima amplitud de copa. Dentro de la región mediterránea de España se ha estudiado la competencia en un rodal de Pinus pinaster (Ait.) a través de este índice de competencia de copa (Lizarralde et al., 2002).
En España existen Tablas de producción para masas de pino silvestre en diversas regiones, como el Sistema Ibérico (García Abejón, 1981), Sistema Central (García Abejón y Gómez Loranca, 1984; Rojo y Montero, 1996) y Pirineos (García Abejón y Tella, 1986). Estas Tablas describen masas ideales que ocuparían toda la superficie, y se entienden como un instrumento de gestión y planificación que describe una media de lo que se hace o se puede hacer (Madrigal, 1991).
Además de Tablas de producción, se han desarrollado otros modelos de crecimiento de masa y de clases diamétricas para pinares silvestres en los Sistemas Central e Ibérico (Río y Montero, 2001; Río et al., 2001 y Bravo y Montero, 2003). Sin embargo, son pocos los modelos desarrollados a nivel de árbol individual (Palahi, 2002), a pesar de la mayor flexibilidad de estos modelos para simular diferentes tipos de selvicultura y estructuras complejas. Generalmente, los modelos de árbol individual incluyen variables de copa en alguna de sus funciones, como crecimiento en diámetro y en altura, mortalidad o en índices de competencia (Wikoff, 1990; Biging y Dobbertin, 1992; Pretzsch, 1995; Soares y Tomé, 2001), por lo que suele ser necesario elaborar funciones que permitan caracterizar adecuadamente la copa.
El objetivo del presente trabajo es elaborar ecuaciones que permitan predecir los parámetros de tamaño de la copa de pino silvestre en el centro de España a partir de los atributos del árbol y de las características del rodal. Estas funciones de copa serán de utilidad para desarrollar índices estructurales y de competencia, así como para integrarlas en futuros modelos de crecimiento de árbol individual para estos pinares silvestres.
Material y Métodos
Área de estudio
Este trabajo se ha realizado en el monte de Valsaín (Segovia, España), situado en altitudes de 1300-2000m (Rojo y Montero, 1996). El pinar de Valsaín presenta una superficie de 7627ha, ocupadas prácticamente en su totalidad por Pinus sylvestris L. El esquema de ordenación propuesto en 1990 para cuarteles de producción de este monte se basa en tratamientos de aclareos sucesivos por cantones y/o bosquetes, con turnos de 120 años con el método de ordenación de tramo móvil en regeneración, admitiendo una forma semirregular de las masas (Rojo y Montero, 1996). El monte Valsaín es una zona especial de protección a las aves, ya que habitan en él 10 especies consideradas amenazadas y 18 vulnerables; así mismo, forma parte de la red Natura 2000 de espacios protegidos de la Unión Europea. (Decreto 1990) dado su carácter protector de cuenca hidrográfica y su alto valor ecológico.
Los datos climáticos se tomaron de la estación termopluviométrica ubicada en Rascafría "El Paular" en Madrid, a una altitud de 1159m (Figura 1), donde la temperatura media anual es de 10ºC y la precipitación media anual es de 1008,9mm.
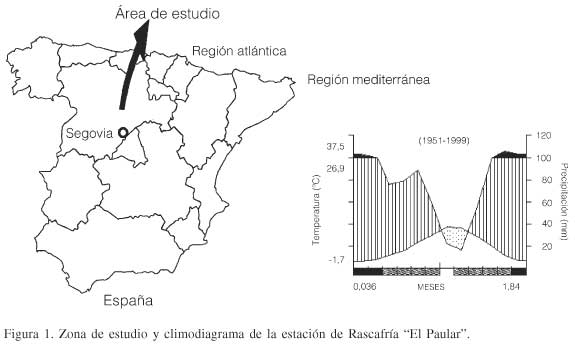
Los suelos en Valsaín son del tipo cambisoles dístricos, luvisoles férricos, con permeabilidad muy alta, textura franca arenosa, el pH varía de 4,9 a 6,2. El monte se asienta sobre terrenos del carbonífero con litofacies gnéisica o granítica, existiendo pinares sobre terrenos precámbricos (Ruiz de la Torre, 1979; Rojo y Montero, 1996).
Origen de los datos
Las parcelas se establecieron en una banda altitudinal de 1200 a 1500m, zona en la que el pino silvestre es más productivo y se aplican con más intensidad los tratamientos selvícolas. En esta banda altitudinal el pino silvestre forma masas monoespecíficas, densas y de estructura regular. En altitudes superiores a 1600m se encuentran masas más claras, irregulares, con un alto valor protector. Por lo contrario, por debajo de 1200m, el pino silvestre se mezcla generalmente con el rebollo (Quercus pyrenaica Willd.) formando masas mixtas (DGCONA, 1998).
Los muestreos se hicieron en tres cantones de clase de edad 60-80, 80-100 y 100-120 años; sin embargo, existen ejemplares en algunas parcelas de clases de edad de 20-40 y 40-60, debido a diversos factores como la masa incorporada y residual, y a la graduación temporal de las cortas. En cada cantón se realizó un muestreo sistemático sobre una malla cuadrada de 100×100m, orientado al norte magnético, con un total de 60 parcelas. Se trabajó con parcelas de radio variable, con centro en el primer árbol inventariable según el método descrito por Prodan (1968), Sloboda (1976) y Reque (2002). El diámetro mínimo inventariable se fijó en 5cm y se midieron el árbol inventariable más próximo al nudo de la malla y sus seis árboles vecinos más próximos, tomando la posición de cada árbol (rumbo y distancia al centro).
De cada árbol inventariable se midieron las siguientes variables:
Diámetro normal o diámetro a la altura del pecho (DBH). Según las indicaciones del Segundo Inventario Forestal Nacional (ICONA, 1990), considerando dos diámetros perpendiculares uno de otro, tomados a la altura de 1,3m.
Altura total (HT). Se midió con hipsómetro.
Altura a la base de la copa (HCB). Se consideró como base de la copa al punto donde se inserta el primer conjunto de ramas que ocupan las tres cuartas partes de la circunferencia del árbol y que representen la base de una copa continua. Se ignoraron las ramas aisladas por debajo del nivel general de la copa, o las ramas muertas.
Altura de máxima amplitud de copa (HLCW). Se midió con un hipsómetro la altura del punto estimado de forma visual en el que la copa posee su mayor anchura.
Máxima amplitud de copa o diámetro de copa (LCW). Se midió la proyección de la copa mediante dos diámetros perpendiculares, el primero de ellos en dirección al árbol central.
Además se midió la edad normal, a 1,3m del suelo, del árbol dominante de cada parcela. A partir de las mediciones realizadas en campo se generaron variables para elaborar posteriormente los modelos de copa. La Tabla I muestra las variables y las ecuaciones utilizadas en el presente trabajo para su definición. Las variables calculadas son:
Relación de copa (CR). Resulta de dividir la longitud de copa entre la altura total.
Área basimétrica (BA). Se considera el área basimétrica de la parcela de acuerdo al método de muestreo, es decir como la sumatoria del área de los árboles 0-5, más la mitad del área del árbol 6, dividido por la superficie de la parcela.
Área basimétrica de los árboles de mayor diámetro (BAL). Es la suma del área basimétrica de los árboles de mayor diámetro que el árbol dado, considerando los árboles para el cálculo del BAL de la misma forma que en el caso del cálculo del BA.

Modelos de copa
Se han desarrollado cuatro modelos para estimar los siguientes atributos de la copa: relación de copa (CR), altura a la base de la copa (HCB), máxima anchura de copa (LCW) y altura al punto de máxima anchura de copa (HLCW). Dado que los modelos de CR y HCB, una vez conocida la HT, ofrecen la misma información, se seleccionará el que tenga mejor ajuste.
Relación de copa. La forma básica utilizada generalmente en los modelos de relación de copa (Hasenauer y Monserud, 1996; Hann, 1997; Soares y Tomé 2001) es
CR = 1/(1+Exp(-X)) (1)
donde X es una función lineal que incluye variables que representan el tamaño de los árboles, la competencia entre árboles y la productividad de la estación.
La variable de productividad no ha sido incluida en el presente trabajo porque no existe suficiente variación de calidad de estación entre los cantones estudiados. El tamaño fue representado por HT y DBH, ya que estas variables han dado buenos resultados en trabajos previos (Ortega, 2001), mientras que la competencia fue representada por el área basimétrica de los árboles mayores más gruesos que el árbol considerado (BAL). Con el objeto de encontrar los modelos de regresión no lineal que mejor represente a las variables, se han utilizado como parámetros iniciales los valores propuestos por Hasenauer y Monserud (1996) para pino silvestre en Austria, b o= -1,67698; b1 = 2,94; b2= 0,02638; b4= 0,01305. El parámetro utilizado para b3= 0, ya que la variable DBH2 no se incluye en el modelo propuesto por Hasenauer y Monserud (1996). El siguiente modelo de relación de copa fue ajustado:
CR=1/(1+Exp(-(bo+b1×HT/DBH+b2×HT+ b3×DBH2+b4×BAL))) (2)
Altura a la base de la copa. De acuerdo a trabajos previos de Ritchie y Hann (1997), y de Hanus et al. (2000), se ha utilizado como modelo general de HCB el siguiente:
HCB = HT/(1+Exp(X)) (3)
donde X es una función lineal que incluye variables que representan el tamaño del individuo, la densidad de la masa, la competencia entre árboles y la productividad de la estación. Como en el modelo CR, la variable de productividad no ha sido incluida. El tamaño fue representado por HT, la densidad por el área basimétrica (BA), mientras que la competencia fue representada por el área basimétrica en los árboles más grandes (BAL).
En algunos casos fue necesaria la transformación logarítmica para mejorar los ajustes. De acuerdo con los modelos generales previamente propuestos, el modelo usado fue el propuesto por Ritchie y Hann (1997):
HCB = HT/(1+Exp(bo+b1×HT+b2×BAL+b3×LogG(BA)+b4(DBH/HT))) (4)
y los parámetros utilizados inicialmente para obtener el ajuste del modelo fueron b= 0 para todas las variables.
Máxima anchura de copa. El modelo de LCW utilizado en este estudio fue usado previamente por Hann (1997):
LCW = MCW×CRZ (5)
donde MCW es la máxima anchura de copa potencial de un árbol de la especie considerando que ha vivido siempre sin sufrir competencia.
El MCW fue sustituido por una función de DBH, ya que en este trabajo no se incluye información sobre árboles que estén creciendo en condiciones abiertas; los rodales trabajados crecen en condiciones cerradas donde existe competencia. Ortega (2001) utilizó el mismo procedimiento. El modelo usado es
LCW = (bo+b1×DBH+b2×DBH2)(CRb3) (6)
Para encontrar el modelo de regresión no lineal que mejor represente a las variables, se utilizó como parámetros iniciales en el modelo de LCW los valores propuestos por Ortega (2001) para P. pinaster. (bo= 4,7952, b2= 0,0027 y b3= 0,4076). Como valor del parámetro b1, al igual que en el caso del modelo de CR, se consideró inicialmente el valor de cero.
Altura en el punto de máxima anchura de copa. La estructura de la Ec. 4 fue usada como modelo básico para estimar el HLCW en un modelo no lineal. Los parámetros usados inicialmente fueron b= 0 para todas las variables. El modelo probado es
HLCW = HT/(1+Exp (b o+b 1×HT+b 2×BAL+b 3×(DBH/HT)+b 4×CR)) (7)
Análisis estadístico
Aleatoriamente se extrajeron de los datos 305 observaciones para construir los modelos de copa y los 115 árboles restantes se utilizaron para validar los modelos ajustados. En la Tabla II se presentan las características de las principales variables en el total de los datos, para el ajuste del modelo y para su validación. En el ajuste de los modelos se utilizó regresión no lineal con el procedimiento NLIN en el paquete SAS (SAS, 1995). Cada una de las variables de los modelos es significativa con una probabilidad a=0,05 rechazándose la hipótesis de que los valores de los intervalos de confianza contengan el valor cero. Cuando en algún caso existían variables no significativas eran eliminadas de los modelos.

En el análisis de regresión no lineal se expresa la variable dependiente como una función no lineal de las variables independientes. La estimación depende tanto del procedimiento como de los parámetros iniciales elegidos. Entre los procedimientos para el ajuste de los modelos no lineales, se ha utilizado el método DUD (Don't use derivatives). Esta metodología ha sido usada anteriormente en otros trabajos, como por ejemplo Álvarez (1997) que no encontró diferencias con otros métodos de ajuste.
Validación de los modelos
Con los datos de los 115 árboles separados para realizar la validación de los modelos se han calculado los siguientes índices (Soares et al., 1995):
![]() (8)
(8)
![]() (9)
(9)
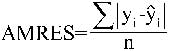 (10)
(10)
![]() (11)
(11)
donde MRES: error medio del modelo, AMRES: diferencia media absoluta, Yi: valor observado o real, ![]() : valor estimado con el modelo,
: valor estimado con el modelo,![]() : valor promedio de los valores
: valor promedio de los valores
observados o reales, n: número de observaciones en la validación de los modelos (115).
En la validación, además de estos criterios se comprueba gráficamente que las predicciones sean razonables (valores predichos frente a valores observados).
Error relativo (%) = 100 × ![]() (12)
(12)
Para comprobar la consistencia biológica de cada uno de los modelos, se elaboraron gráficas analizando la variación de la variable independiente en el eje de las abscisas en relación con la variable dependiente que define el modelo. Para ello, se tomaron como base los datos de muestreo de un árbol dominante en una parcela determinada para fijar los valores de las otras variables que intervienen en el modelo. Este análisis ofrece información sobre la consistencia biológica del modelo en función de las clases de factores o atributos como el tamaño del árbol, el vigor del árbol, el nivel de competencia y la productividad de la masa.
Resultados Discusión
Relación de copa
En el modelo de la relación de copa (Ec. 2), todas las variables que conforman el modelo resultaron significativas a un nivel de confianza del 95%, quedando el modelo de CR como
CR= 1/(1+Exp(-(1,505760-(0,706481)×HT/DBH-(0,078039)×HT+(0,000182)×DBH2 -(0,007262)×BAL))) (13)
Los resultados del ajuste del modelo no lineal y de los parámetros del modelo de CR se muestran en las Tablas III y IV.
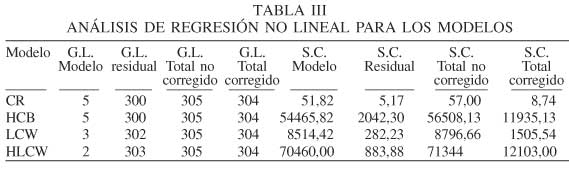

La relación de la copa, que representa el vigor del árbol, se estima en función de la relación de esbeltez, el diámetro al cuadrado, la altura y el BAL como variable de competencia. Las tres primeras variables están muy relacionadas con el vigor del árbol, especialmente la esbeltez (HT/DBH), ya que los árboles dominados suelen presentar esbelteces elevadas. Al respecto Biging y Gill (1997) mencionan que expresiones de dimensiones de copa están fuertemente correlacionadas con variables como la altura y el crecimiento en diámetro, así como con variables de rodal como el volumen. La variable DBH2 resulta significativa, indicando una relación cuadrática entre DBH como variable independiente y el CR como variable dependiente. Hasenauer y Monserud (1996) encontraron que para pino silvestre en Austria es significativo HT/DBH y HT, pero no DBH, dentro de las variables de tamaño.
En la Figura 2a se hace una representación gráfica del modelo de relación de copa, para ver la consistencia biológica de las variables. Se muestra la variación de CR con cada una de las variables independientes del modelo fijando el resto de las variables. A mayor desarrollo del árbol en diámetro en un mismo rodal, la relación de copa tiende a incrementar, de manera que cuando el pino silvestre presenta un diámetro de 60cm, la relación de copa incrementa manteniéndose entre 0,47 y 0,58. Los valores grandes de CR también reflejan a los árboles dominantes representados por el BAL= 0 (Figura 2b).
Se puede decir que el nivel de competencia del árbol es reflejado por el área basimétrica de los árboles de mayor diámetro (BAL), que estima que los árboles competidores son aquellos de mayor diámetro que el árbol sujeto y que la competencia es mayor, cuanto mayor es el diámetro de dichos árboles. Los árboles dominantes obtienen un BAL= 0, presentando una relación de copa mayor, debido a la mayor capacidad de captar la energía solar, por lo tanto, esos árboles presentan mayor vigor. Esta relación de copa se ve disminuida, hasta encontrar árboles en situación dominada generada por la mayor densidad del rodal, donde la CR disminuye gradualmente. Esta variable de competencia ha sido estudiada por Bravo et al. (2001) en comparación con el factor de competencia de copa (CCH), encontrando una disminución leve en el cuadrado medio del error cuando se utiliza esta última.
La estructura del rodal influye fuertemente en el crecimiento diamétrico de P. sylvestris L, encontrándose una mayor eficiencia de los modelos de crecimiento en diámetro cuando contienen un índice de competencia como el BAL, y un índice de vigor como el CR (Marcos, 2002). Estas variables han sido determinadas considerando en su trabajo características como el tamaño, el vigor del árbol, la competencia, la productividad de la estación y la diferenciación horizontal y vertical (Bravo et al., 2001).
Por otra parte, el vigor del árbol representado a través de la relación de copa muestra una relación directa con el grosor del fuste, incrementando el vigor, en árboles más jóvenes (Figura 2c).
Altura a la base de la copa
En el modelo de HCB (Ec. 4), la variable de competencia representada por el BAL no resulta significativa, quedando el modelo dependiente de las variables HT, relación DBH/HT, que representa el tamaño del árbol, y el logaritmo del área basimétrica, que representa la competencia de los árboles a través de la densidad del rodal:
HCB=HT/(1+Exp((0,845435)-(0,040666)×HT+(-0,418976)×Log(BA)+(0,637408)×DBH/HT)) (14)
Esta última variable fue también incluida en el modelo ajustado por Ritchie y Hann (1997). Dichas variables presentan valores de los parámetros con signo positivo, excepto para la altura total del árbol, cuyo parámetro estimado presenta signo negativo. Los resultados del análisis de regresión no lineal se muestran en las Tablas III y IV.
Por su parte, la altura a la base de la copa manifiesta un incremento a través de la variable de competencia representada por el área basimétrica, de manera que cuando esta variable aumenta, la HCB incrementa también de manera gradual con la altura del árbol, siendo mayor este incremento con mayores áreas basimétricas (Figura 3a). La altura a la base de la copa muestra menor incremento a través del área basimétrica al incrementar el DBH (Figura 3b), no así para la altura del árbol al incrementar el DBH (Figura 3c), que presenta una tendencia exponencial de la altura a la base de la copa a través de la variable de HT, indicando que para una misma altura, los árboles con mayor diámetro (dominantes) presentan una altura de copa viva menor.
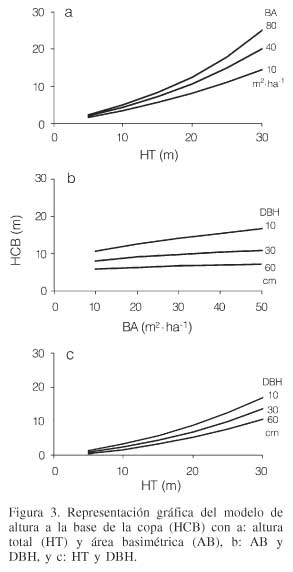
La variable de la altura a la base de la copa (HCB) representa la altura del fuste del árbol hasta la base de la copa, por tanto un valor más alto de (HCB) implica menor longitud de copa viva; estas variables han sido anteriormente utilizadas en la eficiencia del crecimiento en P. pinaster (Ortega, 2001) y en el crecimiento diamétrico de P. sylvestris (Marcos, 2002).
Máxima anchura de copa
En el modelo de máxima anchura de copa probado inicialmente (Ec. 6) se incluyeron las variables DBH, DBH2 y CR, de las cuales el DBH2 no resultó significativo a un nivel de confianza del 95% en el análisis de regresión no lineal. Por lo tanto el modelo (Ec. 15) queda definido con la variable de tamaño DBH y la variable que representa el vigor del árbol CR. En este modelo se presenta una relación lineal de la variable DBH, a diferencia del modelo de CR que queda mejor ajustado con la relación cuadrática (DBH2).
LCW = (1,303632+(0,149361)×DBH)×CR0,175496 (15)
Los resultados del análisis de regresión no lineal del LCW se presentan en las Tablas III y IV, mostrando un valor del cuadrado medio residual igual a 0,93. Los parámetros estimados para cada una de las variables que representan este modelo resultan positivos, así como también para el caso del término independiente b0.
El valor de LCW representa además del tamaño del árbol la situación de competencia del mismo. Los árboles que presentan un mayor valor de esta variable indican que se desarrollan bajo condiciones de menor competencia de espacio y de luz, por tanto tienen mayor capacidad de recibir energía solar. Al realizar la representación gráfica del modelo de LCW se puede ver que existe una relación lineal en el aumento de la máxima anchura de copa al incrementar el diámetro normal de los árboles, haciéndose más notable en los árboles con mayor relación de copa, en los individuos más vigorosos (Figura 4a). Por su parte al analizar el LCW con la CR como variable que representa el vigor del árbol se puede notar una tendencia potencial, presentando un leve incremento al aumentar el vigor del árbol a través de la relación de copa. La diferencia del LCW se hace más notable en este caso en árboles con mayor diámetro (Figura 4b).
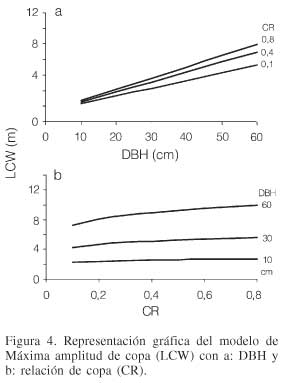
Altura en el punto de máxima anchura de copa
El modelo de la altura al punto de máxima anchura de copa fue representado inicialmente por las variables HT, BAL, DBH/HT y CR (Ec. 7), de las cuales solo resultó significativo a un nivel de confianza del 95% la relación de copa. Los resultados del ajuste se presentan en las Tablas III y IV. El modelo expresa la influencia del vigor del árbol en la altura en el punto de máxima anchura de copa:
HLCW=HT/(1+Exp(-2,158175+(3,049517)×CR)) (16)
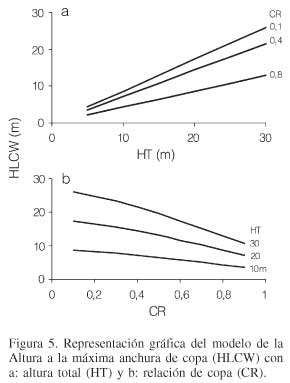
El valor de HLCW representa en parte a la competencia y vigor del árbol y a la producción foliar de la masa. Al representarse en la Figura 5a el modelo HLCW muestra el desarrollo de esta variable en una relación lineal a través del incremento en la altura total. Por su parte, al relacionar a HLCW con la variable que representa al vigor del árbol, se aprecia una tendencia de tipo logarítmica, disminuyendo la altura a la máxima amplitud de copa con el aumento de la relación de copa (Figura 5b). La relación de copa alta suele corresponder a árboles jóvenes y árboles de mayor vigor, por lo que el punto de máxima anchura de copa en el árbol baja, de manera similar al caso de la HCB. Al realizar las mediciones de campo se observó que, en algunos casos, coincidía la altura a la base de la copa con el punto de máxima anchura de copa.
Validación
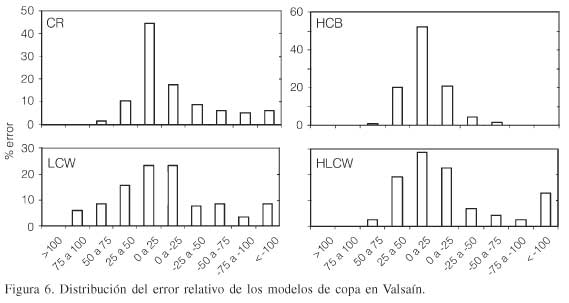
El error relativo de cada modelo se obtuvo a través de la Ec. 12 para indicar la validez del mismo. En el caso del modelo CR el 80,85% de los 115 datos se encuentran distribuidos en el área del 50% de error relativo y un 6% se encuentran fuera del 100% (Figura 6); sin embargo en el modelo de HCB el 97,37% de los datos están distribuidos dentro del rango del 0 al 50% de error relativo y no se presenta error que rebase el 100%, lo cual muestra un modelo mejor representado. Los modelos LCW y HLCW dan como resultado valores similares encontrando que un 70,41 y 77,37% respectivamente de los datos están distribuidos dentro del 0 al 50% de error relativo y el 8,69 y 13,04% rebasan el 100% respectivamente para valores negativos (Figura 6).
Los estadísticos realizados en la validación con una muestra independiente dan como resultados los menores valores tanto del error medio del modelo en porcentaje como de la diferencia media absoluta para el modelo de altura a la base de la copa (10,59% y 18,50%), respectivamente. Al comparar el modelo de relación de copa con el modelo de la altura a la base de la copa, que representan el crecimiento de la misma sección del árbol, resulta menos predictivo la CR que el modelo de altura a la base de la copa, por lo tanto este último se ajusta de mejor manera a través de sus variables de forma y competencia del árbol (altura total, relación del diámetro dividido por la altura y logaritmo del área basimétrica), respectivamente.
Los modelos de relación de copa, máxima anchura de copa y altura en el punto de máxima anchura de copa manifiestan un valor predictivo sensiblemente inferior, este último presenta errores medios del modelo en porcentaje y la diferencia media absoluta menos predictivo que los anteriores (Tabla V). La diferencia media absoluta de los modelos LCW y HLCW presentan los valores más altos, lo que es lógico ya que son dos variables que se miden de manera más imprecisa debido a la altura de los árboles.

El trabajo de Ortega (2001) en P. pinaster determinó que el valor predictivo del modelo de la altura a la base de la copa es inferior al de otros modelos ensayados como LCW y HLCW; sin embargo, los errores medios del modelo en porcentaje y especialmente la diferencia media absoluta del modelo de la altura a la base de la copa de Ortega son similares a los valores encontrados en este trabajo. El modelo de Ortega (2001) queda ajustado únicamente por la altura total y considerando un número reducido de observaciones a diferencia del modelo aquí desarrollado donde queda ajustado por altura total, la relación del diámetro dividido por la altura y logaritmo del área basimétrica.
Conclusiones
Se han evaluado cuatro modelos de copa: relación de copa (CR), altura a la base de la copa (HCB), máxima anchura de copa (LCW) y altura en el punto de máxima anchura de copa (HLCW), de los cuales el CR y HCB estiman a la misma variable, por lo que si podemos estimar la altura total del árbol, entonces la altura a la base de la copa y la relación de la copa resultan modelos redundantes, ya que una variable se puede calcular a partir de la otra, por lo tanto sólo una de ellas es necesaria para caracterizar la longitud de la copa.
De los modelos (CR y HCB), el modelo HCB presenta los valores más bajos en error medio del modelo (10,59%) y diferencia media absoluta (18,50%), por lo tanto HCB es considerado el modelo mejor ajustado de los dos.
HLCW es el modelo que presenta el máximo error medio del modelo en porcentaje y la diferencia media absoluta.
Los cuatro modelos probados para estimar los atributos de copa, pueden ser usados para desarrollar índices estructurales y de competencia de árbol individual. Estos índices pueden servir para explorar las respuestas de los árboles de pino silvestre a diferentes alternativas estructurales. Estos modelos son aplicables a rodales de entre 60 y 120 años; aún cuando algunos árboles del muestreo tienen menos de 60 años, debe tenerse en cuenta que son árboles dominados procedentes de regeneración avanzada por lo que no se justifica utilizar los modelos en masas de menos de 60 o más de 120 años.
Agradecimiento
Este trabajo ha sido realizado en el marco del proyecto MCYT (AGL 2000-1545) "Influencia de los tratamientos selvícolas sobre la diversidad de las masas de pino silvestre: caracteres selvícolas, florísticos y genéticos".
References
1. Álvarez GJG (1997) Análisis y caracterización de las distribuciones diamétricas de Pinus pinaster Ait. En Galicia. Tesis. Universidad Politécnica de Madrid. España. 270 pp. [ Links ]
2. Blanco CE, Casado GMA, Costa, TM, Escribano BR, García AM, Génova FM, Gómez MA, Gómez MF, Moreno SJC, Morla JC, Regato PP, Sainz OH (1997) Los bosques Ibéricos. Una interpretación geobotánica. Planeta. Madrid, España. 572 pp. [ Links ]
3. Biging GS, Dobbertin M (1992) A Comparison of Distance-Dependent Competition Measures for Height and Basal Area Growth of Individual Conifer Trees. For. Sci. 38: 695-720. [ Links ]
4. Biging GS, Dobbertin M (1995) Evaluation of competition indices in individual-tree growth models. For. Sci. 41: 360-377. [ Links ]
5. Biging GS, Gill S (1997) Stochastic models for conifer tree crown profiles. For. Sci. 43: 25-34. [ Links ]
6. Bravo F, Hann DW, Maguire DA (2001) Impact competitor species composition on predicting diameter growth and survival rates of Douglas-fir trees in southwest Oregon Can. J. For. Res. 31: 2237-2247. [ Links ]
7. Bravo F, Montero G (2003) High-grading effects on Scots pine volume and basal area in pure stands in northern Spain. Ann. For. Sci. 60: 11-18. [ Links ]
8. Decreto (1990) Real Decreto 439/1990, de 30 de Marzo de 1990. Catálogo Nacional de especies amenazadas. B.O.E. Nº82, 5 de Abril. pp. 9468-9471. [ Links ]
9. DGCONA (1998) Segundo Inventario Forestal Nacional 1986-1996 España. Direccion General de Conservacion de la Naturaleza. Madrid, España. 337 pp + cartografía. [ Links ]
10. García Abejón JL (1981) Tablas de producción de densidad variable para Pinus sylvestris L. en el Sistema Ibérico. Comunicaciones INIA, Serie Recursos Naturales Nº10. 47 pp. [ Links ]
11. García AJL, Gómez LJA (1984) Tablas de producción de densidad variable para Pinus sylvestris L. en el Sistema Central. Comunicaciones INIA, Serie Recursos Naturales Nº29. 36 pp. [ Links ]
12. García AJL, Tella FG (1986) Tablas de producción de densidad variable para Pinus sylvestris L. en el Sistema pirenaico. Comunicaciones INIA, Serie Recursos Naturales Nº43. 28 pp. [ Links ]
13. Hann DW (1997) Equations for predicting the largest crown width of stand-grown trees in Western Oregon. Research contribution 17. Forest Research Laboratory. Corvalis, Oregon, EEUU. 14 pp. [ Links ]
14. Hann DW (1999) An adjustable predictor of crown profile for stand-grown Douglas-fir trees. For. Sci. 45: 217-225. [ Links ]
15. Hann DW, Ritchie MW (1988) Height growth rate of Douglas-fir: A comparison of model forms. For. Sci. 34: 165-175. [ Links ]
16. Hanus M, Hann D, Marshall D (2000) Predicting height to crown base for undamaged and damaged trees in Southwest Oregon. Research contribution 29. Forest Research Laboratory. Corvalis, Oregon, EEUU. 35 pp. [ Links ]
17. Hasenauer H, Monserud RA (1996) A crown ratio model for Austrian forest. For. Ecol. Manag. 84: 49-60. [ Links ]
18. Hedman CW, Binkley D (1988) Canopy profiles of some Piedmont hardwood forest. Can. J. For. Res. 18: 1090-1093. [ Links ]
19. Hunter ML (1999) Maintaining biodiversity in forest ecosystems. Cambridge University Press. Cambridge, Inglaterra. 698 pp. [ Links ]
20. ICONA (1990) Segundo Inventario Forestal Nacional. Explicaciones y métodos 1986-1995. Instituto Nacional para la Conservación de la Naturaleza. Madrid, España. 174 pp. [ Links ]
21. Kramer H (1988) Waldwachstumslehre. Paul Parey. Hamburg-Berlin, Alemania. 374 pp. [ Links ]
22. Kramer PJ, Kolowski TT (1979) Physiology of woody plants. Academic Press. New York, EEUU. 811 pp. [ Links ]
23. Kurth W (1994) Morphological models of plant growth. Possibilities and ecological relevance. Ecol. Mod. 75/76: 299-308. [ Links ]
24. Lizarralde I, Guerra N, Bravo F (2002) Competition and diameter growth in maritime pine in a mediterranean area. En Workshop on reality, models and parameter estimation. Sesimbra. Portugal. [ Links ]
25. Madrigal C (1991) Tablas de producción. Seminario sobre inventarios y ordenación de montes. Valsaín, Segovia, España. Vol. II, pp. 32-70. [ Links ]
26. Marcos LD (2002) Estudio de la influencia de la estructura del rodal sobre el crecimiento diamétrico de Pinus sylvestris en el monte "Pinar de Valsaín" (Segovia). Proyecto. Universidad de Valladolid. Palencia, España. 130 pp. [ Links ]
27. Mitchell KJ (1975) Dynamics and simulated yield of Douglas fir. For. Sci. Monogr. 17. 39 pp. [ Links ]
28. Moeur M (1981) Crown width and foliage weight of northern Rocky Mountain conifers. USDA For. Serv. Res. Par. INT-283. 14 pp.
29. Morrison ML, Timossi IC, Kimberly AW (1987) Development and testing of linear regression models predicting bird-habitat relationships. J. Wild. Manag. 51: 247-253. [ Links ]
30. Oker-blom P, Kellomäki S, Valtonen E (1988) Structural Development of Pinus sylvestris Stands with varying Initial Density: a Simulation Model. Scan. J. For. Res. 3: 185-200. [ Links ]
31. Ortega M (2001) Estudio de la eficiencia de crecimiento de Pinus pinaster Ait. en relación con la competencia y los grupos familiares. Proyecto. Universidad de Valladolid. Palencia, España. 127 pp. [ Links ]
32. Palahi M (2002) Modelling the stand development and optimizing the management of even-aged Scots pine forests in North-east Spain. Tesis. Univ. of Joensuu. Joensuu. Finland. 58 pp. + App. [ Links ]
33. Pretzsch H (1995) Zum EinfluSS des Baumverteilungsmusters auf den Bestandeszuwachs. Allg. Forst-u. J. Ztg. 166: 190-201. [ Links ]
34. Prodan M (1968) Punktstichprobe für die Forsteinrichtung. FHW 23: 225-226. [ Links ]
35. Reque JA (2002) Prescripciones selvícolas para roble albar (Quercus petraea) en la Cordillera Cantábrica a partir de un análisis sincrónico. Investigación Agraria. Sistemas y recursos forestales. Vol. 11. pp. 283-297. [ Links ]
36. Río M del, Montero G (2001) Modelo de simulación de claras en masas de Pinus sylvestris L. Monografías INIA: Forestal Nº 3. 114 pp. [ Links ]
37. Río M del, Montero G, Bravo F (2001) Analysis of diameter-density relationships and self-thinning in non-thinned even-aged Scots pine stands. For. Ecol. Manag. 142: 79-87. [ Links ]
38. Ritchie MW, Hann DW (1988) Equations for predicting height to crown base for fourteen tree species in Southwest Oregon. Forest Research Laboratory, Oregon State University. Research Paper 50. Corvalis, Oregon, EEUU. 14 pp. [ Links ]
39. Rojo A, Montero G (1996) El pino silvestre en la Sierra de Guadarrama. Ministerio de Agricultura, Pesca y Alimentación, Madrid, España. 293 pp. [ Links ]
40. Rottmann M (1985) Waldbauliche Konsequenzen aus Scheneebruch katastrophen. Schweiz. Z. Forstwes. 136: 167-184. [ Links ]
41. Ruiz de la Torre J (1979) Árboles y arbustos de la España peninsular. Escuela Técnica Superior de Ingenieros de Montes. Madrid, España. 512 pp. [ Links ]
42. SAS (1995) SAS Users Guide. Version 6, Vol. 2, 4th ed. SAS Institute, Inc. Cary, NC, EEUU. [ Links ]
43. Sloboda B (1976) Mathematische und stochastische modelle zur Beschreibung und Beständen. Insbesondere das bestandesspezifische wachstum als stochastischer Prozeb. Tesis. Univ. Freiburg. Freiburg, Alemania. [ Links ]
44. Soares P, Tomé M (2001) A tree crown ratio prediction equation for eucalypt plantations. Ann. For. Sci. 58: 193-202. [ Links ]
45. Soares P, Tomé M, Skovsgaard J, Vanclay K (1995) Evaluating a growth model for forest management using continuous forest inventory data. For. Ecol. Manag. 71: 251-265. [ Links ]
46. Wikoff WR (1990) A Basal Area Increment Model for Individual Conifers in the Northern Rocky Mountains. For. Sci. 36: 1077-1104. [ Links ]












 uBio
uBio 
