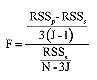Comparación de métodos de estimación de parámetros de crecimento del camarón blanco Litopenaeus schmitti en el occidente de venezuela

Glenys Andrade de Pasquier y Eduardo P. Pérez E.

 M.Sc., Universidad Católica del Norte (UCN), Chile. Ph.D., CINVESTAV-IPN, México. Investigadora, Instituto Nacional de Investigaciones Agrícolas (INIA), Venezuela. e-mail: gandrade@inia.gov.ve

Biólogo Marino, UCN, Chile. M.Sc. y Ph.D., CINVESTAV-IPN, México. Profesor, UCN e Investigador, Centro de Estudios Avanzados en Zonas Áridas, Chile. Dirección: UCN, Casilla 117, Coquimbo, Chile. e-mail: eperez@ucn.cl

RESUMEN

Para el camarón blanco Litopenaeus schmitti se han reportado diferentes parámetros de crecimiento en el occidente de Venezuela. Tales diferencias han sido atribuidas tanto a los distintos métodos como a las distintas bases de datos empleadas en la estimación. Para evaluar esta explicación se reanalizaron los parámetros de crecimiento para la especie, utilizando dos bases de datos y dos métodos de ajuste: ELEFAN y una minimización de cuadrados. La primera base de datos consistió de frecuencias de longitudes de juveniles capturados en el Lago de Maracaibo en el periodo 1991-1993. La segunda consistió de frecuencias de longitudes de juveniles y adultos capturados en el Golfo de Venezuela y el Lago de Maracaibo durante el periodo 2001-2003. Para ajustar los parámetros mediante ELEFAN se empleó el software FiSAT, en tanto que para el método de mínimos cuadrados se usaron planillas de cálculo. Los resultados mostraron que los tamaños registrados en las bases de datos tienen un mayor impacto que los métodos utilizados. Usando información de ambas bases de datos los resultados fueron similares entre métodos, pero diferentes cuando fueron comparados entre bases de datos, las cuales diferían en términos de los intervalos de tamaños representados en cada una. Para Litopenaeus schmitti, en el occidente de Venezuela la base de datos con una mejor representatividad de tallas juveniles y adultas arrojó estimaciones más confiables que el ajuste basado solo en juveniles.

Comparison of methods for estimation of white shrimp (litopenaeus schmitti) growth parameters in western venezuela

SUMMARY

Different estimates of growth parameters for the white shrimp Litopenaeus schmitti have been reported for Western Venezuela. The differences have been attributed to the different methods and data bases employed. In order to evaluate these explanations, a re-evaluation of growth parameters for this species was carried out using two data bases and two fitting methods: the ELEFAN approach and the least squares minimization technique. The first data base consisted only of juvenile length frequency distributions recorded in the 1991-1993 period in the Maracaibo Lake. The second one consisted in both juvenile and adult frequency distributions recorded in the 2001-2003 period in the Maracaibo Lake and the Gulf of Venezuela. In order to fit parameters by the ELEFAN method, the FiSAT package was used, while worksheet spreads were used for fitting parameters by least squares minimization. Results showed a greater impact of the size range recorded in the data base than of the method employed. Using information contained in both data bases results were similar among methods, but were different when comparison was between data bases, which were different in terms of the size ranges represented. For Litopenaeus schmitti in Western Venezuela, data bases with adequate representation of juvenile and adults led to more reliable estimates than fitting based exclusively in juveniles.

comparação do métodos de estimação de parâmetros de crescimento do camarão branco litopenaeus schmitti no occidente da venezuela

RESUMO

Para o camarão branco Litopenaeus schmitti se tem relatado diferentes parâmetros de crescimento no ocidente da Venezuela. Tais diferenças têm sido atribuídas tanto aos distintos métodos como as distintas bases de dados empregadas na estimação. Para avaliar esta explicação se reanalizaram os parâmetros de crescimento para a espécie, utilizando duas bases de dados e dois métodos de ajuste: ELEFAN e uma minimização de quadrados. A primeira base de dados consistiu de freqüências de longitudes de juvenis capturados no Lago de Maracaibo no período 1991-1993. A segunda consistiu de freqüências de longitudes de juvenis e adultos capturados no Golfo de Venezuela e no Lago de Maracaibo durante o período 2001-2003. Para ajustar os parâmetros mediante ELEFAN se empregou o software FiSAT, em tanto que para o método de mínimos quadrados se usaram planilhas de cálculo. Os resultados mostraram que os tamanhos registrados nas bases de dados têm um maior impacto que os métodos utilizados. Usando informação de ambas as bases de dados os resultados foram similares entre métodos, mas diferentes quando foram comparados entre bases de dados, as quais diferiam em termos dos intervalos de tamanhos representados em cada uma. Para Litopenaeus schmitti, no ocidente da Venezuela a base de dados com uma melhor representatividade de tamanhos juvenis e adultas arrojou estimações mais confiáveis que o ajuste baseado somente em juvenis.

PALABRAS CLAVE / Crecimiento / Distribución Multinomial / ELEFAN / Golfo de Venezuela / Lago de Maracaibo / Litopenaeus schmitti /

Recibido: 22/08/2006. Modificado: 12/12/2006. Aceptado: 15/12/2006.

Introducción

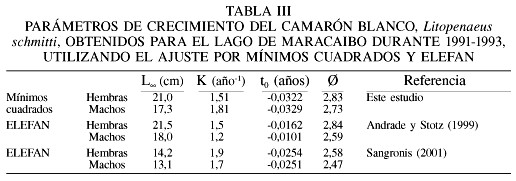
Los parámetros de crecimiento de una especie constituyen elementos indispensables en las evaluaciones de stock que se basan en el conocimiento de su estructura por edades y contribuyen a definir una estrategia de explotación acorde con políticas de administración pesquera. El camarón blanco, Litopenaeus schmitti (Burkenroad, 1938), es el camarón peneido de mayor importancia comercial en Venezuela (Novoa et al., 1998). En el Golfo de Venezuela y Lago de Maracaibo existen grandes poblaciones de L. schmitti y allí ocurre una de las pesquerías de mayor rendimiento en toda su área de distribución (Andrade, 2005). El patrón de crecimiento de esta especie ha sido reportado para el Lago de Maracaibo con distintos resultados dependiendo del intervalo de tamaños evaluados o de la metodología empleada. Andrade y Stotz (1999) y Sangronis (2001) mediante ELEFAN estimaron el crecimiento y la composición etaria de L. schmitti, empleando frecuencias de talla de la fracción juvenil de la población presente en el Lago de Maracaibo y extrapolando el crecimiento hacia la fracción de adultos presentes en el Golfo de Venezuela, la cual no fue muestreada. La comparación de los resultados entre ambos trabajos indicó que, aunque ambos sexos presentaron parámetros de crecimiento diferentes, para un mismo sexo los valores fueron diferentes. Dado que el método de estimación fue el mismo tales diferencias pueden ser atribuidas a los intervalos de tallas analizados, entre 6 y 20cm (Andrade y Stotz, 1999) y entre 1,3 y 14cm (Sangronis, 2001) de longitud total. Según Gulland y Rosenberg (1992), la falta de individuos de tallas grandes puede subestimar la longitud asintótica y sobrestimar la tasa de crecimiento. Igualmente la estimación del crecimiento basado sólo en los individuos más grandes puede ser sesgada.

Recientemente (Andrade y Pérez, 2004) reevaluaron el crecimiento de L. schmitti utilizando el intervalo completo de tallas presentes tanto en el Golfo de Venezuela como en el Lago de Maracaibo usando la técnica de minimización de cuadrados basándose en una distribución multinomial. Sus resultados se aproximaron a los de Andrade y Stotz (1999), pero difirieron de los de Sangronis (2001). Del mismo modo estos autores hicieron una comparación entre los resultados obtenidos por ellos con lo evaluado por otros autores para especies del mismo género en otras latitudes. Para el caso específico de L. schmitti en la zona occidental de Venezuela, existen tres estimaciones con dos métodos diferentes, lo que fue discutido por Andrade y Pérez (2004), planteando la necesidad de averiguar si tales diferencias podrían deberse a variaciones debida a los métodos y no necesariamente a variaciones biológicas. Así, el presente trabajo tiene por finalidad analizar, con los dos métodos utilizados anteriormente, una base de datos común y determinar hasta qué punto las diferencias detectadas son debidas al método o a la base de datos utilizada, a fin de resolver la duda planteada por Andrade y Pérez (2004)

Materiales y Métodos

Se utilizaron dos bases de datos disponibles para los análisis, las que fueron construidas a partir de muestreos en los principales sitios de desembarque de L. schmitti en el Lago de Maracaibo y en el Golfo de Venezuela (Figura 1). Ambas bases de datos son las únicas con suficiente representatividad temporal, de manera que no obedecen a ninguna otra situación particular. La primera consistió en una serie temporal de distribuciones de frecuencias de longitud (dfl) obtenidas mensualmente de la pesquería artesanal del camarón blanco en el Lago de Maracaibo, entre abril de 1991 y diciembre de 1993. Anteriormente estos datos fueron analizados por Andrade y Stotz (1999) mediante los algoritmos de la rutina ELEFAN I (Electronic LEngth Frequency ANalysis) contenida en el programa FAO-ICLARM Stock Assessment Tools (FiSAT; Gayanilo et al., 1995). En el presente estudio esta misma base de datos fue analizada con la metodología sugerida por Andrade y Pérez (2004) basada en la progresión de clases modales identificadas mediante una distribución multinomial y en un ajuste por mínimos cuadrados para la estimación de los parámetros. La segunda base de datos utilizada consistió de dfl provenientes de las capturas de la pesca artesanal en el Lago de Maracaibo entre abril de 2001 a junio de 2003 y de la pesca industrial en el Golfo de Venezuela, entre febrero y julio de 2003. Esta base fue utilizada por Andrade y Pérez (2004) aplicando el ajuste por mínimos cuadrados y la distribución multinomial para identificar modas en el tiempo. Para comparar los resultados esta misma base de datos fue analizada en este trabajo mediante ELEFAN I (Gayanilo et al., 1995).

Se construyeron dfl mensuales de L. schmitti, en clases de 1cm según lo recomendado por Andrade (1996). Los sexos fueron analizados separadamente dados los reportes sobre diferencias en el crecimiento entre machos y hembras (Andrade 1996, Andrade y Stotz 1999, Sangronis 2001, Andrade y Pérez 2004).

Para obtener los parámetros del modelo de crecimiento de von Bertalanffy (L_¥, K y t₀) se utilizó:

1) El método ELEFAN I (Gayanilo et al., 1995), el cual consta de dos etapas principales, a) la reestructuración de las frecuencias de tallas y b) el ajuste de la curva de crecimiento. El proceso de reestructuración utiliza promedios móviles para obtener los diferentes grupos de tallas o cohortes asignándoles un puntaje máximo y mínimo sin considerar el número de individuos en cada cohorte. El ajuste de la curva de crecimiento más convincente se basa en la inclusión del mayor número de puntos máximos o suma de máximos explicada (SME) y en la suma de todos los puntajes máximos ajustados en la curva o suma de máximos disponibles (SMD). De este modo, la razón SME/SMD se convierte en una forma de bondad de ajuste para medir cuán cerca está una curva del mejor ajuste posible (Sparre y Venema, 1995). Este método permite a partir de una sola muestra de frecuencia de longitud repetir dicha frecuencia por varios años, simular y ajustar el crecimiento bajo el supuesto de que todas las cohortes siguen la misma curva de crecimiento.

2) La minimización de cuadrados entre el incremento en longitud observado entre dos periodos de tiempo y el esperado por la ecuación de von Bertalanffy. Para identificar la posición de las modas entre tiempos sucesivos se empleó la distribución multinomial (Haddon, 2001), la cual permite separar las n distribuciones normales presentes en una distribución de frecuencias de longitud. La función de densidad probabilística para la distribución multinomial fue descrita por Hastings y Peacock (1975) como:

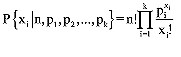(1)

donde x_i: número de veces que un evento de tipo i ocurre en n pruebas, n: tamaño de la muestra o el número de pruebas, y p_i: probabilidades separadas para cada uno de los k tipos de eventos posibles. La esperanza de ocurrencia de cada tipo de evento es E(x_i)=np_i, donde n: tamaño de la muestra, y p_i: probabilidad del evento tipo i.

La distribución normal se usó para describir la distribución de tamaños para cada cohorte (Zar, 1999):

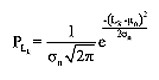(2)

donde L_k: longitud observada para cada una de las k categorías y n clases de edad, μ_n y s_n: media y desviación estándar de la distribución, respectivamente. La probabilidad estimada para la multinomial está dada por (Haddon, 2001):

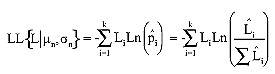(3)

donde μ_n y μ_n: medias y desviaciones de las n cohortes en la distribución de frecuencia, donde existen k clases de longitud, L_i y : frecuencias observadas y esperadas para la clase i, respectivamente, y : proporción esperada de la clase i de las distribuciones normales combinadas. La combinación óptima para las n distribuciones se obtuvo minimizando las diferencias entre las frecuencias observadas y esperadas mediante mínimos cuadrados.

Se asumió que la desviación estándar de la longitud media incrementa a medida que se detectan nuevos grupos de edad (Sullivan et al., 1990) y que el coeficiente de variación tiene un valor fijo de 3,5% (Andrade y Pérez, 2004). Se utilizó el índice de separación (IS) de clases de edad para la separación de las diferentes cohortes (Sparre y Venema, 1995):

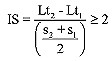(4)

donde Lt₁, Lt₂, s₁ y s₂: longitudes medias y desviaciones estándar al tiempo 1 y 2, respectivamente. Si IS<2, entonces no es factible separar los componentes normales de las frecuencias observadas (Sparre y Venema, 1995).

Una vez calculadas las medias y desviaciones para las dfl de todos los meses, se ajustó la ecuación de crecimiento de von Bertalanffy:

(5)

donde L_¥: longitud asintótica, K: parámetro de curvatura, t₀: edad teórica a la longitud cero, y t: edad.

Finalmente, los parámetros de la Ec. 5 fueron ajustados por mínimos cuadrados, utilizando como función objetivo (Gallucci et al., 1996)

(6)

donde DL: diferencia observada en longitud para una misma cohorte en un intervalo Dt de tiempo.

Para comparar las curvas de crecimiento resultantes se utilizó el análisis de suma de cuadrados de los residuos (Chen et al., 1992), el cual consiste en comparar la suma de cuadrados residuales (RSS) y los respectivos grados de libertad (DF) para cada curva de crecimiento contra los RSS y DF de una curva de ajuste general para ambos sexos agrupados. El estadígrafo F se calcula como (Chen et al., 1992),

(7)

donde RSS_p: RSS de la curva de crecimiento común para ambos sexos, RSS_s: RSS de cada curva de crecimiento por sexo, N: tamaño de la muestra agrupada, y J: número de curvas comparadas. La diferencia entre ambos sexos fue evaluada al comparar el valor de F calculado por la Ec. 7, y el valor crítico de F con 3(J-1) y (N-3J) DF para el numerador y denominador, respectivamente.

Resultados

Cálculos con la base de datos 1991-1993

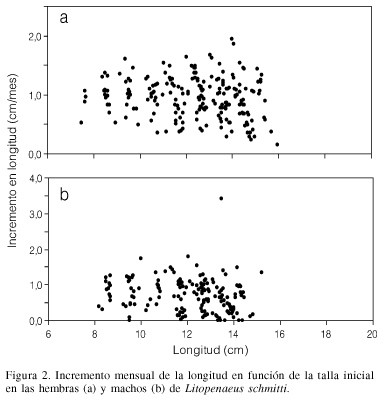
Esta base de datos contiene 115 muestras de los desembarques de camarones en el Lago de Maracaibo. Se identificaron 368 grupos modales de los cuales 211 correspondieron a hembras y 157 a machos, que cumplieron con la regla de decisión de estar entre meses contiguos. El intervalo de modas fue de 7,5 a 16,0cm para las hembras (Tabla I) y de 8,2 a 15,2cm de longitud total para los machos (Tabla II). La relación entre el tamaño y el incremento en longitud por mes mostró una relación inversa (p<0,05; Figura 2) para ambos sexos. Los parámetros de la ecuación de crecimiento obtenida por mínimos cuadrados para las hembras fueron

Lt=21,0(1-e^{-1,51(t+0,0322)}),

mientras que para machos fueron

Lt=17,3(1-e^{-1,81(t+0,0329)}).

La curva de crecimiento calculada para hembras y machos fue estadísticamente diferente (F-test= 95,04; p<0,001). El valor de f’ fue de 2,83 para hembras y 2,73 para machos (Tabla III).

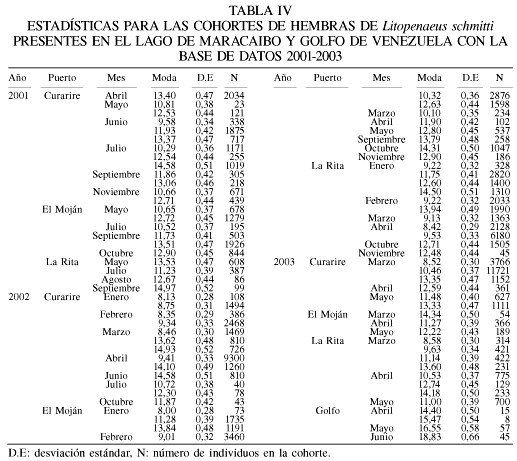
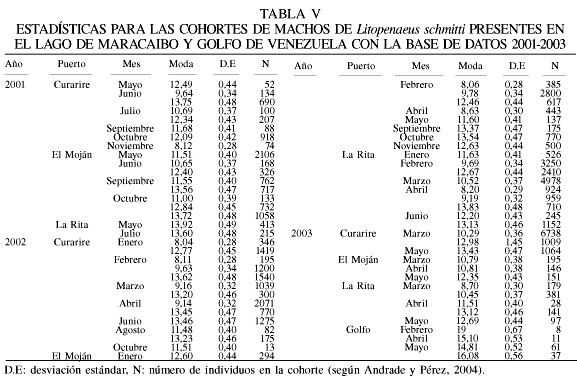
Cálculos con la base de datos 2001-2003

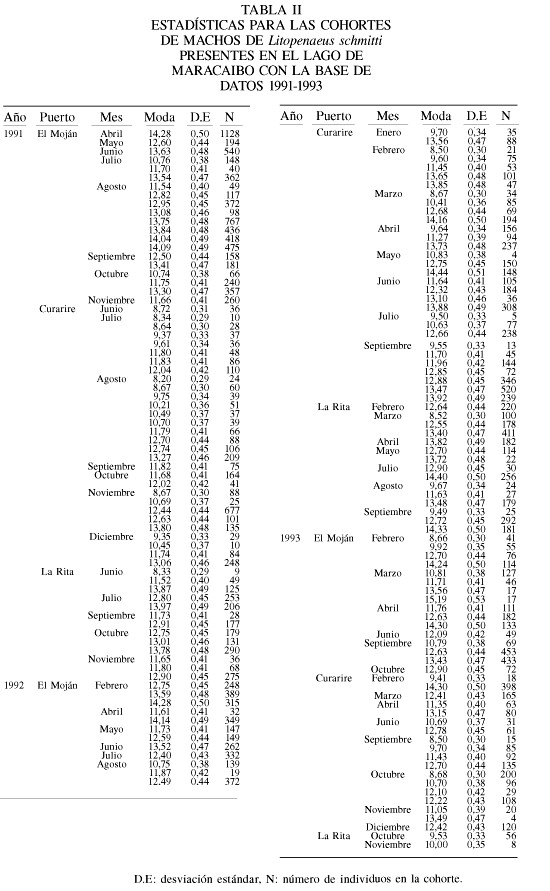
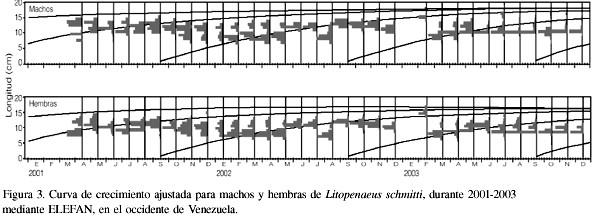
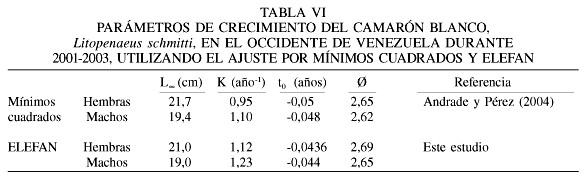
La base de datos para este período 2001-2003 incluye 75 muestras de los desembarques en el Lago de Maracaibo y el Golfo de Venezuela. El intervalo de modas obtenido fue de entre 8,0 y 18,8cm para hembras (Tabla IV), mientras que para los machos estuvo entre 8,0 y 19,0cm de longitud total (Tabla V). Los parámetros de la ecuación de crecimiento obtenidos en este estudio con el método ELEFAN (Figura 3), para las hembras fueron

Lt=21,0(1-e^{-1,12(t+0,0436)}),

mientras que para machos fueron

Lt=19,0(1-e^{-1,23(t+0,044)}).

El valor de f’ fue similar entre los sexos, obteniéndose 2,69 para hembras y 2,65 para machos (Tabla VI).

Discusión

Existen diferencias entre los resultados obtenidos en este trabajo y en el de Andrade y Stotz (1999) con los reportados por Sangronis (2001). En este último caso los valores de L_¥ parecen estar subestimados, dado que son valores por debajo de las modas detectadas en la información de captura comercial (Tablas II y III). Trabajos (Andrade y Pérez, 2004) reportan modas de hasta 19cm en el Golfo de Venezuela, por encima de los 14cm reportados por Sangronis (2001) como tamaños máximos para hembras y machos en el Lago de Maracaibo. Por este motivo, no se consideraron los resultados reportados por este último autor en las comparaciones posteriores.

Comparación dentro de los métodos de ajuste

Para el ajuste por mínimos cuadrados, el valor de K estimado para la base de datos 2001-2003 disminuyó tanto para hembras como para machos, en comparación con la base de datos 1991-1993. En este mismo sentido, el valor de L_¥ aumentó de 17,7 a 19,4cm en la base de datos más reciente. Este mismo efecto se observó para el método ELEFAN I, solo que el cambio fue menor en el valor de K. La razón más evidente para la similitud de estos cambios es una mejor representatividad de tamaños presente en la base de datos 2001-2003. En efecto, al comparar las modas presentes en ambas bases de datos, la base de datos 1991-1993 presenta las menores modas de tamaño, principalmente por el hecho de que los datos provienen del Lago de Maracaibo, donde viven las tallas menores antes de migrar al Golfo de Venezuela (Ewald, 1964, 1965; Godoy, 1971; Cadima et al., 1972; García y Le Reste, 1987). En este sentido, más que por el método en sí, los resultados serían afectados por los tamaños presentes en las muestras, lo que plantea una dificultad al momento de trabajar con datos de captura de stocks muy explotados, donde los tamaños mayores han desaparecido por efecto de la pesca.

Comparación entre los métodos de ajuste

Comparando entre métodos de ajuste se repite el mismo patrón anterior: similitud entre los resultados para hembras y diferencias en el coeficiente K para machos. Es decir, hay diferencias en el patrón de crecimiento al comparar los resultados entre las dos bases de datos utilizadas. Sin embargo, las estimaciones entre los enfoques empleados no son diferentes en términos del patrón de crecimiento usando la misma base de datos. En efecto, el patrón de crecimiento es el mismo al realizar los ajustes mediante ELEFAN I y por mínimos cuadrados tanto en la base 1991-1993 como en la de 2001-2003.

Los resultados anteriores indican que más importante que el método usado (ELEFAN I o ajuste por mínimos cuadrados) es la estructura de datos (modas) representadas en las muestras. Por lo mismo, entre métodos los resultados son comparables. Dado lo anterior, entre bases de datos el resultado más confiable es aquel que contenga modas identificables en un intervalo mayor de tallas. La especie Litopanaeus schmitti presenta su fase juvenil en el lago de Maracaibo y la adulta en el Golfo de Venezuela (Andrade y Pérez, 2004; Andrade, 2005), de modo tal que datos provenientes de ambos hábitats generarán un mayor contraste en la información, con modas distribuidas entre todos los tamaños posibles. En este sentido, los resultados aportados por Andrade y Pérez (2004) y en este trabajo pueden ser considerados como representativos del crecimiento de L. schmitti en el Lago de Maracaibo y en el Golfo de Venezuela. Lo anterior es principalmente cierto para el caso de los machos, donde anteriormente (Andrade y Stotz, 1999; Sangronis, 2001) se dispuso de datos provenientes solo del Lago de Maracaibo y no del Golfo de Venezuela, donde ocurren los tamaños mayores. Así, el valor probable del parámetro f’ estaría en el intervalo de 2,62-2,69; lo cual puede ser de utilidad para futuros estudios de crecimiento para el género y la especie. Del mismo modo es imperativo que trabajos futuros generen bases de datos que contemplen el intervalo total de distribución de la especie entre sus distintos hábitats con el fin de dar mayor solidez a nuevas estimaciones.

AGRADECIMIENTOS

La primera autora agradece al Instituto Nacional de Investigaciones Agrícolas (INIA), Venezuela, por el financiamiento otorgado (proyecto Nº 612-21001). Este trabajo es parte de su Tesis Doctoral en el CINVESTAV–IPN, Unidad Mérida, México.

REFERENCIAS

1. Andrade de Pasquier G (1996) Análisis de la pesquería del camarón blanco, Penaeus schmitti Burkenroad 1936, en el Lago de Maracaibo, Venezuela. Tesis. Universidad Católica del Norte, Sede Coquimbo. Chile. 105 pp.        [ Links ]

2. Andrade de Pasquier G (2005) Análisis bioeconómico de la pesquería secuencial del camarón blanco, Litopenaeus schmitti, y su aplicación para el manejo del recurso en el Occidente de Venezuela. Tesis. CINVESTAV, Unidad Mérida. Yucatán, México. 165 pp.        [ Links ]

3. Andrade de Pasquier G, Stotz W (1999) Crecimiento y mortalidad del camarón blanco, Penaeus schmitti, en el Lago de Maracaibo, Venezuela. Zootecnia Tropical 17: 63-89.        [ Links ]

4. Andrade de Pasquier G, Pérez EP (2004) Age and growth of the white shrimp Litopenaeus schmitti in Western Venezuela. Interciencia 29: 212-218.        [ Links ]

5. Cadima E, Ewald J, Montesinos H, Díaz W, Novoa D, Racca E, Godoy G (1972) La pesquería de camarones en el occidente de Venezuela. Informe Técnico. Nº 52. MAC-PNUD-FAO. Caracas, Venezuela. 46 pp.        [ Links ]

6. Chen Y, Jackson DA, Harvey HH (1992) A comparison of von Bertalanffy and polynomial functions in modelling fish growth data. Can. J. Fisheries Aquat. Sci. 49: 1228-1235.        [ Links ]

7. Ewald JJ (1964) La biología y pesquería del camarón en la zona Occidental. FONAIAP. Caracas, Venezuela. 29 pp.        [ Links ]

8. Ewald JJ (1965) Investigaciones sobre la biología del camarón comercial en el Occidente de Venezuela. FONAIAP. Caracas, Venezuela. 147 pp.        [ Links ]

9. Gallucci V, Amjoun B, Hedgepeth J, Lai HL (1996) Size-based methods of stock assessment of small-scale fisheries. En Gallucci VF, Saila SB, Gustafson DJ, Rothschild BJ (Eds.) Stock Assessment. Quantitative Methods and Applications for Small-Scale Fisheries. Lewis. Boca Ratón, FL, EEUU. 527 pp.        [ Links ]

10. García S, Le Reste L (1987) Ciclos vitales, dinámica, explotación y ordenación de las poblaciones de camarones peneidos costeros. Documento Técnico de Pesca. Nº 203. FAO. Roma, Italia. 180 pp.        [ Links ]

11. Gayanilo FC Jr, Sparre P, Pauly D (1995) The FAO-ICLARM Stock Assessment Tools (FiSAT) User’s Guide. FAO Computerized Information Series (Fisheries) Nº 8. Roma, Italia. 126 pp.        [ Links ]

12. Godoy G (1971) Maduración y desove del camarón blanco Penaeus schmitti Burkenroad, 1936, en el Occidente de Venezuela. Tesis. Universidad Central de Venezuela. 52 pp.        [ Links ]

13. Gulland JA, Rosenberg AA (1992) Examen de los métodos que se basan en la talla para evaluar las poblaciones de peces. Documento Técnico de Pesca. Nº 323. FAO. Roma, Italia. 112 pp.        [ Links ]

14. Haddon M (2001) Modelling and quantitavive methods in fisheries. CRC Press. Boca Ratón, FL, EEUU. 406 pp.        [ Links ]

15. Hastings NAJ, Peacock JB (1975) Statistical Distributions. En Haddon M (2001) Modelling and quantitavive methods in fisheries. CRC Press. Boca Ratón, FL, EEUU. 406 p.        [ Links ]

16. Novoa D, Mendoza J, Marcano L, Cárdenas JJ (1998) Atlas Pesquero Marítimo de Venezuela. MAC-SARPA-CONGEPESCA. Caracas, Venezuela. 71 pp.        [ Links ]

17. Sangronis C (2001) Estructura etaria del camarón blanco Litopenaeus schmitti presente en la Ciénaga Los Olivitos, Zulia-Venezuela. Tesis. Universidad del Zulia. Venezuela. 84 pp.        [ Links ]

18. Sparre P, Venema SC (1995) Introducción a la evaluación de recursos pesqueros tropicales. Documento Técnico de Pesca Nº 306/1. FAO. Roma, Italia. 420 pp.        [ Links ]

19. Sullivan PJ, Lai HL, Gallucci VF (1990) A catch-at-length analysis that incorporates a stochastic model of growth. Can. J. Fisheries Aquat. Sci. 47: 184-198.        [ Links ]

20. Zar JH (1999) Biostatistical analysis. 2^nd ed. Prentice-Hall. Englewood Cliffs, NJ, EEUU. 718 pp.        [ Links ]