MÉTODO PARA OPTIMIZAR LAS MEDICIONES TOPOGRÁFICAS CON APARATOS GPS

Rafael Ortiz-Marín, María Gloria del Río-Cidoncha, Juan Martínez-Palacios y Carlos Cobos-Gutiérrez

Rafael Ortiz-Marín. Ingeniero Industrial, Universidad de Valladolid, España. M.B.A., Escuela de Administración de Le Mans, Francia. Doctor, Universidad de Sevilla (US), España. Profesor, Escuela Superior de Ingenieros (ESI), US, España. e-mail: rafortiz@esi.us.es

María Gloria del Río-Cidoncha. Arquitecta, Doctora Ingeniero Industrial y Master en E-Learning, US, España. Dirección: Departamento de Ingeniería Gráfica, ESI, Av. De los Descubrimientos s/n, Isla de la Cartuja, 41092 Sevilla, España. e-mail: cidoncha@esi.us.es

Juan Martínez-Palacios. Ingeniero Industrial y DEA en Gestión de la Producción, ESI-US, España. Profesor, ESI-US, España. e-mail: juanmp@esi.us.es

Carlos Cobos-Gutiérrez. Ingeniero de Caminos Canales y Puertos, Universidad Politécnica de Madrid, España. Doctor, Universidad Politécnica de Cataluña, España. Profesor ESI, US, España. e-mail: ccobos@esi.us.es

RESUMEN

Hasta hoy, en el levantamiento topográfico mediante satélites artificiales, para conocer las coordenadas de un lugar, o bien se medía reiteradamente en él un determinado número de veces y se hacía la media para obtener el valor más probable, o con una sola medición se suponía que ésa era la coordenada del sitio. Éstas eran las técnicas usadas, independientemente del número de épocas o del tiempo de colocación en el punto. En el primer caso se tenía una nube de puntos, de los que no se sabía cuales eran las mediciones qué más se aproximaban a las coordenadas del sitio donde estaba posicionada la antena GPS. Ahora, aplicando un método basado en técnicas Geoestadísticas, concretamente el cokrigeado, se puede extraer de esa nube de puntos, un subconjunto, cuya media mejora la exactitud de la media que se obtenía con el conjunto de todos ellos. La aplicación de esta metodología es la que se desarrolla en este artículo.

A METHOD TO OPTIMIZE TOPOGRAPHIC MEASUREMENTS USING GPS DEVICES

SUMMARY

Until today, to know the coordinates of a place one could measure several times and after that calculate the average in order to obtain the more probable value. Another option was doing only one measure and suppose that was the coordinate of that place. These were the techniques always used. First case, had a cloud of points but it didn’t know which measurements were nearest to the place were the GPS antenna was situated. Now applying a method based on geostatistic techniques, concretely the cokriging one, it can extract a subgroup of that cloud of points, whose average improves the exactitude of the average that it can obtain with the group of all of them. This methodology is developed in this paper.

UM MÉTODO PARA OPTIMIZE MEDIDAS TOPOGRAFICAS USANDO DISPOSITIVOS DO GPS

RESUMO

Até hoje, no exame topográfico por meio dos satélites artificiais, para saber as coordenadas um lugar, ou era repetidamente moderado nele um determinado número de vezes e média foi feito para obter mais o valor provável, ou com uma única medida supos aquela que um era a coordenada do local. Estas eram as técnicas usadas, independentemente do número das épocas ou da época de posicionar no ponto. No primeiro caso uma nuvem dos pontos foi tida, de que não se soube porque eram as medidas o que veio perto de mais às coordenadas do local onde a antena GPS foi posicionada. Agora, aplicando um método baseado em técnicas de Geoestadísticas, concreta o cokrigeado um, pode ser extraído dessa nuvem dos pontos, um subgrupo, cuja melhoria média o exactitude da média que foi obtida com o jogo de todo. A aplicação desta metodologia é essa que é desenvolvida neste artigo.

PALABRAS CLAVE / Autocorrelación Espacial / Cokrigeado / GPS / Semivariograma / Variables Regionalizadas /

Recibido: 12/07/2006. Modificado: 26/07/2007. Aceptado: 30/07/2007.

Introducción

Se pretende mejorar los resultados obtenidos a partir de series de observaciones de distinta duración de un mismo punto. Dichas observaciones fueron realizadas con equipos de código y se calcularon, en postproceso, empleando una estación de referencia fija y próxima. La idea esencial es la obtención, a partir de todas las observaciones realizadas de un punto, de aquel subconjunto de las mismas cuya media se aproxime más a las coordenadas que se suponen exactas.

La distribución de las mediciones alrededor del punto en cuestión sigue una distribución de Rayleigh, que es una distribución normal bidimensional con desviaciones típicas iguales. Esto permite hablar de la probabilidad de que en una medición tal o cual punto se encuentre fuera de un circulo de un diámetro determinado, pero no se conoce qué puntos aceptar y cuales rechazar.

Desde punto de vista teórico, el empleo de la geoestadística se fundamenta en el hecho de ser una herramienta útil para el estudio de las variables numéricas distribuidas en el espacio (Chauvet, 1994). Se puede entonces sugerir la idea de interpretar esto en términos de función aleatoria. Así, a cada punto del espacio se le asocia una variable aleatoria (VA) Z(), para dos puntos diferentes e , se tendrán entonces dos VAs Z() y Z() diferentes pero no independientes, y es precisamente su grado de correlación el encargado de reflejar la continuidad de cualquier fenómeno en estudio, de modo que el éxito de esta técnica es la determinación de la función de correlación espacial de los datos (Zhang et al., 1995).

En base a ello se ha aplicado la teoría de la variable regionalizada, que permite seleccionar los puntos que más se aproximan al valor real de las coordenadas del vértice en cuestión, rechazando los demás puntos. Las coordenadas planimétricas (X,Y) se analizan independientemente, dado que los mejores valores obtenidos no tienen porqué corresponder a la misma serie, ni mucho menos a una misma observación.

El método consiste en asignar a cada una de las mediciones obtenidas y a cada par de coordenadas X e Y, las variables regionalizadas para las coordenadas X, las coordenadas Y y las variables regionalizadas cruzadas XY. Estas variables permiten definir el semivariograma teórico, y a partir de éste, el semivariograma modelo. Por medio de la interpolación por krigeado y cokrigeado, y utilizando el semivariograma modelo, se calculan de nuevo estas variables regionalizadas en los puntos de las mediciones. De todas las mediciones se seleccionan aquellas que tienen la variable regionalizada con un menor valor. Las mediciones así seleccionadas coinciden con las coordenadas que más se aproximan a las coordenadas reales del vértice.

Conceptos Teóricos.

Elementos geoestadísticos utilizados

Este epígrafe presenta los principales conceptos teóricos necesarios para el desarrollo de este trabajo. Se inicia con una definición de la variable regionalizada, luego se define el variograma y se calcula el estimador del variograma y, por último, se ofrece una rápida visión del cálculo de los pesos para la interpolación mediante el krigeado y el cokrigeado.

Variable regionalizada

Según (Blais y Carlier, 1968), citados por Olea (1975), una variable regionalizada es una función numérica con distribución espacial que varía de un punto a otro con continuidad aparente, pero cuyas variaciones no pueden ser representadas por una función matemática simple. La teoría de la variable regionalizada presupone que una variación de una variable puede ser expresada por la suma de tres componentes (Burrough, 1986), a saber: i) una componente estructural, asociada a un valor medio constante o a una tendencia constante; ii) una componente aleatoria espacialmente correlacionada; y iii) un ruido aleatorio o error residual.

Sí representa una posición en una, dos o tres dimensiones, entonces el valor de la variable Z en , está dada (Burrough, 1986) por

   (1)

donde m(): función determinística que describe la componente estructural de Z en , e'(): término estocástico que varía localmente y depende espacialmente de m(), y e'': ruido aleatorio no correlacionado, con distribución normal de media cero y varianza s².

El variograma

El variograma es una herramienta básica de soporte de las técnicas de krigeado, que permite representar cuantitativamente la variación de un fenómeno regionalizado en el espacio (Huijbregts, 1975).

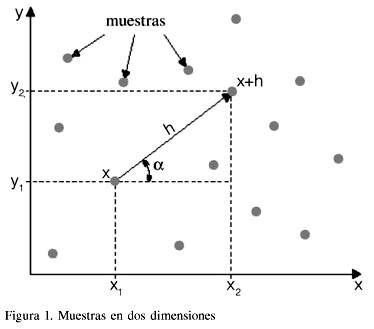
Sean dos variables regionalizadas, X e Y, donde X= Z() y Y= Z(+). En el caso objeto de este trabajo se hallan referidas a un mismo atributo medido en dos posiciones diferentes, conforme se ilustra en la Figura 1, donde define una posición, de componentes (x_i,y_i), y un vector distancia (módulo y dirección) que separa los dos puntos.

El nivel de dependencia entre esas dos variables regionalizadas X e Y, este representado por el variograma, 2g(), y éste está definido como la esperanza matemática del cuadrado de la diferencia entre los valores de puntos en el espacio, separados por un vector distancia :

2)

Generalizando a una muestra z() i=1,2,...,n, el variograma se estima (Journel y Huijbregts, 1978) según

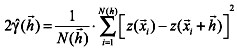  (3)

donde 2(): variograma estimado; N(): número de pares de valores medidos, z(_i) y z(_i+), separados por un vector distancia h; y z(_i) y z(_i+): valores de la i-ésima observación de la variable regionalizada, recogidos en los en los puntos _i y _i+ (i=1,...n), separados por un vector .

Muchos autores definen el variograma de forma distinta a la Ec. 3, considerando lo que comúnmente se describe como semivariograma:

(4)

Análogamente la función semivariograma se puede estimar por

  (5)

donde N(), z(_i) y z(_i+) tienen el mismo significado que en fórmulas anteriores.

El semivariograma y la covarianza están relacionados (Journel y Huijbregts, 1978) por la ecuación

(6)

El krigeado

Conocido el semivariograma de la variable y existiendo dependencia espacial entre las muestras, se pueden interpolar valores en cualquier posición del campo de estudio, sin sesgo y con varianza mínima. El método de interpolación se llama krigeado, nombre que fue dado por (Matheron, 1963) en homenaje al matemático sudafricano Krige. El krigeado consiste en efectuar una ponderación, es decir, atribuir un peso a cada valor observado. Los pesos son calculados de manera que minimice la varianza de estimación resultante, teniendo en cuenta las características geométricas del problema (Matheron, 1970). Al minimizar la varianza de estimación se garantiza el uso óptimo de la información disponible (Zhang et al., 1995).

Estimador del krigeado. Suponiendo que se quieran estimar valores z*, para cualquier posición x₀, donde no se tiene valores medidos, y que la estimación debe ser una combinación lineal de los valores medidos. Es decir:

  (7)

donde N: número de valores medidos, z(_i), que intervienen en la estimación, y l_i: pesos asociados a cada valor medido z(_i).

Sistema de ecuaciones del krigeado. Para que un estimador sea óptimo, no puede ser sesgado y debe tener varianza mínima (David, 1977). En términos matemáticos,

  (8)

y

  (9)

Aplicando el método de los multiplicadores de Lagrange (David, 1977), el sistema de krigeado quedará según las Ecs. 10 u 11 dependiendo que sea en función de la covarianza o el semivariograma.

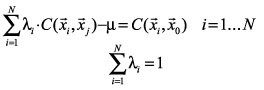  (10)

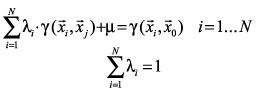  (11)

El cokrigeado

El método estadístico de interpolación expuesto en el apartado anterior, el krigeado, es un caso particular del cokrigeado que se analizará enseguida. Una vez que exista dependencia espacial para cada una de las variables Z₁ y Z₂, y que también exista dependencia espacial entre Z₁ y Z₂, entonces es posible utilizar el cokrigeado para estimar valores. Esta estimación puede ser más precisa que el krigeado de una variable simple (Vauclin et al., 1983), cuando el semivariograma cruzado muestra dependencia entre las dos variables.

Estimador del cokrigeado. Suponiendo que se quisiera estimar valores de z^*₂, para cualquier localización ₀, y que la estimación deba ser una combinación lineal de ambos z₁ y z₂, es decir

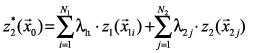  (12)

donde N1 y N2: los números de puntos vecinos a considerar de Z₁ y Z₂, respectivamente; y l_1i y l_2j: los pesos asociados a cada valor de Z₁ y Z₂. Tomando z₁(_1i) y z₂(_2i) como solo una realización de las funciones aleatorias Z₁(_1i) y Z₂(_2i), respectivamente, y asumiendo la estacionariedad de orden 2, el estimador puede ser rescrito

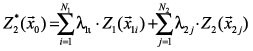  (13)

La Ec. 13 expresa que la estimación de la variable Z₂ deberá ser una combinación lineal de ambas Z₁ y Z₂, con los pesos l₁ y l₂ distribuidos de acuerdo con la dependencia espacial de cada una de las variables entre sí y la correlación cruzada entre ellas.

Sistema de ecuaciones del cokrigeado. Para que el estimador sea óptimo, no puede ser sesgado y tiene que tener varianza mínima. En otras palabras, para que el estimador sea el mejor posible es necesario que no superestime ni subestime valores y que la confianza en las estimaciones sea máxima. Matemáticamente hablando,

  (14)

y

  (15)

El sistema de ecuaciones para el cokrigeado queda:

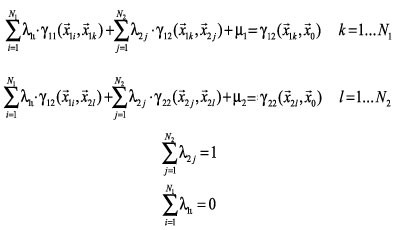  (16)

Posicionamiento Espacial. Elección de las variables regionalizadas

Se presentará una fórmula para calcular el GDOP y sus componentes, como una función de la geometría de cuatro satélites GPS. Para la navegación de cuatro satélites GPS, las ecuaciones de navegación linealizadas son dadas en Jorgensen (1980) como

  (17)

donde : vector de dimensión cuatro de las correcciones de la posición y el tiempo, : vector de los residuales de las pseudodistancias, y H₄: matriz de los cosenos directores asociados al vector de cada satélite.

La varianza de los errores de la posición y el tiempo son funciones de los elementos de la diagonal de [H₄^T · H₄]^-1. Esto conduce al concepto de GDOP (dilución geométrica de la precisión) que se define (Sturza, 1983) como

  (18)

De manera que

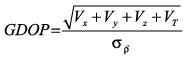  (19)

GDOP se puede dividir en las diluciones de precisión en posición y tiempo, PDOP y TDOP respectivamente:

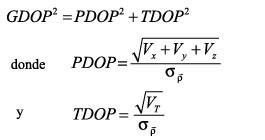 (20)

A su vez, el PDOP se puede dividir en HDOP y VDOP, diluciones de precisión en planimetría y altimetría respectivamente, de manera que

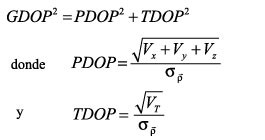(21)

El HDOP se puede resolver más a fondo en sus componentes X e Y. Si el eje de las X se orienta en una dirección de Oeste a Este, un "al este" DOP (EDOP) y un "al norte" DOP (NDOP) puede definirse (USAF, 1996) como

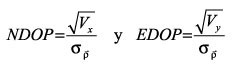   (22)

El equipo GPS después del post-procesamiento de los datos, devuelve además del error cuadrático medio (emq) para cada medición, la matriz Q que es la inversa de la matriz normal de la ecuación del ajuste por mínimos cuadrados (Leica GeoSystem, 1994) y está definida como:

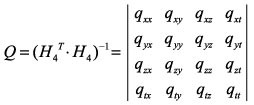  (23)

El error cuadrático medio en las soluciones posición, tiempo (PT) se relaciona (USACE, 2003) con la geometría según la ecuación

  (24)

donde s_UERE: error en la medida de la pseudodistancia, equivalente a s_r; GDOP: factor de geometría que se calcula como

  (25)

Por el mismo razonamiento se pueden definir PDOP, TDOP, HDOP y VDOP, y por supuesto el NDOP y el EDOP (USAF, 1996) como

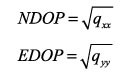    (26)

donde q_xx y q_yy pertenecen a la traza de la matriz Q definida en la Ec 23:

Esta descomposición permite estudiar separadamente la mejor "X" y la mejor "Y", que no tienen por qué coincidir en el mismo punto.

La varianza de la posición se puede determinar a partir de la matriz C=emq²·Q de cada una de las líneas base de las mediciones, identificando s_UERE con el emq.

s²_x=emq²·q_xx

Para cada base línea de las n_mediciones

s²_y=emq²·q_yy

Para cada base línea de las n_mediciones (27)

Para cada serie de observaciones se pueden especificar dos variables regionalizadas Z₁() y Z₂() donde indica el par (X_i,Y_i) de la medición en coordenadas UTM, definidas como

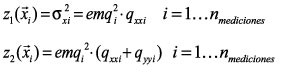  (28)

para obtener, la o las mejores coordenadas X de la serie y

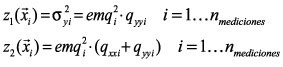  (29)

para obtener la o las mejores coordenadas Y de la serie.

Evidentemente, el número de mediciones coincide con el número de líneas base. Como se observa en las Ecs. 28 y 29, para definir las variables regionalizadas Z₁() y Z₂() se han usado las definiciones de NDOP, EDOP y HDOP.

Metodología

De campo

Una vez en el campo, la observación se efectuó introduciendo en la unidad de control una serie de parámetros, a saber: i) método de posicionamiento, en este caso estático diferencial (la base situada en la Escuela Superior de Ingenieros de Sevilla); ii) máscara de elevación, de 15º; y iii) establecimiento del intervalo de grabación en segundos (épocas). Cada época es un tiempo de grabación de datos; a menor valor de época, mayor cantidad de datos almacenados en la tarjeta, y por ende, se deberá elegir un menor tiempo de puesta de observación para no agotar su capacidad.

En cada uno de los vértices se realizaron series de mediciones de 5, 8, 15, 20, 25, 30, 35, 45, 60, 120 épocas. Cada serie está compuesta al menos por 30 observaciones del vértice en cuestión. En algunos casos ciertos archivos se han repetido, dando lugar a un mayor número de observaciones.

En resumen, se puede decir que el archivo de 8 épocas del vértice Atalaya de los Barros, por ejemplo, comprende 33 observaciones de ese vértice de 8 épocas de duración cada una (Tabla I). Esta metodología de trabajo viene impuesta por el objetivo de analizar la precisión de la medida tanto aisladamente como en función del tiempo de observación y por tanto del número de épocas.

De laboratorio.

Aplicación de la geoestadística

Al igual que en la observación para el cálculo de las líneas bases, aquí hay parámetros correctores. Entre otros se tiene: i) corrección ionosférica y troposférica; ii) tipo de efemérides usadas; iii) tipo de datos usados (solo código); iv) para cada observación se han obtenido específicamente las coordenadas GPS en el Sistema WGS 84 formadas por la terna latitud, longitud y altura elipsoidal, las coordenadas Cartesianas (X,Y,Z) y las matrices de varianza-covarianza.

Para cada una de las series de mediciones realizadas en los distintos vértices y a distintas épocas, se define el valor de las variables regionalizadas en cada uno de los puntos de estas mediciones utilizando las Ecs. 28 y 29. Para cada serie de mediciones se deben obtener: i) la "mejor X" de las mediciones, es decir, la coordenada que más se aproxima al vértice; y ii) la "mejor Y" de las mediciones, ídem de lo mismo. En ambos casos esto se conseguirá mediante el cokrigeado, definiendo para obtener la "mejor X" unas variables regionalizadas Z₁ y Z₂ según las Ecs. 28 y para obtener la "mejor Y" otras variables regionalizadas Z₁ y Z₂ según las Ecs. 29. Nótese que la definición de la variable Z₂ es idéntica en ambos casos.

Una vez definidas las variables regionalizadas en cada uno de los puntos del plano, para hallar la "mejor X" o la "mejor Y" se procede a calcular los semivariogramas experimentales g₁₁ que corresponde a la variable Z₁, g₂₂ que corresponde a la variable Z₂, y g₁₂ (semivariograma cruzado) que corresponde a las variables Z₁ y Z₂.

Conseguido el semivariograma omnidireccional deben encontrarse los posibles patrones de anisotropía calculando los variogramas direccionales, para lo cual es de gran ayuda el conocimiento del fenómeno bajo estudio.

Establecidas las direcciones de máxima y mínima continuidad, se debe seleccionar la tolerancia direccional. Idealmente, debería ser lo menor posible. Lo que ocurre es que con tolerancias direccionales reducidas, el número de datos abarcados es muy pequeño, dando lugar a valores erráticos en los variogramas. En la práctica, se prueban varias tolerancias y se escoge la menor que genera los mejores resultados.

Conviene indicar que los semivariogramas son muy sensibles a los datos anómalos (outliers) con valores muy grandes o muy pequeños. De forma práctica, si unos pocos puntos erráticos hacen que la forma de estas funciones se vea alterada, es necesario examinarlos cuidadosamente y comprobar que no son fruto de algún tipo de error.

A partir de los semivariogramas experimentales se debe hallar los semivariogramas modelos. Una vez que se han definido los puntos del variograma experimental, será necesario ajustar un modelo a dichos puntos, denominado variograma teórico. Esto se debe a la imposibilidad de trabajar con un variograma como el experimental, carente de una función matemática precisa (o al menos difícil de caracterizar), y a la necesidad de extender los valores del variograma más allá de la distancia máxima definida. También, por el contrario, será necesaria la extensión del variograma a las proximidades del origen, o sea, para distancias próximas a 0.

Cuando se realiza el modelado del semivariograma teórico, se proponen diversos modelos que se ajusten a los datos experimentales. La elección de un modelo concreto suele basarse en apreciaciones subjetivas bien documentadas y en la experiencia previa. Sin embargo, puede justificarse la elección de un modelo en función de una serie de criterios estadísticos, como con el método de mínimos cuadrados ponderado (Cressie, 1985) o con el método de Jacknife o de validación cruzada (Isaaks y Srivastava, 1989). Cuando el modelo ha sido identificado, se dice que el variograma ha sido calibrado o validado.

Con los semivariogramas modelos se aplicará el cokrigeado, que es solo una modificación del krigeado ordinario. La variable principal se estima en un punto mediante una combinación lineal de los datos obtenidos en distintos lugares para las variables primaria y secundaria (una o varias), en este caso solo una. En el cokrigeado es menester la especificación de las relaciones de dependencia espacial mediante los semivariograma de las diferentes variables y los semivariogramas cruzados.

Aplicación al vértice Atalaya de los Barros (8 épocas de 1seg)

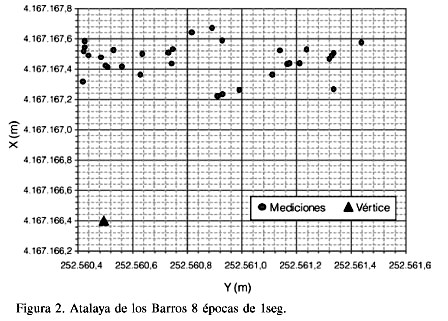
Las coordenadas UTM ED50 del vértice Atalaya de los Barros son (X_vértice, Y_vértice) = (252.560,495; 4.167.166,400) en metros. La representación en el plano XY de todos los valores observados y del vértice se muestra en la Figura 2

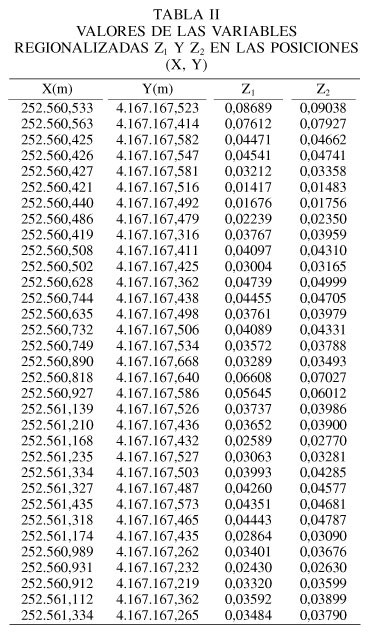
Para calcular la "mejor X", se halla para cada una de las líneas base los valores de las variables regionalizadas Z₁ y Z₂ según las Ecs. 28. Estos valores se encuentran en la Tabla II.

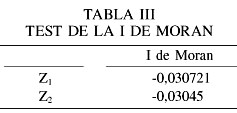
Para ver si las variables Z₁ y Z₂ que anteriormente se han definido tienen autocorrelación espacial, se les aplicará el test de la I de Moran, con resultados positivos ya que los valores son superiores a la E[1] (Cliff y Ord, 1981). Los resultados para las dos variables se muestran en la Tabla III.

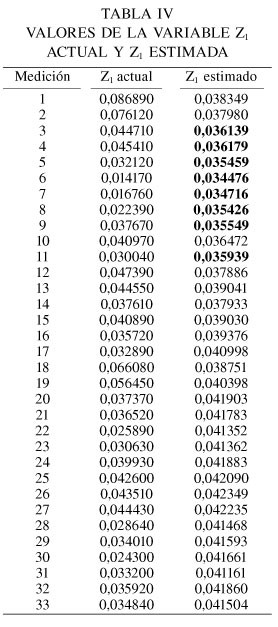
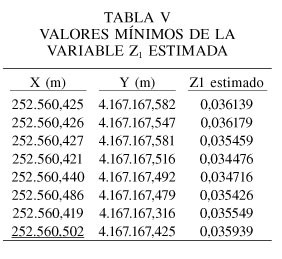
Siguiendo los pasos detallados en el epígrafe anterior se llega a estimar la variable primaria Z₁ en los puntos muestrales (Tabla IV); a continuación las estimaciones de mayor a menor se agrupan en clases (se recomienda crear de 10 a 15 clases) y por último se eligen los valores correspondientes a la última clase. En el caso presente, la última clase es 0,03618 y sus valores muestrales se exponen en la Tabla V. Por definición de la variable, estos valores representan el DOP. Cuanto más pequeño sea el DOP más exacto es el ajuste de la línea base y, por lo tanto, debe ser la medición de la coordenada del punto. Los puntos muestrales con la variable estimada Z₁ más pequeña, serán los que tengan la coordenada X más cercana al vértice.

Análisis de los resultados

Para comprobar que el método es válido se hicieron mediciones en distintos vértices con distintas épocas, y a unos 30 y 60km (Gibarrayo) del vértice de referencia, advirtiéndose que los resultados obtenidos tenían una mejora en la exactitud de las coordenadas UTM X e Y. Solo se mostrarán los datos para hallar la "mejor X" en el vértice de Atalaya de los Barros. Atendiendo a lo dicho en el último párrafo del epígrafe anterior, en la Tabla V que resulta de todo ello el valor de la X subrayado se corresponde con el valor más próximo a la coordenada "X" del vértice Atalaya de los Barros. Este valor y el resto de los valores, se han obtenido atendiendo al criterio de valor mínimo de la variable Z₁.

En la Tabla VI se compara la media de las X de la Tabla V, la X del vértice Atalaya y la media de las X de todas las observaciones. Como se aprecia, el cálculo de la "mejor X" usando el método de la variable regionalizada, es superior a hacer la media de las X de todas las observaciones.

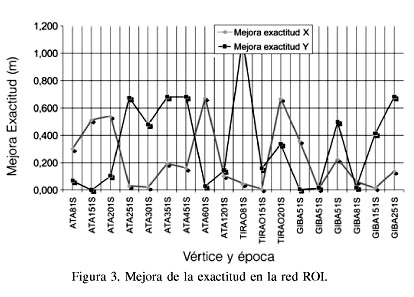
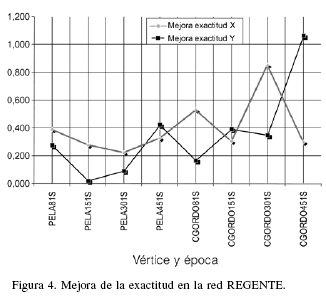
En una recopilación de todos los resultados obtenidos, se compararon las mediciones realizadas en los distintos vértices. Se obtuvo tanto la mejora de la exactitud en la coordenada X como en la coordenada Y, como la diferencia entre la exactitud de la media de todas las observaciones y la exactitud de la media de las observaciones seleccionadas según el criterio de mínimo valor de la VR. Ambos valores se representan en las Figuras 3 y 4, para vértices de la red ROI (Red de Orden Inferior) y la red REGENTE (Red Geodésica Nacional por Técnicas Espaciales).

Conclusiones

Las técnicas geoestadísticas, y en particular el cokrigeado, son de aplicación a las mediciones GPS. Se han realizado 1234 tomas de datos, de las que en 1099 casos (89,06%) se han obtenido resultados favorables en el test de la I de Moran, lo que indica que existe correlación espacial (ver Tabla I). Las 135 tomas (10,94%) en las que el test de Moran no ha proporcionado un resultado favorable se han localizado en el vértice de Gibarrayo, en cuya proximidad existen antenas de telefonía que han podido influir en la medición por el efecto multicamino y la mayor distancia de este vértice a la base (la distancia de este vértice al máster es de 60km, mientras que la distancia media del resto de vértices analizados es de 30km).

La aplicación de la geoestadística mejora la exactitud de los resultados en las coordenadas planimétricas (X,Y), con relación a las medias de los valores calculados.

Las mejoras obtenidas en la exactitud de la determinación de las coordenadas UTM X e Y no dependen de la dirección considerada. En algunos casos la mayor mejora corresponde a una dirección y en otros a la contraria.

No se aprecian influencias del número de épocas en las mejoras que se obtienen aplicando técnicas geoestadísticas. Por ello, se propone la realización de series de mediciones cortas, entre 8 y 20 épocas, para no alargar excesivamente el tiempo de estacionamiento en un punto.

A la vista de los resultados obtenidos se aconseja un número de mediciones por serie, entre 33 y 50 veces para cada punto, mejorándose así el semivariograma experimental a costa de un mayor tiempo de computación.

Desarrollo Futuro

Partiendo de los modelos teóricos elementales de semivariogramas, se propone desarrollar metodologías de cálculo de los pesos de éstos con el fin de conseguir un nuevo modelo teórico lineal que se ajuste lo mejor posible al semivariograma experimental. Igualmente, desarrollar nuevas técnicas para obtener el semivariograma teórico, como por ejemplo técnicas de bootstrapping.

Para elegir de todos los puntos vecinos posibles los que proporcionan una varianza mínima en el cokrigeado deben desarrollarse técnicas de filtrado.

La influencia de la distancia de los vértices al máster en la aplicación de esta metodología a las mediciones con GPS, así como la incidencia de otro tipo de señales (telefonía, radio, etc.) sobre la exactitud conseguida con este método geoestadístico requieren de análisis ulterior.

Referencias

1. Blais RA, Carlier PA (1968) Applications Of Geostatistics In Ore Evaluation. En Ore Reserve Estimation And Grade Control. Special Vol. 9. Canadian Institute of Mining and Metalurgy. Montreal, Canada. pp. 41-48.        [ Links ]

2. Burrough PA (1986) Principles of geographical information systems for land resources assessment. Clarendon Press, Oxford, RU. 193 pp.        [ Links ]

3. Chauvet P (1994) Aide-Memoire de Géostatistique Miniere. École des Mines. Paris, Francia. 210 pp.        [ Links ]

4. Cliff A, Ord JK (1981) Spatial Process: Models and Applications. Pion. Londres, RU. 266 pp.        [ Links ]

5. Cressie N (1985) Fitting variogram models by weighted least square. Math. Geol. 17: 563-586.        [ Links ]

6. David M (1977) Geostatistical ore reserve estimation. Elsevier. Nueva York, EEUU. 364 pp.        [ Links ]

7. Huijbregts CJ (1975) Regionalized variables and quantitative analysis of spatial data. En Davis JC, McCullagh MJ (Eds.) Display and analysis of spatial data. Wiley. Londres, RU. pp. 38-53.        [ Links ]

8. Isaaks EH, Srivastava RM (1989) An introduction to applied geostatistics. Oxford University Press. Nueva York, EEUU. 592 pp.        [ Links ]

9. Journel AG, Huijbregts, ChJ (1978) Mining Geostatistics. Academic Press. Londres, RU. 600 pp.        [ Links ]

10. Jorgensen PS (1980) NAVSTAR/Global Positioning System 18-Satellite Constellation. Navigation 27: 89-100.        [ Links ]

11. Matheron G (1963) Principles of geostatistics. Econ. Geol. 58: 1246-1266.        [ Links ]

12. Matheron G (1970) La Théorie des Variables Regionalisées et ses Applications. Ecole de Mines de Paris. Francia. 212 pp.        [ Links ]

13. USAF (1996) NAVSTAR GPS User Equipment Introduction. US Space Systems Division. LA, EEUU. 215 pp.        [ Links ]

14. Olea RA (1975) Optimum mapping techniques using regionalized variable theory. Series on Spatial Analysis Nº 2. University of Kansas, EEUU. 137 pp.        [ Links ]

15. Sturza MA (1983) GPS Navigation Using Three Satellites and a Precise Clock. Global Positioning System. Navigation 30: 122-132.        [ Links ]

16. USACE (2003) Engineering and Design - NAVSTAR Global Positioning System Surveying. US Army Corps of Engineers. Washington DC, EEUU, 328 pp.        [ Links ]

17. Vauclin M, Vieira SR, Vachaud G, Nielsen DR (1983) The Use Of Cokriging With Limited Field Soil Observations. Soil Sci. Soc. Am. J. 47: 175-184.        [ Links ]

18. Leica Geosystem (1994) WILD GPS - System 200 User Manual For SKI 2.30. Heerbrugg, Suiza, 137 pp.        [ Links ]

19. Zhang XF, Van Eijkeren JCH, Heemink AW (1995) On the Weighted Least Squares Method for Fitting a Semivariogram Model. Comput. Geoscie. 21: 605-608.        [ Links ]