Estimación de componentes de (co)varianza para la producción de leche del día del control en ganado siboney utilizando un modelo de regresión aleatoria.

Dianelys González-Peña, Danilo Guerra Iglesias, José Luis Espinoza Villavicencio, Alejandro Palacios Espinosa y Rafael de Luna de la Peña

Dianelys González-Peña. Doctora en Ciencias Veterinarias, Instituto de Ciencia Animal (ICA), La Habana, Cuba. Investigadora, Centro de Investigaciones para el Mejoramiento Animal de la Ganadería Tropical, (CIMAGT) La Habana, Cuba

Danilo Guerra Iglesias. Doctor en Ciencias Veterinarias, ICA, La Habana, Cuba. Profesor, CIMAGT, La Habana, Cuba.

José Luis Espinoza Villavicencio. Doctor en Filosofía, Universidad Autónoma de Chihuahua (UACh), México. Profesor Investigador, Universidad Autónoma Baja California Sur (UABCS), México. Dirección: Nicolás Bravo # 419, entre Guillermo Prieto y Serdán, Col. Centro. CP 23000, La Paz, B.C.S., México. e-mail: jlvilla@uabcs.mx.

Alejandro Palacios Espinosa. Doctor en Filosofía, UACh, México. Profesor Investigador, UABCS, México.

Rafael de Luna de la Peña. Doctor en Ciencia Animal, Universidad Autónoma de Nayarit, México. Profesor Investigador, UABCS, México.

Resumen

Con el fin de estimar los componentes de (co)varianza para la producción de leche del día del control en ganado Siboney (5/8 Holstein 3/8 Cebú Cubano) se utilizó un modelo de regresión aleatoria y se analizó el comportamiento de los estimadores al tener en cuenta la heterogeneidad de varianza residual (s_r²). Se analizaron 17034 registros de producción de leche del día del control (PDC) de 2086 vacas Siboney de primer parto que parieron entre 1995 y 2003. Las vacas, provenientes de 50 hatos, fueron hijas de 153 padres y 1179 madres. El pedigrí estuvo conformado por 5471 individuos y se garantizó que las hembras tuvieran, como mínimo, los primeros cuatro controles de producción de leche. Se trabajó con modelos de regresión aleatoria probando diferentes órdenes de polinomios de Legendre, para luego seleccionar mediante el logaritmo de convergencia y el criterio de Akaike el modelo de orden 4 para la varianza aditiva y de orden 5 para el ambiente permanente (AG4PE5), al cual se le aplicó heterogeneidad de s_r². Los estimados de heredabilidad oscilaron entre 0,21 y 0,31 con valor máximo a los 177 días de lactancia. Las correlaciones genéticas fueron elevadas y a la mitad de la lactancia tomaron valores >0,95. Los resultados destacan la importancia de modelar la heterogeneidad de s_r², debido a que se obtiene un mejor ajuste en la estimación de los componentes de (co)varianza para la producción de leche del día del control.

Estimation of (co)variance components for the test-day milk yield in siboney cattle using a random regression model.

Summary

In order to estimate (co)variance components for test-day milk in Siboney (5/8 Holstein 3/8 Cuban Zebu) cattle a random regression model was used and it was determined whether a heterogeneous residual variance (s_r²) adjustment was necessary. Data were test-day yields of 17034 first lactations of 2086 Siboney cows, collected from 1995 through 2003. The cows were daughters of 153 sires and 1179 dams of 50 herds. The genealogy file was comprised by 5471 animals. It was guaranteed that the cows had, at least, the first four test-day milk controls. Random regression models were used testing Legendre polynomials of different order. The 4^th order was selected for the additive variance and the 5^th for the permanent effects (AG4PE5), based on the logarithm of convergence and the Akaike criterion. The s_r² heterogeneity was applied to the model. The estimated heritability varied between 0.21 and 0.31 with maximum at 177 days of lactation. The genetic correlations were elevated and reached values >0.95 at mild lactation. The results emphasize the importance of modeling the s_r² heterogeneity, because a better adjustment of (co)variance components for milk yield is obtained.

Estimação de componentes de (co) variâncias para a produção de leite no dia do controle no gado siboney utilizando um modelo de regressão aleatória.

Resumo

Com o fim de estimar os componentes de (co) variância para a produção de leite no dia do controle no gado Siboney (5/8 Holstein 3/8 Zebu Cubano) se utilizou um modelo de regressão aleatória e se analisou o comportamento dos estimadores ao levar em conta a heterogeneidade de variação residual (s_r²). Analisaram-se 17034 registros de produção de leite no dia do controle (PDC) de 2086 vacas Siboney de primeiro parto que pariram entre 1.995 e 2003. As vacas, provenientes de 50 fazendas, foram filhas de 153 pais e 1179 mães. O pedigree esteve conformado por 5471 indivíduos e se garantiu que as fêmeas tivessem, no mínimo, os primeiros quatro controles de produção de leite. Trabalhou-se com modelos de regressão aleatória provando diferentes ordens de polinômios de Legendre, para logo selecionar mediante o logaritmo de convergência e o critério de Akaike o modelo de ordem 4 para a variação aditiva e de ordem 5 para o ambiente permanente (AG4PE5), ao qual foi aplicado heterogeneidade de s_r². Os estimados de heredabilidade oscilaram entre 0,21 e 0,31 com valor máximo aos 177 dias de lactância. As correlações genéticas foram elevadas e na metade da lactância tomaram valores >0.95. Os resultados destacam a importância de modelar a heterogeneidade de s_r², devido à obtenção de um melhor ajuste na estimação dos componentes de (co) variâcia para a produção de leite no dia do controle.

Palabras Clave / Componentes de (co)varianza / Ganado Siboney / Producción de Leche / Regresión Aleatoria /

Recibido: 23/02/2007. Modificado: 10/09/2007. Aceptado: 11/09/2007.

Introducción

La estimación de los componentes de varianza y covarianza son necesarios para la evaluación genética del ganado bovino (Danell, 1982) y para ese fin se han utilizado varios modelos con diferentes grados de complejidad (Mark, 2004). La primera función aplicada para modelar la parte aleatoria de la curva de lactancia en un modelo de regresión aleatoria fue la curva de Ali y Schaeffer (1987). Otras funciones, como la de Wood (1967) y la de Wilmink (1987), también han sido empleadas con el mismo objetivo.

Recientemente se han utilizado los polinomios de Legendre, aplicados por Kirkpatrick et al. (1994) en ganado lechero, los cuales han desplazado a las funciones lactacionales por sus propiedades matemáticas, ya que tienen bajas correlaciones entre sus parámetros y una mayor flexibilidad (Macciotta et al., 2005). Presentan numerosas ventajas; entre ellas, que la función es ortogonal, lo cual es útil para analizar patrones de variación genética (Kirkpatrick et al., 1990). Los registros perdidos pueden ser predichos con más exactitud que con la curva de Wilmink (1987) y para mejor convergencia se pueden estimar altos órdenes de ajuste cuando fallan los polinomios convencionales (Pool y Meuwissen, 2000).

Aunque la homogeneidad de las (co)varianzas es una suposición común de los modelos de evaluación genética, dicho supuesto es a veces incorrecto a lo largo de la lactación (Gengler y Wiggans, 2002). De manera similar a la varianza de la producción de leche, la varianza residual (s_r²) cambia en el transcurso de la lactación y esto puede afectar directamente las evaluaciones genéticas (Rekaya et al., 2000). La utilización de ajuste de la heterogeneidad de la varianza en modelos de regresión aleatoria aplicados en la producción de leche del día del control es relativamente reciente (Muir et al., 2007). Garrick y Van Vleck (1987) encontraron una reducción de 3,3% en la ganancia genética cuando fue omitida la heterogeneidad de s_r² en la evaluación, concluyendo que al ser ignorada la heterogeneidad de varianza genética y/o residual se puede ocasionar una reducción de los valores genéticos predichos y consecuentemente una reducción en la respuesta a la selección.

Los objetivos de este estudio fueron estimar los componentes de (co)varianza para la producción de leche del día del control (PDC) en ganado Siboney de Cuba, utilizando un modelo de regresión aleatoria, y valorar el comportamiento de los estimados con y sin heterogeneidad de la varianza residual.

Materiales y Métodos

Se analizó información proveniente de ganado Siboney (5/8 Holstein 3/8 Cebú Cubano) de 50 hatos explotados bajo un sistema de pastoreo en Cuba, situada en la entrada del Golfo de México (20-23°N y 74-85°O; IMRC, 2006). En la localidad hay dos estaciones claramente definidas, la de lluvias (verano) de mayo a octubre, en la que ocurre 70-80% de la precipitación (960mm), y la estación seca (invierno) de noviembre a abril (240mm). La temperatura media anual es de 23,1°C, con humedad relativa de 60-70% durante el día y de 80-90% durante la noche (Hernández et al., 1998).

Se utilizaron 17034 pesajes de leche en 2086 vacas de primer parto, las que parieron entre 1995 y 2003. Las vacas fueron hijas de 153 padres y 1179 madres. El pedigrí estuvo conformado por 5471 individuos y se garantizó que las hembras tuvieran, como mínimo, los primeros cuatro controles de producción de leche.

Los registros de la producción de leche del día del control (PDC) fueron modelados con polinomios de Legendre (Meyer y Hill, 1997) de orden 0 hasta 6. La varianza genética aditiva (s_a²) y la varianza del medio ambiente permanente (s²_pe) fueron modeladas con igual y diferente orden de polinomios de Legendre, de forma tal que cuando se utilizó el orden 2 para la s_a² y el orden 3 para la s²_pe, la simbología utilizada es AG2PE3. La s_r², debido a su distribución, fue modelada con una función cuadrática con un coeficiente de determinación de 97,6%.

El modelo en notación matricial fue

y = Xb + Z₁a + Z₂p + e

donde y: vector de los pesajes mensuales; b: vector de los efectos fijos, siendo estos la combinación hato-fecha del día del control y la edad de la vaca al día del control como covariable lineal y cuadrática; a: vector con w coeficientes de regresión aleatoria por animal para el efecto genético del animal, donde w= m+1 y m: orden de ajuste del polinomio; p: vector con w regresiones aleatorias para el ambiente permanente; e: vector del efecto residual; y X, Z₁, Z₂: matrices de incidencia para los efectos fijos, para el efecto genético aditivo y del ambiente permanente.

Se supuso que la s_r² fue diagonal y constante para el modelo, cuando este incluyó la heterogeneidad de la s_r².

Para calcular s_a² y s²_pe se utilizaron los días en lactación (DEL) estandarizados entre +1 y -1 como

Todos los análisis fueron realizados con el ASREML (Gilmour et al., 2002). Se utilizó el criterio de información de Akaike (AIC; Akaike, 1973) para seleccionar el modelo que mejor ajusta, según la ecuación

AIC= -2(log máxima verosimilitud) + 2 (número de parámetros)

Cuando se comparan dos modelos, aquel con el AIC más bajo es considerado el mejor (Huisman et al., 2002). A partir de esta ecuación se utilizó el orden de ajuste seleccionado para la estimación de los parámetros genéticos con homogeneidad de la s_r², denominado Modelo 1 (M1), y con 10 clases de heterogeneidad de s_r² (M2)

Las correlaciones genéticas entre las PDC se calcularon de acuerdo a la ecuación

y las (co)varianzas fueron calculadas a través de la ecuación

Cov(PDC_i, PDC_j)=z’_i G z_j

donde z'_i es el vector con los coeficientes de los polinomios de Legendre correspondientes a un DEL específico y G es la matriz de (co)varianzas genéticas de los coeficientes de regresión aleatoria.

Resultados y Discusión

Selección del modelo

Los logaritmos de convergencia estimados variaron entre 7956,92 y 8256,89 con valores del AIC de 7878,92 y 8164,89 en los modelos AG4PE5 y AG6PE4, respectivamente. Tomando en cuenta el logaritmo de convergencia menor y de acuerdo con el AIC, el modelo seleccionado fue AG4PE5. Menéndez y Caunedo (2005) seleccionaron el orden del polinomio de mejor ajuste en base al logaritmo de convergencia. Sawalha et al. (2005) utilizaron además del logaritmo, el criterio de Akaike (1973) y plantearon que el logaritmo de convergencia es un criterio muy objetivo a la hora de seleccionar modelos. Meyer (2000) planteó que es preferible el modelo más sencillo, respetando el criterio de selección establecido, pues los modelos con muchos parámetros tienden a tener problemas de convergencia y generalmente la exactitud se ve afectada. Los polinomios de Legendre de orden 4 para modelar la s_a² han sido utilizados por Barret et al. (2005) y De Roos et al. (2004). Órdenes de ajuste del ambiente permanente superiores al del efecto genético aditivo han sido postulados por Pool et al. (2000) y López-Romero y Carabaño (2003)

Varianza aditiva

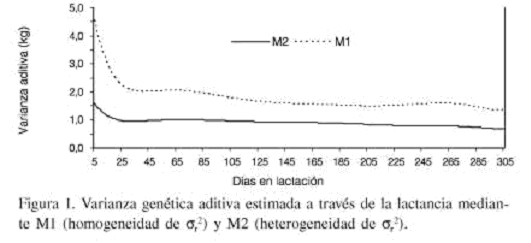
En la Figura 1 se observa que la s_a² estimada con M1 (homogeneidad de s_r²) fue mayor en el día 5 de la lactancia (4,5) y menor en el día 302 (1,34) mientras que la obtenida por M2 (heterogeneidad de s_r²) se comportó de manera similar que la del modelo M1 pero su valor más elevado fue de 1,6 en el día 5 y su valor mas bajo de 0,67 en el día 302. De forma general, la curva de M2 estuvo 0,87 unidades en promedio por debajo de la obtenida por M1. Una tendencia similar fue estimada por Strabel y Jamrozik (2006) usando polinomios de Legendre de orden 4, aunque en ese estudio la s_a² se mantuvo constante desde el inicio de la lactancia, a diferencia de lo observado en el presente trabajo, en el cual, la s_a² fue más elevada en el día 5 de la lactación para luego mantenerse relativamente invariable. Una tendencia diferente fue reportada por Fujii y Suzuki (2006) en vacas Holstein de Japón, en un estudio en el que utilizaron modelos con heterogeneidad de s_r², donde la s_a² más baja se registró al inicio de la lactación y la más alta al final de la misma. Una directriz similar a la anterior fue observada en otro estudio, realizado en Brasil con vacas Holandesas utilizando polinomios de Legendre de orden 3, 4 y 5 (Vieira et al., 2006). En otro trabajo en el que se usaron polinomios de Legendre de orden 4, la s_a² más baja se presentó en los extremos de la lactación y los valores más altos estuvieron en una etapa intermedia de la misma (Pool et al., 2000).

Varianza del ambiente permanente

La s²_pe en M1 presentó tres valores máximos y tres valores mínimos evidentes (Figura 2); el primer incremento en el día 5 de la lactancia con un estimado de 27,71; el segundo a los 95 días con un valor de 4,7269 y el tercero a los 238 días. Los valores mínimos se establecieron a los 40 (0,6193), 167 (0,5012) y a los 297 días (0,7974) de lactación.

La s²_pe en M2 se expresó de forma diferente a la s²_pe estimada por M1, con 24,66 unidades por debajo al inicio de la lactación y tendencia decreciente hasta los 182 días (1,1407), para luego crecer discretamente y terminar a los 305 días con el 49% de la varianza inicial (Figura 2). Resultados similares fueron reportados por Strabel y Jamrozik (2006). Fujii y Suzuki (2006) observaron que la s²_pe disminuyó desde el inicio de la lactación hasta los 250 días, aproximadamente, para incrementarse al final de la misma por encima de los valores iniciales. Vieira et al. (2006) utilizando polinomios de Legendre de orden 3, 4 y 5 determinaron que la s²_pe disminuye en forma marcada en los primeros 30 días, se mantiene relativamente constante durante la mayor parte de la lactación y se incrementa al final de la misma. En un estudio indicado por Mostert et al. (2006), los componentes de varianza estimados utilizando los registros de producción del día del control con heterogeneidad de la s_r² fueron mayores para los efectos directos y del ambiente permanente a expensas de la s_r², en comparación con las estimaciones obtenidas con homogeneidad de la s_r².

Heredabilidad

El comportamiento de la s²_pe en M1 determinó la conducta de la heredabilidad, por lo que esta presentó máximos de 0,54; 0,50 y 0,43 a los 40, 167 y 297 días de la lactación, respectivamente (Figura 3), debido probablemente a los valores bajos de la s²_pe en esas etapas (Vieira et al., 2006). Los valores de heredabilidad estimados en el presente estudio mediante M1 son similares a los obtenidos por Kettunen et al. (1998) y Olori et al. (1999) quienes reportaron heredabilidades mayores de 0,50 en algunas etapas de la curva de lactación. Este tipo de oscilaciones de la heredabilidad a través de la lactación no tienen una explicación biológica clara y se presume que pueden derivar del uso de funciones de alto orden para explicar efectos aleatorios en el modelo (Strabel y Jamrozik, 2006). La heredabilidad obtenida por M2 presentó valores entre 0,21 y 0,31; correspondientes a los 302 y 177 días de la lactancia, respectivamente. Curvas parecidas han sido obtenidas por Jakobsen et al. (2002). De manera similar, Strabel y Jamrozik (2006) determinaron que la heredabilidad se incrementa conforme transcurre la lactación hasta los 150 días aproximadamente, para luego reducirse hasta el final, aunque los valores estimados en ese estudio fueron inferiores a los del presente trabajo, fluctuando entre 0,1 y 0,2. Así mismo, Druet et al. (2003) estimaron el valor de heredabilidad más bajo (0,16) al inicio la lactación, el más alto (0,39) a los 200 días y posteriormente un descenso hasta el final de la misma. Vieira et al. (2006), basados en polinomios de Legendre de orden 4 determinaron valores de heredabilidad que se incrementaron de manera constante desde el inicio (0,12) hasta los 240 días (0,27) para descender posteriormente a los 305 días de la lactación (0,23). Valores superiores a los anteriores pero con una tendencia similar durante la lactación fueron obtenidos utilizando el mismo procedimiento (Pool et al., 2000; Cobuci et al., 2006). Otros autores han estimado mayores heredabilidades en ambos extremos de la curva de lactación (Strabel y Misztal, 1999; Samoré et al., 2002).

Los resultados de diferentes estudios con modelos de regresión aleatoria han sido heterogéneos (Misztal et al., 2000) y los valores de heredabilidad a través de la lactancia varían considerablemente entre estudios en intervalos que van de 0,10 (Strabel y Misztal, 1999) a 0,60 (Jamrozik y Schaeffer, 1997).

Varianza residual

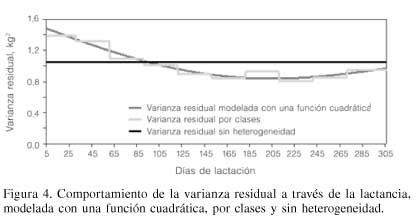
El comportamiento de la varianza residual se presenta en la Figura 4, donde se aprecia que la función cuadrática utilizada para modelar la varianza del error, teniendo en cuenta la heterogeneidad de la s_r², se ajusta bien, con excepción de la clase siete. De manera similar, en otros estudios se ha encontrado que la s_r² decrece a través de la lactación con un ligero incremento al final (Rekaya et al., 1999; Pool et al., 2000). Así mismo, Mostert et al. (2006) observaron que la s_r² fue mayor al inicio que a la mitad de la lactación; sin embargo, Druet et al. (2003) encontraron que la s_r² fue mayor al inicio y menor al final.

Correlaciones genéticas

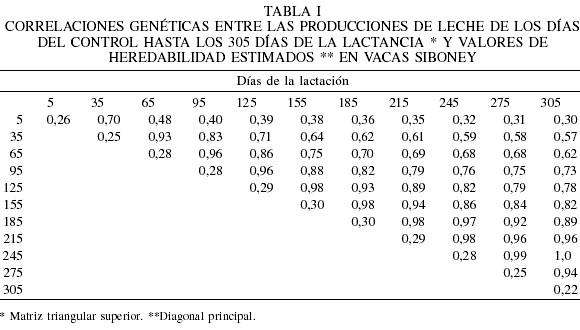
Las correlaciones genéticas entre los días en producción presentaron valores bajos entre los extremos de la lactación. A medida que aumentó el intervalo de los días en producción la correlación genética se incrementó con valores próximos a la unidad en algunos periodos adyacentes (Tabla I). Estos resultados coinciden con las estimaciones hechas por Vieira et al. (2006). En general, las correlaciones fueron >0,95 a partir de la mitad. Todos los valores fueron positivos y la correlación genética entre los extremos fue de 0,30 indicando que la selección para el aumento de la producción de leche en determinado punto de la lactación tendrá un reflejo positivo sobre todas las demás etapas. Resultados semejantes fueron reportados por Olori et al. (1999) y Brotherstone et al. (2000) al utilizar polinomios de Legendre. Strabel y Misztal (1999) utilizando un polinomio de Legendre de segundo orden, encontraron correlaciones genéticas altas entre controles adyacentes, con estimaciones próximas a cero entre los controles más extremos.

Los resultados del presente estudio concuerdan con lo planteado por López-Romero y Carabaño (2003) quienes reportan que las correlaciones genéticas entre las producciones de leche medidas en tiempos t1 y t2 disminuyen a medida que t2 se aleja de t1.

Estos resultados están de acuerdo también con los obtenidos por Druet et al. (2003) quienes estimaron correlaciones genéticas >0,90 a partir de la mitad y de 0,35 entre los extremos de la lactación. Las correlaciones genéticas entre las PDC obtenidas en el presente estudio están de acuerdo también con aquellas estimadas mediante análisis multivariado por Kettunen et al. (1998). También se han reportado correlaciones genéticas superiores, obtenidas mediante análisis multivariado (White et al., 1999). Finalmente, Rekaya et al. (1999) obtuvieron correlaciones genéticas negativas para las parte extremas de la lactación cuando utilizaron un modelo de regresión aleatoria y explicaron ese comportamiento por el hecho que suponen el efecto aleatorio del ambiente permanente como constante a lo largo de la lactación, lo que podría sobreestimar la varianza genética aditiva en los extremos de la curva de lactación (Vieira et al., 2006).

Conclusiones

De los modelos estudiados de acuerdo al logaritmo de convergencia y al criterio de Akaike, el mejor fue AG4PE5 con heterogeneidad de la s_r². Las estimaciones de heredabilidad basadas en este modelo oscilaron entre 0,21 y 0,31 presentando el valor máximo a los 177 días de lactancia. Las correlaciones genéticas fueron elevadas y alcanzaron valores >0,95 a la mitad de la lactancia.

Los resultados indican la importancia de modelar la heterogeneidad de la s_r² en virtud del mejor ajuste en la estimación de los componentes de (co)varianza para la producción de leche del día del control, comparado con aquellos modelos en los cuales no se considera tal heterogeneidad.

REFERENCIAS

1. Akaike H (1973) Information theory and an extension of the maximum likelihood principle. En Petrov BN, Caski F (Eds.) Proc. 2^nd Int. Symp. Information Theory. Budapest. Akademiai Kiado. Budapest, Hungría. pp 287-261.        [ Links ]

2. Ali TE, Schaeffer LR (1987) Accounting for covariances among test day milk yields in dairy cows. Can. J. Anim. Sci. 67: 637-644.        [ Links ]

3. Barret R, Miglior F, Jansen G, Jamrozik J, Schaeffer LR (2005) Joint international evaluation of milking Shorthorn dairy cattle for production traits. J. Dairy Sci. 88: 3326-3336.        [ Links ]

4. Brotherstone S, White IMS, Meyer K (2000) Genetic modeling of daily milk yield using orthogonal polynomials and parametric curves. Animal Sci. 70: 407-415.        [ Links ]

5. Cobuci JA, Costa CN, Teixeira NM, Freitas AF (2006) Utilização dos polinômios de Legendre e da função de Wilmink em avaliações genéticas para persistência na lactação de animais da raça Holandesa. Arq. Bras. Med. Vet. Zootec. 58: 614-623.        [ Links ]

6. Danell B (1982) Studies on lactation yield and individual test-day yield of Swedish dairy cows: II. Estimates of genetic and phenotypic parameters. Acta Agric. Scand. 32: 82-92.         [ Links ]

7. De Roos APW, Harbers AGF, de Jong G (2004) Random herd curves in a test day models for milk, fat and protein production of dairy cattle in the Netherlands. J. Dairy Sci. 87: 2693-2701.        [ Links ]

8. Druet T, Jaffrezic F, Boichard D, Ducrocq V (2003) Modelling lactation curves and estimation of genetic parameters for first lactation test day records of French Holstein cows. J. Dairy Sci. 86: 2480-2490.        [ Links ]

9. Fujii Ch, Suzuki M (2006) Comparison of homogeneity and heterogeneity of residual variance using random regression test-day models for first lactation Japanese Holstein cows. Animal Sci. J. 77: 28-32.        [ Links ]

10. Garrick DJ, Van Vleck LD (1987) Aspects of selection for performance in several environments with heterogeneous variances. J. Anim. Sci. 65: 409-421.        [ Links ]

11. Gengler N, Wiggans GR (2002) Adjustment for heterogeneous genetic and non-genetic (co)variance structures in test-day models using a transformation on random regression effect regressors. Interbull Bulletin 29: 79–83. www-interbull.slu.se/bulletins/ bulletin29/Gengler.pdf        [ Links ]

12. Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R (2002) ASREML. User Guide. Release 1.10.        [ Links ]

13. Hernández IR, Milera MC, Simón LA, Hernández DG, Iglesias JN, Lamela LO, Toral OL, Matías CA, Francisco GS (1998) Avances en las investigaciones en sistemas silvopastoriles en Cuba. Memorias de la Conferencia Electrónica FAO-CIPAV sobre agroforestería para la producción animal en Latinoamérica. Abril-Septiembre. pp. 47-59.        [ Links ]

14. Huisman AE, Veerkamp RF, Van Arendock JAM (2002) Genetics parameters for various random regression models to describe the weight data of pigs. J. Anim. Sci. 80: 575-582.         [ Links ]

15. IMRC (2006) Instituto Meteorológico de la República de Cuba. www.met.inf.cu/asp/ genesis.asp?TB0=PLANTILLAS & TB1=INICIAL.         [ Links ]

16. Jakobsen JH, Madsen P, Jensen J, Pederson J, Christensen LG, Sorensen DA (2002) Genetic parameters for milk production and persistency for Danish Holstein estimated in random regression models using REML. J. Dairy Sci. 85: 1607-1616.        [ Links ]

17. Jamrozik J, Schaeffer LR (1997) Estimates of genetic parameters for a test day model with random regressions for yield traits of first lactation Holsteins. J. Dairy Sci. 80: 762-770.        [ Links ]

18. Kettunen A, Mäntysaari EA, Strandén I, Pöso J, Lidauer M (1998) Estimation of genetic parameters for first lactation test day milk production using random regression models. Proc. 6^th World Congr. Genet. Appl. Livest. Prod. Armidale, Australia. XXIII: 307-310.        [ Links ]

19. Kirkpatrick M, Lofsuold D, Bulmer M (1990) Analysis of inheritance, selection and evolution of growth trajectories. Genetics 124: 979-993.         [ Links ]

20. Kirkpatrick M, Hill WH, Thompson R (1994) Estimating the covariance structure of traits during growth and aging, illustrated with lactations in dairy cattle. Gen. Res. 64: 57-69.        [ Links ]

21. López-Romero P, Carabaño MJ (2003) Comparing alternative random regression models to analyse first lactation daily milk yield data in Holstein Friesian cattle. Livest. Prod. Sci. 82: 81-96.        [ Links ]

22. Macciotta NPP, Vicario D, Cappio-Barlino A (2005) Detection of different shapes of lactation curve for milk yields in dairy cattle by empirical mathematical models. J. Dairy Sci. 88: 1178-1191.        [ Links ]

23. Mark T (2004) Applied genetic evaluations for production and functional traits in dairy cattle. J. Dairy Sci. 87: 2641-2652.        [ Links ]

24. Menéndez A, Caunedo JR (2005) Utilización de los resultados del control de la producción de leche en cada ordeño para la evaluación genética de sementales, mediante modelos de regresiones aleatorias. Mem. III Cong. Int. Mejoramiento Animal. La Habana, Cuba. pp. 92-95.        [ Links ]

25. Meyer K (2000) Random regression to model phenotypic variation in monthly weights of Australian beef cows. Livest. Prod. Sci. 65: 19-38.        [ Links ]

26. Meyer K, Hill WG (1997) Estimation of genetic and phenotypic covariance functions for longitudinal or repeated records by restricted maximum likelihood. Livest. Prod. Sci. 47: 185-200.        [ Links ]

27. Misztal I, Strabel T, Jamrozik J, Mäntysaari EA, Meuwissen THE (2000) Strategies for estimating the parameters needed for different test day models. J. Dairy Sci. 83: 1125-1134.        [ Links ]

28. Mostert BE, Theron HE, Kanfer FHJ, van Marle-Köster E (2006) Adjustment of heterogeneous variances and a calving year effect in test-day models for national genetic evaluation of dairy cattle in South Africa. S. Afr. J. Anim. Sci. 36: 165-174.        [ Links ]

29. Muir BL, Kistemaker G, Jamrozik J, Canavesi F (2007) Genetic parameters for a multiple-trait multiple-lactation random regression test-day model in italian holsteins. J. Dairy Sci. 90:1564-1574.        [ Links ]

30. Olori VE, Hill WG, McGuirk BJ, Brotherstone S (1999) Estimating variance components for test day milk records by restricted maximum likelihood with a random regression animal model. Livest. Prod. Sci. 61: 53-63.        [ Links ]

31. Pool MH, Meuwissen THE (2000) Reduction of the number of parameters needed for a polynomials random regression test day model. Livest. Prod. Sci. 64: 133-145.         [ Links ]

32. Pool MH, Janss LLG, Meuwissen THE (2000) Genetic parameters of Legendre polynomials for first parity lactation curves. J. Dairy Sci. 83: 2640-2649.        [ Links ]

33. Rekaya R, Carabaño MJ, Toro MA (1999) Use of test day yields for the genetic evaluation of production traits in Holstein-Friesian cattle. Livest. Prod. Sci. 57: 203-217.        [ Links ]

34. Rekaya R, Carabaño MJ, Toro MA (2000) Assessment of heterogeneity of residual variances using change points techniques. Genet. Sel. Evol. 32: 383-394.         [ Links ]

35. Samoré AB, Boettcher P, Jamrozik J, Bagnato A, Groen AF (2002) Genetic parameters for production traits and somatic cell scores estimated with a multiple trait random regression model in Italian Holsteins. Proc. 7^th World Congr. Genet. Appl. Livest. Prod. Montpellier, France. Communication Nº 01–07.        [ Links ]

36. Sawalha RM, Keown JF, Kachman D, Van Vleck LD (2005) Evaluation of autoregressive covariance structures for test-day records of Holstein cows: Estimates of parameters. J. Dairy Sci. 88: 2632-2642.        [ Links ]

37. Strabel T, Jamrozik J (2006) Genetic analysis of milk production traits of Polish Black and White cattle using large-scale random regression test-day models. J. Dairy Sci. 89: 3152-3163.        [ Links ]

38. Strabel T, Misztal I (1999) Genetic parameters for first and second lactation milk yields of Polish Black and White cattle with random regression test-day models. J. Dairy Sci. 82: 2805–2810.        [ Links ]

39. Vieira C, Torres RA, Costa CN, Torres RA, Araújo SI, Lopes PS, Regáis AJ, Silva C, Araújo J, Rocha JL (2006). Uso de funções ortogonais para descrever a produção de leite no dia de controle por meio de modelos de regressão aleatória. Rev. Bras. Zootec. 35: 967-974.        [ Links ]

40. White IMS, Thompson R, Brotherstone S (1999) Genetic and environmental smoothing of lactation curves with cubic splines. J. Dairy Sci. 82: 632-638.        [ Links ]

41. Wilmink JBM (1987) Adjustment of test day milk, fat, and protein yields for age season and stage of lactation. Livest. Prod. Sci. 16: 335-348.        [ Links ]

42. Wood PDP (1967) Algebraic model of lactation curve in cattle. Nature 216: 164-165.        [ Links ]