Aplicación de lógica difusa y algoritmos genéticos para clasificación de tratamientos contra enfermedades neoplásicas malignas

Application of fuzzy logic and genetic algorithms for classification of malignant neoplastic diseases treatments

Miguel León, MgSc¹, Belkys L. de Lameda¹*, Carlos Lameda, MgSc², José Gerardo Chacon, MgSc, PhD⁴, María Sofía Martínez, MD⁵, Joselyn Rojas, MD, MgSc^3,5, Julio Contreras -Velásquez, MgSc⁴, Modesto Graterol -Rivas, MgSc, PhD⁶, Sandra Wilches Durán, MgSc⁴, Miguel Aguirre, MD, MgSc⁵, Miguel Vera, MgSc, PhD⁴, Marcos Cerda, MgSc⁴, Carlos Garicano, MD⁴, Juan Diego Hernández MD, MgSc⁴, Victor Arias, Ing⁴, Rosemily Graterol, MgSc⁴, Maricarmen Chacín, MD, MgSc⁵, Valmore Bermúdez, MD, MPH, MgSc, PhD⁵

¹ Universidad Centroccidental Lisandro Alvarado (UCLA), Barquisimeto, Venezuela

² Universidad Nacional Experimental Politécnica "Antonio José de Sucre", Barquisimeto, Venezuela

³ Pulmonary and Critical Care Medicine Department. Brigham and Women’s Hospital. Harvard Medical School. Boston, MA. USA 02115.

⁴ Grupo de investigación Altos Estudios de Frontera (ALEF), Universidad Simón Bolívar, Cúcuta, Colombia

⁵ Centro de investigación de Enfermedades Endocrino-Metabólicas. Universidad del Zulia, Maracaibo, Venezuela.

⁶ Centro de Estudios de la Empresa. Universidad del Zulia, Maracaibo, Venezuela.

*Autor para correspondencia: Belkys L. de Lameda. Universidad Centroccidental Lisandro Alvarado (UCLA). E-mail: belkislopez@cantv.net

Resumen

Un clasificador difuso es un sistema que asigna una etiqueta de clase a un objeto basado en la descripción del mismo y hace uso de conjuntos difusos como parte de su operación. Su funcionamiento puede ser optimizado mediante algoritmos genéticos, garantizando soluciones viables. El artículo propone un clasificador difuso optimizado utilizando un algoritmo genético hibridado con una técnica de agrupamiento difuso. Se implementa un prototipo y se evalúa con conjuntos de datos referenciales sintéticos como posibles problemas de clasificación de tratamientos contra enfermedades neoplásicas malignas. Se compara los resultados con otros clasificadores encontrados en la literatura sobre los mismos datos de prueba. La conclusión es que el método propuesto obtuvo resultados similares a los comparados con funciones de pertenencia más fáciles de interpretar.

Palabras Clave: lógica difusa, algoritmos genéticos, clasificador difuso, algoritmo genético híbrido, enfermedades neoplásicas malignas.

Abstract

A fuzzy classifier is a system that assigns a class label to object based on a description of it and makes use of fuzzy sets as part of its operation. Its functioning can be optimized using genetic algorithms, ensuring viable solutions. The paper proposes a fuzzy classifier optimized using a genetic algorithm hybridized with a fuzzy clustering technique. A prototype is implemented and evaluated with synthetic reference data sets as possible classification problems treatments for malignant neoplastic diseases. The results are compared with other classifiers found in the literature on the same test data. The conclusion is that the proposed method obtained similar results with functions easier to interpret.

Keywords: fuzzy logic, genetic algorithms, fuzzy classifier, hybrid genetic algorithm, malignant neoplastic diseases

Introducción

En la actualidad los sistemas de clasificación son usados en aplicaciones de diversas áreas, desde clasificación automática de correo electrónico (spam), sugerencias de productos en tiendas virtuales, hasta en módulos de identificación de objetos en el creciente número de desarrollos de visión artificial¹. Para ampliar su uso se deben mejorar cualidades como interpretabilidad y exactitud. La interpretabilidad de un sistema de clasificación es la capacidad de utilizar y producir elementos necesarios para el proceso de clasificación que sean fáciles de comprender y tengan sentido para un usuario humano. En un sistema difuso, estos elementos pueden ser: la base de reglas, los atributos y variables lingüísticas utilizados para representar un objeto. Por otra parte, la exactitud de un clasificador puede entenderse como la proporción de objetos clasificados correctamente.

Un clasificador difuso es un sistema de clasificación que incluye el uso de conjuntos difusos o lógica difusa como parte de su operación o entrenamiento². El clasificador predice la etiqueta de clase, mientras la descripción del objeto se presenta en forma de un vector que contiene los valores de las características (atributos) considerados relevantes para la tarea de clasificación. Por lo general, el clasificador aprende a predecir las etiquetas de clase usando un algoritmo de entrenamiento y un conjunto de datos de entrenamiento.

Cuando un conjunto de datos de entrenamiento no está disponible, un clasificador puede ser diseñado a partir de conocimientos previos y experiencia. Una vez entrenado, el clasificador está preparado para funcionar en los objetos no conocidos^2,3 Por esta razón, podría considerarse que un clasificador entrenado, se desempeña de manera autónoma sobre nuevos conjuntos de datos, sin que haya sido explícitamente programado para tratar con cada caso específico. Se espera que los clasificadores difusos puedan separar correctamente un máximo número de patrones, mientras que el número de características y el número de reglas difusas puede mantenerse bajo para incrementar la generalidad del sistema y mejorar su interpretabilidad.

Para un clasificador sencillo, se puede obtener un sistema de clasificación basado en información proporcionada por expertos humanos; sin embargo, es difícil construir un sistema de clasificación difusa para un sistema complejo, donde la experiencia del experto es incompleta⁴. Uno de los tipos de clasificador difuso, quizás el más común, es el basado en reglas si-entonces, donde cada una de las características del objeto es asociada a una variable lingüística a la cual pertenece con cierto grado. Este grado de pertenencia es representado dentro del sistema con una función que se denomina función de pertenencia.

Los clasificadores difusos incluyen una variedad de parámetros configurables, usualmente dependientes de la apreciación del diseñador o de la experiencia aportada por personas que se desempeñan en el área determinada. La identificación de los parámetros en un sistema difuso se compara a un problema de optimización, donde se busca determinar valores para los parámetros que optimicen el clasificador basándose en un criterio de evaluación dado. Por lo tanto, pueden también aplicarse técnicas de optimización y búsqueda para la identificación de parámetros⁵. Una técnica de optimización y búsqueda ampliamente estudiada, son los algoritmos genéticos, destacados por un buen balance entre exploración y explotación del espacio de búsqueda⁶.

El aprendizaje efectivo de los datos para el correcto funcionamiento del clasificador difuso depende de parámetros asociados a los elementos del mismo. La selección puede ser realizada de manera manual con la ayuda del experto, sin embargo, a menudo resulta conveniente y más efectivo que estos sean generados automáticamente mediante la utilización de una técnica de optimización y búsqueda. Los algoritmos genéticos, son una técnica de optimización y búsqueda que imita el proceso de evolución natural y en teoría presentan un óptimo balance entre la exploración (búsqueda global) y explotación (búsqueda local) del espacio de búsqueda⁷. Pueden ser usados para la identificación de parámetros en el sistema de clasificación difuso.

Estos algoritmos usan principios inspirados por la genética de la población natural, y proveen una búsqueda robusta en espacios complejos; de este modo ofrecen un enfoque válido a problemas que requieren búsquedas eficientes y eficaces⁶. También pueden ser hibridados con otras técnicas de optimización y búsqueda con el fin de aumentar sus capacidades. Por ejemplo, incorporar métodos de búsqueda local dentro de la operación de un algoritmo genético puede ayudar a superar la mayoría de los obstáculos que surgen como resultado de tener tamaños de población finitos⁷. Además, un sistema híbrido puede acelerar la velocidad de convergencia mientras se preserva la capacidad del algoritmo genético de evitar quedar atrapado fácilmente en mínimos locales.

Tomando como base lo expuesto, la investigación propone diseñar un clasificador difuso optimizado mediante un algoritmo genético híbrido.

Metodología

La investigación es proyectiva⁸, se inicia con una revisión documental de alternativas de optimización de los clasificadores difusos, el uso de las técnicas de agrupamiento para la generación inicial de la base de reglas, maneras de optimizar los parámetros de las funciones de pertenencia, cómo aplicar algoritmos genéticos para la identificación automática de dichos parámetros, cómo utilizar una función de objetivo múltiple para la maximización de la exactitud del clasificador, al igual que la minimización del conjunto de reglas para la conservación de la interpretabilidad de las variables lingüísticas en el clasificador difuso.

La siguiente fase es diseñar la arquitectura de construcción y las partes que lo conforman, incluyendo el sistema difuso de clasificación y el algoritmo genético híbrido a dos fases para el entrenamiento, que optimiza los objetivos expuestos previamente. Luego, se implementa y evalúa el prototipo. Se evalúa teniendo en cuenta atributos como la exactitud del clasificador en relación al conjunto de datos de entrenamiento, es decir, la capacidad de aprender el patrón de datos de entrenamiento. La exactitud se mide con la capacidad de generalización, es decir, la capacidad de predecir correctamente la etiqueta de clase de objetos no vistos anteriormente por el clasificador.

También se tiene en cuenta la forma de las funciones de pertenencia, la cantidad de variables lingüísticas utilizadas, el tamaño del conjunto de reglas y la cantidad de variables utilizadas en las reglas, para realizar un análisis sobre la interpretabilidad del sistema de clasificación y la capacidad de ser asimilado por un usuario humano para describir la tarea de clasificación. Finalmente, se compararan los resultados obtenidos sobre rendimiento e interpretabilidad con otros trabajos y clasificadores reportados en la literatura sobre los mismos datos de prueba, para concluir sobre la efectividad del clasificador diseñado.

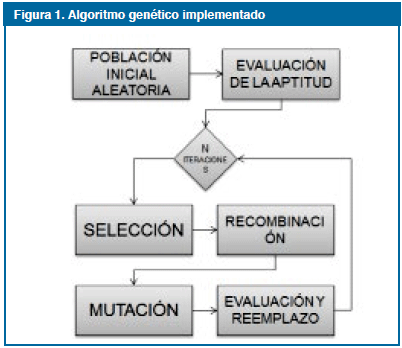
El desarrollo del trabajo se realiza siguiendo una metodología de desarrollo iterativo e incremental. Se implementa un sistema de clasificación basado en reglas difusas de la forma si-entonces, que utiliza un algoritmo genético para optimizar la selección de los parámetros de las funciones de pertenencia y la base de reglas durante el proceso de entrenamiento del clasificador (Figura 1).

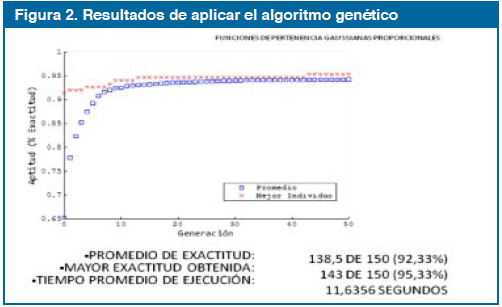
El algoritmo genético está a su vez hibridado con la técnica de búsqueda Fuzzy C-Means Clustering, para mejorar su efectividad. El híbrido es un algoritmo a dos fases, que ejecuta la técnica de agrupamiento clustering para construir una base de reglas inicial, con el fin de aumentar la calidad de las soluciones y producir un sistema final considerablemente interpretable. Posteriormente, se aplica un algoritmo genético modificado, que optimiza simultáneamente la base de reglas y los parámetros de las funciones de pertenencia, utilizando el sistema inicial como punto de partida para acelerar la velocidad de convergencia en las regiones más prometedoras, sin dejar atrás su capacidad de exploración del espacio de búsqueda, los resultados de aplicar este algoritmo se muestran en la Figura 2.

La función de evaluación utilizada en el algoritmo genético está orientada a optimizar un objetivo múltiple: la maximización de la exactitud del clasificador y aunado a la minimización del número de reglas. Para la función multiobjetivo, el algoritmo genético incorpora una población con cadenas de implementación doble de codificación real para las funciones pertenencia y codificación binaria para el conjunto de reglas. Se utiliza, para cada uno de los atributos que describen el objeto a clasificar, un número de variables lingüísticas pequeño «tres», para contribuir en la mejora de la interpretabilidad.

Resultados

En la evaluación del sistema, se comprueba con conjuntos de datos referenciales «benchmark»; el primer caso puede constituir un problema de clasificación de datos sintéticos que pueden representar un tipo de enfermedad «E1», cuyo estudio es común entre investigaciones de sistemas de clasificación; y el segundo caso representa una variación en los datos que pueden representar una segunda enfermedad «E2». Con los resultados obtenidos se realizan comparaciones de desempeño con otras investigaciones y sistemas desarrollados.

El problema de clasificación de la data sintética 1 «DA1», es un problema referencial (benchmark) en estudios de clasificación y reconocimiento de patrones. Contiene 150 medidas que representan dos tratamientos para la enfermedad 1, con cuatro características; dos características para el tratamiento 1 y dos características para el tratamiento 2; en 50 muestras para cada una de tres tipos de pacientes clasificados por edad: pacientes menores de 20 años, pacientes entre 20 a 40 años, y pacientes mayores de 40 años.

El sistema propuesto, consta de tres funciones de pertenencia representativas de tres variables lingüísticas: «corto», «mediano» y «largo»; para cada una de las cuatro variables de entrada del clasificador, correspondientes a las características en el conjunto de datos. En la elaboración del sistema de clasificación, se utiliza dentro del ambiente MATLAB, la herramienta Fuzzy Logic Toolbox, que provee funciones y aplicaciones para el análisis, diseño y simulación de sistemas basados en lógica difusa.

En una primera iteración se utilizaron funciones de pertenencia triangulares para representar los valores de las variables lingüísticas. La base de reglas, presenta cuatro reglas previamente definidas por⁹, luego se establecen restricciones a las posibles variaciones en la distribución de funciones de pertenencia para simplificar el sistema de inferencia e incrementar la interpretabilidad del sistema por un experto humano. Se construye el algoritmo genético básico que tendría el objetivo de mejorar el porcentaje de exactitud en la clasificación de los datos de entrenamiento, únicamente optimizando los parámetros de las funciones de pertenencia de las variables de entrada.

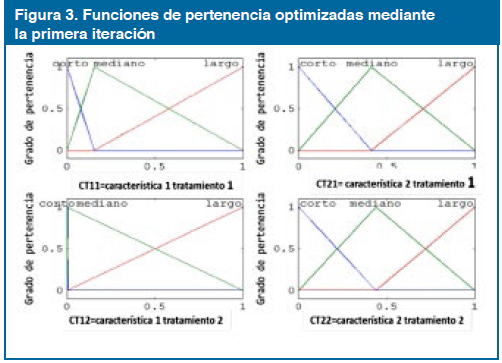
Luego de la ejecución de este sistema inicial, se observa un techo en el mejoramiento de la exactitud del clasificador en el problema de la Flor de Iris, que permite establecer criterios para la generación de sistemas de clasificación difusos fácilmente interpretables y explicables por parte de humanos (Figura 3). En la segunda iteración, se disminuye las restricciones establecidas en la primera iteración, con lo cual el espacio de búsqueda para la evolución de funciones de pertenencia resulta demasiado grande como para atender a condiciones de interpretabilidad. La cantidad de posibles soluciones no compensó la carga computacional agregada para el problema de E1.

Varios autores^10,11, sugieren el uso de funciones de pertenencia Gaussianas, exponen que estas sirven para no dejar partes del espacio de entrada sin cubrir como sucede con las funciones de pertenencia triangulares², al mismo tiempo que los modelos resultantes presentan mayor exactitud¹². En la tercera iteración se utilizan funciones de pertenencia Gaussianas para representar los valores de las variables lingüísticas, obteniendo un mejor desempeño. Se diseñan dos versiones: una que permita la evolución independiente de los parámetros de las funciones; la otra tiene una restricción que mantiene una concordancia entre las funciones de pertenencia. El uso de funciones de pertenencia Gaussianas, en particular, las funciones de pertenencia independientes, muestran un incremento en techo de exactitud, aunque se obtiene una menor interpretabilidad.

En la cuarta iteración, se propone evolucionar la base de reglas del clasificador, junto con los parámetros de las funciones de pertenencia, con el fin de aumentar el proceso de optimización y crear un clasificador más complejo. Para evolucionar la base de reglas simultáneamente con los parámetros de las funciones de pertenencia, se modifica el algoritmo genético y la codificación de los cromosomas. Una parte de los cromosomas se codifican de forma mixta, conservando la codificación original para guardar los valores para los parámetros de las funciones de pertinencia. La otra porción de los cromosomas se codifican con una representación binaria, siendo más conveniente para representar la base de reglas.

El uso de codificaciones de población mixtas resulta ser práctico para la optimización simultánea de elementos de diferente naturaleza, al mismo tiempo que los operadores modificados del algoritmo genético siguen manteniendo sus propiedades. El algoritmo genético funciona con buena efectividad sobre la optimización de objetivos múltiples, comprobando que se puede generar un clasificador con un alto desempeño y mínimo número de reglas, aunque se utilicen pocas funciones de pertenencia.

Para la quinta iteración se desea mejorar la velocidad de convergencia del algoritmo genético y aumentar su capacidad para conseguir mejores soluciones en la configuración del clasificador. Para ello se modifica el proceso de optimización, combinando el algoritmo genético con otra técnica de optimización y búsqueda, en sus estudios^12,13,14 proponen la inicialización del espacio de búsqueda, utilizando métodos iterativos como algoritmos de agrupamiento para descubrir reglas difusas a partir de los datos de entrenamiento. El propósito de los algoritmos de agrupamiento es identificar agrupaciones naturales en la información de conjuntos de datos amplios para producir una representación concisa del comportamiento de un sistema¹⁵. Fuzzy Logic Toolbox provee funciones para el análisis de datos a través de algoritmos de Clustering, entre ellos el algoritmo Fuzzy C-Means Clustering (FCM), el cual es una técnica de agrupamiento de datos, en el que cada punto de dato pertenece en cierto grado a cada grupo (cluster).

El FCM produce principalmente dos resultados, el conjunto difuso que indica el valor de pertenencia de cada punto para cada grupo, y las coordenadas n-dimensionales de los centroides o baricentros de los grupos. En otras investigaciones^16,12, se utiliza Fuzzy Clustering para producir un número de grupos igual o mayor al número de clases posibles. Luego se formula una regla para cada grupo, de forma que cada variable de entrada corresponda a una sola función de pertenencia.

Se propone utilizar un nuevo método heurístico para la formulación de reglas utilizando FCM como paso previo, en combinación a la optimización interpretada por el algoritmo genético, para lograr una hibridación en forma de algoritmo a dos fases. El método fija inicialmente la cantidad de funciones de pertenencia (variables lingüísticas) para determinar, a partir de los grupos, los parámetros de estas funciones en anticipación a la formulación de las reglas.

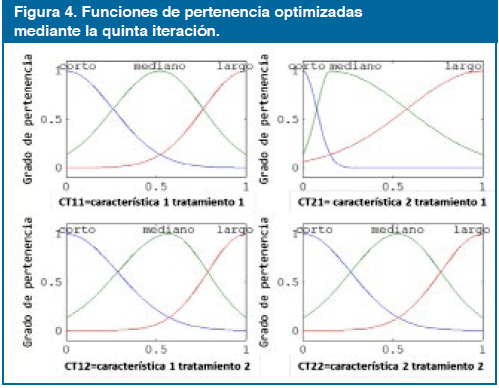
El nuevo método propuesto para generar sistemas iniciales, evidencia ser más efectivo; utilizar un procedimiento heurístico para derivar las funciones de pertenencia manteniendo las restricciones resulta ser práctico y de bajo costo computacional. Además, la inicialización del espacio de búsqueda genera mejores soluciones con respecto a la exactitud del clasificador, aunque el número de reglas no se pueda llevar al mínimo, las reglas pertenecientes a una misma clase resultan muy similares, permitiendo ser combinadas intuitivamente por un humano o algún algoritmo objeto de otro trabajo. La proposición del uso de tres variables lingüísticas facilita la formulación de las reglas en lenguaje humano aumentando aún más las interpretabilidad del sistema. La Figura 4 muestra las Funciones de Pertenencia Optimizadas mediante la quinta iteración.

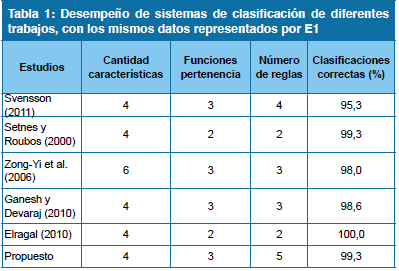
Los problemas utilizados para la comprobación del presente trabajo, son problemas referenciales (benchmark) en estudios de clasificación y reconocimiento de patrones. Esto permite la comparación de los resultados con otros trabajos en la literatura. La Tabla 1 muestra los resultados de diferentes trabajos sobre el problema de clasificación con los mismos datos empleados en el caso de para tratamiento 1. Los trabajos que obtienen mayor porcentaje de exactitud en la clasificación fueron los de^12,17 sin embargo éstos usan un modelo de clasificador que emite como salida un único valor numérico, el cual es extrapolado para obtener la etiqueta de clase.

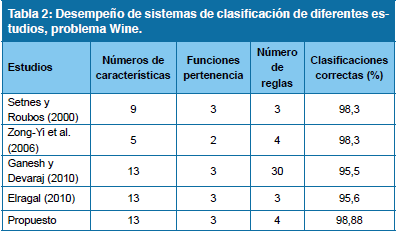
Trabajar con un número de reglas menor al número de dos clases, que se interpolan para generar salidas de tres clases distintas, descarta la posibilidad de interpretación del sistema por parte de humanos. En contraste, el sistema utilizado en este trabajo emite una salida para cada clase y determina la etiqueta de clase mediante el principio de “el ganador se lo lleva todo” (winner-take-all). En cualquier caso, las funciones de pertenencia y las variables lingüísticas de este trabajo, podrían considerarse como las que poseen mayor sentido semántico. Por otra parte, la Tabla 2 muestra los resultados de diferentes trabajos sobre el problema representados por E2.

Los estudios de^12,13, incorporan un método de selección de características para reducir la cantidad de variables de entradas; sin embargo, no superan el porcentaje de exactitud de este estudio, que resulta ser el mayor de entre los trabajos comparados, con una cantidad viable de reglas. La minimización de características podría ser un punto interesante de incorporar como objetivo adicional al método de optimización.

Conclusiones

El principal hallazgo es que el procedimiento heurístico para derivar las funciones de pertenencia manteniendo las restricciones, de la quinta iteración resulta ser más efectivo y de bajo costo computacional. El clasificador propuesto genera resultados con exactitud, así como funciones de pertenencia con mayor sentido semántico, comparados con resultados de otros estudios contrastados.

Los resultados de esta investigación sugieren la posibilidad de implementar clasificadores difusos semejantes al diseñado en entornos donde se requiera la verificación o entendimiento de los procesos automáticos por parte del humano, reemplazando procesos de caja negra.

Referencias

1. Tan P, Steinbach M, Kumar V. Introduction to Data Mining. Boston:Pearson;2005.        [ Links ]

2. Kuncheva L. Studies in Fuzziness and Soft Computing, Fuzzy Classifier Design. UK:Physica-Verlag; 2000.        [ Links ]

3. Toosi AN, Kahani M. A new approach to intrusion detection based on an evolutionary soft computing model using neuro-fuzzy classifiers. Computer communications, 2007;30(10):2201-12.        [ Links ]

4. Zong-yi X, Yuan-long H, Zhong-zhi T, Li-min J. Construction of Fuzzy Classification System Based on Multi-objective Genetic Algorithm. Sixth International Conference on Intelligent Systems Design and Applications, ISDA’06 IEEE Computer Society. 2006;2: 1029–34.        [ Links ]

5. Yen J, Langari R. Fuzzy logic: intelligence, control, and information. USA:Prentice-Hall Inc;1999.        [ Links ]

6. Cordón O, Herrera F, Hoffmann F, Magdalena L. Genetic fuzzy systems. Singapore: World Scientific Publishing Company;2001.        [ Links ]

7. El-Mihoub T, Hopgood A, Nolle L, Battersby A. Hybrid Genetic Algorithms: A Review. Engineering Letters, 2007;13(2):124-37.        [ Links ]

8. Hurtado de Barrera J. Metodología de la Investigación Holística. Venezuela: Fundación SYPAL; 2012.        [ Links ]

9. Ishibuchi H, Nozaki K, Yamamoto N, Tanaka H. Selecting fuzzy ifthen rules for classification problems using genetic algorithms. IEEE Transactions on Fuzzy Systems, 1995;3(3):260-70.        [ Links ]

10. Abe S. Pattern Classification: Neuro-fuzzy methods and their comparison. UK:Springer Verlag;2001.        [ Links ]

11. Chiu, S. Extracting fuzzy rules from data for function approximation and pattern classification. Fuzzy Information Engineering: A Guided Tour of Applications. New Jersey:John Wiley & Sons;1997.        [ Links ]

12. Setnes M, Roubos H. GA-fuzzy modeling and classification: complexity and performance. IEEE Transactions on Fuzzy Systems, 2000;8(5):509-22.        [ Links ]

13. Zong-Yi X, Yuan-Long H, Yong Z, Li-Min J. A Multi-objective GA based Fuzzy Modeling Approach for Constructing Pareto-optimal Fuzzy systems. International Journal of Computer Science and Network Security, 2007;6(5):213-19.        [ Links ]

14. Pulkkinen P. Multiobjective identification of fuzzy models with hybrid methods. International Journal of Approximate Reasoning, 2008;48(2):526-43.        [ Links ]

15. D’Urso P, Massari R. Fuzzy clustering of human activity patterns. Fuzzy Sets and Systems, 2013;215:29-54.        [ Links ]

16. Abonyi J, Szeifert F. Supervised fuzzy clustering for the identification of fuzzy classifiers. Pattern Recognition Letters, 2003;24(14):2195- 207.        [ Links ]

17. Elragal H. Using Swarm Intelligence for Improving Accuracy of Fuzzy Classifiers. International Journal of Electrical and Computer Engineering, 2010;5(2):105-12.        [ Links ]