Optimización de la Deshidratación Osmótica con Pulso de Vacío de Láminas de Sardinas

Genara Reyes M. ¹, Otoniel Corzo ¹, Nelson Bracho ² y Yusbelis Rodríguez ¹

¹ Departamento de Tecnología de Alimentos. Venezuela.

² Departamento de Estadística. Núcleo de Nueva Esparta. Universidad de Oriente. Venezuela. E-mail: genareyes@cantv.net

RESUMEN

El objetivo principal de este estudio fue optimizar la transferencia de masa ocurrida durante la deshidratación osmótica con pulso de vacío de láminas de sardina mediante los métodos gráfico y función deseada. Las sardinas se cortaron en láminas y se sumergieron simultáneamente en una salmuera de concentración y temperatura dada según un diseño compuesto central de 3 bloques. Las condiciones experimentales fueron concentraciones de 17; 19; 22; 25; 27 y 28,6% de NaCl, temperaturas de 28,6; 30; 32; 34 y 35,4°C y tiempos de 113; 140; 180; 220 y 247 min. A cada lámina se le determinó el peso, contenido de humedad y NaCl, se calculó la pérdida de agua, pérdida de peso y ganancia de sal. Los datos se analizaron mediante un ANOVA y regresión lineal múltiple para obtener los modelos de las variables estudiadas, luego se determinó la zona óptima de la deshidratación osmótica utilizando los métodos gráfico y la función deseada. Por el método gráfico se obtuvo una zona óptima correspondiente a una concentración entre 23,9 y 24,6% de NaCl, un tiempo entre 204 y 207 min y una temperatura de 32,2°C para tener una pérdida de agua de 0,23 g agua/g, una ganancia de sal de 0,07 g NaCl/g y una pérdida de peso de 0,17 g/g. Por el método de la función deseada, las condiciones óptimas correspondieron a 23,9% NaCl, 207 min y 32,2°C.

Palabras clave: Optimización, superficie de respuesta, deshidratación osmótica con pulso de vacío, sardina.

Optimization of Vacuum Pulse Osmotic Dehydration of Sardine Sheets

ABSTRACT

The aim of this study was to optimize the mass transfer occurred during the vacuum pulse osmotic dehydration of sardine sheets by surface response and desired function methodologies. Sardines were cut into sheets and simultaneously immersed into a brine at given concentration and temperature according to a composite central rotatable design with 3 blocks. The experimental condition were 17; 19; 22; 25; 27 and 28.6% NaCl, 28.6; 30; 32; 34 and 35.4°C and 113; 140; 180; 220 y 247 min. Each sheet was weighed and moisture and salt contents were determined, then water and mass loss, and salt uptake were calculated. Data were analyzed by ANOVA and multiple lineal regressions to obtaining the models for studied variables, and then optimum zone for osmotic dehydration was found by response surface and desired function methodologies. By response surface, an optimum zone of concentration from 23.9 to 24.6% of NaCl, time from 204 to 208 min and temperature of 32.2°C was attained related to a water loss of 0.23 g water/g, uptake salt of 0.07 g NaCl/g and mass loss of 0.17 g/g. The optimum conditions of 23.9% NaCl, 207 min and 32.2°C were attained by desired function.

Key words: Optimization, response surface, vacuum pulse osmotic dehydration, sardine.

Recibido: 21 / 03 / 2006. Aceptado: 06 / 09 / 2007.

INTRODUCCIÓN

La sardina (Sardinella aurita) es un pez pelágico de pequeño tamaño, de hábito filtrador en su alimentación, planctófaga, y que abunda en el océano atlántico tropical, tanto en las costas africanas como americanas. En las costas venezolanas se encuentra principalmente en el área de surgencia de la región nororiental [29]. Para el año 2004, a nivel mundial la captura de Sardinella aurita estuvo por el orden de 470.000 toneladas. En Venezuela las estadísticas de captura de sardinas se han mantenido relativamente constantes en un valor aproximado de 155.000 toneladas anuales en los últimos diez años hasta el año 2004, a partir del cual se observó un descenso brusco en las capturas debido a la pesca indiscriminada y factores climáticos, entre otros, alcanzando niveles aproximados de 25 toneladas anuales [19]. El 70% de la producción se utiliza en la industria conservera y el 30% restante se consume fresca, se exporta en forma de troncos congelados principalmente a Brasil o se emplea como carnada para la captura de especies de mayor valor comercial [19].

Un método de conservación de los alimentos es la deshidratación osmótica en el cual se remueve parte del agua de un alimento sumergiéndolo en una solución hipertónica. Durante el proceso fluye agua desde el alimento hacia la solución mientras que se transfiere soluto de la solución al alimento. La deshidratación osmótica se ha utilizado como un pre-procesamiento o paso previo al secado y refrigeración de alimentos, incluyendo frutas y vegetales, carnes y productos marinos. El efecto beneficioso de la deshidratación osmótica incluye la alta calidad del producto final y el bajo requerimiento de energía [2].

La velocidad a la cual ocurre la transferencia de masa durante la deshidratación osmótica aumenta al incrementar la concentración de la solución osmótica, tiempo de inmersión, temperatura, relación de solución osmótica-alimento, área superficial del alimento y agitación de la solución [5, 6, 9, 24, 31]. La transferencia de masa se puede acelerar mediante la aplicación de un pulso de vacío durante un corto tiempo al inicio del proceso [7, 8]. Esto permite la introducción de la solución osmótica dentro de los poros del alimento por un mecanismo hidrodinámico, aumentando así el área de transferencia de masa, la transferencia de agua y soluto, y a la vez se manifiesta el efecto de la estructura del alimento en la transferencia de masa [15].

La metodología de superficies de respuesta se ha usado amplia y efectivamente en la investigación del desarrollo, mejoramiento de productos y procesos debido a su utilidad en la optimización de éstos [1, 21, 22, 25, 32, 33]. Esta metodología requiere del uso de técnicas de diseño experimental para investigar y conocer la forma funcional del proceso que genera una o más variables respuesta influenciadas por varios factores o variables independientes (superficie de respuesta). Un diseño experimental apropiado es fundamental para permitir explorar el proceso y llevarlo a su optimización, obteniendo el máximo o el mínimo si ellos existen, o determinar la región en el espacio total de los factores en la cual se satisfacen ciertas condiciones [27].

La deshidratación osmótica se debe optimizar para minimizar los costos, maximizar las ganancias, reducir el empleo de ingredientes o preservantes costosos, incrementar las características deseables del alimento sin comprometer su inocuidad durante el desarrollo de un nuevo producto o para el mejoramiento de uno existente [3]. Optimizar es seleccionar la mejor alternativa a partir de un grupo específico y para ello se requiere una relación que describa las opciones potenciales y el criterio para decidir cuál es la mejor [23]. Hay diversos métodos para optimizar, tales como el gráfico convencional [13, 20, 33, 36], el gráfico mejorado [14, 16, 17], la función deseada [10, 18, 31] y el procedimiento de la superficie extendida [18, 31].

Los objetivos de este estudio fueron modelar los efectos de la concentración y temperatura de la solución osmótica y el tiempo de deshidratación sobre los cambios de masa (pérdida de agua, pérdida de peso y ganancia de sal) en la sardina durante la deshidratación osmótica con pulso de vacío, y obtener la región experimental en la cual la deshidratación sea óptima.

MATERIALES Y MÉTODOS

Preparación de las muestras

Se utilizaron sardinas recién capturadas y sin daños mecánicos, compradas en el mercado de los Cocos de la ciudad de Porlamar, estado Nueva Esparta, Venezuela, durante el periodo agosto a septiembre del 2001, con longitud entre 14 y 18 cm, peso entre 38 y 65 g, humedad de 81 ± 1%, sal de 0,25 ± 0,05% NaCl y grasa entre 3,5 y 4,5%. Se mantuvieron en hielo durante su traslado y preparación posterior. Las sardinas se filetearon, y luego los filetes se cortaron por la zona más cercana a la cabeza con un molde cortador de acero inoxidable para obtener láminas de 20 ± 0,5 mm de largo, 13 ± 0,5 mm de ancho y 6,3 ± 0,2 mm de espesor. Se obtuvieron dos láminas por cada filete y para el estudio se utilizaron 250 sardinas. Se determinó el contenido de humedad por diferencia de peso hasta peso constante en estufa a 105°C [4], el contenido de sal (%NaCl) por el método de Mohr [4] utilizando 1,000 g de muestra y una solución de Nitrato de Plata 0,100 N, y el contenido de grasa mediante extracción continua en éter etílico en un equipo Goldfish Labconco (Labconco Co, EUA) [4].

Deshidratación osmótica

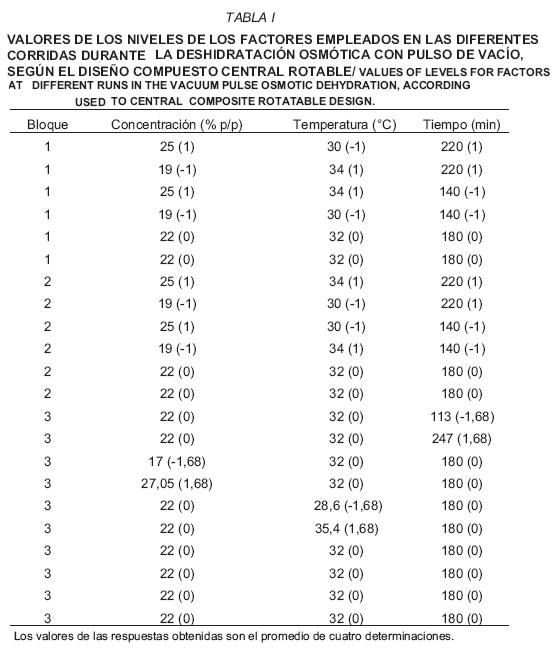
Al azar se tomaron cuatro láminas de sardina y se colocaron en una celda de cuatro compartimientos (grupo experimental), para así asegurar que las láminas no interfirieran unas con otras durante la deshidratación y lograr la inmersión y extracción simultánea en la solución osmótica. A cada lámina del un grupo se le determinó su peso inicial. El proceso de deshidratación osmótica se llevó a cabo en un desecador con conexión de vacío marca Pirex, modelo 3,8 l con llave 8 para vacío (Corning Incorporated Life Sciences, EUA 2000) que contenía la solución osmótica, el cual fue colocado en un baño de agua regulado marca Julabo SW-20C (Julabo Labortechnik GmbH, Alemania 2000) a una temperatura constante y provisto de agitación. El grupo experimental se sumergió en una solución de NaCl de concentración y temperatura dadas según el diseño compuesto central rotable (TABLA I), luego se aplicó un vacío de 11,1 kPa durante 10 min seguido de 10 min de relajamiento, se continuó la deshidratación a presión atmosférica, y se extrajo al cabo de un tiempo determinado según el diseño experimental (TABLA I). Cada lámina del grupo, se escurrió, se secó superficialmente colocándola sobre papel absorbente para retirar la salmuera adherida superficialmente, luego se pesó y se le determinó el contenido de humedad y NaCl.

La pérdida de agua (PA), pérdida de peso (PP) y ganancia de sal (GS), que experimentaron las láminas de sardina como consecuencia del tratamiento osmótico, se calcularon mediante las siguientes ecuaciones, según [5]:

(1)

(2)

(3)

Donde M_o y M_t son las masas inicial y final de la lámina de sardina respectivamente, X_wo y X_wt son las fracciones en peso de agua de la lámina al inicio y al final del tratamiento osmótico, respectivamente, X_so y X_st son las fracciones en peso de NaCl de la lámina al inicio y al final del tratamiento osmótico, respectivamente.

Superficies de respuesta

Las superficies de respuesta, o modelos, son funciones matemáticas aproximadas que relacionan las variables respuesta con los factores, tales como polinomios de segundo orden [18]:

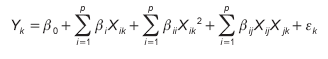(4)

Donde Y_k es la respuesta observada cuando los p factores son aplicados en los niveles X_ik, b₀ es la constante,b_i, b_ii, y b_ij, son los coeficientes de los términos lineales, cuadráticos y cruzados, e_k el error experimental y k = 1, 2, …, n.

Optimización

Para la optimización de la deshidratación osmótica se emplearon los métodos gráfico y la función deseada. El método gráfico consiste en obtener las gráficas de contorno de cada respuesta, de acuerdo a los modelos correspondientes, y luego sobreponerlas para lograr una optimización multirrespuesta. El método de la función deseada consiste en estandarizar cada respuesta en una función d_n cuyo valor varía de 0 (fuera del rango deseado) a 1 (en el rango deseado). Derringer y Suich [11] usaron la siguiente función deseada:

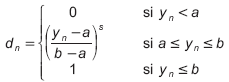  (5)

Donde a y b son valores constantes correspondientes a las restricciones de la respuesta y es una constante positiva.

Para todas las funciones deseadas de las diferentes respuestas, se define una función total D (0 £ D £ 1) como:

D=F (d₁,d₂,...,d_n)     (6)

Igual al promedio geométrico de las n funciones deseadas individuales:

(7)

Un valor alto de D indica las mejores funciones del sistema, lo cual se considera como las soluciones óptimas. Los valores óptimos se determinan a partir de los valores individuales de las funciones deseadas que maximizan D.

Tratamiento estadístico de los datos

Se utilizó un diseño compuesto central rotable [26] de tres factores con tres niveles, dos puntos estrella, seis repeticiones del punto central, con bloques incompletos y aleatorios. Los bloques se formaron con sardinas capturadas en una misma fecha. Dos bloques eran de 6 corridas cada uno y el otro bloque era de 8 corridas, teniéndose así un total de 20 experiencias. En la TABLA I se presentan los niveles reales y codificados de los factores concentración, temperatura y tiempo. Las superficies de respuesta, modelos, se obtuvieron al estudiar las relaciones de las variables respuestas en función de los factores analizados mediante regresión lineal múltiple y análisis de varianza. Para los ajustes correspondientes de los modelos explicativos de la variación de masa, se analizó la suma secuencial de éstos considerando el promedio de la respuesta, los efectos lineales, los efectos cruzados o interacciones y los efectos cuadráticos de los factores concentración (C), temperatura (T), y tiempo de deshidratación (t). Con el fin de evitar en lo posible la inestabilidad numérica se mantuvo la jerarquía de los modelos [28, 30], o sea que los efectos lineales de los tres factores estudiados fueran significativos o no, se incluyeron dentro de los modelos. La adecuación de los modelos se realizó eliminando aquellos efectos no significativos (P>0,05), evaluando los coeficientes de determinación (R²) del modelo ajustado, utilizando la validación cruzada [34, 35]. y considerando la suma de cuadrados del error de predicción (PRESS). Un valor bajo de PRESS, y un valor alto del R² de predicción comparable con el R² ajustado, implica que el modelo ajustado es adecuado para predecir. Para optimizar el sistema constituido por las tres respuestas de interés, se empleó el método gráfico convencional [16] y el de la función deseada [11]. Para todos los análisis se empleó el paquete estadístico Design Expert 6,01 (Stat-Ease, Inc. Minneapolis. EUA) [12].

RESULTADOS Y DISCUSIÓN

Variación de masa

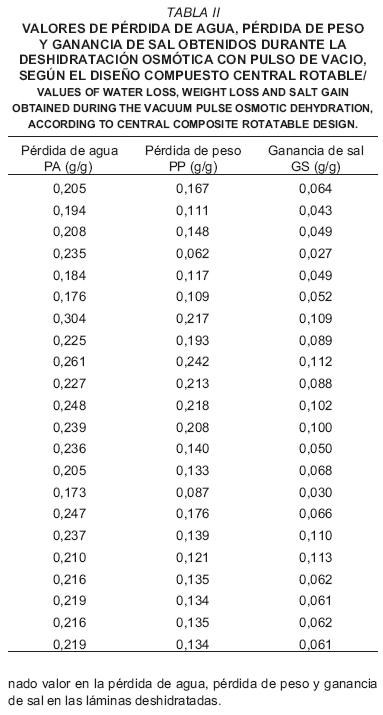
En la TABLA II se muestran los valores promedios de las respuestas pérdida de agua, pérdida de peso y ganancia de sal obtenidas durante la deshidratación osmótica de la sardina, según el diseño compuesto central rotable empleado. Se puede observar que los valores de pérdida de agua variaron entre 0,173 y 0,304 g agua/g, de pérdida de peso entre 0,062 y 0,242 g/g y de ganancia de sal entre 0,027 y 0,113 g NaCl/g.

Obtención de los modelos

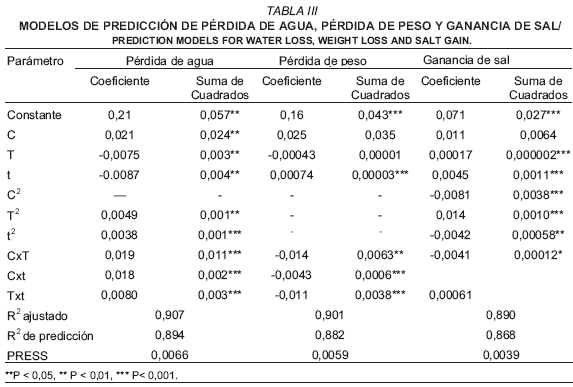
Los modelos ajustados se presentan en la TABLA III, y explican el 90,7; 90,1 y 89,0% de la variabilidad en la pérdida de agua, pérdida de peso y ganancia de sal, respectivamente, con al menos 95% de nivel de confianza. Los valores PRESS son bajos y los coeficientes de determinación para la predicción son muy cercanos a los correspondientes para el ajuste, por lo tanto estos modelos son adecuados para predecir los cambios de masa estudiados.

Los modelos correspondieron a:

PA = 0,21+0,021 C - 0,0075 T - 0,0087 t + 0,0049 T² + 0,0038 t² + 0,019 C T + 0,018 C t + 0,0080 T t     (8)

PP = 0,16 + 0,025 C - 0,00043 T + 0,00074 t - 0,014 C T - 0,0043 C t - 0,011 T t   (9)

GS = 0,071 + 0,011 C + 0,00017 T + 0,0044 t - 0,0081 C² + 0,014 T² - 0,0042 t² - 0,0041 C T - 0,00061 C t   (10)

Similares modelos fueron obtenidos para explicar los cambios de masa en láminas de sardina deshidratadas osmóticamente a presión atmosférica [33]. Los modelos permiten determinar las condiciones de temperatura, concentración y tiempo de deshidratación requeridas para obtener un determinado valor en la pérdida de agua, pérdida de peso y ganancia de sal en las láminas deshidratadas.

Optimización

La optimización de los niveles de los factores se realizó utilizando el método gráfico y el método de la función deseada, considerando que las láminas de sardina deshidratadas osmóticamente con pulso de vacío tuvieran la mayor pérdida de agua, la mayor ganancia de sal, y la menor pérdida de peso.

Método gráfico

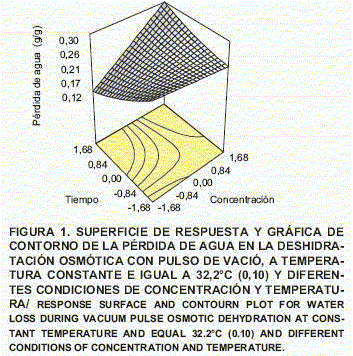
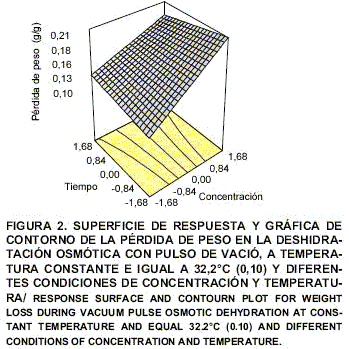
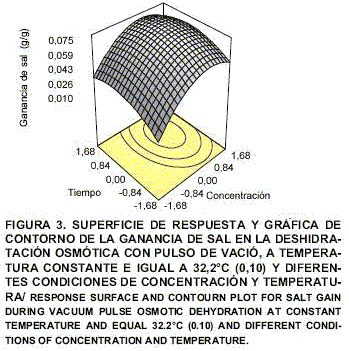
Con el fin de obtener la representación gráficas de la superficie de repuesta y de contorno se realizó el análisis de perturbación, consistente en variar el valor de uno de los factores, manteniendo constantes los de los otros factores, y examinar la sensibilidad de la variable respuesta a dicho cambios. Se encontró que las tres respuestas eran poco sensibles a los cambios en el valor de la temperatura, por lo tanto se consideró tomar un valor constante de este factor para lograr la optimización. Con la finalidad de conocer el valor de la temperatura dentro del rango experimental que fuera el más apropiado para la optimización, se obtuvieron gráficas de contorno en función de la concentración y tiempo a diferentes temperaturas, encontrándose que para un valor codificado de temperatura igual a 0,10 (32,2°C) se satisfacían las restricciones de la optimización. En las FIGS. 1, 2 y 3 se presentan las superficies de respuesta y las gráficas de contorno correspondientes. Se puede observar en ellas que: 1) la pérdida de agua y la pérdida de peso aumentan al incrementar el tiempo y la concentración de la solución osmótica, 2) la ganancia de sal aumentan al incrementar el tiempo y la concentración hasta lograr un máximo y luego disminuye, 3) las variaciones siguen las tendencias correspondientes a las formas matemáticas de una silla, una loma ascendente y un punto máximo, respectivamente.

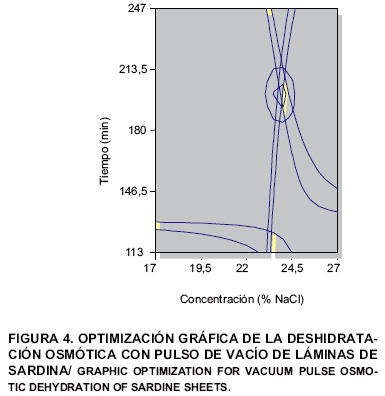
La zona óptima correspondiente a la sobreposición de las gráficas de contorno de pérdida de agua, pérdida de peso y ganancia de sal se presenta en la FIG. 4. Esta se logra a una concentración de la solución osmótica entre 23,9 y 24,6% de NaCl, tiempo de deshidratación entre 204 y 207 min y una temperatura de 32,2°C. En esta zona óptima, la pérdida de agua varió entre 0,230 y 0,245 g agua/g, la pérdida de peso entre 0,168 y 0,170 g/g y la ganancia de sal entre 0,075 y 0,076 g NaCl/g. En la deshidratación osmótica a presión atmosférica 33 la zona óptima se logró a una concentración de 26,5% de sal, una temperatura de 31,7°C y un tiempo de 245 min, donde la pérdida de agua fue de 0,260 g/g, la pérdida de peso de 0,145 g/g y la ganancia de sal de 0,187 g/g. Estos resultados hacen evidente el efecto positivo del pulso de vacío en la deshidratación osmótica de la sardina.

Método de la función deseada

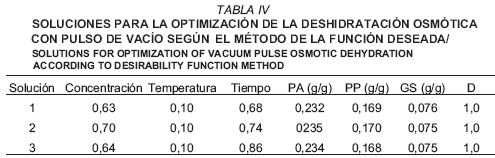
Para la optimización se tomaron las siguientes restricciones: a) concentración y tiempo entre 17 y 27% NaCl y 113 y 247 min, respectivamente, b) pérdida de agua entre 0,230 y 0,245 g agua/g, c) pérdida de peso entre 0,168 y 0,170 g/g, y d) ganancia de sal entre 0,075 y 0,076 g NaCl/g. Las tres soluciones obtenidas se presentan en la TABLA IV y se puede ver que todas tienen una función deseada igual a la unidad, por lo tanto cualquiera de ellas se puede considerar como la solución óptima. Sin embargo, tomando en cuenta la economía del proceso de deshidratación osmótica, se considera que la solución 1 es la más adecuada, o sea que a las condiciones óptimas de concentración igual a 23,9% de NaCl, temperatura igual a 32,2°C, y tiempo de 207 min se tienen 0,232 g agua/g, 0,169 g/g y 0,076 g NaCl/g de pérdida de agua, pérdida de peso y ganancia de sal, respectivamente. Es conveniente anotar que con el método de la solución deseada se obtiene un punto óptimo, mientras que con el método gráfico se obtiene una zona óptima donde este punto se encuentra. La optimización no es cuestión de tener precisión en los valores, si no de poder decidir cuál alternativa es la más adecuada en función de los valores obtenidos.

CONCLUSIONES

La metodología de superficies de respuesta permite modelar los efectos de la concentración y temperatura de la solución osmótica y el tiempo de deshidratación sobre la pérdida de agua, pérdida de peso y ganancia de sal en la sardina durante la deshidratación osmótica con pulso de vacío, para luego aplicar métodos de optimización del proceso. Empleando el método gráfico se obtuvo una zona óptima correspondiente a una concentración entre 23,9 y 24,6%, un tiempo entre 204 y 208 min y una temperatura de 32,2°C para tener una pérdida de agua entre 0,230 y 0,245 g agua/g, una ganancia de sal entre 0,075 y 0,076 g NaCl/g y una pérdida de peso entre 0,168 y 0,170 g/g. Utilizando el método de la función deseada las condiciones óptimas para la deshidratación fueron concentración de 23,9% de sal, tiempo de 207 min y temperatura de 32,2°C, para tener una pérdida de agua de 0,232 g agua/g, una ganancia de peso de 0,169 g/g y una ganancia de sal de 0,076 g NaCl/g. Dado que en este estudio sólo se consideraron los cambios de masa, se hacen necesarias investigaciones posteriores que permitan determinar las características sensoriales de la sardina deshidratada y la aceptación general por parte del consumidor. Así el industrial podrá tener un criterio más amplio para poder decidir la alternativa más adecuada para tener una mejor producción.

AGRADECIMIENTO

Este estudio fue posible gracias al financiamiento otorgado por el FONACIT al proyecto S1-2000000773 titulado “Estudio de la Deshidratación Osmótica de la Sardina”.

REFERENCIAS BIBLIOGRÁFICAS

1. ALIZADEH, M.; HAMEDI, M.; KHOSROSHAHI, A. Optimizing sensorial quality of Iranian white brine cheese using response surface methodology. J. Food Sci. 70(4): S299-303. 2005.        [ Links ]

2. ANDRÉS, A.; RODRÍGUEZ, S.; BARAT, J.; FITO, P. Application of vacuum impregnation technology to salting and desalting cod (Gadus morhua). In: Fito P.; Chiralt A.; Barat J.; Spiess W.; Beshnilian D. (Eds). Osmotic Dehydration and Vacuum Impregnation. Applications in Food Industries. Technomic Publishing Lancaster, USA. 185-192 pp. 2001.        [ Links ]

3. ARTEAGA, G.; LI-CHANG, E.; VASQUEZ-ARTEAGA, M.; NAKAI, S. Systematic experimental designs for product formula optimization. Trends Food Sci. Technol. 5: 243-254. 1994.        [ Links ]

4. ASSOCIATION OF OFFICIAL ANALYTICAL CHEMISTS (A.O.A.C). Official Methods of Analysis. 14^th Ed. Washington, USA. 1285 pp. 1985.        [ Links ]

5. BARAT, J.; ANDRÉS, A.; FITO, P. Modelización de Operaciones Unitarias. Capítulo 2. En: Deshidratación Osmótica de Alimentos. Universidad Politécnica de Valencia, Servicio de Publicaciones, Valencia, España, 23-52 pp. 1998.        [ Links ]

6. BOLIN, H.; HUXSOLL, C.; JACKSON, R. Effects of osmotic agents and concentration on fruit quality. J. Food Sci. 48: 202-204. 1983.        [ Links ]

7. CHAFER, M.; GONZALEZ-MARTINEZ, C.; ORTOLA, M. D.; CHIRALT, A. Long term osmotic dehydration processes of orange peel at atmospheric pressure and by applying a vacuum pulse. Food Sci. Technol. Int. 7(6): 511-520. 2001.        [ Links ]

8. CHIRALT, A.; FITO, P.; BARAT, J.; ANDRÉS, A.; GONZÁLEZ, C.; ESCRICHE, I.; CAMACHO, M. Use of vacuum impregnation in food salting process. J. Food Eng. 42: 435-446. 2001.        [ Links ]

9. CORZO, O.; BRACHO, N. Effects of brine concentration and temperature on equilibrium distribution coefficients during osmotic dehydration of sardine sheets. Lebensm. Wiss. u Technol 37(4): 475-479. 2003.        [ Links ]

10. CORZO, O.; GÓMEZ, E.R. Optimization of osmotic dehydration of cantaloupe using desired function methodology. J. Food Eng. 64: 213-219. 2004.        [ Links ]

11. DERRINGER, G.C.; SUICH, R. Simultaneous optimization of several response variables. J. Quality Technol. 12 (10): 214-219. 1980.        [ Links ]

12. DESIGN-EXPERT SOFTWARE. User’s guide, version 6.0. Stat-Ease Inc. Minneapolis, USA. 224 pp. 2006.        [ Links ]

13. FERMÍN, W.; CORZO, O. Optimization of vacuum pulse osmotic dehydration of cantaloupe using response surface methodology. J. Food Proc. Preserv. 29: 20-32. 2005.        [ Links ]

14. FICHTATI, J.; VAN DE VOORT, F. R.; KHURY, A. I. Multiresponse optimization of acid casein production. J. Food Proc. Eng. 12(4): 247-258. 1990.        [ Links ]

15. FITO, P.; CHIRALT, A. An approach to the modeling of solid food-liquid operations: Application to osmotic dehydration. In: Fito, P.; Ortega, E.; Barbosa-Canovas, G. (Ed.) Food Engineering 2000. Chapman & Hall, New York. USA. 231-252 pp. 1997.        [ Links ]

16. FLOROS, J.; CHINNAN, M. Computer graphics-assisted optimization for product and process development. Food Technol. 42:72-78, 84. 1988.        [ Links ]

17. GARROTE, R.; COUTAZ, V.; LUNA, J.; SILVA, E.; BERTONE, R. Optimizing processing conditions of chemical peeling of potatoes using response surface methodology. J. Food Sci. 58: 821-826. 1993.        [ Links ]

18. GUILLOU, A. A.; FLOROS, J. D. Multiresponse optimization minimizes salt in natural cucumber fermentation and storage. J. Food Sci. 58:1381-1389. 1993.        [ Links ]

19. INSTITUTO NACIONAL DE PESCA. Estadísticas Pesqueras. Caracas, Venezuela. 167 pp. 2007.        [ Links ]

20. KENNY, S.; GRAU, H.; ARENDT, E. Use of response surface methodology to investigate the effects of processing conditions on frozen dough quality and stability. Eur. Food Res. Technol. 213(3): 323-328. 2001.        [ Links ]

21. KOBLITZ, M. G. B.; PASTORE, G. M. Contribution of response surface design to the synthesis of monoacylglycerols catalyzed by Rhizopus ss. lipase. J. Food Sci. 70(8): C503-505. 2005.        [ Links ]

22. LANEUVILLE, S. I.; PAQUIN, P.; TURGEON, S. L. Formula optimization of a low-fat food system containing whey protein isolate-xanthan gum complexes as a fat replacer. J. Food Sci. 70(8): S513-519. 2005.        [ Links ]

23. LAWSON, J.; MADRIGAL, J. L.; ERJAVEC, J. Criterios de Selección. Capítulo 4. En: Estrategias Experimentales para el mejoramiento de la calidad en la industria. 1^era Ed. Grupo Editorial Iberoamérica, México, 54-87 pp. 1992.        [ Links ]

24. LERICI, C.; PINNAVAIA, G.; DALLA R, A.; BARTOLUCCI, L. Osmotic dehydration of fruits: influence of osmotic agents on drying behavior and product quality. J. Food Sci. 50: 1217-1219. 1985.        [ Links ]

25. LIU, S.; ZHANG, C.; HONG, P.; Ji, H. Concentration of docosahexaenoic acid (DHA) and eicosapentaenoic acid (EPA) of tuna oil by urea complexation: optimization of process parameters. J. Food Eng. 73(3): 203-209. 2006.        [ Links ]

26. MULLEN, K.; ENNIS, D. Rotatable designs in product development. Food Technol. 33:74-80. 1979.        [ Links ]

27. MYERS, R. H; MONTGOMERY, D. C. Multiple response surface. Chapter 6. En: Response Surface Methodology. Process and Product Optimization Using Designed Experiments. John Wiley & Sons. New York. USA. 235-32.pp. 2002.        [ Links ]

28. NELDER, J. A. The selection of terms in response-surface models. How strong is the weak-heredity principle? Ame. Stat. 52(4): 97-102. 1998.        [ Links ]

29. NOVOA, D.; MENDOZA, J.; MARCANO, J.; CÁRDENAS, J. El Atlas Marítimo Pesquero de Venezuela. SARPA, Caracas, Venezuela. 197 pp. 1998.        [ Links ]

30. PEIXOTO, J. A property of well-formulated polynomial regression models. Ame. Stat. 44(1): 52-60. 1990.        [ Links ]

31. OZEN, B.; DOCK, L.; OZDEMIR, M.; FLOROS, J. Processing factors affecting the osmotic dehydration of diced green peppers. J. Food Sci. Technol. 37:497-502. 2002.        [ Links ]

32. RAVI, R.; SUSHEELAMMA, N. S. Simultaneous optimization of a multi-response system by desirability function analysis of boondi-making: a case study. J. Food Sci. 70(8): S539-547. 2005.        [ Links ]

33. REYES, G.; CORZO, O.; BRACHO, N. Optimización de la deshidratación osmótica de sardina mediante la metodología de superficies de respuesta. Rev. Científ. FCV-LUZ. XV(4): 377-384. 2005.        [ Links ]

34. SNEE, R. D. Validation of regression model: methods and examples. Technometr. 19: 415-428. 1977.        [ Links ]

35. STONE, M. Cross-validating choice and assessment of statistical predictions (with discussion). J. Royal Stat. Soc. (Series B). 36(11): 111-147. 1974.        [ Links ]

36. VIJAYALAKSHMI, G.; SHOBHA, B.; VANAJAKSHI, V.; DIVAKAR, S.; MANOHAR, B. Response surface methodology for optimization of growth parameters for the production of carotenoids by a mutant strain of Rhodotorula gracilis. Eur. Food Res. Technol. 217(3): 230-234. 2003.        [ Links ]