Revista Científica
versión impresa ISSN 0798-2259
Rev. Cient. (Maracaibo) v.18 n.6 Maracaibo dic. 2008
Predicción del crecimiento de lactococcus lactis subsp. Lactis en leche descremada estéril en función a la temperatura.
Growth prediction of lactococcus lactis subsp. Lactis in sterile skimed milk as a function of temperature.
Emiro Valbuena1, José Barreiro3, Edgar Sánchez2, Gustavo Castro1, Valero Kutchinskaya y Wilfido Briñez1
1 Unidad de Ciencia y Tecnología de Alimentos. Venezuela.
2 Unidad de Bioestadística. Facultad de Ciencias Veterinarias. Universidad del Zulia, Maracaibo. Apartado 15252, Venezuela.
3 Departamento de Tecnología de Procesos Biológicos y Bioquímicos. Universidad Simón Bolívar. Sartenejas, Venezuela. E-mail: eavalbue@cantv.net
RESUMEN
Diversos modelos matemáticos han sido desarrollados con el objeto de predecir el comportamiento de las poblaciones bacterianas en fase de crecimiento en condiciones controladas a nivel de laboratorio, muchos de estos han sido validados en condiciones de producción, transporte y almacenamiento de alimentos. El objetivo del presente trabajo fué adaptar un modelo matemático utilizando ecuaciones obtenidas como resultado del análisis con modelos secundarios de los coeficientes de regresión de la ecuación de Gompertz, a efectos de lograr predecir las poblaciones en crecimiento de Lactococcus lactis subsp. lactis en leche en polvo reconstituida y esterilizada, controlando la temperatura en el rango desde 9 a 39°C. Con este fin, los coeficientes A y B se analizaron con el modelo de la raíz cuadrada, obteniéndose valores de R2 = 0,819 y 0,991, respectivamente, mientras que el modelo hiperbólico se utilizó para modelar los coeficientes D (R2= 0,812) y M (R2= 0,995). Finalmente se obtuvo una expresión reparametrizada del modelo original de Gompertz, sustituyendo cada coeficiente de regresión por la ecuación que lo describe, en función a las diferentes temperaturas estudiadas, siendo este modelo utilizado para predecir directamente las poblaciones del microorganismo en estudio a cualquier temperatura dentro del rango estudiado. Se obtuvieron diferencias muy pequeñas entre la población observada experimentalmente y la ajustada según la aplicación del modelo desarrollado, observándose una distribución bastante equilibrada de los valores residuales. Se recomienda utilizar este tipo de modelo para describir el crecimiento de poblaciones combinadas en productos como leche pasteurizada comercial.
Palabras clave: Lactococcus lactis, modelo de Gompertz, microbiología predictiva, crecimiento bacteriano.
ABSTRACT
Several mathematic models have been developed to predict the behavior of bacteria populations in growing phase and controlled conditions at the laboratory. Many of these models have been validated under food production, transportation and storage conditions. The objective of this study was to adapt a mathematical model using equations obtained as a result of the analysis with secondary models of regression coefficients from the Gompertz equation, to predict population of Lactococcus lactis subsp. lactis in the growing phase in reconstituted and sterilized powder milk, controlling temperature in a range of 9 to 39°C. Prediction was done by the analysis of A and B coefficients, using the square root model, obtaining R2 values = 0.819 and 0.991, respectively. Furthermore, a hyperbolic model was used for modeling D (R2= 0.812) and M (R2= 0.995) coefficients. Finally, a reparametrized expression of the original Gompertz model was obtained replacing each regression coefficient by the described equation, in relation to the different studied temperatures. Thus, this model was used to directly predict the population of microorganism under study at any temperature in the studied range. Small differences were obtained between both, the experimental and the adjusted populations, according to the application of the developed model. A well balanced distribution of the residual values was observed. The use of this type of models is recommended to describe growth of combined microorganism populations in products such as commercial pasteurized milk.
Key words: Lactococcus lactis, Gompertz model, predictive microbiology, bacterial growth.
Recibido: 13 / 12 / 2007. Aceptado: 15 / 02 / 2008.
INTRODUCCIÓN
El Lactococcus lactis subsp. lactis (conocido anteriormente como Streptococcus lactis) es un microorganismo mesófilo, capaz de fermentar la lactosa produciendo ácido láctico en gran cantidad, de la misma forma es capaz de producir algunas substancias antibacterianas conocidas en forma genérica como bacteriocinas, entre las cuales destacan la nisina y la diplococcina [3, 4, 12].
Entre las bacterias ácido-lácticas se encuentran diversos microorganismos utilizados como cultivos iniciadores en diversos productos fermentados, pero especialmente en productos lácteos, destacándose el Lactococcus lactis subsp. lactis, el cual ha sido ampliamente utilizado en diversos productos como quesos madurados, el suero de mantequilla madurado, cremas de leche maduradas y muchos otros [6, 12].
La importancia de lograr predecir en una forma aproximada el crecimiento de Lactococcus lactis subsp. lactis, en leche, tomando como única variable la temperatura de incubación, radica en que esta bacteria acido láctica, muy frecuente en forma natural en leche, puede ser utilizada tecnológicamente como biopreservador, controlando el crecimiento de bacterias patógenas como el Staphylococcus aureus, Listeria monocytogenes, Escherichia coli O157;H7 e incluso algunas especies del género Clostridium, los cuales son responsables de serios problemas de conservación en diversos productos lácteos [5, 12].
Modelos de predicción aplicados al crecimiento bacteriano
Entre los modelos primarios más ampliamente utilizados para describir el crecimiento bacteriano encontramos la ecuación de Gompertz, la cual representa un modelo de regresión no lineal con tres o cuatro parámetros o coeficientes. En su forma sigmoidal de cuatro parámetros se representa según la siguiente ecuación;
Log N = A + D exp ( -exp (-B (t-M))) (Ec. 1)
Donde: Log N: logaritmo común de las ufc/mL, representando la variable dependiente del modelo.
t: tiempo transcurrido (variable independiente).
Los parámetros que deben ser ajustados por el modelo y de los cuales son necesarios estimados iniciales, serian;
A: Log10 del número inicial (inóculo).
D: Log10 la diferencia entre el número inicial de microorganismos y el número final de los mismos en la fase estacionaria (cantidad de ciclos logarítmicos).
B: representa la pendiente de la curva y describe la tasa de crecimiento.
M: tiempo en el cual se da el punto de inflexión (tasa de crecimiento más alta).
Utilizando estos coeficientes de regresión, y con los mismos datos de crecimiento bacteriano, en un trabajo previo [14] fue posible hallar los descriptores de la cinética de crecimiento, entre ellos la fase de adaptación (l), tasa específica de crecimiento (µ), tiempo de generación (TG) [15].
Sin embargo, a pesar de lograr obtener datos relacionados con la cinética específica para las condiciones dadas e incluso luego de modelar los mismos en función a la temperatura, solo pueden ser utilizadas para evaluar momentos aislados dentro de la cinética de crecimiento pero haciendo muy difícil predecir poblaciones para un tiempo y temperatura dado.
Así, para obtener esta predicción poblacional dentro del rango de temperatura estudiado, se hizo necesario desarrollar un nuevo modelo matemático utilizando la ecuación de Gompertz modificada, en la cual sus coeficientes de regresión fueron a su vez modelados en forma secundaria en función a la temperatura, logrando entonces un modelo de predicción poblacional de tipo primario, capaz de estimar poblaciones en función a otra variable distinta al tiempo, en este caso, la temperatura. Este procedimiento, no ha sido descrito en la bibliografía consultada, resultando el objetivo fundamental de este trabajo la aplicación del mismo.
Los coeficientes de la ecuación de Gompertz de cuatro parámetros, fueron entonces modelados utilizando los siguientes tipos de ecuaciones;
Modelo de la raíz cuadrada: este modelo se basa, como su nombre lo indica, en la raíz cuadrada de la tasa de crecimiento constante y la temperatura, con la cual se obtiene una relación lineal (Ratkowsky y col. [11]; McMeekin y col. [9]);
Öµ = b (T - Tmin) (Ec. 2)
Donde;
Öµ: raíz cuadrada de la tasa máxima de crecimiento.
b: pendiente de la regresión.
T: temperatura en grados Kelvin o centígrados.
Tmin: temperatura donde la tasa de crecimiento es igual a cero.
El modelo hiperbólico: desarrollado por Adair y col. [17] resulta bastante sencillo y de muy buen ajuste a los datos, la ecuación descrita es la siguiente;
Ln l= p / ( T – q ) (Ec. 3)
Donde;
Ln l: representa el Logaritmo de la fase de adaptación.
p: disminución de la fase de adaptación en la medida en que aumenta T.
T: temperatura de incubación.
q: temperatura en la cual la fase de adaptación se hace infinita.
En un trabajo anterior [14] se describieron las curvas de crecimiento a 9°, 12°, 15°, 18°, 21°, 24°, 27°, 30°, 33°, 36° y 39°C, correspondientes al Lactococcus lactis subsp. lactis en leche. A partir de los datos usados para la construcción de estas curvas, lograron obtenerse los coeficientes de regresión del modelo de Gompertz (TABLA I), en la cual puede apreciarse que, aunque el número de muestras representativas de cada curva, es relativamente pequeño (entre 9 y 15 puntos), los coeficientes de determinación (R2 corregido) son bastante elevados, mientras que la desviación de los datos obtenidos por la curva ajustada (suma de residuales) son muy bajos.
TABLA I. Parámetros de ajuste del modelo primario / Adjusted parameters from primary model.
| Temp. (°C ) | A | D | B | M | R2 Corregido | n | å Resid. |
| 9 | 2,172 | 7,826 | 0,010 | 84,933 | 0,976 | 15 | 1,612 |
| 12 | 2,324 | 7,140 | 0,030 | 25,553 | 0,992 | 14 | 0,408 |
| 15 | 2,570 | 6,382 | 0,080 | 9,896 | 0,986 | 10 | 0,537 |
| 18 | 2,646 | 7,298 | 0,083 | 14,642 | 0,997 | 14 | 0,245 |
| 21 | 2,505 | 7,026 | 0,126 | 5,790 | 0,993 | 11 | 0,292 |
| 24 | 3,604 | 6,063 | 0,197 | 7,299 | 0,998 | 12 | 0,100 |
| 27 | 3,045 | 6,486 | 0,234 | 4,003 | 0,995 | 9 | 0,196 |
| 30 | 3,664 | 5,746 | 0,312 | 4,217 | 0,997 | 10 | 0,122 |
| 33 | 3,261 | 6,624 | 0,262 | 3,863 | 0,999 | 9 | 0,041 |
| 36 | 4,038 | 5,237 | 0,409 | 3,712 | 0,999 | 9 | 0,023 |
| 39 | 3,123 | 5,783 | 0,335 | 4,355 | 0,993 | 9 | 0,272 |
Como datos de inicialización, los parámetros representan;
A: Población inicial.
D: Pendiente de la curva.
B: Log(10) de la diferencia entre las poblaciones inicial y final.
M: Tasa de crecimiento mas elevada.
n: Número de puntos muestreados en cada curva de crecimiento.
åResid. : Sumatoria de los residuales para los datos de cada temperatura.
El objetivo principal del presente trabajo fue desarrollar una ecuación matemática que permita establecer con la mayor precisión posible las poblaciones a tiempos determinados de la bacteria ácido láctica Lactococcus lactis subsp. lactis en leche estéril descremada, utilizando para ello datos obtenidos previamente, con los cuales se describieron las curvas de crecimiento del microorganismo, dentro del rango de 9 a 39°C [14].
MATERIALES Y MÉTODOS
Medio y condiciones de crecimiento
Se utilizó leche en polvo descremada reconstituida al 10% (P/V), libre de inhibidores y esterilizada en autoclave (Huxley, modelo HL 340, EUA) a 110°C / 10 min. Se colocaron 25 mL de leche en tubos de ensayo previamente esterilizados, los mismos fueron inoculados con el microorganismo hasta alcanzar un nivel inicial cercano a 1*103 ufc/mL. El cultivo de Lactococcus lactis subsp. lactis (ATCC 29146) fue utilizado en fase logarítmica de crecimiento, lograda en la misma leche por incubación previa a 30°C durante 12 horas y diluyendo en forma seriada en leche estéril hasta alcanzar el título requerido.
Las temperaturas en cuales se estudió el crecimiento fueron: 9°, 12°, 15°, 18°, 21°, 24°, 27°, 30°, 33°, 36° y 39°C con una variación de ± 0,1°C, lo cual se consiguió utilizando un baño de circulación termorregulado de alta precisión, modelo 2161, Forma Scientific (Ohio-EUA).
Para cada nivel de temperatura se efectuaron dos ensayos, en cada uno de ellos se incubaron 15 tubos en las condiciones descritas, cada cierto tiempo, dependiendo de la temperatura en estudio, fueron retirados del baño cada uno de ellos y se tomaron alícuotas de la muestra para medir por duplicado la población del L. lactis, en forma tal de obtener una representación muestral en toda la curva de crecimiento, fase de adaptación, de crecimiento exponencial y comienzo de la fase estacionaria.
Análisis microbiológico
Con el fin de garantizar la ausencia de inhibidores que afecten el crecimiento microbiano, la leche en polvo utilizada en los experimentos fue sometida previamente a un análisis para detectar posibles substancias inhibidoras del crecimiento bacteriano, para ello se utilizó la prueba del DelvotestSP (Gist-brocades, DSM Food Specialities, Delft-Holanda). Una vez obtenida cada una de las muestras de 25 mL, se procedió en primera instancia a la extracción aséptica de una alicuota de 1,0 mL, con la cual se efectuó la siembra en profundidad y los contajes según la metodología de la American Public Health Association (APHA) [1], reportando los resultados como ufc/mL de leche, con posterior transformación a Log ufc/mL.
El medio de cultivo fue el M-17 (Difco, Michigan-EUA), con glicerofosfato como regulador de pH, el azúcar a incorporado fue lactosa al 10%, la cual se añadió en forma estéril al medio previamente tratado a 121°C/15 min. Esta técnica ha sido ampliamente utilizada para el microorganismo en cuestión y fue originalmente descrita por Terzaghi y Sandine [13].
Análisis computacional de los modelos
El proceso de ajuste se efectuó utilizando el módulo NONLIN del paquete estadístico SYSTAT, empleando para ello las descripciones que hacen sobre el mismo Ato y López [2]. Al incorporar los datos correspondiente a la variable dependiente del modelo; población (log (ufc/mL), o coeficientes de regresión en el caso de los modelos secundarios (A, D, B, M), e independiente; tiempo ó temperatura, la ecuación de regresión no lineal a utilizar y los valores de inicialización, el módulo descrito comienza un proceso iterativo que tiene como objetivo disminuir paulatinamente el error en la suma de cuadrados, valiéndose para esto, de una modificación del proceso matemático de Gauss-Newton, este proceso iterativo continua hasta que se consigue el criterio de convergencia deseado, la tolerancia permitida para alcanzar este punto, se fijó en 0,0005.
Al alcanzar la convergencia en el proceso, el programa aporta los valores numéricos de los coeficientes de regresión incorporados en la ecuación con su intervalo de confianza, la matriz de correlación, de la misma forma, se puede solicitar como salida, la variable respuesta ajustada, los residuales de la suma de cuadrados y los puntuales en cada observación, el coeficiente de determinación (R2), los grados de libertad, etc.
La evaluación estadística de los modelos empleados en cada caso, se llevó a cabo mediante la valoración del coeficiente de determinación (R2), el estudio del intervalo de confianza al 95% para cada coeficiente de regresión estudiado, el análisis de la normalidad en la distribución de los residuales mediante gráficos de dispersión de los mismos y finalmente, la construcción de gráficos, en lo cuales se contrastaron contra la variable independiente, las curvas de las variables respuesta ajustadas y observadas experimentalmente.
Por otra parte, las matrices de correlación también se tomaron en cuenta para el análisis de cada proceso, aunque no se presentan en la discusión de resultados, en ellas se evalúa la interdependencia de los distintos coeficientes de regresión empleados en cada modelo, observando que la correlación presente, no supere el valor de 0,95, ya que, más allá del mismo, se considera que el modelo está supraparametrizado y por lo tanto alguno de dichos coeficientes está de más en la ecuación [2, 7, 10].
Análisis del modelo primario
Tal como se ha planteado en un trabajo anterior [14] se habían obtenido los contajes del microorganismo en estudio bajo las condiciones enunciadas, expresados como logaritmo de las ufc/mL para cada temperatura y el tiempo de incubación, se elaboraron los gráficos de crecimiento y se acopió la extensa base de datos para las poblaciones a diversos tiempos dentro del rango de temperatura estudiado.
Utilizando estos datos, se aplicó el proceso computacional utilizando las ecuaciones de regresión no lineal de Gompertz modificada [9], empleando como valores de inicialización los propuestos por el autor citado, los datos fueron procesados hasta alcanzar el mejor ajuste entre los observados y los calculados con el modelo, así fue posible describir todas las curvas de crecimiento [15].
Análisis del modelo secundario
Los valores de los coeficientes de regresión o constantes, originados del modelo de Gompertz, fueron incorporados al modelo secundario de la raíz cuadrada [11], o al modelo hiperbólico presentado por Zwietering y col. [18], en los cuales se integraron los datos provenientes de todas las temperaturas en estudio a efectos de obtener la ecuación final de predicción, calculados para cada temperatura en particular.
A efectos de evaluar la capacidad predictiva del modelo desarrollado, se procedió a generar nuevos datos experimentales utilizando la misma metodología descrita y dentro del rango térmico estudiado, pero a temperaturas distintas de aquellas utilizadas para generar los datos originales y como paso posterior al desarrollo del modelo final. A cada nueva temperatura ensayada con crecimientos, le fueron calculados los respectivos coeficientes de regresión (A, D, B y M) usando el modelo desarrollado, los cuales fueron en cada caso integrados a la ecuación de Gompertz para construir entonces una curva de crecimiento de población ajustada o esperada según la predicción generada por los cálculos matemáticos. Los nuevos datos experimentales obtenidos a distintos tiempos de crecimiento fueron entonces comparados con las poblaciones ajustadas por el modelo matemático.
RESULTADOS Y DISCUSIÓN
Valores iniciales para iniciar los parámetros de ajuste
En la TABLA I se resumen los coeficientes de ajuste, A, D, B y M, obtenidos como salida del proceso iterativo para cada conjunto de datos, a partir de éstos se procedió a modelar mediante el uso de modelos matemáticos secundarios para cada uno de ellos, con la finalidad de lograr representarlos en la forma más aproximada posible para cualquier temperatura dentro del rango estudiado, haciendo posible un modelo final de predicción poblacional, como el planteado por Zwietering y col. [17], o Witjzes y col. [16], lo cual representa el objetivo principal de este trabajo.
Modelo secundario para el parámetro A del modelo de Gompertz
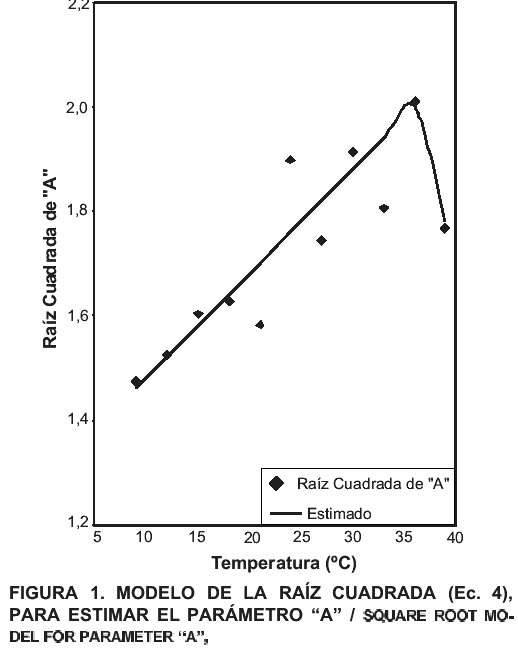
En la FIG. 1, se aprecia como el coeficiente A aumenta en forma proporcional a la temperatura, con un comportamiento aparentemente lineal, sin embargo, al aplicar diversos modelos matemáticos, se logró establecer que el comportamiento de este parámetro no era realmente lineal, lo cual es lógico, conociendo que la temperatura óptima del Lactococcus lactis está alrededor de los 37°C, por lo tanto las funciones relativas a la temperatura no deberían presentar un comportamiento lineal cuando este punto óptimo se encuentra dentro del rango en estudio. En este caso pudo comprobarse que el parámetro A era mejor modelado aplicando el modelo de la raíz cuadrada [11].
Luego de calcular la raíz cuadrada del coeficiente A, e incorporar estos datos junto con la ecuación modificada por Ratkowsky al paquete estadístico, se calcularon los parámetros de regresión b, Tmin, c y Tmax, los cuales se presentan en la TABLA II, acompañados de sus respectivos intervalos de confianza, quedando la ecuación definitiva para este parámetro como sigue;
ÖA = (0,02 * (T – (-64,003))) * (1 – Exp (6,102 * ( T – 39,328))) (Ec. 4)
TABLA II. Parámetros de ajuste del Modelo de la raíz cuadrada aplicado al coeficiente A/ SQUARE ROOT ADJUSTED PARAMETERS APPLIED TO COEFFICIENT A.
| Parámetro | Estimado | Intervalo de Confianza (95%) | |
|
|
| Inferior | Superior |
| b | 0,020 | 0,013 | 0,027 |
| c | 6,102 | -2,440 | 14,644 |
| Tmin | -64,003 | -95,732 | -32,273 |
| Tmax | 39,328 | 38,906 | 39,749 |
b, c, Tmin, Tmax: son los parámetros de ajuste del modelo de la raíz cuadrada (Ec. 4).
En la TABLA III, se presentan los valores ajustados al emplear esta ecuación sustituyendo T por cada una de las temperaturas en estudio, junto con los valores de origen correspondientes, los residuales registrados para cada uno de estos puntos y el coeficiente de determinación (R2) alcanzado.
TABLA III. Raíz cuadrada del parámetro A, valores de origen y residuales / PARAMETER A SQUARE ROOT, ORIGINAL VALUES AND RESIDUALS.
| Temperatura (°C) | ÖA | Estimado | Residual |
| 9 | 1,474 | 1,449 | 0,025 |
| 12 | 1,524 | 1,508 | 0,016 |
| 15 | 1,603 | 1,568 | 0,035 |
| 18 | 1,627 | 1,628 | -0,001 |
| 21 | 1,583 | 1,687 | -0,104 |
| 24 | 1,898 | 1,747 | 0,151 |
| 27 | 1,745 | 1,806 | -0,061 |
| 30 | 1,914 | 1,866 | 0,048 |
| 33 | 1,806 | 1,925 | -0,119 |
| 36 | 2,009 | 1,985 | 0,024 |
| 39 | 1,767 | 1,767 | -0,000 |
R2 (corregido)= 0,819
ÖA: raíz cuadrada del parámetro A, obtenido del modelo de Gompertz.
Estimado: valor calculado al utilizar la Ec. 4.
En la FIG. 1, se presenta la curva de ajuste obtenida al representar gráficamente los valores presentados en la TABLA III. En el mismo se aprecia como la línea de valores ajustados representa un buen compromiso entre los puntos obtenidos como parámetros de regresión A, calculado en el modelo primario, se observa como la curva ajustada por el modelo establece una disminución del valor de este parámetro más allá de la temperatura de 36-37°C, considerada como óptima para el crecimiento del microorganismo en cuestión, lo cual sí corresponde a lo esperado teóricamente.
Modelo secundario para el parámetro D del modelo de Gompertz
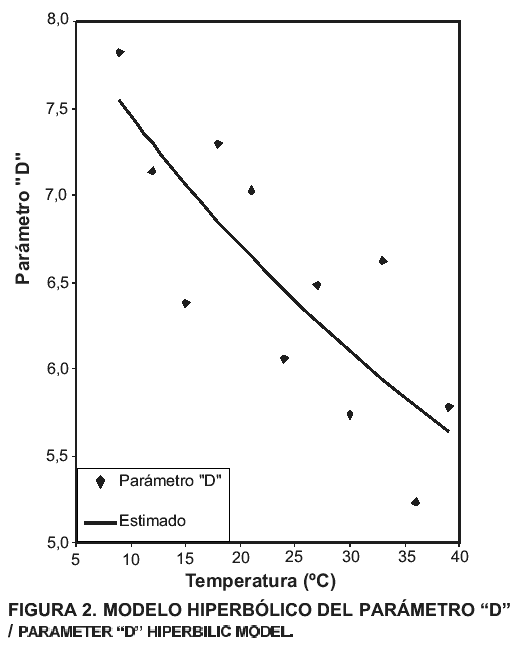
En la FIG. 2, se observan los valores del parámetro D obtenidos en el modelo primario, para cada una de las temperaturas en estudio, los mismos presentan una relación inversamente proporcional con respecto a la temperatura, éstos a simple vista parecieran encajar en una regresión lineal simple, pero al aplicar diversos modelos presentados en la literatura, se logró establecer que este parámetro puede ser mejor ajustado por una función hiperbólica, como la utilizada por Zwitering y col. [17]. Para utilizar la misma, no fue requerida ninguna transformación previa de los valores originales del parámetro estudiado, luego de utilizar el modelo descrito con los valores de origen y lograr la convergencia del sistema, fueron obtenidos los coeficientes p y q, al incluir éstos en la ecuación 3, se obtiene que;
D = 671,206 / ( T – (-79,975)) (Ec. 5)
Donde; T: temperatura (°C).
En la TABLA IV, se presentan los coeficientes descritos junto con el intervalo de confianza correspondiente, en la misma destaca la gran variación existente en el intervalo de confianza para ambos coeficientes, lo cual indica que el ajuste del modelo debe perder precisión, esto es sin duda, producto de la dispersión relativamente amplia de los datos. En la TABLA V se reportan lo valores originales del parámetro D, los valores ajustados con este modelo (Ec. 5), los residuales y el coeficiente de determinación obtenido, allí se evidencia que, a pesar de los problemas mencionados, los valores ajustados son muy afines con los observados, por lo que se concluye que es viable la aplicación del modelo descrito.
TABLA IV. Parámetros de ajuste del modelo hiperbólico aplicado al coeficiente D / HIPERBOLIC MODEL ADJUSTED PARAMETERS APPLIED TO COEFFICIENT D.
| Parámetro | Estimado | Intervalo de Confianza (95%) | |
|
|
| Inferior | Superior |
| p | 671,206 | 303,786 | 1038,627 |
| q | -79,975 | -135,243 | -24,708 |
p y q : parámetros de ajuste del modelo hiperbólico (Ec. 5).
TABLA V. Parámetro D, valores de origen y residuales / PARAMETER d ORIGINAL VALUES AND RESIDUALS.
| Temperatura (°C) | D | Estimado | Residual |
| 9 | 7,826 | 7,544 | 0,282 |
| 12 | 7,140 | 7,298 | -0,158 |
| 15 | 6,382 | 7,067 | -0,685 |
| 18 | 7,598 | 6,851 | 0,447 |
| 21 | 7,026 | 6,647 | 0,379 |
| 24 | 6,063 | 6,455 | -0,392 |
| 27 | 6,486 | 6,274 | 0,212 |
| 30 | 5,746 | 6,103 | -0,357 |
| 33 | 6,624 | 5,941 | 0,683 |
| 36 | 5,237 | 5,788 | -0,551 |
| 39 | 5,783 | 5,642 | 0,141 |
R2 (corregido) = 0,812.
D: parámetro obtenido del modelo de Gompertz.
Estimado: valor calculado al utilizar la Ec. 5.
Al graficar los valores de origen y ajustados del parámetro D (FIG. 2) puede apreciarse como la línea de ajuste se presenta con una concavidad muy suave, prácticamente asemeja una recta, sin embargo, el coeficiente de determinación de 0,812 fue ligeramente superior al obtenido para la regresión lineal, lo cual sumado a los valores residuales más bajos, justifican plenamente la elección de el modelo hiperbólico para este parámetro.
Modelo secundario para el parámetro B del modelo de Gompertz
En este caso, el modelo matemático que resultó con un mejor ajuste fue el de Ratkowsky, por supuesto con la transformación previa del parámetro B en su raíz cuadrada, con el objeto de estabilizar la varianza según Neter y col. [10]. La TABLA VI, presenta los valores obtenidos para los coeficientes de regresión de la ecuación modificada por Ratkowsky [11], representados por b, Tmin, c y Tmax, acompañados de sus intervalos de confianza para una probabilidad del 95%.
TABLA VI. Parámetros de ajuste del modelo de la raíz cuadrada aplicado al coeficiente B/ SQUARE ROOT ADJUSTED PARAMETERS APPLIED TO COEFFICIENT B.
| Parámetro | Estimado | Intervalo de Confianza (95%) | |
|
|
| Inferior | Superior |
| b | 0,021 | 0,018 | 0,024 |
| c | 0,399 | -0,097 | 0,895 |
| Tmin | 3,648 | 1,350 | 5,947 |
| Tmax | 42,704 | 38,311 | 47,097 |
b, c, Tmin y Tmax: son parámetros de ajuste de la Ec. 6.
Es importante resaltar que en los valores numéricos para el intervalo de confianza referidos al coeficiente de regresión c , el valor cero queda incluido, puesto que va desde –0,097 hasta 0,895, lo cual indica que este coeficiente no hace un aporte significativo dentro del modelo aplicado [2], sin embargo, al efectuar los cálculos que conducen a hallar los valores ajustados utilizando la ecuación descrita, conseguimos un excelente ajuste, con valores residuales muy bajos y un altísimo coeficiente de determinación (R2= 0,991), por lo cual se aceptó como válido el presente modelo. La ecuación resultante utilizada, fue la siguiente;
ÖB= (0,021 * (T – 3,648)) * (1 – EXP (0,399 * (T- 42,704))) (Ec. 6)
En la TABLA VII, aparecen los resultados obtenidos al aplicar esta ecuación para cada una de las temperaturas en estudio, además de los valores de B originalmente obtenidos del modelo primario y los residuales correspondientes a las diferencias puntuales entre estos últimos y los calculados con este modelo.
TABLA VII. Raíz cuadrada del parámetro B, valores de origen y residuales / PARAMETER B SQUARE ROOT, ORIGINAL VALUES AND RESIDUALS.
| Temperatura (°C) | ÖB | Estimado | Residual |
| 9 | 0,100 | 0,114 | -0,014 |
| 12 | 0,173 | 0,177 | -0,004 |
| 15 | 0,283 | 0,241 | 0,042 |
| 18 | 0,288 | 0,304 | -0,016 |
| 21 | 0,355 | 0,368 | -0,013 |
| 24 | 0,444 | 0,432 | 0,012 |
| 27 | 0,484 | 0,495 | -0,011 |
| 30 | 0,559 | 0,556 | 0,003 |
| 33 | 0,512 | 0,608 | 0,096 |
| 36 | 0,639 | 0,639 | 0,000 |
| 39 | 0,579 | 0,579 | 0,000 |
R2 (corregido) = 0,991.
ÖB: raíz cuadrada del parámetro B, obtenido del modelo de Gompertz.
Estimado: valor calculado al utilizar la Ec. 6.
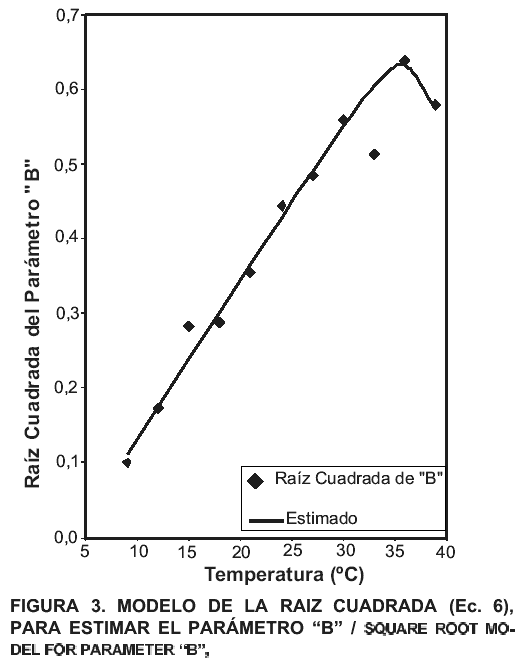
En la FIG. 3, puede apreciarse la bondad del ajuste encontrado al emplear el modelo descrito, en éste solo se observa un punto relativamente alejado de la curva calculada, correspondiente a la temperatura de 33°C, lo cual puede examinarse también el la TABLA VII, donde se aprecia como los valores de la raíz cuadrada de B, suben progresivamente en relación a la temperatura hasta los 36°C (temperatura óptima), para disminuir al llegar al valor de 39°C, pero para el punto en cuestión (33°C), se observa como el mismo baja de 0,559 para 30°C hasta 0,512 a 33°C, para luego llegar a 0,639 a 36°C, por lo cual se puede inferir que se trata de un valor atípico, el cual dificulta en gran medida conseguir la convergencia cuando se introducen los datos en el sistema computarizado, haciendo necesaria la exclusión del mismo del conjunto de datos.
Modelo secundario para el parámetro M del modelo de Gompertz
Este parámetro fue modelado utilizando el mismo modelo hiperbólico empleado para el parámetro D; de la misma forma no fue necesario transformar matemáticamente el parámetro original obtenido del modelo primario. Tal como puede apreciarse en la TABLA VIII, el intervalo de confianza para el coeficiente p, es bastante amplio, lo cual es producto de la dispersión de los datos y la poca cantidad de estos [10]. La ecuación resultante fue la siguiente;
M = 101,955 / (T – 7,8) (Ec. 7).
TABLA VIII. Parámetros de ajuste del modelo hiperbólico para el coeficiente M / HIPERBOLIC MODEL ADJUSTED PARAMETERS APPLIED TO COEFFICIENT M.
| Parámetro | Estimado | Intervalo de Confianza (95%) | |
|
|
| Inferior | Superior |
| p | 101,955 | 81,227 | 122,682 |
| q | 7,800 | 7,539 | 8,061 |
p y q: parámetros de ajuste del modelo hiperbólico (Ec. 12).
Como resultado de aplicar esta ecuación para todas las temperaturas correspondientes al estudio, se generan los valores ajustados, que se presentan en la TABLA IX, acompañados por los valores que dieron origen al modelo y las diferencias entre ambos, es decir, los residuales.
TABLA IX. Parámetro M, valores de origen y residuales / PARAMETER d ORIGINAL VALUES AND RESIDUALS.
| Temperatura (°C) | M | M Ajustado | Residual |
| 9 | 84,933 | 84,968 | -0,035 |
| 12 | 25,553 | 24,275 | 1,278 |
| 15 | 9,896 | 14,161 | -4,265 |
| 18 | 14,642 | 9,996 | 4,646 |
| 21 | 5,790 | 7,724 | -1,934 |
| 24 | 7,299 | 6,294 | 1,005 |
| 27 | 4,003 | 5,310 | -1,307 |
| 30 | 4,217 | 4,593 | -0,376 |
| 33 | 3,863 | 4,046 | -0,183 |
| 36 | 3,712 | 3,615 | 0,097 |
| 39 | 4,355 | 3,268 | 1,087 |
R2 (corregido) = 0,995.
M : parámetro obtenido del modelo de Gompertz.
Estimado: valor calculado al utilizar la Ec. 16.
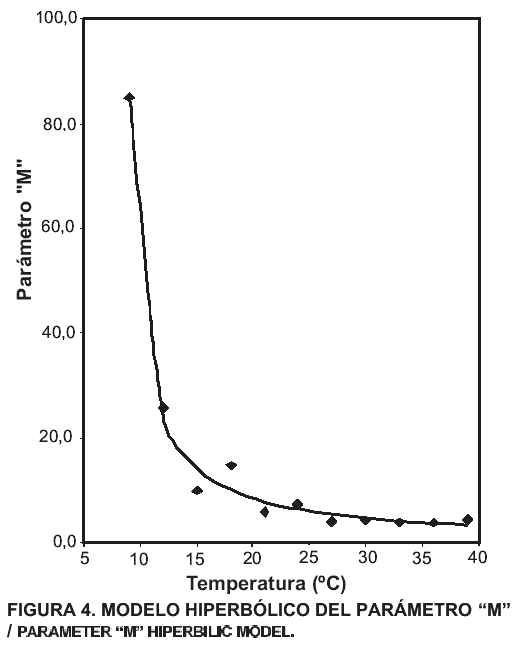
Es importante destacar, que la magnitud de los residuales es grande, si se compara con la mayoría de los modelos ajustados con anterioridad en este mismo trabajo, lo cual sin duda es producto de la alta dispersión de los valores originales, al observar los mismos, se notó como varios de los puntos escapan de la tendencia evidenciada por los puntos previos y posteriores, así por ejemplo, se aprecia como la magnitud de este parámetro viene decreciendo desde el punto correspondiente a los 9°C (84,9), 12°C (25,6) y 15°C (9,9) para elevarse nuevamente (14,6) a la temperatura de 18°C, este tipo de comportamiento le resta precisión al modelo e indudablemente debe causar cierta desviación en las predicciones del modelo final, no obstante el modelo descrito posee un elevado coeficiente de determinación (R2) de 0,995.
En la FIG. 4, se puede observar como la línea que representa el modelo para el parámetro M, representa un buen ajuste para los datos que le dieron origen, lo que permite validar el uso de el modelo hiperbólico en este conjunto de datos, tomando en cuenta que la dispersión de los residuales es bastante homogénea, según se aprecia en la TABLA IX.
Modelo Final de Predicción
Una vez finalizada la etapa de ajuste de los coeficientes de regresión originados del modelo primario (Gompertz), en modelos secundarios relativos a la temperatura, es posible generar una ecuación final de predicción, con la cual pueden ser construidas curvas esperadas de crecimiento para Lactococcus lactis subsp. lactis a cualquier temperatura dentro del rango estudiado, de esta forma se pueden generar los valores de población microbiana a temperaturas en las cuales no se efectuó experimento alguno, con una precisión bastante aceptable.
Cabe destacar que las diferencias encontradas entre los valores ajustados por el modelo final y los aportados por la data original en cada temperatura estudiada, no son imputables exclusivamente al modelo, ya que los datos observados representan también una muestra de los datos de crecimiento que pueden originarse en las condiciones experimentales, máxime en este trabajo, en el cual apenas se usaron dos curvas de datos de crecimiento para cada temperatura. El modelo final aporta valores poblacionales que representan un compromiso entre todas las curvas ensayadas, lo cual puede corregir desviaciones puntuales presentes en alguna de ellas, siempre y cuando la mayoría de las mismas presenten un comportamiento típico del microorganismo en estudio.
En la bibliografía revisada, son pocos los trabajos que refieren en forma explícita el modelo final empleado para la predicción de poblaciones microbianas, la mayoría de éstos concluyen resolviendo el modelo secundario para los parámetros de interés microbiológico, como la fase de latencia, tasa de crecimiento y densidad poblacional máxima, con estos parámetros es posible comparar la respuesta obtenida en diferentes condiciones de crecimiento, o comparar la respuesta de diferentes microorganismos en las mismas condiciones experimentales, sin embargo, en muchos casos es más provechoso lograr predecir las poblaciones bacterianas y para ello es imprescindible concretar una expresión matemática que permita calcular estas poblaciones, lo cual es presentado en este trabajo.
El modelo de predicción resultante, funciona a partir del modelo primario empleado para describir cada una de las curvas de crecimiento ensayadas, es decir, el modelo de Gompertz [8], modificado con cuatro parámetros (Ec. 1);
Log N = A +D * EXP {-EXP {-B * {tiempo – M} } }
Al sustituir cada uno de los coeficientes de regresión, A, D, B y M, por las ecuaciones detalladas para cada parámetro (Ec. 4, 5, 6 y 7), las cuales permiten describir el comportamiento de los mismos en relación a la temperatura, se obtuvo;
Log N = {0,02*(T-(-64,003)) * (1-EXP(6,102*(T-39,328)))}2 + {671,206/(T-(-79,975))} * EXP { -EXP { - {0,021*(T-3,648)*(1-EXP(0,399*(T-2,704)))}2* {Tiempo – {101,955/(T-7,8) } } } } (Ec. 8)
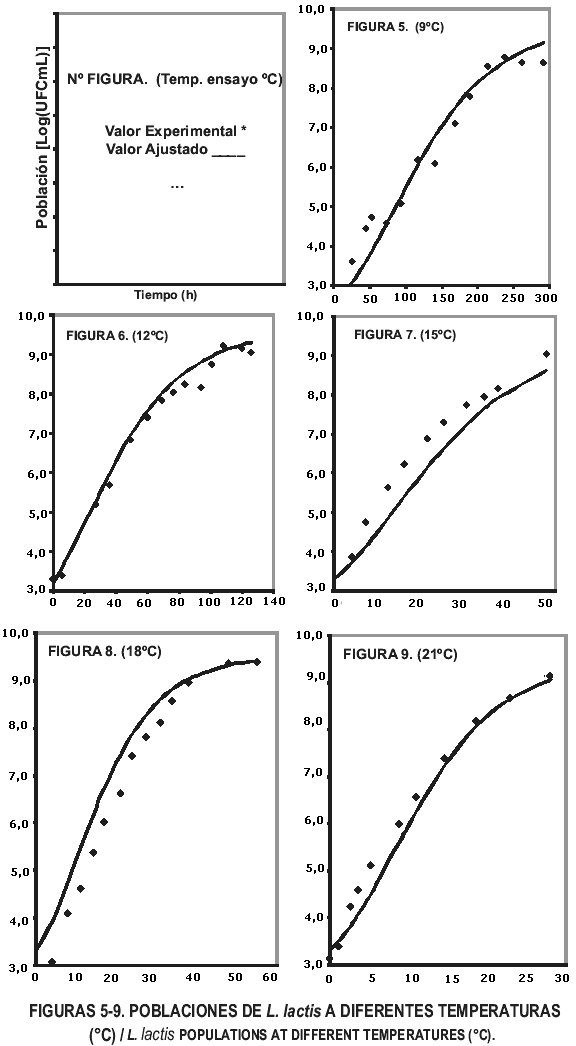
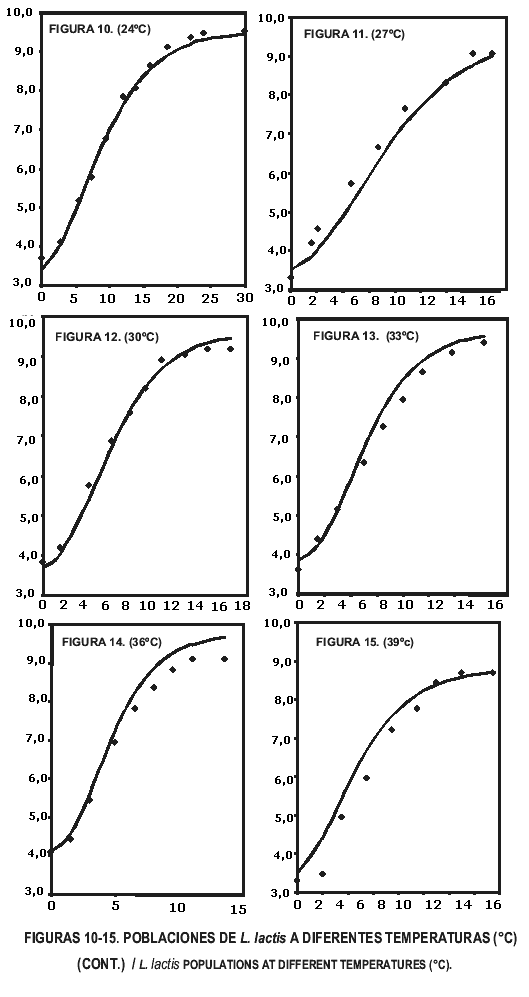
Al sustituir todas las T por el valor de la temperatura en grados Celsius y hacer lo propio con la variable independiente, tiempo (h), es posible predecir la población puntual para esas condiciones, siempre y cuando el inóculo inicial esté muy aproximado a 1,0 x 103 ufc/mL y el medio (leche) sea comparable a la utilizada en este trabajo. En caso de partir de un inóculo diferente, sería necesario construir la curva de crecimiento, para lo cual es necesario repetir el cálculo descrito, en varias oportunidades y a diferentes tiempos hasta describir la misma, luego se debe entrar en ella con la población del inóculo, restar el tiempo correspondiente a la fase de adaptación del tiempo a transcurrir, obteniendo el tiempo de crecimiento efectivo, el cual se utiliza para recorrer el eje de las ordenadas (tiempo) y lograr así una aproximación a la población final (FIGS. 5-9 y del 10-15).
Estos resultados establecen que el modelo no manifiesta sesgo alguno en relación a la temperatura, ya que en las desviaciones del mismo, no aumentan ni disminuyen en relación a ésta, lo cual es de gran importancia por tratarse de un modelo secundario relativo exclusivamente a ese factor. En este sentido, al analizar los ajustes del modelo final presentados en el trabajo de Zwietering y col.[17] para el Lactobacillus plantarum, se concluye que el mismo manifiesta una gran desviación con respecto a los datos observados cuando trata de integrar el modelo y confrontarlo con los valores de origen a temperaturas bajas, a pesar de tratarse de crecimientos en medios de cultivo y no en alimentos, sin embargo a temperaturas más altas, el ajuste obtenido es también excelente.
A efecto de corroborar las bondades del modelo final generado, en las FIGS. 5 hasta 15 (ambas inclusive), se presentan las curvas esperadas de crecimiento del Lactococcus lactis subsp. lactis contra los valores observados que dieron origen al modelo en cada una de las temperaturas ensayadas, en las mismas se puede apreciar como a las temperaturas de 9°, 12°, 21°, 24°, 30° y 39°C, la predicción es excelente, mientras que en otras sin ser tan preciso, refiere una aceptable estimación de la magnitud de las poblaciones, así, a 15 y 27°C, el modelo subestima ligeramente las poblaciones reales, por otra parte, a 18°, 33°, y 36°C, sobreestima las mismas. En todos los casos, las poblaciones se presentan como logaritmos de base 10, a efectos de facilitar el manejo numérico.
En la TABLA X, se presentan los resultados obtenidos al aplicar este modelo a varias temperaturas dentro del rango en estudio, se presentan los valores calculados o ajustados por el modelo y los valores observados al realizar los experimentos adicionales correspondientes, esto, con la finalidad de comprobar el funcionamiento integral del modelo, sin embargo, es necesario aclarar que en los casos presentados, el inóculo inicial se encontraba bastante cercano al calculado a tiempo cero por el modelo.
TABLA X. Parámetros y poblaciones obtenidas al emplear el modelo desarrollado (Ec. 8) / PARAMETERS AND POPULATIONS OBTAINED WHEN THE DEVELOPED MODEL WAS APPLIED (EQ.8).
| T | A | D | B | M | Tiempo | Población Esperada | Población Observada |
| 31°C | 3,610 | 6,048 | 0,324 | 4,395 | 0,0 2,5 7,0 | 3,71 4,56 7,54 | 3,36 5,08 7,60 |
| 32°C | 3,687 | 5,994 | 0,345 | 4,213 | 0,0 2,5 7,0 | 3,77 4,67 7,78 | 3,59 4,90 7,63 |
| 34°C | 3,842 | 5,889 | 0,381 | 3,891 | 0,0 2,5 7,5 | 3,91 4,92 8,42 | 3,72 4,95 8,04 |
| 36°C | 4,000 | 5,788 | 0,400 | 3,615 | 00 2,5 7,0 | 4,03 5,21 8,47 | 3,36 4,45 7,52 |
A, D, B, y M: parámetros de ajuste correspondientes a cada temperatura.
T: temperatura (°C).
Población Esperada: obtenida al utilizar la Ec. 8 para cada temperatura y tiempo (Log(ufc/mL)).
Población Observada: obtenida de las curvas de crecimiento para cada temperatura y tiempo (Log(ufc/mL)).
Puede apreciarse como las poblaciones correspondientes a temperaturas dentro del rango estudiado, pero distintas a las once empleadas para originar el modelo (31°, 32° y 34°C), son bastante afines con la esperadas, así mismo, se presentan poblaciones observadas a 36°C (una de las temperaturas ensayadas para dar origen al modelo), siendo necesario aclarar, que éstas corresponden a datos obtenidos luego de generar la ecuación final de predicción, por lo tanto son independientes, permitiendo entonces corroborar la utilidad de la misma.
La razón para efectuar la comprobación específicamente con estas temperaturas, radica en que, para establecer el modelo secundario del parámetro de ajuste B, se eliminó el punto correspondiente a la temperatura de 33°C por los motivos expuestos en su oportunidad, luego, podría suponerse que el modelo no presentase un buen ajuste al tratarse de la zona térmica correspondiente, requiriéndose entonces la evaluación en un nivel cercano a esta temperatura.
CONCLUSIONES Y RECOMENDACIONES
La integración del modelo primario con los modelos secundarios, permitió generar una ecuación matemática para la predicción del crecimiento del Lactococcus lactis subsp. lactis dentro del rango estudiado, con lo cual se cumplió exitosamente el objetivo central de este trabajo, con esta ecuación es posible calcular con bastante precisión, las poblaciones del microorganismo citado cuando crece en leche, siempre y cuando se conozca la temperatura de crecimiento y el tiempo de incubación.
Se recomienda validar las ecuaciones propuestas con alguna de las cepas del Lactococcus lactis productoras de nisina, ya que, esta bacteriocina ha resultado sumamente útil en la preservación de los productos lácteos como los quesos madurados, incluso, resultaría más importante modelar la producción de este metabolito con el crecimiento del microorganismo, en diversas condiciones de crecimiento, que incluyan además de la temperatura y medio de crecimiento, condiciones como actividad de agua, concentración de sal y pH, para lo cual se cuenta con modelos multiplicativos, capaces de incorporar todos estos factores al unísono.
Finalmente, se recomienda utilizar los modelos propuestos en este trabajo para tratar de describir el crecimiento del Lactococcus lactis subsp. lactis en otros productos lácteos, esto es, debido a que su utilidad estaría dada en medios diferentes al ensayado, como leches pasteurizadas y quesos frescos, sobretodo si se toman en cuenta que, en trabajos previos se ha demostrado, que este microorganismo es capaz de mantener sus parámetros de crecimiento en presencia de otros grupos bacterianos activos.
REFERENCIAS BIBLIOGRÁFICAS
1. AMERICAN PUBLIC HEALTH ASSOCIATION (APHA). Compendium of Methods for the microbiological examination of food. 3rd Ed. 75-95 pp. 1996. [ Links ]
2. Ato, M.; López, J.J. Modelos no lineales. En: Fundamentos de Estadística con SYSTAT. Cap. 13. Addison Wesley Iberoamericana, S.A. Delaware-USA. 399-414 pp.1994. [ Links ]
3. Davidson, P.; Hoover, D. Antimicrobial components from lactic acid bacteria. In: Lactic Acid Bacteria. Salminen S.; Von Wright A (Eds.) Academic Press, San Diego, California. 96-114 pp. 1993. [ Links ]
4. Kim, W.S.; May, R.J.; Dunn, N.W. The effect of nisin concentration and nutrient depletion on nisin production of Lactococcus lactis subsp, lactis. Appl. Microbiol. Biotechnol. 48(4): 449-453. 1997. [ Links ]
5. LEROY, F.; DEGEEST, B.; DE VUST, L.A. novel area of predictive modelling: describing the functionality of beneficial microorganism in foods. Int. J. Food Microbiol. 73: 251-259. 2002. [ Links ]
6. Mäyrä-Mäkinen, A.; Bigret, M. Industrial use and production of lactic acid bacteria. In: Salminen S.; Von Wright A. (Eds.) Lactic Acid Bacteria. Chapter 2. Academic Press, San Diego, California. 65-95 pp. 1993. [ Links ]
7. MCKELARR, R.; Lu, X. Model fitting and uncertainty. Modeling Microbial Responses in Food. Chapter 4. CRC Press, Boca Raton-Florida. 151-196 pp. 2004. [ Links ]
8. McMeekin, T.A.; Olley, J.N.; Ross, T.; Ratkowsky, D.A. Basic concepts and methods. In: Predictive Microbiology: Theory and Application. Chapter 2. Research Studies Press, LTD., Taunton, England. 11-70 pp. 1993. [ Links ]
9. McMeeekin, T.A.; Ross, T. Modeling applications. J. Food Prot. 59 (Supl.): 37-42. 1996. [ Links ]
10. Neter, J.; Kutner, M.; Nachtsheim, C.; Wasserman, W. Applied Linear Statistical Models. 4th Ed. Richard D. Irwin, Inc., Chicago. 105-126 pp. 1996. [ Links ]
11. Ratkowsky, D.A.; Lowry, R.K.; McMeekin, T.A.; Stokes, A.N.; Chandler, R.E. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 154(3): 1222-1226. 1983. [ Links ]
12. RODRIGUEZ, E.; CALZADA, J.; ARQUES, J.L.; RODRIGUEZ, J.M., NUÑEZ, M.; MEDINA, M. Antimicrobial activity of pediocin-producing Lactococcus lactis on Listeria monocytogenes, Staphylococcus aureus and Escherichia coli O157:H7 in cheese. Int. Dairy J. 15: 51-57. 2007. [ Links ]
13. Terzaghi, B.E.; Sandine, W.E. Improved medium for lactic streptococci and their bacteriophages. Appl. Microbiol. 29(6): 807-813. 1975. [ Links ]
14. VALBUENA, E.; BARREIRO, J.; SÁNCHEZ, E.; CASTRO, G.; BRIÑEZ, W.; TOVAR, A. Modelos cinéticos aplicados al crecimiento de Lactococcus lactis subsp. lactis en leche. Rev. Científ FCV-LUZ. XI(5): 464-475. 2005. [ Links ]
15. Whiting, R.C.; Buchanan, R.L. Microbial modeling. Food Technol. 48(6): 113-120. 1994. [ Links ]
16. Wijtzes, T.; Wit, J.C.; Huis, J.H.; Vant Riet, K.; Zwietering, M.H. Modelling bacterial growth of Lactobacillus curvatus as a function of acidity and temperature. Appl. Environ. Microbiol. 61(7): 2533-2539. 1995. [ Links ]
17. Zwitering, M.H.; Cuppers, H.G.; de Wit, J.C.; Van´t Riet, K. Evaluation of data transformation and validation of a model for the effect of temperature on bacterial growth. Appl. Environ. Microbiol. 60(1): 195-203. 1994. [ Links ]
18. Zwitering, M.H.; de Koos, J.T.; Hasenack, B.E.; de Wit, J.C.; Van´t Riet, K. Modeling of bacterial growth as a function of temperature. Appl. Environ. Microbiol. 57: 1094-1101. 1991. [ Links ]












 uBio
uBio