Influencia de la longitud del recipiente y la ubicación de las sillas en los esfuerzos circunferenciales de recipientes horizontales usando el método de elementos de contorno

MARCO GONZÁLEZ D. ¹ Y MANUEL J. MARTÍNEZ ²

¹ Departamento de Mecánica, Universidad Simón Bolívar, Caracas - Venezuela, margdleon@usb.ve

² Escuela de Ingeniería Mecánica, Universidad Central de Venezuela, Caracas - Venezuela, mj_martinez@cantv.net

RESUMEN

En este artículo se presenta el análisis de esfuerzos de un recipiente cilíndrico horizontal a presión soportado en dos sillas, basado en el Método de Elementos de Contorno en tres dimensiones, dirigido a determinar la influencia de la longitud del recipiente y la ubicación de las sillas en los esfuerzos circunferenciales en el contacto silla – cuerpo. La Ecuación Integral generada en este problema incorpora la integral de volumen relacionada con el peso del acero del recipiente. La ecuación de volumen se transforma en una integral de superficie usando el esquema recomendado por Beer. En este trabajo se plantearon tres valores distintos de ubicación de sillas (relación A / R₁) y cinco valores distintos de longitud tangente – tangente del recipiente. Los resultados numéricos alcanzados fueron comparados con el método de Zick, que es el más utilizado en este tipo de diseño, obteniendo resultados concordantes.

Palabras clave: Ubicación de silla, Longitud del recipiente, Recipiente a presión horizontal, Esfuerzos circunferenciales, Método de elementos de contorno en 3D.

INFLUENCE OF THE VESSEL LENGTH AND SADDLES LOCATION ON THE CIRCUNFERENTIAL STRESS IN HORIZONTAL PRESSURE VESSELS USING BOUNDARY ELEMENT METHOD

ABSTRACT

In this article, a stress analysis based on the 3-D Boundary Element Method to determine the influence of the parameters:vessel length and saddles location, on the values of circumferential stress at horn of the saddles in horizontal pressure vessels on two saddles, is presented. The  ntegral equation obtained for this problem includes the volume integral of the body forces, represented by self-weight of vessel. The domain integral is transformed into boundary integral using the method recommended by Beer. In this work, three different saddle locations (A/R₁ ratio) and five different tangent-totangent lengths of vessel are used. The numerical results obtained are compared to Zick analysis, most popular method to design horizontal vessels, obtaining agreed results.

Keywords: Saddle location, Length of vessel, Horizontal pressure vessels, Circumferential stress, 3-D Boundary element method.

Recibido: abril de 2006  Revisado: julio de 2006

INTRODUCCIÓN

El análisis de esfuerzos circunferenciales en el contacto silla – cuerpo en recipientes horizontales largos ha sido realizado por largos años usando el método de Zick (Zick, 1951), el cual se basa en un conjunto de correlaciones teóricas - empíricas que se ajustan a resultados de mediciones experimentales de deformaciones en un recipiente de almacenamiento de propano. Posteriormente se han realizado investigaciones para determinar esfuerzos en recipientes horizontales (Widera et al., 1988; Ong, 1995; Nash y Tooth, 1996) que utilizan el Método de Elementos Finitos, para compararlos con los resultados obtenidos por Zick y/ o para plantear métodos paramétricos de cálculo.

La aplicación del Método de Elementos de Contorno (MEC) para este tipo de problemas de elastostática fue desarrollado en 1967 por Rizzo, para análisis en dos dimensiones, siendo extendido a tres dimensiones por Cruse (1969). Estas soluciones planteaban la ausencia de fuerzas de cuerpo, debido a su poca relevancia para los ejemplos numéricos desarrollados por ellos; además, dichas cargas al depender del volumen y no del contorno, le quitan algunas ventajas computacionales inherentes del MEC.

González y Martínez (2004) aplicaron el MEC en dos dimensiones sin fuerzas de cuerpo, para el análisis de esfuerzos circunferenciales en la sección transversal de un recipiente a presión horizontal, obteniéndose resultados satisfactorios; sin embargo, el análisis bidimensional no permitió incluir variables que tienen relevancia en el problema, tales como el peso propio y del fluido entre apoyos, el ancho de silla, y la distancia entre sillas y cabezales. En dicha publicación se recomienda extender el problema a un análisis tridimensional, tema objeto de este trabajo.

El análisis en tres dimensiones realizado tiene como factor fundamental la presencia de las fuerzas de cuerpo representadas en el peso propio del material que conforma el recipiente, ya que las otras variables mencionadas son incluidas mediante adecuadas condiciones de borde. En este caso se requiere resolver la Ecuación Integral del Contorno (EIC) con la integral de volumen que incluye la variable peso propio. Wen et al. (2000) reportan un conjunto de investigaciones dirigidas a resolver el problema de ecuaciones integrales de contorno con integrales de volumen incorporadas. Para este trabajo se utilizó el procedimiento planteado por Beer (2000), de transformación de la integral de volumen en una integral de superficie, el cual fue incorporado como rutina a un software basado en el MEC en tres dimensiones (MEC-3D) previamente desarrollado.

Para validar el software de MEC – 3D se desarrolló el análisis numérico de un problema de solución exacta conocida, cuyos resultados presentan González y Martínez (2006). Basados en esa validación, se muestra en este trabajo el análisis numérico de los esfuerzos generados en un recipiente a presión horizontal, cuyos resultados fueron comparados con la solución de Zick (1951).

1. FORMULACIÓN DEL PROBLEMA

El recipiente a presión horizontal apoyado en dos sillas se considera como un cuerpo sólido deformable que ocupa un volumen V, tiene una superficie de contorno S y está sometido a: un campo vectorial de fuerzas de cuerpo b, que se refieren al peso del recipiente; un campo vectorial de fuerzas de superficie t⁰, que actúan únicamente en la superficie de contorno del cuerpo, y representan las cargas que el recipiente deberá soportar: presión interna y/o la carga distribuida ocasionada por el peso del fluido contenido; y desplazamientos u⁰ que son conocidos en algunos sectores de S, debido a las restricciones de movimiento que tiene el recipiente, por las sillas donde se apoya.

El análisis permite obtener una matriz de esfuerzos σ simétrica que representa el estado de esfuerzos en un punto cualquiera del sólido, y el vector desplazamiento u de cualquier punto del mismo sólido. Para obtener los valores de la matriz σ y el vector u en un punto genérico del sólido, se deben resolver las ecuaciones de equilibrio en forma diferencial que gobiernan el comportamiento de un cuerpo sometido a los campos vectoriales indicados:

Para completar las ecuaciones necesarias que permiten determinar nueve valores desconocidos, seis valores de esfuerzos y tres valores de desplazamiento, se requiere la utilización de las relaciones esfuerzos – deformación, denominadas constitutivas, las cuales se expresan de la siguiente manera:

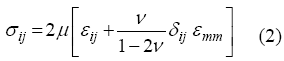
donde μ es el módulo de corte y ν es la relación de Poisson del material.

La ecuación (2) es válida para materiales lineales, homogéneos, isotrópicos y elásticos, y se basa en la ley generalizada de Hooke. El material más utilizado en la fabricación del cuerpo de recipientes, acero al carbono laminado, cumple con los requisitos indicados para la ecuación (2).

Las relaciones constitutivas aportan seis ecuaciones al sistema, pero generan seis incógnitas adicionales, que son las componentes de la matriz de deformaciones ε. Para completar el sistema de ecuaciones, se agregan seis ecuaciones correspondientes a las relaciones deformación – desplazamiento, que se expresan:

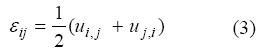
El sistema de quince ecuaciones con quince valores desconocidos obtenido con las expresiones (1), (2) y (3), puede ser simplificado sustituyendo la ecuación (3) en la ecuación (2):

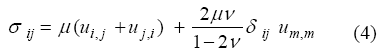
De esta manera, se tiene un sistema de nueve ecuaciones expresadas por (1) y (4), con nueve incógnitas representadas por los valores de la matriz σ y el vector u; este sistema se puede resolver numéricamente mediante la aplicación del Método de Elementos de Contorno (MEC)

Finalmente, se sustituye la expresión (4) en (1), obteniéndose las denominadas ecuaciones de Navier (Cruse, 1969) de elasticidad lineal:

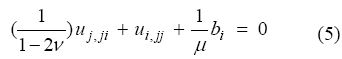
Las soluciones fundamentales de la Ec. (5) U_ij (desplazamiento en dirección j) y T_ij (tracción en dirección j) fueron obtenidas por Lord Kelvin al analizar el comportamiento de un cuerpo infinito al serle aplicada una carga puntual unitaria en una dirección determinada i. Aplicando el Teorema de Recíprocos de Betti, se pueden relacionar dos estados de equilibrios de un cuerpo elástico: uno definido por el problema de Kelvin (U_ij y T_ij conocidos), y otro cuyos vectores desplazamiento u_j y tracción t_j requieren ser conocidos. Así se obtiene la Ecuación Integral del Contorno del problema, conocida como la Identidad de Somigliana:

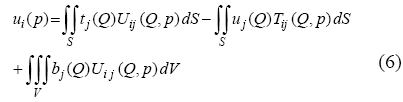
donde p es el punto de aplicación de la carga unitaria, y Q un punto perteneciente al contorno.

Por su naturaleza, el inconveniente de este campo vectorial b_j se encuentra en que requiere trabajar con todo el dominio, y MEC utiliza únicamente el contorno.

El método de este trabajo para incluir las fuerzas de cuerpo en el MEC es el esquema recomendado por Beer (2001), el cual se basa en la transformación de la integral de volumen correspondiente a las fuerzas de cuerpo a una integral de superficie:

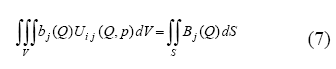
donde

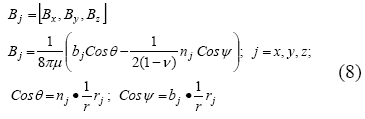
FORMULACIÓN DEL MÉTODO DE ELEMENTOS DE CONTORNO

La forma discretizada de la ecuación (6), habiendo incorporado la ecuación (7), que representa la transformación de las fuerzas de cuerpo al contorno, es:

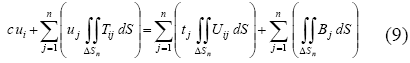
Luego la ecuación 9 se re-expresa de la siguiente manera:

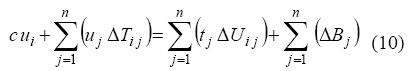
La ecuación (10) puede ser expresada en forma matricial de la siguiente manera:

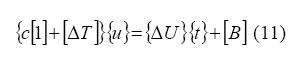
Las matrices [ΔT] y [ΔU] contienen todos los valores de esfuerzo y desplazamiento calculados por la integración de las soluciones fundamentales en el contorno. Al aplicar las condiciones de borde mixtas, donde sobre una parte de la superficie se conocen los desplazamientos, mientras que en la otra parte se conocen los valores de los esfuerzos, se obtienen matrices {u} y {t} con unos valores conocidos y otros desconocidos. Si estos términos se arreglan, incorporando todas las incógnitas a una nueva matriz {X}, y los valores conocidos se suman a los términos de la matriz [B] para formar una nueva matriz [F], se obtiene la expresión [A]{X}=[F], que al resolverse genera los valores de desplazamiento y esfuerzo requeridos, determinando la matriz de esfuerzo en el contorno, así como la matriz de esfuerzo en puntos internos del recipiente.

ANÁLISIS NUMÉRICO

Datos

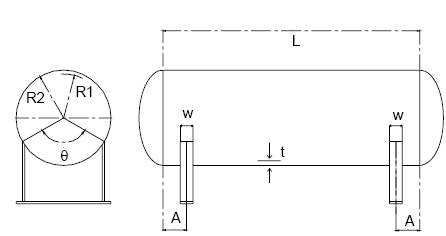
Se plantea la simulación del recipiente horizontal apoyado en dos sillas (ver Figura 1) sometido a las cargas de peso propio más el peso del fluido contenido, durante la etapa de prueba hidrostática. Para este trabajo se usa un programa de computación validado mediante la simulación de un problema de elasticidad tridimensional con carga de peso propio y de solución exacta conocida. González y Martínez (2006) presentan los resultados de esta validación.

Figura 1. Vistas lateral y frontal esquemáticas de Recipiente a Presión Horizontal

En este trabajo se evalúa la influencia de la longitud tangente – tangente del recipiente y de la ubicación de las sillas, en los esfuerzos circunferenciales en el cuerno de la silla generados por cargas gravitatorias.

A continuación se indican los datos utilizados para la simulación:

Dimensiones: Radio interno (R₁): 1828,8 mm; Radio externo (R₂): 1854,2 mm

Longitud cilíndrica tangente – tangente (L): variable desde 6,10 m hasta 16,76 m

Distancia entre cada silla y la línea tangente (A): 914,4 mm (A/R₁ = 0,50); 2139,7 mm (A/R₁ = 1,17); 2852,9 mm (A/R₁= 1,56)

Material: Acero ASTM-A-516-485: E = 200 GPa y n = 0,25

Ángulo de contacto sillas – cuerpo (θ): 120 º y Ancho de silla (ù ): 0,38 m

Discretización del Contorno

Se utilizó un modelo discretizado con base en elementos cuadriláteros compuestos por ocho nodos. Aprovechando la simetría del problema, se modeló la mitad lateral y la mitad longitudinal del recipiente horizontal, para luego extender los resultados a todo el perímetro y a toda la longitud del recipiente. Por otra parte, se sustituyen los cabezales ubicados en ambos extremos del recipiente horizontal por condiciones de borde adecuadas.

Los elementos que conforman el cuerpo fueron distribuidos en función del contorno a discretizar. Para la dirección axial (eje de coordenadas X) se considera siempre un elemento de 0,76 m de longitud axial. Para la dirección radial (dirección más crítica por la forma cilíndrica del cuerpo en evaluación), se realizó un análisis del número de elementos idóneo, que resultó ser 18. El espesor de pared del recipiente se discretizó con un único elemento.

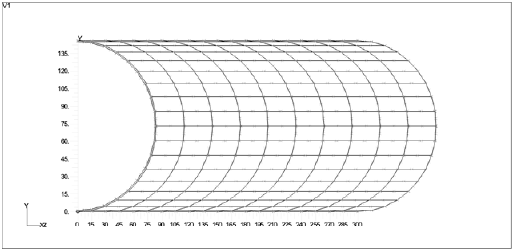
En la Figura 2 se presenta la discretización de un recipiente horizontal de longitud 15,24 m, con 10 elementos en dirección axial (mitad de longitud axial igual a 7,62 m) y 18 elementos en dirección radial (mitad lateral)

Figura 2. Discretización de Recipiente Horizontal

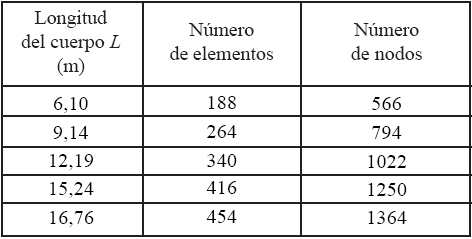
El número de elementos y nodos de la discretización del cuerpo del recipiente para todos los valores considerados de longitud en el análisis se presenta en la Tabla 1.

Tabla 1. Datos de discretización del contorno del cuerpo

Condiciones de Borde

Las condiciones de borde establecidas para la simulación del recipiente horizontal soportado por dos sillas son las siguientes:

Desplazamiento normal de las paredes laterales del recipiente igual a cero (u_z = 0); esto representa la rigidez que se aportan mutuamente ambas mitades laterales del cuerpo

Desplazamiento en dirección axial en el extremo conectado al cabezal recipiente, igual a cero (u_x = 0); esto representa a rigidez de la presencia del cabezal

Desplazamiento axial en el extremo del cuerpo conectado a la segunda mitad longitudinal del recipiente igual a cero (u_x = 0); esto representa la continuidad del cuerpo

Desplazamiento restringido en dirección de los ejes coordenados Y y Z (u_y = u_z = 0), en los elementos del cuerpo en contacto con las sillas de apoyo

Para el peso del fluido se considera que los elementos internos están sometidos a un estado de esfuerzos que representa la carga estática del fluido sobre esos elementos

Análisis de resultados

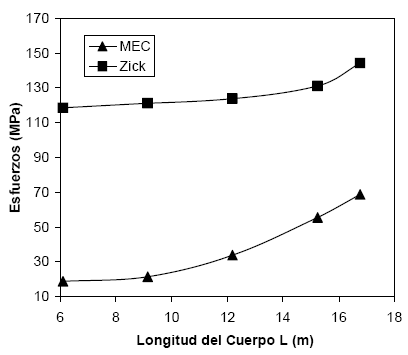
Los cálculos más aceptados de esfuerzos circunferenciales en el extremo de las sillas de recipientes horizontales son aquellos que utilizan las ecuaciones que presenta Zick (1951), las cuales fueron re-expresadas por Megyesy (1992). Por otra parte, se realiza la simulación del recipiente con el Método de Elementos de Contorno para diferentes valores de L, desde 6,10 m hasta 16,76 m, con el objeto de alcanzar los rangos de valores requeridos por las ecuaciones de Zick. Los resultados numéricos de esfuerzos circunferenciales en el extremo de las sillas obtenido de las simulaciones con MEC son comparados con los resultados de la solución teórico - empírica de Zick, para distintos valores de longitud del recipiente y para relaciones A/R₁ de 0,50; 1,17 y 1,56, las cuales se consideran relaciones relevantes en las ecuaciones de Zick.

Es conveniente mencionar que los esfuerzos circunferenciales en el extremo de las sillas son a compresión, pero se presentan en valor absoluto para mayor facilidad de representación gráfica.

Relación A/ R₁ = 0,50

Los esfuerzos circunferenciales en el extremo de las sillas obtenidos utilizando MEC para una relación A/R₁ = 0,50 se comparan con los esfuerzos obtenidos de aplicar las ecuaciones de Zick (1951). Los resultados numéricos son presentados en la Tabla 2

Tabla 2. Esfuerzos Circunferenciales en Unión Silla– Cuerpo (MPa) (A/ R₁ = 0,50)

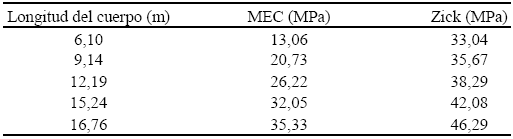
Los resultados muestran que el programa del Método de Elementos de Contorno predice un comportamiento similar en los esfuerzos circunferenciales en el punto de contacto silla / cuerpo del recipiente, al reportado utilizando las ecuaciones de Zick, esto es a mayor longitud, los esfuerzos generados son mayores.

Sin embargo, los valores obtenidos por MEC son menores en valor absoluto a los esfuerzos reportados por las ecuaciones de Zick.

La diferencia entre ambos resultados disminuye a medida que se incrementa la longitud: desde 60,5% para una longitud de 6,1 m hasta 23,7% para una longitud de 16,8 m.

La estructura de las ecuaciones de Zick genera que la variación de la longitud sea poco relevante en los resultados de los esfuerzos circunferenciales en el extremo de las sillas (el valor del esfuerzo para L = 16,8 m es 1,4 veces mayor que el valor para L = 6,1 m), mientras que los resultados por MEC reconocen en mayor medida el impacto de la longitud (2,7 veces mayor).

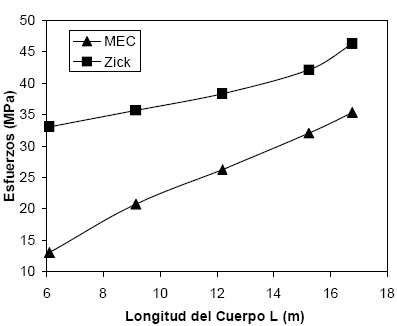
En la Figura 3 se presentan gráficamente dichos resultados.

Figura 3. Esfuerzos circunferenciales en contacto cuerpo – extremo de silla A/R1 = 0,50

Tabla 3. Esfuerzos Circunferenciales en Unión Silla – Cuerpo (A/ R₁ = 1,17)

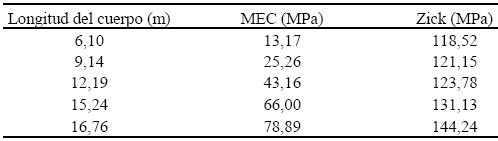
Los esfuerzos circunferenciales reportados por MEC para una relación A/R₁ = 1,17 (A = 2139,7 mm), son mayores que los obtenidos para una relación A/R₁ = 0,50, lo cual está de acuerdo con la consideración de que al alejarse las sillas de los cabezales, el cuerpo pierde la rigidez que le otorgan estos para resistir los esfuerzos circunferenciales, generando mayores esfuerzos en el cuerpo. Sin embargo, los valores obtenidos por MEC siguen siendo menores en valor absoluto a los esfuerzos reportados por Zick.

La estructura de las ecuaciones de Zick genera que la variación de la longitud sea menos relevante aún en los resultados de los esfuerzos circunferenciales en el extremo de las sillas (el valor del esfuerzo para L = 16,8 m es apenas 1,08 veces mayor que el valor para L = 6,1 m), mientras que los resultados obtenidos por MEC reconocen en mayor medida el impacto de la longitud (6,00 veces mayor).

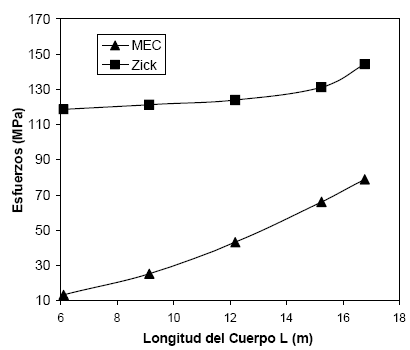
En la Figura 4 se presentan gráficamente dichos resultados.

Figura 4. Esfuerzos Circunferenciales en Unión Silla / Cuerpo – A/ R₁ =1,17

El cambio de la relación A/ R₁ (de 0,50 a 1,17) en las ecuaciones de Zick genera valores de esfuerzos circunferenciales que varían desde 3,59 veces para L = 6,1 m hasta 3,11 veces para L = 16,8 m; mientras que con MEC, la variación es contraria y sensiblemente menor: desde 1,01 veces hasta 2,23 veces.

Relación A/ R₁ = 1,56

Zick plantea que los esfuerzos circunferenciales en la unión silla - recipiente son constantes para cualquier valor de A/ R e» 1,0 y una longitud dada. Para determinar si esta predicción es coherente, se realiza la simulación por MEC para una relación A/R1 = 1,56 (A = 2852,9 mm). Los resultados numéricos de este caso son presentados en la Tabla 4.

Tabla 4. Esfuerzos Circunferenciales en Unión Silla – Cuerpo (A/ R1 = 1,56)

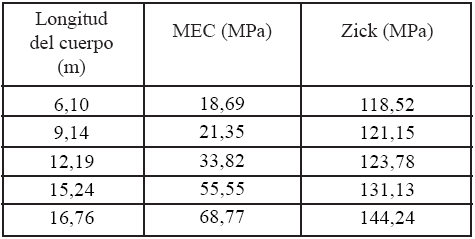
En general, los esfuerzos obtenidos con MEC para una relación A/R = 1,56 son menores que para A/R₁ = 1,17, lo cual indica que el punto crítico de un recipiente horizontal, desde el punto de vista de esfuerzos, se presenta para una relación A/R alrededor de 1,0.

Este hecho lo establece el método de Zick, al reportar sus máximos valores de esfuerzos para dicha relación. Sin embargo, Zick sobre-estimaría los valores de esfuerzos circunferenciales para valores de A/ R₁ > 1,5.

En la Figura 5 se presentan gráficamente los resultados obtenidos por ambos métodos.

Figura 5. Esfuerzos Circunferenciales en Unión Silla / Cuerpo – A/ R₁ =1,56

CONCLUSIONES

El cálculo de esfuerzos circunferenciales en el extremo del contacto cuerpo – silla de un recipiente cilíndrico horizontal a presión fue analizado por el Método de Elementos de Contorno en tres dimensiones utilizando la formulación de la Ecuación Integral de Borde, que incorpora la integral de volumen de las fuerzas de cuerpo (peso propio del recipiente), convertida en una integral de superficie.

Los resultados numéricos fueron comparados con el método de Zick (1951), y demuestran que el Método de Elementos de Contorno puede ser aplicado en el campo de recipientes con buenos resultados. Al incorporar los cabezales y las sillas en el modelo, los resultados deben ser más precisos. De igual forma, se esperan resultados con mayor precisión si se incrementan el número de elementos en la discretización del cuerpo, en las direcciones radial y axial.

Estos valores muestran que el programa del Método de Elementos de Contorno predice un comportamiento esperado, esto es a mayor longitud del recipiente mayor valor tienen los esfuerzos circunferenciales en la unión silla – cuerpo. Para recipientes a presión horizontales con cargas por reacciones en los apoyos, el análisis tridimensional con Método de Elementos de Contorno, permite obtener resultados más precisos que con el análisis bidimensional reportado por González y Martínez (2004), por lo que se justifica su uso a pesar de ser más compleja su aplicación.

REFERENCIAS

1, BEER, G. (2001). Programming the Boundary Element Method. An Introduction for Engineers, John Wiley & Sons, LTD.        [ Links ]

2. CRUSE, T. A. (1969). Numerical solutions in three dimensional elastostatics, International Journal of Solid Structures, vol. 5, pp. 1259-1274.        [ Links ]

3. GONZÁLEZ D., M. & M. MARTÍNEZ. (2004) Determinación de esfuerzos circunferenciales en recipientes horizontales largos apoyados en dos sillas, utilizando el Método de Elementos de Contorno, pp 150-154, VII CIMENICS.        [ Links ]

4, GONZÁLEZ D., M. & M. MARTÍNEZ. (2006). Aplicación del Método de Elementos de Contorno en tres dimensiones para el Análisis de Esfuerzos en Recipientes Horizontales, VIII CIMENICS.        [ Links ]

5. MEGYESY, E.F. (1992). Pressure Vessel Handbook, 9th Edition, Publishing Co. Tulsa, Inc.        [ Links ]

6. NASH, D.H & A. S. TOOTH. (1996). The influence of the flexibility of the dished end on twin saddle supports pressure vessels, 6th Conference on Pressure Vessels Technology.        [ Links ]

7. ONG, L.S. (1995). Peak stress and fatigue assessment at the saddle support of a cylindrical vessel. Journal of Pressure Vessel Technology, Vol. 117: 305 – 311. 1995.        [ Links ]

8. WEN, P.H., M.H. ALIABADI, A. YOUNG. (2000). Application of dual reciprocity method to plates and shells, Engineering Analysis with Boundary Elements, vol. 24, pp. 583–590.        [ Links ]

9. WIDERA, G.E.O., Z.F. SANG, R. NATAJARAN. (1988). On the design of horizontal pressure vessels Journal of Pressure Vessel Technology, Vol. 110: 393 – 401.        [ Links ]

10. ZICK, L.P. (1951). Stresses in large horizontal cylindrical vessels on two saddles supports, The Welding Research Supplement        [ Links ]