Evaluación de los métodos espectrales para el diseño de columnas de concreto armado de estructuras planas

Dilio A. Godoy B. ¹, Oscar A. López ²

¹ Facultad de Ingeniería, Universidad del Zulia, Venezuela.

² IMME, Facultad de Ingeniería, Universidad Central de Venezuela

RESUMEN

El principal objetivo de esta investigación es evaluar el método tradicional de diseño espectral de columnas que considera los valores máximos probables de la fuerza axial y del momento flector, para estructuras planas de concreto armado sometidas a una sola componente sísmica. Con esta finalidad, este método se compara con métodos más refinados propuestos recientemente, denominados del Esfuerzo Extremo y de la Fuerza Extrema, los cuales utilizan el concepto de valores simultáneos probables de fuerza axial y momento flector. Se comparan también los valores de diseño obtenidos por todos los métodos con el conjunto de valores posibles de fuerza axial y momento flector cuya envolvente está dada por la elipse de interacción de Gupta. Se definieron modelos simplificados de estructuras planas para edificios con vigas rígidas y edificios con vigas flexibles de 1, 2 y 8 pisos, con período corto y largo, y se sometieron a una componente sísmica horizontal de dirección fija coincidiendo con uno de los ejes principales de la estructura. Se determinó el error relativo entre las fuerzas máximas probables y las fuerzas simultáneas probables, tomando estas últimas como valores más confiables para fines de diseño. Los errores encontrados son siempre de sobrestimación. Se concluye que el método tradicional es conservador, los métodos propuestos son más precisos y que las áreas de acero en el diseño de columnas de concreto armado calculadas con las fuerzas máximas probables, pueden estar sobrestimadas hasta un 260% en edificios de mediana altura, en relación a un diseño más confiable basado en los valores simultáneos probables.

Palabras clave: métodos espectrales, columnas de concreto armado, estructuras planas, valores máximos probables, valores simultáneos probables.

Evaluation of spectral methods for the design of reinforced concrete columns for plane structures

ABSTRACT

The main objective of this investigation is to evaluate the traditional method of spectral design of columns that considers the probable maximum values of the axial force and the bending moment, for plane structures of reinforced concrete under a single seismic component. With this purpose, this method is compared with more refined methods recently proposed, the Extreme Stress and the Extreme Force Methods, which use the concept of probable simultaneous values of axial force and bending moment. The design values using those methods are also compared with the set of possible values of axial force and bending moment whose envelope is given by the interaction ellipse of Gupta. Simplified models of 1, 2 and 8-story plane structures for buildings with rigid beams and buildings with flexible beams were defined, with a short and a long period, under a horizontal seismic component along one of the main axes of the structure. The relative error between the probable maximum forces and the probable simultaneous forces was determined, taking the last ones as more reliable values for design purposes. The errors found are always in excess. In conclusion, the traditional method is conservative, the proposed methods are more accurate and the reinforcement bar areas in the design of reinforced concrete columns calculated with the probable maximum forces, can be exceeded up to 260% in buildings of medium height, in relation to a more reliable design based on the probable simultaneous values. spectral methods, reinforced concrete columns, plane structures, probable maximum values, probable simultaneous values.

Recibido: agosto de 2006 Revisado: abril de 2007

INTRODUCCIÓN

El método de análisis espectral es comúnmente usado en ingeniería sísmica para estimar los valores máximos de respuestas en estructuras lineales sujetas a movimientos sísmicos. En este método las respuestas modales máximas son entonces combinadas de una manera apropiada para estimar los valores máximos probables de las respuestas de interés (Chopra, 2001). Es idealmente apropiado para el análisis o diseño de elementos estructurales que son controlados por el valor máximo de una única respuesta, tales el caso de una viga gobernada por el máximo momento flector. Utilizando factores de reducción en los espectroselásticos, el método de análisis espectral también se sueleutilizar en el diseño de estructuras que responden en elrango inelástico, tal como se presenta en normas sismorresistentes nacionales (COVENIN, 2001) einternacionales (ICBO, 1997; ECS, 1998; ICC, 2000). Para aquellos miembros en los cuales la acción simultánea de múltiples respuestas sísmicas deba ser considerada, como por ejemplo una columna sujeta a carga axial y a momentos flectores, un diseño utilizando los máximos valores de estas fuerzas puede no ser el más idóneo.

La respuesta de miembros a movimientos sísmicos multicomponentes se fundamenta en el modelo de Penzien y Watabe (1975), en el cual el movimiento traslacional delterreno es usualmente descompuesto en sus tres componentes principales, no correlacionadas: dos en el plano horizontal y una en la dirección vertical. En este trabajo solo se considera una componente horizontal.

Para miembros en los cuales la acción simultánea de múltiples respuestas sísmicas debe ser considerada en el diseño, se han desarrollando en los últimos años investigaciones comolas de Menun-Der Kiureghian (2000a; 2000b)(MDK) y lasde Anastassiadis-Avramidis-Panetsos (2002)(AAP). Lainvestigación de MDK, predice la envolvente que limita doso más respuestas en una estructura lineal; sin embargo, está limitada a que las componentes horizontales tengan espectros proporcionales. Por otro lado, la determinaciónde la denominada envolvente suprema es extremadamente laboriosa y debe ser realizada punto por punto, además, ladeterminación del punto de contacto entre la superficie decapacidad y la envolvente suprema requiere el uso de unalgoritmo numérico especial en una manera iterativa, cuyaconvergencia a un máximo o mínimo global o local no puede ser predicha desde el principio. La investigación de AAP, deriva las propiedades tensoriales de una respuesta arbitrari  de una estructura sujeta a una excitación sísmica ortotrópica y en base a ello desarrolla los métodos del Esfuerzo Extremo y de la Fuerza Extrema, los cuales permiten considerar espectros con formas distintas, pero está limitado sólo a componentes horizontales. Adicionalmente, ambas investigaciones, sólo ilustraron la aplicación de los métodos propuestos a una única estructura, por lo que los resultadosno pueden ser extrapolables a otras estructuras; por lo tanto, conviene extender esas investigaciones mediante análisis paramétricos de estructuras, tal como los realizados porLópez-Chopra-Hernández (2000), en el caso de una solarespuesta, a fin de evaluar la factibilidad y la incidencia de aplicar estas nuevas metodologías. Por otro lado, interesa conocer el grado de aproximación y los errores que se introducen al usar las metodologías aproximadas de diseño(Marín-Güell, 1984) contenidas en las normas nacionales (COVENIN, 1985) y extranjeras vigentes.

El principal objetivo de esta investigación es evaluar el método tradicional de diseño espectral de columnas que considera los valores máximos probables de la fuerza axial y del momento flector, para estructuras planas de concreto armado sometidas a una sola componente sísmica. Con estafinalidad, este método se compara con otros métodos másrefinados propuestos recientemente por Anastassiadis- Avramidis-Panetsos (2002), denominados del Esfuerzo Extremo y de la Fuerza Extrema, los cuales utilizan el concepto de valores simultáneos probables de fuerza axial y momento flector. Se comparan también los valores de diseño obtenidospor todos los métodos con el conjunto de valores posibles de fuerza axial y momento flector cuya envolvente está dada por la elipse de interacción de Gupta.

VALORES SIMULTÁNEOS DE FUERZA AXIAL Y MOMENTO FLECTOR

Las fuerzas en los elementos inducidas por el sismo varían en el tiempo, independientemente una de otra; por consiguiente, existe un tiempo sobre el intervalo de oscilación de la estructura, diferente para cada componente de fuerza, en el cual alcanzan sus valores máximos probables o extremos. Por ejemplo, en el caso de una columna, un número infinito de conjuntos de tres componentes de fuerza (N, Mx, My) actúan sobre sus secciones transversales durante el intervalo de vibración de la estructura y las tres componentes, por lo general, alcanzan sus valores máximos probables o extremos en tiempos diferentes; así que elconjunto formado por estas últimas no tiene significado físico y la información necesaria para el diseño de la sección transversal de la columna debería ser determinada a travésde la evaluación de unos pocos conjuntos de las trescomponentes de fuerza que consideren los casos más críticos y satisfagan los requerimientos de seguridad. Estos conjuntos forman la requerida «combinación más desfavorable de fuerzas simultáneas» actuando sobre la sección transversal de la columna.

Gupta y Chu (1977), esbozan un procedimiento general para obtener cualquier valor de respuesta, la cual es esperada a ocurrir simultáneamente con un valor de respuesta máxima probable en un sitio dado de la estructura.

Elipse de Interacción

Al utilizar el método de análisis espectral las respuestas modales máximas son combinadas por reglas como la raíz cuadrada de la suma de los cuadrados (Chopra, 2001) (SRSS), o la denominada combinación cuadrática completa (Wilsonet al., 1981) (CQC), para estimar el valor máximo probable de la respuesta de interés. Ésta provee solamente el valor máximo probable (positivo o negativo) de la fuerza axial N o momento flector M en el caso de una columna de unaestructura plana. Un criterio de diseño frecuentemente utilizado en la práctica ingenieril consiste en considerar todas las combinaciones máximas probables dadas por ± N, ± M y diseñar con la más desfavorable de ellas. Gupta y Singh (1977) han derivado un procedimiento analítico para determinar la envolvente de todos los valores posibles de las fuerzas N y M que ocurren durante la respuesta sísmica. Cualquier punto de esta envolvente da una combinación de estas fuerzas que pueden ocurrir simultáneamente.

Para el caso de estructuras planas la envolvente deseada viene dada por la siguiente expresión (Gupta y Singh, 1977):

m² N² + n² M² – 2 l² NM = m² n² – l⁴                                 (1)

donde:

n² = å_i å_j ε_ij N_ki N_kj                         (2)

m² = å_i  å_j ε_ij M_ki M_kj                        (3)

l² = å_i  å_j ε_ij N_ki N_kj                           (4)

En las anteriores ecuaciones ε_ij es el coeficiente de correlación entre los modos i y j; n y m son los valoresmáximos probables de la fuerza axial y el momento flector,respectivamente; N_ki y M_ki son los valores modales máximos, con sus signos correspondientes, en el modo i ante la componente sísmica k, de la fuerza axial y del momento flector, respectivamente.

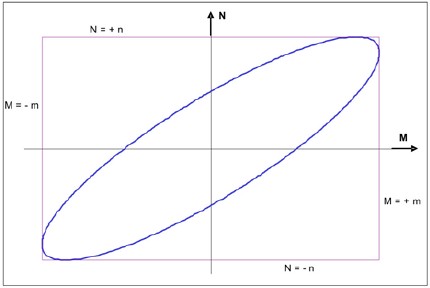
La ecuación (1) simboliza una elipse tal como se muestra en la figura 1. La elipse es la envolvente de todos los valores posibles de N y M que se pueden generar durante la respuesta sísmica, y por ende, es denominada la «elipse de interacción». Esta elipse está limitada por las tangentesdefinidas por los valores máximos probables, N = ± n y M = ± m, las cuales generan un rectángulo que envuelve la elipse (figura 1). Es claro que los valores de n y m no pueden ocurrir simultáneamente.

Figura 1. Elipse de interacción.

Cualquier punto sobre la elipse de interacción da un par devalores de N y M que si pueden ocurrir simultáneamente;por lo tanto, para diseñar una sección que satisfaga requisitos de seguridad, es suficiente que el diagrama de interacción que describe la capacidad de la columna, envuelva completamente a la elipse de interacción.

Método del Esfuerzo Extremo (MEE)

La determinación de las «combinaciones desfavorables» de las fuerzas internas en secciones específicas de los miembros, pertenece a la primera fase del análisis de unaestructura, en la cual se suele adoptar en las normas de diseño que ésta se comporta linealmente elástica; porconsiguiente, es legítimo calcular provisionalmenteesfuerzos normales y cortantes en una sección específica al igual que los correspondientes momentos flectores, fuerzascortantes y fuerzas axiales de acuerdo con las reglas de la Mecánica de Materiales, es decir, adoptando seccioneshomogéneas. Así por ejemplo, en cualquier punto de una sección de una columna rectangular es posible determinarel esfuerzo axial σ correspondiente a una combinación simultánea probable prescrita de fuerzas internas M_ξ , M_η ,N. Ahora, si σ es escogido a ser el esfuerzo máximo probable o extremo σ_k (con signo positivo o negativo) en una de las esquinas k de la sección rectangular, la combinacióncorrespondiente de  M_ξk ,  M_ηk , N_k es una «combinación desfavorable» probable de fuerzas internas simultáneas,porque esta combinación produce un esfuerzo extremo en la sección. Para las cuatro esquinas k = 1, 2, 3, 4 resultan un total de 8 combinaciones desfavorables (4 para el signopositivo σ_k y 4 para el signo negativo  σ_k ), las cuales cubren todos los casos posibles de esfuerzos extremos a ser generados en una sección rectangular.

Basado en las anteriores ideas, Anastassiadis-Avramidis- Panetsos desarrollan un procedimiento general denominado Método del Esfuerzo Extremo (Anastassiadis et al., 2002), para el caso de dos componentes sísmicas que inciden con un ángulo è con respecto a los ejes principales de laestructura (x, y). El método puede ser aplicado en el caso de excitación sísmica de la siguiente manera: Primero, se calculan los esfuerzos normales máximos probables en cada esquina k:

±σ_k , k = 1, 2, 3, 4                             (5)

Luego, el valor simultáneo probable (con σ_k ) de una fuerza S en una sección es determinada así (Gupta y Chu, 1977):

S_σk / C_σks  = σ_k                           (6)

donde:

C_σks  = å_i  å_j ε_ij + (σ_ki,la S_j,la+ σ_ki,IIb S_jIIb                       (7)

El coeficiente C_σks de correlación para el sistema de referencia fijo (x, y) de la estructura, resulta:

C_σks= C_σks,x cos² θ_cr,k                                  (8)

donde:

C _σks,x  = å_i  å_j ε_ij + (σ_ki,xa S_j,xa+ σ_ki,yb S_yb                         (9a)

C_σks,y  = å_i  å_j ε_ij + (σ_ki,xb S_j,xb+ σ_ki,ya S_ya                         (9b)

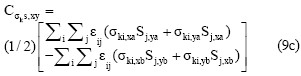
En las anteriores ecuaciones ε_ij es el coeficiente de correlación entre los modos i y j;σ_ki,xa σ es el esfuerzo en la esquina k de la columna en el modo i, con sus signos respectivos, ante la componente sísmica x bajo el espectrode movimiento correspondiente S^a; S _j,xa es la fuerza enuna sección de la columna en el modo i, con sus signos respectivos, ante la componente sísmica x bajo el espectro de movimiento correspondiente S^a.

Para estructuras planas sometidas a una sola componente sísmica en dirección x, se tiene que θ= 0° y las ecuaciones (8) y (9) resultan:

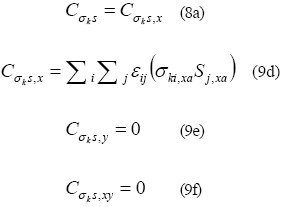
El factor de correlación ks Cσ es calculado con la ecuación (8a), y el valor simultáneo probable (con σ_k ) de una fuerzaS en una sección, es calculado con la ecuación (6). Este procedimiento de cálculo se repite para todas las otrasfuerzas en la sección que deben ser tomadas enconsideración para el diseño de la sección (momento flector, fuerza axial).

Método Aproximado de la Fuerza Extrema (MFE)

Este método está basado en la siguiente regla confiable (Anastassiadis et al., 2002): cada «combinación desfavorable» de dos o más fuerzas en una sección de un miembro estructural comprende el valor máximo probable o extremo de una de estas fuerzas y los valores simultáneos probables de las otras. Los valores máximos probables de cualquier fuerza R en una sección son:

± R                                 (10)

Para una excitación sísmica, el valor simultáneo probable (con R) de cualquier otra fuerza S en una sección es determinada así (Gupta y Chu, 1977):

S_r C_rs = / R                      (11)

donde:

El coeficiente de correlación C_rs para el sistema de referencia fijo (x, y) de la estructura, resulta:

donde:

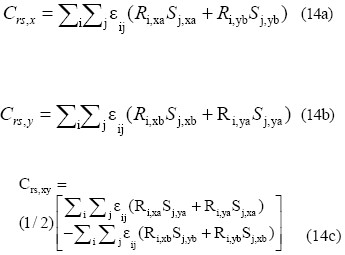
En las anteriores ecuaciones ε_ij es el coeficiente de correlación entre los modos i y j;  R _i,xa y  S _j,xa son las fuerzas en una sección de la columna en los modos i y j,respectivamente, con sus signos respectivos, ante lacomponente sísmica x bajo el espectro de movimiento correspondiente S^a.

Para estructuras planas sometidas a una sola componente sísmica en dirección x, se tiene que  θ= 0° y las ecuaciones (13) y (14) resultan:

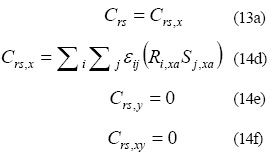
El factor de correlación C_rs es calculado con la ecuación (13a), y el valor simultáneo probable (con R) de una fuerza Sen una sección es calculado con la ecuación (11). Este procedimiento de cálculo se repite para todas las otras fuerzas en la sección que deben ser tomadas en consideración para su diseño (momento flector, fuerza axial).

EDIFICIOS Y MOVIMIENTO SÍSMICO

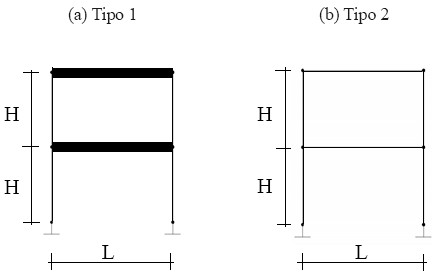
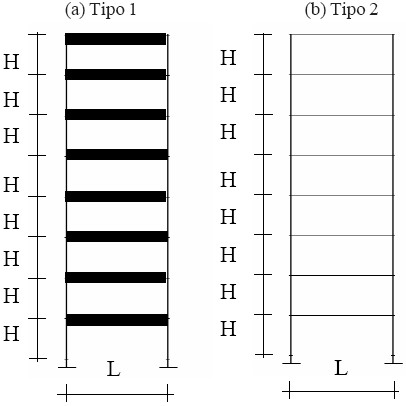
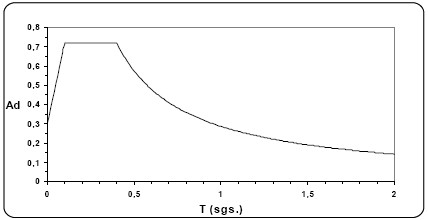
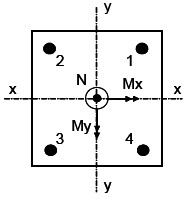
Se definen modelos simplificados de edificios de 1,2 y 8 pisos, cuyas características de los dos últimos se muestran en las figuras 2 y 3. En ellas se observa que para cada uno de los edificios estudiados existen dos casos: el primero, es un edificio con vigas rígidas (tipo 1), y el segundo, es un edificio con vigas flexibles (tipo 2). En el caso particular del edificio de 8 pisos tipo 1, la variación de las dimensiones delas columnas cuadradas son las necesarias para que el primer modo sea lineal. Los distintos edificios se sometieron a una componente horizontal de dirección fija coincidiendo con uno de los ejes principales de la estructura (sismo en la dirección x) de acuerdo al espectro de diseño COVENIN 1756-98: REV. 2001, cuyas características se muestran en la figura 4. Adicionalmente, para cada uno de los tipos de edificios se varió la masa hasta conseguir un período largo T₁=1 s. (rama descendente del espectro) y un período corto T₁=0.1 s. (inicio de la zona plana del espectro). En el método del Esfuerzo Extremo se consideró, para las bases de las columnas analizadas, la numeración de las esquinas y la convención de fuerzas mostradas en la figura 5; por lo cual, siendo planas las estructuras estudiadas (M_x = 0), sólo se analizaron por simetría las esquinas k=1 y k=2. A partir de este momento, se utiliza M_y = M.

Figura 2. Edificio de dos pisos. Columnas de 30x30 cms., H= 3 m, L= 5m. (a) Tipo 1: viga rígida; (b) Tipo 2: viga de 30x50 cms.

Figura 3. Edificio de ocho pisos. H= 3 m, L= 5m. (a) Tipo 1: viga rígida con primer modo lineal; (b) Tipo 2: viga de 40x60 cms. y columnas de 60x60 cms.

Figura 4. Espectro de diseño COVENIN 1756-98, Rev. 2001: Zona 5, Grupo B2, Suelo S1.

Figura 5. Numeración de esquinas y convención de fuerzas para base de columna: método del Esfuerzo Extremo.

Las respuestas se determinan en diversas columnas variando paramétricamente el tipo de edificio, el número de pisos y los períodos de cada uno. En el método del Esfuerzo Extremo, para cada caso, se determinaron los esfuerzos máximos probables en las esquinas ya mencionadas y se compararon con los esfuerzos equivalentes obtenidos a partir de la fuerza axial y del momento flector máximos probables. Para ambos métodos, se determinan y comparan las respuestas máximas probables y las respuestas simultáneas probables que se utilizan en el diseño de acuerdo a la propuesta dada por Anastassiadis et al., 2002. Las respuestas simultáneas probables se calculan, para el métododel Esfuerzo Extremo, a partir de los esfuerzos máximos probables en cada esquina de la columna; y para el método de la Fuerza Extrema, a partir de cada una de las fuerzas máximas probables.

Con el propósito de evaluar la incidencia de aplicación de estas metodologías en términos de las solicitaciones de diseño y de los porcentajes de acero longitudinal, se consideró el edificio de 8 pisos de varios vanos cuyas características se muestran en la figura 6. Este edificio se sometió asismo en la dirección horizontal de acuerdo al espectro de diseño mostrado en la figura 4 pero con un factor de reducción de respuesta R=3, además a cargas de gravedad representadas por una carga permanente de 554 kg /m² para eltecho y 569 kg /m² para el resto de los entrepisos, y una carga variable de 100 kg /m² para el techo y 175 kg /m² parael resto de los entrepisos. Se le realizaron las combinaciones de carga estipuladas en la norma COVENIN 1753 y se diseñaron las columnas del eje 5 por los diferentes métodos: el tradicional, el MEE y el MFE, obteniéndose el acero longitudinal correspondiente a cada uno de ellos.

Figura 6. Edificio de ocho pisos. H= 3 m, L= 6m., vigas de 40x60 cms., columnas de 50x50 cms. para los entrepisos 1- 4, columnas de 35x35 cms. para los entrepisos 5-8.

COMPARACIÓN DE FUERZAS MÁXIMAS PROBABLES Y FUERZAS SIMULTÁNEAS PROBABLES

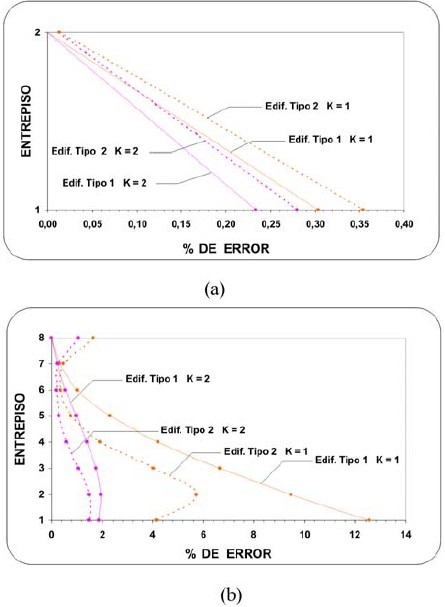
Para edificios de 1 piso todos los métodos de diseño conducen al mismo resultado pues los valores máximos probables del momento flector (M) y la fuerza axial (N) son simultáneos en el tiempo y coinciden por lo tanto con losvalores simultáneos probables. Para edificios de 2 y 8 pisosse determinaron los esfuerzos máximos probables en lasesquinas de varias columnas del edificio, y se compararoncon los esfuerzos equivalentes obtenidos a partir de losmáximos probables de M y N. Se determinó el error en el cálculo del esfuerzo equivalente relativo al esfuerzo máximo probable. Se obtuvieron errores muy pequeños, menores al 1%, en los edificios de 2 pisos y de período largo (T₁=1 s.), tipos 1 y 2; mientras que para el mismo período y tipos en edificios de 8 pisos se obtuvieron errores mayores, hasta de 13% de sobrestimación (figura 7). Los errores se hacen insignificantes para el caso de período corto T₁=0.1 s. (figura 8). Un aumento en el número de pisos o en el período da lugar a un aumento en el error debido a la mayor contribución de los modos superiores.

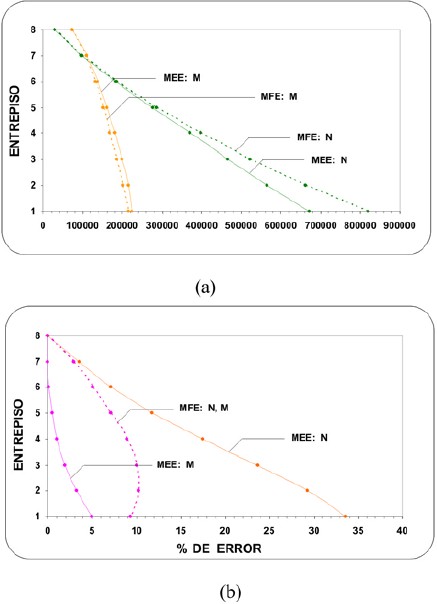
Figura 7. Error en los esfuerzos, método del Esfuerzo Extremo, caso T1=1 s.: (a) Edificios de dos pisos (b) Edificios de ocho pisos.

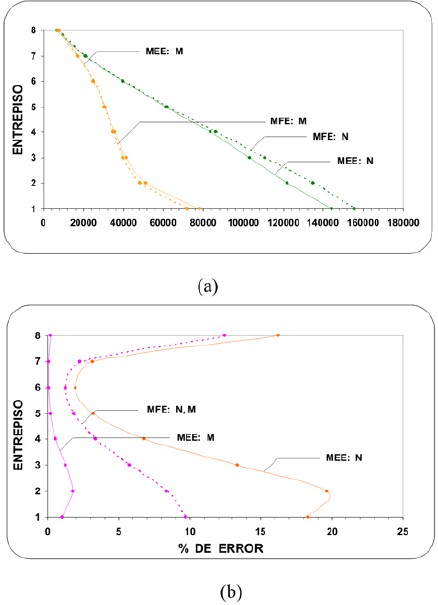
Figura 8. Error en los esfuerzos, método del Esfuerzo Extremo, caso T₁=0.1 s.: (a) Edificios de dos pisos (b) Edificios de ocho pisos.

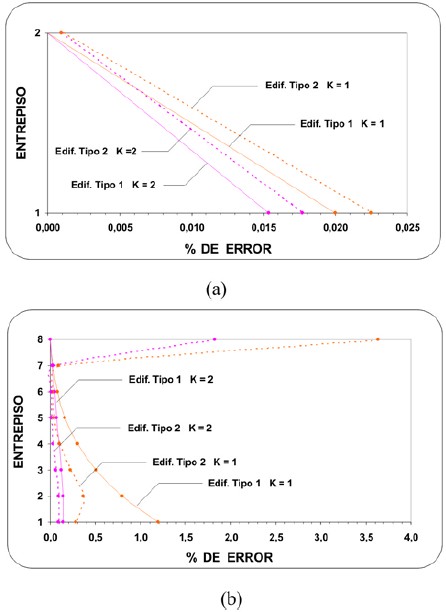
Para estos mismos edificios se calcularon las fuerzas simultáneas probables por los métodos MEE y MFE y se determinó el error relativo entre éstas y las fuerzas máximas probables, tomando las primeras como valores más confiables para fines de diseño. Se obtuvieron para los métodos MEEy MFE errores pequeños, menores al 7% y 6%, respectivamente, para N en los edificios de 2 pisos con período largo (T₁=1 s.), tipos 1 y 2; mientras que para M los errores soncasi nulos (figuras 9 y 10).Un aumento en el número depisos produce un aumento en la contribución de los modos superiores y por ende en la diferencia entre las fuerzas máximas probables y las simultáneas probables. Para el mismo período y tipos en edificios de 8 pisos, por el MEE y el MFE se obtuvieron para N errores mayores, hasta de un 33% y 12%, respectivamente; mientras que para M fueron hastade un 5% y 12%, respectivamente (figuras 11 y 12). Todos estos errores son de sobrestimación. Para el caso de los sistemas con período corto (T₁=0.1 s.) los errores se hacen insignificantes debido a la poca contribución de los modos superiores, por lo que estos resultados no son presentados en figuras.

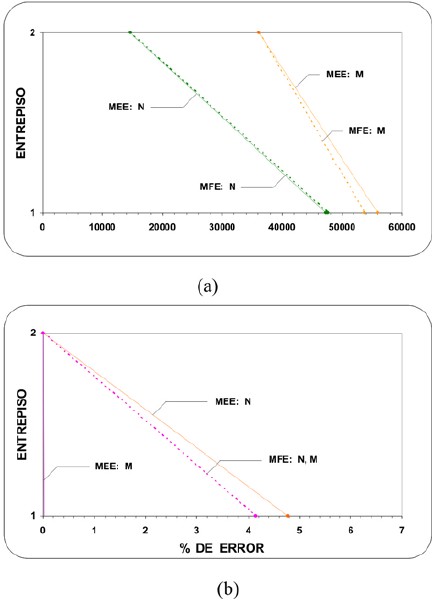
Figura 9. Fuerzas (Kg y Kg-m) y errores para el edificio tipo 1 de dos pisos, caso T₁=1 s., ambos métodos: (a) Fuerzas simultáneas probables (b) Error en las fuerzas máximas probables.

Figura 10. Fuerzas (Kg y Kg-m) y errores para el edificio tipo 2 de dos pisos, caso T₁=1 s., ambos métodos: (a) Fuerzas simultáneas probables (b) Error en las fuerzas máximas probables.

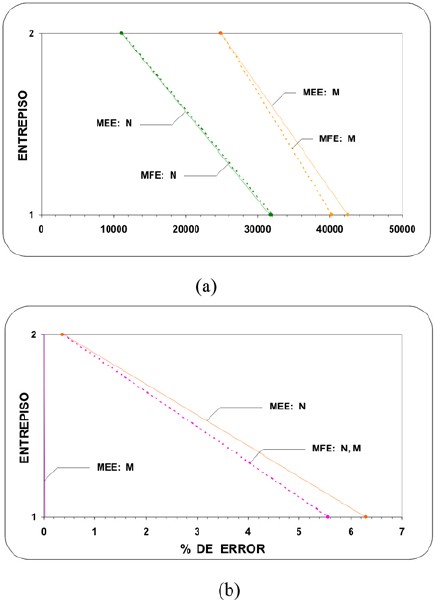
Figura 11. Fuerzas (Kg y Kg-m) y errores para el edificio tipo 1 de ocho pisos, caso T₁=1 s., ambos métodos: (a) Fuerzas simultáneas probables (b) Error en las fuerzas máximas probables.

Figura 12. Fuerzas (Kg y Kg-m) y errores para el edificio tipo 2 de ocho pisos, caso T₁=1 s., ambos métodos: (a) Fuerzas simultáneas probables (b) Error en las fuerzas máximas probables.

COMPARACIÓN DE LAS FUERZAS DE DISEÑO

En esta sección se comparan las fuerzas de diseño (fuerza axial N y momento flector M) provenientes de utilizar el método tradicional de diseño basado en las fuerzas máximas probables y los métodos MEE y MFE basados en las fuerzas simultáneas probables. En cada método, las fuerzas de diseñose obtienen utilizando las combinaciones de carga sugeridaspor las normas COVENIN, 1985. Las fuerzas de diseño sonademás presentadas y comparadas con la elipse de interacción de Gupta (figura 1) que envuelve todos los pares posibles de N y M que ocurren durante la respuesta sísmica. Cada combinación de carga da lugar a una elipse de interacción.

Métodos de Diseño

Cada método de diseño utiliza las siguientes combinaciones de carga:

a) Método Tradicional de Diseño: para Fuerzas Máximas Probables:

C1=1.4CP+1.7CV                             (15)

C2=0.75(1.4CP+1.7CV)±Sx                (16)

C3=0.90CP±Sx                                (17)

El diseño se efectúa con los valores máximos probables de la fuerza axial y el momento flector, que aparecen en el término de acción sísmica Sx de las ecuaciones (16-17). Se consideran cuatro casos de diseño para cada una de las ecuaciones (16) y (17): (+M, +N), (+M, -N), (-M, +N) y (-M, -N). Estos cuatro pares de valores definen las esquinas del rectángulo que envuelve a la elipse de interacción de Gupta. Se tendrá, por tanto, un rectángulo por cada combinación de carga. 

b) Método del Esfuerzo Extremo: para Fuerzas Simultáneas Probables:

C1=1.4CP+1.7CV                                      (18)

C2=0.75(1.4CP+1.7CV)±Sx(k=1)                  (19)

C3=0.75(1.4CP+1.7CV)±Sx(k=2)                 (20)

C4=0.90CP±Sx(k=1)                                 (21)

C5=0.90CP±Sx(k=2)                                (22)

El diseño se efectúa con los valores simultáneos probables de la fuerza axial y el momento flector, que aparecen en el término de acción sísmica Sx de las ecuaciones (19-22). Las combinaciones de carga dadas por las ecuaciones (19) y (20) suministran cuatro pares de valores (M, N) que debieran quedar insertos sobre la elipse de interacción correspondiente. De modo similar ocurre con los pares (M,N) provenientes de las ecuaciones (21) y (22). En la acciónsísmica Sx se utilizan los valores simultáneos probables de la fuerza axial y del momento flector, asociados a las esquinas k=1 y k=2 de la columna considerada (figura 5).

c) Método de la Fuerza Extrema: para Fuerzas Simultáneas Probables

C1=1.4CP+1.7CV                                         (23)

C2=0.75(1.4CP+1.7CV)±Sx(N)                       (24)

C3=0.75(1.4CP+1.7CV)±Sx(M)                       (25)

C4=0.90CP±Sx(N)                                         (26)

C5=0.90CP±Sx(M)                                         (27)

El diseño se efectúa con los valores simultáneos probables de la fuerza axial y el momento flector, que aparecen en el término de acción sísmica Sx de las ecuaciones (24-27). Las combinaciones de carga dadas por las ecuaciones (24) y (25) suministran cuatro pares de valores (M, N) que debieran quedar sobre la elipse de interacción correspondiente. De modo similar ocurre con los pares (M, N) provenientes de las ecuaciones (26) y (27). Sx (N) indica que para el diseño se consideran los valores de la fuerza axial máxima probable y el momento flector simultáneo probable correspondiente. Así mismo, Sx (M) indica que para el diseño se consideran los valores del momento flector máximo probable y la fuerza axial simultánea probable correspondiente.

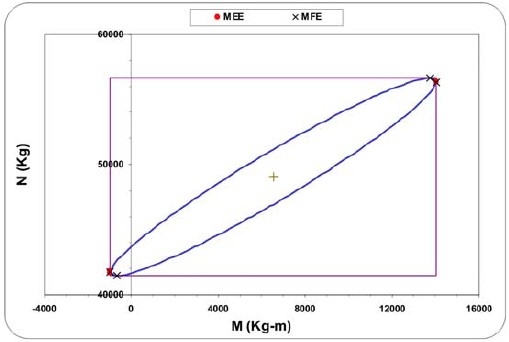
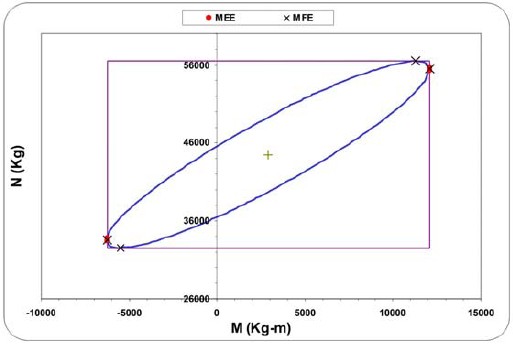
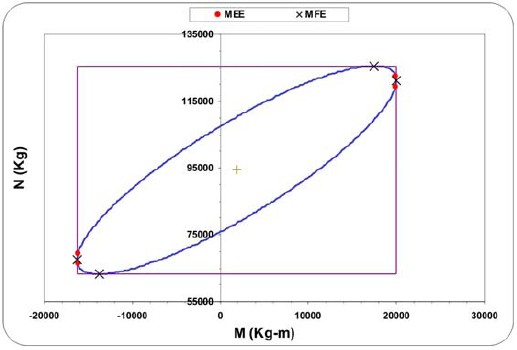
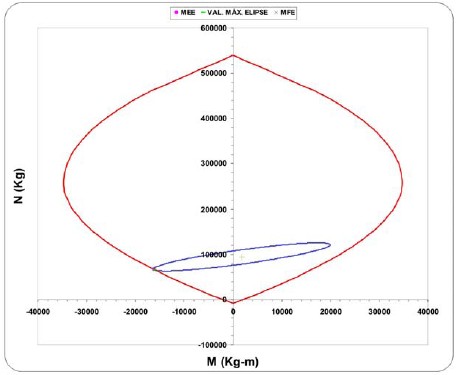
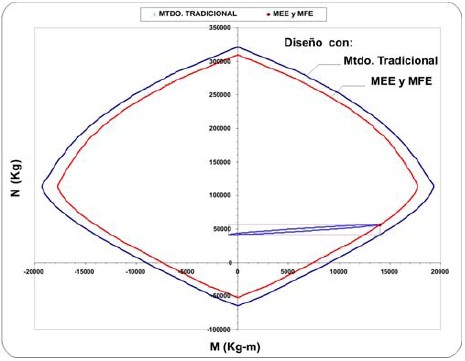
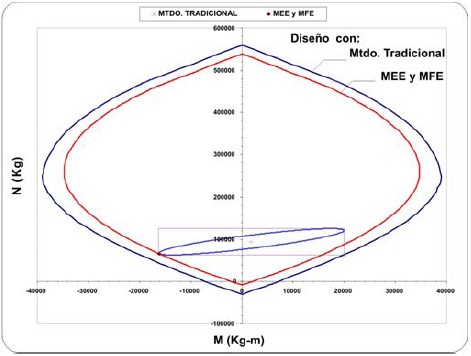
Para comparar las fuerzas de diseño se calcularon y dibujaron las elipses de interacción correspondientes a cada una de las combinaciones que las generan y los rectángulos que las inscriben, ubicándose sobre ellas los valores de diseño provenientes de todos los métodos. Se seleccionó, para cada columna del eje 5 del edificio de ocho pisos mostrado en la figura 6, la elipse generada por la combinación más desfavorable en lo referente a la mayor cantidad de área de acero obtenida. Las figuras 13, 14 y 15 muestran para losentrepisos 6, 5 y 1, respectivamente, las elipses de interaccióndesplazadas por los efectos de las cargas de gravedad y losrectángulos correspondientes. Se observa que las fuerzas de diseño provenientes de utilizar los métodos MEE y MFE, basados en las fuerzas simultáneas probables, están efectivamente localizadas sobre la elipse de interacción y muy próximas entre si; mientras que las provenientes del método tradicional, basadas en las fuerzas máximas probables, forman las esquinas del rectángulo que laenvuelve. Igualmente, se observa que las fuerzas de diseño basadas en las fuerzas simultáneas probables (métodos MEE y MFE) están muy próximas al valor de la elipse de interacción que condiciona el diseño. Este aspecto se evidencia al observar que el diagrama de interacción que describe la capacidad de la columna, es prácticamente el mismo para dichos puntos (figura 16).

Figura 13. Elipse de interacción para la columna del eje 5, entrepiso 6, del edificio de ocho pisos, y valores de diseño correspondientes a las fuerzas máximas probables (rectángulo) y a los métodos MEE y MFE. Casos de carga 16, 19, 20, 24 y 25.

Figura 14. Elipse de interacción para la columna del eje 5, entrepiso 5, del edificio de ocho pisos, y valores de diseño correspondientes a las fuerzas máximas probables (rectángulo) y a los métodos MEE y MFE. Casos de carga 17, 21, 22, 26 y 27.

Figura 15. Elipse de interacción para la columna del eje 5, entrepiso 1, del edificio de ocho pisos, y valores de diseño correspondientes a las fuerzas máximas probables (rectángulo) y a los métodos MEE y MFE. Casos de carga 17, 21, 22, 26 y 27.

Figura 16. Elipse y diagrama de interacción para la columna del eje 5, entrepiso 1, del edificio de ocho pisos.

COMPARACIÓN DE LOS MÉTODOS DE DISEÑO

El objetivo de esta sección es comparar las áreas de acero obtenidas con el método tradicional y con los métodos MEE y MFE. Para ello se diseñaron las columnas del eje 5 del edificio de ocho pisos mostrado en la figura 6, sometidas a las combinaciones de carga ya indicadas en la sección 5.1.

El método tradicional consiste en diseñar las columnas para las fuerzas de diseño expresadas por las ecuaciones (15-17), quienes incluyen los valores máximos probables de la fuerzaaxial y el momento flector, y conforman los cuatro puntos del rectángulo que limitan a la elipse correspondiente a la combinación más crítica y de allí se obtiene el valor que da la cantidad de acero más desfavorable. El otro método consiste en diseñar las columnas con las fuerzas de diseño aportados por los métodos MEE y MFE, debidas a lascombinaciones indicadas en las ecuaciones (18-22) y (23- 27), respectivamente, y donde se utilizan los valores simultáneos probables de la fuerza axial y el momento flector.

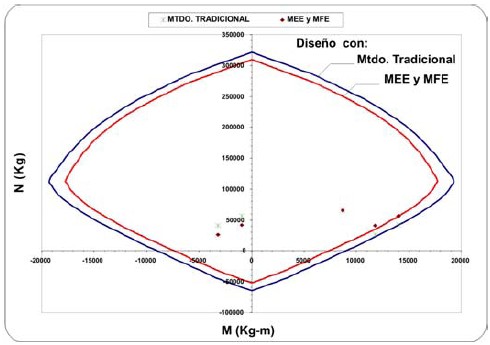
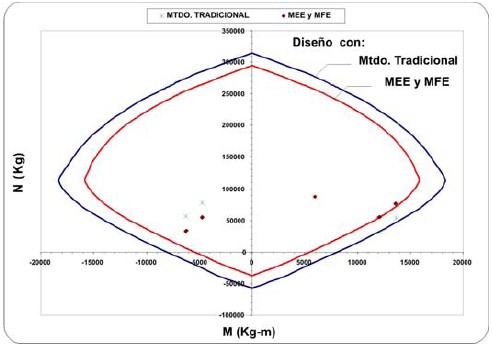
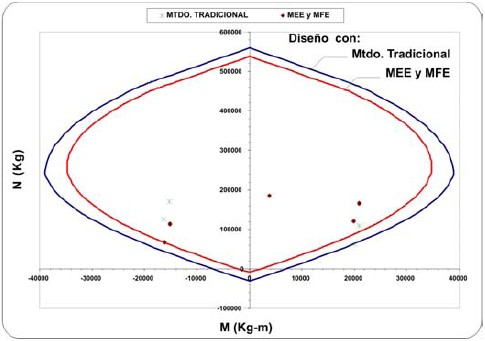
Las figuras 17 a 19 muestran los diagramas de interacción de las columnas del eje 5, entrepisos 6, 5 y 1, respectivamente,del edificio de ocho pisos. Se han graficado los diagramas de interacción asociados al diseño con el método tradicional y al diseño con el método MEE o el MFE, considerando los casos más desfavorables. Se indican también en las figuraslos pares de valores (M, N) provenientes de las combinaciones de carga dadas en la sección 5.1 para cada método de diseño.

Figura 17. Comparación en el diseño con el Método Tradicional y con los Métodos MEE y MFE. Columna del eje 5, entrepiso 6, edificio de ocho pisos.

Figura 18. Comparación en el diseño con el Método Tradicional y con los Métodos MEE y MFE. Columna del eje 5, entrepiso 5, edificio de ocho pisos.

Figura 19. Comparación en el diseño con el Método Tradicional y con los Métodos MEE y MFE. Columna del eje 5, entrepiso 1, edificio de ocho pisos.

La tabla 1 muestra las cantidades de acero y el error relativo. Se determinó el error relativo entre el área de acero calculada por el método tradicional y los métodos que utilizan elconcepto de VSP (MEE y MFE), tomando los valoresaportados por estos últimos como valores más confiables para fines de diseño. Es de destacar que las cantidades de acero calculadas por los métodos MEE y MFE fueron las mismas por estar sus valores de diseño muy próximos.

Tabla 1. Cantidades de acero y porcentajes de error para los distintos métodos.

Se observa que, al calcular las áreas de acero con las combinaciones provenientes de incluir las fuerzas máximas probables, se obtienen valores superiores en un 24%, 54% y 260%, respectivamente, al compararlas con las obtenidas con las combinaciones resultantes de utilizar las fuerzassimultáneas probables; es decir, las áreas de acero en eldiseño de elementos de concreto armado calculadas con lasfuerzas máximas probables, pueden estar sobrestimadashasta en un 260% en edificios de mediana altura. Lo anteriormente comentado indica que el método tradicional es conservador y puede conducir a diseños costosos, lo que muestra la necesidad de utilizar métodos más precisoscomo el método MEE y el método MFE.

Las figuras 20 a 22 muestran, además de los diagramas de interacción asociados al diseño con el método tradicional y al diseño con el método MEE o el MFE, las elipses de interacción y los rectángulos que las inscribencorrespondientes a la combinación más desfavorable, en lo referente a la mayor cantidad de área de acero obtenida. Asociados a dichas áreas, también se indican en las figuras, los dos pares de valores (M, N) correspondientes al diseño con el método tradicional (esquina del rectángulo) y al diseño con el método MEE o el MFE (sobre la elipse de interacción).

Figura 20. Elipse de interacción, rectángulo que la inscribe y diagrama de interacción para la columna del eje 5, entrepiso 6, del edificio de ocho pisos.

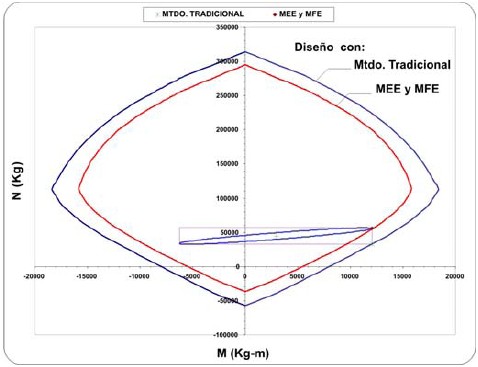
Figura 21. Elipse de interacción, rectángulo que la inscribe y diagrama de interacción para la columna del eje 5, entrepiso 5, del edificio de ocho pisos.

Figura 22. Elipse de interacción, rectángulo que la inscribe y diagrama de interacción para la columna del eje 5, entrepiso 1, del edificio de ocho pisos.

Los resultados de la tabla 1 ponen de manifiesto un mayor error en el área de acero en la columna del entrepiso 1; esto era de esperar al examinar los resultados presentados previamente (figura 12) para el edificio tipo 2 de 8 pisos(figura 3), en el cual se observaron errores mayores en las solicitaciones del primer entrepiso. Aún cuando en el método tradicional el porcentaje de acero de la columna del entrepiso 1 está por debajo del mínimo normativo y en las columnas de los entrepisos 5 y 6 está por encima, se esperaría que los errores en las áreas de acero se mantengan en ese orden para otras dimensiones de columnas, debido a las diferencias entre las fuerzas máximas probables y las fuerzas simultáneas probables mencionadas previamente.

En todo caso se ha demostrado que el método tradicional puede conducir a diseños innecesariamente conservadores, aún cuando la magnitud de los errores va a depender del tipo de estructura a diseñar. Por esta razón se recomienda extender estas evaluaciones a otras estructuras.

CONCLUSIONES Y RECOMENDACIONES

Dentro del marco del método de análisis espectral se han evaluado dos procedimientos de diseño de columnas propuestos recientemente, que permiten la determinación de las combinaciones más desfavorables de dos o más fuerzas internas actuando concurrentemente en una sección de un miembro estructural, los cuales utilizan el concepto de valor simultáneo probable. Estos procedimientos se han comparado con el procedimiento tradicional de diseño que utiliza los valores máximos probables de la fuerza axial (N) y el momento flector (M). De este estudio se desprenden las siguientes conclusiones y recomendaciones:

• Para edificios de un piso todos los métodos de diseño conducen al mismo resultado pues los valores máximosprobables del momento flector y la fuerza axial son simultáneos en el tiempo. La presencia de modos superiores en edificios de varios pisos es el factor que introduce diferencias entre los diversos métodos de diseño.

• Los errores en el cálculo del esfuerzo equivalente calculados con los valores máximos probables de N y M, con respecto al esfuerzo máximo probable, resultaron muy pequeños, menores al 1%, en los edificios de 2 pisos y de período largo (T1=1 s.); mientras que para el mismo período en edificios de 8 pisos se obtuvieron errores algo mayores, hasta de 13% de sobrestimación. Los errores se hacen insignificantes para el caso de períodos cortos (T1=0.1 s.).

• Los errores relativos entre las fuerzas máximas probables y las fuerzas simultáneas probables, tomando estas últimascomo valores más confiables para fines de diseño, resultaronpequeños para los métodos del Esfuerzo Extremo y de laFuerza Extrema, menores al 7% y 6%, respectivamente, para la fuerza axial en los edificios de 2 pisos y de período largo (T1=1 s.); mientras que para el momento flector los errores son muy pequeños. Para el mismo período en edificios de 8 pisos, por el método del Esfuerzo Extremo y el método de la Fuerza Extrema se obtuvieron para la fuerza axial errores mayores, hasta de un 33% y 12%, respectivamente; mientras que para el momento flector fueron hasta de un 5% y 12%, respectivamente. Todos estos errores son de sobrestimación.

• Los valores de diseño obtenidos por los métodos del Esfuerzo Extremo y de la Fuerza Extrema están efectivamente localizados sobre la elipse de interacción de Gupta, para los ejemplos aquí considerados. Los valores de diseño están muy próximos entre si y prácticamente se confunden con el punto de la elipse que condiciona el diseño.

• Las áreas de acero en el diseño de elementos de concreto armado calculadas con las fuerzas máximas probables, pueden estar sobrestimadas hasta en un 260% en edificios de mediana altura, en relación a un diseño más confiable basado en los valores simultáneos probables.

• El método tradicional es conservador y puede conducir a diseños costosos, lo que muestra la necesidad de utilizarmétodos más precisos como el método del Esfuerzo Extremo y el método de la Fuerza Extrema.

• Se recomienda extender las evaluaciones aquí presentadas a otras estructuras planas con diferentes características, así como al caso de estructuras espaciales sujetas a varias componentes sísmicas.

AGRADECIMIENTOS

Agradecemos el financiamiento otorgado a esta investigación por el FONACIT según Proyecto S1- 2000000606, al Instituto de Materiales y Modelos Estructurales (IMME) de la Facultad de Ingeniería de la Universidad Central de Venezuela, así como las sugerencias conceptuales del Ing. Julio J. Hernández y el apoyo computacional del Prof. Norberto Fernández.

REFERENCIAS

1. CHOPRA, A. K., (2001): «Dynamics of structures: Theory and applications to earthquake engineering», Second edition, Prentice Hall, Upper Saddle River, NJ.        [ Links ]

2. COVENIN. «Edificaciones sismorresistentes. Norma Venezolana COVENIN 1756», Caracas, Venezuela, (2001).        [ Links ]

3. INTERNATIONAL CONFERENCE OF BUILDING OFFICIALS (ICBO). «Uniform Building Code, Volume 2, Structural Engineering Design Provisions», Whittier, CA, (1997).        [ Links ]

4. EUROPEAN COMMITTEE FOR STANDARDIZATION (ECS). «Eurocode 8: Design provisions for earthquake resistance ofstructures», Brussels, Belgium, 1998.        [ Links ]

5. INTERNATIONAL CODE COUNCIL, INC. (ICC). «2000 International Building Code», Birmingham, AL, 2000.        [ Links ]

6. PENZIEN, J. AND WATABE, M., (1975): «Characteristics of 3- dimensional earthquake ground motion». Journal of Earthquake Engineering and Structural Dynamics, Vol. 3, pp. 365 - 373.        [ Links ]

7. MENUN, C. AND DER KIUREGHIAN, A., (2000): «Envelopes for seismic response vectors. I: Theory». Journal of Structural Engineering, Vol. 126, pp. 467 – 473.        [ Links ]

8. MENUN, C. AND DER KIUREGHIAN, A., (2000): «Envelopes for seismic response vectors. II: Application». Journal of Structural Engineering, Vol. 126, pp. 474 – 481.        [ Links ]

9. ANASTASSIADIS, K., AVRAMIDIS, I. E. AND PANETSOS, P., (2002): «Concurrent design forces in structures under threecomponent orthotropic seismic excitation». Earthquake Spectra, Vol. 18, pp. 1 – 17.        [ Links ]

10. LÓPEZ, O. A., CHOPRA, A. K. AND HERNÁNDEZ, J. J., (2000): «Critical response of structures to multicomponent earthquake excitation». Earthquake Engineering and Structural Dynamics, Vol. 29, pp. 1759 – 1778.        [ Links ]

11. MARÍN, J. Y GÜELL, A., (1984): «Manual para el cálculo de columnas de concreto armado». MINDUR, Caracas, Venezuela.        [ Links ]

12. COVENIN, (1985): «Estructuras de concreto armado para edificaciones. Análisis y diseño. Norma Venezolana COVENIN 1753», Caracas, Venezuela.        [ Links ]

13. GUPTA, A. K. AND CHU, S. L., (1977): «Probable simultaneous response by the response spectrum method of analysis». Nuclear Engineering and Design, Vol. 44, pp. 93-95.        [ Links ]

14. WILSON, E. L., DER KIUREGHIAN, A. AND BAYO, E. P., (1981): «A replacement for the SRSS method in seismic analysis». Earthquake Engineering and Structural Dynamics, Vol. 9, pp. 187 – 194.        [ Links ]

15. GUPTA, A. K. AND SINGH, M. P., (1977): «Design of column sections subjected to three components of earthquake». Nuclear Engineering and Design, Vol. 41, pp. 129-133.        [ Links ]