Influencia del modelado de las condiciones de borde en la simulacion de ensayos mecanicos de huesos bovinos

^{Marco Ciaccia1,2}, Thalia San Antonio ^1,2, Carmen Muller-Karger ¹, Euro Casanova ¹

¹ Universidad Simon Bolivar, Grupo de Biomecanica. Correo-e: mciaccia@gmail.com 

² Universidad de Carabobo, Centro de Investigaciones en Mecanica (CIMEC).

RESUMEN

En este trabajo se estudio la influencia del modelado de las condiciones de borde en el comportamiento de modelos de elementos finitos utilizados para la simulacion de ensayos mecanicos de dos tibias anteriores bovinas. Se utilizo tomografia computarizada para la reconstruccion geometrica y la asignacion de propiedades mecanicas, incluyendo la heterogeneidad y ortotropia caracteristicas del tejido oseo. Se realizaron ensayos de flexion en tres puntos y compresion a probetas elaboradas a partir de los huesos tomografiados, con la finalidad de validar las simulaciones. Se elaboraron mallas de elementos finitos de las probetas sobre las que se ensayaron distintas variantes de las condiciones de borde presentes en los ensayos mecanicos, con la finalidad de determinar los mejores parametros para el modelado de dichas condiciones. Se encontro que los mejores resultados se obtienen al imponer desplazamientos como condicion de borde de carga, y que las condiciones de borde de apoyo deben reproducir estrechamente las vinculaciones presentes en los ensayos mecanicos para lograr resultados correctos. Tambien se evidencio que los ensayos experimentales son una herramienta invaluable para la validacion y ajuste de las simulaciones con elementos finitos (EF).

Palabras clave: Condiciones de contorno, Simulacion con elementos finitos (EF), Modelos oseos, Tejido oseo, Ensayos mecanicos.

Influence of modelling boundary conditions in the simulation of mechanical tests of bovine bones

ABSTRACT

The aim of this work is to study the influence of different configurations of boundary conditions in the behavior of finite elements models built to simulate mechanical tests of two front bovine tibias. Computerized tomography was used to reconstruct the geometry and to assign mechanical properties which include the heterogeneity and orthotropy of the bone tissue. Three point bending and compression tests were performed to sample tests made from the bones in order to validate the simulations. The models of the sample tests were meshed and different boundary conditions were implemented to simulate the mechanical tests and optimize their applications. The best results were found when the load was applied through the imposition of displacements and when the support boundary conditions reproduced closely the links present in the mechanical tests. Also this study shows that experimental tests are an invaluable tool for the validation and adjustment of FE simulations.

Keywords: Boundary conditions, Finite element simulation, Bone models, Bone tissue, Mechanical tests.

Recibido: enero de 2008 Revisado: mayo de 2008

INTRODUCCION

En la actualidad, el exito en el diseno, fabricacion y prueba de protesis, fijadores externos e internos y otros dispositivos utilizados en el area de traumatologia y ortopedia depende en gran medida de la experiencia del disenador y de los resultados de la prueba directa en los pacientes. Esto trae como consecuencia que el mejoramiento de estos dispositivos sea un proceso lento, puesto que se debe esperar la evolucion del paciente para poder observar sus virtudes y defectos, afectando en muchos casos adversamente al paciente. Para lograr mejores disenos desde el principio, es conveniente contar con huesos <<virtuales>>, modelos computarizados en los que puedan probarse modelos tambien virtuales de estos dispositivos, de forma que pueda observarse, sin afectar al paciente y en un tiempo mucho menor, los defectos que pueda tener el diseno de una protesis o fijador.

El desarrollo de modelos de huesos no es tarea facil debido a la complejidad de estos elementos organicos; deben tomarse en cuenta factores mecanicos y bioquimicos, entre otros, para intentar simular su comportamiento, sobre todo a largo plazo. En la experiencia de los autores, los factores mas importantes a ser considerados en la construccion de un modelo mecanico oseo son: la reconstruccion de la geometria, la generacion de la malla de elementos finitos, la asignacion de las propiedades mecanicas y la aplicacion de las condiciones de borde (CB). Este ultimo aspecto recibe cada vez mayor atencion, haciendose enfasis principalmente en la simulacion de condiciones fisiologicas (Jacobs et al. 1999; Speirs et al. 2006; Phillips et al. 2007a y 2007b) y en la interaccion protesis hueso (Giudice et al. 2005; Pappas et al. 2006; Helwig et al. 2006; Viceconti et al. 2006; Xu et al. 2006). El objetivo, en el primer caso, es mejorar el calculo de esfuerzos y deformaciones con la finalidad de predecir fracturas y mejorar las simulaciones de remodelado oseo; en el segundo caso, el proposito es determinar las razones de las fallas de las protesis y elementos de fijacion para realizar mejoras en el diseno de estos dispositivos. Las publicaciones consultadas no muestran interes explicito en determinar la influencia de la metodologia de aplicacion de las CB en los modelos de EF, aun cuando se tienen indicios de que ello afecta los resultados (Gupta et al. 2004 y Pappas et al. 2006).

Este trabajo se centro en la importancia de la correcta aplicacion de las CB en la calidad de los resultados que se obtienen al analizar un modelo de elementos finitos (EF). Para lograrlo, se reconstruyeron las geometrias de dos huesos bovinos, a partir de las cuales se generaron mallas que se dejaron constantes a lo largo del estudio, asi como las propiedades del material, variando unicamente las CB. Las propiedades mecanicas se calcularon y asignaron mediante procedimientos que incluyen la heterogeneidad y ortotropia caracteristicos del tejido oseo. Finalmente, se compararon los resultados de las simulaciones con los resultados de los ensayos mecanicos realizados a los huesos modelados, con el proposito de validar la metodologia y depurar la aplicacion de las CB.

METODOLOGIA

Construccion de los Modelos

Para generar los modelos, el primer paso consistio en reproducir la geometria externa del hueso con base en las imagenes obtenidas del tomografo. Este proceso se conoce como segmentacion, con el cual se genera un modelo de <<alambre>>.

La segmentacion se realizo con un programa que extrae los contornos para todas las imagenes secuenciales, denominado SURFdriver^® (Moody et al. 1999), que proporciona los contornos como un conjunto de puntos y lineas en un archivo con formato IGES II. Este archivo es leido por el programa de elementos finitos ANSYS^® (ANSYS Inc. (2005)), donde se procede a crear, a partir de los puntos y lineas, un volumen con los siguientes pasos: (a) utilizando las lineas y puntos importados desde SURFdriver^®, se generan curvas suavizadas (splines) que pasan por los puntos definiendo asi el contorno de cada seccion del hueso; (b) se crean superficies que se adaptan a las curvas definiendo asi la geometria del hueso como una superficie cerrada y (c) se genera a partir de esta superficie un volumen que puede ser mallado.

Mallas de Elementos Finitos

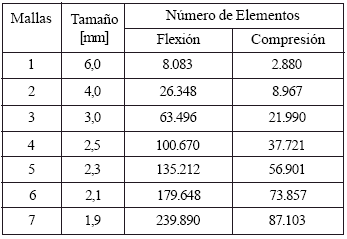
El elemento usado en esta investigacion fue el SOLID92 de ANSYS^®, el cual es un tetraedro de 10 nodos con 3 grados de libertad de desplazamiento por nodo. Este elemento permite una aproximacion cuadratica del desplazamiento y es adecuado para modelar geometrias irregulares, como las superficies de los huesos. En la tabla 1 se presentan las caracteristicas de las mallas para los modelos de flexion y de compresion. Las diferentes mallas se obtuvieron fijando el tamano maximo de la arista del elemento, el cual se disminuyo hasta alcanzar la convergencia de los resultados.

Tabla 1. Mallas de los modelos.

Asignacion de Propiedades Mecanicas

A continuacion se muestra un resumen de la metodologia publicada originalmente por Ciaccia et al. (2006). El procedimiento para determinar las propiedades mecanicas 7 de un hueso usando tomografias axiales computarizadas consiste en: 1) leer el valor de unidad Hounsfield (UH) de la tomografia, 2) convertir este valor en un valor de densidad aparente, y 3) calcular el modulo de elasticidad a partir del valor de la densidad aparente. Para la asignacion de las propiedades mecanicas al modelo heterogeneo y anisotropico se utilizo un programa desarrollado por Muller- Karger (2001).

El valor UH de la tomografia y la densidad aparente se relacionan a traves de la curva de calibracion del tomografo (ecuacion 1):

Existen varios estudios experimentales que presentan las relaciones entre la densidad aparente de las TAC y las propiedades mecanicas del hueso, como el modulo de elasticidad. En este trabajo se utilizo la correlacion de Carter et al. (1977) (ecuacion 2), la cual proporciona muy buenos resultados para valores de densidad aparente mayores a 0,778 g/cm³ que son las que presentan los modelos de diafisis de tibias bovinas utilizados en este estudio.

donde:

E es el modulo de elasticidad a compresion (MPa), ρ es la densidad aparente (g/cm³), ε es la velocidad de deformacion (1/s), E_c es el modulo de elasticidad a compresion del hueso compacto con una densidad ρ_c a una tasa de deformacion de 1 s^-1, y ρ_c es la densidad de la matriz mineral.

Para determinar el parametro velocidad de deformacion (ε) se utilizo la velocidad de desplazamiento del cabezal (5 mm/ min) y la longitud inicial de la probeta (55 mm) del ensayo de compresion, resultando ε = 0,001515 s^-1. Se utilizo la densidad maxima para la matriz mineral reportada por Cardoso et al. (2003) con un valor de nc = 1,96 g/cm³. El modulo de elasticidad a la compresion (Ec) del hueso compacto a una densidad ρ_c y una tasa de deformacion de 1 s^-1 fue calculada con la ecuacion presentada por Hight et al. (1983), la cual expresa el modulo de elasticidad longitudinal del hueso cortical humano en funcion de la velocidad de deformacion. Esta relacion fue ajustada posteriormente por Cowin (1989) con los datos experimentales reportados por Crowninshield et al. (1973) para hueso bovino, resultando en este caso E_c = 10,40 MPa. Sustituyendo estos parametros en la ecuacion (2) se tiene que el modulo de elasticidad para cada elemento se puede calcular como:

El valor de E obtenido con la ecuacion (3) corresponde a la propiedad en la direccion longitudinal del hueso (E₃). Una vez calculada esta propiedad para cada elemento, es decir, se tiene un modelo heterogeneo, se procede a generar el modelo ortotropico calculando una relacion porcentual entre los valores de modulos de elasticidad, modulos de corte y modulos de Poisson de acuerdo con los datos presentados por van Buskirk et al. (1981) para hueso bovino (ecuacion 4):

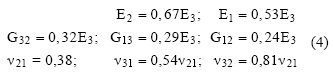
Los subindices 1, 2 y 3 indican las direcciones radial, tangencial y longitudinal, respectivamente. De esta manera, queda definida la forma en que se calculan las propiedades mecanicas de cada uno de los elementos para obtener un modelo heterogeneo y ortotropico.

ENSAYOS EXPERIMENTALES

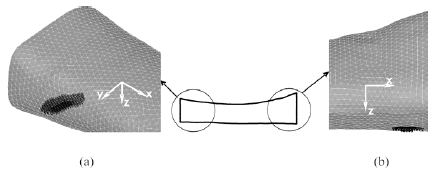
Para la elaboracion de las probetas se utilizaron dos tibias bovinas anteriores de un mismo animal, a las cuales se les eliminaron las epifisis. Para evitar la descomposicion del componente organico, se hirvieron los huesos durante dos horas y luego se secaron en horno durante cuatro horas a 250 °C, quedando finalmente el material oseo compuesto casi exclusivamente por su fase mineral. Una vez preparados los huesos, se les efectuo una tomografia con la finalidad de realizar la construccion del modelo a partir de las imagenes. Se realizaron dos tipos de ensayos mecanicos: ensayo de flexion en tres puntos, y ensayo de compresion (figura 1). La maquina utilizada en los ensayos es marca MTS, modelo 810.

Figura 1. Probetas colocadas en la maquina: (a) ensayo de flexion y (b) ensayo de compresion.

De cada ensayo se obtuvo una curva carga-desplazamiento, la cual se utilizo como parametro de validacion para los ensayos virtuales, puesto que el calculo de esfuerzos y deformaciones reales se dificulta por la irregularidad de la geometria de las probetas. Ademas, en el caso del ensayo de flexion en tres puntos, el tramo de hueso utilizado es poco esbelto, por lo que el uso de las formulas tradicionales para el calculo de las propiedades mecanicas a partir de la carga y el desplazamiento no arroja resultados confiables.

Condiciones de Borde

En este trabajo, las CB se clasifican en dos tipos: (1) los apoyos, o restricciones, y (2) las cargas aplicadas. Se modelaron distintas variantes para ambos tipos de condiciones de contorno en las mallas de EF.

Un aspecto comun a ambas simulaciones es que existe la aplicacion de una carga que impone un desplazamiento a la probeta. Es por ello que en lo que respecta a la CB de carga, se modela en cada caso un desplazamiento impuesto y una fuerza aplicada. Tales valores son correspondientes al punto de ruptura en la curva carga-desplazamiento obtenida de los ensayos experimentales. Por otro lado, las condiciones de apoyo en ambos casos presentan caracteristicas muy particulares que requieren ser tratados de forma individual.

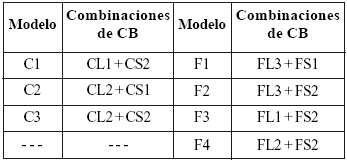
Para cada ensayo simulado (flexion, compresion) se propuso varios modelos de CB, tanto para la aplicacion de la carga como para los apoyos. La combinacion de todas las CB propuestas dio como resultado una gran cantidad de modelos; por razones de espacio, en este trabajo solamente se reportaron las combinaciones que aportan resultados significativos. Para identificar las combinaciones, se le asigno un codigo a cada CB de forma que la referencia a las mismas fuera mas sencilla. Estos codigos empezaron por la letra C para indicar compresion y F para flexion. El siguiente caracter indicara si se trata de una carga o apoyo, para lo que se utilizaron las letras L (load) y S (support), respectivamente. Si hay dos variantes de una CB, se anadiria al final un numero correlativo asociado a cada variante. En la tabla 2 se resumen los modelos analizados y las combinaciones de condicion de borde que se consideraron relevantes.

Tabla 2. Modelos de EF y combinaciones de CB en cada caso.

ENSAYO DE COMPRESION

Condiciones de borde de carga .

• Condicion CL1: se distribuyo la fuerza aplicada a la probeta en cantidades iguales entre los nodos correspondientes a la parte superior de la probeta, como se muestra en la figura 2a.

• Condicion CL2: se impuso el mismo desplazamiento en direccion axial a todos los nodos correspondientes a la parte superior de la probeta, como se muestra en la figura 2b.

Figura 2. Condiciones de borde de carga en la probeta de compresion. (a) CL1, (b) CL2.

Condiciones de borde de apoyo

La primera aproximacion que se suele tomar en estos casos consiste en restringir completamente los desplazamientos de los nodos de la base de la probeta, como si esta estuviese fijada o empotrada al soporte inferior de la maquina. Sin embargo, teniendo el tejido oseo un modulo de Poisson positivo, la tendencia es a aumentar su seccion transversal cuando es comprimido axialmente, lo cual no es permitido con esta CB, incrementando los esfuerzos en el plano transversal. Si bien es cierto que existe friccion entre el hueso y el soporte, lo cual podria impedir o reducir la expansion transversal, tambien es cierto que esta fuerza puede ser inferior a la que se genera por efecto de la expansion.

Debido a que experimentalmente no se determino cual de las dos situaciones ocurre efectivamente, se modelaron ambas, restringiendo en un caso los desplazamientos en todas las direcciones de los nodos de la base de la probeta (condicion CS1) (figura 3a), y restringiendo unicamente los desplazamientos en direccion axial en el segundo caso (condicion CS2) (figura 3b).

Figura 3. Condiciones de borde de apoyo en la probeta de compresion. (a) CS1, (b) CS2.

ENSAYO DE FLEXION

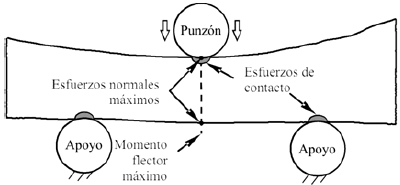
El ensayo de flexion en 3 puntos es mas complejo de modelar debido a la geometria del hueso y el punzon. En las zonas de encuentro entre los apoyos y el hueso, y entre el punzon y el hueso, se producen esfuerzos de contacto que podrian generar una fractura local antes de que ocurra la falla general del hueso. Adicionalmente existe el inconveniente de que la zona de contacto central coincide con la zona de maximo esfuerzo de compresion debido a la flexion, como se muestra en la figura 4. Las zonas de apoyo, en cambio, son menos criticas debido a que el esfuerzo causado por la flexion es teoricamente cero. El problema de contacto se simplifica por el hecho de que el acero tiene un modulo de elasticidad 10 veces superior al del hueso cortical en direccion axial, y al menos 20 veces en direccion radial, siendo esta ultima la direccion predominante del movimiento del punzon de la maquina en el ensayo. Por estas razones, se consideraron las partes de la maquina como infinitamente rigidas en comparacion con el hueso, lo que permite que se impongan desplazamientos en la zona de contacto del modelo de EF, en lugar de realizar un analisis no lineal de contacto, el cual es mucho mas complicado y de mayor demanda computacional.

Figura 4. Esquema de cargas en el ensayo de flexion.

Condiciones de borde de carga

Al igual que en el ensayo de compresion, las cargas pueden aplicarse mediante una fuerza o mediante la imposicion de un desplazamiento. Sin embargo, para el ensayo de flexion la zona de aplicacion no es tan evidente. Si se considera que las tomas de contacto entre el hueso y las partes de la maquina ocurren en un punto, como podria suceder inicialmente, se tendria que seleccionar un solo nodo como lugar de aplicacion de cargas y/o restricciones. Esto trae como consecuencia la aparicion, en el modelo de EF, de desplazamientos mayores y fuerzas de reaccion menores a los encontrados experimentalmente. Sin embargo, lo que sucede en realidad es que el hueso se deforma bajo la presion de contacto de las partes de la maquina, aumentando por ende la zona de contacto y distribuyendo los esfuerzos. Puesto que la geometria del hueso es irregular, esta zona tendra que ser estimada en forma y tamano, de modo que la simulacion produzca resultados similares a los de los ensayos experimentales.

• Condiciones FL1 y FL2: se aplico la fuerza distribuida entre un grupo de nodos seleccionados de un volumen ubicado en la zona de contacto. Este volumen se selecciono de dos formas distintas, en primer lugar (FL1) un paralelepipedo con dos de sus tres dimensiones constantes (en las direcciones axial y tangencial), y la tercera (radial) variable para conocer la influencia de este parametro en el comportamiento del modelo (figura 5a). En el segundo caso (FL2) el volumen es una seccion de un cilindro de dimensiones constantes, orientado transversalmente al hueso (similar al punzon de la maquina). En este modelo el parametro a variar es el tamano de la seccion del cilindro dentro del mallado (figura 5b).

Figura 5. Condiciones de borde de carga en la probeta de flexion. (a) FL1, (b) FL2.

• Condicion FL3: se selecciono una cantidad de nodos en un volumen equivalente al de la CB FL1, pero sin parametro variable, debido a que la profundidad se establecio en el valor del desplazamiento al punto de ruptura del ensayo. Este desplazamiento se impuso a todos los nodos seleccionados (figura 6).

Figura 6. Condiciones de borde de carga en la probeta de flexion. FL3. 11

Condiciones de borde de apoyo

La CB en la zona de los soportes puede considerarse similar a la de la zona de aplicacion de la carga, debido a que la forma de los apoyos es igual a la del punzon (figura 1). Sin embargo, al ser cargado, el hueso rota alrededor de los apoyos, al mismo tiempo que se desplaza por efecto del acortamiento que produce la flexion, aun cuando esten presentes las fuerzas de friccion. Para modelar este ultimo efecto, basta con restringir el desplazamiento en direccion axial en la zona de contacto de uno de los soportes, permitiendo el desplazamiento del otro extremo. Por otro lado, modelar la rotacion de las secciones soportadas del hueso al mismo tiempo que se restringe el desplazamiento transversal es mas complicado. Las dos opciones estudiadas en este trabajo fueron: en primer lugar, en uno de los extremos se selecciono un volumen cilindrico de nodos similar al de la CB FL2, restringiendose el desplazamiento en todas las direcciones, y en el otro extremo se tomo un volumen de nodos equivalente, restringiendose solamente las direcciones transversales (condicion FS1) (figura 7). Este modelo de condicion de contorno, aunque pueda parecer similar a lo que ocurre en la realidad, tiene la desventaja de inducir un momento de reaccion ficticio, el cual es creado por las fuerzas de reaccion distribuidas en una direccion longitudinal.

Figura 7. Condiciones de borde de apoyo en la probeta de flexion. (a) y (b) FS1.

La segunda opcion consiste en seleccionar nodos en una seccion muy delgada del modelo y restringir los desplazamientos en la direccion radial (condicion FS2) (figura 8). Esto se realiza en ambos extremos del modelo de EF. La razon de tomar una seccion muy delgada es que se minimiza la aparicion del momento de reaccion y, al ser seleccionados una gran cantidad de nodos se evita la concentracion de esfuerzos asociada a la restriccion de pocos nodos.

Figura 8. Condiciones de borde de apoyo en la probeta de flexión. (a) y (b) FS2.

Analisis de Convergencia

Las condiciones de borde descritas se aplicaron a cada una de las mallas reportadas en la tabla 1 con la finalidad de observar la convergencia de los resultados. Adicionalmente, los modelos F1, F2 y F3 (tabla 2), los cuales incluyen las condiciones de borde FL1, FL2 y FS1 con un parametro variable, fueron objeto de un analisis de convergencia para determinar el mejor valor de dicho parametro.

RESULTADOS Y DISCUSION

Resultados Experimentales

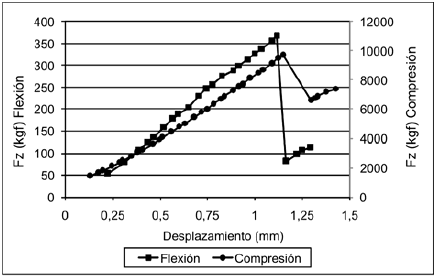
La figura 9 muestra los resultados de los ensayos experimentales (notese las distintas escalas para cada curva). Las curvas carga desplazamiento exhiben el comportamiento lineal y fragil caracteristico del componente mineral del tejido oseo. La ruptura en el ensayo de flexion ocurre para un desplazamiento de 1,118 mm y una carga de 368,6 kgf, mientras que en el ensayo de compresion ocurre para un desplazamiento de 1,15 mm y una carga de 9.723 kgf.

Figura 9. Curvas carga desplazamiento experimentales, ensayos de flexión y compresión.

Simulacion del Ensayo de Compresion

- Modelo C1

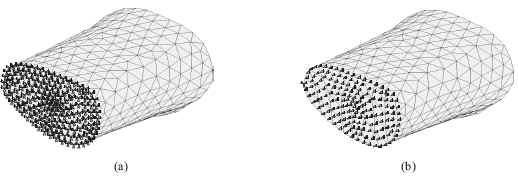
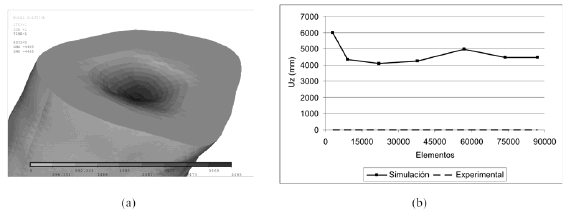
Antes de presentar los resultados de este modelo, es conveniente precisar que la probeta del ensayo de compresion es hueca, puesto que pertenece a una parte de la tibia en la que se encuentra el canal medular. El proceso de segmentacion descrito en la metodologia se realizo solamente a la parte externa del hueso, no asi a la parte interna, por lo que el modelo de EF se presenta solido. Sin embargo, el proceso de asignacion de propiedades utilizando las ecuaciones (1), (3), y (4) establece para esta zona propiedades elasticas muy bajas con relacion a las asignadas a la parte osea, por lo que su aporte a la resistencia de las cargas es practicamente nulo. Es por ello que al distribuir fuerzas uniformemente sobre la superficie del modelo de EF, la zona central del modelo predice desplazamientos enormes que no tienen fundamento fisico, como puede verse en la figura 10a. En dicha figura se muestran los desplazamientos escalados por 10-3, siendo el maximo reportado de 4.465 mm. Debido a esto, se propuso imponer el desplazamiento en lugar de aplicar la fuerza. En la figura 10b se observa la grafica de convergencia del modelo C1.

Figura 10. Modelo C1. (a) desplazamientos resultantes, (b) curva de convergencia.

- Modelos C2 y C3

Estos modelos presentan comportamientos muy similares, siendo C2 el modelo completamente restringido en la base, mientras que a C3 se le permitio expandirse. La figura 11 muestra que en el primer caso se obtuvo resultados mas cercanos a los conseguidos experimentalmente, por lo que probablemente represente mejor lo sucedido durante el ensayo de compresion. El modelo C2 tiene una diferencia del 0,44 % con respecto a los ensayos experimentales, mientras que para el modelo C3 la diferencia es del 1,9 %, en ambos casos son resultados de la malla 6.

Figura 11. Curvas de convergencia, modelos C2 y C3.

Simulacion del Ensayo de Flexion

Los primeros dos modelos de ensayos de flexion (F1 y F2) se realizaron imponiendo el desplazamiento debido a que fue la opcion que arrojo mejores resultados en la simulacion del ensayo de compresion. En los ultimos dos modelos (F3 y F4) se implementa la aplicacion de la fuerza con la finalidad de tener una vision mas amplia del comportamiento del modelo.

- Modelo F1

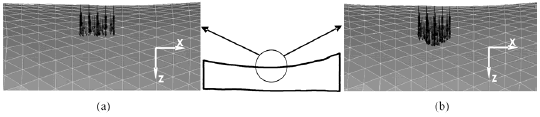
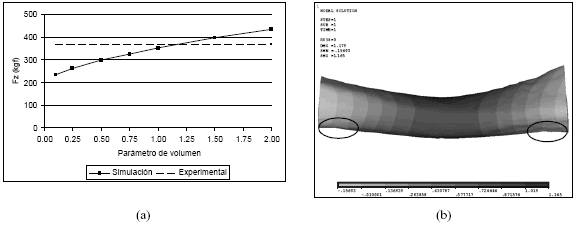
El analisis de convergencia del parametro de volumen para la condicion F1 indica que no es el modelo de apoyo apropiado para la simulacion del ensayo de flexion. Esta curva fue realizada utilizando la malla 6 y variando el parametro de volumen desde 0,1 hasta 2,0. A medida que se aumenta el parametro, la fuerza de reaccion aumenta, sobrepasando ampliamente la fuerza aplicada experimentalmente, y ademas no muestra signos de convergencia, como puede observarse en la figura 12a. En la figura 12b puede advertirse que en la parte inferior de los extremos del modelo, en las zonas marcadas, hay una pronunciada curvatura debida a la imposibilidad de rotacion que genera la condicion impuesta, causando un momento de reaccion que se incrementa a medida que se seleccionan mas nodos.

Figura 12. Modelo F1. (a) curva de convergencia del parametro de volumen, (b) desplazamientos transversales resultantes.

- Modelo F2

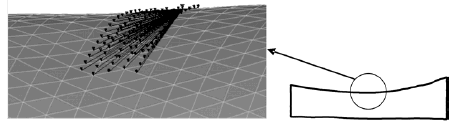
En este caso el volumen de nodos seleccionado se dejo constante. El analisis de convergencia de las mallas muestra que se obtiene valores estables a partir de la malla 6 (figura 13a), con una diferencia entre el valor de la simulacion y el experimental de solo 3,5 %. En la figura 13b se puede advertir que los extremos del modelo han podido rotar, lo cual se refleja en una curvatura mucho menos pronunciada que en el caso del modelo F1. Debido al contraste entre los resultados de F1 y F2, se selecciona la condicion FS2 para los siguientes dos modelos.

Figura 13. Modelo F2. (a) curva de convergencia, (b) desplazamientos transversales resultantes.

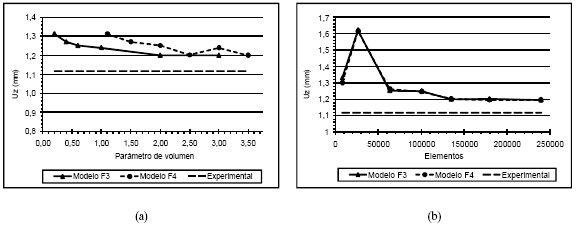
- Modelos F3 y F4

Los modelos F3 y F4 tienen comportamientos similares, como puede observarse en la figura 14. El modelo F3 muestra convergencia del parametro de volumen a partir de 2, mientras que en el modelo F4 ocurre lo mismo a partir de 2,5. Fijando estos valores, se realizo el analisis de convergencia de las mallas, la cual se alcanza en ambos casos a partir de la malla 5. Sin embargo, las diferencias entre los valores de las simulaciones y el valor experimental son mayores que en el modelo F1, siendo del 7% para ambos modelos.

Figura 14. Modelos F3 y F4. (a) curva de convergencia del parametro de volumen, (b) curva de convergencia de las mallas.

CONCLUSIONES

Los resultados obtenidos con las simulaciones permiten afirmar que en ensayos mecanicos realizados a tejido oseo, como los presentados en este trabajo, la imposicion de desplazamientos produce mejores resultados que la aplicacion de fuerzas como metodologia para la simulacion de la carga. Este fenomeno esta estrechamente relacionado con la significativa diferencia en la magnitud de las rigideces de los materiales involucrados, acero y tejido oseo, lo que ocasiona que los accesorios metalicos de la maquina de ensayos practicamente impongan desplazamientos de cuerpo rigido a las zonas del hueso donde se realiza el contacto. Respecto a los apoyos, el correcto modelado de la vinculacion es indispensable para que los grados de libertad restringidos no produzcan efectos ficticios que afecten negativamente la simulacion.

Los ensayos experimentales, por su parte, han probado ser una herramienta invaluable para la validacion y ajuste de la metodologia utilizada. La informacion obtenida de esta investigacion permitira que los resultados obtenidos de la simulacion de ensayos de flexion y compresion en otros huesos, en las mismas condiciones, sean confiables sin la necesidad de realizar los ensayos experimentales.

La metodologia presentada en este trabajo tambien sirve como guia para la simulacion de la interaccion entre protesis metalicas y huesos, un tema que es objeto de intenso estudio debido al interes de la comunidad medica e ingenieril de producir mejores protesis, mas similares al elemento que reemplaza y optimamente integradas al hueso en el que se implanta.

AGRADECIMIENTOS

Este trabajo fue financiado parcialmente por el Consejo de Desarrollo Cientifico y Humanistico de la Universidad de Carabobo (CDCH-UC) y el proyecto FONACIT USB200500172.

REFERENCIAS

1. ANSYSR, Inc. (2005). ANSYS 10.0 Help, Theory Reference, Copyrightc 2005.        [ Links ]

2. CARDOSO, L., MEUNIER, A., ODDOU, C. (2003). Theoretical and experimental ultrasonic characterization of anisotropic properties in cancellous bone. WCU, Paris, Septiembre (7-10): 1169-1172.        [ Links ]

3. CARTER, D. & HAYES, W. (1977). The compressive behavior of bone as a two-phase porous structure. J Bone Joint Surg, A (59): 954-62.        [ Links ]

4. CIACCIA, M., SAN ANTONIO, T., MULLER-KARGER, C., D' ARMAS, H. (2006). Simulacion y validacion experimental de un modelo oseo bovino. III Congreso Venezolano de Bioingenieria BIOVEN, pp 55.        [ Links ]

5. COWIN, S. (1989). Bone mechanics. CRC Press Inc., Boca Raton, Florida.        [ Links ]

6. CROWNINSHIELD, R. & POPE, M. (1973). The response of compact bone in tension at various strain rates. Ann. Biomed. Eng., 2: 217-225.        [ Links ]

7. GIUDICE, F., LA ROSA, G., RUSSO, T., VARSALONA, R. (2005). Evaluation and improvement of the efficiency of the Seidel humeral nail by numerical.experimental analysis of the bone-implant contact. Med Eng & Phys, 28: 682.693.        [ Links ]

8. GUPTA, S., VAN DER HELM, F., STERK, J., VAN KEULEN, F., KAPTEIN, B. (2004). Development and experimental validation of a three dimensional finite element model of the human scapula. J. Eng Med, Proc. IMechE Vol. 218 Part H, 127-142.        [ Links ]

9. HELWIG, P., FAUST, G., HINDENLANG, U., KROPLIN, B., EINGARTNER, C. (2006). Finite element analysis of a bone-implant system with the proximal femur nail. Technology and Health Care, 14:411.419.        [ Links ]

10. HIGHT, T. & BRANDEAU, J. (1983). Mathematical modeling of the stress strain-strain rate behavior of bone using the Ramberg-Osgood equation. J. Biomech, 16: 445- 450.        [ Links ]

11. JACOBS, C., DAVIS, B., RIEGER, C., FRANCIS, J., SAAD, M., FYHRIE, D. (1999). The impact of boundary conditions and mesh size on the accuracy of cancellous bone tissue modulus determination using large-scale finite-element modeling - effects of element size. J. Biomech, 32: 1159- 1164(6).        [ Links ]

12. MOODY, D. & LAZONOFF, S. (1999). SURFdriver 3.5, User Manual.        [ Links ]

13. MULLER-KARGER, C. (2001). Simulacion osea por medio de la version p del metodo de los elementos finitos. Tesis doctoral en ciencias de la ingenieria. Universidad Central de Venezuela. Venezuela.        [ Links ]

14. PAPPAS, C., YOUNG, P. & LEE, A. (2006). Development of the Mennen 3 PeriPro fixation plate for the treatment of periprosthetic fractures of the femur. J. Eng Med, Proc. IMechE Vol. 220 Part H, 775-785.        [ Links ]

15. PHILLIPS, A., HOWIE, C. & PANKAJ, P. (2007a). Free boundary condition modelling of the musculo-skeletal pelvis: assessment of anterolateral and posterolateral approaches. Proceedings of the European Society of Biomechanics Workshop 2007, Finite Element Modelling in Biomechanics and Mechanobiology. 88- 89.        [ Links ]

16. PHILLIPS A., PANKAJ, P., HOWIE, C., USMANI, A., SIMPSON, A. (2007b). Finite element modelling of the pelvis: Inclusion of muscular and ligamentous boundary conditions. Med Eng & Phys, 29:739-748.        [ Links ]

17. VAN BUSKIRK, COWIN, W., S., WARD, R. (1981). Ultrasonic measurament of orthotropic elastic constans of bovine femoral bone. J Biomech Eng, 103: 67-71.        [ Links ]

18. VICECONTI, M., PANCANTI, A., VARINI, E., TRAINA, F., CRISTOFOLINI, L. (2006). On the biomechanical stability of cementless straight conical hip stems. J. Eng Med, Proc. IMechE Vol. 220 Part H, 473-480.        [ Links ]

19. XU, W., XU, D., CROCOMBE, A. (2006). Three-dimensional finite element stress and strain analysis of a transfemoral osseointegration implant. J. Eng Med, Proc. IMechE Vol. 220 Part H, 661-670.        [ Links ]