Nuevo esquema numerico conservativo para la difusion de calor en medios bi-dimensionales no-homogeneos

Jhonnathan Arteaga-Arispe, Juan M. Guevara-Jordan

Universidad Central de Venezuela, Facultad de Ciencias, Escuela de Matematicas, Caracas, Venezuela. e-mail: arteagajt@cantv.net , jguevara@euler.ciens.ucv.ve 

RESUMEN

El presente articulo describe la formulacion de un nuevo esquema numerico conservativo aplicado a la ecuacion no estatica del calor en 2-D. La evaluacion del metodo y su comparacion con los esquemas de diferencias finitas estandar asi como un estudio cualitativo de las tasas de convergencia son analizados. Los resultados obtenidos evidencian la ventaja del nuevo metodo, sobre todo en aquellos problemas fisicos en los cuales las condiciones de borde son determinantes para la correcta aproximacion numerica de la solucion.

Palabras clave: Metodos mimeticos, Metodos de diferencias finitas, Metodos conservativos, Ecuacion del calor, Capa limite.

New conservative numerical scheme for heat diffusion in two-dimensional non-homogeneous medium

ABSTRACT

A new numerical conservative scheme formulation and its application to the 2D transient heat equation is presented. The evaluation of the method and its comparison with the standard finite difference method are analyzed. The results show the advantages of the new method, in particular for those physical problems where the boundary conditions are very important for an accurate numerical solution approximation.

Keywords: Mimetic methods, Finite differences methods, Conservative methods, Heat equation, Boundary layer.

Recibido: febrero de 2007 Revisado: marzo de 2008

INTRODUCCION

Los problemas no estaticos de valor en la frontera de transferencia de calor aparecen recurrentemente en muchas aplicaciones de la ingenieria tales como moldura de metales y no metales por calor, enfriamiento de componentes electronicos, propagacion del calor en yacimientos en los cuales se inyecta vapor, y otros numerosos procesos y/o problemas aplicados. Los metodos numericos han sido usados ampliamente para resolver estas ecuaciones. Sin embargo y a pesar de que estos han ido evolucionando y mejorando continuamente, no se puede afirmar que un metodo pueda ser considerado como el mejor u optimo. En consecuencia, la propuesta de nuevos metodos numericos para resolver la ecuacion del calor es un topico de mucho interes actualmente.

Los metodos numericos mas usados hoy en dia, para resolver de forma general los problemas de transferencia de calor mediante la ecuacion del calor son: diferencias finitas, elementos finitos y elementos de contorno. Cada uno de estos presentan numerosas ventajas (Lapidus et al. 1983) pero tambien algunas desventajas entre las que se pueden citar la imprecision en el manejo de heterogeneidades fuertes en el caso de elementos de contorno (Power, 1995), la complejidad de implementacion computacional en el caso de elementos finitos (Zienckiewicz et al. 1994), consideraciones ficticias para las condiciones de borde y poca generalidad son algunas de las desventajas de los metodos de diferencias finitas estandar (Smith, 1986; Morton et al. 1994).

El tratamiento poco sistematico de las condiciones de borde en diferencias finitas y su incompatibilidad con las moleculas de discretizacion en nodos interiores han originado un nuevo tipo de esquemas en diferencias finitas denominado metodos mimeticos u operadores de soporte (Shashkov et al. 1994; Hyman et al. 1998; Hyman et al. 2002; Castillo et al. 2003). La aplicacion de estos metodos a los problemas de difusion estatica han presentado numerosas ventajas sobre los de diferencias finitas estandar (Freites, 2004; Guevara, 2005). En consecuencia, una extension y aplicacion de estos representa un area de investigacion importante. Mas recientemente en la Escuela de Matematicas de la Universidad Central de Venezuela, se ha estudiado un nuevo metodo conservativo asintoticamente convergente a los esquemas mimeticos, el cual adquiere naturalmente las ventajas de representacion y flexibilidad de los metodos mimeticos pero posee una formulacion mas simple (Guevara, 2005; Guevara et al. 2005). Todos estos estudios corresponden a problemas estaticos o elipticos unidimensionales, las extensiones y analisis al caso multidimensional fueron presentados por Arteaga et al. (2006).

Los primeros indicios de la aplicacion del nuevo metodo conservativo a la ecuacion de calor han exhibido resultados sumamente satisfactorios (Arteaga, 2008). Una exposicion formal de la discretizacion de las ecuaciones, sus diferencias con respecto al metodo de diferencias finitas, las ventajas que posee y su aplicacion a la ecuacion de calor en medios cuyas propiedades de conductividad termica varia dependiendo de la posicion, no han sido reportados y constituyen los objetivos principales de este trabajo.

El presente articulo se encuentra estructurado de la siguiente manera: se exhibe el problema de valor en la frontera gobernado por la ecuacion de difusion de calor y condiciones de borde del tipo mixta o de Robin. Seguidamente se describen los principios basicos de las discretizaciones conservativas, adicionalmente se establece una comparacion con el metodo de diferencias finitas estandar. Posteriormente, se aplica la discretizacion conservativa al problema de valor en la frontera referido anteriormente. Luego se presentan los resultados numericos obtenidos para un caso homogeneo y uno heterogeneo, asi como una comparacion con los resultados obtenidos por el metodo de diferencias finitas estandar. Finalmente se proporcionan las conclusiones del estudio cualitativo y cuantitativo del metodo numerico propuesto en este articulo.

ECUACION DE DIFUSION EN 2D

La ecuacion en derivadas parciales y las condiciones de borde que modelan la transferencia de calor por difusion en un medio no-homogeneo, vienen dadas por las relaciones:

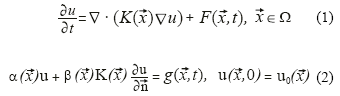
donde:

Ω representa el medio en el cual se estudia la variacion de la temperatura es el coeficiente de conductividad termica y representa la intensidad de las fuentes de calor en el punto en el tiempo t. Las funciones  , definen las condiciones de borde en su forma mas general o, escrito de otra manera, el comportamiento de la temperatura en la frontera de Ω, representa la temperatura inicial del medio.

La solucion general del problema de valor, en la frontera dada por las ecuaciones (1) y (2), no puede ser obtenida de manera general mediante metodos analiticos. Es por esta razon que existe un amplio espectro de metodos numericos que tienen por objetivo aproximar de forma sistematica las soluciones de este problema.

METODO CONSERVATIVO

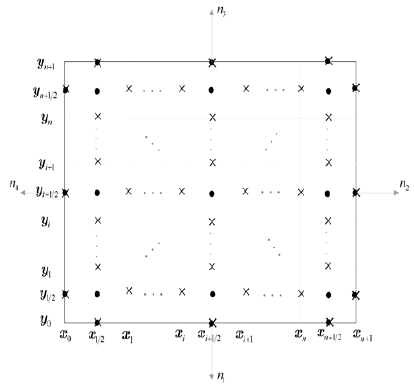
Con la finalidad de simplificar la exposicion del metodo y tal como se ilustra en la figura 1, se tomara el mismo numero de nodos n en la direccion de las abcisas x y de las ordenadas y en las cuales se discretizara el medio, tal que este puede ser representado mediante el producto cartesiano:

Figura 1. Malla punto distribuida.

donde:

x₀= y₀ =0  y x_n+1 = y_n+1. Esta malla posee (n +1)x(n +1) celdas de tamano h x h , cada una de las cuales posee un nodo central, marcado con un circulo en la figura 1, y denotado por (x_i+1/2, y_i+1/2) para i,j=0. Es de hacer notar que cada bloque con un lado en la frontera de Ω tiene un nodo adicional y las celdas en las esquinas poseen, en consecuencia, dos nodos adicionales. Esta malla nouniforme es llamada en los articulos de metodos mimeticos (Castillo, 2003; Guevara, 2005) malla punto distribuida. La distancia h viene dada por la relacion usual:

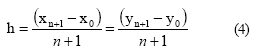
donde:

x_i = x₀ + ih y y_j = y₀ + jh para i,j=0,..n+1. De igual manera, el intervalo de tiempo (denotado por [0, T]) en el cual se resolvio el problema, fue discretizado en n_t subintervalos de longitud Δt donde: t₀ = 0 , t_nt = T y t_m = mΔt  para m = 0,.,n_t . La siguiente notacion sera empleada en todo el articulo u^m_{(i,j) =} u₍x_i, y_j,t_m)

En la malla, la funcion escalar tendra una representacion por un vector de (n +1)² + 4(n + 1) componentes correspondientes a la evaluacion de u en los centros de cada celda y en los nodos adicionales en la frontera, todos estos denotados por puntos negros en la figura 1. Ordenando los nodos de izquierda a derecha y de abajo hacia arriba, la expresion vectorial de vendra dada por:

De acuerdo a la notacion empleada en la figura 1, la aproximacion de la proyeccion del gradiente G en el vector normal a la frontera de Ω tendra la forma:

donde:

para los nodos en la base y en el tope del cuadrado unitario, i₁ =i₂ =i₃ = i + 1/2 para i = 0,..,n, y   j₁ = 0 , j₂= 1/2, j₃= 3/2 . si y= 0, o, j₁= n +1, j₂= n + 1/2, j₃= n - 1/2 si y= 1. Por otra parte, para los nodos en las fronteras izquierdas y derechas del dominio j₁= j₂= j₃= j+ 1/2 para j= 0,..,n, y i₁= 0, i₂= 1/2  , i₃= 3/2  si x=0 , o , i₁= n + 1, i₂= n +1/2 , i₃= n - 1/2 si x = 1. El signo de los coeficientes en la aproximacion de los componentes del gradiente vendra dado por el signo del vector normal a la frontera de Ω.

Esta aproximacion es la misma obtenida para el gradiente mimetico unidimensional en la frontera (Guevara, 2005; Guevara et al. 2005; Castillo 2005) y tiene la ventaja que puede ser obtenida por aplicaciones sistematicas de las series de Taylor (Guevara, 2005). En los puntos internos de la malla, el gradiente y la divergencia coinciden con las discretizaciones estandar en diferencias finitas centradas, esto es:

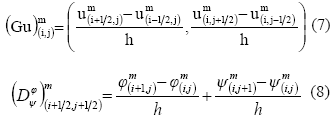
La ecuacion (7) es valida para i,j = 1,.,n mientras que la ecuacion (8) para i,j = 0,..,n . En esta ultima las funciones φ y ψ son los componentes del gradiente.

Los operadores discretizados en las ecuaciones (6), (7) y (8) admiten una representacion matricial de la siguiente manera; en notacion matricial, el operador gradiente G, denotado por G, tiene dimensiones 2ñ x ñ donde ñ = (n + 1)² + 4(n + 1). Sus elementos son ± 8/3h , μ3/h , ±1/3h , en las filas correspondientes a los nodos de la frontera, mientras que en los nodos interiores las elementos son 1/h y -1/h . Por otra parte, la matriz asociada a la discretizacion del operador divergencia D, denotada por D, posee dimensiones (n + 1)² x 2ñ y sus coeficientes son los mismos que para la discretizacion mediante diferencias finitas estandar, esto es, sus elementos son -1/h, -1/h ,y para cada uno de los nodos interiores de la malla punto distribuida y 0 en el resto.

Por otra parte, la derivada temporal fue aproximada por diferencias adelantadas y representada por el operador tal que:

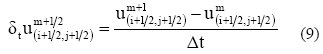
Definiendo el calor total del sistema en un tiempo t mediante la relacion:

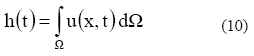
se puede demostrar (Arteaga, 2008), aplicando reglas de cuadratura para las aproximaciones de las integrales, que el esquema de discretizacion propuesto satisface la relacion conservativa:

Este resultado se deriva de las propiedades que satisfacen las versiones discretas de los operadores gradiente y divergencia (Arteaga et al. 2006).

DISCRETIZACION CONSERVATIVA DE LA ECUACION DE DIFUSION

Con la finalidad de representar el esquema numerico en una forma discreta explicita, se supondra sin perdida de generalidad que y se expresara la ecuacion de difusion (1) en terminos de los operadores diferenciales expuestos en la seccion anterior y el θ metodo o metodo de promedio ponderado (Morton et al. 1994), obteniendose la relacion:

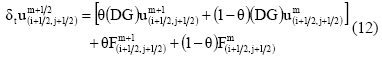
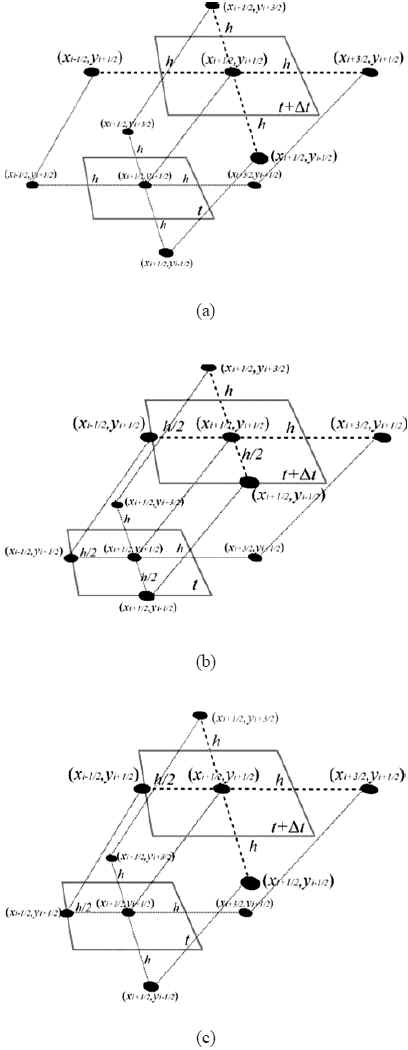
En esta, el peso ƒÆ define el metodo a ser aplicado para la resolucion temporal de la ecuacion diferencial. En el caso de θ= 0 el esquema es explicito mientras que es implicito para el caso θ=1. El metodo de Crank-Nicolson, obtenido para θ=1/2, es de particular interes para el presente trabajo, ya que es de segundo orden de aproximacion (Morton et al. 1994). Por otra parte, el termino DG corresponde a la composicion de los operadores discretos D y G, y varia en funcion de los nodos de la malla punto distribuida. A saber, para los nodos internos (referidos en la figura 2(a) como nodos internos regulares), i,j=1,..n., la composicion viene dada por:

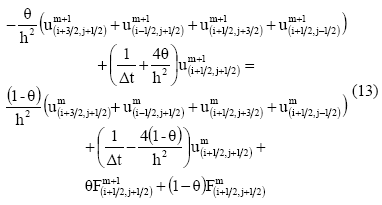
Figura 2. Nodos de discretizacion para la ecuacion del calor. (a) nodos interiores regulares, (b) nodos de las esquinas internas, (c) nodos de los lados internos.

Como se menciono en el parrafo anterior, la figura 2 muestra los tres casos posibles obtenidos para la discretizacion de la ecuacion del calor mediante el metodo conservativo propuesto en el presente articulo. Estos casos se diferencian entre si a partir de la posicion de los nodos en la malla no uniforme punto distribuida. En esta figura se muestra tanto la dependencia temporal como espacial de los nodos segun la notacion empleada para las ecuaciones (7), (8) y (9).

Por otra parte, para los nodos internos proximos a la frontera (nodos de los lados internos en la figura 2), la composicion discreta se define mediante la relacion:

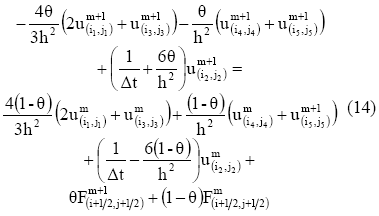
Finalmente, la discretizacion en los nodos de las esquinas internas (figura 2) (i=0, j=0), (i=n, j=0), (i=n, j=n), (i=0, j=n), viene dado por:

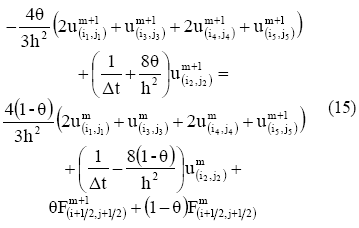
En las ecuaciones anteriores se han empleado indices generalizados para la representacion de la discretizacion de los operadores en cada nodo. La relacion entre estos y los nodos de la malla puede resumirse mediante las relaciones:

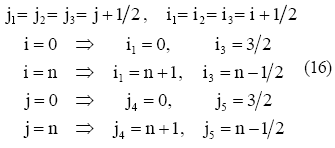
De igual manera, las condiciones de borde (2) en su forma discreta vendran dadas por:

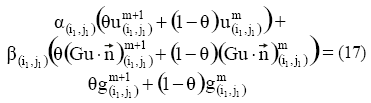
en esta la correspondencia entre los sub-indices generalizados y los nodos de la malla es la misma que para la ecuacion (6).

La discretizacion conservativa del problema de valor en la frontera admite una representacion matricial compacta y mas general, mediante el sistema de ecuaciones lineales:

En esta, los componentes del vector vienen dados por la evaluacion de los terminos fuentes en los nodos interiores y por en las entradas correspondientes a los nodos de la frontera. La matriz M, correspondiente a la discretizacion espacial de la ecuacion en derivadas parciales, viene dada por la ecuacion:

En la ecuacion (19), las matrices A^α y B^β de dimensiones ñ x ñ y ñ x 2ñ, respectivamente, son representaciones matriciales de condiciones de borde, las cuales solo poseen valores no nulos en las filas correspondientes a los nodos en la frontera. Estos valores estan asociados a las evaluaciones de las funciones descritos en la ecuacion (2). K es una matriz diagonal de valores positivos obtenidos de la evaluacion conservativa mediante promedios aritmeticos del coeficiente de difusion termica en los nodos correspondientes (Morton et al. 1994; Freites, 2004), manteniendo asi la correspondencia con la version discreta del operador gradiente. Finalmente, D y G son las representaciones matriciales de los operadores divergencia y gradiente descritos en la seccion anterior, con la adicion en D de 4 (n+1) filas de ceros correspondientes a las condiciones de borde.

RESULTADOS NUMERICO

El esquema conservativo propuesto y el metodo de diferencias finitas estandar fueron implementados computacionalmente para resolver el problema de valor en la frontera gobernado por la ecuacion del calor bidimensional. En esta seccion se presenta un estudio comparativo de ambos esquemas tomando como referencia dos casos o ejemplos.

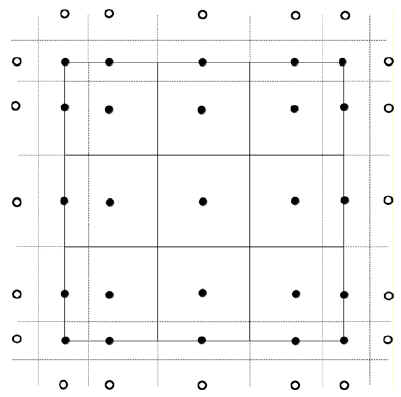
La implementacion del metodo de diferencias finitas para resolver la ecuacion estatica de difusion en 2D requiere mallas extendidas con puntos fantasmas o ficticios, como se ilustra para un caso simple en el cuadrado unitario Ω en la figura 3. En esta, se puede apreciar que los nodos de la malla punto distribuida son un subconjunto de la malla extendida. Los puntos fantasmas fueron representados por circulos blancos, mientras que los negros corresponden a los nodos reales, los cuales coinciden con los nodos de la malla punto distribuida excepto en las esquinas. Las lineas punteadas son bordes imaginarios para los bloques de malla extendidos. En general, una malla rectangular extendida n x n tendra n² + 4n + 4 nodos reales y 4n+ 4 nodos fantasmas, mientras que en la malla punto distribuida se necesitara solamente n²+4n nodos reales y ningun nodo ficticio. Esta observacion presenta en si misma, una ventaja del metodo conservativo sobre diferencias finitas.

Figura 3. Malla extendida de diferencias finitas estandar.

Caso I

Para este primer analisis, se considero el problema de valor en la frontera (1), (2) para un medio homogeneo con esto es:

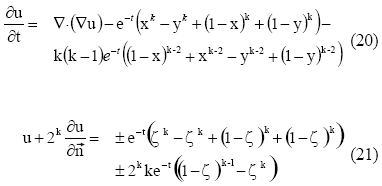
donde:

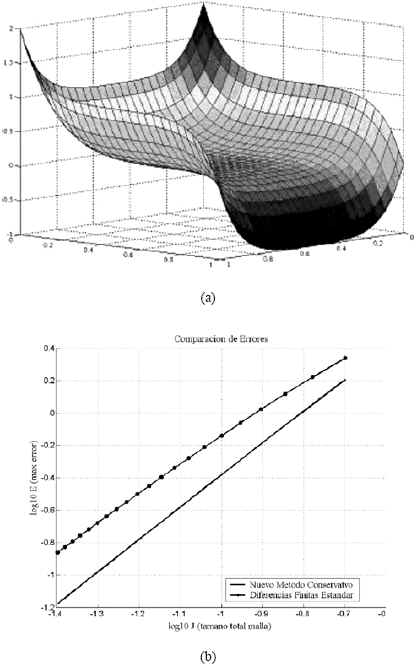
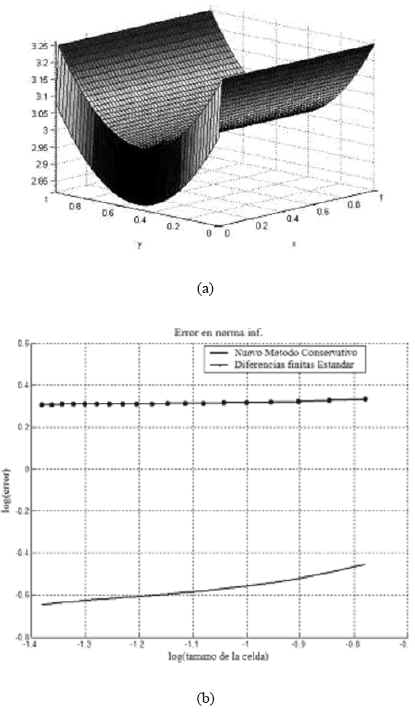
ζ= x o y , dependiendo de la posicion de en la frontera de Ω , y el signo del lado derecho de la condicion de borde vendra dado por el signo del vector normal a әΩ. Por otra parte, la solucion analitica de este problema es , la cual es del tipo capa limite para todos los lados del cuadrado unitario y, mientras mayor es el valor de k, mayores son las dificultades para el metodo numerico porque las capas son mas proximas al borde, como puede observarse en la figura 4(a), y, en consecuencia, mallas muy refinadas son necesarias para una buena aproximacion.

Figura 4. Resultados numericos (caso I). (a) solucion analitica, (b) comparacion de errores en norma ¥.

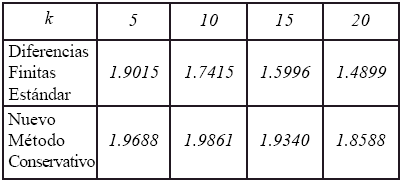
En la figura 4(b) se muestran la comparacion de los errores estimados para el metodo propuesto y diferencias finitas tomando como datos k=10, θ= 1/2 y ∆ t= 1/2h² y . Los resultados obtenidos exhiben una clara ventaja del nuevo metodo conservativo sobre el esquema de diferencias finitas estandar. Adicionalmente y como se muestra en la siguiente tabla, el metodo conservativo posee y mantiene una convergencia cuadratica bajo refinamiento simultaneo en los ejes del tiempo y el espacio, lo cual corresponde a los resultados teoricos descritos en Arteaga (2008).

Tabla 1. Tasas de convergencia (caso I).

Caso II

A continuacion se analizan los resultados obtenidos para un medio no-homogeneo, en el cual el coeficiente de difusion viene dado por:

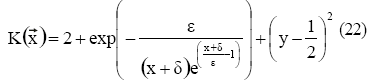
Mientras menor es el valor de ε, mayores son las exigencias a los metodos numericos para alcanzar una buena aproximacion ya que el coeficiente de difusion se acerca al borde, como se ilustra en la figura 5(a). Para este caso se emplearon los valores de ε= 0.005 y δ= 0.001. Las condiciones de borde son, al igual que para el caso I, Mixtas o Robin con . El problema de valor en la frontera vendra dado entonces por las relaciones:

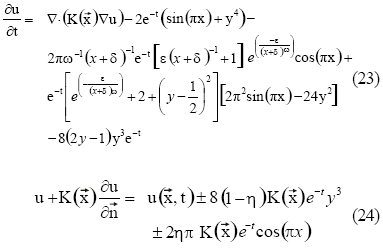
donde:

n= 1 si y= o o y= 1 y la solución analítica

Figura 5. Resultados numericos (caso II). (a) grafica del coeficiente de difusion termica. (b) comparacion de los errores en norma ¥.

Los resultados obtenidos muestran diferencias numericas considerables (figura 5b) y una pobre representacion de la solucion por parte del metodo de diferencias finitas estandar. En este caso, la correcta aproximacion de las condiciones de borde por parte del metodo conservativo incide drasticamente en la buena aproximacion de la solucion del problema de valor en la frontera. A continuacion se tabula la comparacion de los errores absolutos para varios tamanos de malla, lo cual confirma la conclusion presentada anteriormente.

Tabla 2. Comparacion de errores absolutos (caso II) .

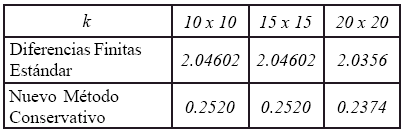
En esta se ha denotado por a la solucion analitica del problema y la estimada por los metodos numericos para .

CONCLUSIONES

En el presente articulo se ha desarrollado un nuevo esquema numerico conservativo para resolver la ecuacion de difusion en 2-D. El analisis cualitativo de la convergencia muestra evidencias claras de tasas de convergencia cuadraticas, el cual es el mejor resultado posible para este tipo de esquema. Esta no es una propiedad obvia debido a su error de truncacion de primer orden en los nodos internos cercanos al borde. El analisis presentado en este articulo constituye una extension en la aplicacion del metodo conservativo reportado y formalizado por Arteaga (2008).

El analisis en varias variables fue restringido al caso bidimensional por ser el mas sencillo. La extension del metodo a varias variables no incorpora ningun elemento adicional de estudio, pero requiere expresiones mas extensas.

Las principales ventajas del esquema numerico presentado en el presente articulo son: es conservativo; su formulacion en los nodos internos y en la frontera es consistente; su implementacion numerica es mas robusta que para los esquemas de diferencias finitas de segundo orden ya que no se basa en tecnicas como nodos fantasmas; su formulacion es rigurosa y consistente con el planteamiento fisico del problema de valor en la frontera ya que no discretiza la ecuacion diferencial en el borde como suele hacerse con los metodos de diferencias finitas estandar; su implementacion computacional es facil y el tratamiento versatil de las condiciones de borde permite resolver con el mismo programa, problemas de valor en la frontera con condiciones del tipo Dirichlet, Neumann y Robin, y combinaciones de estas para varios sectores de la frontera.

El nuevo metodo conservativo fue aplicado a dos casos, ejemplo claves por sus dificultades en la resolucion con esquemas numericos. Los resultados indicaron sus principales ventajas sobre el mas comun y preciso metodo de diferencias finitas estandar de segundo orden.

REFERENCIAS

1. CASTILLO, J. E. & GRONE R. D. (2003). A Matrix Analysis Approach to Higher Order Approximations for Divergence and Gradients Satisfaying a Global Conservation Law, SIAM J. Matrix Analysis and Applications. Vol. 25, 128.        [ Links ]

2. GUEVARA-JORDAN, J. M., FREITES-VILLEGAS, M., ROJAS, S., CASTILLO, J. E. (2005). A New Second Order Finite Differences Conservative Scheme, Divulgaciones Matematicas, Zulia. Vol. 13, 107.        [ Links ]

3. POWER, H. (1995). Boundary Element Applications in Fluid Mechanics, WIT Press.        [ Links ]

4. ARTEAGA-ARISPE, J., GUEVARA-JORDAN. (s.a). Conservative Finite Difference Scheme for Static Diffusion Equation. Divulgaciones Matematicas, Zulia, Venezuela. Aceptado para publicacion.        [ Links ]

5. ZIENCKIEWICZ & TAYLOR. (1994). El Metodo de los Elementos Finitos, Mc Graw-Hill.        [ Links ]

6. CASTILLO, J. E., YASUDA, M. (2005). Linear System Arising for Second Order Mimetic Divergente and Gradient Discretizations, Journal of Mathematical Modelling and Algorithms. Vol. 4, pag. 67.        [ Links ]

7. ARTEAGA, J. (2008). Metodo Conservativo para la Ecuacion de Difusion en 2D. Tesis de Maestria (en preparacion). Facultad de Ingenieria, U.C.V.        [ Links ]

8. HYMAN, J., MOREL, J., SHASHKOV, M., STEINBERG, S. (2002). Mimetic Finite Difference Methods for Diffusion Equations, Computational Geosciences. Vol. 6, 333.        [ Links ]

9. MORTON, K. W. & MAYERS, D. F. (1994). Numerical Solution of Partial Diferential Equations, Oxford University Press.        [ Links ]

10. SMITH, G. D. (1986). Numerical Solutions of Partial Differential Equations: Finite Differences Methods, Oxford University Press.        [ Links ]

11. LAPIDUS, L. & PINDER, G. F. (1983), Numerical Solution of Partial Differential Equations in Science and Engineering, Wiley, NY.        [ Links ]

12. GUEVARA-JORDAN, J. M. (2005). Sobre los Esquemas Mimeticos en Diferencias Finitas para la Ecuacion Estatica de Difusion, Trabajo de Ascenso, UCV Caracas, Venezuela.        [ Links ]

13. SHASHKOV, M. J. & STEINBERG, S. (1995). Support Operators Finite Difference Algorithm for General Elliptic Problems, Journal of Computational Physics. Vol. 118, 131.        [ Links ]

14. HYMAN, J. M. & SHASHKOV, M. J. (1998). The Approximation of Boundary Conditions for Mimetic Finite Difference Methods Operators, Computers & Mathematics with Applications. Vol. 36, 79.        [ Links ]

15. FREITES, M. A. (2004). Un estudio comparativo de los metodos mimeticos para la ecuacion estacionaria de difusion. Tesis de grado. Facultad de Ciencias (U.C.V., Caracas).        [ Links ]