Estudio numérico del ascenso de burbujas de taylor en mini-conductos verticales de sección no-circular: Parte I

Miguel Baritto Y Julio Segura

Universidad Central de Venezuela. Facultad de Ingeniería. Escuela de Ingeniería Mecánica. Caracas, Venezuela. e-mail: miguelbaritto@gmail.com ; e-mail: jsegura@reacciun.ve 

RESUMEN

Este trabajo presenta un estudio numérico del ascenso de burbujas de Taylor en mini-conductos verticales de sección transversal en forma de triángulo equilátero y cuadrado, para flujo bifásico segregado aire-agua. El modelo matemático resuelto corresponde a un modelo Euleriano-Euleriano, heterogéneo y con superficie libre, que incluye la ecuación de continuidad y la ecuación de momentum para ambas fases y para la interfase, y la ecuación de conservación de fracción volumétrica para la interfase. La fuerza de tensión superficial se modeló empleando el método de fuerza continua en la interfase (CFS). La solución numérica al modelo planteado se obtuvo mediante el método de volúmenes finitos basados en elementos (EbFVM), implementado en el software ANSYS® CFX™-10.0. Los resultados se compararon con estudios experimentales, obteniéndose para la velocidad terminal de la burbuja una tendencia de aumentar con el diámetro hidráulico del conducto y de ser mayor en conductos de sección triangular que de sección cuadrada, coincidiendo cualitativamente con la data experimental. De igual manera se encontró que las burbujas con mayor velocidad terminal tienden a ocupar menos porcentaje de la sección transversal del conducto y a tener meniscos menos planos, comportamiento observado experimentalmente, por lo que el modelo empleado describe adecuadamente al fenómeno físico aquí estudiado.

Palabras clave: Burbujas de Taylor, Velocidad terminal, Mini-conductos, Flujo bifásico, Dinámica de fluidos computacional (CFD), Método de volúmenes finitos basado en elementos (EbFVM).

Numerical study of taylor bubble rising in a vertical noncircular mini channel: Part I

ABSTRACT

We present a numerical study for Taylor bubbles rising in a vertical non-circular mini channel filled with stagnant liquid. Triangular and square cross-sections were considered for this study. A Eulerian-Eulerian heterogeneous model for free surface flow was solved by the elements based finite volume method (EbFVM) implemented in commercial software ANSYS® CFX-10.0™. The mathematical model takes into account the effects of surface tension and viscous force. The first behavior was modeled by the Continuous Surface Model (CSF), and the second by solving the conservation equations of both the mass and the momentum of each phase and interphase, coupled with the conservation equation of the volume fraction at the interphase. The bubble drift velocity and the interfacial profiles were compared with published experimental data and good agreement has been obtained. As a result, the model has been validated for the study of this kind of twophase flow.

Keywords: Taylor bubbles, Drift velocity, Mini channels, Two-phase flow, Computational fluid dynamics (CFD), Elements based finite volume method (EbFVM).

Recibido: junio de 2007 Revisado: abril de 2008

INTRODUCCIÓN

En el patrón de flujo ascendente de gas y de líquido en conductos verticales, conocido como flujo tapón o de burbuja de Taylor, se observa la presencia de burbujas alargadas que ocupan casi en su totalidad la sección transversal del conducto y poseen una extensión de muchas veces el diámetro hidráulico del mismo. Cuando la sección transversal del conducto es circular, la burbuja se caracteriza por presentar una forma que hace alusión a una bala, con una nariz redondeada y una cola que puede ser cóncava, plana, convexa, irregular u oscilante, dependiendo de la viscosidad del líquido y de la longitud de la burbuja (Polonsky et al. 1999; Viana et al. 2003), separada de la pared del conducto por una delgada película de líquido descendente. Al igual que la forma de la burbuja, la velocidad constante con la cual asciende dentro de un conducto de longitud infinita, llamada velocidad terminal, ha sido de interés. Dumitrescu (1943) y Davies & Taylor (1950) fueron los primeros en publicar sendas ecuaciones, ambas prácticamente iguales, para la velocidad terminal de una burbuja de Taylor ascendiendo en conductos verticales de sección circular, al suponer flujo potencial de la película de líquido descendente. Ambos trabajos determinaron que dicha velocidad disminuye con la raíz cuadrada del diámetro del conducto. Aun cuando estas ecuaciones funcionan bastante bien para diámetros grandes, para diámetros pequeños fallan, al no considerar el efecto de la tensión superficial. Este inconveniente fue resuelto por Tung y Parlange (1976), quienes obtuvieron una correlación para burbujas ascendiendo en conductos circulares llenos de líquido estancado, influenciadas por la tensión superficial. Experimentalmente, Bi y Zhao (2001) determinaron que existe un diámetro mínimo para el cual no es posible el ascenso de la burbuja en conductos de sección circular, atribuyendo este hecho a que la totalidad de la sección es ocupada por la fase gaseosa, sin que la fuerza de flotación sea capaz de generar el ascenso. Una vez que la burbuja toca la pared del conducto, la continuidad de la fase líquida se interrumpe, haciendo imposible que actúe la fuerza de flotación y por ende el flujo de la burbuja. Para flujo aire-agua, este diámetro mínimo es 2.58 mm. Sin embargo, este mismo estudio determinó que en conductos de sección transversal con esquinas, el ascenso de la burbuja ocurre para diámetros hidráulicos tan pequeños como 0.866 mm en el caso de sección triangular, 1.5 mm en el caso de sección cuadrada, y 1.0 mm en el caso de sección rectangular, debido a que por efecto de la tensión superficial las esquinas del conducto siempre retienen líquido, asegurando la continuidad de esta fase y por consiguiente la acción de la fuerza de flotación. El interés en el estudio de ascenso de burbujas de Taylor en conductos de sección no circular proviene de la existencia del flujo en conductos de diámetros hidráulicos en el orden de los milímetros, llamados mini conductos, ya que la aplicación se ha llevado a escalas tan pequeñas que no es posible el uso de conductos de sección circular. Las aplicaciones incluyen aumento del factor de recobro de crudo (Ransohoff & Radke, 1988; Ratulowski & Chang, 1989), diseño de reactores nucleares (Tomiyama et al. 2003), transferencia de masa en reactores monolíticos (Vandu & Krishna, 2005), entre otras, impulsadas por las novedosas, y cada vez más confiables, herramientas de dinámica de fluidos computacional que complementan, y en algunos casos sustituyen, a los estudios experimentales. En los últimos años ha aumentado el número de estudios basados en simulaciones computacionales del fenómeno de ascenso de burbujas de Taylor en mini conductos verticales de sección no circular, como lo muestran los trabajos de Liao & Zhao (2003), quienes resolvieron un modelo unidimensional mediante el método de Runge-Kutta de cuarto orden, determinando la interfase gas-líquido y la velocidad terminal de la burbuja, para secciones cuadradas y triangulares; y de Taha & Cui (2006) quienes emplearon el método de volúmenes finitos acoplado a un esquema de reconstrucción geométrica de la interfase, para obtener la forma y la velocidad terminal de una burbuja de Taylor ascendiendo en conductos verticales de sección cuadrada de 2.0 mm de diámetro hidráulico. Los primeros obtuvieron resultados cualitativamente acordes a los pocos datos experimentales contra los cuales compararon, mientras que los segundos no realizaron comparación contra resultados de experimentos, evidenciándose la escasez de estudios experimentales en esta área de investigación.

La intención de este trabajo es obtener el comportamiento fluidodinámico de burbujas de Taylor ascendiendo en mini conductos verticales de sección triangular y cuadrada, llenos de líquido estancado, a partir de simulaciones computacionales, y comparar los resultados con la data experimental disponible para validar las simulaciones, a fin de realizar experimentos numéricos con secciones transversales de geometrías no reportadas en la literatura especializada.

MODELO MATEMÁTICO Y EXPERIMENTOS NUMÉRICOS

El comportamiento fluidodinámico del fenómeno es descrito mediante un modelo tridimensional, Euleriano-Eulariano y heterogéneo, constituido por las ecuaciones de conservación de masa y de momentum para cada fase y para la interfase, y de conservación de fracción volumétrica para la interfase. El modelo matemático planteado está sujeto a las siguientes consideraciones:

• Régimen transitorio

• Ambas fases se consideran continuas

• Gas y líquido fluidos incompresibles, newtonianos y de propiedades físicas constantes

• Flujo laminar en ambas fases

• Flujo isotérmico

• Se desprecia la transferencia de masa entre fases

• Tensión superficial entre fases, constante

• Campo gravitatorio actúa en la dirección vertical

La ecuación de conservación de momentum, se expresa como:

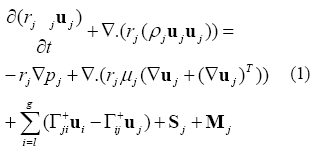
La posición de la interfase en un instante dado, y su evolución en el tiempo, son observados a partir de la distribución de r: la fracción volumétrica de las fases en un volumen finito, donde:

r_l= 1   en la fase líquida

               y

r_g= 0  en la fase gaseosa.

De esta manera la interfase gas-líquido existe en aquellos volúmenes finitos donde se cumpla:

0 < r_j < 1

Todos los términos de la ecuación (1) se aplican a la interfase gas-líquido, mientras que sólo algunos actúan en ambas fases y sus efectos se describen a continuación.

El término de la ecuación (1) representa la transferencia de momentum debido a la transferencia de masa interfacial. Vandu et al. (2005), determinaron experimentalmente que, en conductos capilares, la transferencia de masa (oxígeno) entre la burbuja y la película uniforme de líquido que la rodea, es proporcional a la suma de la velocidad superficial del líquido y del gas. Debido a que el estudio de interés considera el líquido estancado, es de esperarse velocidades superficiales bajas en ambas fases, por lo que este término puede despreciarse.

El término S_j de la ecuación (1) describe fuentes de momentum debido a la acción de fuerzas externas de campo. El ascenso de la burbuja se debe a la diferencia de densidad entre ambas fases, y es asistido por el campo gravitacional, por lo que el efecto de la fuerza de flotación es incorporado a la ecuación (1) como un término fuente, descrito mediante el modelo de diferencia de densidad (DDM) (ANSYS® CFXSolver ™, 2005), que tiene la forma:

donde:

ρ_ref denota una densidad de referencia, correspondiente a la densidad de la fase gaseosa, de manera de excluir la contribución de la presión hidrostática del gas, en la ecuación de momentum.

El efecto de la tensión superficial también es incluido en la ecuación (1) como un término fuente ( S_j ), mediante el método de fuerza continua en la superficie (CSF), propuesto por Brackbill et al. (1992). Este modelo considera la fuerza debido a la tensión superficial, como una fuerza continua de campo y con efecto tridimensional, a través de la interfase, en lugar de una condición de borde superficial.

Considerando al líquido como fase primaria, la fuerza de tensión superficial es expresada, mediante el modelo CSF, como:

donde:

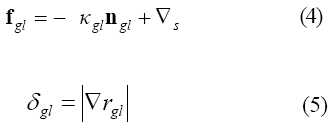
El vector normal n_gl apunta de la fase primaria a la secundaria, y la curvatura de la interfase es definida como:

El primer término del lado derecho de la ecuación (4), representa la componente normal de la fuerza de tensión superficial, la cual es originada por el efecto de la curvatura de la interfase. El segundo término del lado derecho representa la componente tangencial de la fuerza de tensión superficial, originada por la variación del coeficiente de tensión superficial, conocida como efecto Marangoni.

El término δ_gl es llamado función delta interfacial, anulándose lejos de la interfase, y asegurando que la fuerza de tensión superficial actúe sólo cerca de ésta (ANSYS^® CFX-Solver™, 2005), por lo que este término sólo se hace presente en la interfase.

En este trabajo se considera constante la tensión superficial entre fases, por lo que el efecto Marangoni no se presenta y la fuerza de tensión superficial toma la forma:

Ya que la presión se considera como fuerza normal por unidad de área, la expresión anterior es la ecuación de Young- Laplace.

El término M_j de la ecuación (1), describe las fuerzas interfaciales actuantes sobre una de las fases debido a la otra. El modelo de superficie libre, empleado en este trabajo y aplicable si ambas fases son continuas, considera sólo el efecto de la fuerza de arrastre en la transferencia de momentum interfacial, el cual se expresa como:

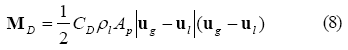
donde:

C_D es el coeficiente de arrastre y A_p es el área proyectada por el cuerpo en la dirección perpendicular al flujo.

Este término sólo se hace presente en la interfase. El modelo de superficie libre requiere conocer el coeficiente de arrastre mantenido sobre la burbuja, el cual es fuertemente dependiente de la forma de ésta. Kamaranev & Nikolov (1992) determinaron que una esfera liviana, ascendiendo por flotación, presenta un valor medio de = 0.95 C_D , sin embargo, para el caso de una burbuja de Taylor, es de esperarse un coeficiente de arrastre mucho menor, por tratarse de un cuerpo más esbelto que una esfera. En este trabajo se consideró a la burbuja de Taylor de forma elipsoidal, obteniéndose un valor aproximado para el coeficiente de arrastre, dependiente de la relación entre la longitud y el eje perpendicular a la dirección del flujo (L/d ), y del régimen del flujo (White, 2004). Taha & Cui (2006) reportaron que una burbuja de aire, ascendiendo en líquido estancado ( ρ_l = 971 kg/m³ , µ_l = 0.971 Pa.s y σ_gl = 0.0222 N/m) dentro de un conducto de sección cuadrada de 2 mm de diámetro hidráulico, presenta una relación entre 3.6 y 5.7 para 0.001 < Ca < 1.35. Considerando que el coeficiente de arrastre para un elipsoide sumergido en flujo laminar no varía significativamente para valores de entre 2 (C_D = 0.27) y 8 (C_D = 0.20), se empleó el valor de C_D = 0.25 (L/d= 4) para todos los experimentos numéricos realizados.

La ecuación de conservación de masa se expresa matemáticamente como:

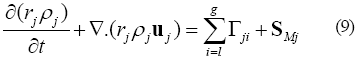
El término representa la transferencia de masa entre las fases. Este término puede despreciarse de la ecuación (9) bajo el mismo planteamiento hecho en la ecuación de conservación de momentum. El término representa fuentes de masa. La fase líquida y la fase gaseosa consideradas en este trabajo son sustancias no reaccionantes, por lo que este término es nulo. Al considerar ambas fases incomprensibles, la ecuación de conservación de masa o ecuación de continuidad se expresa como:

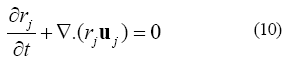
La ecuación (10) aplica en la interfase, ya que la fracción volumétrica de cada fase en esta región es variable. En cada fase, la fracción volumétrica es constante en el tiempo e igual a la unidad, por lo que la ecuación de conservación de masa en ambas fases se simplifica a:

El sistema planteado para cada fase, conformado por la ecuación (1) y la ecuación (11), es suficiente para resolver el comportamiento fluidodinámico en ambas fases. Al sistema planteado para la interfase (ecuación (1) y ecuación (10)) se agrega la condición de conservación de fracción volumétrica en la interfase (ecuación (12)), y la consideración de campo de presión compartido en la interfase, a fin de poder resolver la distribución de fracción volumétrica de cada fase en esta región:

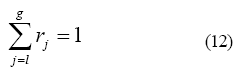
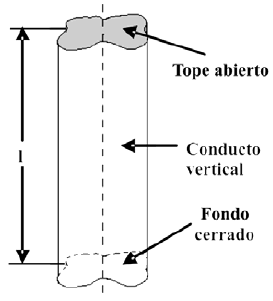
La figura 1 muestra, de manera general, el dominio de solución del modelo matemático anteriormente planteado, compuesto por un conducto vertical de sección transversal no circular, cerrado en el fondo y abierto en el tope.

Figura 1. Dominio de solución del modelo matemático planteado.

Para este dominio de solución, las condiciones de borde están dadas por:

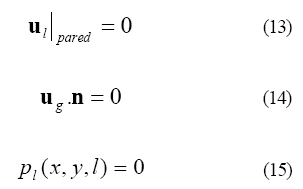
La ecuación (13) representa la condición de flujo sin deslizamiento entre la fase líquida y la superficie del conducto. La ecuación (14) significa que no existe flujo de fase gaseosa hacia la fase líquida a través de la interfase, estableciendo la condición de flujo con superficie libre. La ecuación (15) representa la condición de tope abierto en el conducto, por lo que la presión absoluta en el líquido es la atmosférica, resultando en una presión relativa igual a cero.

Considerando que ambas fases parten del reposo, las condiciones cinemáticas iniciales vienen dadas por:

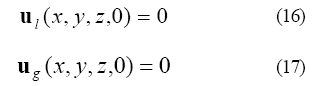
Las condiciones iniciales para la fracción volumétrica de ambas fases, se expresan como:

La ecuación (18) representa una forma inicial prescrita para la fase gaseosa, mientras que la ecuación (19) representa la condición de conservación de la fracción volumétrica. La forma inicial de la burbuja en todos los casos estudiados, correspondió a un esferoide vertical, a fin de iniciar con una forma tendiente a la forma final de la burbuja y así disminuir el tiempo de cómputo para alcanzar la convergencia.

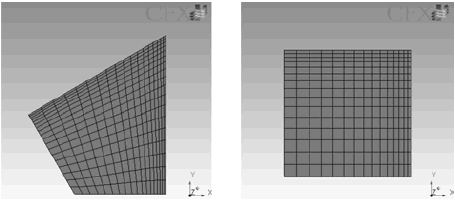
El modelo matemático planteado fue resuelto mediante el método de volúmenes finitos basados en elementos (EbFVM) (Maliska, 2004), implementado en el sofware ANSYS^® CFX™-10.0. El dominio de solución fue un conducto vertical de 30 mm de longitud y sección transversal cuadrada y triangular equilátera de 1.0 y 1.5 mm de diámetro hidráulico. La longitud del conducto empleada fue suficiente para que la burbuja alcanzase su velocidad terminal. La simetría geométrica y fluidodinámica del fenómeno permitió emplear como dominio de solución una cuarta parte de la sección cuadrada, y una tercera parte de la sección triangular, a fin de economizar tiempo de cómputo. Para todos los experimentos numéricos la malla empleada fue estructurada y de elementos hexaédricos, presentando mayor densidad de elementos hacia las paredes del conducto puesto que en esa zona se previó marcados gradientes de propiedades. En la figura 2 se muestran mallas típicas empleadas en las simulaciones.

Figura 2. Vista en planta del dominio discretizado (malla). a) cuarta parte de la sección cuadrada, b) tercera parte de la sección triangular.

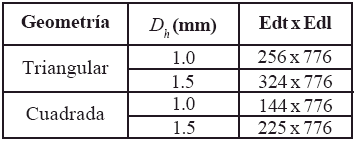
El número de elementos en cada malla es presentado, para cada caso estudiado, en la tabla 1. La independencia de los resultados respecto a la malla se aseguró al realizar simulaciones variando en 1.5 y 2.0 el número de elementos en la dirección longitudinal, y en 1.5 en la dirección transversal, obteniéndose resultados muy similares.

Tabla 1. Número de elementos de las mallas empleadas en cada caso de estudio.

Los términos advectivos presentes en las ecuaciones de conservación fueron interpolados mediante el esquema de alta resolución (HRS), una variante del esquema corriente arriba (US) que disminuye la tendencia de éste último a ser propenso a la difusión numérica. Los términos temporales fueron discretizados a partir del esquema regresivo de Euler de segundo orden (SOBES). Las simulaciones temporales avanzaron en el tiempo con un paso constante de 5x10^-4s y el tiempo total de simulación varió entre 0.5 y 0.7 s. Las simulaciones se realizaron mediante procesamiento paralelo, empleando dos nodos homogéneos, cada uno con dos procesadores de 64 bits AMD^® Opteron^® de 2 GHz, 12 GB de memoria RAM y velocidad de conexión entre nodos de 2Gb/ s, con sistema operativo Linux, distribución SuSE. Estas simulaciones tuvieron una duración aproximada de 120 horas cada una.

ANÁLISIS DE RESULTADOS

Las velocidades terminales de ascenso de la burbuja de Taylor en conductos de sección cuadrada y triangular, obtenidas en este estudio, son comparadas con los datos experimentales reportados por Bi & Zhao (2001) y con los obtenidos mediante simulaciones computacionales por Liao & Zhao (2003), considerando agua como la fase líquida y aire como la fase gaseosa, ambos a 25º C.

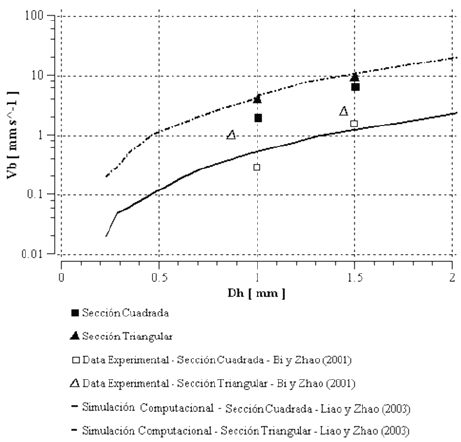
En la figura 3 se observa que, aunque las velocidades terminales obtenidas en este trabajo son mayores que las reportadas a partir de datos experimentales, éstas presentan una tendencia a aumentar con el diámetro hidráulico del conducto, al igual que la data reportada. También es consecuente con los datos experimentales el hecho de que la velocidad terminal de la burbuja es mayor en conductos de sección triangular que en conductos de sección cuadrada con igual diámetro hidráulico.

Figura 3. Velocidad terminal de la burbuja vs. diámetro hidráulico del conducto vertical.

De manera cualitativa, las velocidades de flujo en conductos triangulares y cuadrados obtenidas en este trabajo presentan comportamiento semejante al de la data experimental. La discrepancia entre los valores de las velocidades terminales calculadas y las experimentales reportadas, puede deberse al uso del modelo de superficie libre para considerar la transferencia de momentum a través de la interfase gas – líquido, en donde el coeficiente de arrastre sobre la burbuja debe ser conocido. En este estudio se consideró a la burbuja de Taylor de forma esferoidal, para la cual el coeficiente de arrastre es bajo incluso en régimen laminar; sin embargo, la burbuja tiende a tomar la forma de la sección transversal del conducto, originándose una suerte de aristas a lo largo de la burbuja, lo que aumenta la resistencia al flujo e incrementa el coeficiente de arrastre, resultando en una velocidad terminal menor. Por esta razón era de esperar que la velocidad terminal calculada a partir de este modelo fuera superior a la experimental, para todos los casos estudiados.

Por otro lado, la figura 3 muestra que el modelo tridimensional empleado en este trabajo concuerda con el modelo unidimensional de Liao & Zhao (2003) en el caso de conductos de sección triangular, siendo el primero ligeramente mejor en la determinación de la velocidad terminal; sin embargo existe una notable diferencia entre ambos modelos en el caso de conductos de sección cuadrada.

La influencia del tamaño del conducto se observa al notar el aumento de la velocidad terminal con el diámetro hidráulico, comportamiento independiente de la geometría estudiada. Este hecho se explica a partir del número de Eötvös, parámetro adimensional que muestra la relación entre fuerzas de empuje y fuerzas de tensión superficial, actuantes sobre la burbuja. Al aumentar el tamaño de la sección del conducto, la fuerza de empuje aumenta en mayor medida que la fuerza de tensión superficial, lográndose una velocidad terminal mayor. Por el contrario, si el diámetro hidráulico disminuye, la fuerza de tensión superficial actúa significativamente en contraposición a la fuerza de empuje, reduciendo así la velocidad terminal de la burbuja. En este trabajo se cumple que:

Eö=0.136 para conductos de  D_h =1.0mm, y

Eö=0.306 para conductos de =1.5 mm, corroborando el razonamiento anterior.

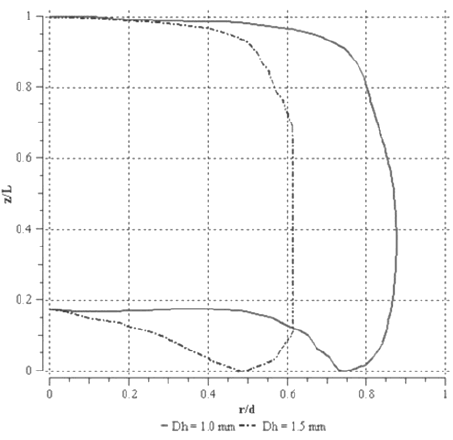
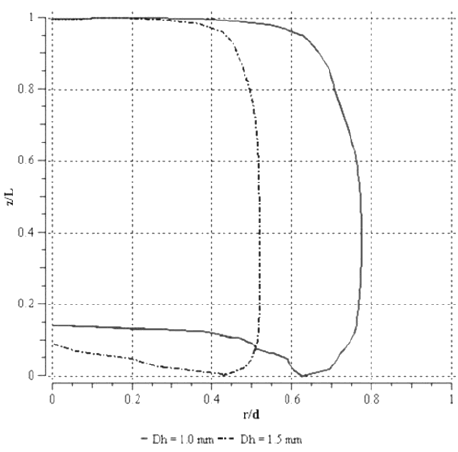
Las figuras 4 y 5 presentan el perfil adimensional de la burbuja, en un plano longitudinal al conducto y diagonal a la sección transversal, para cada caso estudiado. En todos los casos la burbuja presentó, de manera general, una nariz redondeada y una cola con cierta concavidad, sin embargo las características de ambos meniscos depende de la velocidad terminal de la burbuja. Se observó que a menor velocidad terminal de la burbuja, ésta presenta una nariz y una cola más chata. Al aumentar la velocidad terminal de la burbuja, la nariz se alarga y la concavidad en la cola se hace más pronunciada. Este comportamiento se explica a partir del número de capilaridad, el cual muestra la relación entre fuerzas viscosas y fuerzas de tensión superficial actuantes sobre la burbuja. Una velocidad terminal menor implica un número de capilaridad más bajo, es decir las fuerzas viscosas sobre la interfase de la burbuja disminuyen, resultando en meniscos más chatos. El número de capilaridad para los casos estudiados se muestra en la tabla 2.

Figura 4. Perfil adimensional de la burbuja en un plano longitudinal del conducto que pasa por la diagonal de la sección triangular.

Figura 5. Perfil adimensional de la burbuja en un plano longitudinal del conducto que pasa por la diagonal de la sección cuadrada.

Tabla 2. Número de Capilaridad para los casos estudiados.

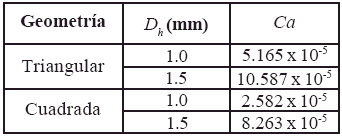
En las figuras 4 y 5 también se aprecia que las burbujas que ascienden en un conducto de diámetro hidráulico igual a 1.0 mm, ocupan mayor porción de la sección transversal que aquellas que ascienden en un conducto de 1.5 mm. Este resultado concuerda con la tendencia mostrada por la velocidad terminal en función del diámetro hidráulico, ya que la mayor velocidad se hace presente en conductos de mayor diámetro hidráulico, donde a mayor porción de la sección transversal ocupada por el líquido se traduce en una mayor tasa de flujo de líquido descendente, necesaria para mantener la continuidad del flujo y reponer el espacio dejado bajo la burbuja en su ascenso.

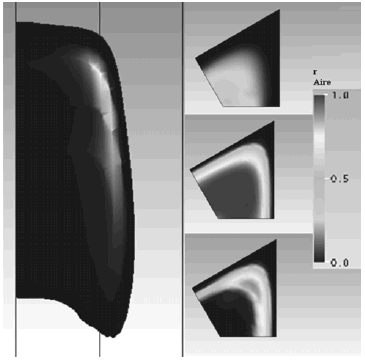
El estudio de la variación de la sección transversal de la burbuja muestra que existen tres zonas bien diferenciadas a lo largo de la burbuja, coincidentes con las descritas por Liao & Zhao (2003). Se puede observar que, transversalmente, la nariz tiende a ser más circular que el resto de la burbuja, correspondiendo a la zona de menisco superior; en la parte central de la burbuja, la película de líquido descendente alcanza su mínimo valor y se mantiene constante a lo largo de la longitud de la burbuja, lo que corresponde a la zona de película uniforme; finalmente se observa una región donde el espesor de película decrece y se hace visible la concavidad en el fondo de la burbuja, correspondiente a la zona de menisco inferior. Las figuras 6 y 7 muestran las zonas características para burbujas ascendiendo en conductos verticales de D_h =1.5 mm.

Figura 6. Interfase de una burbuja de Taylor ascendiendo en conductos de sección triangular de Dh=1.5 mm.

Figura 7. Interfase de una burbuja de Taylor ascendiendo en conductos de sección cuadrada de Dh=1.5 mm.

De la figura 8 a 11 se muestra el campo de velocidad del líquido alrededor de una burbuja para todos los casos estudiados, en el plano longitudinal del conducto que pasa por la diagonal de la sección transversal. En todas las figuras se observa el efecto de pistón que tiene la nariz de la burbuja sobre el líquido arriba de la misma. El líquido es empujado por la nariz de la burbuja y desplazado hacia el canal formado entre la burbuja y la pared del conducto. Este efecto de pistón se desvanece rápidamente, y la velocidad del líquido deja de verse afectada a una distancia de alrededor 0.1 veces la longitud de la burbuja, lo que representa cerca de 0.5 veces el diámetro hidráulico del conducto. Un comportamiento similar fue reportado por van Hount et al. (2002) a partir de estudios experimentales, pero en conductos circulares de diámetros más grandes.

Figura 8. Campo de velocidad del líquido en un plano longitudinal al conducto que pasa por la diagonal de la sección triangular de D_h=1.5 mm.

Figura 9. Campo de velocidad del líquido en un plano longitudinal al conducto que pasa por la diagonal de la sección triangular de D_h=1.0 mm.

Figura 10. Campo de velocidad del líquido en un plano longitudinal al conducto que pasa por la diagonal de la sección cuadrada de Dh=1.5 mm.

Figura 11. Campo de velocidad del líquido en un plano longitudinal al conducto que pasa por la diagonal de la sección cuadrada de Dh=1.0 mm.

La magnitud de la velocidad del líquido desplazado es relativamente baja en la zona más elevada de la nariz, prácticamente igual a la velocidad terminal de la burbuja; sin embargo, la magnitud de la velocidad aumenta a medida que el líquido entra a la zona de película, obedeciendo a una reducción en el área de flujo. El líquido descendente se acelera a medida que se adentra en la zona de película, hasta alcanzar una velocidad terminal. En ese momento el esfuerzo cortante en la pared se iguala con el peso del líquido en la película, ésta se equilibra y por consiguiente su espesor se hace constante, alcanzándose la zona de película uniforme.

La magnitud de la velocidad promedio del líquido a la salida de la zona de menisco inferior es alrededor de 5 y 9 veces la magnitud de la velocidad terminal de la burbuja, en conductos de sección cuadrada y de sección triangular, respectivamente, siendo ligeramente superior para conductos de 1.5 mm de diámetro hidráulico. Esta relación de velocidades es necesaria para que el líquido descendente pueda llenar el espacio dejado bajo sí por la burbuja en su ascenso, y mantener la continuidad en el flujo. Al ser dicha relación de velocidades elevada, el líquido sale de la zona de menisco inferior tomando un efecto jet, lo que ocasiona una zona de recirculación de apariencia toroidal, justo debajo de la burbuja, donde el líquido asciende e impacta contra la parte más baja de la cola de la burbuja, ocasionando la concavidad observada en las figuras, siendo ésta más acentuada en conductos de D_h =1.5 mm, por ser mayor la relación de velocidades.

CONCLUSIONES

El comportamiento fluidodinámico de una burbuja ascendiendo en un conducto vertical de sección cuadrada y triangular de diámetro hidráulico igual a 1.0 y 1.5 mm, fue simulado computacionalmente empleando un modelo tridimensional Euleriano-Euleriano, heterogéneo y de superficie libre, resuelto mediante el método de volúmenes finitos basados en elementos. De los resultados obtenidos se desprenden las siguientes conclusiones:

El modelo matemático empleado describe adecuadamente el comportamiento fluidodinámico del ascenso de burbujas de Taylor en mini conductos de sección transversal triangular y cuadrada.

El método de volúmenes finitos basado en elementos permite resolver el modelo matemático planteado, obteniéndose resultados con el grado de precisión deseado. Sin embargo la complejidad del fenómeno hace que se requiera un tiempo de cómputo elevado.

El comportamiento de la velocidad terminal de la burbuja, obtenido en este trabajo, concuerda cualitativamente con el observado experimentalmente, sobreestimándolo de manera cuantitativa.

A medida que se incrementa el diámetro hidráulico del conducto, los meniscos de la burbuja se tornan chatos y el espesor de película uniforme disminuye. En contraposición, si el diámetro hidráulico disminuye, la nariz se alarga y la cola adopta cierta concavidad. Este comportamiento es independiente de la geometría de la sección transversal del conducto.

El campo de velocidad de líquido alrededor de la burbuja presenta un comportamiento similar en todas las geometrías, caracterizado por la presencia de una zona de recirculación a la salida de la zona de menisco inferior.

AGRADECIMIENTOS

Los autores quieren expresar su agradecimiento al Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuela (UCV) por el financiamiento de los proyectos 08.15.5506.2004 y 08.15.5508.2004. Así mismo, quieren agradecer al Instituto de Mecánica de Fluidos de la Facultad de Ingeniería de la UCV, en la persona del Prof. Iván Saavedra, su director, por permitir el uso del cluster en el que se realizaron las simulaciones, y del Ing. Alejandro Alvarado por la asistencia técnica brindada en el uso del cluster. Finalmente, agradecen al M.Sc. Daniel Riveiro de la empresa brasileña ESSS, proveedora del software ANSYS^® CFX™ para Suramérica, por su esmerada asistencia técnica.

NOMENCLATURA

A_p : área proyectada

Ca : número de capilaridad

C_D : coeficiente de arrastre

d : mitad de la longitud de la diagonal de conductos no circulares

D_h : diámetro hidráulico

Edl: número de elementos en la dirección longitudinal

Edt: número de elementos en la dirección transversal

Eö: número de Eötvös

Fr : número de Froude

g : aceleración de gravedad

l: longitud del conducto

L : longitud de la burbuja

m: flujo másico de líquido

M: fuerzas interfaciales

n: vector normal a la interfase

p: presión

r: radio máximo de la burbuja; fracción volumétrica

S: término fuente

t: tiempo

u: vector velocidad

V_b: velocidad de flujo de la burbuja

Símbolos griegos:

d: función delta interfacial

G: coeficiente de difusión de la ecuación general de conservación

κ: curvatura de la interfase

µ: viscosidad dinámica

ρ: densidad

s: coeficiente de tensión superficial

Subíndices:

g: denota la fase gaseosa

j: fase

l: denota la fase líquida

REFERENCIAS

1. ANSYS® CFX-SOLVER (2005). Release 10.0: Modeling. p 486.        [ Links ]

2. BI, Q. C. & ZHAO, T. S. (2001). Taylor bubbles in miniaturized circular and noncircular channels. International Journal of Multiphase Flow, (27); pp. 561-570.        [ Links ]

3. BRACKBILL, J. U., KOTHE, D. B., ZEMACH, C. (1992). A continuum method for modeling surface tension. Journal of Computational Physics, (100); pp. 335-354.        [ Links ]

4. DAVIES, R. M. & TAYLOR, G. I. (1950). The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Proc. R. Soc. Londres, (200); pp. 375- 390.        [ Links ]

5. DUMITRESCU, D. T. (1943). Strömung an einer luftblase im senkrechten rohr. Z. Angew. Mathematical Mechanics, (23); pp. 139-149.        [ Links ]

6. HOUNT, VAN R., GULITSKI, A., BARNEA, L., SHEMER, L. (2001). Experimental investigation of the velocity field induced by a Taylor bubble rising in stagnant water. International Journal of Multiphase Flow, (28); pp. 579- 596.        [ Links ]

7. KAMARANEV, D.G. & NIKOLOV, L.N. (1992). Freely rising spheres do not obey Newton’s law for free settling. AIChE Journal, (38), núm 1; pp.1843-1846.        [ Links ]

8. LIAO, Q. & ZHAO, T. S. (2003). Modeling of Taylor bubble rising in a vertical mini noncircular channel filled with a stagnant liquid. International Journal of Multiphase Flow, (29); pp. 411-434.        [ Links ]

9. MALISKA, C. (2004). Transferencia de calor e mecánica dos fluidos computacional. Livros Técnicos e Cientificos Editora, Florianópolis. p 453.        [ Links ]

10. POLONSKY, S., BARNEA, D., SHEMER, L. (1999). Averaged and time-dependent characteristics of the motion of an elongated bubble in a vertical pipe. International Journal of Multiphase Flow, (25), pp 795-812.        [ Links ]

11. RANSOHOFF, T. C. & RADKE, C. M. (1988). Laminar flow of a wetting liquid along the corners of a predominantly gas-occupied noncircular pore. Journal of Colloid and Interface Science, (121); 392-401.        [ Links ]

12. RATULOWSKI, J. & CHANG, H. C. (1989). Transport of gas bubble in capillaries. Physics of Fluids, A 1, pp. 1642- 1655.        [ Links ]

13. TAHA, T & CUI, Z. F. (2006). CFD modelling of slug flow inside square capillaries. Chemical Engineering Science, (61); pp. 665-675.        [ Links ]

14. TOMIYAMA, A., NAKAHARA, Y., ADACHI, Y., HOSOKAWA, S. (2003). Shapes and rising velocity of singles bubbles rising through an inner subchannel. Journal of Nuclear Science and Technology. Vol 40. N 3, pp. 136-142.        [ Links ]

15. TUNG, K. W. & PARLANGE, J. Y. (1976). Note on the motion of long bubbles in closed tube influence of Surface Tension. Acta Mechanica, (24); pp. 313-317.        [ Links ]

16. VANDU, C. O., LIU, H., KRISHNA, R. (2005). Mass transfer from Taylor bubbles rising in single capillaries. Chemical Enginnering Science, (60); pp. 6430-6437.        [ Links ]

17. VIANA, F., PARDO, R., YÁNEZ, R., TRALLERO, J., JOSEPH, D. (2003). Universal correlation for the rise velocity of long gas bubbles in round pipes. Journal of Fluid Mechanic (494); pp. 379-398.        [ Links ]

18. WHITE, F. (2002). Mecánica de fluidos. Mc. Graw Hill, Madrid. p 833.         [ Links ] l