Estudio numerico del ascenso de burbujas de taylor en mini-conductos verticales de seccion no-circular: Parte II

Miguel Baritto Y Julio Segura

Universidad Central de Venezuela, Facultad de Ingenieria, Escuela de Ingenieria Mecanica. e-mail: miguelbaritto@gmail.com  / e-mail: jsegura@reacciun.ve 

RESUMEN

Este trabajo presenta un estudio numerico del ascenso de burbujas de Taylor en mini-conductos verticales de seccion transversal en forma de astroide y pseudoastroide, para flujo bifasico segregado aire-agua. Se resolvio el modelo matematico planteado en la primera parte de este trabajo, donde se demostro que los resultados obtenidos son comparables con los datos experimentales publicados en la literatura. El metodo numerico empleado para resolver el modelo fue el metodo de volumenes finitos basados en elementos (EbFVM), implementado en el software ANSYSR CFX.-10.0. Se encontro que la velocidad de flujo de la burbuja presenta la misma tendencia de aumentar con el diametro hidraulico del conducto, observada en la primera parte de este trabajo, siendo mayor en conductos de seccion pseudoastroidal. La forma de la burbuja es reportada, encontrandose meniscos mas planos en aquellas con menor velocidad de flujo; al igual que la distribucion del esfuerzo cortante en la direccion diagonal al conducto, y a lo largo de su longitud, donde se encontro que la distancia relativa a la longitud de la burbuja, corriente arriba y corriente debajo de la misma, a la cual el liquido no se ve afectado por el ascenso de la burbuja, es independiente de la forma de la seccion transversal del conducto.

Palabras clave: Burbujas de Taylor, Velocidad de flujo, Mini-conductos, Astroide, Pseudoastroide, Flujo bifasico, Dinamica de fluidos computacional (CFD), Metodo de volumenes finitos basado en elementos (EbFVM).

Numerical study of taylor bubble rising in a vertical noncircular mini channel: Part II

ABSTRACT

The mathematical model presented in first part of this study was solved for vertical mini channels with astroidal and pseudoastroidal cross-sections, in order to describe behavior of Taylor bubbles rising into these geometries. The model was solved once again by the elements based finite volumen method (EbFVM), implemented in code ANSYSR CFX.-10.0. The drift velocity trend was found to increase with the hydraulic diameter of channel, as in first part of this study. Drift velocities in pseudoastroidal geometries are higer than those in astroidal geometries. Interfacial profiles of bubbles revealed that top and bottom meniscus becomes flatter with a decrease in the channel size. How the shear stress in the diagonal direcction depends on the cross-section shape was also examined.

Keywords: Taylor bubbles, Drift velocity, Mini channels, Astroidal, Pseudoastroidal, Two-phase flow, Computational fluids dynamic (CFD), Elements based finite volumen method (EbFVM).

Recibido: junio de 2007 Revisado: abril de 2008

INTRODUCCION

El estudio de burbujas de Taylor ascendiendo en conductos verticales de seccion no circular, responde a la necesidad de conocer en detalle el patron de flujo bifasico denominado flujo tapon, en aplicaciones cada vez de menor tamano, donde se imposibilita el ascenso de este tipo de burbujas en conductos de seccion circular, como lo demostraron experimentalmente Bi & Zhao (2001). Estas aplicaciones, que van desde refrigeracion de componentes electronicos hasta estudio de flujo de crudo en yacimientos (Ratulowski & Chang. 1989), demandan conductos de diametros 38 hidraulicos en el orden de los milimetros, pudiendose catalogar como mini conductos. Quiza por la simplicidad de las geometrias, el estudio del ascenso de burbujas de Taylor en mini conductos verticales de seccion cuadrada y triangular ha marcado el inicio de la investigacion de este fenomeno, considerando dimensiones tan pequenas. Para secciones triangulares y cuadradas se cuentan con estudios experimentales (Bi & Zhao, 2001) y estudios numericos (Liao & Zhao 2003; Taha & Cui 2006) que demuestran que, aun cuando la velocidad terminal de la burbuja sigue la misma tendencia de aumentar con el diametro hidraulico mostrada en conductos de seccion circular, existe una importante diferencia entre las secciones no circulares y la circular, en cuanto a la forma de la burbuja se refiere, tanto en la forma de la seccion transversal de la burbuja, como en la curvatura de su menisco. La seccion transversal de la burbuja, en la zona de pelicula uniforme, deja de ser circular y tiende a adoptar la forma de la seccion transversal del conducto, mientras que la curvatura del menisco tiende a ser menos redondeada que su contraparte encontrada en conductos de seccion circular, debido a que el efecto de la tension superficial supera al de las fuerzas viscosas, como lo demuestran los bajos numeros de capilaridad que caracterizan a este fenomeno. Se han hecho esfuerzos para extrapolar estos resultados a casos de seccion transversal de forma arbitraria. Clanet et al.(2004) correlacionaron datos experimentales obtenidos para secciones triangulares, cuadradas, rectangulares, circulares y anulares, y determinaron una expresion para la velocidad terminal de la burbuja a bajos numeros de Reynolds, proporcional al area de la seccion transversal e inversamente proporcional a la viscosidad cinematica del liquido. Sin embargo esta expresion fue desarrollada para conductos de grandes diametros hidraulicos y falla en la prediccion para mini conductos por no considerar el efecto de la tension superficial. En este trabajo se realizo un estudio numerico del comportamiento fluidodinamico de burbujas de Taylor ascendiendo en mini conductos verticales de seccion transversal en forma de astroide y pseudoastroide, motivado por la escasa informacion disponible para estos casos, aun cuando estas geometrias han despertado interes en estudios de conveccion de calor (Soto et al. 2005; Maliska, 2004).

Modelo Matematico

Se resolvio un modelo tridimensional Euleriano-Euleriano y heterogeneo para flujo bifasico con superficie libre, considerandose ambos fluidos como incompresibles y al fenomeno en regimen transitorio. El sistema de ecuaciones resuelto para cada fase consistio en las ecuaciones de conservacion de masa y de momentum, ambas descritas a continuacion:

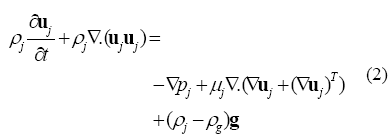
El sistema anterior describe el comportamiento fluidodinamico de cada fase por separado, y aplica en aquellos elementos ocupados por completo por la fase en cuestion, es decir donde la fraccion volumetrica de esa fase sea igual a la unidad. En los elementos donde se hace presente la interfase gas-liquido se cumple que 0 < r_j < 1, y la ubicacion de la misma se determina a partir de la distribucion de r . Las ecuaciones que rigen al fenomeno a nivel de la interfase son las ecuaciones de conservacion de masa y de momentum para cada fase, sujetas a la condicion de que en estos elementos la sumatoria de la fraccion volumetrica de las fases debe ser igual a 1:

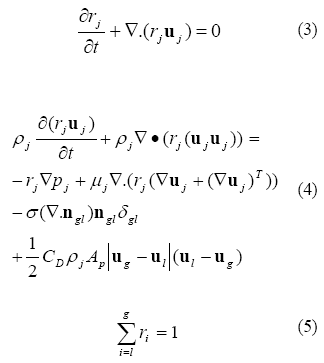
El segundo termino del lado derecho de la ecuacion (4) representa la transferencia de momentum interfacial por efecto de la fuerza de tension superficial (Brackbill et al. 1992), mientras que el ultimo termino incluye la transferencia de momentum debido al arrastre de una fase sobre la otra. El coeficiente de arrastre se fijo en 0.25 para todas las simulaciones, valor tipico para un cuerpo con forma elipsoidal en flujo laminar (White, 2004). Para determinar el campo de presion en la interfase se considero que este es compartido por ambas fases ( p_j = p ). Esta condicion se cumple si la interfase es plana, suposicion que no introduce error significativo si los elementos son suficientemente pequenos como para que el efecto del radio de curvatura de la interfase, en cada elemento, sea despreciable. El modelo planteado se resolvio sujeto a las siguientes condiciones de borde:

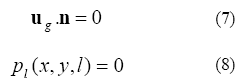
La ecuacion (6) representa la condicion de flujo sin deslizamiento entre la fase liquida y la superficie de la pared del conducto. La ecuacion (7) significa que no existe flujo de la fase gaseosa a traves de la interfase, estableciendo la condicion de flujo con superficie libre. La ecuacion (8) representa la condicion de conducto con tope abierto, por lo que la presion absoluta es igual a la presion de referencia, resultando en una presion relativa igual a cero.

Experimentos Numericos

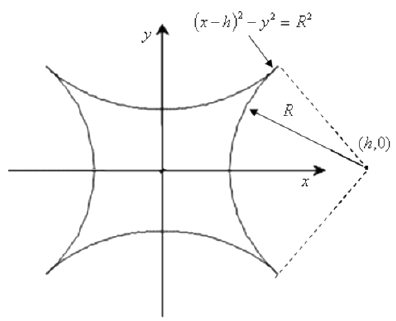
El modelo matematico planteado se aplico a burbujas ascendiendo en conductos verticales de seccion transversal con forma de astroide y pseudoastroide de 1.0 y 1.5 mm de diametro hidraulico. Las curvas generatrices del pseudoastroide se muestran en la figura 1. La longitud de los conductos fue de 30 mm, resultando suficiente para que la burbuja alcanzase su velocidad terminal. La fase liquida fue agua, mientras que la fase gaseosa fue aire, ambos a 25° C.

Figura 1. Pseudoastroide.

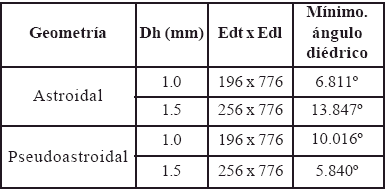
El modelo se resolvio mediante el metodo de volumenes finitos basados en elementos (EbFVM) (Maliska, 2004), implementado en el software CFX-10.0. Todas las mallas empleadas en los experimentos numericos fueron estructuradas y de elementos hexaedricos, presentando mayor densidad de elementos hacia las paredes del conducto por esperarse marcados gradientes de velocidad de liquido y de fraccion volumetrica en esa zona. La simetria geometrica y fluidodinamica del fenomeno permitio emplear solo una cuarta parte de la seccion transversal del conducto como dominio de solucion, a fin de reducir tiempo de computo. Los elementos ubicados hacia las esquinas del conducto, para ambas geometrias estudiadas, fueron manipulados con la finalidad de obtener angulos diedricos lo suficientemente grandes como para evitar problemas de convergencia del metodo, pero lo suficientemente pequenos para describir adecuadamente el fenomeno. El minimo angulo diedrico, asi como tambien el tamano de la malla para todos los casos estudiados, se presentan en la tabla 1.

Tabla 1. Caracteristicas de las mallas empleadas en cada caso de estudio.

Las simulaciones se realizaron en regimen transitorio, avanzando en el tiempo con un paso constante de 5x10-4 s, para un tiempo total de fenomeno simulado que vario entre 0.5 y 0.7 s. Tanto el aire como el agua se consideraron en reposo en el instante inicial. La forma inicial de la burbuja fue un esferoide, forma proxima a la esperada. Emplear otra forma como la inicial para la burbuja genera el mismo resultado pero incrementa el tiempo de computo para alcanzar la convergencia en los primeros pasos de tiempo, originando un mayor tiempo total de computo. Los terminos advectivos presentes en las ecuaciones de conservacion fueron interpolados mediante el esquema de alta resolucion (HRS), una variante del esquema corriente arriba (US) que disminuye la difusion numerica. Los terminos temporales fueron discretizados a partir del esquema regresivo de Euler de segundo orden (SOBES). Las simulaciones se realizaron en un cluster IBM, mediante procesamiento paralelo, empleando dos nodos homogeneos, cada uno con dos procesadores de 64 bits AMD^® Opteron^® de 2 GHz, 12 GB de memoria RAM y velocidad de conexion entre nodos de 2Gb/ s, con sistema operativo Linux, distribucion SuSE. Estas simulaciones tuvieron una duracion aproximada de 120 horas cada una.

Analisis de Resultados

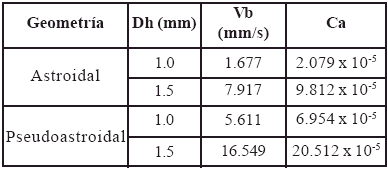
La tabla 2 muestra la velocidad terminal de burbujas ascendiendo en conductos verticales de seccion transversal Geometria Dh (mm) Edt x Edl Minimo. angulo diedrico Astroidal Pseudoastroidal 1.0 1.5 1.0 1.5 196 x 776 256 x 776 196 x 776 256 x 776 6.811o 13.847o 10.016o 5.840o 40 con forma de astroide y pseudoastroide, y su correspondiente numero de capilaridad. Se observa que para ambas geometrias, la velocidad terminal aumenta con el diametro hidraulico del conducto, comportamiento tambien observado, en datos experimentales, en otras geometrias (Bi & Zhao, 2001). Esta tendencia se visualizo en conductos de seccion cuadrada y triangular de igual diametro hidraulico a los aqui estudiados, resolviendo el mismo modelo y aplicando el mismo metodo numerico en la primera parte de este trabajo (Baritto & Segura, 2007), por lo que desde el punto de vista cualitativo el modelo se aplica a las geometrias consideradas en este trabajo. La velocidad terminal resulto mayor en conductos de seccion pseudoastroidal debido a que para esta geometria el efecto de la tension superficial, como fuerza que se opone al movimiento de la burbuja, es menor que para secciones astroidales, como se evidencia en el numero de capilaridad. Un numero de capilaridad elevado significa que la fuerza inercial supera a la tension superficial, disminuyendo el efecto de esta ultima sobre el ascenso de la burbuja. Un menor radio de curvatura de la interfase en una seccion transversal de la burbuja genera una mayor diferencia de presion entre la nariz de la burbuja y la seccion transversal en cuestion. Esta diferencia de presion asiste a la accion de la aceleracion de gravedad en el flujo de la pelicula de liquido descendente, lo que aunado a una mayor area de flujo, resulta en un mayor flujo masico de liquido descendente y una mayor velocidad terminal de la burbuja, como ocurre en conductos de seccion pseudoastroidal.

Tabla 2. Velocidad terminal y numero de capilaridad para todos los casos estudiados.

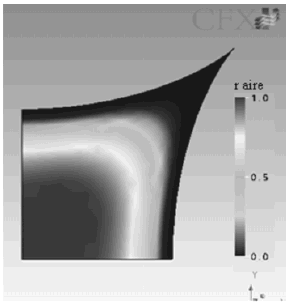
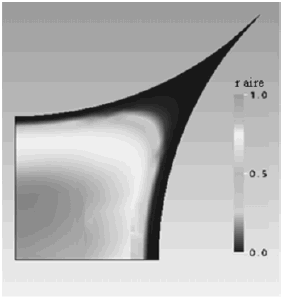
En las figuras 2 y 3 se muestra la mayor seccion transversal de burbujas ascendiendo en conductos de seccion astroidal y pseudoastroidal, respectivamente. Se observa que debido a que un pseudoastroide posee esquinas mucho mas alargadas que un astroide, la seccion transversal de la burbuja se torna tambien alargada hacia esa zona, disminuyendo el radio de curvatura de la interfase.

Figura 2. Maxima seccion transversal de una burbuja ascendiendo en conductos de seccion astroidal de Dh=1.0 mm.

Figura 3. Maxima seccion transversal de una burbuja ascendiendo en conductos de seccion pseudoastroidal de Dh=1.0 mm.

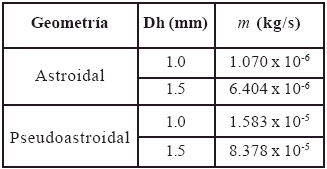
Ademas, debido a la misma caracteristica geometrica, una seccion pseudoastroidal requiere mayor area transversal para tener el mismo diametro hidraulico que una seccion astroidal, lo que resulta en mayor flujo masico de liquido descendente, como se muestra en las tablas 3 y 4.

Tabla 3. Area de la seccion transversal del conducto y de area de flujo para todos los casos estudiados.

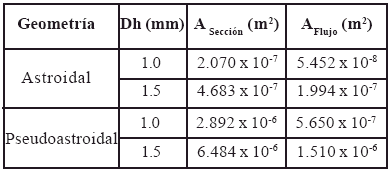
Tabla 4. Flujo masico de liquido descendente para todos los casos estudiados.

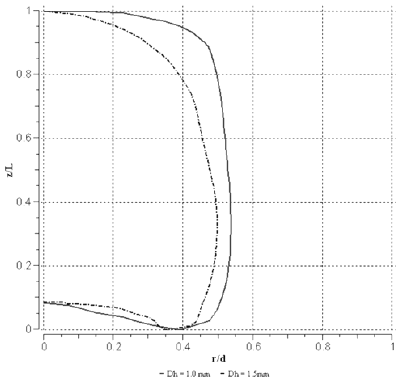
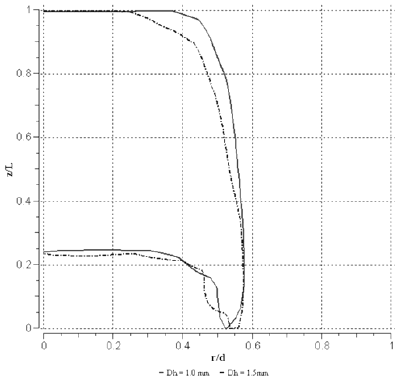
La figura 4 muestra el perfil adimensional de la burbuja, en un plano longitudinal del conducto que pasa por la diagonal de la seccion transversal, para conductos de seccion astroidal. Se observo que a menor velocidad de flujo de la burbuja, esta presenta una nariz mas chata. Al aumentar la velocidad terminal de la burbuja, la nariz se alarga como consecuencia de un mayor efecto de la fuerza viscosa sobre la forma de la interfase. Para esta geometria se tiene que la cola de la burbuja presenta cierta concavidad, acentuandose para una mayor velocidad terminal.

Figura 4. Perfil adimensional de la burbuja en un plano longitudinal del conducto que pasa por la diagonal de la seccion astroidal.

La figura 5 muestra que en conductos de seccion pseudoastroidal no existe diferencia apreciable en la forma de la cola de la burbuja en relacion a la velocidad terminal, debido a que en ambos casos estudiados las fuerzas viscosas superaron a la fuerza de tension superficial, responsable de dar a la cola de la burbuja la concavidad observada en conductos de seccion astroidal.

Figura 5. Perfil adimensional de la burbuja en un plano longitudinal del conducto que pasa por la diagonal de la seccion pseudoastroidal.

En la figura 6 se observa el desprendimiento de una estela de aire para el caso de burbujas ascendiendo en conductos de seccion pseudoastroidal de Dh = 1.5 mm. Este hecho se debe a la predominancia de las fuerzas viscosas sobre la fuerza de tension superficial, esta ultima responsable de mantener unida a la burbuja. Este resultado demuestra que el modelo empleado permite describir la ruptura de una burbuja y, aunque no precisa la distribucion de las burbujas resultantes, brinda un estimado del comportamiento global de las mismas.

Figura 6. Interfase de una burbuja de Taylor ascendiendo en conducto de seccion pseudoastroidal de Dh=1.5 mm.

En las figuras 4 y 5 tambien se aprecia que, independiente de la geometria del conducto, las burbujas que ascienden en un conducto de diametro hidraulico igual a 1.5 mm, ocupan menor porcion de la seccion transversal que aquellas que ascienden en un conducto de 1.0 mm, resultando en una mayor area de flujo y por consiguiente una tasa de flujo de liquido descendente mayor, necesaria para mantener la continuidad del flujo y reponer el espacio dejado bajo la burbuja en su ascenso.

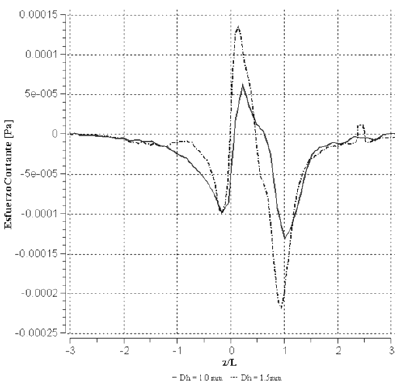
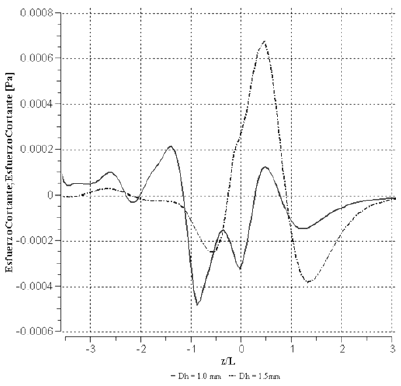
Las figuras 7 y 8 muestran la distribucion de esfuerzo cortante en la esquina del conducto en la direccion diagonal, para secciones astroidales y pseudoastroidales, respectivamente. Se observa que la magnitud del esfuerzo cortante es cero hasta una distancia de aproximadamente 2.5 y 3.5 veces la longitud de la burbuja por encima de la nariz de esta, independientemente del diametro hidraulico del conducto, para conductos de seccion astroidal y pseudoastroidal, respectivamente.

Figura 7. Esfuerzo cortante en la esquina del conducto en direccion diagonal para conductos de seccion astroidal.

Figura 8. Esfuerzo cortante en la esquina del conducto en direccion diagonal para conductos de seccion pseudoastroidal.

El esfuerzo cortante aumenta su magnitud producto del efecto piston que ejerce la burbuja sobre el liquido arriba de la nariz. A medida que el liquido es desplazado alrededor de la nariz de la burbuja, este experimenta el mayor esfuerzo cortante negativo, justo antes de entrar a la zona de pelicula, siendo esta magnitud mayor en conductos de Dh = 1.5 mm. El signo negativo del esfuerzo cortante significa flujo de liquido acercandose de la burbuja. El esfuerzo cortante tiende rapidamente a cero en la zona central de la burbuja, y cambia de signo debido a que el liquido es desplazado al aumentar la seccion transversal de la burbuja, alejandose de esta en la direccion diagonal. En la zona de menisco inferior, a la salida de la zona de pelicula, el esfuerzo cortante cambia de signo nuevamente, debido a que el liquido se acerca a la burbuja a fin de ocupar el vacio dejado por esta en su ascenso. En conductos de seccion astroidal, justo despues de la cola de la burbuja, la magnitud del esfuerzo se hace cero a medida que se aleja de la zona de recirculacion de liquido. En conductos de seccion pseudoastroidal se hacen presentes fluctuaciones del esfuerzo cortante corriente abajo de la burbuja, debido a la presencia de pequenas burbujas que se desprenden de la cola de la burbuja de Taylor, que afectan al campo de velocidad del liquido y por consiguiente al esfuerzo cortante en esa zona.

CONCLUSIONES

El comportamiento fluidodinamico de una burbuja ascendiendo en un conducto vertical de seccion astroidal y pseudoastroidal de diametro hidraulico igual a 1.0 y 1.5 mm, fue simulado numericamente empleando un modelo Euleriano-Euleriano, heterogeneo y de superficie libre, resuelto mediante el metodo de volumenes finitos basados en elementos. Para los casos estudiados se concluye que: La velocidad terminal de la burbuja se incrementa al aumentar el diametro hidraulico del conducto, independientemente de la geometria de la seccion transversal del mismo.

En conductos de seccion pseudoastroidal, la velocidad de flujo es mayor que en conductos de seccion astroidal, para todos los diametros hidraulicos estudiados.

En conductos de igual diametro hidraulico, el efecto de la tension superficial disminuye al aumentar el area transversal de los mismos, haciendose significativa la influencia de las fuerzas viscosas.

El maximo esfuerzo cortante en la esquina del conducto, en la direccion diagonal, aumenta al aumentar el diametro hidraulico del mismo.

La influencia del movimiento de la burbuja en el esfuerzo cortante en la esquina del conducto, desaparece a una distancia menor, en relacion a la longitud de la burbuja y a partir de la nariz de la misma, en conductos de seccion astroidal; siendo esta distancia independiente del diametro hidraulico del conducto.

Mediante un modelo Euleriano-Euleriano de superficie libre es posible estudiar el comportamiento global de grupos de pequenas burbujas, asi como tambien del rompimiento de grandes de ellas.

AGRADECIMIENTOS

Este trabajo fue financiado por el Consejo de Desarrollo Cientifico y Humanistico de la Universidad Central de Venezuela (UCV), a traves de los proyectos 08.15.5506.2004 y 08.15.5508.2004, apoyo que los autores agradecen. De igual forma, quieren agradecer al Instituto de Mecanica de Fluidos de la UCV, en particular a su director, Prof. Ivan Saavedra, por permitir el uso del cluster donde se realizaron las simulaciones, y al Ing. Alejandro Alvarado por su esmerada asistencia tecnica en el uso del cluster. Los agradecimientos se hacen extensivos al M.Sc. Daniel Riveiro de la empresa brasilena ESSS, proveedora del software ANSYS^® CFX^® para Suramerica, por sus valiosos consejos y asistencia tecnica.

NOMENCLATURA

A_p : area proyectada

Ca : numero de capilaridad

C_D : coeficiente de arrastre

d : mitad de la longitud de la diagonal de conductos no circulares

D_h : diametro hidraulico

Edl: numero de elementos en la direccion longitudinal

Edt: numero de elementos en la direccion transversal

Eo: numero de Eotvos

Fr : numero de Froude

g : aceleracion de gravedad

l : longitud del conducto

L : longitud de la burbuja

m: flujo masico de liquido

M: fuerzas interfaciales

n: vector normal a la interfase

p: presion

r: radio maximo de la burbuja; fraccion volumetrica

S: termino fuente

t: tiempo

u: vector velocidad

V_b: velocidad de flujo de la burbuja

Simbolos griegos:

δ: funcion delta interfacial

Γ: coeficiente de difusion de la ecuacion general de conservacion

κ: curvatura de la interfase

μ: viscosidad dinamica

ρ: densidad

σ: coeficiente de tension superficial

Subindices:

g: denota la fase gaseosa

j: fase

l: denota la fase liquida

REFERENCIAS

1. BARITTO, M. & SEGURA, J. (2007). Estudio numerico del ascenso de burbujas de Taylor en mini-conductos verticales de seccion no-circular: Parte I. Revista de la Facultad de Ingenieria de la UCV. Enviado para su arbitraje.        [ Links ]

2. BI, Q. C. & ZHAO, T. S. (2001). Taylor bubbles in miniaturized circular and noncircular channels. International Journal of Multiphase Flow, (27); pp. 561-570.        [ Links ]

3. BRACKBILL, J. U., KOTHE, D. B., ZEMACH, C. (1992). A continuum method for modeling surface tension. Journal of Computational Physics, (100); pp. 335-354.        [ Links ]

4. CLANET, C., HERAUD, P., SEARBY, G. (2004). On the motions of bubbles in vertical tubes of arbitrary cross-sections: some complements to the Dumitrescu-Taylor problem. Journal of Fluid Mechanics, (519); 359-376.        [ Links ]

5. KAMARANEV, D.G. & NIKOLOV, L.N. (1992). Freely rising spheres do not obey Newtonfs law for free settling. AIChE Journal, (38), num 1; pp.1843-1846.        [ Links ]

6. LIAO, Q. & ZHAO, T.S. (2003). Modeling of Taylor bubble rising in a vertical mini noncircular channel filled with a stagnant liquid. International Journal of Multiphase Flow, (29); pp. 411-434.        [ Links ]

7. MALISKA, C. (2004). Transferencia de calor e mecanica dos fluidos computacional. Livros Tecnicos e Cientificos Editora, Florianopolis. p 453.        [ Links ]

8. RATULOWSKI, J. AND CHANG, H. C. (1989). Transport of gas bubble in capillaries. Physics of Fluids, A 1, pp. 1642- 1655.        [ Links ]

9. SOTO, J., GARCIA, F., SEGURA, J. (2005). Estudio numerico del comportamiento termico y fluidodinamico de microtubos de calor multiranurados. Revista de la Facultad de Ingenieria de la UCV, (20); pp. 23-33.        [ Links ]

10. TAHA, T. & CUI, Z. F. (2006). CFD modelling of slug flow inside square capillaries. Chemical Engineering Science, (61); pp. 665-675.        [ Links ]

11. WHITE, F. (2002). Mecanica de fluidos. Mc. Graw Hill, Madrid. p 833.         [ Links ] 44