Análisis fluido-dinámico bidimensional de los gases que pasan a través de dos válvulas de control en la línea de cabecera del regenerador de una planta de desintegración catalítica.

MIGUEL PAIVA¹, ALFREDO RAMOS², TIBISAY ZAMBRANO¹, RODOLFO BERRÍOS¹

¹ Universidad Central de Venezuela, Facultad de Ingeniería, Escuela de Ingeniería Mecánica. Venezuela. e-mail: paivams@yahoo.com; coromotzambrano@gmail.com; rodolfoberrios@hotmail.com

² Petróleos de Venezuela. Intevep. Apdo. 76343. Caracas 1020 A. Venezuela. e-mail: ramosa@pdvsa.com

RESUMEN

El presente trabajo contempla el analisis fluido-dinamico bidimensional de los gases que pasan a traves de dos valvulas de control ubicadas en la linea de cabecera de la unidad de desintegracion catalitica tipica de una refineria de petroleo crudo. La linea presenta vibraciones de alta frecuencia, inducidas por el flujo turbulento. El fluido de trabajo es gas de combustion, compuesto en su mayoria por nitrogeno. El caudal es de aproximadamente 5,54 x 10⁶ m³/dia. El analisis se realizo resolviendo un sistema de ecuaciones no lineales, las cuales describen el comportamiento del flujo. Se utilizo el modelo de turbulencia RNG , mediante simulacion numerica por computadora. Se realizaron diferentes mallas, seleccionando finalmente una malla conformada por 15.957 nodos y 15.364 volumenes de control. Para modelar y resolver el sistema de ecuaciones planteado se utilizo el programa comercial FLUENT 6.0 de dinamica de fluidos computacional (CFD). Se estudio la distribucion de presion, la variacion de presion en el tiempo, el perfil de velocidad, las lineas de corriente y la formacion de vortices en la seccion de la tuberia en estudio.

Palabras clave: Turbulencia, CFD, FLUENT, Linea de Cabecera, RNG .

Bidimensional fluid dynamic analysis of gases that pass through two control valves in the head line of the regenerator in a fluid catalytic cracking plant.

ABSTRACT

In this work the bidimensional fluid dynamic analysis of gases that pass through two control valves located in the headline of a typical catalytic cracking plant in an oil refinery is simulated. The line presents high frequency vibrations induced by turbulent flow. The work fluid is combustion gas, composed in its majority by nitrogen (N2). The volume is approximately 5.54 × 10⁶ m³/day. The analysis was performed solving a non-linear system of equations, which describes the flow behavior. The model of turbulence RNG was used, by means of computer numerical simulation. Different meshes were evaluated; finally selecting a mesh made up by 15,957 nodes and 15,364 cells. In order to model and solve the system of equations, the commercial program FLUENT 6.0 of computational fluid dynamics (CFD) was used. The pressure distribution, pressure variation in time, velocity profile, streamlines and vortex shedding in the section of pipe in study were studied.

Keywords: Turbulence, CFD, FLUENT, Head Line, RNG .

Recibido: enero de 2008 Recibido en forma final revisado: mayo de 2008

INTRODUCCIÓN

En este trabajo de investigación se estudió el fenómeno que se origina en la línea de cabecera del regenerador de una planta de desintegración catalítica que procesa crudos medianos y pesados para producir gasolina y otros La línea de cabecera de la unidad de desintegración catalítica en estudio ha venido presentando problemas de vibraciones de alta frecuencia desde que inició sus operaciones, las cuales han ocasionado fracturas en zonas de alta concentración de esfuerzo.

 Debido a esta problemática, en el año 1999 se comenzó a realizar mediciones de vibraciones para caracterizar las amplitudes y las frecuencias de las vibraciones en varios puntos del tramo afectado por este efecto. Los resultados de estas mediciones arrojaron niveles altos de vibración en el tramo de tubería de 1,42 metros de diámetro, ubicado entre las válvulas reductoras de presión. Además, se concluyó que las altas vibraciones eran consecuencia del estrangulamiento del flujo y de la caída de presión en esas válvulas de control.

De manera simplificada, la función del reactor de la planta de desintegración catalítica es producir una serie de reacciones químicas en presencia de un catalizador para obtener diferentes hidrocarburos. La corriente de hidrocarburos pasa a la torre de fraccionamiento, en donde se separan los diferentes productos. Luego, el catalizador usado se transporta al regenerador, donde es reactivado y el residuo de la reacción (coque) es quemado. Finalmente, los gases que genera la combustión del residual son expulsados por medio de una línea que conduce a la chimenea. Esta tubería es llamada «línea de cabecera», la cual transporta los gases de combustión y sirve como sistema de control de presión en el regenerador. El control de presión es realizado mediante dos válvulas deslizantes, que estrangulan el flujo en el tramo comprendido entre la entrada de la primera válvula y la salida de la segunda válvula, produciendo un descenso de la presión hasta un valor ligeramente superior a la presión atmosférica.

Debido a las caídas de presión y a la obstrucción del flujo que se producen en las válvulas deslizantes, se inducen vibraciones de alta frecuencia en las paredes de la tubería de ese tramo del sistema. En algunas ocasiones, estos efectos dinámicos pueden generar grietas y desajustes. En este sentido, surgió la necesidad de evaluar el origen de dichas vibraciones, realizando un estudio sobre el comportamiento del flujo de fluido en la tubería.

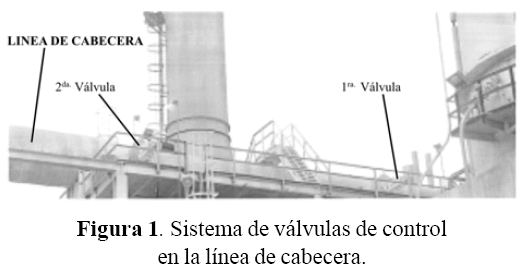
Las válvulas de control están colocadas en un tramo horizontal de tubería aguas abajo del regenerador y se encuentran separadas entre sí en aproximadamente once metros (11 m), tal como se muestra en la figura 1.

Las investigaciones realizadas por Catalano et al. (2003) relacionadas con simulaciones del comportamiento transitorio del flujo turbulento alrededor de un cilindro, establecieron comparaciones entre los modelos matematicos RANS y LES, permitiendoles obtener cambios de presion en pequenos intervalos de tiempo y capturar la presencia de vortices.

Un estudio importante, tomado como base para la elaboracion de este trabajo, fue el realizado por Iaccarino et al. (2002, 2003). Ellos analizaron el comportamiento transitorio del flujo debido a la separacion del flujo turbulento alrededor de un cubo, implementando la metodologia RANS y el codigo FLUENT para resolver los modelos de turbulencia, especificamente el modelo de turbulencia k-ε estandar.

Un modelo de turbulencia de dos-ecuaciones del tipo de k- ε fue derivado por Yakhot & Orszag (1986), para ello se basaron en metodos de renormalizacion de grupos (RNG). Posteriormente, se divulgo que con este modelo se obtienen predicciones substancialmente mejores que con el modelo k-ε estandar. Las evidentes mejoras obtenidas con el modelo de RNG k- fueron atribuidas al mejor tratamiento de los efectos de la turbulencia en la zona cercana a la pared (Speziale & Thangam, 1992).

El presente trabajo contempla el estudio fluido-dinamico del problema existente mediante el modelo matematico de turbulencia RNG k- para la simulacion y como herramienta de calculo se empleo el simulador comercial FLUENT, que permitio evaluar la presion, las lineas de corriente y los perfiles de velocidad que originan el problema de vibracion en el sistema.

PLANTEAMIENTO DEL PROBLEMA

El problema consistio en estudiar el comportamiento del flujo que pasa a traves de la linea de cabecera y los efectos que producen las valvulas deslizantes en el flujo, ya que ellas representan el elemento primario de control de presion en el proceso de regeneracion del catalizador. Sin embargo, las restricciones del flujo que producen las valvulas provocan separaciones bruscas del gas, estas a su vez generan vibraciones de alta frecuencia en la linea, lo que ha originado el desprendimiento de accesorios, la descalibracion de la instrumentacion, fugas por agrietamiento e inclusive fugas en las valvulas de la planta de desintegracion catalitica.

Estos problemas dieron origen a que se realizara esta investigacion para analizar el comportamiento del flujo a traves de la linea de cabecera, en especial cuando atraviesa las valvulas, como se puede observar en la figura 2.

Ecuaciones que gobiernan el flujo en dos dimensiones

La conservación de la masa, aplicada a una partícula de fluido infinitesimal, da lugar a la ecuación diferencial de continuidad, relacionando los campos de densidad y velocidad. Por otra parte, se tiene que la segunda ley de Newton da forma a ecuaciones diferenciales parciales conocidas como ecuaciones de Navier-Stokes, las cuales corresponden con las ecuaciones de conservación de la cantidad de movimiento, solamente para fluidos newtonianos.

Estas ecuaciones describen el comportamiento de los flujos bajo condiciones laminares y turbulentas y se expresan de la siguiente forma:

  (1)

  (2) 

A pesar de la antiguedad de las ecuaciones de Navier-Stokes, estas ecuaciones solo han podido ser resueltas en geometrias relativamente sencillas que permiten soluciones analiticas. En las ultimas decadas, mediante procesos iterativos con computadoras de alto rendimiento, tambien se han podido resolver las ecuaciones de Navier-Stokes usando las mismas geometrias sencillas. Actualmente, estos procesos son las unicas tecnicas que permiten generar soluciones mas aproximadas.

Modelos de turbulencia

El termino estocastico podria ser usado para referirse a la turbulencia. Existen varios modelos para la simulacion de flujos, ya sean turbulentos o laminares, solo en la simulacion de flujos turbulentos es donde se hace necesario estudiar varios modelos de turbulencia, ya que ellos ofrecen un amplio margen de aplicabilidad y son exitosos dependiendo del tipo de analisis que se requiera, de los objetivos que se deseen alcanzar y sobre todo de las condiciones de validacion.

El flujo turbulento, visto desde un punto de vista macroscopico, es un fenomeno en el cual las trayectorias de las particulas se entrelazan caoticamente. Las caracteristicas cinematicas y dinamicas de este flujo estan relacionadas con la magnitud del numero de Reynolds, puesto que si este es incrementado, excediendo un valor critico, el flujo pierde estabilidad y se caracteriza por la interaccion de remolinos de diferentes tamanos y por fluctuaciones rapidas al azar (Zambrano, 2000).

Las fluctuaciones del flujo turbulento pueden ocurrir a pequena escala y alta frecuencia, de manera que al introducirlas en las ecuaciones de momentum y realizar los promedios estadisticos temporales aparece un termino adicional: los esfuerzos de Reynolds. La introduccion de estos nuevos terminos hace que el sistema de ecuaciones no lineales establecido no quede cerrado, con lo que se requiere el desarrollo de modelos de turbulencia para poder cerrar el sistema de ecuaciones. Existe una variedad de metodos para resolver el sistema de ecuaciones, desde los modelos de cero-ecuaciones hasta las mas complejas ecuaciones de transporte de esfuerzos de Reynolds.

Entre los modelos de turbulencia mas populares, pueden citarse:

• Spalart-Allmaras Model .

• Standard k-ε Model .

• Renormalization-Group (RNG) k-ε  Model .

• Realizable k-ε  Model .

• Standard k-ω  Model (SST) .

• Reynolds Stress Model (RSM) .

• Large Eddy Simulation (LES) Model

La eleccion del modelo de turbulencia depende de las consideraciones que se realizan, las condiciones fisicas del fluido, la practica que se adquiere para la resolucion de un determinado tipo de problema, la capacidad de calculo computacional y el tiempo disponible para realizar la simulacion.

Modelo RNG k-ε

El modelo RNG k-ε esta basado en el modelo de turbulencia k-ε y es derivado directamente de las ecuaciones de Navier- Stokes, usando una tecnica matematica llamada metodo de grupo renormalizado (RNG). Este modelo incluye un termino adicional que mejora el analisis de flujos rapidamente forzados, el efecto de remolinos en la turbulencia y los flujos transitorios, lo que permite aumentar la precision para flujos muy turbulentos, con masiva separacion o desprendimiento de vortices.

Tambien incluye una formula analitica para numeros turbulentos de Prandtl. Ademas, el modelo k-ε trabaja con numeros de Reynolds altos, mientras que la teoria RNG da una formula diferencial derivada analiticamente por la viscosidad efectiva, valida tambien para numeros de Reynolds bajos.

METODOLOGÍA DE SOLUCIÓN

La estrategia de solución se estableció definiendo la ecuación de cierre, el fluido de trabajo, las condiciones de borde, la selección de la malla y la simulación.

Como herramienta para modelar el flujo se utilizó la simulación numérica a través del programa comercial de Dinámica de Fluidos Computacional (CFD) FLUENT 6.0.

Programa FLUENT

El programa FLUENT tiene incorporado los modelos de turbulencia mencionados anteriormente. Este programa resuelve los sistemas de ecuaciones discretizadas con la técnica de volúmenes finitos, calculando los valores de las variables en el interior de las celdas computacionales.

Las ecuaciones diferenciales se pueden aproximar con métodos de (CFD). Estos métodos ofrecen una manera práctica de alcanzar la generalidad de la formulación de las ecuaciones diferenciales. Entre la variedad de métodos de CFD desarrollados se tiene que el método de volúmenes finitos es uno de los más utilizados.

Para aplicar el método es necesario definir un espacio temporal de cálculo (dominio), el cual debe ser discretizado para resolver numéricamente las ecuaciones. La discretización del dominio espacial consiste en la división del espacio en un conjunto de pequeñas celdas que son consideradas pequeños volúmenes de control, todo este conjunto conforma la malla computacional.

La malla computacional es un aspecto fundamental de la simulación numérica de flujos. El número y tamaño de las celdas computacionales deben ser suficientes para poder calcular con bastante precisión las distintas zonas del fluido. En este sentido, se debe identificar las zonas del flujo donde los gradientes de las variables sean más pronunciados y disponer de una malla suficientemente fina en esas zonas.

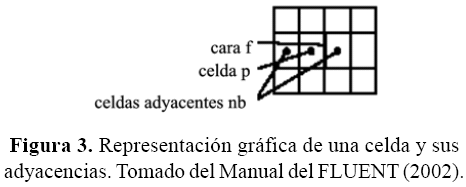
Para discretizar las ecuaciones se deben aproximar las ecuaciones diferenciales por un sistema de ecuaciones algebraicas para las variables termo-fluido-dinámicas en el conjunto de celdas de la malla computacional y en un conjunto discreto de instantes de tiempo. Sistemáticamente, cada ecuación de transporte es discretizada en forma algebraica para cada celda, requiriendo información o datos de campo; tales como propiedades del fluido, velocidad, entre otros; de centros y caras de las celdas (ver figura 3, para la celda «p»). El programa FLUENT utiliza un promedio de los valores de las celdas que comparten cada nodo.

Aun cuando el programa FLUENT es una herramienta poderosa para efectuar simulaciones, él no cuenta con la opción para definir la malla y debe apoyarse en la subrutina GAMBIT, la cual forma parte del pre-procesamiento de los datos. Entonces, para realizar un modelo y la simulación se deben manejar ambos programas, FLUENT y GAMBIT.

Pre-procesamiento en GAMBIT

La subrutina GAMBIT permite definir la geometría del dominio y discretizar el sistema en un número finito de volúmenes de control. Pero antes de crear o definir la malla es preciso dibujar la geometría del sistema que se pretende simular.

Pre-procesamiento en FLUENT

Luego de seleccionada la malla, previamente definida en la subrutina GAMBIT, es importada al programa FLUENT, para luego seleccionar en él el modelo de turbulencia y establecer las condiciones de borde o contorno establecidas.

Procedimiento de Solución

El procedimiento de solución contempló los siguientes pasos:

1. Se usó como ecuación de cierre el modelo de turbulencia RNG  k-ε y se usaron las condiciones transitorias y datos experimentales de campo.

2. Se seleccionó el flujo de trabajo en base al conocimiento del flujo que es transportado en la línea de cabecera, el cual es monofásico y está compuesto por gases de productos de combustión. Comúnmente la concentración de estos productos está conformada por nitrógeno (N₂) en un 80% y el 20% restante se divide en dióxido de carbono (CO₂), monóxido de carbono (CO) y oxígeno (O₂). Como el nitrógeno representa el más alto porcentaje de concentración, este gas fue utilizado como fluido de trabajo.

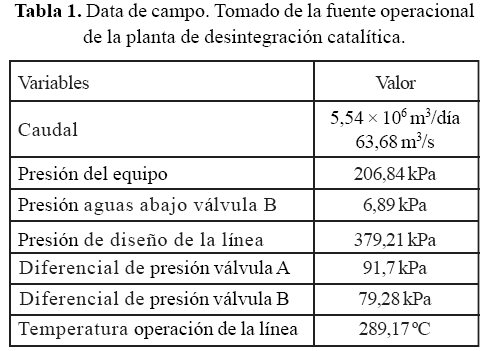
3. Las condiciones de borde a la entrada de la geometría fueron tomadas de los datos operacionales de la refinería, los cuales se indican en las tablas 1 y 2.

4. Al calcular el número de Mach se obtuvo un valor menor a 0,3; esto significa que los cambios de densidad no son significativos en el tramo en estudio. Por lo tanto, se pudo considerar el flujo como incompresible de acuerdo a lo expuesto por Potter et al. (2002).

5. Luego, se establecieron las condiciones de salida, tomando como presión a la salida un valor de 1,0 psi y temperatura constante, mientras que la presión de entrada no fue considerada para efectos de los cálculos.

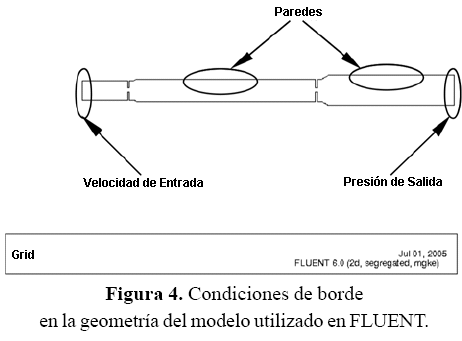
6. Seguidamente, se diseñó la geometría de la malla bidimensional, la cual se muestra en la figura 4, en conjunto con las condiciones de borde. Figura 4. Condiciones de borde en la geometría del modelo utilizado en FLUENT.

7. Antes de seleccionar la malla definitiva para la simulación final fue preciso realizar varias mallas con distintas densidades y formas. Por ello, se elaboraron diferentes mallas gruesas y finas. En la corrida inicial se empleó una malla no muy fina con celdas uniformes en todo el dominio, pero este tipo de mallado mostró resultados físicos no satisfactorios, puesto que no reflejó las fluctuaciones de presión.

8. Posteriormente, se utilizó una malla fina, estructurada y uniforme, pero los resultados correspondientes a esta malla tampoco fueron los esperados.

9. Ante los resultados obtenidos, se decidió afinar más la malla, haciendo énfasis en la zona de estrangulamiento y extendiendo el dominio de forma axial aguas abajo de la segunda válvula de control, con la finalidad de permitir que se observara el desarrollo del flujo en esa zona.

10. Se seleccionó una malla conformada con 15.364 elementos y 15.957 nodos, por haberse obtenido la mejor convergencia con ella. En las figuras 5 y 6 se puede observar que la malla fue afinada hacia la zona de estrangulamiento (válvulas de control A y B), en donde se buscó obtener mayor y mejor información del flujo.

11. En las simulaciones se usó la metodología de las ecuaciones de Navier-Stokes promediadas según Reynolds (RANS). Este módulo del FLUENT permite obtener soluciones más aproximadas, ya que las simulaciones en estado estable omiten un importante componente del promedio del campo de flujo, que es el desprendimiento periódico de vórtices.

12. Para las simulaciones también se empleó inicialmente una solución en estado estable, en la que se obtuvo un amplio número de pasos de tiempo, lo cual indicaba que no existían variaciones a través del tiempo en el campo fluido-dinámico. Luego, la simulación en estado estable se obtuvo y se usó como condición inicial para analizar la condición transitoria, lo que permitió obtener una simulación más precisa respecto al tiempo (con pequeños pasos de tiempo). Para lograr la convergencia de las ecuaciones se usó como paso de tiempo 2 10^-6 segundos y 20 pasos por períodos de tiempo. Estos números se calcularon tomando en cuenta las frecuencias de las vibraciones registradas en la línea de cabecera, las cuales tienen valores entre 700 a 2300 Hz.

RESULTADOS

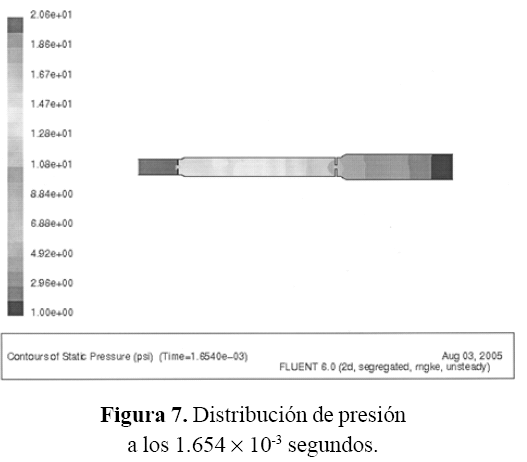
Al resolver el sistema de ecuaciones se obtuvieron variables importantes, dentro de las cuales se encuentran la distribución de presión, variación de presión en el tiempo, distribución de velocidad y dirección del flujo. Distribución de presión La distribución de presión en la tubería, antes de cada válvula fue estable. Luego, cuando el flujo pasaba a través de cada válvula de control, la presión descendía un 50%, coincidiendo con los datos suministrados por la refinería.

En la figura 7 se observa que el mayor valor de presión se encuentra aguas arriba de la válvula A. Luego, se observa una disminución de presión, según la escala de valores del lado izquierdo del gráfico. Finalmente, al sobrepasar la válvula B, el flujo presenta un valor de presión ligeramente superior a la presión atmosférica.

Variaciones de presión en el tiempo

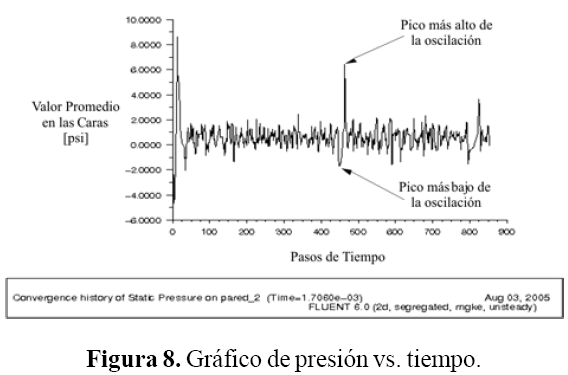
Para poder mostrar con facilidad los cambios en cada uno de los pasos de tiempo, el programa FLUENT construyó una gráfica de las variaciones de la presión versus el tiempo, en donde se pudo observar que variaban entre 0 a 900 pasos de tiempo. Los máximos picos de presión se observaron uno a los 450 pasos de tiempo, con un valor pico a pico de 55,5 kPa, (8 psi), y otro de menor escala a los 825 pasos con un valor de 41,4 kPa (psi) pico a pico. Se entiende como valor pico a pico la señal mostrada en la gráfica del punto más bajo al punto más alto de una oscilación. Finalmente se obtuvo que el promedio de las oscilaciones estuviera en el orden de 20,7 kPa (3 psi).

En la figura 8 se aprecian los ligeros cambios en la distribución de presión en el volumen de control, demostrando que existen condiciones transitorias en el sistema. Es por ello que la presión manométrica no es un factor considerable en esta simulación en dos dimensiones. Además, la gráfica de la figura 8 muestra las oscilaciones promedio de presión en la tubería de 1,42 m de diámetro, entre las válvulas de control de la línea de cabecera del regenerador, la cual es la sección de la tubería que presenta las altas vibraciones inducidas por el flujo.

Perfil de Velocidad

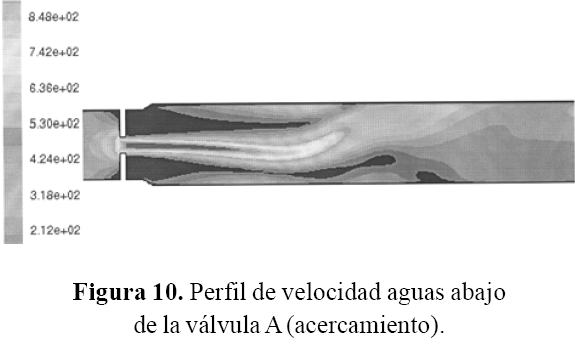
En las figuras 9 y 10 se observan los contornos de velocidad, en donde el flujo formado aguas abajo de la válvula A de control está completamente desarrollado en el tramo de 1,42 m de diámetro. Luego, en esa misma área se nota como el flujo va disipando su estela.

En los gráficos anteriormente presentados se aprecia que el flujo alcanza la mayor velocidad a la salida de la zona de estrangulamiento de ambas válvulas de control, para luego irse disipando y estabilizándose a una distancia no muy lejana de la salida de cada válvula.

Líneas de Corriente

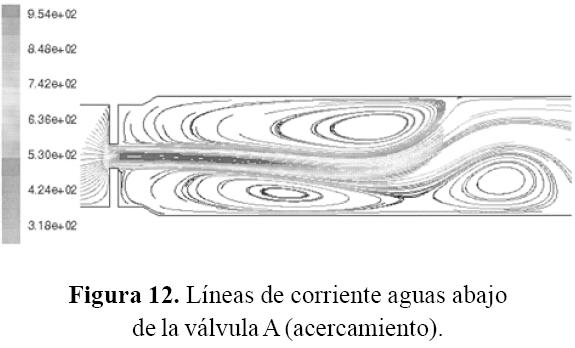
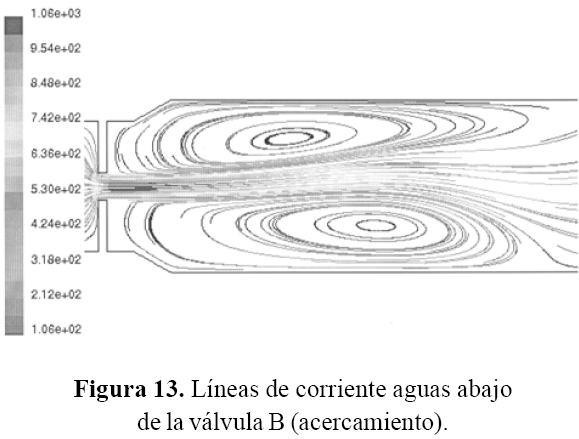
Las líneas de corriente se muestran en las figuras 11, 12 y 13, en ellas se observa la formación de vórtices tanto en la parte superior como en la parte inferior de la salida del flujo, aguas abajo de cada válvula de control. Los vórtices no son simétricos y la mayor concentración de ellos ocurre a la salida de las válvulas A y B.

CONCLUSIONES

• Debido a que el campo de flujo aguas abajo de la válvula A no hace interferencia con la válvula B, se puede asegurar que al separar las válvulas de control no se disiparían las vibraciones en la tubería.

• La separación existente entre las válvulas reductoras de presión no representa un obstáculo para que el flujo se estabilice luego de pasar a través de la válvula A.

• La simulación determinó que la mayor concentración de vórtices se ubica después de la válvula A, lo cual coincide con los datos de altas vibraciones obtenidos en las mediciones de campo.

• Se deben desarrollar simulaciones estructurales con los datos de presión-tiempo obtenidos para estimar zonas críticas y tiempo estimado de fallas en la tubería.

NOMENCLATURA

g Gravedad

p Presión

V Velocidad

ñ Densidad

ì Viscosidad

REFERENCIAS

1. CATALANO, P., WANG, M., IACCARINO, G., MOIN, P. (2003). Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. International Journal of Heat and Fluid Flow. 2003, Vol. 24, No 4, pp. 216-223. Elsevier Science Inc.        [ Links ]

2. FLUENT 5/6. (2002) User´s guide. Fluent Inc. Lebanon, NH, USA.        [ Links ]

3. IACCARINO, G., OOI, A., DURBIN, P.A., BEHNIA, M. (2002). Reynolds averaged simulation of unsteady separated flow. Center of Turbulence Research, Stanford University, USA. Elsevier Science Inc.        [ Links ]

4. IACCARINO, G., OOI, A., DURBIN, P.A., BEHNIA, M. (2003). Reynolds averaged simulation of unsteady separated flow. International Journal of Heat and Fluid Flow, Vol. 24, No. 2, pp. 147-156. Elsevier Science Inc.        [ Links ]

5. POTTER, M.C., HONDZO, M., SHIH, T.I.P., WIGGERT, D.C. (2002). Mecánica de fluidos. Thomson International.        [ Links ]

6. SPEZIALE, C.G. & THANGAM, S. (1992). Analysis of an RNG based turbulence model for separated flows. Institute for Computer Applications in Science and Engineering, Hampton, Va.        [ Links ]

7. YAKHOT, V. & ORSZAG, S.O. (1986). Renormalization group methods in turbulence. Journal Science Comp., 1, p. 3.         [ Links ]

8. ZAMBRANO, T. (2000). Análisis del flujo turbulento sobre un prisma de sección transversal cuadrada mediante simulación de vórtices grandes. Universidad Central de Venezuela.        [ Links ]