Estabilizando patrones binarios asociados a mapas discretos

Gustavo Ramírez, Pedro García

Universidad Central de Venezuela, Facultad de Ingeniería, Laboratorio de Sistemas Complejos, Departamento de Física Aplicada, A.P. 48110, Caracas. 1041-A, Venezuela.

e-mail: gramirez@fisica.ciens.ucv.ve - pedro@fisica.ciens.ucv.ve

RESUMEN

Los esquemas de control, destinados a estabilizar órbitas periódicas inestables asociadas a redes neurales caóticas, requieren por una parte que la metodología sea efectiva en sistemas de alta dimensión y por otra que el objetivo del control pueda alcanzarse utilizando sólo información parcial acerca del mismo. Como una alternativa en este trabajo se propone asociar patrones binarios a la evolución de un mapa unidimensional que pueda ser controlado usando un esquema sencillo. Resultados que pueden ser de utilidad en el diseño de memorias asociativas de baja dimensionalidad son presentados usando como ejemplo el mapa Logístico.

Palabras clave: Sistemas caóticos, Control de caos, Redes neurales, Memoria asociativa, Patrones binarios.

Stabilizing binary patterns in discrete maps

 ABSTRACT

The use of control schemes to stabilize unstable periodic orbits in a chaotic neural network acting as associative memory, require firstly that the control scheme has to be effective in high dimensional systems and secondly that it does not depend on the target. As an alternative, we propose to associate binary patterns to the evolution of a low dimensional chaotic map where a suitable control scheme can be used. By using the Logistic map as an example, results that can be useful in the design of associative memories are shown.

Keywords: Chaotic systems, Control of chaos, Neural networks, Associative memory, Binary patterns.

Recibido: mayo de 2008   Recibido en forma final revisado: abril de 2009

INTRODUCCIÓN

Un sistema dinámico puede ser representado, sin pérdida de generalidad, por una dupla ( fs, {s(t)}), donde fs es la regla dinámica que gobierna la evolución temporal del sistema, {s(t)} el conjunto de todos los estados que le son accesibles al mismo y s es un vector de parámetros. Cuando estos sistemas son espacialmente localizados y su evolución ocurre a intervalos de tiempo discretos, se los conoce como mapas y son representados por ecuaciones en diferencias de la forma x_n+1 = fs (x_n). Por otra parte, cuando los sistemas son espacialmente extendidos, muchas de sus propiedades pueden modelarse mediante el uso de redes de mapas acoplados, en estas redes o grafos los vértices representan los elementos del sistema (mapas) y los bordes las interconexiones entre ellos. Estos sistemas pueden ser pensados como versiones discretas en tiempo y espacio de ecuaciones diferenciales en derivadas parciales, de manera que la discretización las convierte de sistemas de dimensión infinita en sistemas de dimensión finita, pero grande. Por otra parte, si el conjunto {s(t)} tiene un número finito de elementos, al sistema se lo conoce como un autómata celular.

Una red de mapas acoplados en la cual los parámetros de acople son escogidos de manera que el sistema como un todo realice una tarea predeterminada, es lo que se conoce como una red neural.

Cuando las redes neurales son usadas como memorias asociativas, los parámetros de acoplamiento son ajustados de forma que la red tenga como espacio de estados un conjunto de puntos fijos estables, que son considerados las memorias almacenadas en la red. De esta manera, si un patrón contaminado con ruido es presentado a la red, esto es, el patrón es usado como condición inicial para el sistema, entonces la red convergerá al patrón original, si esta condición inicial se encuentra en la cuenca de atracción del punto fijo en cuestión.

El número de patrones que pueden ser almacenados en una memoria asociativa (la capacidad de la red) está relacionado con el número de unidades que constituyen la red. Un aumento en ésta, requiere un aumento en el número de unidades, lo que a su vez redunda en el costo computacional asociado a la determinación de los parámetros de la red (etapa de entrenamiento).

Una alternativa a la solución de este problema la ofrecen las redes neurales de evolución caótica (Adachi & Aihara 1997). Estas redes son principalmente caracterizadas por un espacio de estados, compuesto por un número infinito de orbitas periódicas inestables, además de una marcada sensibilidad de la evolución del sistema a pequeños cambios en las condiciones iniciales o pequeñas variaciones en los parámetros.

Ahora bien, el uso de estas órbitas periódicas, como memorias almacenadas en la red, está limitado por el carácter inestable de las mismas, que evita que el sistema pueda tener como estado estacionario alguna de ellas. Sin embargo, la sensibilidad del sistema a cambios, en las condiciones iniciales, permite que este pueda ser controlado usando perturbaciones pequeñas. Estos dos hechos sugieren que una manera de usar las órbitas periódicas inestables de un sistema caótico, como memorias, es dotando al sistema con un esquema de control que permita la estabilización de esas órbitas (Crook et al. 2007; He et al. 2007). No obstante, debe hacerse notar que el diseño de estrategias de control para sistemas de alta dimensión presenta un grado de dificultad sensiblemente mayor que los esquemas dedicados al control de sistemas de dimensión baja.

Como una alternativa, en este trabajo se presenta un esquema de control que permite estabilizar patrones binarios asociados a los elementos de órbitas periódicas inestables de mapas unidimensionales. Con ese fin, el trabajo está organizado como sigue: en la sección II se resumen algunos esquemas de control de sistemas caóticos, en la sección III se presenta una metodología hibrida para estabilizar orbitas periódicas inestables de mapas caóticos, en la sección IV se usa esa metodología para estabilizar patrones binarios asociados a los elementos de las órbitas.

CONTROL DE SISTEMAS CAÓTICOS

Como ya se mencionó, un sistema dinámico cuya evolución depende sensiblemente de las condiciones iníciales y cuyo espacio de estados está estructurado por un conjunto infinito de orbitas periódicas inestables, es lo que se conoce como un sistema caótico. Estas características confieren a estos sistemas un comportamiento parecido en muchos aspectos, a los de evolución aleatoria.

El control de sistemas caóticos se refiere a la situación donde el sistema evolucionando inicialmente en régimen desordenado es obligado, mediante perturbaciones pequeñas, a seguir una trayectoria predeterminada que en principio puede tener características estructurales bien diferentes a la órbita del sistema no perturbado.

Ahora bien, cuando la tarea es ejercer control sobre un sistema caótico, puede elegirse entre dos alternativas: una consiste en realizar pequeñas variaciones en los parámetros del sistema con el fin de estabilizar la órbita deseada. El método de OGY (Ott et al. 1990) es el ejemplo canónico de esa clase. Otra alternativa consiste en realizar esos cambios en la variable de estado. Un ejemplo resaltante de este tipo de control es el método de Pyragas (1992). En este último esquema, la separación entre el objetivo y la órbita del sistema es penalizada por la diferencia entre el estado actual y el estado T pasos de iteración en el pasado.

Dentro de este esquema no hay dependencia expresa del esquema de control con el objetivo, en vez de eso, se usa sólo información parcial acerca de la órbita periódica, esto es, s(t) = s(t - T). Debido a esta característica, los esquemas de este tipo resultan de particular interés cuando se trata de ejercer control sobre una red neural actuando como memoria asociativa.

Por otra parte, hay evidencia tanto experimental (Corron et al. 2000) como teórica (Hilker, 2006) que indica que un sistema caótico puede ser estabilizado en una órbita periódica inestable mediante una selección adecuada de un límite para el espacio de estados. Particularmente Crook et al. (2007) proponen un esquema de control para mapas unidimensionales, dado por:

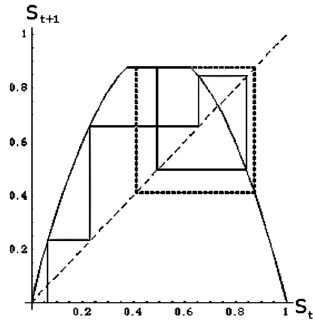
De la figura 1 es claro que cuando la órbita cae en el intervalo de control, ésta colapsa en un ciclo límite estable.

Figura 1. Control limitando el espacio de fase.

Ambas técnicas han sido usadas en la estabilización de orbitas periódicas en redes neurales caóticas (He et al. 2008; 2007, 2003), particularmente en un esquema de retroalimentación del estilo de Pyragas (1992) para estabilizar orbitas periódicas inestables en una red 100 neuronas caóticas. Por su parte (HE et al. 2003) logran el mismo objetivo limitando adecuadamente el espacio de estados asociado a una red del mismo tamaño. En este caso se propone, no el control de una red 100-dimensional, sino la construcción de un mapa unidimensional a cuyas orbitas periódicas inestables puedan ser asociadas los patrones deseados y que posteriormente serán estabilizados mediante control.

Ambas técnicas han sido usadas en la estabilización de orbitas periódicas en redes neurales caóticas (He et al. 2008; 2007, 2003), particularmente en un esquema de retroalimentación del estilo de Pyragas (1992) para estabilizar orbitas periódicas inestables en una red 100 neuronas caóticas. Por su parte (HE et al. 2003) logran el mismo objetivo limitando adecuadamente el espacio de estados asociado a una red del mismo tamaño. En este caso se propone, no el control de una red 100-dimensional, sino la construcción de un mapa unidimensional a cuyas orbitas periódicas inestables puedan ser asociadas los patrones deseados y que posteriormente serán estabilizados mediante control.

UN ESQUEMA DE CONTROL HIBRIDO

En nuestro caso, usaremos una metodología híbrida entre el método anterior y el de Pyragas, de manera que se ejercerá control perturbando la estructura de la regla dinámica como sigue:

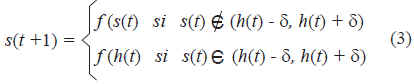
Como fue mencionado antes, acá combinamos ambos métodos de control de forma que una órbita periódica cualquiera puede ser estabilizada perturbando el parámetro como sigue:

donde:

g y d son parámetros a ajustar. Como en el caso anterior, la órbita del sistema, luego de una etapa de transición colapsará en una órbita periódica estable y simultáneamente h(t) convergerá al elemento de la órbita más cercano a la condición inicial h(0).

ESTABILIZACIÓN DE PATRONES BINARIOS ASOCIADOS AL MAPA

Consideremos ahora una representación binaria de los estados s(t) del mapa unidimensional, dado por:

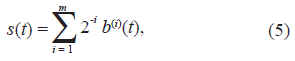
donde:

 

b⁽ⁱ⁾(t) є{0,1} y m representa la precisión del procesador donde se hace la simulación o el aparato que realiza la medición. De esta manera la perturbación D = g(s(t-T) - s(t)), aplicada sobre la posición del segmento de control (h) puede escribirse como:

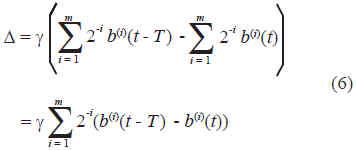
Esta es una representación que jerarquiza los bits de acuerdo al orden en que se encuentran y promedia las diferencias entre las cadenas, esto es, los primeros bits son más importantes que los últimos.

En este trabajo la información sobre la jerarquía es suprimida, de manera que el control se realiza dando sólo la sucesión de bits asociada al estado del sistema. De esta forma, la perturbación es realizada como:

donde la ecuación:

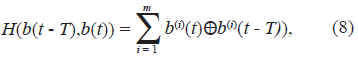
representa la distancia de Hamming entre las dos cadenas binarias y el operador binario representa la suma módulo 2. Es de hacer notar, que la remoción de los pesos constituye una supresión de información importante para cada estado.

Es fácil notar que la perturbación g(s(t - T) - s(t)) penaliza la separación entre el objetivo y la órbita del sistema cambiando de signo según la órbita esté por encima o por debajo del objetivo, s(t - T). En el caso en que la perturbación está dada por H(b(t - T),b(t)) no hay nunca cambio de signo en la perturbación (H(b(t - T),b(t)) ≥ 0) por lo que es necesario introducir un esquema de variación en el signo de la perturbación de forma que ésta sea positiva si la órbita está por debajo del objetivo y negativa si está por encima. En nuestro caso se implementa un esquema de recocido simulado (Kirkpatrick et al. 1983) a temperatura cero, donde la energía está dada por DH=H(b(t - T),b(t))-H(b(t - 1- T),b(t - 1)) y el signo de la perturbación es cambiado en cada iteración sí DH ≥ 0.

La idea de ejercer el control usando como perturbación la distancia de Hamming entre las cadenas binarias asociadas a los estados del mapa, es motivada por el hecho de que el control, usando una representación real de los estados, conduce a estados cuyas representaciones binarias pueden ser marcadamente diferentes a pesar de que su representación real es bastante similar. Este último hecho conduce a su vez a perturbaciones muy pequeñas para patrones binarios que pueden ser marcadamente diferentes.

El esquema de control anterior, basado sólo en la representación binaria de los estados del mapa, permite estabilizar órbitas periódicas inestables de f y sugiere que un sistema dinámico como (3)-(4), puede ser usado como memoria asociativa. Esto es, como un sistema capaz de almacenar patrones que luego pueden ser recuperados usando información parcial acerca de ellos.

En este caso, la información se almacena en forma de órbitas periódicas inestables del mapa y la recuperación es realizada mediante el control de tales órbitas.

RESULTADOS

A manera de ejemplo, en este trabajo se muestran resultados de la aplicación del esquema de control, para el caso particular del mapa logístico x_n+1 = 4xn(1 - xn). En este caso el sistema controlado es representado por:

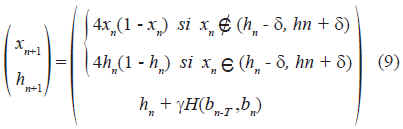
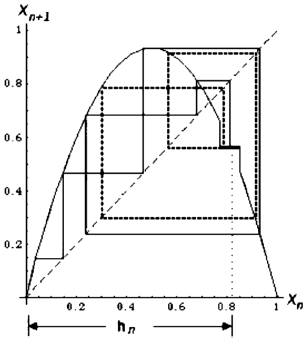
La figura 2 muestra una gráfica de la ecuación (9), junto con un ejemplo de trayectoria.

Figura 2. Esquema de control hibrido propuesto.

Dado que las orbitas periódicas inestables son densas en el atractor de la dinámica f, el intervalo de control quedará ubicado sobre un elemento (digamos, x_m = f ^(m) (x₀)) de alguna de ellas. Por otra parte, la estabilidad de cada una de esas orbitas puede medirse (Ott, 1993), como la estabilidad del np - ésimo iterado del mapa:

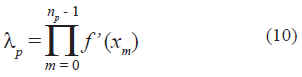
De esta manera, el sistema dinámico constituido por el sistema original más la ecuación de control tiene un comportamiento asintótico periódico ya que f’(x_c) = 0 y por lo tanto l_p < 1, lo que indica que la órbita periódica es estable. Sin embargo, durante el periodo de transición asociado a la evolución de la órbita antes de aterrizar en el intervalo de control d, el comportamiento es caótico, lo que permite el uso de un esquema de control basado en perturbaciones pequeñas. Una vez que la órbita cae en el intervalo el comportamiento del sistema es periódico y además estable.

Las gráficas siguientes muestran la evolución del mapa logístico cuando el esquema de control es usado para estabilizar ciclos límites inestables de periodos uno y dos, con los parámetros d = 0.002 y g = 0.001. En ambos casos, la condición inicial la x es escogida al azar y la condición inicial para h es escogida como h₀ = x_j⁽ⁱ⁾ + x. Aquí, x_j⁽ⁱ⁾ representa el j-ésimo elemento de la i-ésima órbita periódica inestable y x representa una perturbación pequeña de ese elemento.

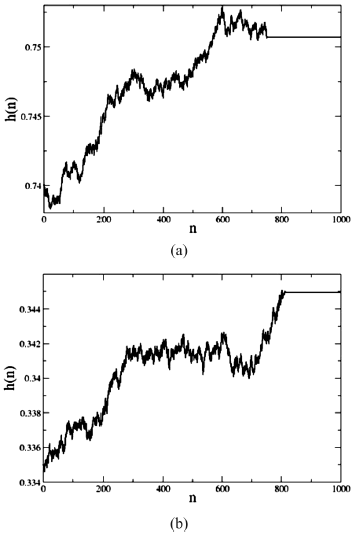
Particularmente, las figuras 3(a) y 3(b) muestran como, cuando la condición inicial h₀ está cerca de algún elemento de un ciclo límite inestable, la aplicación del control obliga a h_n a converger asintóticamente en ese elemento del ciclo.

Figura 3. Evolución de la ubicación del segmento de control h_n para ciclos de orden (a) uno y (b) dos.

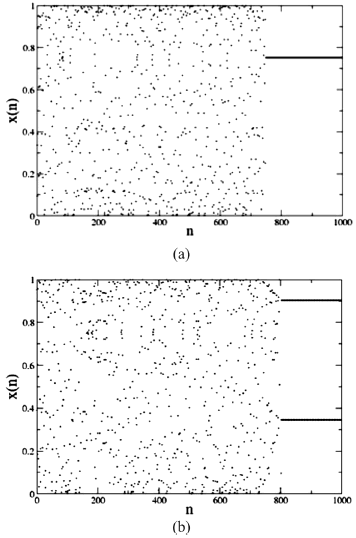
Como un complemento, las figuras 4(a) y 4(b) muestran, la estabilización del resto del estado (x_n) del mapa, sobre las mismas órbitas periódicas inestables anteriores.

Figura 4. Estabilización de órbitas periódicas de periodos (a) uno y (b) dos.

Por último, las figuras 5(a) y 5(b) muestran la evolución de la representación binaria b⁽ⁱ⁾(t) asociada a la evolución del mapa. Cuando el esquema de control es activado los patrones binarios asociados a la evolución pasan de tener una estructura desordenada a una estructura regular.

Figura 5. Los gráficos muestran la estabilización de patrones binarios correspondientes a las órbitas periódicas inestables (a) periodo 1, (b) periodo 2.

Es de hacer notar que aunque en el ejemplo presentado acá, sólo se han considerado órbitas periódicas de periodo uno y dos, el esquema de control propuesto permite la estabilización de orbitas de periodo mayor. La dificultad para lograrlo radica sólo en la identificación de las órbitas, ya que una vez ubicado el segmento de control en la posición correspondiente a uno de los elementos de dicha órbita, el sistema tendrá un comportamiento asintótico periódico.

Particularmente en (Zhou, 2006) se presenta un esquema para la identificación de las orbitas periódicas de periodo grande (mediante el uso de la dinámica simbólica del sistema) y su posterior control a través el establecimiento de límites al espacio de fase.

CONCLUSIONES

Se presenta un esquema de control híbrido que permite estabilizar patrones binarios asociados a orbitas periódicas inestables de mapas discretos unidimensionales. La estrategia propuesta utiliza sólo información parcial del objetivo a controlar.

Los resultados sugieren, por una parte, que esquemas de este tipo pueden ser usados para controlar redes neurales caóticas actuando como memorias asociativas y por otra muestran la posibilidad de diseñar memorias asociativas basadas en dinámicas caóticas de baja dimensión.

AGRADECIMIENTOS

Este trabajo fue parcialmente financiado por el Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuela.

REFERENCIAS

1. Adachi, M. & Aihara, K. (1997). Associative dynamics in chaotic neural network. Neural network. 64(1): 83.         [ Links ]

2. Corron, N.J., Pethel, S.D., Hopper, B.A. (2000). Controlling chaos with simple limiters. Phys. Rev. Lett. 84: 3835.         [ Links ]

3. Crook, N., Goh, W. J., Hawarat, M. (2007). Pattern recall in networks of chaotic neurons. ByoSystems. 87: 267.         [ Links ]

4. He, G., Cao, Z., Chen, H., Zhu, P. (2003). Controlling chaos in a neural network based on the phase space constraint. International Journal of Modern Physics. 17: 4209.         [ Links ]

5. He, G., Chen, L., Aihara, K. (2008). Associative memory with controlled neural network. Neurocomputing. 71: 2794.         [ Links ]

6. He, G., Shrimali, M. D., Aihara, K. (2007). Partial state feedback control of chaotic neural network and its application. Phys. Lett. A. 371: 228.         [ Links ]

7. Hilker, F.M. (2006). Paradox simple limiter control. Phys. Rev. Lett. 73: 52901.         [ Links ]

8. Kirkpatrick, S., Gelatt, C.D., Vecchi, M.P. (1983). Optimization by Simulated Annealing. Science, 220(4598): 671.         [ Links ]

9. Ott, E. (1993). Chaos in dynamical systems. Cambridge University Press, New York.         [ Links ]

10. Ott, E., Grebogi, C., Yorke, J.A. (1990). Controlling chaos. Phys. Rev. Lett. 64: 1196.         [ Links ]

11. Pyragas, K. (1992). Continuous control of chaos by selfcontrolling feedback. Phys. Lett. A. 170: 421.         [ Links ]

12. Zhou, C.T. (2006). Stabilizing long-periodic orbits via symbolic dynamic in simple limiter controller. CHAOS, 16: 013109.         [ Links ]