Optimización de balance de cargas en sistemas de distribución de energía eléctrica

Ebert Brea

Universidad Central de Venezuela, Facultad de Ingeniería, Escuela de Ingeniería Eléctrica, Apartado Postal 47456, Caracas 1041-A, Venezuela. e-mail: ebert.brea@ucv.ve

RESUMEN

El desbalance de fases en un sistema de distribución de energía eléctrica, constituye ser uno de los tantos problemas que suele afectar negativamente la confiabilidad y calidad de los sistemas de distribución. En este artículo se muestra un modelo matemático convexo que permite medir el balance de las fases ante una configuración de conexión dada. Las características del modelo matemático son estudiadas en el trabajo a fin de demostrar que cuando es identificada al menos una solución local, la misma constituye una solución global al problema. Este último aspecto, resulta ser lo suficientemente atractivo para emplearlo como modelo matemático debido a su simplicidad.

Palabras clave: Optimización, Balance de cargas, Optimización entera, Programación cuadrática, Programación combinatorial, Método de particiones anidadas, Método de Monte Carlo.

Optimization of load balance in electrical distribution systems

ABSTRACT

The unbalancing of electrical loads in feeder systems is one of many possible problems that can negatively affect the reliability and quality of an electrical distribution system. This article shows a convex mathematical model, which allow us to measure the balancing of phases. A mathematical study of the objective function is presented here, in order to show that when a local minimum is identified by some algorithmic method, the solution is also global. This main characteristic of the mathematical model really makes it a useful tool to be applied to these type of problems, because of its simplicity.

Keywords: Optimization, Phase balancing, Integer optimization, Quadratic programming, Combinatorial programming, Nested Partitions Method, Monte Carlo Method.

Recibido: noviembre de 2008 Revisado: julio de 2009

INTRODUCCIÓN

El desbalance de las fases en los sistemas de distribución constituye uno de los tantos problemas que presentan las redes de distribución de energía eléctrica. Estos fenómenos pueden incrementar las pérdidas en los sistemas de distribución, así como la merma en la calidad del sistema eléctrico, además de afectar la confiabilidad del mismo.

Podría mencionarse dos puntos de vista en la búsqueda de soluciones ante los problemas de desbalance de cargas conectadas a los sistemas de distribución de energía eléctrica. El primero de ellos parte del principio de la reconfiguración de la alimentación. El otro, el cual será el enfoque empleado en este trabajo, es el referente a la adjudicación de carga en los distintos nudos del sistema a ser conectado en las fases del sistema, haciendo que la decisión sea tomada en relación a cuál fase será conectada la carga ubicada en cada n-ésimo nudo. Este último enfoque fue abordado por Zhu et al. (1999), no obstante, la formulación matemática del problema no corresponde al enfoque empleado en su trabajo, en virtud de que los autores presentan una formulación matemática como si la misma fuese un caso de programación entera mixta lineal. El propósito de esta investigación es mostrar un modelo matemático alterno al empleado por Zhu et al. (1998), para así buscar una solución al problema cuando la carga conectada en los diferentes nudos del sistema de distribución eléctrica es variable, y su magnitud puede ser caracterizada a través de la distribución probabilística de cada carga eléctrica.

Por otra parte, el autor presenta una breve revisión de algunos conceptos matemáticos, a objeto de mostrar las bases en las cuales se sustenta para afirmar que los resultados óptimos obtenidos en los ejemplos numéricos corresponden a óptimos globales.

Es importante indicar que en este estudio sólo fueron tomadas en cuenta cargas monofásicas, es decir, cargas que están conectadas únicamente entre una fase y neutro, y no entre dos o más fases.

Un aspecto que no puede dejar de mencionarse es el referente al método algorítmico de identificación de óptimos empleado en este trabajo, llamado método de particiones anidadas (MPA) (Shi & Ólafsson, 2000a), el cual ha demostrado ser lo suficientemente eficiente en la identificación de óptimas soluciones en el ampliamente conocido problema del agente viajero (Shi & Ólafsson, 2000b), así como en la identificación de la mejor condición en un problema de optimización de redes de colas estudiado por Brea & Cheng (2003). Debe señalarse que se implementó el MPA para estudiar su desempeño en la identificación de la solución del óptimo balance en sistemas de distribución de energía eléctrica, por tratarse de ser un problema de optimización combinatorial.

El resto del artículo está estructurado como sigue: en la primera sección son presentados algunos conceptos matemáticos a fin de demostrar que la solución obtenida en el modelo formulado corresponde a un óptimo global. En la segunda sección es planteado el problema en términos matemáticos estableciendo algunas consideraciones para proponer una formulación aproximada al problema, sin queella represente una desproporción a lo que en la realidad ocurre. Una formulación matemática alterna a la propuesta por Zhu et al. (1998) es presentada en la tercera sección, y cuya características de convexidad es demostrada en el artículo. Una breve explicación del algoritmo de identificación de la óptima solución empleado en el trabajo es mostrada en la cuarta sección, y en donde el lector podrá apreciar la naturaleza aleatoria del MPA. En la quinta sección son reportados algunos ejemplos numéricos, los cuales comprueban la utilidad del modelo matemático propuesto y la eficiencia del método algorítmico implementado. Finalmente, en la sexta sección son enumeradas las principales conclusiones de la investigación reportada aquí.

CONCEPTOS PRELIMINARES

En esta sección se revisarán algunos aspectos matemáticos que deben ser tomados en cuenta, para así poder establecer el tipo de resultado que puede ser alcanzado al aplicar algún método algorítmico de optimización.

Definición 1 (Dominio efectivo). Se denomina dominio efectivo S de una función f (x): Rⁿ ® R È {+oo}, como el conjunto no vacío de todos los puntos x Î Rⁿ tales que f(x)<+oo , (Murota, 2003).

Definición 2 (Función convexa). Una función f (x): Rⁿ ® R È {+oo} se dice ser convexa si para todo x1, x2 Î Rⁿ y para todo l Î {R½0 ≤ l ≤ 1} se cumple que (Bazaraa et al. 1993):

f (lx₁+ (1-l)x₂) ≤ lf (x₁)+(1-l) f (x₂),                    (1)

Una importante consecuencia en el ámbito de las funciones definidas únicamente en el dominio discreto es el referente al punto medio, el cual se obtiene permitiendo a l tomar el valor de 1/2 en la desigualdad (1), la cual resulta:

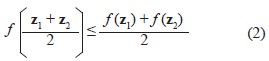
donde:

y

Teorema 1 (Dominio efectivo convexo).

Sea f (x): Rⁿ ® R È {+oo} una función convexa. Entonces, su dominio efectivo en el sentido de la definición 1 es convexo.

Demostración. (Véase Bazaraa et al. 1993).

Teorema 2.

Sea g(x): Rⁿ ® R È {+oo} tal que:

Si cada f (x): Rⁿ ® R È {+oo} es una función convexa para todo k = 1,..., K. Entonces, g(x) es también convexa.

Demostración. De acuerdo a la ecuación (3), se tiene que para todo l Î {R½0 ≤ l ≤ 1} :

Como para cada k = 1,..., K , f k (x) es convexa, se puede afirmar que para todo l Î [0,1] ,

lo cual al aplicar las ecuaciones 3 y 4 en la desigualdad 5, se concluye que la suma de funciones convexa, conforma una función convexa también.

Las definiciones presentadas pueden ser extendidas a funciones cuyo dominio es discreto. En tal sentido, serán contextualizados estos aspectos al análisis de convexidad discreto.

Lema 1 (Función convexa discreta).

Una función f (Z): Zⁿ ® R È {+oo} se dice ser convexa si y sólo si para todo {z - u }, {z + u } Zⁿ se cumple que:

2 f (z) ≤ f (z - u) + f (z + u)                (6)

donde u Î Zⁿ es un vector cuyas componentes u_i Î Z para todo i = 1,..., n.

Demostración. Obviamente la desigualdad 6 se obtiene al sustituir respectivamente z₁, z₂ por {z - u }, {z + u } en la desigualdad 2.

Definición 3 (Función convexa cuadrática). Sea A una matriz simétrica, y sea f (x): Rⁿ ® R È {+oo} una función asociada con la forma cuadrática definida por:

donde x^t representa el vector transpuesto del vector x.

Se dice que f (x) es una función cuadrática convexa si y sólo si la matriz A es semidefinida positiva, es decir, si para cualquier vector x se cumple que x^t Ax ≥ 0. Por otra parte, la función es considerada estrictamente convexa, si y sólo si para cualquier vector x se cumple que x^t Ax > 0, es decir, si la matriz A es definida positiva (Murota, 2003).

Teorema 3 (Función convexa cuadrática discreta).

Sea A una matriz simétrica, y sea f (z): Zⁿ ® R È {+oo} una función de dominio discreto asociada con la forma cuadrática definida por:

Además, sea u Î Zⁿ un vector cualquiera. Entonces, la función cuadrática discreta f (z) es convexa, si su matriz A es positiva semidefinida.

Demostración. Aplicando la ecuación 8 en la desigualdad 6 se obtiene que:

ztAz ≤ (z - u)tA(z - u)+ (z + u)tA(z + u), (9)

donde u Î Zⁿ es un vector cualquiera.

Después de algunas operaciones sobre la desigualdad 9 se llega a que u^t Au ≥ 0, la cual al aplicar la definición 3, se concluye que la función es convexa.

Lema 2.

Si d Î Rⁿ es un vector n dimensional cualquiera. Entonces la matriz simétrica d Rnxn definida por D = dd^t es semidefinida positiva.

Demostración. De la definición 3 se tiene que la matriz D es semidefinida positiva, si para cualquier vector x Î Rⁿ

Ahora como la matriz D = dd^t, se tiene que

donde ½½.½½² es obviamente un número real no negativo.

Además el lema establece que la matriz D Î R^nxn es simétrica, hecho que puede ser fácilmente demostrado al multiplicar los vectores dd^t.

Teorema 4. Sea f (z_a, z_b): Zⁿ x Zⁿ ® R È {+oo} una función con expresión matemática dada por:

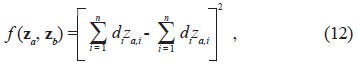
donde z^ta = (z_a,1, z_a,2,..., z_a,n), z^t _b = (z_a,1, z_a,2,..., z_a,n) y cada d_i Î R representa un parámetro. Entonces:

1. f (z_a, z_b) puede ser expresada como:

donde Î R^nxn es una matriz simétrica.

2. f (z_a, z_b) es una función convexa.

Demostración. Parte 1) Como

donde d^t = (d₁, d₂, ... , d_n) es el vector de parámetros y z^t = (z₁, d₂, ... , d_n) el vector de variables, se tiene que al aplicar la ecuación (14) en la ecuación (12), se obtiene que

Claramente, se tiene de la ecuación (15) que:

f (z_a, z_b) = (z_a - z_b)^tdd^t(z_a - z_b),

de donde claramente se puede afirmar que dd^t Î R^nxn es una matriz simétrica, y en consecuencia:

donde la matriz D = dd^t.

Parte 2) Debido a que D = dd^t, del lema 2 se puede afirmar que la matriz D es semidefinida positiva. En consecuencia, de acuerdo a la definición 3 la función f (z_a, z_b) es convexa.

Teorema 5 (Óptimo global).

Sea f (x): Rⁿ ® R una función convexa. Entonces su optimalidad global es garantizada por la optimalidad local.

Demostración. (Véase Murota, 2003).

PLANTEAMIENTO DEL PROBLEMA

Los problemas asociados al desbalance de cargas pueden producir una disminución de la vida útil de los generadores de energía eléctrica, además de los distintos componentes que están conectados a una red de distribución de energía eléctrica.

Obviamente, debido a la naturaleza aleatoria de la carga, los sistemas de distribución tienen una altísima probabilidad de estar sometidos a cargas desbalanceadas. No obstante, el principal propósito del modelo matemático es buscar que el sistema esté lo más balanceado durante el mayor tiempo posible.

En esta sección se presenta un modelo matemático alterno al propuesto por Zhu et al. (1998) y cuya función objetivo es convexa, la cual facilita la identificación de su óptimo, para el caso de un sistema de distribución trifásico de energía eléctrica.

Considere el siguiente problema:

Problema 1.

Sea:

donde i_j,n es la magnitud de la corriente eficaz correspondiente a la fase j medida en el n-ésimo nudo. Entonces, el problema de optimización puede expresarse en términos de lo definido por la ecuación (17), como:

sujeto a:

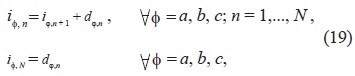
donde:

d_f,n representa la corriente de la carga ubicada en el n-ésimo nudo y conectada a la fase f.

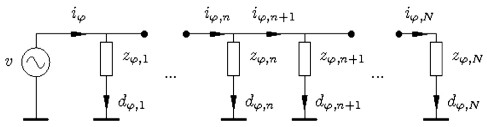
La figura 1 muestra un grupo de cargas eléctricas conectadas a una fase del sistema de alimentación eléctrica. Nótese que únicamente se han representado las conexiones de cargas eléctricas a cada nudo de la red eléctrica, y cuya demanda es denotada por d_f,n.

Figura 1. Red eléctrica.

Es importante señalar que se consideró la magnitud del valor eficaz y no su representación fasorial, debido al hecho de que se consideró que el factor de potencia de todas las cargas son iguales, además de suponer que la caída de tensión a lo largo de la línea de distribución es despreciable, lo cual bajo estas consideraciones la corriente de cada carga conectada a una fase tiene el mismo ángulo, y como resultado de esto, la corriente que entrega cada fase está dada por la suma de las corrientes de las cargas conectadas a una misma fase.

Por otra parte, el hecho de que se haya considerado la suma de las diferencias de las magnitudes de la corriente al cuadrado, es debido a que se está haciendo la estimación sobre el supuesto de que el factor de potencia de las cargas conectadas al sistema de distribución es el mismo y además a la desigualdad de triangular:

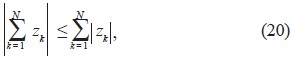
donde:

z_k Î C representa las diferencias de las corrientes.

Obviamente, si se minimiza el lado derecho de la desigualdad (20), se logra identificar el mínimo del problema, desde el punto de vista de su representación en fasores.

Además de estas consideraciones, la distribución probabilística de las cargas se suponen conocidas, bien sea, a través de alguna distribución probabilística típica o mediante alguna distribución probabilística empírica obtenida de los datos.

El problema entonces se fundamenta en definir cuál es la optima configuración de conexión, a objeto de obtener el mayor balance de carga durante el período estudiado, el cual es medido en función de la corriente eléctrica que entrega cada fase del sistema de distribución en los distintos puntos de conexión, siempre y cuando cumpla con la Ley de Corriente de Kirchoff (LCK).

Debido a que el modelo debe responder a qué fase del sistema de alimentación deben ser conectadas las cargas en los diferentes puntos de la red de distribución, se hace necesario replantear el Problema 1 en función de esta variable de decisión, la cual claramente debe ser una variable tipo {0,1}N, para así indicar si la carga está conectada, en este caso su valor será 1, o desconectada que en cuyo caso debe tener el valor de 0.

El nuevo modelo matemático asociado al problema es entonces:

Problema 2.

sujeto a:

 

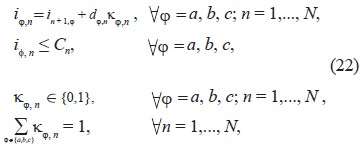
donde:

i_j para todo j = a, b, c está definido por la ecuación  (17), k_{j, n} es la variable de decisión que indica si la carga está o no conectada a la fase j del sistema, C_n es la capacidad máxima de corriente eléctrica que puede entregar el sistema en el n-ésimo nudo.

UN MODELO ALTERNO

En este aparte, se mostrará un modelo matemático alternativo al propuesto en el Problema 2 a objeto de expresarlo explícitamente en función de sus variables de decisión, conexión de la carga.

Del análisis de las ecuaciones de restricciones se tiene que para cada nudo n,

Aplicando la ecuación (23) de forma recursiva, se obtiene:

donde:

q significa el nudo q de la red de distribución eléctrica, e i_j,q representa la magnitud de la corriente eléctrica suministrada por la fase j en el nudo q.

Sea b_q [j₁ j₂] el índice de desempeño de la red, la cual permite medir el balance de corriente entre las fases j₁ y j₂ en el q-ésimo nudo de la red de distribución, y cuya expresión matemática está definida por:

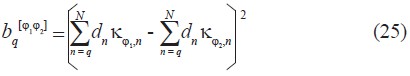
Empleando lo definido por la ecuación (25), para las fases a, b y c, se tiene que:

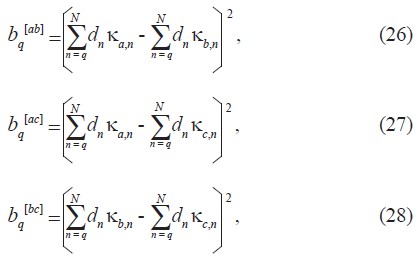
donde:

k_a,n, k_b,n y k_c,n representan las componentes del vector conexión de la carga d_n en el n-ésimo nudo, y q Î {N 1 ≤ q ≤ N} indica el número del nudo desde donde se está determinando el balance de carga.

Aplicando las ecuaciones (24), (26), (27) y (28), en la ecuación (21) se tiene que el balance del sistema medido desde la fuente de generación puede estar definido como:

donde:

k_j^t = k_j,1, . . . ,k_j,N para todo j = a, b, c; b₁[j1j2] es la medida de balance entre las fases j₁ y j₂, y cuantificado desde el nudo 1. Observe que los términos de las variables de decisión k_a,n, k_b,n y k_c,n representan la conexión de la carga d_n en el n-ésimo nudo.

Combinando el modelo representado por las ecuaciones (29) y (22), se tiene que el problema puede ser planteado como:

Problema 3.

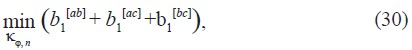
sujeta a:

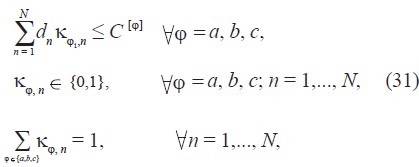
donde:

b_q ^[j1^j2^] para todo j₁ ≠ j₂ = a, b, c están definidos respectivamente por las ecuaciones (26), (27) y (28).

Nótese que el Problema 3 está expresado en función de la variable entera conexión k_j,N de la carga d_n en el n-ésimo nudo.

Es importante señalar que la carga es considerada aleatoria con función de densidad de probabilidad conocida. Este último hecho obliga a estudiar el problema desde una perspectiva estocástica, para lo cual se propone un método de identificación de óptimo por Monte Carlo. No obstante, se estudió su solución primeramente bajo el supuesto de que la carga eléctrica es determinista, para así luego estudiar el problema desde una óptica aleatoria.

Observación 1. De acuerdo a los teoremas 2, 4 y 5, la función objetivo propuesta en el Problema 3 es una función convexa y su mínimo global es identificado por medio de de un mínimo local.

Definición 4 (Matriz de conexión). Denote por K Î {0,1}_3xN la matriz compuesta únicamente por elementos {0,1} tal que cada fila representa una fase del sistema, y cada j-ésima columna representa el correspondiente nudo j del sistema de distribución.

Observación 2. Para cada j-ésima columna, debe satisfacerse que S³_j=1 k_j,_j = 1 debido a que cada carga está exclusivamente conectada a una sola fase del sistema de distribución de energía eléctrica.

Observación 3. Para cada fase j la suma de las magnitudes conectadas a ella debe ser menor o igual a su capacidad. Es decir, S^Nn=1 k_j1,n d_n ≤ C ^[j]. No obstante, a los efectos del alcance de este estudio, se supondrá que la capacidad del sistema de distribución es mucho mayor que la suma de las cargas posibles que pueden ser conectadas.

Un ejemplo de la matriz de conexión, para el caso de 7 nudos es:

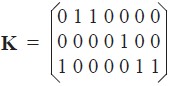
Nótese que la única información necesaria para definir la matriz de conexión es el número de la fila donde está 1, lo cual permite simplificarla a través del vector de conexión k_[N], donde N significa el número de nudos. Siguiendo el ejemplo anterior se tiene que:

k^t _[7] = (3,1,1,0,2,3,3).

Observe que de acuerdo a la matriz de conexión no existe carga conectada al nudo 4, lo cual es indicado en el vector de conexión con un cero en el cuarto elemento del vector. En general el vector k_[N] viene dado por:

k^t _[N] = (k₁,k₂,...,k_N),

donde:

k_n Î {0,1,2,3} representa si la n-ésima carga está desconectada indicándose con un 0, o en el caso de estar conectada a una de las fases, la misma es indicada con el número de la fase a la cual está conectada. De aquí 1, 2 y 3 representan la conexión a las fases a, b y c, respectivamente.

Debe señalarse que el número de distintas conexiones factible es 3^N bajo la consideración que en cada uno de los nudos existe una carga conectada al sistema de alimentación y cada fase del sistema tiene capacidad ilimitada. Esto significa que en un problema de 12 nudos, el número máximo de configuraciones es de 531.441, lo cual representa un número considerablemente elevado.

Esta eventual situación crea la necesidad de emplear algún método eficiente de identificación de óptimos, y más si debe estudiarse el problema para el caso cuando la carga es considerada aleatoria, ya que debe hacerse un número significativo de réplicas a objeto de coleccionar las muestras de cada réplica y así realizar el estudio estadístico de la solución.

EL MÉTODO ALGORÍTMICO

En virtud de que la carga d_n conectada a cada n-ésimo nudo es considerada aleatoria con distribución acumulativa de probabilidades F_Dn(d), se empleó como metodología de identificación de la óptima configuración de conexión, el enfoque de Monte Carlo para simular las distintas cargas asociadas a las aleatoriedades, Law & Kelton (2000), y el método de particiones anidadas (MPA) a objeto de identificar la óptima configuración de conexión, Shi & Ólafsson (2000a).

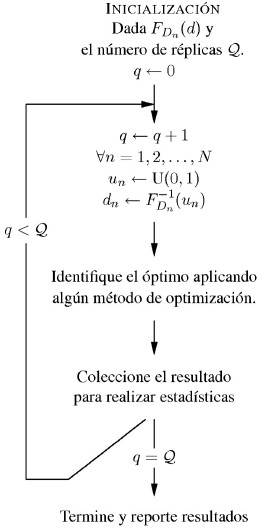
La figura 2 muestra un esquema general en donde se representa cada uno de los principales pasos que son propuesto como método, a fin de identificar la óptima configuración de conexión que permita el mejor balance. En la figura, F_Dn(d) representa la función de distribución acumulativa de probabilidades de cada n-ésima carga, q representa el contador de réplicas, y U(0,1) significa una variable aleatoria distribuida uniformemente entre 0 y 1.

Figura 2. Diagrama de la metodología.

Una forma alterna de identificar el mínimo es a través de la evaluación de cada punto, dado que las variables de decisión son enteras. No obstante, cuando el número de puntos de diseño es elevado, este método resulta sustancialmentecostoso. Por esta razón, se debe emplear algún método que permita identificar sistemáticamente el punto óptimo.

Un aspecto importante en mencionar es el hecho de que este enfoque, aun cuando es analizado bajo un enfoque estático, considera los aspectos aleatorios que tienen las cargas, a través de los valores que pueden tomar las cargas, los cualesson reflejados en las distribuciones probabilísticas quetoman en cuenta la permanencia en el tiempo. Esto es debidoal hecho de que el interés en el trabajo es proponer unmétodo, que a través de un estudio estadístico de las solucionesaportadas por cada réplica, pueda sugerirse la mejorconfiguración de conexión de las cargas. No obstante, este estudio estadístico y un estudio cuando las cargas varían dinámicamente será tema a tratar en un futuro artículo.

Método de particiones anidadas

El método de particiones anidadas (MPA) busca dividir la región de factibilidad en regiones, a objeto de identificar la región prometedora mediante la comparación de una muestra de puntos de diseños tomados de cada región, permitiendo así concentrar la búsqueda, mediante la subdivisión de la región prometedora. Sin embargo, el método permite escapar de los óptimos locales a efecto de identificar el óptimo global, por cuanto una de sus características es su aleatoriedad,en la evaluación de las distintas opciones o puntos de diseños definidos por las combinaciones que conforman el conjunto de soluciones factibles.

Por otra parte, el hecho de contar con una función objetivo convexa permite asegura la identificación de al menos un óptimo global, en virtud de que pueden existir más de una configuración que alcance el óptimo global.

En cuanto a la convergencia del MPA, su estudio fue presentado por Shi & Ólafsson (2000c), el cual está basado en el enfoque de cadena de Markov.

Notación

A fin de mostrar el método, son definidos algunos conceptos básicos del método y la notación empleada por Shi & Ólafsson (2000a).

Q: es la totalidad de la región factible.

S = { s Í Q | es una región válida de una partición }.

S₀ = { s Î S | s está a la máxima profundidad }.

s(k) : la región prometedora en la k-ésima iteración.

d(k) : profundidad de la región s Î S.

s(k) : superregión s Î S.

El algoritmo

El MPA está compuesto de cuatro principales pasos, denominados: partición, muestreo, estimación de la región prometedora y retroceso.

Partición

Denótese por M_s(k) como el número de subregiones de s(k) de la región prometedora. Es decir, la partición de s(k) en M_s(k) subregiones es definida por s₁(k), . . . , s_Ms(k) y la superregión es definida por Q \ s(k) , la cual es indicada como la región M_s(k) + 1.

Muestreo

Este paso ofrece mucha flexibilidad, por cuanto el método permite cualquier esquema de muestreo. Sin embargo, para la aplicación planteada en este artículo, se aplicará un esquema de muestreo uniforme, el cual asegura una competencia entre todas las soluciones con el mismo peso de ser  seleccionado.

Una formulación matemática de este paso es como sigue: sea N_j el número de puntos de diseño provenientes de la región s_j(k) a ser muestreado, definida en la k-ésimo iteración. Emplee cualquier esquema de muestreo para seleccionar N_j de cada s_j(k) región, para todo j = 1, 2,..., M_s(k) + 1. Es decir, como consecuencia del muestreo de cada j-ésima región deben ser seleccionados los diferentes puntos de diseños q^j1, q ^j2,..., q^jN_j para todo j = 1, 2,..., M_s(k) + 1. Además, se estima la función de desempeño para cada punto de diseño muestreado. En términos matemáticos, obtenga f (q^j1), f(q^j2), . . . , f (q^jNj) para cada j = 1,2,..., M_s(k) + 1.

Estimación de la región prometedora

El principio de este paso es identificar la región con la mejor función de desempeño. Para esto, determine:

La ecuación (32) determina el índice de la región que contiene el mejor punto de diseño. Es importante destacar que en el caso de funciones de desempeño aleatorios, la estimación del mínimo puede recurrirse a cualquier método de optimización ordinal, Chen et al. (2000), o algún método directo de optimización.

Retroceso

El MPA ofrece dos reglas de retroceso a los efectos de escapar del proceso de búsqueda sobre una subregión, cuando ella eventualmente no contenga el óptimo global. No obstante, en este estudio se implementó la regla de retroceso en la cual el MPA reinicia su exploración sobre la totalidad de la región de factibilidad. Es decir, si al comparar los diferentes puntos de diseños resulta como región prometedora la correspondiente a la superregión, entonces se reinicia el algoritmo nuevamente.

En términos matemáticos, se tiene: si j_k < M_s(k) + 1, entonces s(k + 1) = s_jk (k) y d(k + 1) = d(k) + 1. En caso contrario, s(k + 1) = Q y d(k + 1) = 1.

EJEMPLOS NUMÉRICOS

En esta sección se presentan dos tipos de ejemplos numéricos, el primero de ellos es determinista, y fue realizado a los efectos de verificar el algoritmo, con diferentes valores de cargas. El segundo, definido por variables aleatorias, las cuales son definidas en el preámbulo de cada experimento.

Es importante destacar que el número de puntos de diseños muestreados, para las subregiones y superregiones, denotados por ns y ns , respectivamente, es determinado de forma dinámica de acuerdo a la profundidad en función del número máximo de posibles casos, es decir, de acuerdo a:

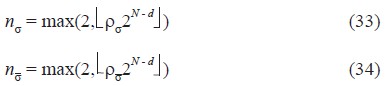
donde:

rs Î (0,1) es el factor de muestreo para cada subregión, rs Î (0,1) es el factor de muestreo para cada superregión definida por el algoritmo, N es el número total de nudos y d es la profundidad de búsqueda definida por el MPA. Este esquema de muestreo dinámico es propuesto por el autor como resultado de laheurística ensayada en el algoritmo, no obstante, su estudio teórico debe constituir un próximo paso en la línea de investigación iniciada en este trabajo.

Además, la eficiencia del método algorítmico es determinada mediante:

donde:

m representa el número de evaluaciones de la función objetivo requeridos para identificar al menos un óptimo.

Con relación al generador de números pseusoaleatorio U(0,1) empleado para la realización en los ejemplos numéricos, se implementó el código de programación propuesto por Law & Kelton (2000).

Caso determinista

A objeto de verificar el desempeño del algoritmo, se realizaron un número importante de pruebas, con distintos valores de carga de enteras, ya que de esta manera puede ser verificado fácilmente el resultado obtenido. Para esto, el factor de muestras por cada subregión y superregión fue de rs= 0,4 y rs = 0,5 , los cuales son empleados para definir el número de puntos de diseños a ser muestreados tanto en las subregiones como en las superregiones definidas en las iteraciones a través de las ecuaciones (33) y (34), respectivamente.

La tabla 1 muestra un conjunto de 20 réplicas con distintos valores de cargas. Nótese que el algoritmo logra identificar al menos un óptimo global con tan sólo 8.390 evaluaciones de la función objetivo, de un total de 531.441 posible combinaciones, debido al hecho de que pudieran existir más deun esquema de conexión óptimo. El esquema de conexiónóptimo para cada réplica es indicado por la primera fila decada réplica del tercer grupo de valores, para una carga por nudo, en cientos de Amperes, las cuales son indicadas enla segunda fila de ese mismo grupo de resultados. Además,en el cuadro en referencia, R significa el número de la réplicao escenario, NE denota en número de evaluaciones de la función objetivo, i₁, i₂ e i₃, representan las sumas de las corrientes entregada por el sistema de distribución para las fases a, b y c, respectivamente. Por ejemplo, la réplica 1, y cuyo reporte es mostrado en las dos primeras filas de la tabla 1 indica: el valor obtenido de la función objetivo f(K₁₂) = 2; número de evaluaciones NE = 8.390; i_a = 119; i_b = 120; i_c = 120; la carga ubicada en el nudo n₁ de magnitud 27 es conectada a la fase 2, es decir, a la fase b; la carga localizada en el nudo n₂ de magnitud 32 es conectada a la fase 3, en otras palabras, a la fase c; la carga ubicada en el nudo n3 de magnitud 28 es conectada a la fase 1, es decir, a la fase a, y así sucesivamente.

Tabla 1. Resumen de experimentos con distintas cargas deterministas.

Como fue definido anteriormente, el esquema de conexión ha sido representado por los número 1, 2 y 3, para indicar que carga es conectada, respectivamente, a las fases a, b y c. Por otra parte, según lo definido por la ecuación (35), puede afirmarse que para este grupo de experimentos la eficiencia en todas las réplicas fue de h = 98,42%, lo cual comprueba la alta eficiencia del método algorítmico para el modelo matemático propuesto.

La tabla 2 presenta los resultados obtenidos para una misma carga determinista. Las condiciones de muestreo fueron las mismas del caso anterior. Observe que el algoritmo identificó diversas configuraciones óptimas de conexión, las cuales corresponden a mínimos locales, y por ende a mínimos globales debido a las características de la función objetivo. Por otra parte, el MPA identificó en cada réplica al menos un mínimo local con una eficiencia h = 98,11%.

Tabla 2. Resumen de experimentos con la misma carga determinista.

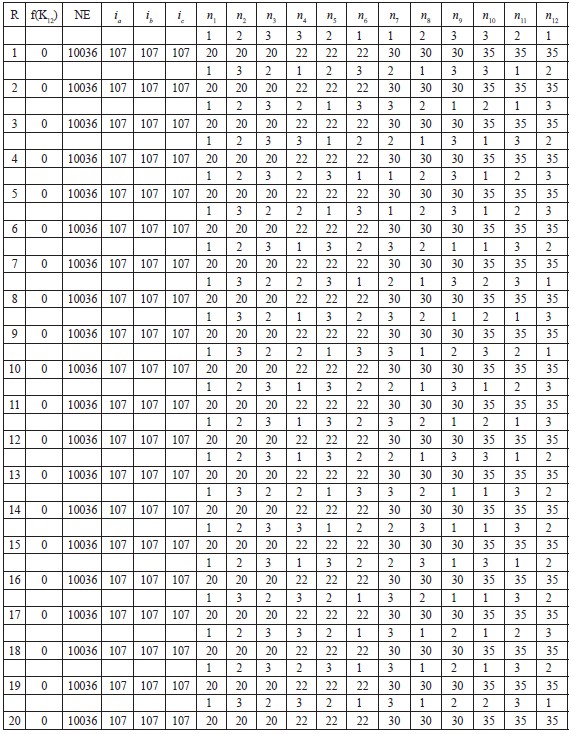
Los resultados obtenidos por el algoritmo, para este específico caso de estudio son fácilmente verificables, en virtud de que obviamente sendas cargas de 20, 22, 30 y 35, tienen que estar conectadas a sendas fases en el sistema de distribución de energía eléctrica.

Caso aleatorio

Para estudiar este caso, se adjudicaron cargas reales aleatorias con distribuciones uniformes continuas tales que D_n ~ U(m_n - √3s, m_n - √3s) para todo n = 1,2,...,N , donde m_n y s denotan la media de la n-ésima carga y su desviación típica, respectivamente.

Para el caso bajo estudio, se tomó como valores medios de las cargas especificadas por la tercera réplica del experimento reportado por la tabla 1, es decir, el vector d^t = (36, 24, 19, 31, 22, 24, 21, 38, 28, 20, 35, 38) y desviaciones típicas s = 0,1; 1; 6.

La tabla 3 muestra el resultado de 20 réplicas, en donde todas las cargas tienen una desviación típica de s = 0,1. En cuanto al factor de muestras por cada subregión y superregión fue, respectivamente, de rs = 0,7 y rs = 0,5.

Tabla 3. Cargas aleatorias con s = 0,1.

Obsérvese que el método no identificó el óptimo en el 20% de los casos. Sin embargo, el método mostró tener una eficiencia h = 97,4%. Además, nótese que la eficiencia del método depende ciertamente del número de muestras que tome en cada subregión y superregión.

En el caso reportado por la tabla 4, el factor de muestras por cada subregión y superregión fue de rs = 0,7 y rs = 0,5, y en cuanto a la desviación típica de las cargas se fijó a un valor de s = 1.

Tabla 4. Cargas aleatorias con s = 1.

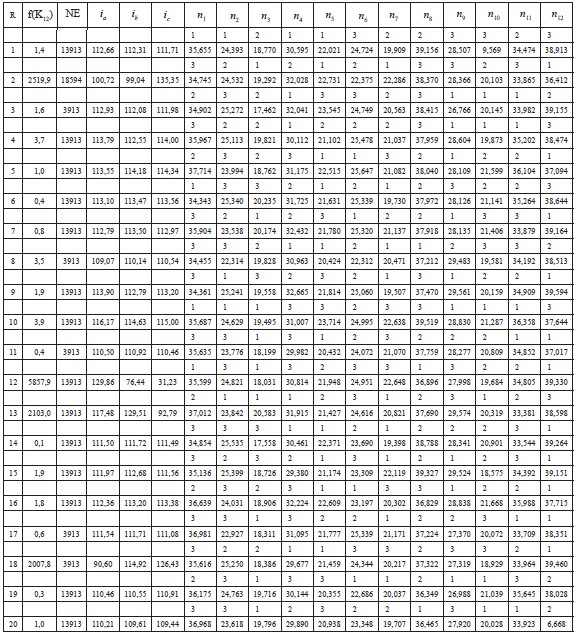
Obsérvese que en este caso, el método no identificó el óptimo en el 20% de los casos, y su eficiencia fue de h = 97,4%, excepto en la réplica 2, que fue de 96,5%.

En la tabla 5 son reportados los resultados de 20 réplicas, cuando la desviación típica se fijó en s = 6. Las condiciones de muestreo se dejaron en los mismos valores de los casos anteriores. El método presentó una eficiencia de h = 97,4% en 18 réplicas, mientras que en las restantes mostró una eficiencia del alrededor de 96%.

Tabla 5. Cargas aleatorias con s = 6.

CONCLUSIONES

De lo reportado en esta investigación se puede concluir que:

El modelo matemático propuesto a los efecto de medir el balance de las cargas conectadas a un sistema de distribución de energía eléctrica es lo suficientemente adecuado, en virtud a sus propiedades de convexidad, las cuales al identificar al menos un óptimo local, el problema es solucionado globalmente.

Aun cuando el método de identificación de óptimo empleado puede fallar, el mismo puede emplearse, en virtud de que a través de las réplicas se identifican al menos un mínimo local, el cual constituye un mínimo global del problema.

En cuanto a la identificación de la óptima configuración bajo restricciones de capacidades en el sistema de distribución de energía eléctrica, puede emplearse algún método de penalización a fin de no seleccionar como solución, si ésta viola la capacidad de carga de la o las fases. No obstante, el tema abordado en esta investigación no limita el enfoque empleado en el trabajo.

De los ejemplos numéricos, puede apreciarse la necesidad de estudiar concienzudamente el método de particiones anidadas, sobre todo en cuanto a la optimización del número de muestras para cada subregión y superregión. Esto último pudiera constituir un interesante tema a ser estudiado a fin de mejorar el método algorítmico de particiones anidadas.

AGRADECIMIENTO

El autor desea agradecer al Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuelapor el financiamiento de esta investigación registrada bajo en número PI 08-00-5690-2004. Además, el autor desea también expresar su gratitud a los árbitros anónimos, quienes con sus observaciones contribuyeron en la mejora de este artículo.

REFERENCIAS

1. Bazarra, M. S., Sherali, H. D., Shetty, C. M. (1993). Nonlinear Programming: Theory and Algorithms. New York: Wiley. 2nd. edition.        [ Links ]

2. Brea, E., Cheng, R. C. H. (2003). Optimisation of four queue network via Nested Partition method. International Journal of Simulation, Systems, Science & Technology 4(1/2); 23-28.        [ Links ]

3. Chen, C-H., Lin, J., YÜcesan, E., Chick, S. E. (2000). Simulation budget allocation for further enhancing the efficiency of ordinal optimization. Discrete Event Dynamic Systems: Theory and Applications 10(3); 251-270.        [ Links ]

4. Law, A. M., Kelton, W. D. (2000). Simulation Modeling and Analysis. Boston: McGraw-Hill. 3rd. edition.        [ Links ]

5. Murota, K. (2003). Discrete Convex Analysis. Philadelphia: Society for Industrial and Applied Mathematics.        [ Links ]

6. Shi, L., Ólafsson, S. (2000a). Nested Partitions method for global optimization. Operations Research 8(3); 390- 407.        [ Links ]

7. Shi, L., Ólafsson, S. (2000b). Nested Partitions method for stochastic optimization. Methodology and Computing in Applied Probability 2(3); 271-291.        [ Links ]

8. Shi, L., Ólafsson, S. (2000c). Stopping rules for the stochastic Nested Partitions method. Methodology and Computing in Applied Probability 2(1); 37-58.        [ Links ]

9. Zhu, J., Bilbro, G., Chow, M-Y. (1999). Phase balancing using simulated annealing. IEEE Transactions on Power Systems 14(4); 1508-1513.        [ Links ]

10. Zhu, J., Chow, M-Y., Zhang, F. (1998). Phase balancing using mixed-integer programming. IEEE Transactions on Power Systems 13(4); 1487-1492.        [ Links ]