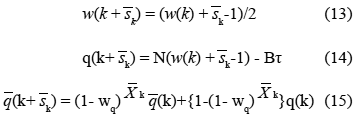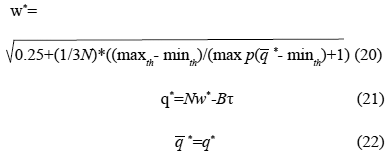Análisis del algoritmo red con la teoría de control moderna

Claudio Parra

Universidad Central de Venezuela. Facultad de Ingeniería. Escuela de Ingeniería Eléctrica. email: claudio942002@yahoo.com

RESUMEN

En este trabajo se presenta un estudio de la estabilidad del sistema formado por el algoritmo de detección temprana aleatoria (RED) en conjunto con el protocolo de control de transmisión (TCP) en función de los parámetros del sistema utilizando la teoría de control moderna. Se deduce la ecuación linealizada del sistema mediante la cual se hace un estudio de la estabilidad en función de la posición de los polos de la matriz del sistema linealizado. Se observa que a medida que crece la cantidad N de conexiones TCP, disminuye la estabilidad. Mediante simulaciones, se comprobaron los resultados obtenidos del análisis teórico. Los experimentos incluyeron diferentes condiciones de operación del sistema con varios valores de máxima probabilidad de marcado de los paquetes, observándose que para valores grandes de probabilidad, la estabilidad relativa también disminuye.

Palabras clave: TCP, RED, Congestión, Simulación, Matriz de estado.

Analysis of the red algorithm with modern control theory

ABSTRACT

This paper presents a study of the stability of the system of the RED (Random Early Detection) algorithm in conjunction with TCP (Transmission Control Protocol) based on the parameters of the system using modern control theory. We deduce the linearized equation of the system through which a study of stability depending on the position of the poles of the linearized system matrix is made. It was noted that as the number (N) of TCP connections grows, stability reduces. Through simulations, the expected results were verified by theoretical analysis. The experiments include different system operating conditions with various values of highest probability of marking packets, noting that for high probability values, the relative stability also decreases.

Keywords: TCP, RED, Congestion, Simulation, State matrix.

Recibido: septiembre de 2009   Recibido en forma final revisado: enero de 2010

INTRODUCCIÓN

El control de congestión en la redes de transmisión de datos requiere de una especial atención debido al crecimiento de demandas de recursos. Se han escrito diferentes trabajos sobre el algoritmo RED y se ha estudiado brevemente el problema del modelaje de la congestión de una red a la luz de la teoría de control clásico. En este trabajo se describe el algoritmo de detección temprana aleatoria como punto de partida en la aplicación de la teoría de control moderna, para estudiar el comportamiento según la variación de la probabilidad de descarte del mismo algoritmo. Para esto se deducen las ecuaciones del sistema basadas en el algoritmo de detección temprana aleatoria y el protocolo de control de transmisión, y luego se derivan las ecuaciones promedio de transición de estado. Luego se genera la matriz de la ecuación de estado linealizada, la cual será utilizada para los experimentos. Dada la complejidad del estudio y su longitud, sólo se estudio la variación de la probabilidad de descarte y el número de fuentes TCP. Los resultados obtenidos concuerdan con los esperados por la teoría.

MARCO TEÓRICO

Uno de los mecanismos más importantes y más utilizado para lograr el control de congestión en redes IP, es el algoritmo RED. La idea de usar un servidor con el algoritmo RED programado, es para mantener un promedio de longitud de la cola de paquetes baja (esto se observa en la memoria buffer a la entrada del servidor). El algoritmo RED descarta aleatoriamente los paquetes de entrada con una probabilidad proporcional al promedio de la longitud de cola. Según los creadores del algoritmo RED (Floyd et al. 1993) éste tiene ventajas sobre otros métodos como Drop Tail, las cuales podemos resumir así:

1. El promedio de la longitud de cola es mantenido bajo, por lo que el retardo de extremo a extremo de una conexión TCP es bajo también.

2. RED no tiene desventajas para el tráfico en ráfagas.

3. La sincronización global de conexiones TCP se toma en cuenta.

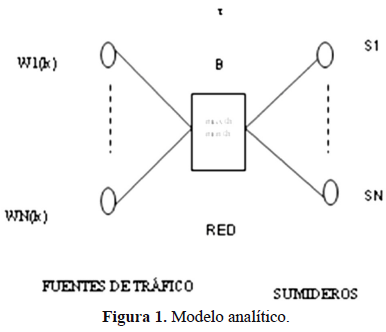
El modelo analítico (Comer, 1997; McCabe, 2003) de una red de datos se muestra en la figura 1:

donde:

N numero de conexiones TCP, t la latencia, B la velocidad de procesamiento, W_n(k) el tamano de la ventana del host n (fuente) y la ranura k (una ranura (slot) es el tiempo RTT (tiempo de ida y vuelta) de la conexion TCP. La longitud de la ranura cambia constantemente debido a los retardos de la cola en el servidor que ejecuta el algoritmo RED), S1-SN son los sumideros, y TCP el protocolo de control de transmision.

Una dificultad importante para la aplicacion del algoritmo RED consiste en que sus parametros son dificiles de ajustar en forma optima en las redes reales (Christiansen et al. 2001). Cada vez que un paquete nuevo llega a la cola del enrutador (servidor con RED), se estima el tamaño promedio de la cola usando un proceso EWMA (Promedio de movimiento de peso exponencial), utilizando la siguiente ecuación:

avg ()= (1-w_q)*avg+w_q*q       (1)

donde:

avg es la longitud promedio de cola estimada, q la longitud instantánea de cola, w_q el factor de peso, y la longitud promedio de cola.

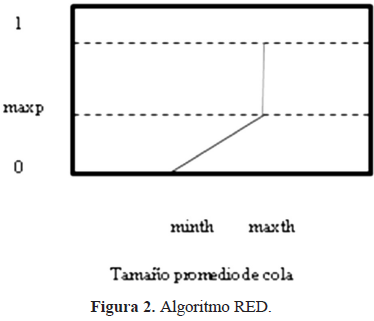
Este valor de avg es comparado por dos umbrales min_th y max_th (figura 2).

Si el valor promedio es menor que min_th, entonces no pasa nada, pero si es más grande que max_th el paquete se desecha. Los valores intermedios son marcados con un valor entre 0 y max_p, donde max_p es un valor probabilístico que se asocia a los paquetes marcados y es directamente proporcional al promedio de la longitud de la cola.

Para nuestro estudio necesitamos definir un modelo analítico donde se tiene que:

1. q(k) es el valor actual de la cola (medido en paquetes).

2. (k) es el tamaño de cola promedio en la ranura k (medido en paquetes).

Se asume que q y no cambian durante cada ranura. Esto ha sido confirmado para valores pequeños de w_q ya que se usa un filtro pasa bajos para calcular (k) (ecuación (1)) (Floyd et al. 1993).

El servidor que ejecuta el algoritmo RED (servidor RED), calcula una probabilidad de marcado de paquetes p_b usando el promedio de longitud de cola para los paquetes que llegan. A continuación se muestra el mecanismo de marcado:

p_b es 0 si (k) < min_th        (2)

es 1 si (k)= ó > max_th ,    (3)

en otro caso:

p_b= max_p( - min_th)/(max_th-min_th )     (4)

Luego, el servidor RED aleatoriamente descarta cada paquete de entrada con probabilidad p_a, según la siguiente ecuación:

p_a=p_b/(1- contador*p_b)         (5)

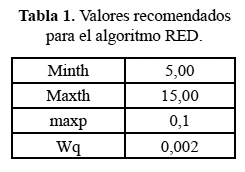
El contador indica el número de paquetes no marcados que han llegado desde el último paquete marcado. El mecanismo de marcado de paquetes no es por flujo sino por el número de paquetes. Para encontrar más información sobre RED se puede consultar (Floyd et al. 1993), donde ellos recomiendan valores para el uso del algoritmo RED (tabla 1).

MARCO METODOLÓGICO

Análisis del estado estable

Para deducir las ecuaciones del sistema que predicen el comportamiento del estado estable, se necesita hallar las ecuaciones de transición. Estas ecuaciones se derivan del control de congestión en TCP y la que rige al algoritmo RED (Floyd et al. 1993).

Para esto se determina la probabilidad de desechar un paquete en la ranura k. En la primera ranura k el transmisor n envía w_n(k) paquetes hacia el sumidero. Como ya sabemos, el servidor RED marca cada paquete basado en el promedio de la longitud de la cola(p_b). Se asume que es fijo en una ranura por lo que p_b es fijo también. Donde p_b se determina por:

p_b(k)=maxp((k)-min_th)/(max_th- min_th)     (6)

Según el algoritmo RED, la probabilidad de marcado definitiva es:

p_a(k) = p_b(k)/(1- contador*p_b(k))       (7)

Luego definimos como el número de paquetes no marcados entre dos consecutivos marcados. es una variable aleatoria uniformemente distribuida: P_k que toma valores {1,2,……1/p_b(k)} y es:

P_k [X = n] = {p_b(k) si 1 <= n <= 1/p_b(k); 0 en otro caso}       (8)

donde:

representa el número de paquetes no marcados entre dos marcados consecutivamente en la ranura k.

Entonces:

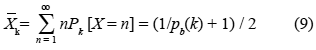
Para este trabajo usaremos la versión de TCP básica, en la que si al menos un paquete es marcado con una probabilidad, el ancho de la ventana en la ranura k+1 será:

w(k +1) ={w(k) /2 con probabilidad , w(k) +1 en otro caso}

Y es:

es el mínimo del intervalo [(w(k)/(1/p_b(k)),1]

Ahora q(k +1) es igual al estado actual q(k) más los anchos de la ventana de todas las conexiones TCP. Si se incluye la velocidad de procesamiento B y la latencia t, se tiene:

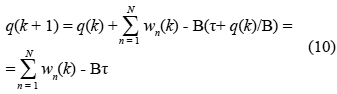
Tomando en cuenta las siguientes condiciones sobre el algoritmo RED:

1. El servidor RED actualiza el promedio de longitud de cola con cada paquete que llega.

2. Esta actualización es veces en la ranura k.

3. q(k) es fijo en cada ranura

Luego podemos decir que la relación entre (k+1) y (k) esta dada por la siguiente ecuación:

(k+1) = (1 - w_q)^a (k) + {1 - (1 - w_q)^a}q(k)      (11)

Derivación de las ecuaciones promedio de transición de estado

Ohsaki et al. (2002) en su estudio introducen la idea de tratar una red de transmisión de datos como un sistema en tiempo discreto en donde se manejan secuencias de datos y a cada secuencia corresponden varias ranuras (ésta es una visión más amplia que la de considerar solamente ranuras individuales). Se define como el número promedio de ranuras en una secuencia determinada, que comienza en la k-ésima ranura.

Para efectos de este trabajo utilizamos las 3 ecuaciones (13), (14) y (15), propuestas por Ohsaki et al. (2002), para determinar los valores de equilibrio de un sistema de transmisión de datos. Estas ecuaciones se basan en el algoritmo RED y en el protocolo TCP, y el análisis de ranuras para este proceso discreto. Asumiendo que es el número de ranuras en una secuencia que guarda la siguiente relación con la ventana w(k):

donde:

N es el número de fuentes TCP

Las 3 ecuaciones de w(k + ), q(k + ) y (k + ) describen las ecuaciones de transición de la ranura k a k+ , y son:

Donde estas ecuaciones de transición describen el comportamiento promedio del tamaño de la ventana, la longitud de la cola actual y el promedio de la longitud de la cola.

Cuando los tamaños de las ventanas de los hosts son idénticos podemos decir que:

En el estado estable se pueden obtener las ecuaciones de equilibrio según las siguientes igualdades. (Para más detalles véase Ohsaki et al. 2002):

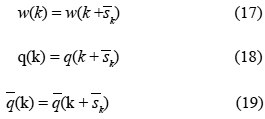
resultando:

donde:

w* representa el mínimo valor esperado de la ventana al comienzo de la secuencia, para obtener el promedio del tamaño de la ventana consultar en Ohsaki et al. (2002).

Analisis de estabilidad y la teoria de control moderno

En esta parte se estudia la estabilidad del sistema (servidor RED). El sistema en cuestion es no lineal, por lo que se linealiza y se estudia su comportamiento alrededor de un punto de equilibrio. Las ecuaciones (13), (14) y (15) definen el comportamiento del sistema TCP y RED.

Dado un vector de estado x(k) tenemos que dx(k) es la diferencia entre el vector en un instante k y el punto de equilibrio:

Linealizando alrededor de (*) w(k), q(k) y (k) de las ecuaciones (13), (14) y(15), obtenemos:

donde:

A es la matriz de la ecuación de estado linealizada:

donde para nuestro caso especifico se obtiene:

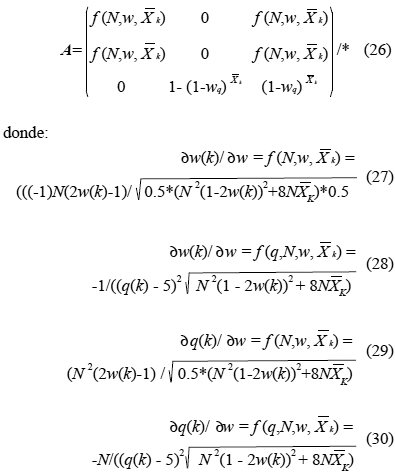
TÉCNICAS EXPERIMENTALES

El propósito del trabajo es estudiar la estabilidad del algoritmo RED y el mecanismo de congestión más simple que usa TCP. Para esto fijamos las condiciones de operación en un punto estable. Además, se determinó la observabilidad y la controlabilidad del sistema TCP-RED.

Una vez determinado el punto de equilibrio (20), (21) y (22) se evaluó la matriz de estado en el punto estable:

A* = f(w*, q* , q *)       (31)

Luego, se tomaron los valores iniciales de las gráficas de los resultados de Ohsaki et al. (2002) para evaluar las ecuaciones (20), (21) y (22), obteniéndose resultados de q y w que permitiesen determinar la Matriz de Estado y su polinomio característico. Se corrieron varios casos con diferentes maxp. También se obtuvo la Matriz para otros casos de B y t, lo cual es propósito de una segunda parte de este trabajo.

Se usaron los valores de la tabla 1 para la consideración de los parámetros del algoritmo RED. Se observó la estabilidad del sistema en cada caso mediante la magnitud de los polos de la Matriz A. Se usaron diferentes valores de la probabilidad de descarte.

RESULTADOS Y DISCUSIÓN

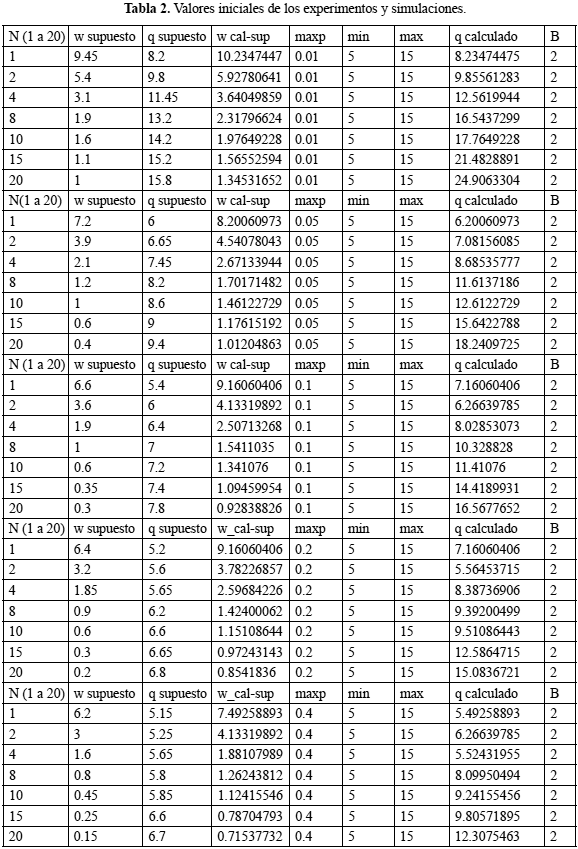
En la tabla 2 se resumen los casos estudiados mediante simulación. Cada uno de ellos comprende fuentes de tráfico en 1 y 20 (N=1,2,4,8,10,15 y 20).

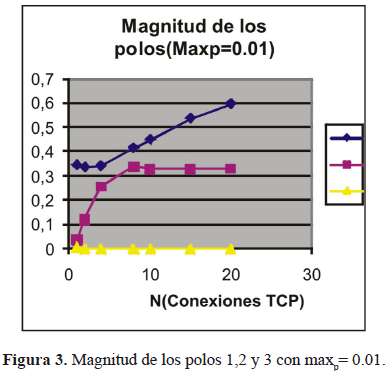
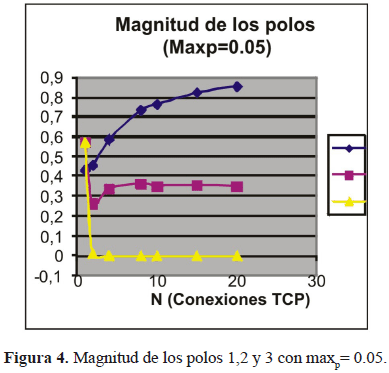
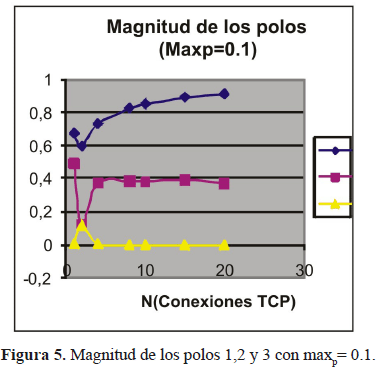
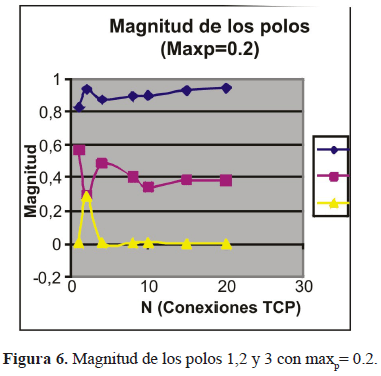
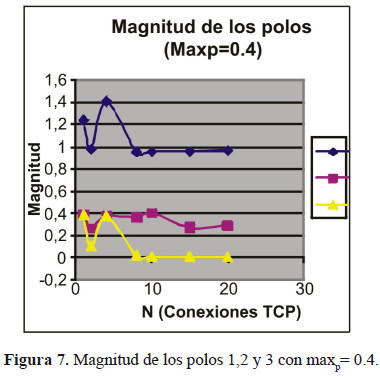
El objetivo final fue determinar la estabilidad del sistema evaluando el polinomio característico de la matriz A. Esta es generada para los casos indicados en la tabla 2. Graficando la magnitud de los polos de los casos mencionados, se puede observar cómo varia la estabilidad relativa del sistema TCP-RED (figuras 3,4,5,6 y 7).

En la figura 3 con maxp=0.01, la magnitud de uno de los polos tiende a 1, pero se mantiene la estabilidad para todos los valores de N.

En la figura 4 con maxp=0.05, la magnitud de uno de los polos tiende a 1 más rápidamente que el caso anterior.

En la figura 5 con maxp=0.1, la magnitud de uno de los polos tiende a 1 más rápidamente que los dos casos anteriores.

En la figura 6 con maxp=0.2, uno de los polos está muy cercano a 1 en todos los casos de N.

En la figura 7 con maxp=0.4 el sistema es totalmente inestable.

En general, se observó en las figuras anteriores que aumentar la probabilidad de marcado de los paquetes tiene un efecto de hacer inestable el sistema, lo cual confirma los resultados de Floyd et al. (1993). Floyd (2003) recomienda usar una probabilidad baja para que los paquetes no sean descartados con alta probabilidad, ya que con alta probabilidad se crea una necesidad de retransmisión de los paquetes que conduce a la congestión de sistema. También se observó que a medida que crece N (Numero de Conexiones TCP) el módulo de un polo (dominante) tiende a 1, lo que significa que la estabilidad relativa disminuye.

CONCLUSIONES

Después del estudio teórico y su verificación con casos prácticos, podemos concluir lo siguiente:

Se observó que a medida que crece N, la magnitud de los polos tiende a 1, por lo que se concluye que el sistema pierde estabilidad relativa. Este resultado es de esperarse, ya que a medida que N aumenta, crece el número de conexiones TCP y aumenta el tráfico que maneja la red, lo que conduce a congestión usando TCP y RED, es decir el sistema se hace ineficiente para manejar el trafico que circula por la red. Este es el principal problema de las redes de datos que usan el algoritmo RED y cursan tráfico TCP.

Los resultados son cónsonos con la propuesta teórica, permitiendo así un análisis amplio y válido del sistema TCPRED. Queda abierta la posibilidad de extender el estudio mediante la variación de los parámetros del algoritmo RED y el uso de otras ecuaciones de TCP. Como alternativas podemos recomendar el trabajo con nuevas versiones de TCP denominadas Illinois y África, así como nuevas versiones de RED, encontradas ambas en Internet.

No es posible usar una probabilidad alta para el descarte de paquetes, ya que en la simulación resultó que el sistema se comporta de forma inestable (módulo de los polos mayor que 1). Este resultado se refuerza con la variación de N.

El estudio abre el camino para otros trabajos que permitan ver la estabilidad del sistema con otros escenarios.

REFERENCIAS

1. Christiansen, M., Jeffay, K., Ott, D., Donelson, S. (2001). Tuning RED for Web Traffic. Recuperado el 20 de Septiembre de 2009, de www.icir.org/floyd/papers/TCPreport.pdf/.        [ Links ]

2. Comer, D. (1997). Redes de Computadores Internet e Interredes. Prentice Hall. p. 189.        [ Links ]

3. De Cnodder, S., Elloumi, O., Pauwels, K. Effect of different packet sizes on RED performance Traffic and Routing Technologies project. Recuperado el 20 de Septiembre de 2009, de http://arxiv.org/pdf/cs/0001005/.        [ Links ]

4. Dorf, R. & Bishop, R. (2005). Sistemas de Control Moderno. Pearson Prentice Hall. p. 386.        [ Links ]

5. Floyd, S. & Fall, K. (1999). IEEE Promoting the Use of End-to-End Congestion Control in the Internet. ACM Transactions on Networking. Recuperado el 20 de Septiembre de 2009, de www.aciri.org/floyd/papers/collapse.may99.pdf/.        [ Links ]

6. Floyd, S. (2000). A Report on Some Recent Developments in TCP Congestion Control. Recuperado el 20 de Septiembre de 2009, de www.aciri.org/floyd/papers/report_Jan01.pdf/.        [ Links ]

7. Floyd, S., Gummadi, R., Shenker, S., (2001). Adaptive RED: An Algorithm for Increasing the Robustness of RED’s Active Queue Management. Recuperado el 20 de Septiembre de 2009, de www.aciri.org/floyd/papers/adaptiveRed.pdf/.        [ Links ]

8. Floyd, S., & Jacobson, V. (1993). Random Early Detection gateways for Congestion Avoidance. Recuperado el 20 de Septiembre de 2009, de http://www.icir.org/floyd/red.html/.        [ Links ]

9. La, R.J., Ranjan, P., Abed, E. Feedback control of random early detection. Recuperado el 20 de Septiembre de 2009, de https://drum.umd.edu/dspace/bitstream/1903/200/1/umi-umd-1313.pdf/.        [ Links ]

10. Le, L., Aikat, J., Jeffay, K., Donelson, S. The Effects of Active Queue Management and Explicit Congestion Notification on Web Performance. Recuperado el 20 de Septiembre de 2009, de www.cs.unc.edu/~jeffay/papers/IEEE-ToN-05.pdf/.        [ Links ]

11. May, M., Bolot, J., Diot, C., Lyles, B. Reason to not deploy RED. Recuperado el 20 de Septiembre de 2009, de ieeexplore.ieee.org/iel5/6221/16606/00766502.pdf/.        [ Links ]

12. McCabe, J. (2003). Network analysis, architecture and design. Elsevier Science. USA. p. 501.        [ Links ]

13. Ohsaki, H. & Murata, M. (2002). Steady State Analysis of the RED gateway:stability, Transient Behavior, and Parameter Setting. IEICE Trans. Commun., Vol. E85- B, No.1. Recuperado el 20 de Septiembre de 2009, de citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.63.4304&rep.        [ Links ]

14. Welzl, M. (2005). Network Congestion Control. Wiley. England. p. 263.        [ Links ]

15. Zhang, H., Liu, M., Vukadinovic, V., Trajkovic, L., Modelling TCP/RED: a dynamical approach. Recuperado el 20 de Septiembre de 2009, de www.ensc.sfu.ca/~ljilja/publications_date.html/.        [ Links ]