Análisis preliminar de la vulnerabilidad de un sistema de potencia mediante interdicción determinista multiobjetivo

Claudio Rocco¹, José Ramírez-Márquez², Daniel Salazar³, César Yajure¹

¹Universidad Central de Venezuela. Escuela Básica de Ingeniería. e-mail: croccoucv@gmail.com; cyajure@gmail.com

²Stevens Institute of Technology. NJ. USA. e-mail: jose.ramirez-marquez@stevens.edu

³Ecole Nationale Supérieure des Mines de Saint Etienne. Francia. e-mail: danielsalazaraponte@gmail.com

RESUMEN

En este artículo se presenta un nuevo enfoque para el análisis de la vulnerabilidad de un sistema de potencia basado en un modelo híbrido que combina conceptos de interdicción determinista de grafos (IDG) y el uso de algoritmos evolutivos de optimización multiobjetivo (AEOM). La IDG aplicada a los sistemas de potencia permite entender la relación que existe entre la puesta fuera de servicio de los componentes que lo forman (ya sea debido a fallas aleatorias o acciones intencionales) y la carga que debe ser racionada. Los autores reconocen que, en el desarrollo de estrategias para prevenir el racionamiento, es posible tomar en cuenta múltiples objetivos contrapuestos y que pueden existir varias soluciones, dependiendo de las preferencias del ente encargado de tomar la decisión. A tal efecto se propone el uso de AEOM, como una herramienta de cálculo simple y eficiente. Para ilustrar el enfoque propuesto, se analizan dos sistemas clásicos en la literatura de sistemas de potencia, como son el IEEE 30-Bus y el IEEE-RBTS y una versión simplificada del sistema eléctrico de potencia de Italia. Los resultados obtenidos se comparan favorablemente con los resultados de otros enfoques reportados en la literatura y sugieren que el enfoque propuesto puede ser utilizado como un análisis preliminar para evaluar la vulnerabilidad de un sistema de potencia.

Palabras clave: Análisis preliminar de contingencias, Interdicción, Optimización evolutiva multiobjetivo, Seguridad de sistemas de potencia, Vulnerabilidad.

Power system vulnerability screening using multiple-objective deterministic interdiction

ABSTRACT

This paper introduces a new approach for the analysis of the vulnerability of power systems based on a hybrid model: an efficient multi-objective optimization evolutionary approach (MOEA) and the use of deterministic network interdiction concepts (DNIP). The paper analyzes the interaction between the power system’s component outages, due to external attacks or random failures and the system load shedding and considers that multiple prospective solutions could be selected, based on the preference of the decision-maker. A simple but powerful evolutionary algorithm can be used to address this multi-objective perspective. To illustrate the proposed approach, classical systems from literature are studied (IEEE 30-Bus and IEEE-RBTS) along with a simplified version of the Italian power system. As presented, the approach can be used as an initial straightforward screening approach to identify severe system disturbances and, to reproduce and/or significantly improve upon the results presented in previous studies.

Keywords: Contingency screening, Interdiction, Power system security, Multi-objective evolutionary optimization, Vulnerability.

Recibido: junio de 2009   Recibido en forma final revisado: diciembre de 2009

INTRODUCCIÓN

El sistema eléctrico de potencia (SEP) es una infraestructura básica en el desarrollo de una nación. La ocurrencia reciente de ciertos eventos tales como los ataques de septiembre en los Estados Unidos o los apagones de Nueva York o Caracas, han mostrado que estas estructuras pueden ser sensibles a la ocurrencia de fallas aleatorias o ataques intencionales.

En el caso de las fallas aleatorias, la ingeniería de confiabilidad y el análisis de riesgo han proporcionado herramientas y procedimientos para estimar, prevenir y manejar estos tipos de eventos. Sin embargo, los eventos debidos a ataques intencionales pueden producir pérdidas considerables y se han convertido en un nuevo reto para los analistas, en particular ante la presencia de una forma de inteligencia maléfica dirigida a maximizar el daño social (Apostolakis & Lemon, 2005).

Para analizar este tipo de eventos, se han desarrollado nuevos enfoques metodológicos que permiten analizar la seguridad de dichas infraestructuras con la intención de proporcionar algún tipo de protección ante la ocurrencia de ataques intencionales. En general, los desarrollos realizados se centran en la protección de infraestructuras que pueden ser modeladas mediante redes, tales como los sistemas de distribución de agua potable (Skolicki et al. 2006; Wadda et al. 2004) o los sistemas eléctricos de potencia (Holmgren et al. 2006; Holmgren, 2006; Johnson, 2007).

Para los SEP, se han definidos atributos de desempeño relacionados, por ejemplo, con la capacidad de suministro de energía. Los analistas, tradicionalmente, se han interesado en evaluar los efectos de las “fallas” de los componentes que forman el SEP y los efectos que producen en éste. En particular, se han usado las técnicas de análisis de contingencia para evaluar sistemáticamente la ocurrencia de eventos establecidos a priori de simple o múltiple contingencias (tales como M-1, M-2, entre otros, siendo M el número de componentes en el SEP).

Sin embargo, ante la posibilidad de eventos intencionales, el análisis se torna más difícil, en particular si la evaluación se realiza con técnicas probabilísticas, basadas principalmente en el uso de información de eventos aleatorios.

En este trabajo se presenta un nuevo enfoque para el análisis de la vulnerabilidad de un sistema de potencia basado en un modelo híbrido que combina conceptos de interdicción determinista de grafos (IDG) y el uso de algoritmos evolutivos de optimización multiobjetivo (AEOM).

La IDG aplicada a los sistemas de potencia permite entender la relación que existe entre la puesta fuera de servicio de los componentes que lo forman (ya sea debido a fallas aleatorias o acciones intencionales) y la carga que es racionada.

La IDG está relacionada con la identificación óptima de los elementos de la red que deben ser puestos fuera de servicio, de tal manera que se minimice el flujo entre dos nodos específicos de la red (nodo fuente s y nodo terminal t), sujeto a una restricción de costo. Se entiende que la acción de colocar un elemento fuera de servicio tiene un costo asociado de interdicción.

Desde la perspectiva de un SEP, la IDG puede instrumentarse como un enfoque para entender la interacción entre la inhabilitación de un elemento (debido a fallas aleatorias o ataques intencionales) y el racionamiento de carga que ésta ocasiona. Por tanto, el enfoque propuesto en este artículo permite determinar el orden de la contingencia k que produce el mayor racionamiento de carga en el SEP. Por ejemplo, para k =1, interesa conocer cuál es la contingencia simple que produce el mayor racionamiento, esto es, interesa encontrar entre la M-1 posibles contingencias simples que pueden ocurrir, cuál es la que ocasiona el mayor racionamiento. Note que en este caso, la IDG supone que el “costo asociado” a la acción de interdicción es el número de elementos que definen la contingencia. Por tanto, el analista está interesado en conocer el mayor racionamiento de carga, para cualquier contingencia M-k.

Es importante resaltar que bajo este enfoque, el problema se convierte en un problema de múltiples objetivos. Por un lado se trata de hallar el máximo racionamiento y por otro determinar la contingencia con el menor número de elementos fuera de servicio que la produce. El conjunto de soluciones que satisface ambos objetivos, es conocido como el conjunto Pareto. Y la técnica utilizada para obtener una aproximación de ese conjunto, está basada en el uso de los AEOM.

El trabajo está organizado en 5 secciones. En la sección 2 se presenta el problema de IDG y su adaptación al SEP. La sección 3 presenta un resumen del enfoque multiobjetivo y los algoritmos más utilizados. La sección 4 ilustra el uso del enfoque propuesto mediante el análisis de tres SEP estudiados en la literatura. Finalmente la sección 5 está dedicada a las conclusiones y trabajos futuros.

EL PROBLEMA DE LA INTERDICCIÓN DETERMINISTA

Reseña y definiciones

El estudio de los modelos de interdicción de redes en Investigación de Operaciones comenzó en la década de los 70, durante la guerra de Vietnam. En 1970, tanto McMasters y Mustin como Ghare, Montgomey y Turner (referido por Pan (2005)), desarrollaron modelos matemáticos deterministas para interrumpir el flujo de materiales y tropas enemigas. A partir de allí, se derivó una gama de nuevos modelos que no sólo ha permitido ampliar su espectro de aplicabilidad, sino que, también ha planteado el reto de diseñar métodos efectivos para su resolución.

A tal efecto, Wood (1993) formuló el problema de la interdicción en redes, mediante la programación entera, incorporándole variantes y generalizaciones; en Israeli & Wood (2002) se enfocó el problema desde la óptica de la programación entera mixta; y Dai & Poh (2002) sugirieron una heurística basada en un algoritmo genético para analizar el problema de la interdicción en redes.

Sea G=(N, A) una red en donde N es un conjunto de nodos y A es un conjunto de arcos tales que (i,j) Î A, si y sólo si hay un arco desde el nodo i al nodo j. Sea s el nodo fuente y t el nodo terminal. Cada arco (i,j) tiene una capacidad de u_ij unidades y requiere de c_ij unidades de recurso para ser puesto fuera de servicio. Sea C la cantidad total de recursos de las que dispone el interdictor.

Se define la variable de decisión x_ij=0 si el arco (i,j) es inutilizado por el interdictor y x_ij=1 en el caso contrario. El problema matemático de interdicción se formula entonces como: determinar el conjunto de enlaces que deben ser inutilizados de forma de minimizar el máximo flujo que atraviesa la red, desde s hasta t, sujeto a las restricciones de balance de conservación de flujo en los nodos. Adicionalmente se debe considerar que el flujo a través de cada arco no puede ser superior a su capacidad máxima y que el costo total de interdicción sea menor o igual a C. Las soluciones que se obtienen al resolver el modelo matemático se denominan en la literatura como estrategias de interdicción. Por tanto, para cada estrategia de interdicción, es necesario evaluar el máximo flujo en la red. En la literatura existen varios enfoques para determinar este máximo flujo (Bertsekas, 1991; Ford & Fulkerson, 1962; Cormen et al. 2001). En este trabajo se utiliza el algoritmo conocido con el nombre de Ford-Fulkerson, descrito en (Ford & Fulkerson, 1962).

La IDG y su adaptación al SEP

El problema anterior puede adaptarse fácilmente para el caso de un SEP. En este caso se trata de hallar la contingencia que ocasiona el máximo racionamiento y por otro determinar la contingencia con el menor número de elementos fuera de servicio que la produce. Por tanto, la cantidad total de recursos que dispone el interdictor es ahora interpretada como el número de elementos puestos fuera de servicio. Por ejemplo, si C=1, el modelo determina qué elemento debe ser puesto fuera de servicio de tal manera que el máximo flujo en la red sea mínimo. Si C=2, el problema consiste en seleccionar la combinación de dos elementos fuera de servicio que hacen que el máximo flujo en la red sea mínimo.

Tradicionalmente en el análisis de contingencias, la determinación del racionamiento se ha evaluado con modelos aproximados de flujo de carga, tales como el flujo de carga DC. Si bien esta opción es aproximada, los beneficios de tiempo de cómputo son significativos.

En este artículo, sin embargo, se usa el modelo de máximo flujo en la red como una forma de aproximar el flujo de carga. Este modelo considera los límites de capacidad máximos de los elementos, el balance de flujo en los nodos, pero no toma en cuenta ni la ley de Ohm, ni la ley de mallas de Kirchhoff. Si bien estas consideraciones parecieran ser desventajosas para el método, los resultados obtenidos en las redes analizadas (sección 4) coinciden con los resultados obtenidos por otros autores (Lesieutre et al. 2008; Salmerón et al. 2004; Donde et al. 2005; Lesieutre et al. 2006), mediante modelos más detallados, como flujo de carga AC o DC. El modelo de máximo flujo en redes ha sido utilizado exitosamente para ubicar dispositivos FACTS, en especial durante situaciones de sobrecarga en los elementos del sistema de potencia (Armbruster et al. 2005).

Sin embargo, como se verá mas adelante, en la utilización de los AEOM, la evaluación del flujo en la red es considerada como una caja negra. Por tanto puede considerarse cualquier modelo de evaluación y el enfoque propuesto sigue siendo válido.

Para aplicar el enfoque de máximo flujo, el SEP es modelado de la siguiente forma:

• Todos los nodos de generación g se conectan a un super nodo s. La capacidad máxima del enlace entre un generador g y s es igual a la capacidad de generación del generador g.

• Todos los nodos de carga d se conectan a un super nodo t. La capacidad máxima del enlace entre una carga d y el nodo t es igual a la carga asociada d.

Bajo estas condiciones, el máximo flujo entre s y t corresponde a la demanda máxima que puede ser suplida por el sistema de potencia.

OPTIMIZACIÓN MULTIOBJETIVO

En la búsqueda de soluciones a problemas del mundo real, puede ser necesario satisfacer de manera simultánea múltiples objetivos, los cuales pueden ser contradictorios entre sí (Fernández & Baran, 2005). A fin de simplificar su solución, muchos de estos problemas tienden a modelarse como monoobjetivo usando sólo una de las funciones originales y manejando las adicionales como restricciones (Coello, 1999). Un problema multiobjetivo consiste en la optimización del vector de funciones (Rocco et al. 2009):

Opt [F(x) =(f₁(x), f₂(x), …, f_k(x))t]

s.t.: g_j(x) ≤ 0, j=1,2,..,q; h_l(x) = 0, l=1,2,..,r (1)

donde:

x = (x₁, x₂, …, x_n)^t Î X es el vector solución o vector de variables de decisión y X representa la región de factibilidad definida por las restricciones g_j y h_l.

En los problemas de optimización multiobjetivo con objetivos contradictorios, no existe una solución única que pueda ser considerada la mejor, sino un conjunto de éstas que representan los mejores compromisos entre los objetivos, en el sentido que cada una es mejor que las otras en algún objetivo, pero ninguna es mejor que otra en todos los objetivos simultáneamente. Dicho conjunto es llamado conjunto de soluciones de Pareto óptimas y sus correspondientes vectores en el espacio objetivo constituyen el denominado frente o frontera de Pareto (Fernández & Baran, 2005).

A continuación se presentan algunas definiciones en términos de minimización (Rocco et al. 2009):

Definición 1: Optimo de Pareto. Un vector x* Î X es solución óptima de Pareto de un problema de optimización con k-objetivos, si y sólo sí:

¬$ x Î X : f_i(x) ≤ f_i(x*) ^ f(x) ≠ f(x*);i = {1,2,...,k}

Definición 2: Dominancia de Pareto. Una solución x¹ domina a x², denotado como x¹ > x², si y sólo sí:

f_i(x¹) ≤ f_i(x²) " i ^ $ j : f_j(x¹) < f_j(x²); i, j {1,2,...,k}

Si no hay soluciones que domine x¹, entonces x¹ es no dominado.

Definición 3: Conjunto de aproximación de Pareto. Un conjunto de soluciones no dominadas

{x* | ¬$ x : x > x* ; x*, x Î D Í X }

se dice que es un conjunto de aproximación de Pareto o simplemente conjunto Pareto. Si D=X, entonces el conjunto se denomina conjunto real Pareto.

Definición 4: Frontera de Pareto. El conjunto de vectores en el espacio objetivo que son imagen del conjunto de aproximación de Pareto, formará la frontera de Pareto o una aproximación a la frontera. Si D=X, entonces el conjunto se denomina frontera real de Pareto.

Bajo el enfoque multiobjetivo, el problema de interdicción determinista consiste en minimizar el máximo flujo en la red y minimizar el costo total de interdicción de los elementos que deben ser puestos fuera de servicio, cumpliendo con las restricciones de balance de conservación de flujo en los nodos y considerando que el flujo a través de cada arco no puede ser superior a su capacidad máxima.

Existen varias técnicas de optimización multiobjetivo en la literatura de investigación de operaciones. Sin embargo, la mayoría de ellas están limitadas a frentes de Pareto con ciertas características (p.ej., convexos) y suelen requerir un punto inicial de búsqueda (Coello, 1999).

Los algoritmos evolutivos de optimización multiobjetivo (AEOM) han demostrado ser especialmente adecuados para la optimización multiobjetivo con la ventaja de no requerir supuestos matemáticos estrictos. Estos algoritmos combinan la potencia de los algoritmos evolutivos tradicionales (p. ej. algoritmos genéticos), con los conceptos de dominancia (ver definiciones).

En líneas generales, estos algoritmos parten de una solución inicial (definida en forma aleatoria o previamente especificada), que iterativamente es mejorada hasta llegar a la mejor solución posible.

Cada solución x es evaluada a través del vector de objetivos F(x)=( f₁(x), f₂(x), …, f_k(x))^t e iterativamente se van seleccionando las soluciones no dominadas. En el caso de estudio, x define cuáles elementos de la red son puestos fuera de servicio y cuáles no, f₁(x), representa el máximo flujo bajo esa configuración y f₂(x) representa el número de elementos que se encuentran fuera de servicio.

Como se mencionó anteriormente, en este trabajo se utiliza el algoritmo de máximo flujo, pero es posible usar cualquier otra técnica (flujo de carga DC, AC, entre otros).

Cabe señalar que, en general, los procedimientos heurísticos no garantizan la optimalidad de la solución. Sin embargo, estudios con funciones test han demostrado la efectividad de dichos algoritmos (Coello, 1999).

En este trabajo se usó el algoritmo MO-PSDA, desarrollado en (Rocco & Ramírez-Márquez, 2009) para la determinación de la aproximación de Pareto. Sin embargo, cualquier otra técnica evolutiva pudiera ser usada.

RESULTADOS EXPERIMENTALES

Para ilustrar el enfoque propuesto, se han seleccionado dos SEP usados comúnmente en la literatura (IEEE-30 Bus y IEEE RTS y una versión simplificada del sistema de potencia de Italia. En cada caso se analizan un máximo de 5x10³ soluciones. Los experimentos se replican 10 veces y la aproximación final de Pareto se obtiene combinando las aproximaciones de cada réplica, de acuerdo con las definiciones de dominancia.

Ejemplo 1: SEP IEEE 30-Barras

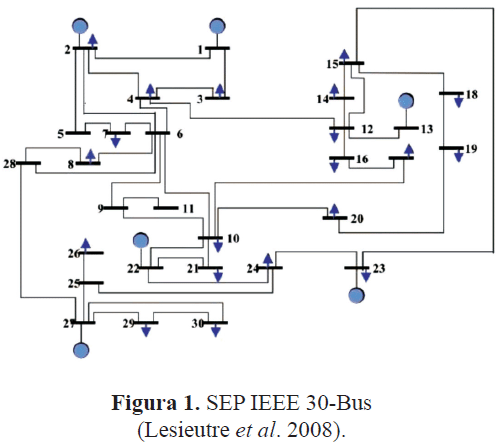
El primer ejemplo considera el SEP de 30 barras mostrado en la figura 1 (Lesieutre et al. 2008). El SEP posee 6 generadores y 41 líneas de transmisión, con capacidad máxima de 500 p.u.

La tabla 1 lista los valores de potencia activa (p.u.) asociados a cada barra (valores positivos representan generación, valores negativos representan demanda). Bajo estas condiciones la demanda máxima del sistema es de 822 p.u.

Bajo el enfoque propuesto, el problema de optimización posee solamente 41 variables, esto es, el número de elementos que pueden ser puestos fuera de servicio. De las 2⁴¹ posibles soluciones, la aproximación de Pareto está caracterizada mediante la evaluación de un total de 5000 estrategias (aproximadamente el 2.27x10^-7 % del espacio de soluciones).

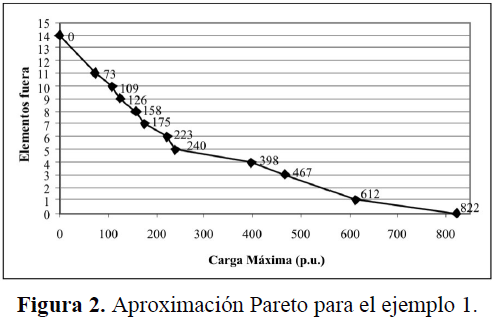
La figura 2 muestra la aproximación de Pareto. Cada punto de la aproximación de Pareto representa una estrategia particular de interdicción.

Por ejemplo, el punto ubicado en (822,0) representa el caso en el que no hay interdicción. El otro punto extremo ubicado en (0,14) corresponde a la interdicción de 14 líneas que producen la pérdida total de carga en el sistema. Otros puntos de interés a lo largo de la frontera son:

• El punto ubicado en (612,1), corresponde a la interdicción de la línea que une las barras 12 y 13. En otras palabras, la contingencia simple más severa produce un racionamiento de 822-612 = 210 p.u.

• El punto ubicado en (240,5), corresponde al caso en que se ponen fuera de servicio 5 líneas. En este caso las líneas entre las barras 12-13, 15-23, 10-21, 10-22 y 27-28 son colocadas fuera de servicio y se raciona un total de 822-240 = 540 p.u. (aproximadamente 71 % de la carga nominal del SEP).

La aproximación de Pareto permite analizar cómo diferentes grados de contingencia afectan el racionamiento. La tabla 2 muestra las estrategias de interdicción óptimas hasta contingencias de 5 elementos. Como se nota, la línea que une las barras 12-13 es la más crítica ya que aparece en todas las estrategias de interdicción. Esta preselección de líneas puede ser estudiada posteriormente con mayor detalle. Por ejemplo, el enfoque detallado presentado por Donde et al. (2005) identifica que las peores contingencias están asociadas a la puesta fuera de servicio de las líneas 10-22, 21-22 y 27-28. El resultado obtenido mediante MO-PSDA y otros enfoques aproximados (Lesieutre et al. 2008; Donde et al. 2005; Lesieutre et al. 2006) incluyen estas contingencias.

Ejemplo 2: IEEE RBTS

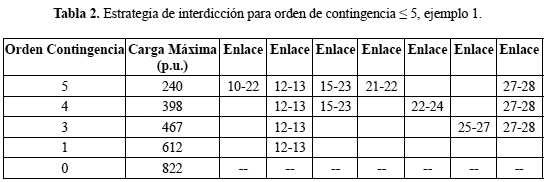
El segundo ejemplo considera el SEP IEEE RBTS de un área (Billinton & Li, 1994), mostrado en la figura 3. El sistema posee 24 barras, 38 elementos de transmisión (33 líneas), 32 unidades de generación y 17 barras de carga. Como se considera en (Arroyo & Galiana, 2005), solamente las líneas de transmisión pueden ser puestas fuera de servicio. A diferencia de estos autores, que consideran como interdicción simple la puesta fuera de servicio de líneas de transmisión en paralelo, en la evaluación que se presenta, cada elemento de transmisión es considerado como un posible elemento de interdicción.

El modelo propuesto en Arroyo & Galiana (2005), formulado como un problema de optimización no lineal enteromixto, está constituido por 1220 restricciones funcionales, 226 variables binarias y 597 variables continuas. La formulación basada en MO-PSDA solamente considera 33 variables, correspondientes al número de elementos que pueden ser puestos fuera de servicio. El máximo flujo antes de interdicción es de 2850 MW.

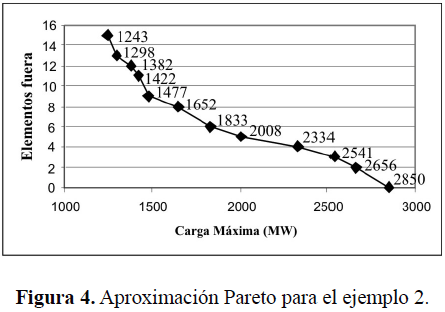
La figura 4 muestra la aproximación de Pareto obtenida mediante la evaluación de tan solo 5000 estrategias de interdicción, de un total de 2³³ posibles soluciones. En esta figura, el punto ubicado en (2850,0) representa el caso sin interdicción. El punto ubicado en (2656,2), representa el primer caso de interdicción, correspondiente al caso de máximo racionamiento ante una doble contingencia. Nótese que no existen puntos de la frontera con simple contingencia, por lo que el sistema está diseñado para soportar la puesta fuera de servicio de una línea. Otros puntos de interés son:

• El punto ubicado en (2008,5), representa el caso de 5 líneas en contingencia con una carga máxima servida de 2008 MW, esto es, un racionamiento de 2850-2008 = 802 MW. Las líneas seleccionadas (11-13, 12-13, 12-23, 14-16 y 15-24) coinciden con los resultados reportados en (Salmerón et al. 2004; Arroyo & Galiana, 2005).

• El punto extremo ubicado en (1243,16), representa el caso en que se ponen fuera de servicio 16 líneas para un racionamiento de 1607 MW. Este punto es interesante ya que en (Arroyo & Galiana, 2005) los autores mencionan que “la destrucción de los 38 elementos de transmisión produce el máximo racionamiento de 1607 MW”. Sin embargo, es la interdicción de solo 16 componentes la responsable del máximo racionamiento.

Los resultados para otras contingencias coinciden con los resultados que se presentan en (Arroyo & Galiana, 2005) tanto en el valor de la carga racionada como en los elementos involucrados. Estos autores utilizan un flujo de carga DC para evaluar el comportamiento del SEP mientras en este artículo se usa un modelo de máximo flujo.

Ejemplo 3: Sistema de potencia italiano

La red de transmisión de alta tensión (380 kV) del sistema de potencia italiano (HVIET) es representada como un grafo no dirigido de 310 nodos y 361 elementos de transmisión (Rosato et al. 2009).

El máximo flujo, antes de cualquier acción de interdicción, es de 23869 MW. La red HVIET ha sido analizada desde el punto de vista puramente topológico y en detalle, respectivamente (Rosato et al. 2007; 2009).

Este último análisis presenta los resultados de la vulnerabilidad de la red, tomando en cuenta los flujos de potencia que se originan en condiciones normales y ante la falla de uno o más elementos. El análisis es realizado mediante flujo de carga DC.

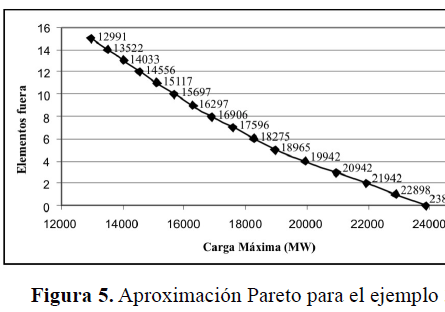
La figura 5 muestra la aproximación de Pareto obtenida mediante la evaluación de sólo 5000 estrategias de interdicción, de un total de 2361 posibles soluciones. En la figura, el primer punto extremo localizado en (23869,0) representa la solución sin interdicción. El punto localizado en (22898,1) representa el primer caso de interdicción, correspondiente al caso de máximo racionamiento ante una contingencia simple (línea entre los nodos 106 y 167). La diferencia entre el flujo para la solución sin interdicción y este caso (23869-22898 = 971 MW) representa el máximo racionamiento que se produciría en el sistema (alrededor del 4% de la máxima carga), ante la pérdida de un elemento.

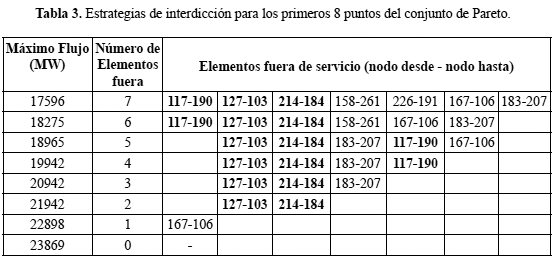
En la tabla 3 se listan las líneas de transmisión que conforman el conjunto de Pareto, esto es, aquellos elementos de la red que deben ser puestos fuera de servicio para provocar la máxima reducción de potencia. El análisis detallado realizado en (Rosato et al. 2009) reconoce que los elementos críticos para el HVIET son las líneas que están relacionadas con los nodos 214, 184, 117, 190, 127, 103 (estos elementos están resaltados en negrita en la tabla 3). Como se puede observar, los resultados obtenidos, mediante el enfoque propuesto, generan un conjunto de elementos de transmisión, que incluyen los obtenidos en (Rosato et al. 2009).

CONCLUSIONES

El artículo presenta un enfoque basado en optimización multiobjetivo para la determinación preliminar de la vulnerabilidad de un SEP. La propuesta proporciona resultados que coinciden con modelos más detallados del SEP (tales como flujo DC o AC), o, en otros casos, determina un conjunto de soluciones que incluyen al conjunto generado con estos modelos detallados.

El enfoque puede ser usado como una herramienta rápida de selección de contingencias simples o múltiples, capaz de identificar los elementos críticos en un SEP. Por una parte, el uso de los AEOM proporciona una manera eficiente de explorar el espacio de búsqueda. Por otra parte, el enfoque utiliza como herramienta de evaluación de las posibles soluciones un modelo estructurado como caja negra. Los ejemplos reportados están basados en un algoritmo de máximo flujo en redes pero pudiera utilizarse otra herramienta que modele en forma más real al SEP, tal como un flujo de carga DC, AC o hasta un flujo de carga óptimo. Nótese que para los sistemas analizados, la aproximación de Pareto se obtiene con un número reducido de evaluaciones, por lo que es factible el uso de modelos más detallados.

El enfoque presentado puede extenderse fácilmente en dos direcciones. La primera, al considerar más objetivos. Por ejemplo pudiera estudiarse el problema de seleccionar el esquema de interdicción que adicionalmente haga máximo el tiempo de restauración, con lo que se estaría determinando la peor contingencia en términos de carga racionada y duración.

La segunda, orientada a evaluar el impacto ante acciones de interdicción ocasionadas directamente en las subestaciones del SEP. En este caso, el costo de la acción de interdicción, puede suponerse como una función del número de elementos de transmisión asociados a cada nodo. Y, naturalmente, es posible considerar un esquema combinado de interdicción de elementos de transmisión y subestaciones.

AGRADECIMIENTO

Parte de este trabajo ha sido financiado por el CDCH-UCV, proyecto PG-08-7309-2008.

REFERENCIAS

1. Armbruster, A., Gosnell, M., McMillin, B., Crow, M. (2005). The Maximum Flow Algorithm Applied To The Placement And Distributed Steady-State Control Of Facts Devices, Proceedings Of The 37th Annual North American Power Symposium (NAPS), pp. 77–83.        [ Links ]

2. Apostolakis, G.E., Lemon, D.M. (2005). A Screening Methodology for the Identification and Ranking of Infrastructures Vulnerability Due to Terrorism. Risk Analysis, VOL. 25(1), pp. 361-376.        [ Links ]

3. Arroyo, J.M., Galiana, F.D. (2005). On the Solution of the Bilevel Programming Formulation of the Terrorist Threat Problem IEEE Transactions on Power Systems, Vol. 20, No. 2, pp. 789-797.        [ Links ]

4. Bertsekas, D. (1991). Linear Network Optimization: Algorithms and Codes, MIT Press, Cambridge, Mass.        [ Links ]

5. Billinton, R., Li, W. (1994). Reliability Assessment of Electric Power Systems Using Monte Carlo Methods Plenum Press, New York, s/n.        [ Links ]

6. Coello, C. (1999). A Comprehensive Survey of Evolutionary- Based Multiobjective Optimization Techniques, Knowledge Information Systems, Vol. 1, No. 3, pp. 129-156.        [ Links ]

7. Cormen, T., Leiserson, C., Rivest, R., Stein, C. (2001). Introduction to Algorithms, 2nd Ed, MIT Press, Cambridge, Mass, s/n.        [ Links ]

8. Dai, Y., Poh, K. (2002). Solving the Network Interdiction Problem with Genetic Algorithms, Proceedings of the Fourth Asia-Pacific Conference on Industrial Engineering and Management System, Taipei, December 18-20, pp. 151-154.        [ Links ]

9. Donde, V., López, V., Lesieutre, B.C., Pinar, A., Yang, C., Meza, J. (2005). Identification of Severe Multiple Contingencies in Electric Power Networks, proceedings of the North American Power Symposium, Ames, IA, pp. 59-66.        [ Links ]

10. Donde, V., López, V., Lesieutre, B.C., Pinar, A., Yang, C., Meza, J. (2008). Severe Multiple Contingencies Screening in Electric Power Systems, IEEE Transactions on Power Systems, Volume 23, pp. 406-417.        [ Links ]

11. Fernández, J., Baran, B. (2005). Equipo de Algoritmos Evolutivos Multiobjetivo Paralelos Asunción: Universidad Nacional de Asunción. http://www.cnc.una.py/cms/invest/download.php?id=181909, 112,4 Consulta: 2008, Junio 3. s/n        [ Links ]

12. Ford, L., Fulkerson, D. (1962). Flows in Networks, Princeton Univ. Press, Princeton, NJ, s/n.        [ Links ]

13. Holmgren, Å.J. (2006). Using Graph Models to Analyze the Vulnerability of Electric Power Networks. Risk Analysis, 26(4), pp. 955-968.        [ Links ]

14. Holgren, Å.J., Jenelius, E., Westin, J. (2006). Evaluating Strategies for Defending Electric Power Networks Against Antagonistic Attacks. IEEE Transactions on Power Systems, 22(1), pp. 76-84.        [ Links ]

15. Israeli, E., Wood, K. (2002). Shortest-path Network Interdiction, (NETWORKS, Vol. 40 (2), pp. 97-111.        [ Links ]

16. Johnson, C.W. (2007). Understanding the Interaction Between Public Policy, Managerial Decision-Making and the Engineering of Critical Infrastructures. Reliab Engng Sys Safety, 92(9), pp. 1141-1154.        [ Links ]

17. Lesieutre, B.C., Pinar, A., Roy, S. (2008). Power System Extreme Event Detection: The Vulnerability Frontier, Proc. Hawaii International Conference on System Sciences, pp. 184,188.        [ Links ]

18. Lesieutre, B.C., Roy, S., Donde, V., Pinar, A. (2006). Power System Extreme Event Screening using Graph Partitioning, proceedings of the North American Power Symposium, Carbondale, IL, pp. 503-510.        [ Links ]

19. McMasters, A., Mustin, T. (1970). Optimal Interdiction of a Supply Network, Naval Research Logistics Quarterly, Vol. 17, pp. 261-68.        [ Links ]

20. Pan, F. (2005). Stochastic Network Interdiction: Models and Methods, Doctoral Dissertation, The University of Texas at Austin, s/n.        [ Links ]

21. Rocco, C.M., Salazar, D.E., Ramírez-Márquez, J.E. (2009). Multiple-Objective Deterministic Network Interdiction Using Evolutionary Algorithms, IEEE The Annual Reliability and Maintainability Symposium, USA, pp. 170-175.        [ Links ]

22. Rocco, C.M., Ramírez-Márquez, J.E. (2009). Deterministic Network Interdiction Optimization Via An Evolutionary Approach, Reliability Engineering and System Safety, Volume 94, Issue 2, pp. 568-576.        [ Links ]

23. Rosato, V., Bologna, S., Tiriticco, F. (2007). Topological Properties of High-Voltage Electrical Transmission Networks Electric Power Systems Research, Vol. 77, N°. 2, pp. 99-105.        [ Links ]

24. Rosato, V., Issacharoff, L., Bologna, S. (2009). Influence of the Topology on the Power Flux of the Italian High- Voltage Electrical Network, Europhysics Letters (in press), s/n.        [ Links ]

25. Salmerón, J., Wood, K., Baldick, R. (2004). Analysis of electric grid security under terrorist threat, IEEE Transactions on Power Systems, Vol. 19, N° 2, pp. 905-912.        [ Links ]

26. Skolicki, Z., Wadda, M.M., Houck, M.H., Arciszewski, T. (2006). Reduction of Physical Threats to Water Distribution Systems, Journal of Water Resources Planning and Management, Special Issue: Drinking Water Systems Security, Vol. 132, Issue 4, pp. 211-217.        [ Links ]

27. Wadda, M., Skolicki, Z., Arciszewski, T. (2004). Generation of Terrorist Scenarios for Water Distribution Systems: An Evolutionary Computation Approach. In A. Woodcock and C. Pommerening, editors, Proceedings of the workshop Critical Infrastructure Protection Project, G. Mason Univ. pp. 162-170.        [ Links ]

28. Wood, K. (1993). Deterministic Network Interdiction, Mathematical & Computer Modelling, Vol. 17, pp. 1-18.        [ Links ]