Simulación de bomba radial multietapa para flujo bifásico aire-agua

Carlos Luis Moreno ¹, Miguel Asuaje ², Frank Kenyery ², Jesús de Andrade ²

¹ Universidad Simón Bolívar. Departamento de Termodinámica y Fenómenos de Transferencia. Baruta. Venezuela. e-mail: cluismoreno@cantv.net

² Universidad Simón Bolívar. Laboratorio de Conversión de Energía. Baruta. Venezuela e-mail: {asuajem; fkenyery; jesusandrade}@usb.ve

RESUMEN

El siguiente trabajo tiene como objetivo principal la simulación de una bomba radial multietapas para flujo bifásico aireagua, en dos etapas consecutivas. Se utilizaron los módulos BladeGen y Ansys-WorkBench para generar las geometrías de los rotores, diafragmas y bloques. Se hizo la validación de las mallas. Se ensambló el sistema y se ejecutaron nueve corridas, correspondientes a los siguientes caudales: 80% de caudal nominal, caudal nominal y 120% de caudal nominal. Se consideraron casos monofásico, y bifásico con 1% y 2% de fracción volumétrica de gas. Se observó que para flujo bifásico con 1% de FVG a la entrada al sistema, la segunda etapa en relación a la primera etapa, presenta menor altura teórica (disminución en 1,65%), mayor altura de bombeo (aumento en 7,94%) y mayor eficiencia hidráulica (aumento en 10%). La tendencia de este comportamiento, se acentúa a medida que aumenta la fracción volumétrica de gas a la entrada de la bomba. Se concluye entonces que el deterioro en la altura de bombeo para flujo bifásico a 1% y 2% de FVG se debe a las pérdidas de carga por fricción, contracción y choque en rodetes, y deflexión en diafragmas. (El flujo está mejor direccionado a la entrada del rodete 2, y hay menor desviación en el diafragma 2), siendo más importante las pérdidas hidráulicas que los factores de deslizamiento, para los rodetes.

Palabras clave: Rodete, Diafragma, Etapas, Bifásico, Carga.

SIMULATION OF A MULTISTAGE RADIAL PUMP FOR BIPHASIC WATER-AIR FLOW

ABSTRACT

The main aim of this study is the simulation of a multistage radial pump for biphasic water-air flow in two consecutive stages. Bladegen and AnsysWorkBench Modules were used for rotor, stator and block geometry generation. Firstly, grid validation was performed. The system was assembled, and nine runs were carried out, corresponding to 80% nominal discharge, nominal and 120% nominal discharge. Monophasic flow, biphasic flow with 1% and 2% of gas void fraction were considered. It was observed that for biphasic flow with 1% GVF, the second stage presents, compared to the first stage, an increase of 10% for pumping head, a similar increase in hydraulic efficiency, and a decrease of 1,65% for theoretical head. The larger the gas void fraction at the entrance of the pump, the more noticeable these tendencies were observed. It was concluded that the decrease in pumping heads is due to flow contraction, friction and choke in rotors, and deflection in stators. The flow is better directed in the rotor 2 entrance, and there is less deflection in stator 2. (Hydraulic Efficiency is more important than slip factor).

Keywords: Rotor, Stator, Stages, Biphasic, Head.

Recibido: octubre de 2008 Recibido en forma final revisado: agosto de 2009

INTRODUCCIÓN

El comportamiento de las bombas centrífugas en flujo bifásico es un asunto que ha adquirido gran importancia hoy en día, debido a la incidencia que se presenta en las industrias nuclear, química y petrolera. En el caso de la industria nuclear, han ocurrido eventualmente descompresiones por fuga de refrigerante, por lo cual el flujo a través de las bombas es de naturaleza bifásica. En cuanto a la industria petrolera, el uso de bombas centrífugas ha probado ser un sistema artificial de producción eficiente y económica. Las bombas sumergibles son bombas centrífugas de varias etapas, usadas para extraer crudo. En la industria química, se presenta flujo bifásico en bombas centrífugas que manejan fluido proveniente de condensadores, principalmente.

El patrón de flujo bifásico a través del impulsor y difusor de las bombas centrífugas es bastante complejo. De hecho, es una tarea ardua visualizar el campo de flujo experimentalmente para obtener el perfil de velocidades para cada uno de las fases. De esta forma, está claro por qué el intento de predecir el comportamiento de las bombas centrífugas operando con mezclas multifásicas no ha dado fruto con exactitud, hasta ahora. La disminución en la altura entregada por una bomba centrífuga en condiciones bifásicas con respecto al caso de flujo monofásico depende de varios factores, tales como, geometría, fracción volumétrica de gas, tamaño y distribución de burbujas, la presión de succión, la velocidad de rotación y caída de presión a través de la bomba.

Debido a las dificultades relacionadas con el modelo analítico del comportamiento del flujo bifásico en una bomba sumergible, la mayoría de los modelos existentes de simulación numérica estiman la reducción de carga de bombeo en forma empírica. Por consiguiente, se necesitan desarrollar nuevos estudios al respecto. Las correlaciones de degradación por gas y de predicción de bombeo son específicas para determinadas bombas, y se basan en el desempeño promedio para cierto número de etapas.

En cuanto a los trabajos previos correspondientes a la revisión bibliográfica, se pueden citar los siguientes:

Pak & Lee (1998)

Para flujo bifásico, en una bomba centrífuga, debido a un gradiente de presión positivo, la burbuja de aire entra al cauce del impulsor más despacio que el agua, pero en la región de succión en la entrada del impulsor donde prevalece un gradiente de presión negativo, las burbujas se mueven más rápidamente que el agua. Estos cambios provocan una alteración general del modelo de flujo en el rodete y también causan una caída en la altura de bombeo. Mediante una simulación, se logra resultados congruentes cuando los valores predichos de estas variables se comparan con los resultados medidos experimentalmente dentro del rango de condiciones de flujo con burbujas.

Estos resultados son útiles al compararlos con los correspondientes a la simulación numérica de este trabajo, y permiten dar una idea de cómo deberían resultar los perfiles de presión y velocidad en el caso bifásico (con 1% y 2%) FVG, para las dos etapas consecutivas de la bomba sumergible en cuestión.

Lee et al. (2003)

Este artículo describe la simulación tridimensional del flujo interno en tres tipos diferentes de bombas centrífugas (una bomba tiene cuatro álabes de grosor pequeño y los otros dos tienen seis álabes curvos). La comparación de los resultados computacionales para varios tipos de bomba, mostraron resultados adecuados en el caso de las bombas de álabes “curveados” de gran espesor. Sin embargo, en el caso de la bomba de álabes “rectos” de poca envergadura, los resultados computacionales fueron diferentes a los resultados experimentales. Sin embargo, los perfiles de velocidad y presión calculados, concuerdan con las hipótesis desarrolladas anteriormente.

Este trabajo sirvió para ilustrar las posibles condiciones de borde que se pueden considerar al tratar de simular el comportamiento de bombas centrífugas.

Pessoa & Prado (2001)

Condujeron un estudio experimental con una bomba de 22 etapas, en condiciones de flujo bifásico. Aire y agua fueron utilizados como fluidos de trabajo. Este estudio se diferencia de los demás, porque los cambios de presión fueron monitoreados etapa por etapa. Los resultados de trabajos previos corresponden a un promedio entre las condiciones de entrada y descarga, y dependen del número de etapas usadas. Los fenómenos de bombeo y bloqueo de gas fueron observados durante las pruebas. Los resultados indican que el comportamiento promedio de la bomba es significativamente diferente al observado en cada etapa.

Caridad (2004)

Se realizaron varios intentos con el objetivo de predecir el desempeño de bombas sumergibles en flujo bifásico. Sin embargo, el éxito ha sido limitado debido a la complejidad de la dinámica del flujo dentro del rodete. La geometría, la fracción volumétrica de gas, y la presión de succión parecen ser los principales parámetros que afectan el desempeño de las bombas sumergibles. En más detalle, a mayor fracción volumétrica de gas de la mezcla, mayor es la degradación de la altura de bombeo. En este trabajo un modelo de dos fluidos es usado en simulaciones de Dinámica Computacional de Fluidos 3D, con el objetivo de obtener la presión, los campos de velocidad del líquido y gas, así como distribución de fracción volumétrica de gas en un rodete de bomba. Se usaron tasas de flujo, diámetro de burbuja y fracciones volumétricas de gas como variables independientes. La FVG en el álabe del rotor reportado por otros investigadores se comparó con resultados experimentales, y coincidieron.

Duplat (2004)

En esta tesis se presentaron los resultados del estudio de la modificación del número de álabes para un mismo rodete de una bomba sumergible, manejando flujo monofásico (agua), así como flujo bifásico (agua-aire) con una fracción volumétrica de gas de 5%. Se realizó la simulación del paso del fluido de trabajo a través del rodete mediante dinámica de fluidos computacional, empleando Turbogrid y CFX. Se puede considerar que se predijo con certeza el desempeño del rodete manejando una mezcla líquido-gas de fracción volumétrica de gas del 5%. Por otra parte, se calcularon las pérdidas hidráulicas y los coeficientes de disminución de trabajo, y dichos resultados se analizaron. Se pudo concluir en este estudio, como en anteriores, que se genera un detrimento de la altura por formación de un bolsillo de gas en el manejo de flujo bifásico que modifica el canal interálabe. Además de esto, se concluyó que la modificación del número de álabes incide en la formación del bolsillo modificando por ende la altura efectiva alcanzada.

Caridad & Kenyery (2004)

En este trabajo se concluyó que en los impulsores de bombas centrífugas, el factor de deslizamiento está bastante influenciado por el caudal y la fracción volumétrica de gas. Para una fracción constante, el factor de deslizamiento aumenta cuando el caudal disminuye. Para flujo constante, el factor disminuye cuando la fracción aumenta.

López (2006)

Se llevó a cabo el estudio del efecto del tamaño de la burbuja de gas en el desempeño de una bomba sumergible con flujo bifásico (líquido-gas). Se acondicionó un banco de pruebas para la bomba. Empleando una mezcla agua-aire, se incrementó la fracción de gas (FVG), desde 0 hasta 2% y se midió el diámetro de burbuja en la succión, para establecer argumentos prácticos que permitan mejorar la predicción del desempeño de la bomba, del tamaño de burbujas y el diámetro promedio de éstas, medido en la succión, los perfiles de presiones interetapas, etc. Los resultados obtenidos fueron los intervalos de confianza del diámetro, variación de la temperatura, y las curvas de desempeño (ΔP. vs. Ql), para diferentes condiciones de operación. El diámetro promedio de una burbuja de aire medida en la succión de la bomba fue de 1 mm. para presiones de succión entre 20 a 30 psig y a una temperatura de 25°C. Se determinó que el efecto combinado de la dinámica de la burbuja (fuerzas de arrastre y flotación), junto a la FVG y la presión de succión juega un papel preponderante en la predicción del desempeño de la bomba sumergible. Se observó que variables como la tasa de líquido y la FVG no influyen sobre el diámetro de burbuja, por lo que la única sensibilidad encontrada en torno a esta variable está representada por la presión de succión.

METODOLOGÍA

Descripción de la bomba

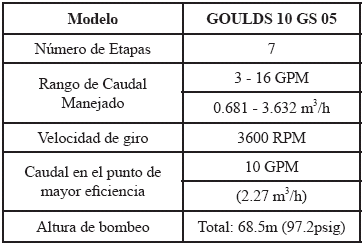
En la figura 1 se presentan el rodete y el diafragma del sistema a estudiar. En la tabla 1 se muestran las características de dicho sistema.

Figura 1. Componentes de una etapa en bomba radial multietapas a simular. Rodete (izquierda). Diafragma (derecha).

Tabla 1. Datos de bomba sumergible cuyo flujo se desea simular.

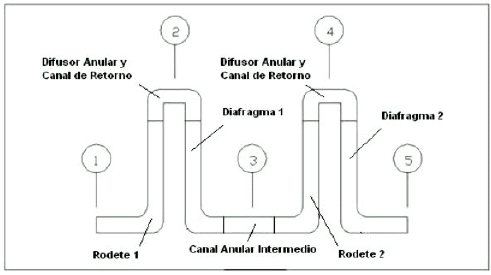
Las 2 etapas consecutivas se presentan en la figura 2.

Figura 2. Plano meridional de dominio a considerar en la simulación.

Generación de la geometría del rodete y del diafragma

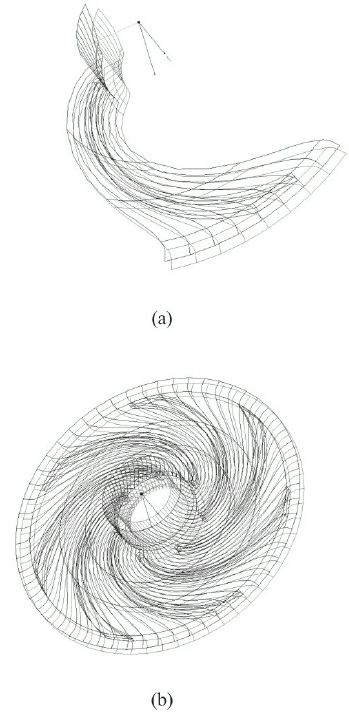
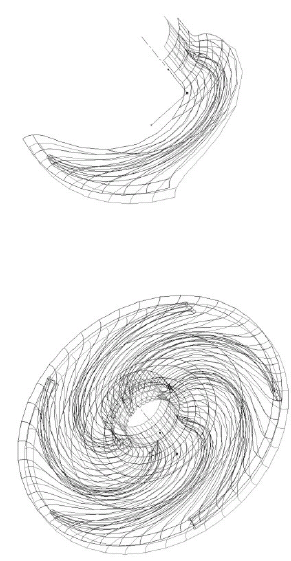
Mediante el módulo Bladegen, se procedió a generar la geometría del rodete y del diafragma. A continuación se presentan los volúmenes de control objeto de la simulación, para el rodete y el diafragma (figuras 3 y 4).

Figura 3. Volúmenes de control correspondiente al rodete (a). Volumen de control correspondiente al rodete completo (b).

Figura 4. Volúmenes de control correspondientes al diafragma.

Generación de la geometría del bloque rodete-diafragma, y bloque entre ambas etapas

Mediante este módulo (Ansys-WorkBench) se procedió a crear los bloques rodete-diafragma, así como el bloque entre las dos etapas consecutivas. Los tres bloques del sistema se generaron primero dibujando en el espacio de trabajo cortes transversales de las geometrías a crear, y luego haciendo uso de la herramienta “revolución”.

Luego se procedió a crear las superficies externas que conforman los bloques.

Construcción del canal interálabe en rodete, diafragma y bloques

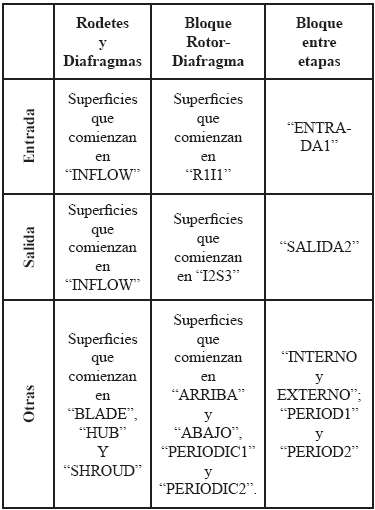
Para la obtención de cada uno de los elementos en estudio, se empleó BladeGen como herramienta de construcción de los rodetes y diafragmas, y Ansys-WorkBench para la construcción de los bloques. Por otra parte, se usó TurboGrid y Ansys-WorkBench como herramienta de mallado de rodetes, diafragmas, y bloques. Se determinaron las superficies de entrada y salida en el volumen control de rodetes, diafragmas, bloques rodetediafragma, y bloque entre etapas. Dichas superficies se muestran en la tabla 2.

Tabla 2. Superficies consideradas en nuestro dominio de simulación.

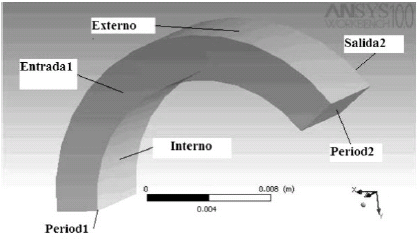
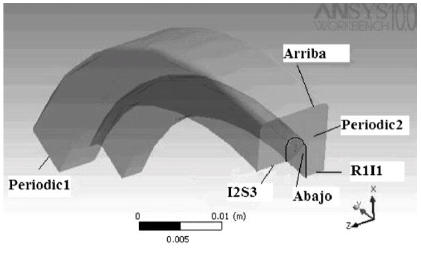
En las figuras 5 y 6 se presentan los bloques rotor-diafragma y bloque entre ambas etapas, señalando las superficies que rodean el dominio.

Figura 5. Superficies que rodean el bloque entre ambas etapas.

Figura 6. Superficies que rodean el bloque entre rotor y diafragma.

Utilización de Turbogrid para la generación de la malla de rodete y diafragma

La generación de la malla, es un paso imprescindible en cuanto al análisis de dinámica computacional de fluidos de una turbomáquina, ya que se desea generar una malla que se adapte fielmente a la geometría del elemento estudiado. El TurboGrid, es una herramienta que logra este objetivo con la interacción mínima entre usuario y computador, ya que la mayoría de los pasos necesarios son automáticos en este módulo de CFX. Se emplearon hexaedros como elementos de las mallas de rotor y diafragma.

Utilización de Ansys-Workbench para la generación de la malla de bloques

Para la discretización de los bloques rotor-diafragma y bloque entre ambas etapas, se utilizó el módulo Ansys-Work- Bench, y se emplearon variables tomadas por defecto. La cantidad de elementos empleados en cada bloque (en especial el correspondiente al bloque rodete-diafragma), fue mucho mayor que en el volumen de control de rodetes y diafragmas. Se emplearon tetraedros como elementos de la malla.

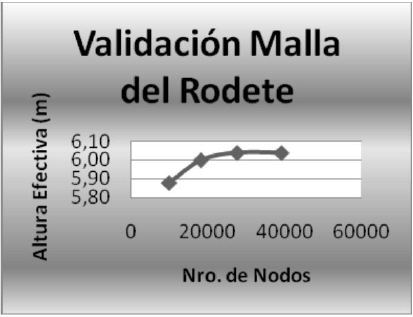
Validación de las mallas del rodete y diafragma

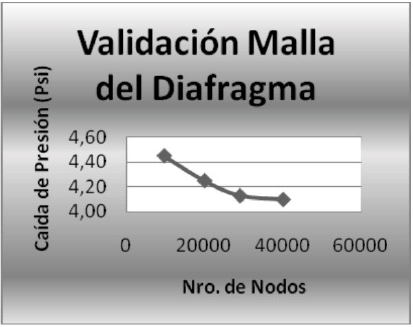
Se discretizó en primer lugar el dominio para un álabe del rotor. Se consideraron 4 corridas para el rotor considerando 8020, 15180. 23520 y 33920 nodos. Se observó que a partir de 33920 nodos, la altura de bombeo del rodete no cambia significativamente. Se realizaron 4 corridas más para el diafragma considerando 7600, 16640, 24735 y 34748 nodos. Se observó que a partir de 34748 nodos, el cambio de presión del diafragma no se modifica significativamente. A continuación se muestran las figuras 7 y 8, correspondientes a la validación de las mallas del rotor y diafragma, respectivamente.

Figura 7. Resultado de validación de malla del volumen de control del rodete.

Figura 8. Resultado de validación de malla del volumen de control del diafragma.

Dominio de la simulación

El dominio se estableció como se presenta en la figura 9.

Figura 9. Dominio a considerar en la simulación de dos etapas consecutivas.

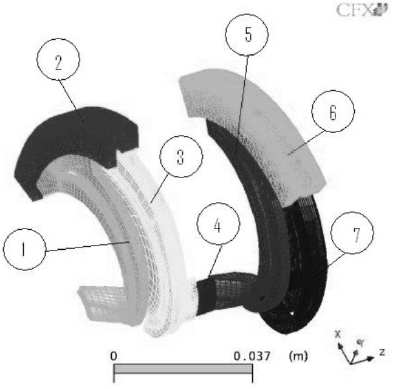
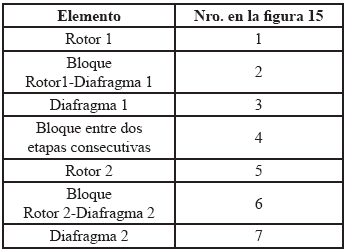
Los elementos a considerar en el dominio de la simulación son los mostrados en la tabla 3.

Tabla 3. Componentes de dominio a simular en 2 etapas consecutivas.

Condiciones de borde

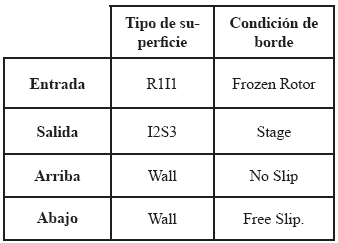
Una vez reconocidas las fronteras del volumen de control correspondiente a las dos etapas consecutivas, se procedió a establecer las condiciones de borde, según se indica en las tablas 4, 5 y 6.

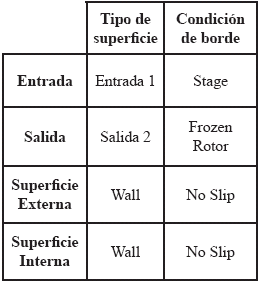
Tabla 4. Condiciones de borde en el sistema a simular. (En rotor y diafragma). Caso monofásico y bifásico.

Tabla 5. Condiciones de borde en bloque rotor-diafragma.

Tabla 6. Condiciones de borde en bloque entre etapas.

Las condiciones de borde para el bloque rodete-diafragma se presentan en la tabla 5.

A la entrada del dominio se estableció como condición de borde la presión total, la cual depende de la velocidad promedio de entrada (calculada como caudal de entrada entre área) y la presión estática relativa tomada como 25 psig. Las superficies tipo pared, como lo son el cubo, la bóveda y el álabe adoptaron condiciones de borde predefinidas por el programa.

La modificación de la condición de borde a la salida es la clave para el estudio comparativo entre el caso monofásico y bifásico. Para el caso monofásico, se empleó la rata de flujo másico usando la densidad del agua a la salida del sistema, mientras que para el caso bifásico se manipuló la velocidad meridional a la salida del rodete para cada una de las fases, asumiendo que dicha velocidad es igual tanto para la fase continúa como para la dispersa. Sin embargo, aun cuando la condición de borde es velocidad y no flujo másico, los términos se mantienen directamente relacionados por el área. Entonces las condiciones son equivalentes y permiten la comparación entre los resultados de las diferentes FVG (tabla 6).

Al igual que en el caso de los bloques rotor-diafragma, en el bloque que divide ambas etapas, se consideró la ausencia de movimiento relativo entre la salida del diafragma 1 y el bloque central inter-etapa (Stage), así como la presencia de movimiento relativo entre la salida del bloque central y la entrada del rotor 2 (Frozen Rotor). Además, el fluido no desliza en las paredes externa ni interna del bloque central (no deslizamiento o no Slip).

Modelo matemático

Para realizar el estudio de una forma computacional sencilla, simplificando matemáticamente los cálculos, se establecieron diferentes hipótesis que se muestran a continuación:

Caso monofásico

• Flujo monofásico: agua.

• Modelo de turbulencia K-Epsilon.

• Condición de entrada: presión total en sistema estacionario (25.97 psig para caudal nominal), Presión estática (25 psig).

• Condición de salida: flujo másico (flujo normal. 0.63 Kg/s).

• Esquema de avección: alta resolución.

• Escala de tiempo física: 0.0027284 s.

• Tolerancia residual: 1e-04.

• Tolerancia de conservación: 0.01.

Caso bifásico

Las hipótesis consideradas para el caso bifásico fueron las siguientes:

• Flujo bifásico agua (fase continua) y aire (fase dispersa).

• Modelo multifluido no homogéneo.

• Presencia de flotación. Diferencia de densidad.

• Modelos de turbulencia dependientes del fluido: K-Epsilon para fase continua y ecuación cero de fase dispersa para el aire.

• Condición de entrada: presión total con Opening (25.97 psig para caudal nominal), Presión Estática (25 psig). FVG 1%.

• Condición de salida: velocidades de fases (3,62 m/s para caudal nominal), Caudal (10 GPM caudal nominal). Flujo normal.

• Modelo de transferencia de movimiento: Grace.

• Diámetro de burbuja, 0.1 mm.

• Densidad de Referencia: 1000 Kg/m3.

• Tensión Superficial del agua. (0.072 Nw/m).

• Esquema de avección: Upwind. Escala de tiempo física: 0.0027284 s.

• Tolerancia residual: 1e-04.

• Tolerancia de conservación: 0.01.

RESULTADOS Y DISCUSIÓN

Curvas de altura vs caudal

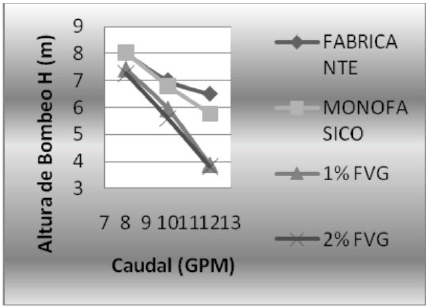
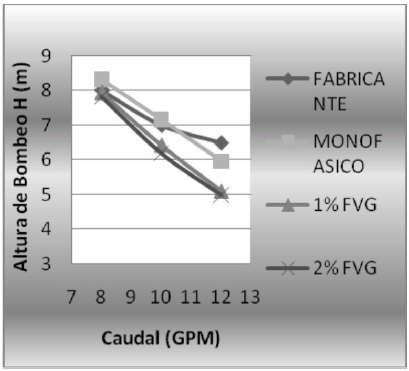
Se observó en las figuras 10 y 11 que en ambas etapas para flujo monofásico, la curvas de altura de bombeo vs. caudal simuladas, coinciden de una manera aceptable con la del fabricante, lo cual sirve para validar los resultados obtenidos en la simulación. (Diferencia de 2,8% y 2,2%, en alturas debombeo de primera y segunda etapa, respectivamente). A medida que aumenta la FVG de entrada al sistema, la caída de altura de bombeo es mayor, a caudal nominal. Dicha caída de altura de bombeo es mayor en la primera etapa que en la segunda (caída del 12,6% y 10,3%, en primera y segunda etapa, respectivamente) desde monofásico a bifásico con 1% de FVG. Todo este comportamiento cualitativo era el esperado, siendo consistente con la teoría de bombas centrífugas para flujo bifásico, mostrada en los trabajos anteriores de Pessoa & Prado, 2001; López, 2006.

Figura 10. Altura de bombeo vs. Caudal de agua para primera etapa, para fabricante, flujo monofásico, bifásico con 1% de FVG y 2% FVG a 3500 RPM, con diámetro de burbuja de 0,1 mm.

Figura 11. Altura de bombeo vs. caudal de agua para segunda etapa, para fabricante, flujo monofásico, bifásico con 1% de FVG y 2% FVG a 3500 RPM, con diámetro de burbuja de 0,1 mm.

Comparación de curvas experimentales y simuladas para dos etapas consecutivas, para flujo bifásico

Se observa bastante similitud entre las curvas experimentales y simuladas, para primera y segunda etapas, a caudales nominales, al considerar las curvas presentadas en el trabajo de López, 2006. (Se observa mayor cercanía en los resultados a 2% de FVG, a caudal nominal). La diferencia entre las curvas experimentales y simuladas difiere en un porcentaje relativamente bajo (alrededor de 2,3% para 2% de FVG a la entrada al Sistema). No obstante, a caudales menores y mayores al nominal, las curvas simuladas no reproducen correctamente el comportamiento real de las etapas.

Cambio de velocidades meridionales y circunferenciales, y efecto en alturas de bombeo y teóricas, así como factores de deslizamiento

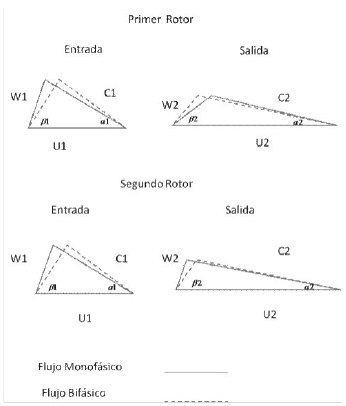
Los triángulos de velocidad resultantes de la simulación se muestran en la figura 12.

Figura 12. Triángulos de velocidades inherentes a los resultados de la simulación, para caudal nominal.

En el caso monofásico las componentes tangenciales de las velocidades absolutas a la entrada (Cu1) disminuyen con aumento de caudal, en ambas etapas, llegando a un valor mínimo a un caudal de 10 GPM en segunda etapa, y 12 GPM en primera etapa. Para estos caudales hay mínima prerrotación y por lo tanto menor pérdida por choque, para cada rotor respectivo, porque el fluido está bien direccionado a la entrada de cada rodete.

Para flujo monofásico, el rotor 2 experimenta una mayor altura de bombeo en relación al rotor 1, (aumento en 1,81%), lo cual es una variación muy pequeña. Por otra parte, la altura teórica en la segunda etapa es mayor a la de la primera etapa, lo que constituye un aumento en 1,85%. Como consecuencia de esto el factor de deslizamiento aumenta en 2,63% de primera a segunda etapa. Así pues, tanto el cambio en el factor de deslizamiento, como el de las pérdidas hidráulicas, es muy pequeño, desde la primera a la segunda etapa, al igual que para la altura de bombeo, como predice la teoría para flujo monofásico (Mataix & Wiggert, 1991; Potter, 1997).

Para flujo bifásico 1% de FVG, La variación de Cu1 y Cu2, hace que la altura teórica en la primera etapa sea mayor a la de la segunda etapa, lo cual constituye un decrecimiento del 1,65%. El factor de deslizamiento disminuye en 1,32% de primera a segunda etapa. Se puede notar que la eficiencia hidráulica, la cual depende de la altura de bombeo y altura teórica, aumenta de primera etapa a segunda etapa, y es más influenciada por la disminución de pérdidas hidráulicas (debido a la mejor conducción de flujo de fluido a la entrada de la segunda etapa, que a la primera), que por la disminución del factor de deslizamiento.

Efecto de pérdidas por choque y fricción en eficiencia hidráulica

Se observó que la eficiencia hidráulica disminuye de monofásico a bifásico, a caudal nominal, en 13,8% para primera etapa y en 8,33% para segunda etapa. Esto se debe a la disminución notable de la altura de bombeo, debido al aumento en las pérdidas hidráulicas, por acumulación de cavidades de aire en el canal interálabe tanto en los rodetes como diafragmas. Es de hacer notar que predomina la variación por pérdida hidráulica sobre la variación por factor de disminución de trabajo y altura teórica.

En los rotores al acumularse burbujas, el área transversal del canal interálabe disminuye, (se forma una contracción). En el diafragma, la acumulación de burbujas ocasiona el mismo efecto de contracción del canal y por lo tanto la caída de altura en este componentes, (la cual es de 13,6% en el primer diafragma y 11,1% para el segundo diafragma), ocurre para flujo bifásico. Al haber deslizamiento entre el agua y el aire, la fuerza de roce aumenta las pérdidas hidráulicas, además de la formación de la contracción.

Al haber mayor caída de altura de bombeo en la primera etapa (caída del 12,6%) que en la segunda etapa (caída del 10,3%), siendo las alturas teóricas iguales o levemente distintas (caídas promedio de 2% aproximadamente), la eficiencia hidráulica en la primera etapa tiene mayor caída (13,8%) que la segunda etapa (8,33%), para el caso de flujo bifásico.

La presencia de cavidades también modifica el patrón de flujo, en el sentido de que se forman “contracciones locales” en los canales interálabes, lo cual aumenta las pérdidas de altura por fricción y pérdida localizada. La unión de ambos tipos de pérdidas hidráulicas, modifican las alturas efectivas, lo cual unido al cambio en las alturas de los diafragmas, lleva a los cambios en alturas de bombeo y eficiencias hidráulicas, en las proporciones ya referidas.

Se observa que la pérdida de altura desde flujo monofásico hasta flujo bifásico, a 80% de caudal nominal es menor que a 120% caudal nominal. Esto se debe a que en el primer caso, la diferencia de densidad de las fases es menor, que en el segundo caso, por lo que el flujo es más homogéneo y hay menos deslizamiento. Por lo tanto hay menos pérdidas hidráulicas para 80% de caudal nominal, que para el caso de 120% caudal nominal (Hay menor deterioro de la altura de bombeo a 80% de caudal nominal, que a 120% de caudal nominal).

Deflexión en los diafragmas

Se observa que desde flujo monofásico a bifásico, la deflexión en cada diafragma disminuye. Esto se debe a que los ángulos de flujo a la entrada de los diafragmas son relativamente constantes, y los ángulos de salida disminuyen (este cambio de perfil de velocidades se debe a la presencia de cavidades de aire). Así pues, la desviación disminuye, en cada diafragma. Se observó que a caudal nominal, la deflexión disminuye de monofásico a bifásico (13,1% para primer diafragma y 11,6% en segundo diafragma, a 1% de FVG). No obstante, debido a que ya para caso monofásico, la deflexión del diafragma 2 era menor que para el diafragma 1, en el caso bifásico el diafragma 2 presenta menor deflexión que el diafragma 1 para caso bifásico, y por eso presenta menos pérdidas en el estator 2.

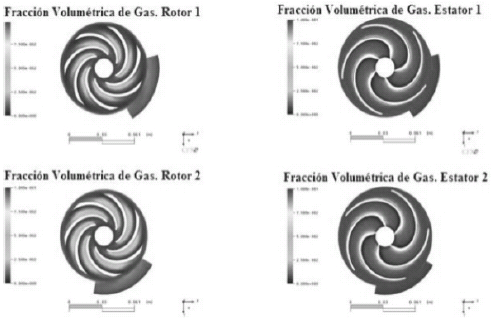
Distribución de FVG en rodetes y diafragmas para 100% de caudal nominal con 1% de fvg a la entrada, y su efecto sobre las alturas efectivas

Se puede observar que para un caudal nominal (10 GPM), con una FVG de 1% a la entrada, la distribución de FVG en cada componente de las dos etapas consecutivas (rotor 1, rotor 2, diafragma 1 y diafragma 2), indica que se forman cavidades de gas. Estas cavidades se forman en el lado de presión de los álabes en los rotores, y en el lado de baja presión en los diafragmas.

En el caso de los rodetes, ocurre que las burbujas en el lado de presión de los álabes, al ser las presiones mayores, las velocidades son menores, por lo que las fuerzas de arrastre son menores a las de flotación, y es por ello que se acumulan en ese lugar.

En los rodetes, a medida que el agua fluye hacia la localización de las cavidades, el área de flujo disminuye y se forma una contracción.

La distribución de FVG en los rodetes y diafragmas para caudal nominal, se muestran en la figura 13.

Figura 13. Fracción volumétrica de gas para flujo bifásico con tamaño de burbuja de 0.1 mm y 1.2 caudal nominal 1% presión de succión 25 Psig.

CONCLUSIONES

El modelo empleado refleja en forma aceptable, el comportamiento de cada etapa, para caso monofásico. (Diferencias entre curvas empíricas del fabricante y simuladas por el orden de 2%).

Las alturas de bombeo en primera y segunda etapa, experimentan caídas de 12,6% y 10,3%, respectivamente al considerar flujo bifásico con 1% de FVG, en relación a flujo monofásico. Esto se debe a la alteración de flujo en rotores y diafragmas, debido a la presencia de cavidades de aire.

Las eficiencias hidráulicas en flujo bifásico experimentan caídas de 13,8% y 8,33% en primera y segunda etapa, respectivamente, al compararlas con el flujo monofásico. Esto se debe a la presencia de burbujas en los canales interálabe.

El aumento en la altura teórica para caudal nominal, desde flujo monofásico a bifásico en la primera etapa es de 1,65%, mientras que en la segunda etapa la disminución es de 1,83%, lo cual ocasiona un cambio 2,63% en el factor de deslizamiento de primera a segunda etapa, en caso bifásico.

Para el caso monofásico, desde la primera a segunda etapa, las alturas y eficiencias aumentan en 1,81% y 3,45%, respectivamente, y tiene la misma importancia el aumento en el factor de deslizamiento (2,63%), que el cambio en pérdidas hidráulicas.

Para el caso bifásico, desde la primera a la segunda etapa, las alturas y eficiencias hidráulicas aumentan en 7,94% y 9,1%, respectivamente, y disminuye en menor proporción el factor de deslizamiento (1,32%), en relación a la disminución de pérdidas hidráulicas.

El cambio de pérdidas hidráulicas en flujo bifásico se debe a la acumulación de burbujas en el canal interálabe, tanto en los rodetes como diafragmas.

En los diafragmas, de flujo monofásico a bifásico, la desviación disminuye en 13,6% para primera etapa y 11,1% en segunda etapa. Además la desviación en el diafragma 2 es menor que el diafragma 1, y por lo tanto las pérdidas hidráulicas en el diagrama 2 son menores que para el diafragma1.

En flujo bifásico 1% FVG, las cavidades de aire que se alojan en la entrada de los rodetes, y a la entrada de los diafragmas, ocasionan un detrimento en las alturas de bombeo de las etapas, ya que modifican velocidades y presiones del flujo (agregan un componente de fricción en la interfase agua-líquido por deslizamiento, el cual es bajo a menores caudales como 80% del valor nominal).

El cambio de altura de bombeo entre la primera y segunda etapa, se debe a un compromiso entre alturas teóricas, y pérdidas hidráulicas (de choque y de fricción) en rotores y por deflexión en diafragmas, influenciados por la presencia de cavidades de aire en todos los canales interálabes (hay mayor predominio de las pérdidas hidráulicas, sobre los cambios por deslizamiento).

REFERENCIAS

1. Caridad, J. & Kenyery, F. (2004). Slip factor for centrifugal impellers under single and two-phase flow conditions. Journal of Fluids Engineering, 1028, pp.1-7.        [ Links ]

2. Caridad, J. (2004). Cfd analysis of electric submersible pumps (esp) handling two-phase mixtures. Vol. 126, pp. 99-104.        [ Links ]

3. Duplat, P. (2004). Simulación 3d del flujo bifásico en rodetes de bombas centrífugas. B.S. Tesis, Universidad Simón Bolívar. s/n.        [ Links ]

4. Lee, T.S., Winoto, S.H., Zao, Z., Zhou, W. (2003). Investigation of flow through centrifugal pump impellers using computational fluid dynamics. International Journal of Rotating Machinery, 9(1), pp. 49-61.        [ Links ]

5. López, D. (2004). Efecto del tamaño de burbuja en el desempeño de una bes manejando flujo bifásico. M.S. Tesis, Universidad Simón Bolívar. s/n.        [ Links ]

6. Mataix, C. (1998). Turbomáquinas hidráulicas. Editorial Icai, España. s/n.        [ Links ]

7. Pak, E.T. & Lee, J.C. (1998). Performance and pressure distribution changes in a centrifugal pump under twophase flow. Proc. Instn. Mech. Engrs., Vol. 212, Part A, pp. 165-171.        [ Links ]

8. Pessoa & Prado, M. (2001). Experimental investigation of two-phase flow performance of electrical submersible pump stages. SPE 71552.        [ Links ]

9. Potter, M. & Wiggert, D. (1997). Mechanics of fluids. Prentice-Hall, USA. s/n.        [ Links ]