Evaluating block preconditioners in the solution of saddle point systems

Zenaida Castillo¹, Jean Piero Suárez²

¹Universidad Central de Venezuela, Facultad de Ciencias, Escuela de Computación, Caracas, 1041-A, Venezuela, e-mail: zenaida.castillo@ciens.ucv.ve

²San Diego State University, Computational Science Research, San Diego CA 92182 -1245, USA, email: jsuarez@sciences.sdsu.edu

ABSTRACT

This paper presents a new approach to precondition linear systems of the saddle point kind. Specifically we consider block diagonal, block triangular and block indefinite preconditioning techniques on nonsymmetric systems. These preconditioners require the computation of some inverses and we propose to use sparse approximate inverses (SPAI) to construct these approximations. The computation of these inverses involves solving a set of uncoupled least squares problems, which can be easily parallelized on a memory distributed machine. Comparison with other techniques suggests that block diagonal and block triangular preconditioning can be more effective if they are combined with SPAI techniques in the computation of approximate inverses. Results are promising and show the effectiveness of these preconditioners when improving the convergence of Krylov methods such as GMRES, which suggests the application of this approach in the large-scale setting.

Keywords: Saddle point linear systems, Block preconditioners, Sparse approximate inverses, SPAI techniques, Krylov methods, GMRES.

Evaluación de precondicionadores en bloque en la solución de sistemas de punto de ensilladura

RESUMEN

Este artículo presenta una nueva técnica para precondicionar sistemas lineales conocidos en la literatura como sistemas de punto de ensilladura. Específicamente consideramos precondicionadores en bloque del tipo diagonal, triangular e indefinido, sobre sistemas de punto de ensilladura no simétricos. Estos precondicionadores requieren el cálculo de inversas y proponemos usar la técnica de aproximación de inversa conocida como SPAI (Aproximación dispersa de la inversa) por sus siglas en inglés. La construcción o cálculo de estas inversas requiere de la resolución de un conjunto de problemas desacoplados de mínimos cuadrados, que puede fácilmente paralelizarse en máquinas con memoria distribuida o máquinas vectoriales. Se presenta un análisis comparativo de tres precondicionadores propuestos. Los resultados numéricos muestran que los precondicionadores en bloque del tipo diagonal y triangular pueden ser más efectivos si se combinan con técnicas SPAI para el cálculo aproximado de las inversas, una vez que se mejoran sustancialmente las características de convergencia de métodos de Krylov como GMRES. Esto nos permite sugerir la aplicación de esta técnica en la resolución de sistemas de gran magnitud.

Palabras clave: Sistemas lineales de punto de ensilladura, Precondicionadores en bloque, Aproximación dispersa de inversas, Técnicas SPAI, Métodos de Krylov, GMRES.

Recibido: febrero de 2009 Recibido en forma final revisado: julio de 2010

INTRODUCTION

The numerical solution of many important problems in sciences and engineering, such as computational fluid dynamics, electromagnetism, nonlinear quadratic programming, constrained optimization and computer graphics is often obtained by solving saddle point linear systems (SPLS), see for example the works in (Glowinsky, 2003; Gould et al. 2001; Wright, 1997). The general structure for these linear systems is:

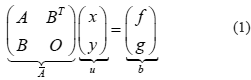
where A Î R^nxn, B Î R^mxn and n ≥ m. This kind of linear systems are known as saddle point problems due to the equivalence with the solution of the equality constrained quadratic programming problem:

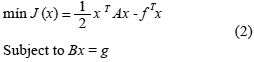
In this problem, the vector y in the linear system (1) represents Lagrange multipliers and the solution of this system is a saddle point of the Lagrangian:

In practical applications, system (1) comes from the discretization of partial differential equations (PDE), thus, the coeffient matrix Ā is large and sparse. For that reason, we are interested in a good approximation of the solution, which can give us important information about the modeled system. In these cases, non analytical or iterative methods are preferred, although direct methods like Gaussian elimination and its variants can be used if the size of the system is moderated (Benzi et al. 2005).

Spectral and symmetry properties of matrix Ā, the upper left block of A, play an important role when choosing a numerical method to solve the linear system (1). In particular, the case when A is symmetric and positive definite has been studied and developed widely by several authors; see for example the works in (Axelson et al. 2003; Sylvester et al. 2001; Elman et al. 1996).

However, SPLS in which the matrix A is no symmetric are of great importance and solving them efficiently has been a topic of research in recent years. Numerical solution of this kind of systems will be considered in this work.

It is known that when the coefficient matrix Ā is large and ill conditioned an iterative preconditioned Krylov subspace solver such as preconditioned GMRES is the best choice to get a good approximation. Several preconditioners based on incomplete factorizations, sparse approximate inverses and algebraic multilevel methods have been proposed for SPLS (Benzi, 2002; Van der Vorst, 2003), some of which have turned out to be well-suited for general saddle point systems. In particular, considering the block structure of the coefficient matrix, some authors have independently proposed block preconditioners to solve SPLS, see for example the references (Ipsen 2001; Murphy et al. 2000; Perugia et al. 2000; Rozloznk, 2002).

The main contribution of this work is to provide an evaluation of current block preconditioners when using a SPAI (Sparse Approximate Inverse) technique for the computation of the inverses involved. The construction of each one of these block preconditioners requires exact inverses of matrices which are smaller in magnitude than the matrix Ā, and we propose to replace those inverses by sparse approximations of them.

CURRENT APPROACHES

Algorithms for saddle point problems can be classified in segregated and coupled. Segregated methods take advantage of the block structure of (1) and compute vectors x and y separately, by solving linear systems with coefficient matrices of smaller dimensions than Ā.

The main representations of these techniques are based on Schur complement reduction (Vavasis, 1994; McGuire et al. 1979) and null space methods (Arioli et al. 2002), which solve the equivalent problem:

Ax + B^T y = f

Bx = g      (4)

Schur complement reduction is a technique commonly used in problems where the matrix A is symmetric positive definite and B has full column rank. Based on these considerations, vector x in (4) can be eliminated, obtaining a symmetric positive definite linear system of m x m:

Sy = BA^-1 f - g    (5)

where the matrix S = BA^-1B^T is known as the Schur complement.

When the inverse of A exists, the linear system (5) can be solved using conjugate gradient without explicitly constructing the matrix S, which is in general dense and its computation is expensive. This technique is very effective when the order m is not large. The main disadvantage of Schur complement reductions is that the inverse of A is required, thus, when A is dense and large, null space methods are preferred.

Null space methods are used generally when matrix A is symmetric positive semidefinite (singular) and B has full column rank. These methods compute a particular solution 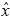of Bx = g and a matrix Z Î R^{nx(n - m)} whose columns form a basis for the null space of B; then, the general solution of Bx = g is given by x = Zv + 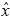, where the unknown vector v is the solution of the reduced symmetric positive definite linear system:

(Z ^T AZ )x = Z ^T ( f - A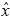)       (6)

of dimension (n-m)x(n-m). The solution of (6) can be obtained using a conjugate gradient method (Hestenes et al. 1952; Saad, 2003), which is especially attractive when n - m is small.

On the other hand, coupled methods deal with the linear system as a whole, computing the unknown vectors x and y simultaneously.

Finally, for both kinds of methods, segregated and coupled, one could use iterative or direct solvers, however, it is known that in the large scale setting, iterative Krylov subspace methods play an important role.

Krylov subspace methods

Iterative methods in Krylov subspaces consider an initial approximation u₀ R^{n + m} of (1) and a residual vector r₀ = b - Au₀ to define an iteration that in i steps generates an approximated to the solution in the space:

K_i (Ā,r₀) = span{r₀,Ār₀, Ā²r₀,...,Ā ^{i - 1} r₀}     (7)

which is called Krylov subspace generated by the matrix Ā and the initial vector r₀ (Saad, 2003).

Conjugate gradient (CG) (Hestenes, 1952), minimum residual (MINRES) (Paige et al. 1975) and generalized minimal residual (GMRES) (Saad,1986) are examples of Krylov subspace methods used frequently for solving large-scale SPLS. In particular, the CG method is used for symmetric positive definite systems, MINRES for symmetric and possibly indefinite systems, and GMRES for nonsymmetric systems. Additionally, CG and MINRES have been proposed to solve saddle point problems in its segregated form when the matrix Ā is symmetric.

Since we are interested in analyzing the behavior of block preconditioners for nonsymmetric saddle point linear systems, we solve the coupled linear system (1) using the method of generalized residuals GMRES.

Generally, iterative Krylov solvers require the application of preconditioning techniques to accelerate the convergence. This work considers block diagonal, block triangular and block indefinite preconditioners, which will be presented in details in the next section.

PRECONDITIONING SPLS

Preconditioning a linear system means to convert it into an equivalent and more tractable system with a better condition. This can be done by premultiplicating and (or) post-multiplicating by some suitable preconditioner matrix P. Preconditioning (1) by the left results in the following linear system:

PĀu = Pb       (8)

and by the right:

ĀPy = b, x = Py         (9)

One should take P as an inexpensive approximation of the inverse of Ā, such that the preconditioned system has a low degree minimum polynomial, i.e., the coefficient matrix of the new system should have a few distinct eigenvalues; in this case, iterative methods like GMRES generally present faster convergence.

In the present work, we apply block preconditioned GMRES to the coupled system (1). This approach can be superior to others for very large matrices since the cost of computing several matrix-vector products with matrices A and B simultaneously is comparable to the computation of one matrix-vector product with matrix Ā, considering memory references. In particular, block methods enable the use of level 3-BLAS, which usually results in a better performance on high level computer architectures supporting vector and parallel processing.

Block diagonal preconditioner

For saddle point problems, Murphy, Golub and Wathen in 2000 proposed an efficient preconditioner, which has the following structure when A is nonsingular:

 

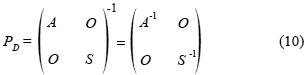
In this case, the right preconditioned linear system has a coefficient matrix given by:

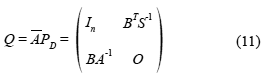
It has been proved in (Murphy et al. 2000) that Q is diagonalizable having just four distinct eigenvalues:

therefore, for any arbitrary rÎR^{n + m}, the Krylov subspace:

span{r , Qr , Q²r , Q³r ,...}       (13)

has at most dimension three if Q is nonsingular, and dimension four if Q is singular. In particular, one could expect that iterative methods like GMRES applied to the preconditioned linear system will terminate in at most 3 or 4 iterations in exact arithmetic.

Block triangular preconditioner

This kind of preconditioners, introduced by Bramble & Pasciak in 1998, has the following structure:

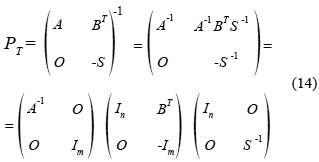
Thus, the coefficient matrix of the right preconditioned linear system is:

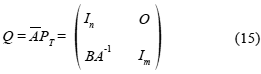
and the spectrum of Q is {1}, which implies faster convergence for Krylov methods like GMRES.

Indefinite preconditioner

In this case, the preconditioner has the same block structure than the original problem (1):

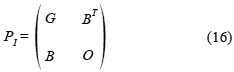
where G ≠ A is some approximation of A, chosen in such a way that the preconditioned linear system is significantly easier to solve than the original problem (1). Some implementations of this preconditioner can be found in (Bergamaschi et al. 2004; Keller et al. 2000).

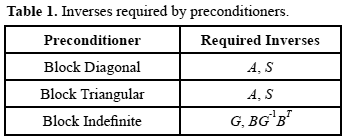
The construction of each block preconditioner involves the inverses of some matrices. This requirement per preconditioner is summarized in Table 1.

This paper proposes to replace these exact inverses by SPAI approximations, using the methodology studied by Grote and Huckle in 1997. The general idea of this technique will be described in the next section.

SPARSE APPROXIMATE INVERSE (SPAI)

Given a nonsingular matrix A Î R^nxn, the basic idea of this technique (Grote & Huckle, 1997), is to compute a sparse matrix P ≈ A^-1 which minimizes the Frobenius norm of the residual matrix I_n - AP, denoted by ||AP - I_n|| _F . By definition:

where e_k y p_k are the k-th column of the identity and P matrices respectively. Thus, one could minimize globally the Frobenius norm  ||AP - I_n|| _F as a function of P. Another possibility is to minimize the function f_k for each k = 1,...,n defined by:

f_k( p_k ) = ||Ap_k - e_k||₂     (18)

This last strategy is very suitable when working in parallel architectures, since the problem of minimizing ||AP - I_n|| can be separated into n independent least squares problems:

The preconditioner P should be a sparse matrix; this condition allows the reduction of (19) to n least squares problems of small dimension that can be solved easily using traditional methods based on QR factorizations.

The main difficulty of this preconditioning technique is the selection of a sparsity structure of P that results in an effective preconditioner. The sparsity pattern should retain the sparse structure of A in P, dropping those entries that do not contribute to the quality of the preconditioner. For example, it is desirable to ignore those entries that are small in absolute value with respect to some tolerance, and retain those with greater values. Nevertheless, the location of the entries in A^-1 with greater values is not normally known, thus, the choosing of a sparsity pattern could be a very difficult task.

To determine the sparsity pattern of P one could use adaptive strategies in which nonzero elements are dynamically defined, or one can select static strategies where the structure of P is fixed a priori.

Once the sparsity pattern is defined, the number of nonzero entries in P increases until the Euclidean norm of the residual vector r_k = Ap_k - e_k satisfies a criterion of the type ||r_k|| ₂ < e for a given tolerance e, or when a maximum number of nonzero elements in the column p_k is reached. Examples of successful implementations of this technique can be found in (Castillo, 2009; Baggag et al. 2004; Broker et al. 2002; Elman et al. 2002).

NUMERICAL EXPERIMENTS

This section presents numerical results obtained after the application of the three block preconditioners described previously, on some interesting test problems. The package IFISS, developed by Elman, Ramage et al. 1996, was used to produce our test problems. This package allow us to define linear systems arising in the discretization of steady state Navier Stokes equations governing a incompressible viscous flows:

-vD²u + u . Du + Ñp = f

div u = 0   (20)

Here, v > 0 is the viscosity of the fluid, u is the velocity in the point x on the domain, p is the pressure in x, and f represents the action of gravity and the interaction between the fluid forces.

Specifically, we consider the following Navier Stokes test problems generated by IFISS:

1. Channel domain (NS1).

2. Flow over a backward facing step (NS2).

3. Lid driven cavity (NS3).

4. Flow over a plate (NS4).

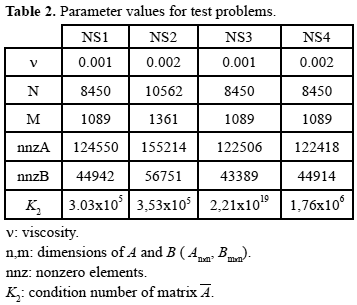
Each one of these problems is discretized using the Taylor-Hood method (Elman et al. 2005) with uniform grids for NS1, NS2 and NS4 and stretched grid for NS3 (with grid parameter equal to six and horizontal parameter equal to two). After discretization, linear systems with the saddle point structure (1) are obtained. In all cases, A is nonsingular and nonsymmetric, and B is a full column rank matrix. Viscosity and characteristics of matrices A and B for all test problems were chosen by default. Table 2 shows the values of these parameters.

Since the block A is nonsymmetric in all test cases, a Schur complement reduction combined with conjugate gradient method is discarded. In addition, due to the size of the systems, null space methods are not attractive, thus, a preconditioned GMRES was used to get an approximated solution for the whole system Ā u = b .

Versions of block diagonal, block triangular and block indefinite preconditioned GMRES were constructed to solve each linear system numerically. In the construction of block diagonal and block triangular preconditioners the inverse of A was replaced by its SPAI approximation.

The inverse of the Schur complement was also replaced by a SPAI approximation of BD_A^-1 B^T , where D_A is a diagonal matrix whose elements are the same as the diagonal of A. This last approximation was also used to construct the block indefinite preconditioner, choosing G = D_A .

It is important to point out that numerical experiments using full inverses to construct each preconditioner were done, but this strategy was not feasible, due to the memory requirements for these calculations and the prohibitive computational cost.

The construction of SPAI approximations for the required inverses for each preconditioner (table 1) is based on the Grote and Huckle strategy with a static pattern for the preconditioner M. A dynamic pattern was also attempted, but it was not effective and its construction was time consuming.

In all cases, e = 0.35 was used as level of tolerance for the residual in the construction of each column of SPAI approximation. This value of e was enough to produce approximations of the inverses with the same nonzero density of the respective matrices, which is desirable since it does not increase the computational cost by iteration of the iterative method.

Sparse inverse approximations were constructed by the right, thus, the system was preconditioned by the same side. Full GMRES was applied, with zero as initial guess, a tolerance of 10^-8 for the relative error and a maximum of 1500 iterations. All experiments were performed using Matlab 7.0 on a Toshiba computer with a Core Duo T2400 1.83 Ghz processor, with 3.25 GB RAM memory.

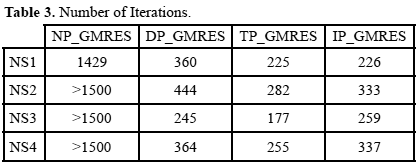
In each case, the linear system was solved with and without preconditioning. Table 3 presents, for each test problem, the number of iterations required for each solver. GMRES block preconditioned versions were named as:

NP_GMRES: No preconditioned GMRES.

DP_GMRES: Diagonal preconditioned GMRES.

TP_GMRES: Triangular preconditioned GMRES.

IP_GMRES: Indefinite preconditioned GMRES.

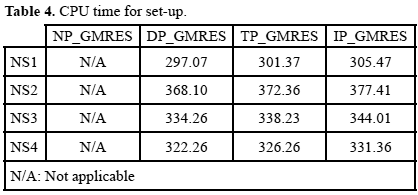
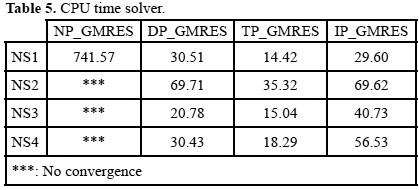
Table 4 reports set-up time (preconditioner construction and preconditioner application), while table 5 shows CPU time consumed by GMRES when it reaches convergence.

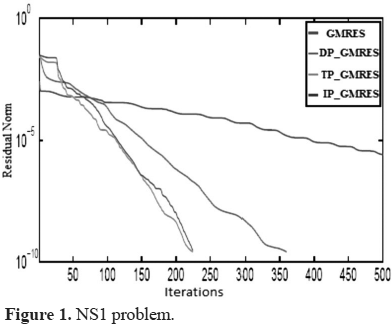
On the other hand, figures 1-4 below illustrate the reduction of the residual norm when using GMRES without preconditioning and GMRES with the inexact versions of block diagonal, block triangular and indefinite preconditioners, denoted in the figures as GMRES, DP_GMRES, TP_GMRES and IP_GMRES respectively.

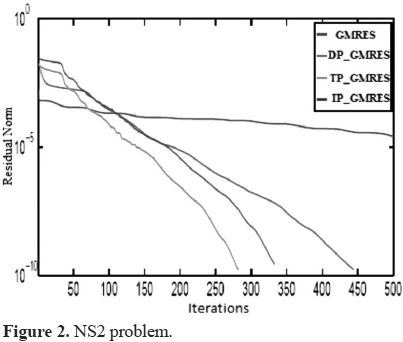
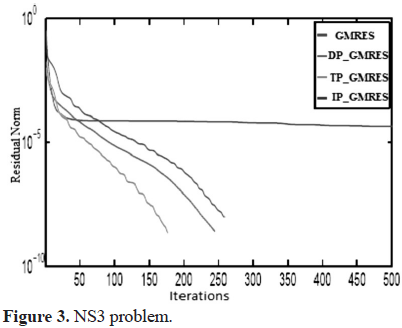
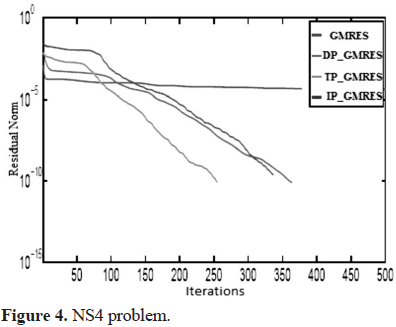
For all test problems, preconditioned GMRES converged in less than 400 iterations. Nevertheless, GMRES without preconditioning only reached convergence for the NS1 problem with a number of iterations close to the maximum, which clearly suggest the need of a preconditioner to solve these problems.

With respect to the block preconditioned versions of GMRES, in all cases, the best results, considering time and number of iterations, were obtained with block triangular preconditioners. Additionally, although the construction and application of block diagonal preconditioner consume the smaller amount of time (table 4), GMRES with this preconditioner requires more iterations to converge than the others (table 3).

Block indefinite preconditioners were in general denser than the others preconditioners; thus, its construction and application consumed more time.

CONCLUSIONS AND FUTURE WORK

Sparse approximations of inverses were used to construct versions of block diagonal, block triangular and block indefinite preconditioners for the solution of saddle point problems. The application of these blocks preconditioners along with GMRES on nonsymmetric saddle point linear systems (SPLS) is promising. The proposed technique of constructing block preconditioners using sparse approximation of inverses reduced time and the number of iterations, leading a faster convergence of GMRES in each test problem.

It is important to recognize that others preconditioners, such as ILU and its variants, have been more effective in the solution of the test problems when sequential codes are used. However, it is well known that ILU preconditioners do not perform well and suffer from breakdowns over ill-conditioned systems, and it is very difficult to implement ILU type preconditioners on distributed memory parallel computers, where the communication overhead is significantly large. On other hand, SPAI preconditioners are highly parallelizable and it does not suffer from the usual drawbacks of incomplete factorization methods.

In this article we evaluated and compared a non-preconditioned version of GMRES and three block preconditioned versions of GMRES on a sequential machine. Results show the reliability of these approaches for different test problems, and suggest that they can be competitive for solving large-scale saddle point linear systems. Due to these results, and taking into account that the SPAI constructions are highly parallelizable, the next step in this direction should be to evaluate the scalability of this approach in the solution of very large saddle point systems in a parallel environment.

ACKNOWLEDGMENT

The authors thank Andy Wathen from Oxford University for providing the test matrices used in the numerical experiments.

REFERENCES

1. Arioli, M. & Manzini, G. (2002). A null space algorithm for mixed finite-element approximation of Darcy’s equation, Comm. Numer. Meth. Engng., 18, pp. 645–657.        [ Links ]

2. Axelsson, O. & Neytcheva, M. (2003). Preconditioning methods for linear systems arising in constrained optimization problems, Numer. Linear Algebra Appl., 10, pp. 3–31.        [ Links ]

3. Baggag, A. & Sameh, A. (2004). A nested iterative scheme for indefinite linear systems in particulate flows, Comput. Methods Appl. Mech. Engrg., 193, pp. 1923–1957.        [ Links ]

4. Benzi, M. & Golub, G. (2002). Preconditioning techniques for large linear systems: a survey, J. Comput. Phys., 182, pp. 418–477.        [ Links ]

5. Benzi, M. & Golub, G. (2005). Numerical solution of saddle point problems, Acta Numerica, pp1-137.        [ Links ]

6. Bargamaschi, L., Gondzio, J., Zilli, G. (2004). Preconditioning indefinite systems in interior point methods for optimization, Comput. Optim. Appl., 28, pp. 149—171.        [ Links ]

7. Bramble, J. H. & Pasciak, J. E. (1998). A preconditioning technique for indefinite systems resulting from mixed approximations of elliptic problems, Math. Comp., 50, pp. 1–17.        [ Links ]

8. Broker, O., Grote, M., Mayer, C., Reusken, A. (2001). Sparse approximate inverse smoothers for geometric and algebraic multigrid, Appl. Numer. Math., 41, pp. 61–80.        [ Links ]

9. Castillo, Z., Xui, X., Sorensen, D., Embree, M., Pasquali, M. (2009). Parallel solution of large-scale free surface viscoelastic flows via sparse approximate inverse preconditioning. Journal of Non-Newtonian Fluid Mechanics. Vol 157, Nos. 1-2, pp. 44-54.        [ Links ]

10. Elman, H. C., Ramage, A. R., Silvester, D. J. (1996). Incompressible Flow Iterative Solution Software Package, http://www.cs.umd.edu/~elman/ifiss/.        [ Links ]

11. Elman, H. C. & Silvester, D. J. (1996). Fast nonsymmetric iterations and preconditioning for Navier-Stokes equations, SIAM J. Sci. Comput., 17, pp. 33–46.        [ Links ]

12. Elman, H. C., Silvester, D. J., Wathen, A.J. (1997). Iterative methods for problems in computational fluid dynamics, Iterative Methods in Scientific Computing, Chan R., Chan T. and Golub G. (Eds), Springer-Verlag, pp. 271–327.        [ Links ]

13. Elman, H. C., Silvester, D. J., Wathen, A.J. (2002). Block preconditioners for the discrete incompressible Navier- Stokes equations, Internat. J. Numer. Methods Fluids, 40, pp. 333–344.        [ Links ]

14. Elman, H. C., Silvester, D. J., Wathen, A.J. (2005). Finite Elements and Fast Iterative Solvers, Oxford University Press.        [ Links ]

15. Glowinsky, R. (2003). Finite element methods for incompressible viscous flow. Vol. IX of Handbook of Numerical Analysis, part 3: Numerical methods for fluids, North-Holland, Amsterdam.        [ Links ]

16. Gould, N. I. M., Hribar, M. E., Nocedal, J. (2001). On the solution of equality constrained quadratic programming problems arising in optimization, SIAM J. Sci. Comput., 23, pp. 1376–1395.        [ Links ]

17. Grote, M. J. & Huckle, T. (1997). Parallel preconditioning with sparse approximate inverses, SIAM J. Sci. Comput., 10, pp. 838–853.        [ Links ]

18. Hestenes, M. R. & Stiefel, E. (1952). Methods of conjugate gradients for solving linear systems, J. Res. Nat. Bureau of Standards, 49, pp. 409–436.        [ Links ]

19. Ipsen, I. (2001). A note on preconditioning nonsymmetric matrices, SIAM J. Sci. Comput., 23, pp. 1050–1051.        [ Links ]

20. Keller, C., Gould, N. I. M., Wathen, A. J. (2000). Constraint preconditioning for indefinite linear systems, SIAM J. Matrix Anal. Appl., 21, pp. 1300–1317.        [ Links ]

21. McGuire, W. & Gallagher, R. H. (1979). Matrix Structural Analysis, Wiley, New York.        [ Links ]

22. Murphy, M.F., Golub, G.H., Wathen, A. J. (2000). A note on preconditioning for indefinite linear systems, SIAM J. Sci. Comput., 21, pp. 1969–1972.        [ Links ]

23. Paige, C. C., Saunders, M. A. (1975). Solution of sparse indefinite systems of linear equations, SIAM J. Numer. Anal., 12, pp. 617–629.        [ Links ]

24. Perugia, I. & Simoncini, V. (2000). Block diagonal and indefinite symmetric preconditioners for mixed finite element formulations, Numer. Linear Algebra Appl., 7, pp. 585–616.        [ Links ]

25. Rozloznk, M. & Simoncini, V. (2002). Krylov subspace methods for saddle point problems with indefinite preconditioning, SIAM J. Matrix Anal. Appl., 24, pp. 368–391.        [ Links ]

26. Saad, Y. (2003). Iterative Methods for Sparse Linear Systems, SIAM, Philadelphia, PA.        [ Links ]

27. Saad, Y. & Schultz, M. H. (1986). Gmres: A generalized minimal residual algorithm for solving nonsymmetric linear systems, SIAM J. Sci. Statist. Comput., 7, pp. 856–869.        [ Links ]

28. Silvester, D. J., Elman, H. C., Kay, D., Wathen, A. (2001). Efficient preconditioning of the linearized Navier- Stokes equations, J. Comput. Appl. Math., 128, pp. 261–279.        [ Links ]

29. Van Der Vorst, H. A. (2003). Iterative krylov methods for large linear systems, Cambridge Monographs on Applied and Computational Mathematics, 13.        [ Links ]

30. Vavasis, S. A. (1994). Stable numerical algorithms for equilibrium systems, SIAM J. Matrix Anal. Appl., 15, pp. 1108–1131.        [ Links ]

31. Wright, S. J. (1997). Primal-Dual interior point methods, SIAM, Philadelphia, PA.        [ Links ]