Modelaje y simulación de un biorreactor enzimático no isotérmico para una reacción serie-paralelo

Yamilet Sánchez Montero ¹, Alexis Bouza ², Jenny MontBrun-Di Filippo ¹

¹ Universidad Simón Bolívar, Departamento Procesos y Sistemas. Caracas, Venezuela. e-mail: [ysanchez;montbrun]@usb.ve

² Universidad Simón Bolívar, Departamento Termodinámica y Fenómenos de Transferencia. e-mail: abouza@usb.ve

RESUMEN

Se desarrolla el modelo matemático para un biorreactor de tipo flujo pistón no isotérmico para una reacción serie-paralelo catalizada enzimáticamente, considerando que las enzimas están coinmovilizadas y las reacciones siguen la cinética de tipo Michaelis-Menten. El modelo se fundamenta en el acoplamiento de la cinética de reacción propuesta, así como en los balances de masa y energía de la microcápsula y de la fase fluida. El modelo presentado es adimensionalizado, permitiendo obtener parámetros adimensionales característicos tales como Péclet, Biot y Damköhler. El modelo del biorreactor es resuelto a través de un método explícito de diferencias finitas implantado en un módulo de Visual Basic^® en Excel^®. Se realiza un análisis paramétrico del comportamiento del biorreactor y se obtienen como resultados que los mismos están dentro de lo esperado para un sistema físico de estas características. Adicionalmente, el modelo desarrollado es validado con datos reportados por la literatura especializada, obteniéndose un error promedio de 9,59% en el peor de los casos.

Palabras clave: Modelo matemático, Biorreactor, No-isotérmico, Enzima, Simulación.

MODELLING AND SIMULATION OF A NON-ISOTHERMAL ENZIMATIC BIOREACTOR FOR A SERIE-PARALEL REACTION

ABSTRACT

A model for a non-isothermal enzymatic bioreactor for a serie-paralel reaction is developed where the enzymes are coimmobilized and the reactions follow Michaelis-Menten kinetics. The model is based on the coupling of reaction kinetic and mass and energy balances for microcapsule and fluid phase. The model was reduced to the corresponding dimensionless form obtaining parameters such as Péclet, Biot and Damköhler. The model was solved using explicit numerical method of finite difference developed on a Visual Basic^® module in Excel^®. A parametric analysis of the bioreactor performance is made, and the results were expected for a physical system of these features. The model is validated with data reported by Ching et al. (1990) and the average error obtained was 9.59% in the worst case.

Keywords: Mathematical model, Bioreactor, No-isothermal, Enzyme, Simulation.

Recibido: febrero de 2008 Revisado: marzo de 2011

INTRODUCCIÓN

Un biorreactor se puede definir como un sistema que proporciona un medio ambiente controlado permitiendo el crecimiento eficaz de las células y la formación de un producto, el cual debe tener niveles óptimos de temperatura, pH, substrato, sales y oxígeno, para así convertir la materia prima en productos específicos de interés.

Las reacciones que ocurren dentro del biorreactor son catalizadas por enzimas, las cuales son proteínas que funcionan como aceleradores de las reacciones químicas en los sistemas biológicos. Una enzima puede formar enlaces covalentes con una molécula mientras ocurre la transformación de la misma para luego, posteriormente, volver a su estado original una vez que el producto es liberado. Otra característica fundamental en la catálisis enzimática es que incrementa la velocidad, a la cual la reacción alcanza el equilibrio, esto implica que la catálisis incrementa la velocidad pero no cambia las propiedades termodinámicas del sistema con el cual está interactuando (Aiba et al. 1973; Shuler & Kargi, 1991).

El modelado de bioprocesos es una tarea compleja debido a que las reacciones biológicas son influenciadas por el ambiente químico (tales como los niveles de concentración de nutrientes y productos) y por las condiciones físicas del proceso. El metabolismo y los mecanismos de regulación de muchos de estos sistemas biológicos aún no son totalmente comprendidos, por lo cual las descripciones matemáticas de los mismos deben ser simplificadas sin pérdida de información que permita el desarrollo de modelos adecuados para la simulación, diseño y optimización de bioprocesos.

Los antecedentes en el estudio del comportamiento de reacciones que se llevan a cabo en biorreactores con enzimas inmovilizadas, muestran la inexistencia de un modelo que reúna las diferentes complejidades de los procesos que ocurren en un biorreactor, así como de sistemas de control avanzado adaptados a los mismos.

En la literatura se pueden encontrar importantes avances en el área de modelado de procesos que han comenzado a impactar el desarrollo de los bioprocesos. Beg et al. (1996) presentan un estudio fluidodinámico en el cual la fase líquida es dividida en una región dinámica y una región estancada. El modelo propuesto considera flujo pistón con dispersión axial para la región dinámica y transferencia de masa entre la región estancada y la región dinámica de la fase líquida, en ausencia de reacción química.

En el trabajo de Hassan et al. (1996) se estudió el efecto de la forma de las microcápsulas sobre el desempeño de un reactor tubular empacado no isotérmico, en el cual se llevaba a cado una reacción simple de primer orden siguiendo una cinética de Michaelis-Menten. En el trabajo se desarrolla un modelo no isotérmico que incluye balances de masa y energía tanto en la fase fluida como en la microcápsula, considerando flujo pistón con dispersión axial de calor y masa. Por otra parte, Indlekofer et al. (1996) desarrollaron un modelo para representar el comportamiento de un reactor de lecho fijo donde ocurría la reacción de racemic-2-metil- 1-pentanol catalizada por lipasa. El modelo considera la transferencia de masa sólido-líquido, así como la difusión en el poro.

Nath & Chand (1996) realizaron un análisis cuantitativo de la transferencia de masa combinada con la reacción bioquímica. Así mismo, utilizaron un modelo de flujo pistón para representar el modelo del reactor para una reacción de primer orden de la conversión de azúcar en etanol utilizando células de Saccharomycess cerevisiae inmovilizadas. En el mismo año, Shieh & Barker (1996) estudiaron la hidrólisis de lactosa utilizando la enzima lactasa en un biorreactor separador cromatrográfico contracorriente simulado. El sistema fue operado de manera continua y por carga, y los datos experimentales medidos fueron modelados a través de un reactor de mezcla completa para la operación continua.

Shiraishi et al. (1996) desarrollaron un método computacional para determinar el coeficiente de transferencia de masa en un biorreactor con enzimas inmovilizadas en un lecho empacado. El modelo propuesto plantea un reactor de tipo flujo pistón con una cinética de reacción del tipo Michaelis- Menten y considera, además, el efecto de la transferencia de masa en el sólido.

Miyakawa & Shiraisi (1997) estudiaron los efectos difusionales de película sobre los parámetros cinéticos aparentes en un reactor de lecho empacado con enzimas inmovilizadas en la superficie de un soporte no poroso. Para ello, se planteó un modelo de reactor tipo flujo pistón considerando la resistencia a la transferencia de masa en el sólido. Benthack et al. (2001), presentan un modelo de reactor tipo mezcla completa para el tratamiento de aguas residuales.

Xiu et al. (2001) desarrollaron un modelo matemático para un reactor de lecho fijo con enzimas inmovilizadas tomando en cuenta una cinética de reacción del tipo Michaelis- Menten acoplada con difusión intrapartícula, transferencia de masa externa y flujo pistón con dispersión axial.

Simon (2005) estudió el crecimiento de microorganismos en un reactor de lecho fijo y para ello utilizó un modelo de reactor de tipo flujo pistón con dispersión axial isotérmico, utilizando una cinética de reacción (de crecimiento) de segundo orden. En el mismo año Al-Muftah & Abu-Reesh (2005), desarrollaron un modelo matemático de un reactor de lecho fijo para la reacción de hidrólisis de lactosa. En el desarrollo del modelo se tomó en cuenta los efectos de transferencia de masa interno y externo, de manera exotérmica.

Berendsen et al. (2007) estudiaron la resolución exotérmica de 1-metoxi-2-propanol con vinil acetato catalizada por Candida antárctica lipasa B inmovilizada en un reactor de lecho empacado. El modelo desarrollado es de tipo flujo pistón con dispersión axial de masa y calor, tanto en la fase fluida como en la microcápsula.

Como puede observarse, los modelos encontrados en la literatura corresponden a casos específicos que difícilmente pueden ser extrapolados a otras condiciones o esquemas de procesos, o que fueron desarrollados para reacciones simples que ocurrían de manera isotérmica, donde sólo se considera las transferencias de masa en la fase fluida y en la microcápsula. En algunos casos, se despreciaron los efectos de la transferencia de masa y los modelos del reactor correspondían a flujo pistón. En otros casos, si bien se planteaban los balances de energía y de masa considerando las resistencia a la transferencia de masa en la fase fluida y en la microcápsula, la aplicación correspondía a una reacción simple muy específica.

En este trabajo se desarrolla un modelo matemático de un biorreactor de tipo flujo pistón con dispersión axial de masa y calor, no isotérmico para una reacción serie-paralelo catalizada enzimáticamente. Dicho modelo también es expresado en términos de variables y números adimensionales para simplificar su resolución numérica y para posteriormente realizar un análisis de sensibilidad paramétrica.

DESARROLLO DEL MODELO MATEMÁTICO

El biorreactor que se va a modelar corresponde a un reactor de tipo flujo pistón con dispersión axial en donde el perfil de concentraciones del substrato y de los productos a lo largo del mismo, dependerá de variables de operación, tales como temperatura y pH.

El modelo que represente el comportamiento dinámico del biorreactor debe incluir el comportamiento cinético (enzimático) y el del reactor como tal (fenomenológico). El acoplamiento de ambos modelos, sujeto al menor número de consideraciones posibles, debe proveer una buena exactitud en un tiempo de cómputo aceptable.

Modelo cinético

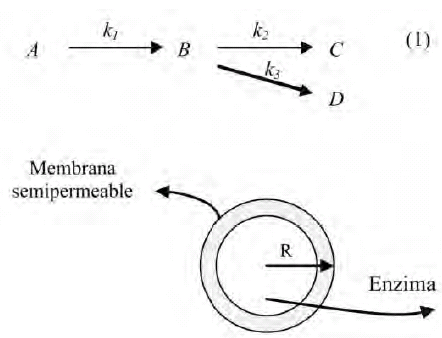
La reacción a estudiar es del tipo serie-paralelo (ecuación 1), la cual ocurre dentro de una microcápsula de geometría esférica de radio R con características enzimáticas y que actúa como catalizador para promover la reacción (figura 1). En todo momento se supondrá que los substratos se distribuyen homogéneamente en la referida microcápsula.

Figura 1. Microcápsula enzimática esférica de radio R

Cada una de las reacciones involucradas será descrita como una cinética del tipo Michaelis-Menten de la siguiente manera:

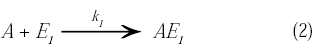
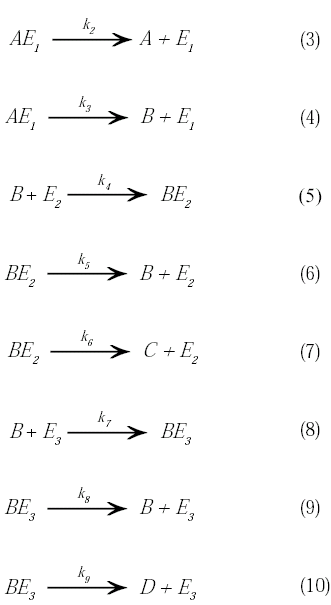
La concentración total de cada enzima dentro del biorreactor puede expresarse como:

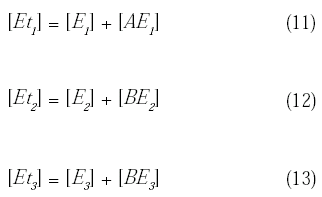
Despejando la concentración de enzima que está libre del complejo enzima-substrato se tiene:

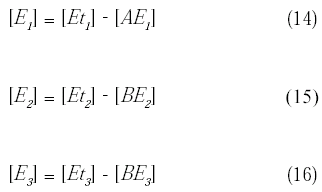
A partir de estas reacciones se obtiene la velocidad de reacción de cada una de las especies involucradas:

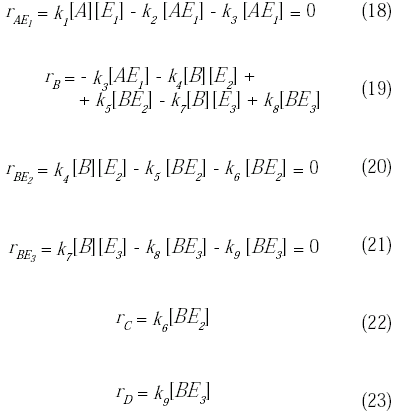
Tomando la ecuación (14) y sustituyéndola en la ecuación (18) se obtiene:

Despejando la concentración del complejo de A y la enzima se tiene:

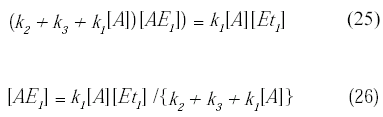
Dividiendo el numerador y el denominador por k₁ se obtiene:

donde:

De igual forma se puede obtener expresiones similares para los demás complejos:

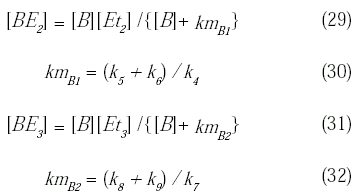
Reagrupando y sustituyendo se pueden obtener las expresiones  de las concentraciones de enzima libre [E₁], [E₂] y [E₃] de las ecuaciones (14) a (16) y (27) a (32):

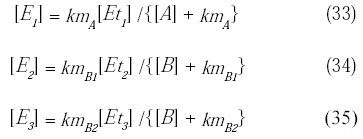
Conociendo la expresión de la concentración de la enzima libre y de los complejos enzima-substrato [AE₁], [BE₂] y [BE₃], se puede obtener la expresión de la velocidad de reacción de cada especie:

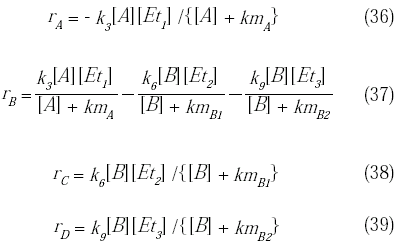
Balance de masa y energía

Para el desarrollo del modelo matemático del biorreactor de lecho empacado se considera que el mismo posee una geometría tubular, tal y como se muestra en la figura 2.

Figura 2. Reactor tubular de lecho empacado con microcápsulas enzimáticas

Adicionalmente, se hicieron las siguientes suposiciones (Aiba et al. 1973; Shuler & Kargi, 1992; Hassan et al. 1996; Nath & Chand, 1996):

i. La temperatura de la pared del biorreactor es constante e igual a la temperatura de alimentación

ii. La resistencia a la transferencia de masa y calor a través de la membrana que recubre a las enzimas es despreciable

iii. La reacción entre el substrato y la enzima sigue una cinética del tipo Michaelis-Menten, sin inhibición del producto ni del substrato

iv. Todas las propiedades físicas y de transporte se consideran constantes. Generalmente en los sistemas reactivos enzimáticos las reacciones involucradas son débilmente exotérmicas o endotérmicas, lo cual conlleva a variaciones de la temperatura poco significativas

v. Los niveles de actividad dentro de la microcápsula son uniformes. La concentración de enzimas dentro de la microcápsula es constante en cada punto de la misma

vi. La distribución de las microcápsulas dentro del biorreactor es uniforme

vii. No hay perfiles de concentración radial dentro del biorreactor

viii. La caída de presión a lo largo del biorreactor es despreciable. Este tipo de sistemas generalmente son reactores verticales que operan bajo la modalidad de flujo descendente en donde la pérdida de carga no es un parámetro de importancia

ix. La desactivación térmica de las enzimas es despreciable (válido sólo si se trabaja a una temperatura inferior a la temperatura de desactivación)

x. Las enzimas no compiten entre sí

Balance de masa en la microcápsula y en la fase fluida

Considerando la ley de conservación de masa en coordenadas esféricas para un fluido contenido en el interior de un elemento de volumen en un determinado instante de tiempo, suponiendo que la densidad y la difusividad son constantes, que los efectos convectivos son despreciables y que sólo existen efectos difusivos en la dirección radial, se puede obtener la expresión general de transferencia de masa del compuesto i dentro de la microcápsula:

Sustituyendo las velocidades de reacción correspondientes del substrato (A), del intermediario (B) y de los productos (C y D) (ecuaciones 36 a 39), se obtiene:

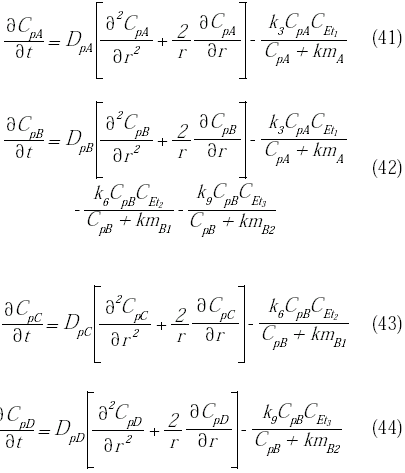
Las condiciones de borde en el centro (r = 0) y en la superficie (r = r_p) de la microcápsula son:

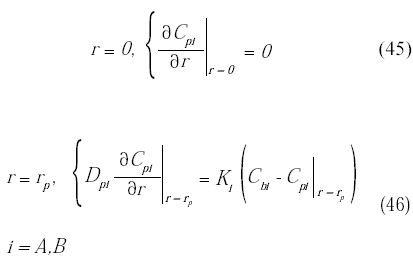
donde: K_A y K_B son los coeficientes de transferencia de masa para los compuestos A y B respectivamente en la interfase sólido-líquido.

Las expresiones correspondientes a la ecuación de continuidad en la fase fluida para los compuestos A, B y C, se obtienen partiendo de la ecuación de continuidad en coordenadas cilíndricas, y considerando sólo los efectos difusivos y convectivos en la dirección longitudinal del biorreactor, y la transferencia de masa entre la microcápsula y la fase fluida:

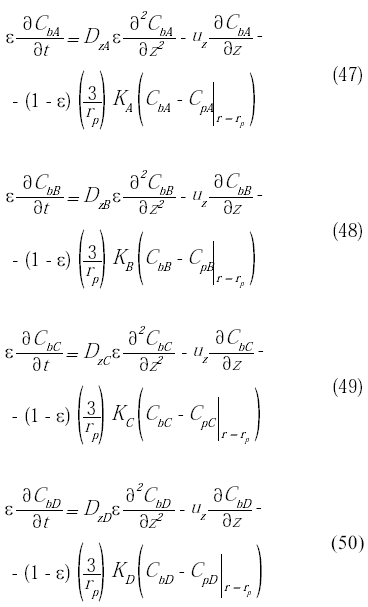
Las condiciones de borde a la entrada y salida del biorreactor:

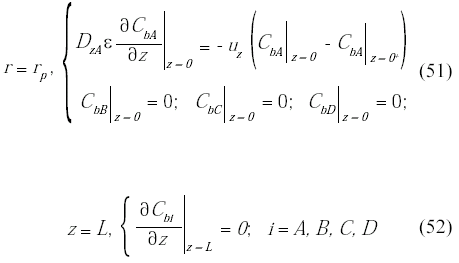
Balance de energía en la microcápsula y en la fase fluida

Partiendo de la ecuación de conservación de energía en coordenadas esféricas y suponiendo que las propiedades físicas del fluido son constantes, que los gradientes de velocidad son despreciables (de forma que la disipación viscosa puede despreciarse), y despreciando la transferencia de calor en dirección angular para tomar en cuenta sólo la contribución en la dirección radial, se obtiene:

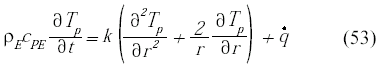
La generación de calor q dependerá de la velocidad de reacción  de cada compuesto, y en este caso se supone que todas las reacciones son exotérmicas. De esta manera se tiene que la temperatura en la microcápsula es una función del tiempo y el radio de la partícula como:

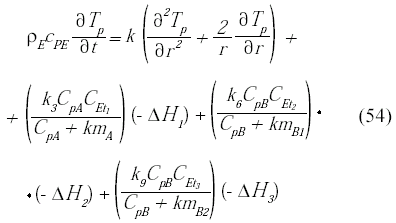
Las condiciones de borde en el centro y en la superficie de la partícula son:

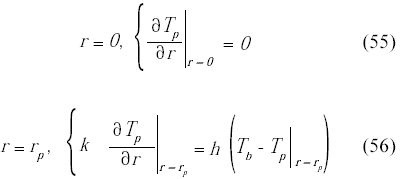
En cuanto al balance de energía en la fase fluida, se considera la variación de la temperatura en la dirección longitudinal, además de tomar en cuenta la transferencia de calor entre la fase fluida y la microcápsula, así como de la fase fluida y la pared del reactor, junto con las condiciones de borde a la entrada y salida del biorreactor son:

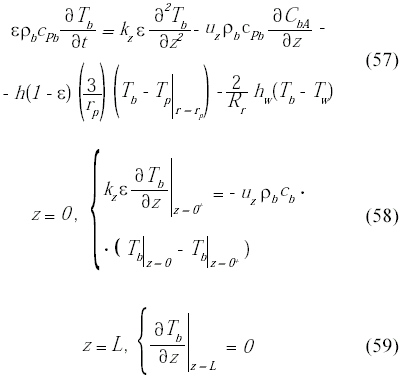
Adimensionalización del modelo

El modelo matemático del biorreactor está conformado por las ecuaciones diferenciales parciales con sus respectivas condiciones de borde dadas por las ecuaciones (41) a (52) y (54) a (59). Para facilitar su resolución, el mismo se adimensionaliza a través de la definición de una serie de parámetros, los cuales se definen en la tabla 1. A continuación

Tabla 1. Parámetros adimensionales

se presenta el sistema de ecuaciones diferenciales que conforman el modelo adimensional junto con sus condiciones de borde.

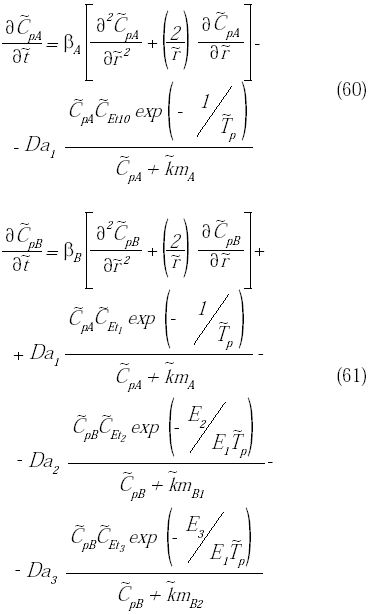
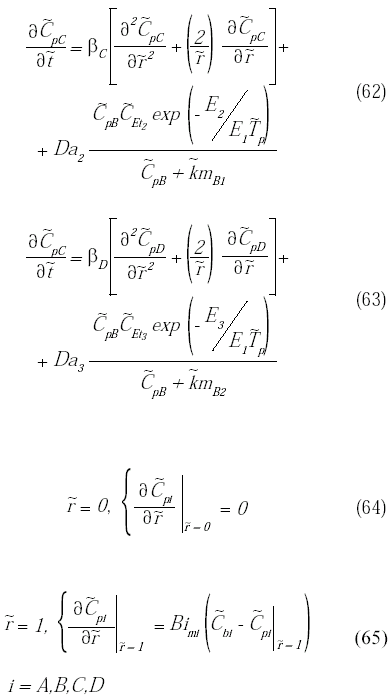
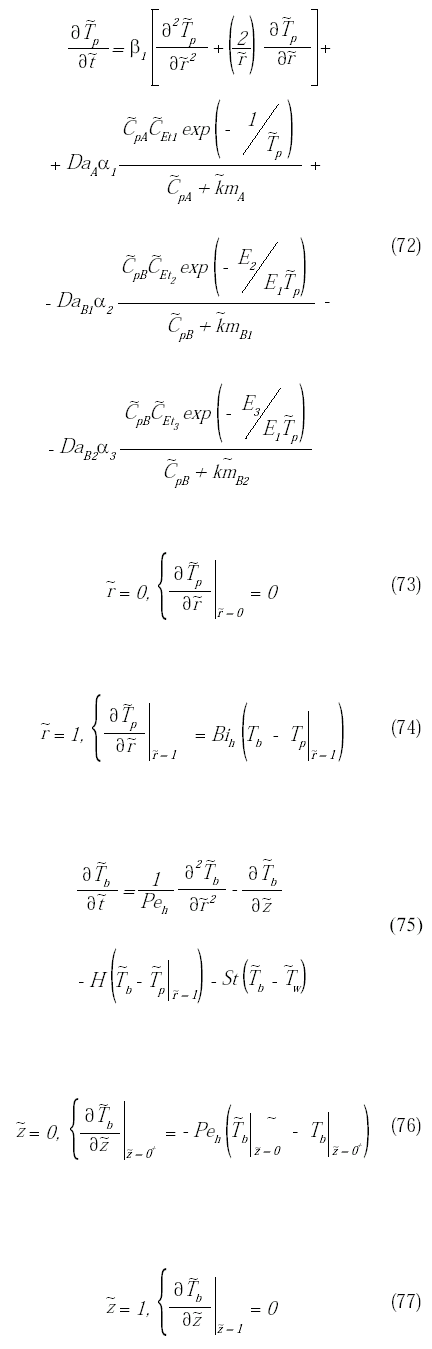
Para resolver el sistema de ecuaciones diferenciales que conforman el modelo adimensional junto con sus condiciones de borde (ecuaciones 60 a 77), se reemplazaron las derivadas parciales por aproximaciones en diferencias finitas y utilizando un método explícito se resolvieron simultáneamente todas las ecuaciones espaciales para cada instante de tiempo a través de un módulo de Visual Basic^® programado en Excel^®. Luego se realizó un análisis de independencia de malla variando el número de nodos temporales, el número de nodos longitudinales del reactor y el número de nodos radiales de la partícula. Los resultados indicaron que para un número de nodos temporales de 4500, un número de nodos longitudinales de 50 y un número de nodos radiales de 10, es suficiente para declarar la independencia de malla.

VALIDACIÓN DEL MODELO

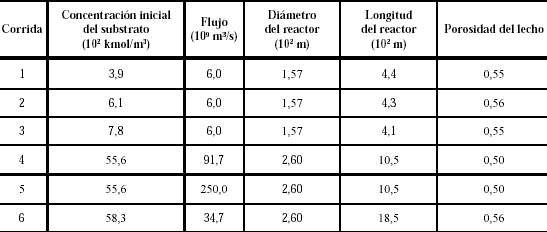
A fin de validar el modelo se utilizaron los datos reportados por Ching et al. (1990), quienes estudiaron el desempeño de un biorreactor de lecho empacado inmovilizado para la fermentación continua de glucosa utilizando como enzima la S. uvarum para producir etanol. El reactor utilizado con las dimensiones dadas en la tabla 2 poseía una chaqueta de enfriamiento para mantener la temperatura en 30°C, y estaba empacado con microcápsulas inmovilizadas de 4 mm de diámetro. El substrato era alimentado al reactor desde un tanque de almacenamiento que lo mantenía a una temperatura constante de 30°C. El flujo de alimentación es garantizado a través de una bomba peristáltica. La cinética de fermentación se rige por la ecuación siguiente en donde [S] representa el substrato:

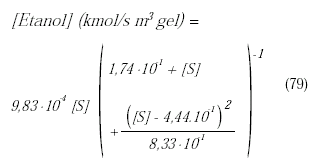
Tabla 2. Condiciones de reacción y dimensiones del reactor Ching et al. (1990)

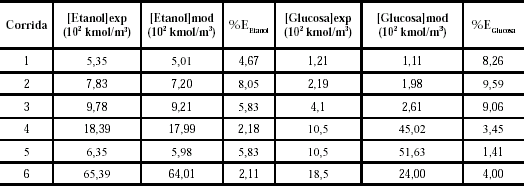
En la tabla 3 se muestra la comparación entre los resultados experimentales reportados por Ching et al. (1990) y los obtenidos por el modelo propuesto. Como se puede observar, el modelo desarrollado presenta un error porcentual menor de 8,05% para el caso del etanol (corrida 2) y menor de 9,59% para la glucosa (corrida 2).

Tabla 3. Comparación entre los valores experimentales reportados por Ching et al. (1990) y los obtenidos por el modelo desarrollado para el etanol y la glucosa

SIMULACIÓN Y ANÁLISIS PARAMÉTRICO

Para estudiar el comportamiento de la reacción en el biorreactor, se tomaron valores para los parámetros que caracterizan el sistema en base a estudios publicados en la literatura con reacciones enzimáticas en biorreactores coinmovilizados no isotérmicos (Hassan et al. 1996; Bouza et al. 2000).

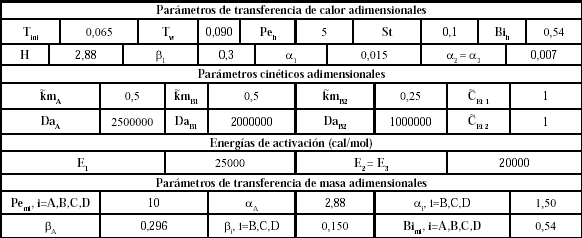
En la tabla 4 se presentan los valores de energías de activación para cada reacción; los valores seleccionados para los parámetros que caracterizan la transferencia de masa; los parámetros seleccionados que intervienen en la transferencia de calor en el sistema y los parámetros cinéticos. Todos los resultados presentados son adimensionales.

Tabla 4. Valores utilizados en la simulación

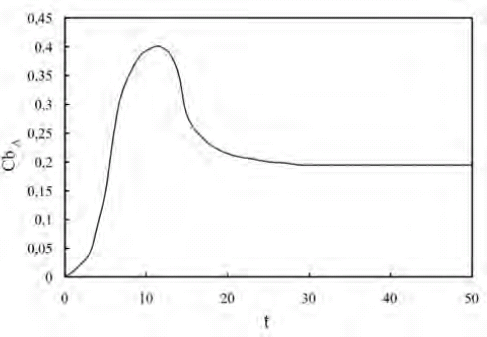
En las figuras 3 y 4 se muestra el comportamiento dinámico del biorreactor a través de la concentración de A a la salida y de la temperatura para las condiciones de simulación antes dadas. Se puede observar que la concentración de A inicialmente crece hasta alcanzar un máximo y luego disminuye hasta alcanzar el valor de estado estacionario. Esto se debe a que el transporte de A a través del reactor está influenciado por dos efectos: el primero debido al flujo de esta especie a través de la fase fluida y el segundo por el flujo de la misma desde la fase fluida hacia las partículas enzimáticas, seguido por la reacción química. En los primeros instantes de tiempo donde ocurre el llenado del reactor, alrededor de un tiempo adimensional de 12, los efectos convectivos predominan sobre los difusivos y los de la reacción química. Una vez que se alcanza esa máxima concentración comienza a prevalecer el flujo hacia el interior de la microcápsula en donde ocurre la reacción química que genera al componente B. Esto conduce a una disminución de la concentración del substrato hasta alcanzar condiciones de estado estacionario.

Figura 3. Variación de la concentración de A adimensional a la salida del biorreactor en función del tiempo adimensional

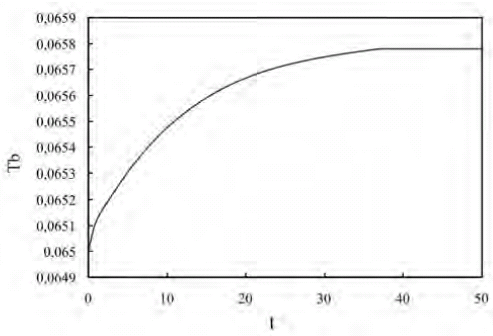
Figura 4. Variación de la temperatura adimensional de la fase fluida a la salida del biorreactor en función del tiempo adimensional

En el caso del perfil de temperatura adimensional en el reactor, la curva es monótona creciente y muestra un incremento de 1,23% aproximadamente con respecto a la temperatura de entrada. En los primeros instantes de tiempo adimensional, el gradiente de temperatura adimensional entre la fase fluida y la microcápsula es despreciable. A medida que transcurre el tiempo, el gradiente comienza a desarrollarse debido al carácter exotérmico de las reacciones involucradas.

También se puede observar que el biorreactor, bajo estas condiciones de simulación, alcanza el estado estacionario en un tiempo adimensional de aproximadamente 35. A partir de este número no se pueden hacer observaciones acerca de la velocidad de respuesta del sistema en virtud de que el tiempo real de establecimiento depende de la velocidad con la que se inyecta el fluido en el sistema, la porosidad generada por las microcápsula y de la longitud del reactor. Sin embargo, mientras menor sea este valor más rápido será el sistema.

Influencia del retromezclado sobre los perfiles de concentración y temperatura

El número de Péclet (Pe) en el modelo representa un número adimensional de transferencia de masa (Pe_m) o de calor (Pe_h). Cuando el Pe tiende a cero, la operación del biorreactor se aproxima a la de uno de mezclado perfecto, es decir, los efectos difusivos predominan sobre los efectos convectivos. Por el contrario, cuando el valor de Pe tiende a infinito, la operación corresponde a uno de flujo pistón, observándose que los efectos convectivos predominan sobre los efectos difusivos.

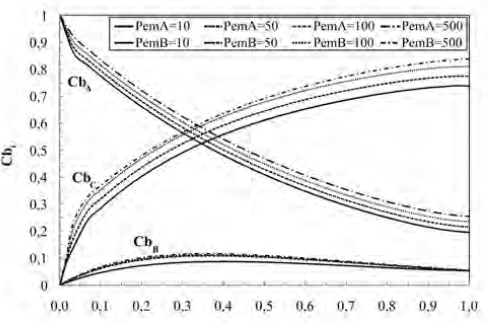
En el perfil de concentración del intermediario ante variaciones del Pe_mB mostrado en la figura 5, se puede observar que la mayor variación de la concentración de B ocurre en la primera mitad del reactor, presentándose un máximo a diferencia del perfil de concentración del substrato A. El aumento y disminución del perfil de concentración de B se puede explicar considerando que el intermediario se forma debido a la reacción del substrato A y la enzima, para luego reaccionar con otra enzima y producir los productos C y D, haciendo que su concentración disminuya. Como era de esperarse, la concentración del producto final C se incrementa a lo largo del reactor y su perfil aumenta a medida que el Pe_mC crece.

Figura 5. Perfiles de concentración de A, B y C a lo largo del biorreactor para variaciones de Pe_m

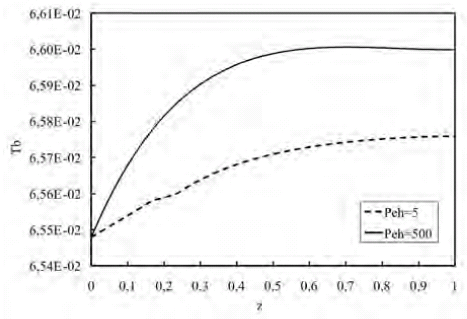
En la figura 6 se muestra como el Pe_h afecta el perfil de temperatura en la fase fluida a lo largo de la longitud del biorreactor, en donde se puede observar como el perfil evoluciona desde un sistema que se comporta como un biorreactor de flujo pistón (Pe=500) a un sistema que tiende a un comportamiento de tanque agitado (Pe=5).

Figura 6. Perfil de temperatura en la fase fluida a lo largo del biorreactor para variaciones de Pe_h

Un valor tendiendo a infinito de Bi puede representar dos situaciones diferentes. La primera en la que la resistencia a la transferencia de calor por conducción en la microcápsula es muy alta, lo cual genera diferencias de temperatura importantes dentro de la misma; y la segunda, aquella en donde la resistencia a la transferencia de calor por convección en la superficie de la microcápsula es prácticamente nula.

Un valor tendiente a cero de Bi también puede representar dos situaciones diferentes y contrarias al caso anterior, respectivamente, es decir, aquel en donde la resistencia a la transferencia de calor por conducción en la microcápsula es prácticamente nula, lo cual conduce a que no exista un gradiente de temperatura en la misma; y la segunda, en donde la resistencia a la transferencia de calor por convección en la superficie de la microcápsula es muy alta generando importantes diferencias de temperatura entre la superficie de la microcápsula y la fase fluida. Este concepto puede extenderse por analogía a la transferencia de masa, en donde se tendrá la relación entre la resistencia a la transferencia de masa por difusión dentro de la partícula (r_p/D_pi) y la resistencia a la transferencia de masa convectiva en la superficie de la misma (1/K_i).

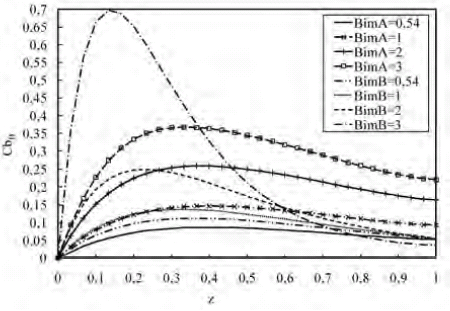
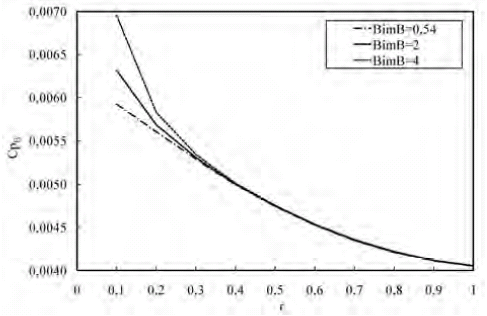
En la figura 7 se muestran los perfiles de concentración del intermediario a lo largo del biorreactor para variaciones del Bi_mA y Bi_mB; en donde se puede observar que al aumentar el Bi_mA, el perfil de concentración del intermediario se incrementa ya que se está disminuyendo la resistencia a la transferencia de masa externa en la microcápsula, lo cual permite que la misma sea alcanzada con mayor facilidad por el substrato, incrementando la conversión.

Figura 7. Perfil de concentración de B a lo largo del biorreactor para variaciones de Bi

Al variar el Bi del intermediario se observa que el perfil de concentración aumenta a medida que aumenta el Bi. Cuando el Bi es mayor que la unidad y va aumentando, la resistencia de transferencia de masa dentro de la partícula es mucho mayor que la resistencia de transferencia de masa en su capa límite; por lo que el intermediario tiende a salir con mayor facilidad de la microcápsula. Por otra parte, al difundir a través de la partícula, éste va reaccionando para producir C y D, lo que ocasiona la disminución de la concentración de B en la fase fluida. Mientras mayor es el Bim existe una menor resistencia de transferencia de masa entre la microcápsula y la fase fluida, generando un perfil mayor del intermediario en el biorreactor.

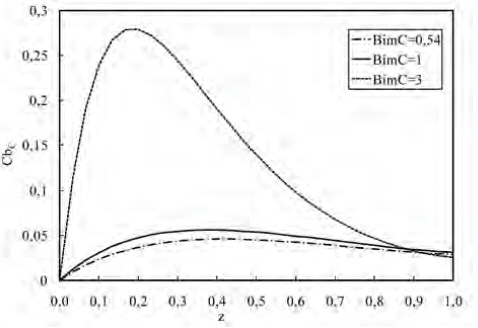
En la figura 8 se muestra el perfil de concentraciones del producto C a lo largo del biorreactor ante variaciones del Bi_mC. Se puede observar que el perfil aumenta a medida que el Bi_m es mayor a la unidad, es decir, se incrementa a medida que la resistencia externa a la transferencia de masa se hace menos significativa. Ello facilita la transferencia desde la partícula hacia la fase fluida aumentando la concentración del producto, por lo que al incrementarse el Bi_m se obtiene una reacción más eficiente.

Figura 8. Perfil de concentración de C a lo largo del biorreactor para variaciones de Bi_mC

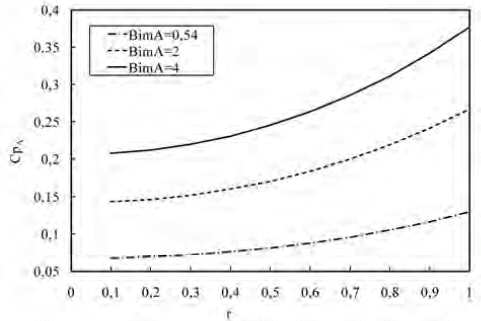
El perfil de concentraciones del substrato a través de la microcápsula enzimática en donde ocurre la reacción de formación de B para variaciones del BimA se presenta en la figura 9. Se puede observar que la concentración de A es mayor en la superficie y disminuye a medida que se acerca al centro, lo cual se debe a que a medida que A difunde en la partícula va reaccionado para dar lugar a B.

Figura 9. Perfil de concentración de A a lo largo de la microcápsula para variaciones de Bi_mA

Adicionalmente, la microcápsula presenta una resistencia a la transferencia de masa interna que se ve incrementada con Bi_m elevados, lo que provoca que el substrato no pueda difundir fácilmente hacia el centro de la microcápsula. Para un Bi_m grande, el perfil de concentración de A es mayor dentro de la microcápsula debido a que la resistencia externa de transferencia de masa es menor y el substrato tiene una mejor penetración en la microcápsula pero no difunde tan efectivamente como en el caso de un Bi_m más pequeño.

Para el caso del perfil de concentraciones de B a través de la microcápsula (figura 10) se observa que a medida que disminuye el Bi_mB, la pendiente del perfil disminuye. Esto se debe a que cuando el Bi_m aumenta, se incrementa la resistencia interna a la transferencia de masa, haciendo que el intermediario le sea más difícil difundir hasta la superficie de la microcápsula, por lo que se consume por reacción para formar los productos finales.

Figura 10. Perfil de concentración de B a lo largo de la microcápsula para variaciones de Bi_mB

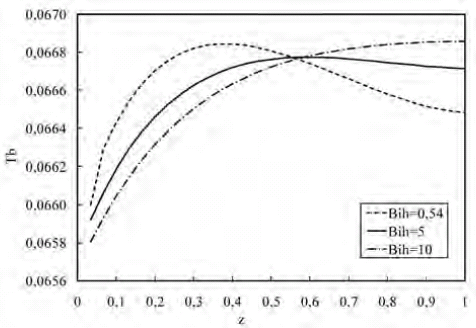
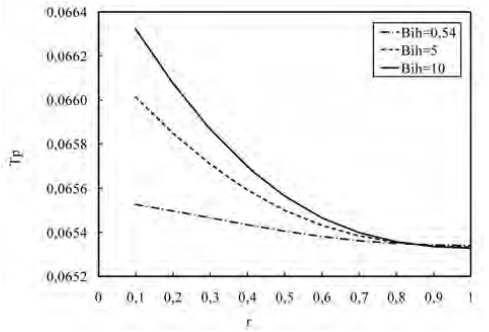
Las figuras 11 y 12 muestran los perfiles de temperatura a lo largo del biorreactor y dentro de la microcápsula para variaciones del Bi de calor (Bi_h). En la figura 11 se observa cómo, en la primera mitad del biorreactor (z < 0,5) donde la reacción se lleva a cabo a mayor velocidad, se produce más energía, y al aumentar la resistencia a la transferencia de calor por convección en la superficie de la microcápsula, el perfil de temperatura se incrementa. Sin embargo, en la segunda mitad del biorreactor, la situación se invierte debido a que la reacción ocurre con menos velocidad generándose menos energía, y al aumentar la resistencia a la transferencia de calor por convección, el perfil de temperatura disminuye. La figura 12 muestra como al disminuir la resistencia interna a la transferencia de calor, el perfil de temperatura es más bajo, lo cual se debe a la facilidad que hay para que el calor se transfiera por conducción.

Figura 11. Perfil de temperatura a lo largo del biorreactor para variaciones de Bi_h

Figura 12. Perfil de temperatura a lo largo de la microcápsula para variaciones de Bi_h

Influencia de la velocidad de reacción sobre los perfiles de concentración y temperatura

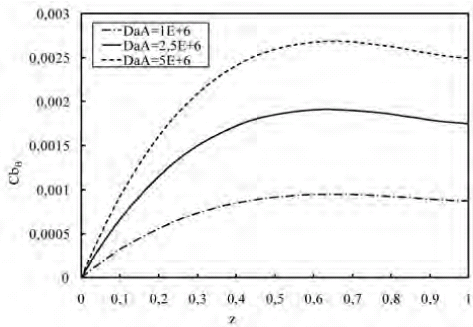
El Damköhler (Da) es un número adimensional proporcional a la constante de reacción, y por ende, lo es a la velocidad de reacción. El valor elegido puede afectar la concentración obtenida de productos y por lo tanto, la conversión en el reactor. En la figura 13 se presenta el efecto de la velocidad de reacción sobre los perfiles adimensionales de concentración del intermediario. Se puede observar que al aumentar la velocidad de reacción para producir el intermediario (DaA), lo cual se traduce en un incremento del consumo de substrato, se produce una acumulación del intermediario aumentando su perfil de concentración.

Figura 13. Perfil de concentración de B a lo largo del biorreactor para variaciones de Da_A

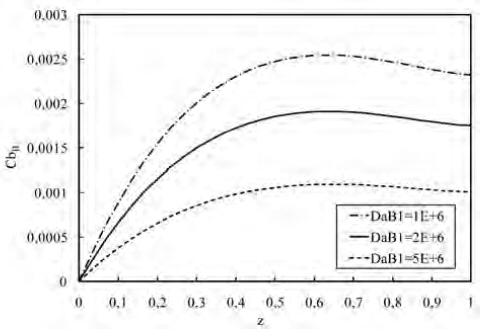
En la figura 14 se puede observar que la concentración de B a lo largo del biorreactor aumenta a medida que disminuye el Da_B1. Mientras mayor es el Da_B1 mayor es la velocidad de reacción pero menor la velocidad de difusión, por lo que para valores de Da_B1 muy altos existe una alta velocidad de reacción para la formación de C y D, y además, una pequeña velocidad para su difusión a través del biorreactor haciendo que la concentración de B sea menor. Por otro lado, cuando el valor del Da_B1 es menor se consume menos cantidad de B para formar los productos, y éstos difunden rápidamente hacia la fase fluida haciendo que la concentración de B sea mayor cuando DaB1 es menor.

Figura 14. Perfil de concentración de B a lo largo del biorreactor para variaciones de Da_B1

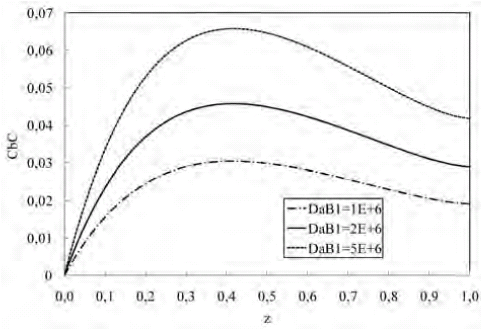
En la figura 15 se observa como al incrementarse Da_B1, aumenta la velocidad de reacción para producir el producto deseado C y por lo tanto, su concentración en la fase fluida. Cuando Da_B1 disminuye, la velocidad de difusión aumenta, pero la cantidad de C que se forma es pequeña debido a la disminución de la velocidad de reacción.

Figura 15. Perfil de concentración de C a lo largo de la biorreactor para variaciones de Da_B1

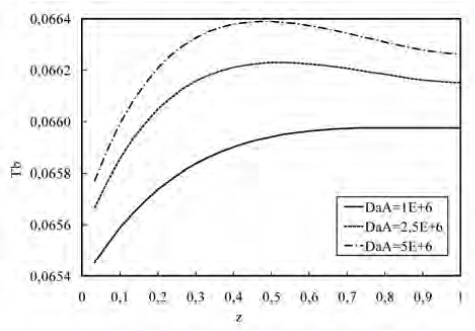
En la figura 16 se aprecia que la velocidad de reacción modifica el perfil de temperatura a lo largo de la longitud del biorreactor. Al aumentar Da_A aumenta la cantidad de calor generado debido al consumo del substrato y del intermediario, lo que trae como consecuencia un incremento en la temperatura del biorreactor.

Figura 16. Perfil de temperatura a lo largo del biorreactor para variaciones de Da_A

Finalmente, en la figura 17 se observa que al aumentar la velocidad de reacción para producir el producto deseado (Da_B1) el perfil de temperatura disminuye, debido a que el calor de reacción adimensional para la reacción B → C (a₂=0,007) es menor que el calor de reacción adimensional para la reacción A → B (a₁=0,015), por lo que favoreciendo la segunda reacción, se producirá menos energía, y por lo tanto, el perfil de temperatura será menor.

Figura 17. Perfil de temperatura a lo largo de la microcápsula para variaciones de Da_B1

CONCLUSIONES

En este trabajo se formuló un modelo matemático de un biorreactor no isotérmico con dispersión axial de masa y de calor a lo largo de su longitud, tomando en consideración la difusión dentro y fuera de las microcápsulas, para una reacción serie-paralelo. El modelo obtenido fue validado con datos publicados por Ching et al. (1990) con un error promedio en el peor de los casos de 9,59%. Las ecuaciones que modelan los fenómenos que ocurren en el biorreactor se adimensionalizaron con el fin de obtener parámetros adimensionales característicos de tales procesos. Las variaciones de dichos parámetros (Péclet, Biot y Damköhler) y en la resolución del modelo, permiten observar sus efectos sobre los perfiles de concentración del substrato, intermediario y productos final, además de establece condiciones óptimas de operación. Las observaciones de los resultados obtenidos estuvieron dentro de lo esperado para un sistema físico de estas características.

LISTA DE SÍMBOLOS Y ABREVIATURAS

A substrato

B intermediario

Bi_h número adimensional Biot de calor (-)

Bi_mi número adimensional Biot de masa de i (-)

C producto

C_bi concentración del compuesto i en el fluido del biorreactor (M / L³)

C_Eti concentración de la enzima i en la microcápsula (M / L³)

CE_ti0 concentración inicial de la enzima i en la microcápsula (M / L³)

c_Pb calor específico a presión constante del fluido de bulto del biorreactor (L² / t² T)

c_PE calor específico a presión constante de la solución enzimática (L² / t² T)

C_pi concentración en la partícula del compuesto i (L / t)

Da_i número de Damköhler del compuesto i (-)

D_pi difusividad efectiva del compuesto i en la partícula (L² /t)

D_zi coeficiente de dispersión axial del componente i (L² / t)

E_i enzima i

h coeficiente de película de transferencia de calor en la interfase sólido-líquido (M / t³ T)

H número adimensional (-)

h_W coeficiente de película del fluido para la transferencia de calor hacia la pared del biorreactor (M / t³ T)

k conductividad térmica intrapartícula (M L / t³ T)

K_i coeficiente de transferencia de masa para el compuesto i en la interfase sólido-líquido (L / t)

k_i constante de la velocidad de la reacción i (1 / T)

km_i constante de Michaelis-Menten (M / L³)

k_z conductividad térmica del fluido (M L / t³ T)

Pe_mi número adimensional Péclet de masa de i (-)

Pe_h número adimensional Péclet de calor (-)

q flujo de calor producido o consumido por reacción química por unidad de volumen (M / L t³)

r longitud radial (L) o dirección radial

r_i velocidad de aparición o desaparición del elemento i (M / L³ t)

r_p radio de la microcápsula (L)

R_r radio interno del biorreactor (L)

St número adimensional de Stanton (-)

t tiempo (t)

T_b temperatura del fluido de bulto del biorreactor (T)

T_p temperatura de la solución enzimática dentro de la microcápsula (T)

T_W temperatura de la pared del biorreactor (T)

u_i velocidad del fluido en la dirección i (L / t)

z longitud del biorreactor (L) o dirección axial

Griegas

a_i calor de reacción adimensional en la Ec. (73) (-) o número adimensional de las Ecs. (67) a (70) (-)

b_i número adimensional de las Ecs. (61) a (64) y (73) (-)

e Porosidad (-)

r_E densidad de la solución enzimática (M / L³)

r_b densidad del fluido de bulto del biorreactor (M / L³)

Símbolos

~ adimensional

[I] concentración de I (M / L³)

REFERENCIAS

1. AiBa, S., humphreY, a. e. milliS, n. F. (1973). Biochemical Engineering, (2da. Ed.). New York: Academic Press, Inc. 11-37, 78-127, 393-413.        [ Links ]

2. Al-muFtah, a.e., aBu-reeSh, i. m. (2005). Effects of internal mass transfer and product inhibition on a simulated immobilized enzyme-catalyzed reactor for lactose hydrolysis. Biochem. Eng. J. 23(2); 139-153.        [ Links ]

3. Beg, S. a., haSSan, m. m., naqvi, m. S. m. (1996). Hydrodynamics and mass transfer in a cocurrent packed column: A theoretical study. Chem. Eng. J. 63; 93-103.        [ Links ]

4. Benthack, c., SrinivaSan, B., Bonvin, D. (2001). An optimal operating strategy for fixed-bed bioreactors used in wastewater treatment. Biotechnol. Bioeng. 72(1); 34-40.        [ Links ]

5. BerenDSen, W.r., lapin, a., reuSS, m. (2007). Non-isothermal lipase-catalyzed kinetic resolution in a packed bed reactor: Modeling, simulation and miniplant studies. Chem. Eng. Sci. 62(9); 2375-2385.        [ Links ]

6. Bouza, V.A.L., Sánchez, M.Y., Revollar, Ch., S.R. (2000). Modelaje y simulación de un biorreactor con microcápsulas coinmovilizadas. Proceedings V Jornada de Sistemas de Instrumentación y Control & IV Jornadas Panamericanas de Automatización (CD), Caracas, Venezuela, Mayo.        [ Links ]

7. Brahim, S., narineSingh, D., GuiSeppi-elie, A. (2002). Kinetics of glucose oxidase immobilized in p(HEMA)- hydrogel microspheres in a packed-bed bioreactor. J. Mol. Catal. B: Enzym. 10(1); 69-80.        [ Links ]

8. Ching, C.B., Teo, W.K., Chu, K.H. (1990). Performance analysis of an immobilized yeast packed-bed reactor for ethanol fermentation. J. Chem. Technol. Biotechnol. 47; 345-355.        [ Links ]

9. HaSSan, M.M., Atiqullah, M., Beg, S.A., ChoWDhurY, M.H.M. (1996). Effects of enzyme microcapsule shape on the performance of a nonisothermal packed-bed tubular reactor. J. Chem. Technol. Biotechnol. 66(1); 41-55.        [ Links ]

10. InDlekoFer, M., Brotz, F., Bauer, A., ReuSS, M. (1996). Stereoselective bioconversions in continuously operated fixed bed reactors: Modeling and process optimization. Biotechnol. Bioeng. 52(4); 459-471.        [ Links ]

11. MiYakaWa, H., ShiraiShi, F. (1997). A film diffusional effect on the apparent kinetic parameters in packed-bed immobilized enzyme reactors. J. Chem. Technol. Biotechnol. 69(4); 456-462.        [ Links ]

12. Nath, S., Chand, S. (1996). Mass transfer and biochemical reaction in immobilized cell packed bed reactors: Correlation of experiment with theory. J. Chem. Technol. Biotechnol. 66; 286-292.        [ Links ]

13. Shieh, M.T., Barker, P.E. (1996). Combined bioreaction and separation in a simulated counter-current chromatographic bioreactor-separator for hydrolysis of lactose. J. Chem. Technol. Biotechnol. 66; 265-278.        [ Links ]

14. ShiraiShi, F., HiromitSu, M., HaSegaWa, T., kaSai, S. (1999). A computational method for determination of the mass-transfer coefficient in packed-bed immobilized enzyme reactors. J. Chem. Technol. Bioechnol. 66; 405-413.        [ Links ]

15. Shuler, M.L., Kargi, F. (1991). Bioprocess Engineering. Basic Concepts (1era. Edic.). EEUU: Prentice Hall College Div. 61-96.        [ Links ]

16. Simon, l. (2005). Observing Biomass Concentration in a fixed-bed bioreactor. Chem. Eng. Commun. 192(3); 272-285.        [ Links ]

17. Sonnleitner, B. (2000). Instrumentation of Biotechnical Processes. Adv. Biochem. Eng./Biotechnol. Springer Beling/Heidelberg. 66; 1-64, Enero.        [ Links ]

18. Xiu, G.H., Jiang, L., Li, P. (2001). Mass-transfer limitations for immobilized enzyme catalyzed kinetic resolution of racemate in a fixed-bed reactor. Biotechnol. Bioeng. 74(1); 29-39.        [ Links ]