Control y compensación aw robusta en sistemas lineales a tiempo discreto inciertos

Addison Ríos Bolívar

Universidad de Los Andes. Facultad de Ingeniería. Escuela de Ingeniería de Sistemas Mérida, 5101, Venezuela

RESUMEN

En esta contribución se presenta un método para la síntesis de controladores con compensación de la saturación en los actuadores. La técnica se aplica en sistemas lineales a tiempo discreto con incertidumbres politópicas, tomando como base un índice de desempeño sobre una función de transferencia que involucra la diferencia entre la señal de salida del actuador y la salida del controlador, y su efecto sobre la señal de control. Para ello, la saturación en los actuadores es considerada como una perturbación en el desempeño de la acción de la señal de control, lo que permite establecer índices de funcionamiento para el diseño de la ley de control (realimentación estática de la salida) y para la síntesis de una ganancia de compensación para el problema de windup. Así, el método exhibe ciertas propiedades de robustez frente a cambios en el funcionamiento de los actuadores. Para la síntesis de las ganancias de realimentación estática de la salida y de la ganancia de compensación, se propone un método derivado de las técnicas de control óptimo robusto en H₂-H_¥ para sistemas lineales con incertidumbres politópicas, basado en desigualdades lineales matriciales. Para verificar las propiedades de la técnica propuesta se presenta un ejemplo numérico.

Palabras clave: Sistemas lineales a tiempo discreto, Realimentación estática de la salida, Control robusto. Incertidumbre politópica, Desigualdades matriciales lineales, Normas H₂-H_¥.

Robust control and aw compensation in uncertain discrete-time linear systems

ABSTRACT

In this contribution an approach for the synthesis of robust controller with compensation of saturation in the actuators is presented. The technique is applied in discrete-time linear systems with polytopic uncertainties, taking into account a performance index on a transfer function that involves the difference between the actuator output signal and the controller output, and its effect on the control signal. For it, the saturation in the actuators is considered like a disturbance in the performance of the action of the control signal, which allows to establish operation indices for the design of the control law (static output feedback), and for the synthesis of a gain of compensation for the problem of windup. Thus, the method exhibits certain properties of robustness in front of changes in the operation of the actuators. For the synthesis of the gains of static output feedback and the compensation gain, an approach derived from the techniques of robust optimal control in H₂/H_¥ for linear systems with polytopic uncertainties is proposed, which is based on linear matrix inequalities (LMIs). In order to verify the properties of the propose technique a numerical example is also presented.

Keywords: Discrete-time linear systems, Static output feedback, Robust control, Polytopical uncertainty, Linear matrix Inequalities (LMI), H₂/H_¥ Norms.

Recibido: mayo de 2010 Recibido en forma final revisado: agosto de 2011

INTRODUCCIÓN

En la actualidad, es común encontrar esquemas de control de procesos industriales complejos que deben satisfacer múltiples objetivos y por lo tanto deben operar en diferentes modos de control. La habilidad de un sistema de control de operar en múltiples ambientes y con multi-objetivos, partiendo del reconocimiento de la situación específica y sirviéndola adecuadamente, se puede definir como control inteligente (Narendra & Balakrishnan, 1997). Cada situación específica define el modo de operación y cada uno de los modos tiene un controlador que se ha diseñado para satisfacer los objetivos de desempeño correspondiente a ese modo. La conmutación entre regímenes de operación se logra por una selección de la entrada de la planta a partir de las salidas de un número de controladores en paralelo, cada uno de los cuales corresponde a un modo en particular. Entonces la conmutación de modos es la sustitución de la entrada a la planta en virtud de que la salida de un controlador se reemplaza por otro.

Como consecuencia de las limitaciones (saturación) y de conmutación de controladores, la entrada de control a los procesos será distinta a la salida de dichos controladores. Cuando esto sucede, la salida de los controladores no conduce apropiadamente la planta y los estados del mismo se actualizan fuertemente, situación que se denomina windup (Åström & Rundqwist, 1989). En términos generales, el windup es una inconsistencia entre la entrada de control al proceso y los estados internos del controlador. Los efectos adversos del rebote son un deterioro significativo del desempeño, sobre-disparo y en algunos casos inestabilidad (Campo & Morari, 1990).

El problema de análisis y síntesis de sistemas de control para sistemas lineales invariantes en el tiempo (LTI) sujetos a limitaciones y sustituciones en la entrada de la planta tiene dos formas de ser abordados: una es incorporando las limitaciones y sustituciones en el diseño del sistema de control (Zheng et al. 1993). La otra es que se puede atacar el problema mediante compensación, la cual consiste en dos etapas: una primera etapa considera el diseño del sistema de control sin tomar en cuenta las restricciones físicas de los actuadores, de manera que se pueden imponer distintos objetivos de funcionamiento. La segunda etapa se refiere al diseño de alguna compensación a través de una realimentación adicional a fin de minimizar los efectos negativos de la saturación de los actuadores.

En general, esta técnica se estudia como el problema de transferencia sin salto anti-rebote (AWBT, por sus siglas en inglés) o problema de compensación anti-windup (AW). A los fines de obtener compensadores globales, en Kothare et al. (1994) se presenta un marco general para el problema de AWBT, el cual está basado en el paradigma de diseñar un controlador lineal que ignore las entradas no-lineales e incorpore compensación a objeto de minimizar los efectos adversos del efecto windup. La generalidad de ese trabajo permite considerar cualquier estructura de sistema de control incluyendo realimentación de estados, pre-adelanto (feedforward), grados de libertad múltiples, cascadas y controladores no cuadrados en general. La principal desventaja de estos métodos es que no se consideran los efectos de la saturación de los actuadores sobre los índices de desempeño que se imponen para el diseño del controlador. Además, cambios en los límites de saturación de los actuadores tampoco son tomados en cuenta lo cual, desde el punto de vista de robustez, puede resultar muy inconveniente.

Otra desventaja, no menos importante, es que en todos los esquemas de compensación es fundamental la medición de la salida no-lineal de los actuadores (Kothare & Morari, 1997; Zheng et al. 1993). En consecuencia, esta medición puede resultar una limitante a los fines de implementar la compensación en los procesos industriales (Ríos-Bolívar & García, 2004).

De manera de considerar la robustez en el diseño de la compensaciónAWBT, en Mulder et al. (2001) se presenta una formulación general del problema de síntesis AWBT multivariable. La compensación resultante se obtiene por minimización de una ganancia pesada en L₂, usando desigualdades lineales matriciales, pero los cambios de acción de los actuadores no se consideran y no se evalúan los efectos respecto a los índices desempeño del sistema en lazo cerrado cuando se está en saturación.

Por otro lado, en Wada & Saeki (2003) se presenta un método basado en el desempeño L₂, con el cual se obtiene un compensador anti-rebote estático. En este caso, tanto el desempeño nominal como el desempeño robusto se reducen a un problema de autovalores generalizados. En Hu & Lin (2001) se aborda el diseño de compensación AW con rechazo a perturbaciones para sistemas LTI a tiempo discreto, donde, considerando realimentación de estados solamente, establece condiciones para un conjunto invariante ante la presencia de perturbación persistente para el diseño de la compensación.

En Mulder & Kothare (2002) se muestra el diseño de un controlador dinámico y una ganancia de compensación estática de manera simultánea, en la cual se considera el efecto de la saturación sobre el desempeño en lazo cerrado, pero no se toma en consideración los posibles cambios en los límites de operación de los actuadores, no hay robustez.

Un enfoque empleado para la síntesis de la ganancia de compensación AW bajo criterios de robustez basado en LMIs es presentado en Gomes da Silva Jr. & Tarbouriech (2005). Mientras que en Cao & Lin, (2006), se presenta un diseño de compensación anti-windup para sistemas politópicos. Allí se utilizan funciones de Lyapunov dependientes de parámetros para reducir el conservatismo. La robustez se considera para la incertidumbre del sistema dinámico.

Por otro lado, en Ríos-Bolívar et al. (2005), se presenta una técnica para compensación AWBT en controladores PID basada en la caracterización de las normas H₂ y H_¥ como desigualdades matriciales lineales, al igual que en Ríos-Bolívar & Godoy (2005) y Ríos-Bolívar & Godoy (2006), para controladores multivariables. La robustez se considera asegurando el desempeño en lazo cerrado a pesar de cambios desconocidos en los límites de saturación de los actuadores, pero no se considera sobre el funcionamiento en lazo cerrado de acuerdo a las premisas de diseño del controlador.

En Ríos-Bolivar et al. (2010), se presenta un método para la síntesis de sistemas de control con compensación de saturación en los actuadores para sistemas lineales a tiempo continuo con incertidumbres politópicas, tomando como base un índice de desempeño basado en la descripción dada en Ríos-Bolivar & Godoy (2005) y Ríos-Bolivar & Godoy (2006).

En este trabajo se presenta un método de diseño de controladores dinámicos con compensación robusta para sistemas LTI basado en las normas H₂-H_¥. La síntesis del controlador dinámico y la ganancia de compensación se realizan simultáneamente, tomando en consideración el desempeño en lazo cerrado y cambios en los limites de saturación de los actuadores. La característica de desempeño robusto se analiza sobre la función de transferencia del lazo cerrado de la salida del actuador respecto a la diferencia entre la señal de control efectiva al proceso y la salida del controlador, la cual se considera como una señal de perturbación. Así, se considera la minimización de las normas H₂-H_¥, descritas como un problema de optimización convexa, de esa función de transferencia, en conjunción con las especificaciones de desempeño en lazo cerrado en ausencia de saturación.

Notación. Â es el conjunto de números reales. Para una matriz A, A^T denota su transpuesta. L₂ es el espacio de Hilbert de señales vectoriales definidas en (-∞,∞), tal que: < ∞, "x Î l₂. diag(A,B) es una matriz diagonal con entradas A y B en su diagonal. En las particiones de matrices simétricas * denota cada uno de sus bloques simétricos. define la matriz identidad de dimensión apropiada.

PRELIMINARES

En esta sección se establecen algunos resultados preliminares a los fines de dar condiciones de desempeño adicionales en el análisis de los sistemas lineales a tiempo discreto (DTLS, por sus siglas en inglés). Considérese el sistema:

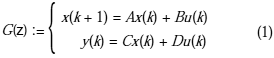
donde: x(k)ÎÂⁿ son los estados, u(k)ÎÂ^m son los controles y y(k)ÎÂ^p son las variables medidas. Las matrices A,B,C,D son bien conocidas y de dimensiones apropiadas.

Se sabe que G(z) es estable si los autovalores de A pertenecen a la región estable del plano complejo, esto es:

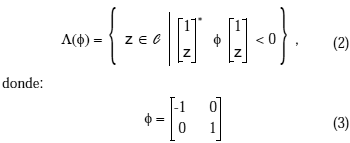
En términos de Lyapunov, esa condición de estabilidad se describe por el siguiente Lema:

Lema 2.1 (LMI Estándar) Considérese el sistema (1). Entonces, todos los autovalores de A pertenecen a L(f) dado por (2) si y solamente si existe una matriz PÎ S_n que satisface el siguiente conjunto de LMIs: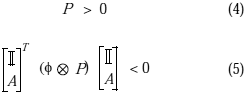

Demostración (Pipeleers et al. 2009)

Para estudiar el desempeño de ese sistema, en la teoría de control óptimo robusto, es tradicional aplicar criterios basados en normas. Así, existen versiones mejoradas del Lema Real Acotado de manera de minimizar el conservatismo (Oliveira et al. 2002; Xu et al. 2007; He et al. 2005), o en el caso de desempeño en H₂ (Oliveira et al. 2002; Pipeleers et al. 2009), esto nuevamente, con la finalidad de reducir el conservatismo. Seguidamente, algunos de estos métodos serán presentados y sirven de base para el desarrollo de los resultados que se muestran en esta contribución.

Condiciones LMI extendidas para DTLS

Lema 2.2 (H₂ extendido en tiempo discreto)

Considérese un sistema como el dado por (1). Las siguientes declaraciones, con P = P^T > 0 , son equivalentes:

i) A es estable y < m.

ii) Existe P y Z, tal que:

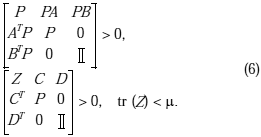
iii) Existe P, Z y G tal que:

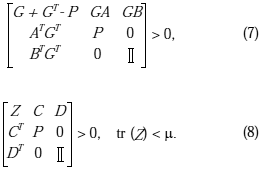
Demostración. La demostración esta basada en la aplicación de lema de proyección. Esta prueba puede ser evaluada en Duan et al. (2006).

Lema 2.3 (H_¥ extendido a tiempo discreto)

Considere el sistema a tiempo discreto (1), con matrices (A, B, C, D). Las siguientes declaraciones, con P = P^T > 0 son equivalentes:

i) A es estable y

ii) Existe P, tal que:

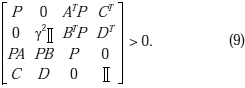
iii) Existe P y G tal que:

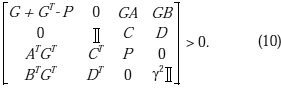
Demostración. La demostración se construye a partir del lema de proyección. Los detalles pueden ser evaluados en Duan et al. (2006).

Estos resultados serán útiles para el diseño de controladores robustos por realimentación estática de la salida extendida, tal como se muestra a continuación.

PROBLEMA INTRODUCTORIO

De manera de introducir el problema de robustez para el diseño de compensación anti-rebote, considérese el siguiente sistema lineal:

x(k + 1) = Ax(k) + B₁w(k) + B₂s(u)

z(k) = C₁x(k) + D₁₁w(k),

y(k) = C₂x(k) + D₂₁w(k),     (11)

donde: xÎÂⁿ son los estados, wÎÂ^r son las perturbaciones, uÎÂ^m son los controles, zÎÂ^q son las salidas controladas, y yÎÂ^p son las salidas medidas. A, B₁, B₂, C₁, C₂, D₁₁, D₂₁ son matrices conocidas de dimensiones apropiadas.

La función no-lineal s(o) denota la saturación del actuador, la cual es definida por: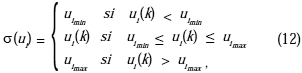

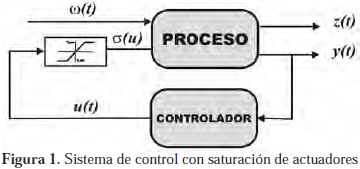
para i = 1, 2, ..., p. Esta función no-lineal describe las limitaciones y/o sustituciones debido al funcionamiento de los accionadores (Figura 1).

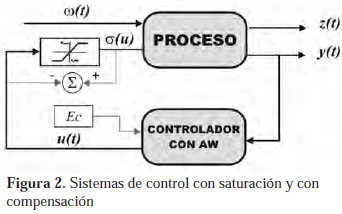
El control efectivo aplicado al proceso s(u) es una función no-lineal de la salida u(k) del controlador.

A objeto de satisfacer los requerimientos de control, se considera un controlador dinámico con compensación, el cual es dado por:

z(k + 1) = A_C z(k) + B_C y(k) + E_C[s(u) - u]

u(k) = C_C z(k) + D_C y(k),     (13)

donde: A_C, B_C, C_C, D_C corresponden a las matrices dinámicas del controlador, las cuales son parámetros de diseño. E_C representa la ganancia de compensación, la cual es también un parámetro de diseño (Figura 2).

Cuando la saturación ocurre, la señal J = s(u) - u es distinta de cero y los efectos adversos se presentan. Considerando la minimización de dichos efectos mediante compensación, las matrices dinámicas del controlador A_C, B_C, C_C, D_C son diseñadas sin tomar en cuenta la saturación, mientras que se sintetiza la ganancia de compensación E_C para poder mejorar el desempeño del lazo cerrado. La compensación toma lugar cuando la señal J = s(u) - u es no nula y la realimentación adicional, es incorporada de manera de hacer nula dicha señal, en el menor tiempo posible, mediante la actualización de la señal de control u, la cual entrará nuevamente en sus límites de acción.

Así, el sistema en lazo cerrado está dado por:

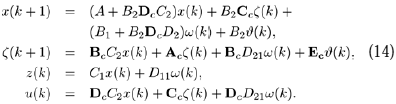
El desempeño del sistema en lazo cerrado y sin saturación se estudia a partir de la función de transferencia de la perturbación w a la salida controlada z. Sea T_zw tal función de transferencia: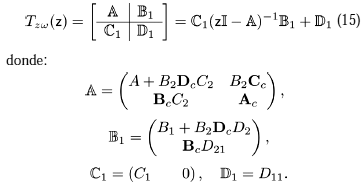

Problema 1: Por requerimientos de desempeño, sin saturación, es necesario diseñar un controlador dinámico (13) tal que:

1. El sistema en lazo cerrado (14) sea asintóticamente estable.

2. ||T_zw||₂ < m ||T_zw||_¥ < g donde m > 0 y g > 0.

Este es un problema típico en la literatura de control óptimo robusto.

Cuando la saturación se activa es necesario preservar las propiedades de estabilidad. Dichas propiedades se garantizan por medio de la estabilidad global de los sistemas de entrada acotada, la cual debe ser utilizada en el diseño de la ganancia de compensación. Entonces, el problema de síntesis consiste en obtener E_C que garantice la efectividad de la compensación bajo alguna condición de estabilidad robusta para sistemas perturbados. Así, en primer lugar, la estabilidad en lazo cerrado se satisface por la adecuada selección de las matrices dinámicas del controlador. La segunda condición, ligada a la estabilidad de los sistemas de entrada acotada, permitirá la compensación bajo condiciones de estabilidad robusta.

Por otro lado, es necesario considerar aspectos de robustez en relación con la operación de los accionadores. En este sentido, se debe diseñar la ganancia de compensación a objeto de garantizar la estabilidad en lazo cerrado y minimizar el efecto de la señal perturbación J sobre una salida controlada que dependa de la señal de control , bajo saturación. Por ejemplo, sea z_u(k) una salida controlada definida por

z_u = D_CC₂x + C_Cz      (16)

que corresponde al control u(k) considerando sin efecto la perturbación w(k). Entonces, el problema de diseño de la ganancia de compensación se puede focalizar a partir de las normas H₂ y H_¥.

Considérese la función de transferencia de la perturbación J a la salida controlada z_u: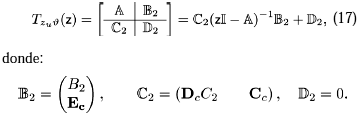

Problema 2: Dado el sistema dinámico (11), diseñar la ganancia de compensación E_C para el controlador (13), tal que:

1. El sistema en lazo cerrado (14) sea asintóticamente estable.

2. El efecto de J sobre z_u sea mínimo, en algún sentido.

En consecuencia, el índice de desempeño robusto respecto a cambios en los límites de saturación puede ser alcanzado.

Este funcionamiento robusto es una demanda típica en un ambiente de control industrial ya que los elementos actuadores (válvulas de control, dispositivos hidráulicos, entre otros), sufren deterioros debido al uso intensivo, obsolescencia de partes, degradación de los materiales de construcción, entre otros aspectos. Por lo tanto, es necesario diseñar los mecanismos de compensación con características de robustez.

En resumen, se han formulado dos problemas: un problema típico de control óptimo robusto y un problema de síntesis de la ganancia de compensación para AWBT robusto. Ambos problemas pueden ser considerados bajo una misma óptica como un problema de control multiobjetivo:

Problema 3: Dado el sistema dinámico (11), diseñar el controlador con compensación (13) tal que:

1. El sistema en lazo cerrado (14) sea asintóticamente estable.

2. ||T_zw||₂ < m ||T_zw||_¥ < g donde m > 0, g > 0; sujeto a que

3. El efecto de J sobre z_u sea mínimo, en algún sentido.

Bajo esta formulación, los objetivos de síntesis pueden ser una mezcla de desempeño H₂, desempeño H_¥, rechazo a perturbación, los cuales pueden ser descritos mediante desigualdades matriciales lineales, tal como ha sido establecido en la síntesis de controladores multi-objetivos. En este contexto, es posible desarrollar una técnica sistemática de diseño que combine aspectos importantes de la síntesis de control realimentado con el diseño de compensación anti-rebote, tomando ventaja de la formulación con criterios múltiples (Ríos-Bolívar, 2007; Ríos-Bolívar, 2008). Así en Ríos-Bolívar (2008), se ha resuelto este problema para sistemas con matrices dinámicas conocidas de acuerdo al siguiente resultado:

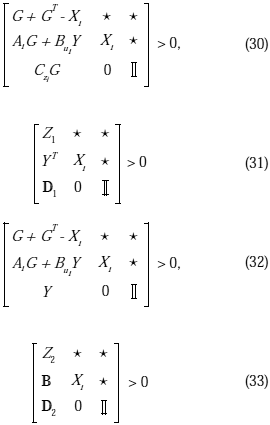
Teorema 3.1 Sea el sistema definido por (11). Dicho sistema es estabilizable por el controlador por realimentación dinámica de la salida con compensación AW, tal que ||T_zw||_¥ < g y ||T_zuJ||²₂ < m si y solamente si, existen matrices de orden n, X > 0 y Y > 0; matrices Q, L ÎÂ^nxn ; matrices F ÎÂ^nxp, N ÎÂ^pxq, M ÎÂ^nxp y la matriz simétrica W ÎÂ^mxm tal que las siguientes LMIs son factibles:

La matriz de ganancia de compensación E_C está dada por E_C = V^-1M donde V y U son matrices no singulares que satisfacen YX + VU = ΙΙ

Demostración: (Ríos-Bolívar, 2008)

El resultado anterior, desde una perspectiva muy conservativa, resuelve el problema para el manejo de perturbaciones y ciertas variaciones en los límites de acción de los actuadores, pero no considera incertidumbres en el modelo dinámico del sistema objeto de control.

Así, para garantizar robustez tanto en la dinámica de los procesos como por efecto del deterioro del funcionamiento de los accionadores, se debe considerar el diseño de sistemas de control para el manejo de perturbaciones e incertidumbres, tal como será presentado a continuación.

CONTROL Y COMPENSACIÓN AW ROBUSTA

A partir de este momento, se está interesado en diseñar controladores y compensadores robustos, en procesos donde existen incertidumbres politópicas. Sea el sistema incierto:

x(k + 1) = A(a)x(k) + B_w(a)w(k) + B_u(a)s(u)

z(k) = C_z(a)x(k) + D_w(a)w(k)

y(k) = C_y x(k),     (22)

donde, tal como ha sido indicado, xÎÂⁿ son los estados, wÎÂ^r son las perturbaciones, uÎÂ^p son los controles, zÎÂ^m son las salidas controladas, y yÎÂ^q son las salidas medidas. Adicionalmente, las matrices desconocidas del sistema conforman un politopo incierto, es decir, pertenecen a una cáscara convexa, con lo cual: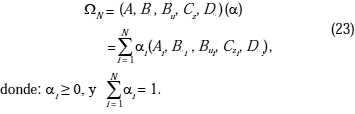

Dado que a está restringida a un conjunto unitario, ya que a_i ≥ 0, ∑^N_i=1 a_i = 1, entonces las matrices (A, B , C_z, D_w)(a) son funciones afines del vector de parámetros inciertos aÎÂ^N descrito por la combinación convexa de las matrices vértices A_i, B_wi , B_ui, C_zi, D_wi , i = 1, 2,..., N.

Como se puede observar, la matriz C_y se considera conocida. Eso tiene correspondencia con el hecho de que ella representa, desde el punto de vista práctico, un elemento fundamental y preciso para la implantación de los sistemas de control, que son los sensores, los cuales nos permiten construir controladores por realimentación de la salida medida.

Ahora, aplicando un control por realimentación de la salida estática y de acuerdo al problema introductorio, entonces:

u(k) = Ky(k) + E_cJ(k)     (24)

donde: K es la ganancia de realimentación estática de la salida, a diseñar. Así, las matrices del lazo cerrado para T_zw (z) son:

A = A(a) + B_u(a)KC_y ,

B = [B_w(a) B_u(a) + B_u(a) E_c] ,    (25)

C₁ = C_z (a), D₁ = [D (a) 0].

De manera similar, si de acuerdo a (24), zu(k) = K y (k) + E_cJ (k), entonces las matrices del lazo cerrado para T_zu J(z) son:

A = A(a) + B_u(a)KC_y ,

B = [B_w(a) B_u(a) + B_u(a) E_c] ,    (26)

C₂ = KC_y , D₂ = [0 E_c].

Es evidente que para realimentación de estados C_y=II. De acuerdo al Problema 3 y siguiendo las directrices del diseño de la ganancia de compensación para el problema de saturación de los accionadores, dicha ganancia se puede obtener, en base a nuestro planteamiento, por dos vías: 1) Diseñando, en primer lugar, la ganancia de realimentación estática de la salida, tomando en consideración solamente la función de transferencia T_zw (z), y luego determinar la compensación, a partir de la función de transferencia T_zuJ(z). 2) Diseñando, simultáneamente, ambas ganancias. Este es el caso que seguiremos a continuación.

Control y Compensación AW en H₂

Del Lema 2.2 se obtiene el siguiente resultado:

Teorema 4.1 Considérese el sistema (22) sobre el politopo (23), con z_u(k) = Ky(k) + E_cJ(k). Se obtiene una ley de control por realimentación estática de la salida y compensación AW, de la forma (24), garantizando un desempeño subóptimo en H₂ para T_zw (z) y T_zuJ (z) a partir del siguiente problema de optimización:

min

G, Y, R, Z_j, X, X_i         tr(Z_j);

i = 1,..., N, j = 1, 2.

los siguientes conjuntos de LMIs son equivalentes:

i)

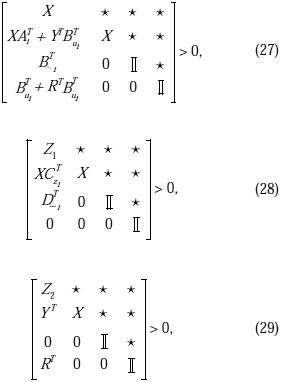
para i = 1,..., N, j = 1, 2, X = X^T > 0ÎÂ^nxn, YÎÂ^pxq , Z_jÎÂ^sxs . A partir de lo cual, las ganancias de realimentación estática de la salida y de compensación están dadas por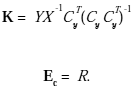

ii)

para i = 1,..., N, j = 1, 2, y donde: GÎÂ^nxn, YÎÂ^pxn, Z_jÎÂ^sxs, Xi = Xi > 0ÎÂ^nxn.

A partir de lo cual, las ganancias de realimentación estática de la salida y de compensación están dadas por:

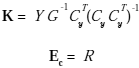
Demostración:

Considérese que existe una solución factible para el problema de realimentación estática de la salida, según el control (24). Entonces, a partir de las matrices dinámicas del lazo cerrado y según el Lema 2.2, para la parte i) se aplica una transformación congruente diag(X, X, II) para la primera LMI en (6), y la transformación diag(II, X, II) para la segunda LMI en (6), con X = P^-1. Así, se obtienen las siguientes LMIs, para las matrices de lazo cerrado A, B, C y D: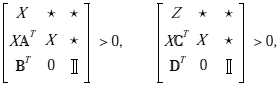

Utilizando las matrices de lazo cerrado (25) y (26), las desigualdades matriciales son linealizadas a partir del cambio de variables Y = KC_y X y E_c = R, entonces se llega al resultado mostrado en el apartado i). Para el apartado ii) se utiliza el sistema dual, entonces se obtienen las siguientes desigualdades matriciales: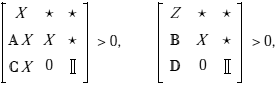

las cuales, siguiendo el procedimiento mostrado en Duan et al. (2006), empleando funciones de Lyapunov dependientes de parámetros, se obtiene:

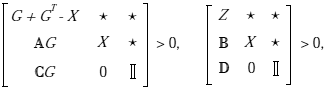
por lo tanto, sustituyendo las expresiones para las matrices de lazo cerrado y aplicando el cambio de variables Y = KC_yG y E_c = R, se obtienen los resultados dados en el apartado i).

Control y Compensación AW en H_¥

Del Lema 2.3 se deriva el siguiente resultado:

Teorema 4.2 Considérese el sistema (22) sobre el politopo (23), con z_u = K y (t) + E_cJ(k). Se obtiene una ley de control por realimentación estática de la salida y compensación AW, de la forma (24), garantizando un desempeño subóptimo en H_¥ para T_zw (z) y T_zuJ(z), a partir del siguiente problema de optimización:

min

G, Y, R, X, X_i   g_j² tal que

i = 1,..., N, j = 1, 2.

los siguientes conjuntos de LMIs son equivalentes:

i)

ii)

para i = 1,..., N, j = 1, 2, donde: GÎÂ^nxn, YÎÂ^pxn. A partir de lo cual, las ganancias de realimentación estática de la salida y de compensación están dadas por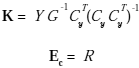

Demostración

Considérese que existe una solución factible para el problema de realimentación estática de la salida, según el control (24). Entonces, a partir de las matrices dinámicas del lazo cerrado y según el Lema 2.3, para la parte i) se aplica una transformación congruente diag(X, II, X, II) para la LMI en (9), con X = P^-1. Así, se obtiene la siguiente LMI, para las matrices de lazo cerrado A, B, C y D: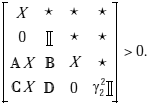

Utilizando las matrices de lazo cerrado (25) y (26), las desigualdades matriciales son linealizadas a partir del cambio de variables Y = KC_yG y E_c = R, entonces se llega al resultado mostrado en el apartado i). Para el apartado ii), siguiendo el procedimiento mostrado en Duan et al. (2006), empleando funciones de Lyapunov dependientes de parámetros, se obtiene:

por lo tanto, sustituyendo las expresiones para las matrices de lazo cerrado y aplicando el cambio de variables Y = KC_yG y E_c = R, se obtienen los resultados dados en el apartado ii.

Los resultados así obtenidos en H_¥ y en H₂ se pueden combinar a fin de obtener controladores con multiobjetivos. En las técnicas multiobjetivos clásicas, las expresiones de la forma A^TP + PA involucran productos entre las matrices de Lyapunov y las matrices de diseño, tal como ha sido mostrado en los casos no relajados, lo que se traduce en conservatismo. A fin de garantizar la convexidad del problema, es necesario hacer una consideración fundamental, reforzando todas las especificaciones a partir de una única función de Lyapunov. En el caso presentado, debido a las versiones extendidas de las caracterizaciones de las normas H₂/ H_¥ como LMIs, no se generan productos que involucren matrices de Lyapunov, y las matrices de diseño K, E_c no dependerán de ellas, evitándose la necesidad de usar la misma matriz de Lyapunov para todas las especificaciones.

Así, este hecho es muy importante debido a que no solamente hay una matriz de Lyapunov dependiente de parámetros para cada formulación, sino que hay, además, una función de Lyapunov para cada especificación de desempeño, lo que permite reducir el conservatismo.

Corolario 4.1 Considérese el sistema (22) sobre el politopo (23), con z_u = K y (t) + E_cJ(k). Se obtiene una ley de control por realimentación estática de la salida y compensación AW, de la forma (24), garantizando un desempeño subóptimo en H₂ para T_zw (z) y un desempeño sub-óptimo en H_¥ para T_zuJ(z), a partir del siguiente problema de optimización:

min

G, Y, R, X, X_i   tr (Z₁) tal que

i = 1,..., N, j = 1, 2.

los siguientes conjuntos de LMIs son equivalentes:

i)

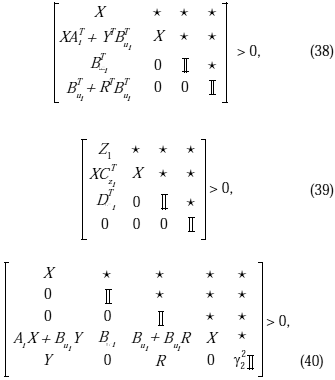
para i = 1,..., N, donde X = X^T > 0ÎÂ^nxn, YÎÂ^pxn. A partir de lo cual, las ganancias de realimentación estática de la salida y de compensación están dadas por: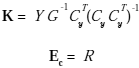

ii)

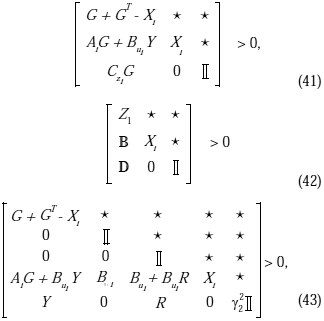
para i = 1,..., N, donde GÎÂ^nxn, YÎÂ^pxn. A partir de lo cual, las ganancias de realimentación estática de la salida y de compensación están dadas por: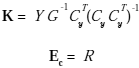

EJEMPLO NUMÉRICO

Para un ejemplo ilustrativo, considérese una variante del sistema dinámico inestable mostrado en Lee et al. (2006):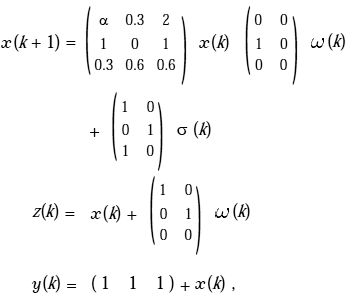

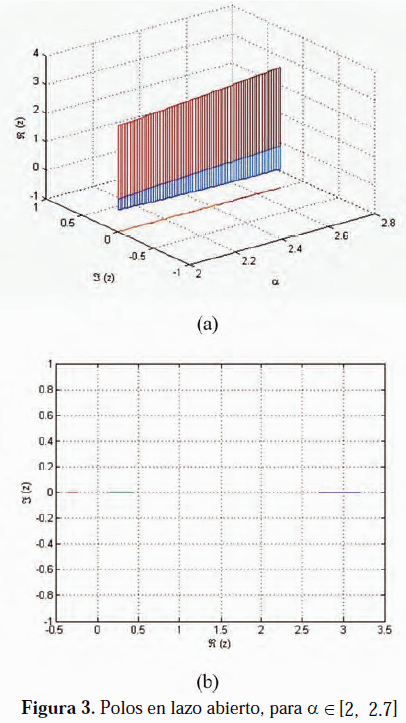
donde: el parámetro aÎ [2, 2.7]. Tal como se puede observar en la Figura 3, para los diferentes valores de a, el sistema en lazo abierto es inestable.

En este ejemplo, se considera la saturación de los actuadores en el sentido de que s(u)Î [-6.2, 6.2].

En primer lugar, a los fines de evaluar la estabilidad bajo incertidumbre, se considera el diseño de una ganancia de realimentación estática de la salida sin tomar en cuenta la saturación de los actuadores. Entonces, aplicando el Teorema 4.2 se obtiene la siguiente ganancia: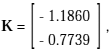

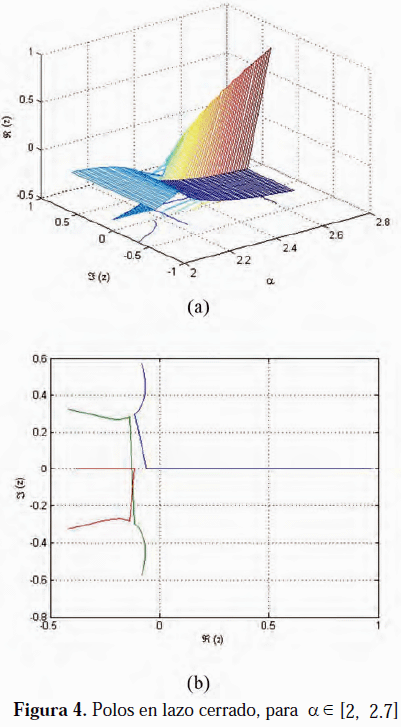
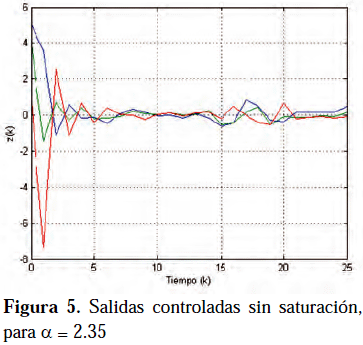
la cual permite garantizar la estabilidad en lazo cerrado para todos los valores de a, tal como se muestra en la Figura 4, con un índice de desempeño ||T_zw(z)||_¥ < 1.2611.

Para a = 2.35, la Figura 5 muestra el comportamiento temporal de las salidas controladas cuando no existe saturación en los actuadores.

En ella se puede observar la estabilización del sistema en lazo cerrado.

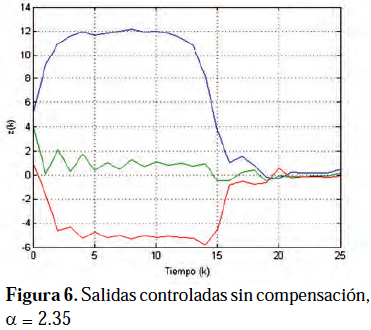
Cuando la saturación en los actuadores se hace presente y no hay compensación, el comportamiento temporal se deteriora (Figura 6). Esto sugiere el diseño de la ganancia de compensación.

Por lo tanto, nuevamente aplicando el Teorema 4.2 para la síntesis de la ganancia de realimentación estática de la salida y de la ganancia de compensación se obtienen:

con los índices de desempeño ||T_zw (z)||_¥ < 0.9255 y ||T_zuJ(z)||_¥ < 0.2700.

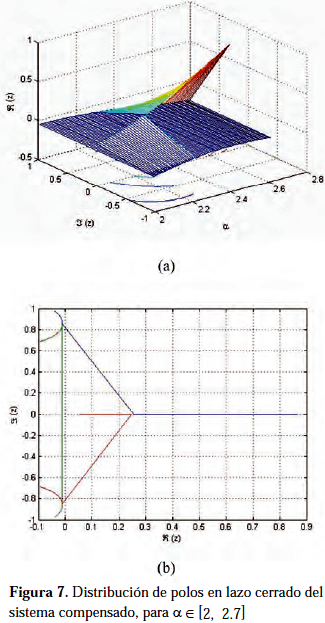
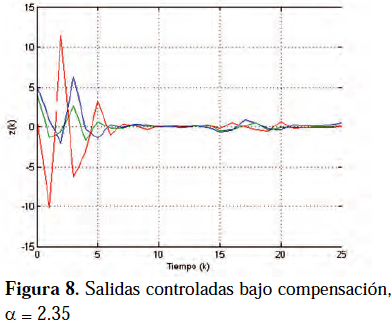
En consecuencia, al tomarse en cuenta la saturación de los actuadores en el diseño del controlador se mejora el índice de desempeño del efecto de las perturbaciones sobre la salida controlada. Para verificar la estabilidad, la Figura 7 muestra la distribución de los polos con respecto a la variación del parámetro a. Todos estos polos pertenecen a la región estable, por lo tanto el sistema en lazo cerrado es robustamente estable.

Para evaluar el efecto de la compensación, en primer lugar, consideremos el diseño del control sin tomar en cuenta la saturación e induciendo, para la simulación, que la misma se hace presente, a partir de lo cual se evalúa el desempeño con la ganancia compensación, que se obtiene en un segundo cálculo. Tal como se muestra en la Figura 8, el comportamiento temporal, con respecto a la evolución sin compensación, se mejora. El efecto de la saturación es minimizado en el sentido de que se alcanza el estado estacionario en un tiempo inferior respecto al comportamiento sin compensación (Figura 6), aproximándose a la evolución temporal sin la presencia de saturación en los accionadores.

Una segunda evaluación se refiere a considerar el diseño de la ganancia de realimentación estática y de la ganancia de compensación de manera conjunta. La Figura 9 muestra la evolución temporal de las salidas controladas, con realimentación de la salida y con compensación. Se puede observar que esta dinámica es más oscilatoria con respecto a la mostrada en la Figura 8, por cuanto la ubicación de los polos en lazo cerrado es distinta respecto al primer cálculo de la ganancia de estabilización estática.

CONCLUSIONES

A partir de la salida, se ha planteado y resuelto el problema de control por realimentación estática de la salida y con compensación AW en sistemas lineales tiempo discreto con incertidumbres politópicas.

El método de síntesis consiste en diseñar dos ganancias, una que corresponde a la realimentación estática de la salida y otra que corresponde a la ganancia de compensación AW. Así, se toman en cuenta dos funciones de transferencia.

La primera que corresponde al desempeño en lazo cerrado de las salidas controladas respecto a las perturbaciones.

La segunda corresponde a tomar en cuenta el efecto de la saturación de los accionadores en la señal de control, de tal manera que la diferencia entre la salida del actuador y la salida del controlador se considera como una señal de perturbación adicional. Por lo tanto, bajo las premisas de estabilidad robusta y manejo de perturbaciones, se plantea el diseño en el marco del control óptimo robusto con criterios multi-objetivos, a partir de lo cual se obtienen las ganancias bajo las premisas de la definición de las normas H₂ y H_¥ como desigualdades matriciales lineales, y aplicadas a las funciones de transferencias señaladas. En consecuencia, las ganancias de realimentación de la salida extendida y de compensación AW se obtienen por solución de conjuntos de LMIs, según los criterios multi-objetivos que se impongan.

Dado que los resultados obtenidos se han derivado de versiones extendidas de las caracterizaciones de las normas H₂/H_¥ como LMIs, se reduce el conservatismo, porque se utiliza una función de Lyapunov para cada especificación de desempeño.

Los resultados, además de su verificación formal, han sido evaluados numéricamente e indican la efectividad de la compensación AW robusta.

AGRADECIMIENTOS

Este trabajo ha sido financiado por el CDCHT de la Universidad de Los Andes, a través del proyecto No. I-1268-11-02-A, por lo que gratamente se reconoce este soporte.

REFERENCIAS

1. Åström, K. J. & Rundqwist, L. (1989). Integrator windup and how to avoid it. In: Proc. of the American Control Conference. pp. 1693–1698.        [ Links ]

2. Campo, P. J. & Morari, M. (1990). Robust control of processes subject to saturation nonlinearities. Comp. & Chem. Enginnering 14, 343–358.        [ Links ]

3. Cao, Y-Y. & Zongli, L. (2006). An anti-windup design for polytopic systems by a parameter dependent lyapunov function approach. Intern. J. Syst. Sci. 37(2), 129–139.        [ Links ]

4. Duan, Z., Zhang, J., Zhang, C., Mosca, E. (2006). Robust H₂ and H_∞ filtering for uncertain linear systems. Automatica 42, 1919–1926.        [ Links ]

5. Gomes Da Silva Jr., J. M. & Tarbouriech, S. (2005). Antiwindup design with guaranteed regions of stability: An LMI approach. IEEE Tran. on Autom. Control 50(1), 106–111.        [ Links ]

6. He, Y., Wu, M., She, J. H. (2005). Improved boundedreallemma representation and H_∞ control of systems with polytopic uncertainties. IEEE Trans. on Autom. Control 52(7), 380–383.        [ Links ]

7. Hu, T. & Lin, Z. (2001). Disturbance rejection with saturation actuators for discrete-time linear systems. In: Proc. 40th IEEE Conf. on Control and Decision. Vol. WeM01-3. Orlando, Florida, USA. pp. 1723–1728.        [ Links ]

8. Kothare, M. V. & Morari, M. (1997). Stability analysis of anti-windup control systems: A review and some generalizations. In: Proc. European Control Conference ECC97.        [ Links ]

9. Kothare, M. V., Campo, P. J., Morari, M., Nett, C.N. (1994). A unified framework for the study of antiwindup designs. Automatica 30(12), 1869–1883.        [ Links ]

10. Lee, K. H., Joon, H. L., Wook, H. K. (2006). Sufficient lmi conditions for H_∞ output feedback stabilization of linear discrete-time systems. IEEE Trans. on Automatic Control 51(4), 675–680.        [ Links ]

11. Mulder, E.F. & Kothare, M.V. (2002). Static antiwindup controller synthesis using simultaneous convex design. In: Proceedings of the American Control Conference. Anchorage. pp. 651–656.        [ Links ]

12. Mulder, E.F., Kothare, M.V., Morari, M. (2001). Multivariable anti-windup controller synthesis using linear matrix inequalities. Automatica 37, 1407– 1416.        [ Links ]

13. Narendra, S. K. & Balakrishnan, J. (1997). Adaptive control using multiple models. IEEE Trans. Autom. Control Vol. 42(2), 171-187.        [ Links ]

14. Oliveira, M. C., Geromel, J. C., Bernussou, J. (2002). Extended H₂ and H_∞ norm characterizations and controller parametrizations for discrete-time systems. Int. J. of Control 75(9), 666–679.        [ Links ]

15. Pipeleers, G., Demeulenaerea, B., Sweversa, J., Vandenberghe, L. (2009). Extended lmi characterizations for stability and performance of linear systems. Systems & Control Letters 58, 510–518.        [ Links ]

16. Ríos-Bolívar, A. (2007). Controller synthesis with compensation AW and performance in H₂/H_∞. Revista Técnica de Ingeniería 30(3), 263–272.        [ Links ]

17. Ríos-Bolívar, A. (2008). Un método para el diseño de compensación AW robusta en sistemas lineales a tiempo discreto. Rev. Ciencia e Ingeniería 29(2), 173–182.        [ Links ]

18. Ríos-Bolívar, A. & Garcia, G. (2004). Control with saturation compensation and fault detection filter design. Rev. Ciencia e Ingeniería 25(1), 51–59.        [ Links ]

19. Ríos-Bolívar, A. & Godoy, S. (2005). Multivariable anti-windup controller design using H₂/H_∞ multiobjectives. In: ICGST Int. Conf. on Automatic Control and System Engineering. Vol. 1. Cairo, Egypt. pp. 28–34.        [ Links ]

20. Ríos-Bolívar, A. & Godoy, S. (2006). Multiobjective approaches for robust anti-windup controller synthesis in LTI systems. WSEAS Transaction on Systems 5(1),164–171.        [ Links ]

21. Ríos-Bolívar, A., Rivas, F., Garcia, G. (2005). Robust anti-windup compensation for PID controllers. In: 7th WSEAS Int. Conf. on Automatic Control, Modelling and Simulation, ACMOS-05. Prague - Czech Republic. pp. 242–247.        [ Links ]

22. Ríos-Bolívar, A., Delgado, V., Márquez, R. (2010). Control y compensación Anti-Windup robusta para sistemas lineales inciertos. Rev. Iberoamericana de Automática e Informática Industrial. (Por aparecer).        [ Links ]

23. Wada, N. & Saeki, M. (2003). Design of a static antiwindup compensator that optimizes L2 performance: An LMI based approach. In: Proc. of the IEEE International Conference on Robotics & Automation. Taipei-Taiwan. pp. 2628–2633.        [ Links ]

24. Xu, S., Lam, J., Zou, Y. (2007). New versions of bounded real lemmas for continuous and discrete uncertain systems. Circuits Syst. Signal Process 26, 829–838.        [ Links ]

25. Zheng, A., Kothare, M. V., Morari, M. (1993). Antiwindup design for internal model control. Technical Report CIT-CDS Technical Memo. CalTech.        [ Links ]