Estudio numérico de la receptividad en la capa límite de rejillas de álabes utilizando criterios de vorticidad

Geanette Polanco¹, Luis Rojas Solórzano², Cristina Amon³

¹Universidad Simón Bolívar, Dpto. de Mecánica, Edo. Miranda, Venezuela. Email: gpolanco@usb.ve

²Universidad Simón Bolívar, Dpto. de Conversión de Energía, Edo. Miranda, Venezuela. Email: rrojas@usb.ve

³University of Toronto, Faculty of Applied Science and Engineering, Toronto, Canada. Email: cristina.amon@utoronto.ca

RESUMEN

El presente trabajo estudia el inicio de la transición del flujo laminar al flujo turbulento, fenómeno denominado receptividad, en la capa límite de rejillas de álabes. El estudio se realiza partiendo de la solución o simulación numérica directa (SND) de la ecuación reconservación de momentum lineal y la ecuación de continuidad, para analizar el decrecimiento de la capacidad de transporte de vorticidad en la dirección del flujo, la dependencia de la vorticidad del gradiente de presión local, la creación y destrucción de la vorticidad y la relación de estos fenómenos con la receptividad dentro de la capa límite. El estudio abarca la consideración de la receptividad bajo condiciones de flujo imperturbado y bajo la influencia de perturbaciones temporales superpuestas al flujo. Las propiedades del campo de vorticidad se obtienen mediante la manipulación matemática de los datos de presión y velocidad obtenidos punto a punto a partir de la SND. De allí resulta que el fenómeno de transición se evidencia claramente en la variable vorticidad, especialmente en el cambio de longitud de onda que sufre esta señal dentro de la capa límite, así como también en el desprendimiento de “bolsas” de vorticidad aguas abajo del canal inter-álabes, para el caso imperturbado como el perturbado bajo el régimen super-crítico, mientras que para el régimen sub-crítico no se evidencian cambios relevantes en la variable vorticidad.

Palabras clave: Vorticidad, Receptividad, Capa límite, SND.

Numerical study of boundary layer receptivity of airfoil cascade using vorticity criteria

ABSTRACT

Receptivity is the beginning of the transition phenomenon between laminar and turbulent flow. Direct Numerical Simulation (DNS) approach is used to solve the momentum and continuity equations in the domain. The purpose of the study is to characterize the decrement of the transport of vorticity in the flow direction, the dependence relationship of vorticity and the pressure gradient, the creation and destruction of vorticity and the relation between those phenomena and the receptivity inside the boundary layer. The study covers considerations related to different conditions as normal flow and perturbed flow with time dependent signals superimposed to the normal flow. The characterization of the vorticity field in the domain is product of the mathematical analysis of the pressure and velocity field in every location of the domain. For both cases, the normal flow and the perturbed flow conditions corresponding to the super-critic flow condition, the results show the receptivity phenonmenon is clearly represented by the vorticity parameter, especially in the change of the wavelength that vorticity suffers inside the boundary layer, as well as, the detached of some structure of vorticity from the airfoil surface in the inter channel section. However, in sub-critic flow condition neither normal nor perturbed flows do not show any relevant change in the behaviour of the vorticity parameter.

Keywords: Vorticity, Receptivity, Boundary layer, SND.

Recibido: noviembre de 2008 Recibido en forma final revisado: julio de 2011

INTRODUCCIÓN

La receptividad es el mecanismo físico mediante el cual la energía es transferida desde una perturbación de longitud de onda larga a una inestabilidad transicional de longitud de onda corta en un plano, caracterizando el comienzo del fenómeno de la transición en este tipo de geometrías (Richez et al. 2008) e incluso extendiéndose a diferentes geometrías con la aplicación de otros modelos de turbulencia, como lo son Large Eddy Simulation y RANS (Hickel, 2008); mostrando la comparación de los resultados obtenidos aplicando varios métodos al estudio (Monokrousos et al. 2008). En particular, se espera caracterizar el inicio del fenómeno de la transición natural, correspondiente a la evolución de inestabilidades primarias (inestabilidades lineales 2D, también denominadas ondas Tollmien- Schlichting) dentro de la capa límite (Umit & Chauvin, 1994), utilizando la variable vorticidad como base de la metodología de estudio.

La simulación numérica directa (SND) permite resolver las ecuaciones que rigen el flujo, a saber: continuidad y conservación de momentum, bajo un esquema de discretización espacial y un esquema temporal. Una vez resueltas las ecuaciones de momentum y continuidad toda la información, es postprocesada para la obtención de las variables necesarias; es decir, vorticidad, variaciones de vorticidad, entre otras, involucradas en el análisis propio de este trabajo.

Los fenómenos hidrodinámicos que aparecen en la capa límite dentro de geometrías variadas, han sido tema de interés desde hace mucho tiempo, en especial aquellos relacionados con la transición del régimen de flujo laminar a turbulento. Trabajos anteriores han desarrollado diversos estudios tanto experimentales (Kachanov & Kozlov, 1982; Nishioka & Morkovin, 1986), como teóricos basados en la Teoría de Estabilidad Lineal (Schlichting, 1979) y numéricos (Fasel, 1976) de la capa límite en geometrías sencillas, como placas planas y álabes aislados. Sin embargo, la geometría de cascada es considerada una geometría compleja, para la cual se han desarrollado correlaciones experimentales que estiman la localización del punto de inicio de la transición (Robert, 1975; Umit & Chauvin, 1994), bajo ciertas limitaciones de flujo. Todos estos estudios han estado sustentados en el análisis del perfil de velocidad y sus componentes. Particularmente el desarrollo de estudios numéricos en la geometría propuesta, se limita al caso bidimensional para el estudio de la receptividad en la capa límite, sometida en algunos casos a perturbaciones externas de tipo sinusoidal, tal como plantearon Rojas-Solórzano & Amon (1995) y Rojas-Solórzano (1997).

MODELO FÍSICO-MATEMÁTICO PARA LA VORTICIDAD

Para flujos con un gradiente de presión adverso, se observa que el momentum en la dirección del flujo “x” empleado para transportar vorticidad decrece en la misma dirección (Gorski, 1995). Cuando la tasa de este decrecimiento no es compensada por la difusión transversal de la vorticidad hacia el borde de la capa límite, se dan las condiciones para el inicio de la separación. Para flujos bidimensionales, en la ausencia de fuerzas no conservativas, la vorticidad no puede ser creada o destruida en el interior de un fluido homogéneo; ésta debe ser creada o destruida solamente en la frontera del fluido - capa límite (Hunt, 1964).

A diferencia de la ecuación de conservación de momentum, la ecuación de vorticidad (Ec. 1), no contiene término de gradiente de presión, aunque el flujo de vorticidad cerca del borde es controlado por el gradiente de presión local.

La conservación del momentum en la dirección del flujo “x” junto con la suposición  ∂p/∂y = 0, basada en que el flujo permanece “cuasi-paralelo” a la superficie del álabe, aplica para el flujo de vorticidad cerca del borde de la capa límite de la siguiente forma:

La validez de esta relación, no implica que el exceso de vorticidad pueda difundirse hacia la pared con algún nivel de desaceleración del flujo. Esta representa la relación entre la variación de presión y de energía cinética en una línea de corriente paralela al álabe. En flujos desacelerados, la difusión de vorticidad hacia el borde es contrarrestada por la convección del fluido en la dirección transversal al flujo “y”. A mayor desaceleración, mayor es la convección que impide la difusión de la vorticidad (y el momentum) hacia el borde de las capas límite. Además, a mayor desaceleración mayor es la tasa de decrecimiento de la vorticidad media en la dirección del flujo “x”. Por lo tanto, debe existir un nivel de desaceleració del flujo sobre el cual la tasa de decrecimiento de la vorticidad media no es balanceada por la difusión de la vorticidad hacia el borde. Cuando esta condición es alcanzada, ocurre lo que se denomina el “nrrollamiento”(roll-up) de la vorticidad.

La eventual separación de la capa límite está determinada por el valor de un número adimensional () que tiene la forma del número de Reynolds, basado en la velocidad en la dirección transversal al flujo “y”, J, y en el espesor local de la capa límite (d). Este paráetro refleja la tendencia dominante entre los procesos de convección y difusión.

La presencia de un gradiente adverso de presión implica la presencia de un punto de inflexión en el perfil de velocidades dentro de la capa límite (Goldstein et al. 1987). El punto de inflexión es la posición de máxima vorticidad y en el caso del flujo dentro de la capa límite, éste es en parte formado por el desplazamiento transversal del fluido desde la vecindad inmediata a la pared hacia el borde de la capa límite. Una propiedad importante del punto de inflexión es que no puede ocurrir difusión de vorticidad media a través de él. Esto es importante porque, en ausencia de “enrrollamiento”, la vorticidad del fluido en el punto de inflexión no tiene acceso al borde (O’Malley et al. 1991).

Para un estado estacionario y una difusión despreciable en la dirección del flujo “x”, la conservación de vorticidad en forma integral puede escribirse como:

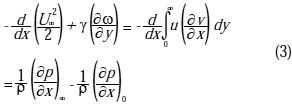
Una de las consecuencias de la presencia de un gradiente de presión adverso, es que el desarrollo de la capa límite debe ser relativamente rápido. El desplazamiento del fluido desde la pared, implica cambios significativos en la velocidad normal al borde en la dirección transversal al flujo “y”. Además, en flujos desacelerados, las líneas de flujo medias exhiben curvaturas convexas impuestas por la curvatura de la superficie, por ejemplo, la curvatura de un álabe. Esta situación crea un gradiente de presión en la dirección transversal al flujo “y”, que es indispensable para la separación del flujo.

METODOLOGÍA

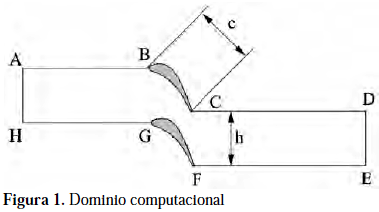
En este caso particular, el estudio se concentra en el estudio del problema hidrodinámico para una rejilla de álabes del estator de una turbina axial. El modelo seleccionado, representa la región inter-álabes extendida horizontalmente en las regiones de entrada y salida, tal como se muestra en la Figura 1. Las características geométricas del dominio son: cuerda de longitud “c” de 0,21m (0.7 ft), espesor de canal en la zona extendida “h” de 0.20 m (0,64 ft), solidez “s = h/c” de 0,914 y ángulo de ataque “a”, de 45 grados. La velocidad uniforme de entrada al dominio U_∞ = 0,152 m/seg (0.5 ft/seg). Dicho modelo está basado en el patrón resultante después de abrir y proyectar la sección cilíndrica coaxial (en el radio medio) sobre un plano, llamado canal inter-álabes (Deconcinck & Hirsch, 1981). El fluido incompresible de densidad 0,0325 kg/m³ (0,002024 lbm/ft³) es aire a una temperatura aproximada de 815,6 ºC (1500 ºF). La transferencia de calor es despreciada despreciada para la solución de las ecuaciones que rigen el flujo.

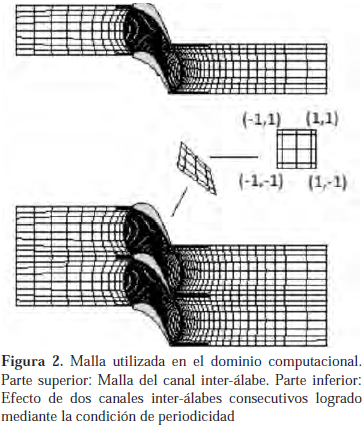
La discretización espacial del dominio se llevó a cabo mediante la técnica de elementos espectrales (Patera, 1984; Korczak & Patera, 1986; Amon, 1993). Cada uno de estos, denominados macro-elementos, posee 25 nodos, 5 por cada lado del macro-elemento. La malla resultante consta de 784 macro-elementos (Rojas-Solórzano, & Amon, 1995), como se puede observar en la Figura 2. El término convectivo, es tratado explícitamente por un esquema de discretización temporal de tipo Adams-Bashfort de tercer orden y el término viscoso por un esquema implícito de primer orden de diferencias hacia atrás.

Se establecieron dos sets de simulaciones: uno para el caso de flujo simple o básico y otro para el caso de flujo perturbado en la entrada. Las condiciones aplicadas a las fronteras del dominio computacional se establecieron comunes para ambos casos, el básico y el perturbado. Estas son la condición de flujo desarrollado a la salida y presión manométrica constante igual a cero a la salida del canal. Condición de no-deslizamiento en las paredes del álabe y condición de periodicidad en las fronteras meridionales (periodicidad AB-HG), que permite reproducir la presencia de varios canales inter-álabes, tal como se muestra en la parte inferior de la Figura 2. En la entrada, se aplicó una velocidad uniforme en la dirección del flujo “x”, para el caso básico y una velocidad constante más una perturbación periódica de tipo sinusoidal función del tiempo en el caso de flujo perturbado.

Se realizaron las simulaciones numéricas para el caso de flujo básico sin perturbación y caso perturbado, con los valores de Re sub y super-crítico de 231 y 1000 (Rojas- Solórzano & Amon, 1995), siendo el Reynolds crítico para la geometría estudiada, Re = 400. Para el caso perturbado se simularon tres valores de frecuencia de la perturbación: por debajo, igual y por encima la frecuencia natural (f = 44) y tres amplitudes diferentes establecidas como un porcentaje de la velocidad media a la entrada del dominio (0,5% U_∞, 1% U_∞, 2% U_∞). La información obtenida de las simulaciones son los datos instantáneos en diferentes tiempos (fracciones del período de la perturbación) así como los valores promedios punto a punto dentro de las variables involucradas; es decir, presión y velocidad.

Los resultados serán expresados utilizando ocho (8) líneas normales a la superficie del álabe, denominadas N1 hasta N8 y seis (6) líneas paralelas a la superficie del alabe, denominadas A, B, C, D, E y F.

ANÁLISIS DE RESULTADOS

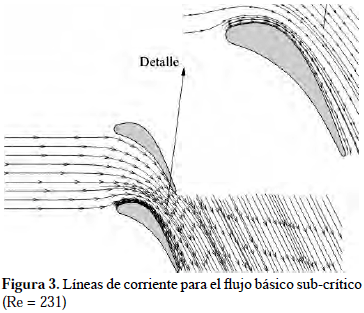
El flujo básico sub-crítico es acelerado de acuerdo a las restricciones de la geometría, manteniendo un campo de líneas de corriente sin separación de la capa límite (Figura 3). El flujo se comporta como flujo cuasi-potencial. El campo de presiones generado muestra una disminución gradual en toda la sección transversal del canal inter-álabes. El valor máximo de presión se localiza hacia la nariz del álabe donde se produce un punto de estancamiento. Se observa una zona centrada alrededor de un punto de la superficie del álabe inferior, creando una “bolsa” de contornos concéntricos que genera aguas abajo del punto un aumento de presión; es decir, se produce un gradiente de presión adverso al flujo. Este comportamiento coincide con la expansión del área de paso de flujo en el canal inter-álabes hacia la expansión aguas abajo del dominio, creando las condiciones favorables para la disminución de la velocidad y un aumento de la presión (Figura 4).

De la variación de presión en la superficie del álabe se evidencia la presencia de un gradiente de presión adverso al flujo, condición necesaria pero no suficiente para determinar la separación de la capa límite, ubicado aproximadamente a x = 0,82. Los valores de vorticidad que se generan justo en la cara de succión del álabe van disminuyendo a medida de que se aumenta la distancia lejos de los bordes y a medida de que el fluido se desplaza por el canal inter-álabes, debido a los fenómenos de convección y difusión de la vorticidad dentro de la capa límite. El valor de máxima vorticidad en la pared está ubicado en la posición x = 0,26.

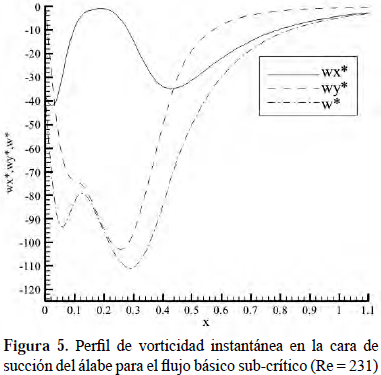
La Figura 5 muestra el perfil de vorticidad y cada una de sus componentes en la cara de succion del alabe. El perfil de vorticidad presenta dos picos (negativos), producto de la superposicion de sus componentes, “-∂u/∂y = w_x” y “∂v/∂x = w_y”.

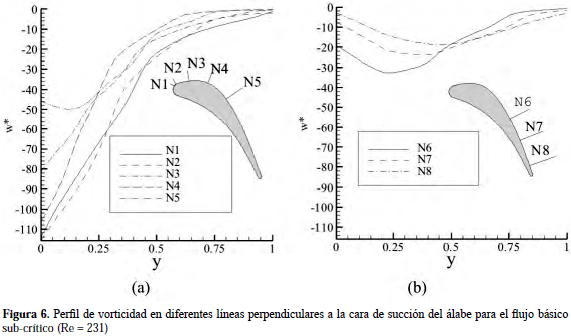
Cualitativamente, se observa que la vorticidad debe su comportamiento esencialmente a la variación del término “w_x” y no a la variación de la “w_y”. Esto se debe al hecho de que el flujo, una vez dentro del canal inter-álabes, está sometido a un cambio de área transversal que lo obliga a aumentar su velocidad localmente y de hecho existe una disminución de la presión. Sin embargo, como esta restricción no es constante en la dirección del flujo, debido a que está delimitada por una combinación de superficies curvas, la aceleración que se produce no es uniforme, y el vector velocidad cambia de dirección, ocasionado una variación en la magnitud de cada una de sus componentes, pero manteniendo su movimiento predominantemente cuasi-paralelo a la superficie del álabe, generando un cambio como el observado.

La Figura 6 muestra el comportamiento de la vorticidad para distintas posiciones sobre la superficie del álabe en dirección transversal al flujo “y”. Allí se observa un cambio de concavidad de los perfiles obtenidos para las posiciones N1 a N5 y N6 a N8. En las primeras posiciones (N1 a N5) la vorticidad máxima se ubica sobre la pared y disminuye siguiendo un comportamiento cóncavo hacia abajo hasta un valor cero a medida de que se aleja hacia el borde exterior de la capa límite, mientras que para las posiciones N6 a N8, la vorticidad comienza en un valor cercano a cero, pero sin llegar a él, presentando una tendencia decreciente-creciente, debido al enfrentamiento de los fenómenos de difusión y convección en la capa límite, en unión con la presencia de un gradiente de presión adverso al flujo como se pudo observar en la Figura 4, que no es lo suficientemente fuerte como para producir la separación de la capa límite y, por lo tanto, generar una recirculación sobre el álabe (que se transformaría en la presencia de una vorticidad positiva).

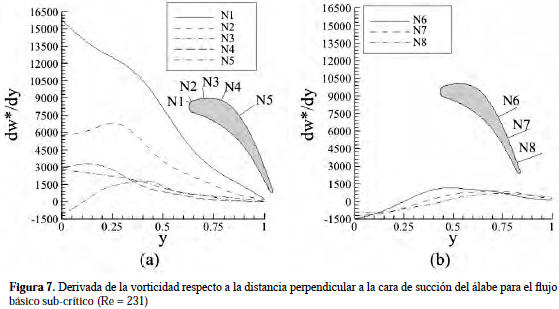
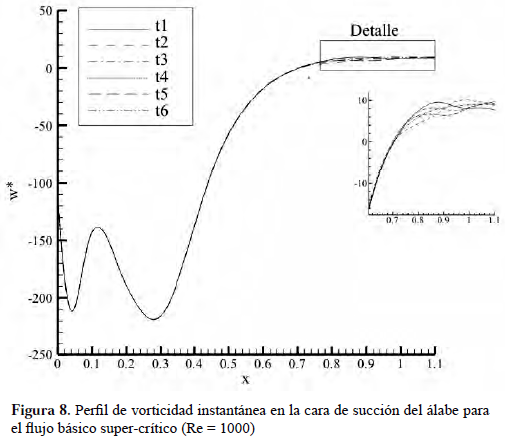
La Figura 7 muestra la derivada de la vorticidad para la dirección perpendicular a la superficie de succión del álabe. Allí se observa como, para todas las posiciones mostradas, la derivada de la vorticidad en dirección perpendicular a la superficie de la pared tiende a valores nulos fuera de la capa límite, en concordancia con el enunciado de la ecuación de conservación de masa en su forma integral, es decir, ∂w/∂y≈∂/∂x, esto sobre el borde de la capa límite, mientras que dentro de la misma sucede el fenómeno difusivo de la vorticidad hacia el flujo medio. Por otro lado, se manifiesta el hecho de que el fenómeno de difusión disminuye en la direcció del flujo.

Se determinó en la geometría estudiada que el fenómeno de transición natural, caracterizado por la presencia de ondas Tollmien-Schlichting (T-S) se inicia para Re = 400 (Rojas-Solórzano, 1997), coincidiendo con el fenómeno de separación de la capa límite, creando una zona de recirculación en las cercanías de la pared con alta dependencia del tiempo. La Figura 8 muestra el perfil de vorticidad sobre la cara de succión del álabe para un Re > Re_cr en seis tiempos distintos. En dicha figura se observa que cualitativamente la vorticidad, para cada tiempo mostrado, tiene el mismo comportamiento obtenido en el caso subcrítico; sin embargo, a partir de x = 0.7 aproximadamente, se observa un desfase entre el perfil de vorticidad de los diferentes tiempos, detallado dentro de la misma figura, en la cual se observa la disminución en la longitud de onda de la señal, que hasta tal sección podría catalogarse como de onda larga, hasta transformarse en una señal de onda corta. Puede inferirse que este comportamiento es debido a la presencia de las ondas T-S en el sistema, que se comportan como inestabilidades transitorias previamente analizadas por Rojas-Solórzano & Amon (1995).

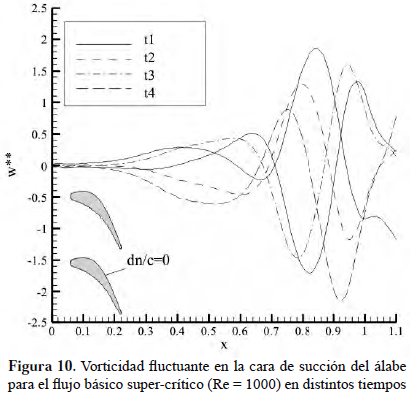
Debido a que las ondas T-S están relacionadas con las inestabilidades en el sistema, más que con el flujo medio durante el comienzo del fenómeno de la transición, se puede apreciar en la componente transitoria (instantánea) de la vorticidad, que ésta se genera de las componentes fluctuantes de las inestabilidades en el campo de velocidad y que se superpone a la vorticidad media. Las Figuras 10 y 11 muestran la vorticidad fluctuante en la cara de succión del álabe y para una línea paralela a la misma, respectivamente. En ambas figuras se observa como la señal de la vorticidad pasa de una longitud de onda larga a una longitud de onda corta en la dirección del flujo, además de aumentar su amplitud, indicando entonces que la vorticidad sí refleja la presencia de las ondas T-S y además estas señales siguen la misma tendencia que la observada para las componentes fluctuantes de la velocidad en trabajos previos (Rojas- Solórzano, 1997), donde se determinó expresamente que este paso de longitud de onda larga a longitud de onda corta que ocurre en todos los casos alrededor del punto x = 0.7, representa el inicio del fenómeno de transición. Además, se observa como las inestabilidades disminuyen su amplitud, más no la longitud de onda, a medida que se alejan de la superficie del álabe.

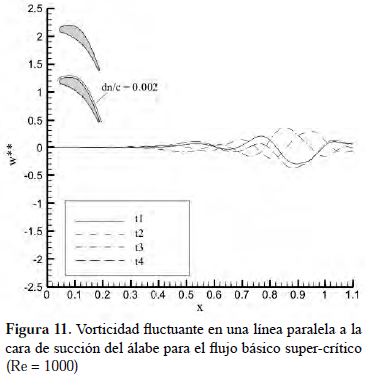
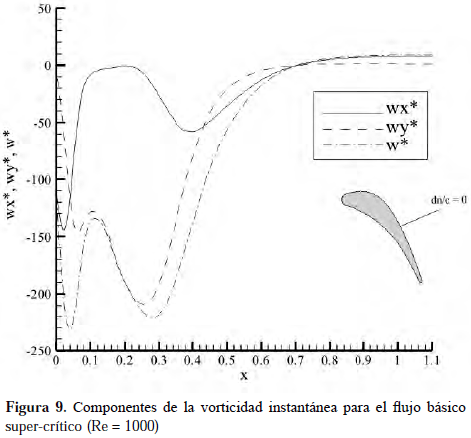
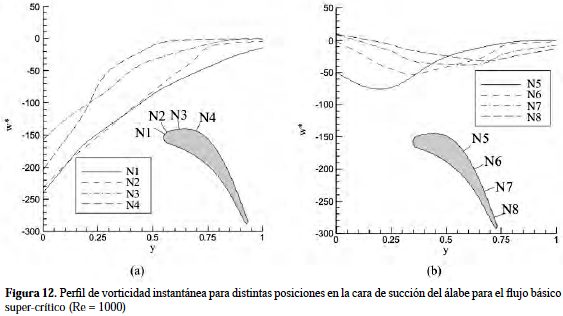
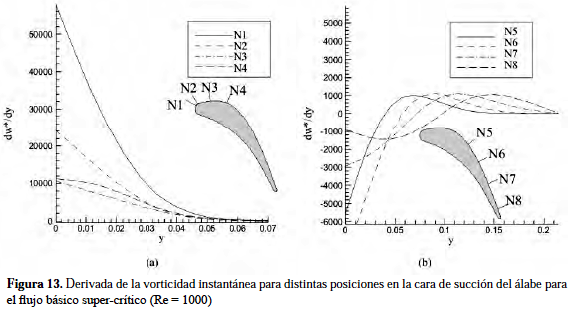
La Figura 9 muestra la descomposición de una de las señales registradas en la Figura 8, obteniéndose que la vorticidad sigue el mismo comportamiento que el caso sub-crítico; es decir, el término “∂u/∂y” es el que aporta la mayor contribución al perfil de vorticidad y no “∂v/∂x”

Al estudiar el campo de flujo en la dirección perpendicular a la superficie del álabe para el caso supercrítico, se obtiene el mismo comportamiento cualitativo encontrado en el flujo básico subcrítico, para la vorticidad y su derivada. Sin embargo, se detecta que para las posiciones N7 y N8 de la Figura 12, la vorticidad instantánea sobre la superficie es positiva, lo que indica que sí existe una separación de la capa límite y por lo tanto una zona de recirculación sobre el álabe, revelando la presencia de un gradiente de presión adverso, suficientemente fuerte para provocar la separación y generando una variación del comportamiento de la derivada de la vorticidad (ver Figura 13), que representa una disminución del fenómeno de difusión en la capa límite.

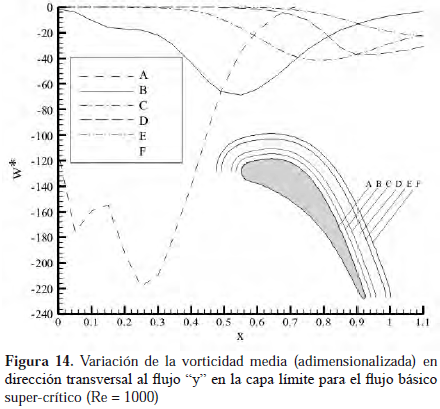
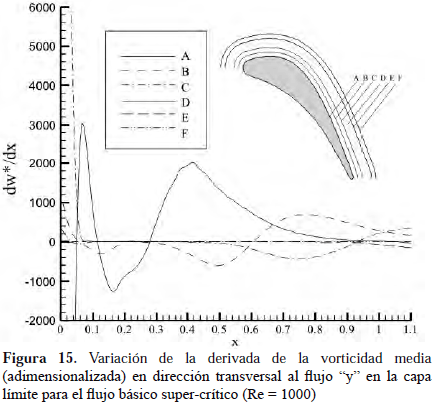
En la Figura 14 se muestra la variación a diferentes distancias equiespaciadas de la superficie del álabe, detalladas dentro de la misma figura, a lo largo de la dirección del flujo. Allí se observa que en las cercanías de la pared la convección es mucho más fuerte que en otra posición y que ésta representa aproximadamente el 50% del total del cambio de la vorticidad en dirección transversal al flujo “y”. Esto puede deberse a la combinación de varios factores: entre ellos la presencia de una aceleración local producto de la geometría y la condición de no-deslizamiento en el borde que maximiza el efecto de tendencia de giro de las partículas (vorticidad). En cuanto a la “velocidad” con la que sucede este fenómeno, en la Figura 15 se observa que a mayor distancia de la pared, el fenómeno de difusión en dirección transversal al flujo “y” disminuye, y que la convección disminuye lejos de las paredes en la dirección del flujo. Este comportamiento obedece a que la vorticidad sólo está presente en el seno de la capa límite y a medida que ésta interactúa con el medio exterior, los efectos viscosos pierden relevancia.

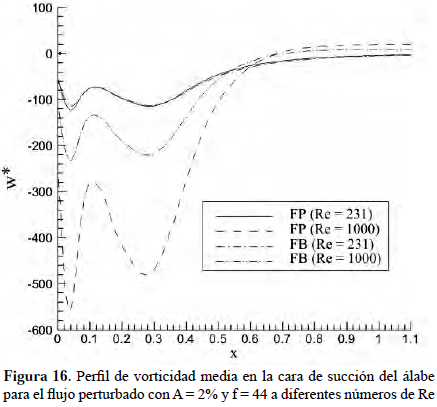
Una vez estudiado el comportamiento de la variable vorticidad en el flujo básico, se procede a imponer perturbaciones de tipo sinusoidal al sistema, que se traducen en una condición transitoria externa. La Figura 16 muestra el efecto de una perturbación de amplitud A = 2%U_∞ y una frecuencia f = 44 sobre el flujo básico para distintos números de Reynolds. Se observa que la presencia de la perturbación no altera el comportamiento cualitativo de la vorticidad media sobre la superficie del álabe para los distintos números de Reynolds, así como se distingue la proporcionalidad entre Re y los valores máximos de vorticidad alcanzados. Para el caso sub-crítico la presencia de la perturbación no produce alteraciones en el orden de magnitud de la vorticidad, mientras que para el caso supercrítico sí ocurre un incremento de aproximadamente el doble en los valores de esta variable.

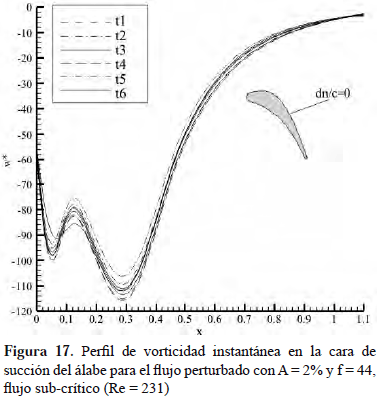
La Figura 17 muestra el perfil de vorticidad instantánea sobre el álabe para el caso perturbado de flujo sub-crítico, sometido a una perturbación de frecuencia f = 44 (f > f_n). En esta figura no se observan alteraciones apreciables del perfil de vorticidad en la dirección del flujo respecto al perfil obtenido para el caso de flujo básico. Sin embargo, estos perfiles pueden ser acotados en una banda, situación que no se presentó en el flujo básico. Ahora bien, esta situación se debe precisamente al hecho de que la perturbación se superpone al flujo en todo el dominio, incluida la capa límite, pero sin interactuar con él; es decir, utiliza el fluido sólo como medio de transporte para viajar a través de él. Entonces, se esperaría que al desaparecer la perturbación del sistema, éste vuelva a comportarse como en el caso básico.

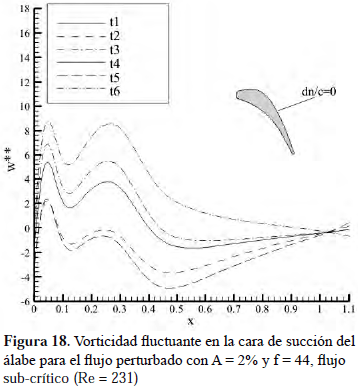
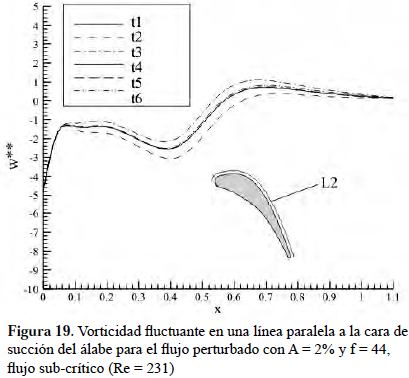
Las Figuras 18 y 19, muestran la componente fluctuante de la vorticidad para el caso perturbado sobre el álabe y una línea paralela al mismo, en la cual se manifiesta un comportamiento similar para todos los tiempos mostrados, a diferencia del caso básico sub-crítico donde esta variable es nula, debido a que el resultado obtenido es un caso estrictamente estacionario.

Si la frecuencia de la perturbación a la cual está sometido el sistema es cercana a la frecuencia natural del flujo, se encuentra un comportamiento similar al caso básico super-crítico donde se inicia la transición del flujo laminar al turbulento, sólo que esta vez artificialmente, es decir, se generan ondas tipo T-S en un medio donde naturalmente no existirían (Rojas-Solórzano, 1997).

La magnitud de la perturbación juega un papel multiplicador de la magnitud de la señal. A mayor amplitud de la perturbación se genera una mayor magnitud de la vorticidad, más no tiene un efecto tan decisivo sobre el inicio de la transición como lo tiene la frecuencia.

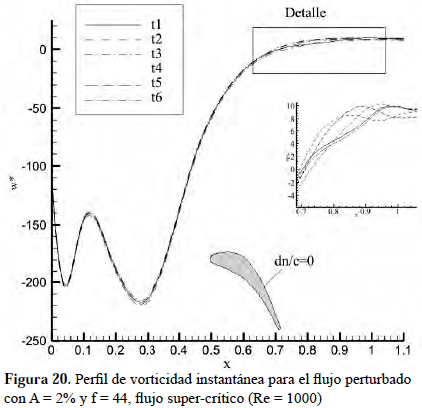
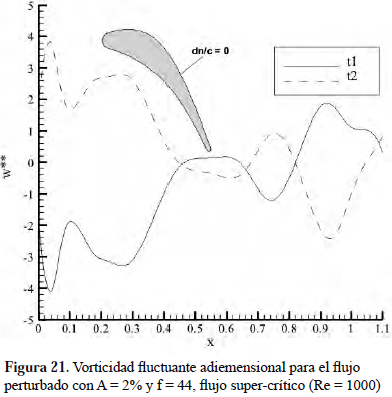
El perfil de vorticidad instantánea para el flujo perturbado con A = 2% y f = 44, flujo super-crítico (Re = 1000) en diferentes tiempos, se mantiene igual para todos los casos hasta el punto x = 0.7, a partir del cual se produce un desfase entre las señales, al mismo tiempo que se observa un cambio en la longitud de onda de las señales, que evidencia la presencia del inicio de la transcisión, como se detalla en la parte superior de la Figura 20, al igual que ocurrió en el caso de flujo básico. Esto indica que la presencia de las perturbaciones no altera esencialmente la receptividad en la capa límite. La vorticidad fluctuante sí presenta una variación importante con respecto al caso básico super-crítico, como se puede observar en la Figura 21, basada en que antes del punto de separación este valor era simplemente nulo, mientras que para el caso perturbado esta componente fluctuante es distinta de cero a lo largo de todo la capa límite, debido a la interacción de la componente temporal impuesta de la velocidad sobre el flujo medio.

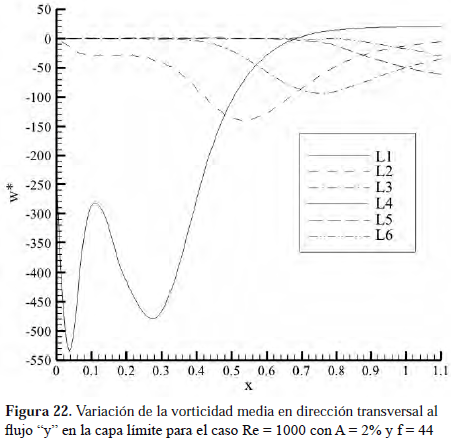
La Figura 22 muestra el comportamiento de la vorticidad media para distintas trayectorias paralelas a la superficie del álabe y distintas posiciones en la dirección del flujo, donde se observa un perfil cualitativo igual al caso básico. No obstante, existe un factor de escala de aproximadamente 2 que multiplica la magnitud del perfil, situación que se repite para las distintas perturbaciones consideradas. Por lo tanto se infiere que la presencia de la perturbación incrementa los niveles de vorticidad que se generan en la capa límite, más no interfiere en la tendencia general de esta variable.

CONCLUSIONES

El análisis de los resultados permite las siguientes conclusiones:

• El fenómeno de transición se evidencia claramente en el cambio de longitud de onda de la señal de la componente fluctuante de la vorticidad.

• El perfil de vorticidad sobre la superficie del álabe, para todos los casos: sub y super-rítico, con y sin perturbación, confirma la suposición de que el flujo en la capa límite se mantiene cuasi-paralelo a la superficie.

• El transporte de vorticidad decrece en la dirección del flujo y en la dirección transversal a éste.

• Si la frecuencia de la perturbación a un flujo subcrítico es cercana a la frecuencia natural del flujo, se puede generar artificialmente el inicio del fenómeno de transición para el caso sub-crítico.

• La magnitud de la perturbación juega un papel multiplicador de la magnitud de la señal, es decir, a mayor amplitud de la perturbación se genera una mayor magnitud de la vorticidad, más no tiene un efecto tan decisivo sobre el inicio de la transición como lo tiene la frecuencia.

• La presencia de las perturbaciones super impuestas al flujo básico incrementa los niveles de la vorticidad que se genera en la capa límite, más no interfiere en la tendencia general de esta variable.

AGRADECIMIENTOS

Al Laboratorio de Mecánica de Fluidos de la Universidad Simón Bolívar por facilitar el uso de sus espacios y recursos computacionales.

REFERENCIAS

1. Amon, C. (1993). Spectral Element-Fourier Method for Transitional Flows in Complex Geometries. AIAA 91-1608, Proc. 10th AIAA Computational Fluid Dynamics Conference; pp. 915-925, 1991. Reprinted in AIAA Journal, 1993, Vol. 31, No. 1; pp. 42-48.        [ Links ]

2. Deconcinck, H. & Hirsch, C. (1981). Finite Element Methods for Transonic Blade Calculation in Turbomachines. Journal of Engineering for Power, Vol. 103, Nº 4; pp. 665-677.        [ Links ]

3. Fasel, H. (1976). Investigation of the Stability of Boundary Layers by Finite-Difference Model of the Navier Stokes Equations. Journal of Fluid Mechanics, Vol. 78, Nº 2; pp. 355-383.        [ Links ]

4. Goldstein, M., Durbin, P., Leib, S. (1987). Roll-up of vorticity in adverse pressure gradient boundary layers. Journal of Fluid Mechanics, Vol. 183; pp. 325-342.        [ Links ]

5. Gorski, J. (1995). Vorticity Transport Analysis of Turbulent Flows. Transactions of the ASME, Vol. 117, Nº 3; pp. 410-416.        [ Links ]

6. Hickel, N. (2008). Implicit LES Applied to Zero-Pressure-Gradient and Adverse-Pressure-Gradient Boundary-Layer Turbulence. International Journal of Heat and Fluid Flow, Vol. 29, Nº 3; pp. 626-639.        [ Links ]

7. Hunt, J. (1964). Incompressible Fluid Dynamics (Mathematical Physics Series). Longmans, Green and Co., LTD, First edition, London.        [ Links ]

8. Kachanov, Y. & Kozlov, V. (1982). Origin of Turbulence in Boundary Layers. Nauka Publishing. Siberian Division, Novosibirsk.        [ Links ]

9. Korczak, K., Patera, A. (1986). An Isoparametric Spectral Element Method for Solution of the Navier-Stokes Equations in Complex Geometry. Journal of Computational Physics, Vol. 62, Nº 2; pp. 361-382.        [ Links ]

10. Monokrousos, A., Brandt, L., Schlatter, P., Henningson, D. (2008). DNS and LES of Estimation and Control of Transition in Boundary Layers Subject to Free-Stream Turbulence. International Journal of Heat and Fluid Flow, Vol. 29, Nº 3; pp. 841-855.        [ Links ]

11. Nishioka, M. & Morkovin, M. (1986). Boundary Layer Receptivity to Unsteady Pressure Gradient: Experiments and Overview. Journal of Fluid Mechanics, Vol. 171; pp. 219-261.        [ Links ]

12. O´Malley, K., Fitt, A., Jones, T. (1991). Models for High Reynolds Number Flow Down a Step. Journal of Fluid Mechanics, Vol. 222; pp. 139-155.        [ Links ]

13. Patera, A. (1984). A Spectral Element Method for Fluid Dynamics: Laminar Flow in a Channel Expansion. Journal of Computational Physics, Vol. 54, Nº 3; pp. 468-488.        [ Links ]

14. Richez, F., Glieze, M., Basdevant, C. (2008). Near Stall Simulation of the Flow Around an Airfoil Using Zonal RANS/LES Coupling Method. Computers and Fluids, Vol. 37, Nº 7; pp. 857-866.        [ Links ]

15. Robert, W. (1975). The Effect of Reynolds Number and Laminar Separation on Axial Cascade Performance. Journal of Engineering for Power, Vol. 97; pp. 261-274.        [ Links ]

16. Rojas-Solórzano, L. & Amon, C. (1995). Direct Numerical Simulations of Boundary Layer Instabilities in Subsonic Cascade Flows Triggered by Free-Stream Disturbances. Proceedings of the Third Caribbean Congress on Fluid Dynamics and the Third Latin-American Symposium on Fluid Mechanics, Caracas, Venezuela.        [ Links ]

17. Rojas-Solórzano, L. (1997). Boundary Layer Receptibity and Resonance caused by tuned Disturbances within Cascade Flows. Doctoral thesis. Carnegie Mellon University, Pittsburgh, Pennsylvania. USA.        [ Links ]

18. Schlichting, H. (1979). Boundary Layer Theory. McGraw-Hill, 7th ed., New York.        [ Links ]

19. Umit, K. & Chauvin, J. (1994). A Rapid Method for Predicting Global and Local Performance of Cascades with Special Emphasis on the Calculation of the Transition Region. International Gas Turbine and Aeroengine Congress and Exposition. The Hague, Netherlands.        [ Links ]