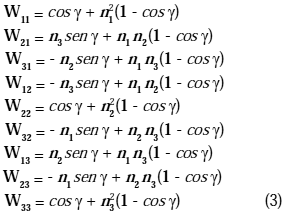Evaluación del elemento co-rotacional viga columna no lineal para el análisis de estructuras espaciales elásticas

Jorge David Cruz Moreno

Departamento de Diseño. Escuela de Ingeniería Mecánica. Facultad de Ingeniería. Universidad Central de Venezuela. Caracas. Venezuela e-mail: jorge.cruz@ucv.ve

RESUMEN

Se presentan los resultados del análisis de estructuras espaciales elásticas modeladas con elementos co-rotacionales vigacolumna. Se toma en cuenta los desplazamientos y rotaciones grandes de las juntas separándolos de las deformaciones de los miembros, en conjunción con el método de la carga incremental y el procedimiento de la matriz de orientación de las juntas. El cual permite distinguir y calcular en cada configuración deformada, la orientación espacial de juntas y miembros. Los valores reportados se comparan con los obtenidos numéricamente con otro tipo de elemento finito y experimentalmente.

Palabras clave: Estructuras espaciales, No lineal, Carga incremental, Matriz orientación, Matriz de rotación.

Co-rotational beam-column non lineal element evaluation for elastic space frames analysis

ABSTRACT

This paper shows the results of the analysis of elastic space structures modelled with co-rotational beam-column elements, that takes into account large displacements and rotations of the joints that separate them, from the deformations of the members. This work combines the incremental load method and the procedure of joint orientation matrix, which allow to distinguish and to calculate, in each deformed configuration, the spatial orientation of joints and members. The reported values obtained numerically here are compared with those calculated via other finite element type and with experimentally data.

Keywords: Space structures, Non lineal, Incremental load, Orientation matrix, Rotation matrix.

Recibido: junio de 2009 Recibido en forma final revisado: julio de 2011

INTRODUCCIÓN

En el análisis de los desplazamientos grandes, la diferencia principal entre las estructuras bidimensionales y las tridimensionales, desde el punto de vista teórico, es el hecho de que en las últimas, las rotaciones no pueden tratarse como cantidades vectoriales. Oran (1973) presenta una solución de este problema al introducir el concepto que denomina matriz de orientación de juntas para representar la orientación de cada junta en la condición deformada de la estructura tridimensional. También presenta la relación fuerza-desplazamiento y la matriz de rigidez tangencial para elementos viga-columna elásticos tridimensionales utilizando un sistema de coordenadas local co-rotacional; es decir, un sistema solidario en todo instante con la cuerda del miembro en su condición deformada.

El desarrollo de Oran (1973), aunque teóricamente consistente, supone que los incrementos de desplazamiento y rotación de las juntas son infinitesimales, lo que conduce a matrices de orientación de juntas no ortogonales. Aunque estas matrices son utilizables en conjunción con los procesos de solución incremental, en los que los cambios de configuración del sistema se deben a incrementos pequeños de las cargas, en cada uno pueden acumularse errores.

Kassimali & Abbasnia (1991) desarrollan una metodología que, basándose en la de Oran (1973), adiciona la que denominan matriz de rotación de juntas que es ortogonal y que permite obtener las matrices de orientación de juntas en la condición deformada de la estructura y es válida para rotaciones de cualquier magnitud. Con la ubicación y orientación de dos juntas adyacentes en la condición deformada de la estructura, se determina la orientación del miembro unido a ese par de juntas y sus deformaciones relativas.

Los desarrollos anteriores requieren su evaluación. El objetivo de este trabajo es presentar los resultados que se obtuvieron al analizar dos estructuras espaciales de las cuales se tienen los reportes de sus estudios hechos en forma numérica mediante otro tipo de elemento finito y en forma experimental.

LIMITACIONES

Las siguientes limitaciones se aplicaron en las estructuras evaluadas:

1. Los miembros son prismáticos

2. Los miembros inicialmente son rectos y libres de esfuerzos residuales y de imperfecciones

3. Las secciones transversales son planas y permanecen planas

4. Las deformaciones son pequeñas, pero se admiten desplazamientos y rotaciones grandes

5. Se desprecian las deformaciones por corte

6. El material permanece lineal y elástico durante toda la historia de carga de la estructura

7. Las cargas actúan en los planos de simetría de los miembros

MATRIZ DE ROTACIÓN DE JUNTAS

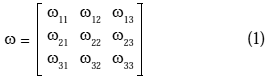
Como demuestra Oran (1973), la orientación de las juntas de un pórtico espacial en la condición deformada puede representarse por una matriz de orientación de junta, w, cuyas columnas son los cosenos directores, con respectos a un sistema de coordenadas global fijo, de tres líneas ortogonales entre sí que se suponen rígidamente unidas a la junta y se mueven con ella.

Por conveniencia, las líneas de referencia de las juntas en la configuración indeformada de la estructura, pueden suponerse paralelas al sistema de coordenadas global.

En la determinación de la respuesta de una estructura espacial en la metodología incremental, uno de los problemas es cómo obtener la referida matriz de orientación de junta para cada configuración deformada. Para este fin, considérese una junta de la estructura y asígnese a w las componentes de la matriz de orientación de dicha junta en una conocida configuración deformada. Supóngase que la junta seleccionada rota un ángulo finito g alrededor de un eje cuyos cosenos directores son n₁, n₂ y n₃. La matriz de orientación de junta v, en la configuración nueva, viene dada por:

v = Ww       (2)

Siendo W la matriz de rotación y puede demostrarse que:

Cuando g es pequeño, puede considerarse como representación vectorial y utilizarse para la rotación con componentes g, g₂ y g₃ respecto a los ejes n₁, n₂ y n₃, anteriormente indicados.

La matriz de rotación, definida en (3), puede utilizarse para interpretar los resultados obtenidos en un procedimiento de carga incremental. Supóngase que en el nivel de carga Pⁱ se conoce la configuración Xⁱ del sistema y se desea determinar la configuración Xⁱ⁺¹ correspondiente al nivel de carga Pⁱ⁺¹ = Pⁱ + DP, donde: DP representa el incremento de carga. Aun en una estructura espacial con rotaciones grandes (donde el vector desplazamiento X no está necesariamente definido), los cambios que ocurren en la configuración del sistema como resultado de DP pueden ser descritos mediante el vector DX cuyos elementos representan los incrementos de los desplazamientos y rotaciones de las juntas de la estructura con respecto a un sistema global de coordenadas.

Denominando Dg₁, Dg₂ y Dg₃ los incrementos de las componentes de la rotación para una junta de la estructura, la matriz de orientación de las juntas wⁱ⁺¹ correspondiente al nivel de carga Pⁱ⁺¹ viene dado por:

wⁱ⁺¹ = Wwⁱ      (4)

En la cual W viene dado por la ecuación (3) reemplazando a g por Dg con: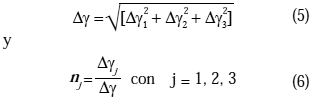

Kassimali & Abbasnia (1991) indican que aunque las rotaciones sean pequeñas, los valores de sen g y cos g no deben aproximarse a g y a 1, respectivamente en la ecuación (3), porque las columnas de W no serían vectores unitarios y tampoco serían exactamente ortogonales entre sí. En consecuencia, este valor aproximado de W conduce a resultados erróneos.

MATRIZ DE ORIENTACIÓN DEL MIEMBRO

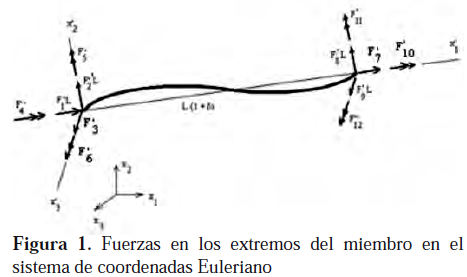
Para separar los desplazamientos de cuerpo rígido de un miembro de sus deformaciones, las cuales se suponen pequeñas, (Oran 1973; Kassimali & Abbasnia, 1991) se utiliza un sistema de coordenadas local co-rotacional, como se indica en las figuras Nº 1 y 2. El sistema de referencia es dextrógiro, en el cual el eje x’₁ une los centroides de las secciones extremas del miembro y los ejes x’₂ y x’₃ son paralelos a los ejes de inercia principales de la sección transversal. Debido a la deformación del miembro, las orientaciones de los ejes principales de las dos secciones transversales extremas varían ligeramente, por lo que las orientaciones de los ejes x’₂ y x’₃ se obtienen promediando las orientaciones de dichos ejes de las dos secciones extremas.

El sistema de coordenadas local co-rotacional del miembro se define mediante la matriz de orientación del miembro r (Kassimali & Abbasnia, 1991) cuyas columnas son los cosenos directores de los ejes x’₁, x’₂ y x’₃ del miembro respecto a los ejes globales.

Cuando se conoce la configuración deformada de dos juntas adyacentes, la orientación de los ejes del elemento asociado a esas dos juntas se determina de la siguiente forma:

La primera columna, r₁, de la matriz de orientación del miembro en la condición deformada (la cual define la dirección del eje x’₁) se calcula directamente a partir de las coordenadas actuales de las juntas.

Definiendo por p⁽¹⁾ y p⁽²⁾ las matrices de orientación de las secciones extremas del miembro, sus columnas son los cosenos directores de las líneas normal y direcciones principales de dichas secciones extremas. Cuando los extremos del miembro están rígidamente conectados a las juntas, puede escribirse

p⁽¹⁾ = w⁽¹⁾ r⁽⁰⁾ ; p⁽²⁾ = w⁽²⁾r⁽⁰⁾       (7)

en las que w⁽¹⁾ y w⁽²⁾ son las matrices de orientación de las juntas a las cuales las secciones extremas del miembro están conectadas rígidamente, y r⁽⁰⁾ es la matriz de orientación del miembro en la configuración indeformada. La segunda y la tercera columnas, r₂ y r₃ de la matriz de orientación del miembro, r, se determinan mediante la evaluación de las rotaciones q₁ y q₂ de las secciones extremas 1 y 2 del miembro, a partir de los productos vectoriales

sen q_in₁ = p₁⁽ⁱ⁾ x r₁  con i = 1, 2      (8)

En la que r₁ es el vector unitario en la dirección del eje del miembro; p₁⁽ⁱ⁾ es el vector normal unitario perpendicular a la sección i extrema del miembro; y n_l es el vector unitario perpendicular al plano que contiene a p₁ y r₁. Cada sección extrema rota el correspondiente ángulo q_i alrededor de un eje en dirección n_l. Mediante la matriz de rotación W, reemplazando a g por qi y a n₁, n₂ y n₃ por los cosenos directores de la dirección n_l, se obtiene:

e⁽ⁱ⁾ = W⁽ⁱ⁾p⁽ⁱ⁾  con i = 1, 2     (9)

En la que e⁽ⁱ⁾ representa la matriz orientación de la sección extrema i perpendicular al eje x₁ del miembro. Finalmente las orientaciones de los ejes x₂ y x₃ del miembro se definen como la segunda y tercera columnas de:

que se normaliza para obtener la nueva matriz de orientación r del miembro.

Las componentes de las rotaciones de las secciones extremas se obtienen por medio de:

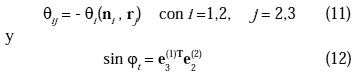
Siendo j_t el ángulo de torsión del miembro.

RELACIONES FUERZA-DEFORMACIÓN DEL MIEMBRO

Considerando un miembro arbitrario prismático de una estructura espacial, y denotando por F y F’ las fuerzas nodales del miembro en los sistemas de coordenadas globales y local co-rotacional del miembro, respectivamente, la relación entre estos dos sistemas de fuerzas nodales puede escribirse como:

F = RF’   (13)

En la cual R es transformación matricial de 12 x 12 dado por: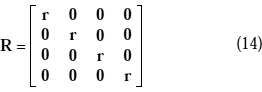

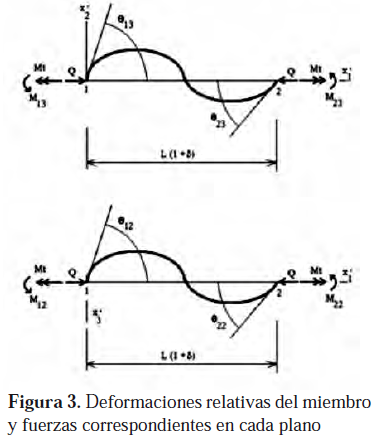
Nótese que la matriz de orientación del miembro corresponde a su configuración deformada. De manera análoga, las fuerzas nodales F’ se relacionan con las fuerzas S asociadas con las deformaciones relativas del miembro mediante (figura 3):

F’= BS (15)

y L y L(1+d) corresponden a las longitud de la cuerda del miembro en sus condiciones indeformada y deformada, respectivamente.

ESTRATEGIA NUMÉRICA

La respuesta no lineal se obtiene mediante el método de la carga incremental utilizando la técnica iterativa Newton-Raphson, realizada en cada nivel de carga hasta satisfacer las ecuaciones de equilibrio de la juntas. En el caso de los desplazamientos grandes, los pasos numéricos en cada incremento de carga pueden resumirse así:

1. Se determina la matriz de rigidez tangencial para cada elemento respecto al sistema global de coordenadas mediante la última información de geometría y fuerzas.

2. Mediante la conectividad, se ensambla la matriz de rigidez tangencial de la estructura.

3. Con el incremento de carga DP, se obtiene la solución DX del sistema de ecuaciones.

4. A continuación se establece la nueva configuración de la estructura:

a. Se determina la nueva ubicación de las juntas. Nótese que las componentes de traslación son las que indican dicha ubicación. Mientras que las componentes de rotación no tienen necesariamente significado físico y sus valores son sólo utilizados en el establecimiento del criterio de convergencia.

b. Con los valores incrementales de las rotaciones, se calculan las nuevas matrices de orientación de las juntas mediante las ecuaciones (4) – (6).

5. Se determina la nueva geometría de cada miembro. Con los datos actualizados de localización y orientación de las juntas, se obtienen las deformaciones relativas de los miembros y sus matrices de orientación. Ecuaciones (7) – (12).

6. Se calculan las fuerzas en las secciones extremas de cada miembro. Primero el vector S y luego mediante las ecuaciones (13) – (15), las fuerzas en coordenadas globales.

7. La solución obtenida representa una aproximación de la configuración verdadera, en el sentido que las ecuaciones de equilibrio de las juntas no necesariamente se satisfacen. Aquí es donde se aplica la iteración Newton-Raphson. Esto se consigue utilizando los desbalances de las juntas como cargas para reajustar la configuración de la estructura hasta la satisfacción de un criterio de convergencia previamente establecido.

En este trabajo se estableció como criterio de convergencia la norma L₂: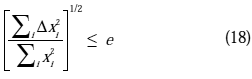

donde: e representa la tolerancia prescrita. En la aplicación de este criterio los desplazamientos y las rotaciones fueron tratados como grupos individuales y la convergencia se consideró lograda cuando se satisfacía en cada grupo de manera individual y simultánea.

SOLUCIONES NUMÉRICAS

Para estudiar problemas con la metodología planteada, al código desarrollado por Crisfield (1996) para el análisis no lineal de sólidos discretizados con elementos finitos unidimensionales de tres grados de libertad por nodo, se le incluyeron las subrutinas necesarias para obtener la matriz de rigidez del elemento co-rotacional viga-columna y su posterior ensamblaje en la matriz de rigidez de la estructura. Adicionalmente se realizaron cambios en la rutina de entrada de datos y en el cálculo de la convergencia para separar los desplazamientos de las rotaciones. Se incluyeron también las subrutinas para el cálculo iterativo de la carga axial en cada elemento como lo indican Kassimali & Abbasnia (1991).

La evaluación de la metodología expuesta se realiza mediante la aplicación de la misma a dos estructuras espaciales y comparando los resultados numéricos, con los datos de un análisis experimental realizado por terceros.

Primer caso

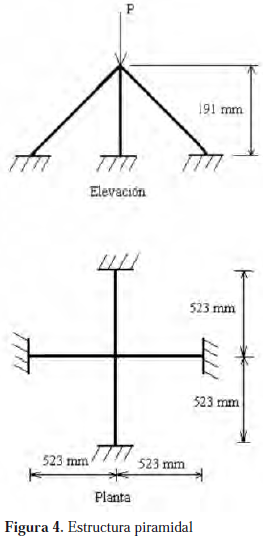
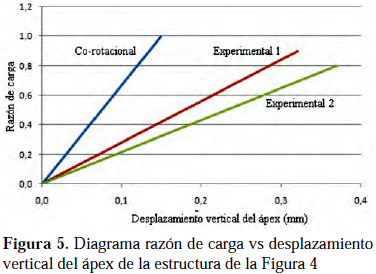
La primera de estas comparaciones con resultados experimentales se realizó utilizando la estructura piramidal mostrada en la figura Nº 4, análisis que fue realizado por See & McConnel (1986). Todos los elementos son de sección circular sólida de diámetro 4,71 mm y módulo elástico 195,4 GPa.

En la figura 5 se muestran las gráficas de razón de carga vs desplazamiento vertical del ápex. En este caso la razón de carga se define como la división de la carga aplicada en el ápex entre la carga de pandeo de la estructura. Las leyendas experimental 1 y experimental 2 se refieren a que realizaron dos estudios experimentales de la misma estructura y sus resultados fueron reportados en forma separada. Los errores relativos entre los desplazamientos experimentales y numéricos se muestran en la Tabla 1. En la técnica numérica se tomó como carga de pandeo, el primer valor que solicitaba la estructura que producía que la matriz de rigidez dejase de ser definida positiva.

Segundo caso

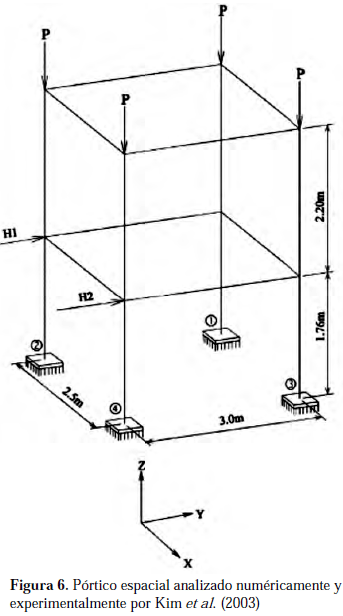
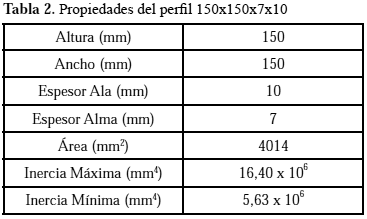
Como segundo caso de comparación se utilizó el pórtico espacial de acero mostrado en la figura Nº 6, el cual fue analizado por Kim et al. (2003) en forma numérica mediante el programa comercial ABAQUS discretizado con elementos tipo cáscara S4R y en forma experimental. La sección transversal de cada columna tiene el eje de inercia mayor paralelo al eje x. En las vigas, las secciones transversales tienen el eje de inercia mayor paralelo el eje x o el eje y dependiendo de su orientación. En el análisis numérico, Kim et al. (2003) modelaron los empotramientos con resortes, cuyas rigidices se determinaron mediante un análisis experimental previo, por la imposibilidad de construir un empotramiento perfecto. En el análisis numérico de este trabajo, se modelaron las bases de las columnas con empotramientos perfectos.

Todos los perfiles utilizados son H-150 x 150 x 7 x 10, cuyas propiedades se muestran en la tabla Nº 2.

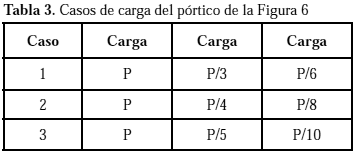
Kim et al. (2003), analizaron esta estructura para tres condiciones de carga diferentes las cuales se indican en la tabla 3.

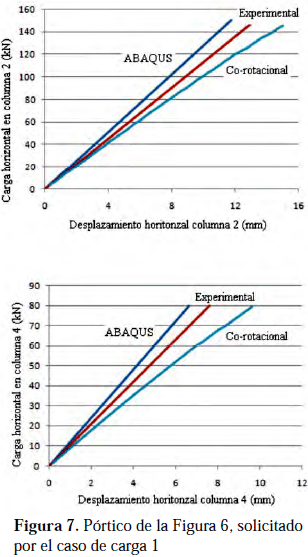
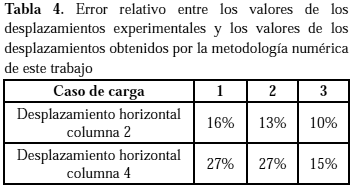
La comparación gráfica entre los resultados obtenidos, (1) mediante el programa comercial ABAQUS discretizando la estructura con elementos tipo cáscara S4R (Kim et al. 2003), (2) experimentalmente, y (3) discretizando la estructura con elementos co-rotacionales, es la que se presenta en las Figuras 7, 8 y 9, para los tres casos de carga indicados en la Tabla 3, respectivamente.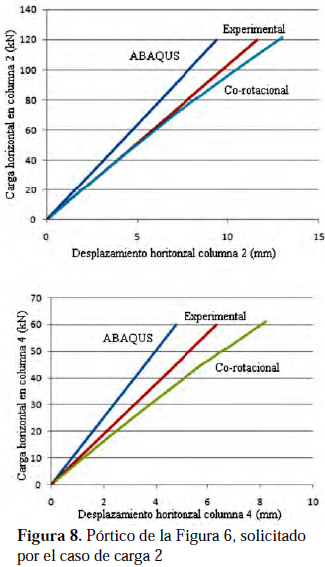

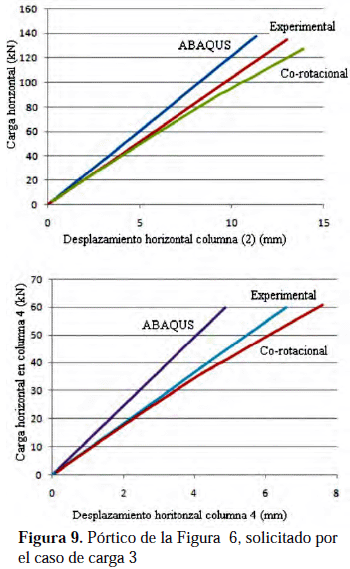
Los valores de desplazamiento reportados corresponden a las secciones transversales donde actúan las cargas horizontales y en las direcciones de dichas cargas.

La comparación cuantitativa entre los resultados de la solución experimental y la discretización con elementos co-rotacionales se presenta en la tabla 4.

ANÁLISIS DE RESULTADOS

See & McConnel (1986) no reportan el valor de la carga crítica encontrada en sus cálculos, pero en su trabajo también analizan la estructura en forma numérica y la gráfica de ese resultado coincide con la de este trabajo, lo que hace suponer que obtuvieron un valor similar al de este trabajo que es de 430 kN.

Tampoco indican el criterio utilizado experimentalmente para considerar que la estructura había alcanzado la carga de pandeo. A pesar de ello, se consideró como estructura de comparación porque reportaban valores experimentales. Pero dichos resultados indican que el valor de carga crítica obtenida mediante la modelación con elementos corotacionales viga-columna es semejante a la obtenida en el análisis experimental.

La discrepancia está en los valores de desplazamiento. See & McConnel (1986) reportan también esta discrepancia entre un método numérico empleado por ellos, el cual reducen introduciendo en el modelo numérico que imperfecciones iniciales, pero no detallan con claridad la cuantificación de las mismas.

Esta discrepancia entre los resultados numéricos y los experimentales de los desplazamientos puede atribuirse, entre otros factores, a la vinculación.

En el método numérico se trabajó con empotramientos perfectos, mientras que en la estructura real la vinculación tiene un grado de flexibilidad no cuantificada.

La discrepancia en los resultados experimentales reportados por See & McConnel (1986) demuestra que, como cualquier data experimental, para que sea confiable es necesario realizar el suficiente número de pruebas bajo las mismas condiciones, de manera de obtener estadísticamente valores de comparación que sí puedan considerarse representativos de la realidad.

En el caso de Kim et al. (2003) la información experimental está bien detallada lo que permitió una buena evaluación del elemento co-rotacional viga-columna. La correlación reportada se considera aceptable además de conducir a valores conservadores si se utiliza la metodología para el diseño.

También el error aumenta conforme aumenta la carga, probablemente debido a que la metodología numérica no considera ni la plasticidad ni imperfecciones. Los valores máximos de cargas mostrados en las Figuras 7, 8 y 9, corresponden a la carga presente en el instante que se alcanzaban valores de efectos internos que iniciaban la cedencia en la estructura, de acuerdo al análisis numérico de este trabajo. La tabla 4 muestra los errores relativos entre los resultados numéricos mediante la metodología expuesta y los datos experimentales. Estos errores fueron calculados en el punto de máxima carga. Esto indica que a niveles de carga de diseño el error se reduce apreciablemente.

Los valores obtenidos en este trabajo se realizaron modelando cada columna y cada viga con un solo elemento co-rotacional viga-columna. También se efectuaron pruebas numéricas modelando cada viga y cada columna con dos elementos viga-columna, pero sus resultados no se reportan puesto que coincidieron con los obtenidos cuando se modelaron con un solo elemento. Esto permite decir que el costo computacional es bajo comparado al modelado de la misma estructura con elementos tipo cáscara.

CONCLUSIONES

Se logró la codificación de las ecuaciones que permiten la obtención de la orientación de las juntas y de los miembros en estructuras espaciales en las cuales las rotaciones, al no ser vectores, son de difícil tratamiento.

Se demostró que las metodologías de la matriz de orientación de juntas y de la matriz de orientación de miembros, en conjunción con el elemento co-rotacional viga-columna, la carga incremental y la solución Newton-Raphson dieron una adecuada correlación con los valores experimentales de las estructuras comparadas.

El tiempo de cálculo es considerablemente menor cuando una estructura espacial se discretiza con elementos vigacolumna en comparación a cuando se modelan con elementos tetraédricos, hexaédricos o cáscara, motivado al menor número de grados de libertad involucrados, lo que conlleva a un sistema con menos ecuaciones simultáneas. Adicionalmente hay que considerar el menor trabajo requerido en la generación de la malla.

REFERENCIAS

1. Crisfield, M. A. (1996). Non linear finite element analysis of solids and structures. Vol 2. Advance. John Wiley and Sons Ltd. England.        [ Links ]

2. Kassimali, A. & Abbasnia, R. (1991). Large deformation analysis of elastic space frames. Journal of Structural Engineering. 117 (7): 2069 – 2087.        [ Links ]

3. Kim, S., Kang, K., Lee, D. (2003). Full-scale testing of space steel frame subjected to proportional loads. Engineering Structures. 25: 69-79.        [ Links ]

4. Oran, C. (1973). Tangent stiffnessin space frames. Journal Structural Division. ASCE. 99 (6): 987 – 1001.        [ Links ]

5. See, T. & McConnel, R. (1986). Large displacement elastic buckling of space structures. Journal of Structural Engineering. 112 (5): 1052 – 1067.        [ Links ]