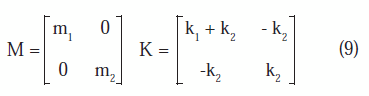Evaluación probabilística de la respuesta de sistemas lineales ante solicitaciones sísmicas

Angelo Marinilli

Universidad Central de Venezuela. Facultad de Ingeniería. Instituto de Materiales y Modelos Estructurales – IMME Caracas, Venezuela. e-mail: angelo.marinilli@ucv.ve

RESUMEN

El trabajo presenta una metodología que permite realizar análisis probabilísticos simplificados de las respuestas de sistemas estructurales discretos, de comportamiento elástico lineal, bajo la acción de movimientos sísmicos. La respuesta dinámica estructural se determina en el dominio del tiempo mediante análisis modal y el análisis probabilístico simplificado se realiza mediante el Método de los Estimadores Puntuales. La masa y la rigidez del sistema son consideradas como variables aleatorias independientes. El desarrollo de un ejemplo de aplicación permite ilustrar la implementación de la metodología propuesta. Los resultados obtenidos con el Método de Simulación de Monte Carlo permiten validar dicha metodología así como destacar sus ventajas para fines prácticos.

Palabras clave: Análisis probabilístico, Respuesta dinámica, Solicitaciones sísmicas, Estimadores puntuales, Simulación.

Stochastic analysis of linear systems under seismic actions

ABSTRACT

The paper presents a methodology to perform a simplified stochastic analysis of discrete linear structure responses under seismic actions. The structural dynamic response is determined in time domain by means of modal analysis, and the simplified stochastic analysis is performed by means of the Point Estimate Method. Structural system’s mass and stiffness are considered as independent stochastic variables. The development of an application example allows us illustrating the implementation of the proposed methodology. The results obtained with the Monte Carlo Simulation Method allow us to validate the methodology as well as to emphasize its advantages for practical purposes.

Keywords: Stochastic analysis, Dynamic response, Seismic loads, Point estimate, Simulation.

Recibido: diciembre de 2010 Recibido en forma final revisado: agosto de 2011

INTRODUCCIÓN

La ecuación (1) permite determinar la respuesta de un sistema discreto de comportamiento elástico y lineal bajo la acción de un movimiento sísmico. Dicha ecuación es conocida como la ecuación de movimiento del sistema (Chopra, 2001).

MÜ + CÚ + KU = - Mb_lü_g (1)

En dicha ecuación M, C y K representan las matrices de masa, amortiguamiento y rigidez del sistema, respectivamente. Por su parte U, Ú y Ü representan los vectores de desplazamientos o rotaciones, velocidades y aceleraciones del sistema, respectivamente. Finalmente, ü_g y b_l representan la historia de aceleraciones del terreno y el vector de influencia del movimiento sísmico. El vector b_l es un vector unitario cuando se analizan edificios de corte en el plano.

Al analizar la ecuación (1) se puede observar que la respuesta dinámica del sistema depende de las cargas que lo excitan y de sus propiedades dinámicas básicas: masa, amortiguamiento y rigidez. Adicionalmente se puede intuir que la respuesta también dependerá del modelado que se haga del sistema y del tipo de análisis que se realice para obtener dicha respuesta. En la literatura especializada se pueden encontrar técnicas que permiten considerar la incertidumbre asociada con las cargas externas sobre la respuesta dinámica de un sistema discreto de comportamiento elástico lineal, considerando dicha respuesta como un proceso estocástico estacionario o no estacionario (Clough & Penzien, 2003). También pueden encontrarse técnicas que permiten considerar la variabilidad o la incertidumbre asociadas con las propiedades dinámicas del sistema, particularmente la masa y la rigidez, sobre la respuesta dinámica del mismo (Melchers, 1999; Schuëller, 2001). En general, estas técnicas pueden resultar de difícil implementación, por lo que resulta útil desarrollar una metodología simplificada para aplicaciones prácticas, que permita realizar el análisis probabilístico de la respuesta dinámica considerando la variabilidad o la incertidumbre asociada con las propiedades dinámicas del sistema.

El objeto de este trabajo es desarrollar una metodología para realizar análisis probabilísticos simplificados de la respuesta de sistemas estructurales discretos, de comportamiento elástico lineal bajo la acción de cargas sísmicas, prestando especial atención a la incertidumbre asociada con las propiedades modales de dichos sistemas. La respuesta dinámica en el dominio del tiempo se determinará mediante análisis modal y el análisis probabilístico simplificado se realizará mediante el Método de los Estimadores Puntuales (MEP), considerando la masa y la rigidez como variables aleatorias independientes. Los resultados obtenidos con el método propuesto serán validados mediante el Método de Simulación de Monte Carlo (MSMC).

ANÁLISIS DINÁMICO

La respuesta dinámica del sistema, vale decir la solución de la ecuación (1), puede ser obtenida mediante análisis modal. Para ello se plantea el problema de autovalores y autovectores mostrado en la ecuación (2) para un sistema discreto, no amortiguado y de comportamiento elástico lineal (Chopra, 2001).

[K – λ_i M ] Ф_i = 0  (2)

La solución de la ecuación (2) permite obtener “n” autovalores (λ_i = ω_i ²) y “n” autovectores (Ф_i) del sistema, siendo “n” el número de grados de libertad dinámicos (gdld) que posea dicho sistema. Los autovectores representan las formas modales o modos de vibración del sistema y los autovalores representan el cuadrado de la frecuencia de vibración correspondiente a cada forma modal.

La ecuación (3) representa la ecuación de movimiento desacoplada de la forma modal “i”, donde: m_i* = Ф_i ^TM Ф_i es la masa modal, ξ_i es la fracción de amortiguamiento crítico y k_i* = Ф_i^T KФ_i es la rigidez modal. Por otra parte,  son las respuestas modales en términos de desplazamiento o rotación, velocidad y aceleración del modo i, respectivamente.

La ecuación (3) representa la ecuación de movimiento de un sistema de 1 gdld, cuya solución puede ser obtenida mediante la integral de Duhamel o mediante la integración numérica en el tiempo (Chopra, 2001). Esta última opción resulta particularmente adecuada para el caso sísmico donde la historia de aceleraciones del terreno (ü_g) usualmente se conoce de manera discreta. Finalmente, la respuesta total del sistema en el dominio del tiempo puede obtenerse por medio de la superposición de las respuestas modales indicada en la ecuación (4).

ANÁLISIS PROBABILÍSTICO

La probabilidad de falla de un sistema estructural se obtiene al evaluar la integral multidimensional indicada en la ecuación (5) (Melchers, 1999).

Donde: y = f(X) es la función que describe el comportamiento del sistema, definida para este caso particular de tal manera que cuando y ≤ 0 ocurre la falla del sistema, X es el vector de las variables aleatorias y f_X(X) es la función de densidad conjunta de X. La evaluación analítica de la ecuación (5) resulta irrealizable en la mayor parte de los casos prácticos, por lo que resulta más conveniente evaluar la integral multidimensional mediante métodos numéricos.

Análisis modal probabilístico La estrategia de solución de la ecuación (1) mediante análisis modal sugiere que la incertidumbre o la variabilidad presentes en las matrices de masa y rigidez del sistema estructural incidirán sobre las respuestas dinámicas que sean obtenidas. Debido a esto es necesario considerar el uso de metodologías probabilísticas para cuantificar la incertidumbre asociada con dichas respuestas. En este trabajo se considera con especial interés el efecto de la variabilidad o la incertidumbre asociada con la masa y la rigidez del sistema estructural sobre su respuesta dinámica bajo la acción de solicitaciones sísmicas. Como antecedente inmediato a este trabajo, Marinilli & Fuentes (2010) realizaron un análisis de sensibilidad para evaluar el efecto de la variabilidad de la masa y la rigidez de sistemas de uno y varios grados de libertad dinámicos sobre sus propiedades dinámicas (períodos y formas modales). Los autores utilizaron el Método de Simulación de Montecarlo, el Método de los Estimadores Puntuales y la Expansión de las Series de Taylor.

En la literatura técnica pueden ser encontradas diversas referencias sobre esta línea de investigación, entre las cuales se pueden citar las siguientes. Schuëller (2001) al revisar los más recientes avances en análisis estructural y mecánica estructural desde el enfoque estocástico indicó que existen diversas técnicas para resolver el problema de autovalores y autovectores para sistemas discretos de comportamiento lineal. En este sentido el autor indica que las estrategias basadas en el Método de Simulación de Monte Carlo son particularmente útiles para sistemas relativamente pequeños y cuando se dispone de computadores suficientemente rápidos; adicionalmente indica que las estrategias basadas en el Método de Simulación de Monte Carlo pueden también ser útiles para analizar el comportamiento de sistemas no lineales bajo la acción de excitaciones estocásticas no estacionarias. Adhiakri & Friswell (2004) proponen un método basado en la aproximación asintótica de las integrales multidimensionales para obtener los momentos estadísticos y las distribuciones probabilísticas de los autovalores de sistemas estructurales de comportamiento lineal. Los autores comparan los resultados obtenidos para un sistema de tres grados de libertad dinámicos (3 gdld) con aquellos obtenidos mediante el Método de Simulación de Monte Carlo, observando un buen ajuste de los mismos y validando de esta manera el método propuesto. Guerra et al. (2006) realizaron un estudio de confiabilidad de una estructura aporticada de concreto reforzado de dos pisos, sometida a la acción de un grupo de historias de aceleración del terreno. Los autores calcularon los desplazamientos de la estructura mediante el Método de los Elementos Finitos usando análisis dinámico lineal y determinaron la probabilidad de falla por el método de primer orden (FORM), observando que los elementos estructurales ubicados en niveles inferiores presentaron mayor probabilidad de falla.

En general, estas técnicas pueden resultar de difícil implementación por lo que es conveniente desarrollar una metodología para aplicaciones prácticas, la cual permita realizar análisis probabilísticos simplificados de la respuesta dinámica considerando la variabilidad o la incertidumbre asociada con las propiedades dinámicas del sistema. La metodología que se propone en este trabajo está basada en el Método de los Estimadores Puntuales, considerando la masa y la rigidez del sistema como variables aleatorias independientes. A continuación se presentan los fundamentos básicos del Método de los Estimadores Puntuales (MEP). También se presenta brevemente el Método de Simulación de Montecarlo (MSMC) el cual será empleado para validar la metodología propuesta.

Posteriormente se desarrollará un ejemplo de aplicación que permite ilustrar la implementación de la metodología así como las ventajas y desventajas que presenta.

Método de los Estimadores Puntuales (MEP)

El MEP fue originalmente propuesto por Rosenblueth (1975). Este método considera básicamente que una función de una variable aleatoria (y = f(x)) puede ser concentrada en los dos puntos indicados en la ecuación (6).

y₊ = f (x+) = f (m_x + sx)  (6)

y_- = f (x-) = f (m_x - sx)

Donde: m_x y s_x son la media y la desviación estándar de la variable x, respectivamente. La media y la varianza de la función y = f(x) pueden ser estimadas por medio de las ecuaciones (7) y (8).

m_y = y₊ P₊ + y_- P_-   (7)

s_y² = ( y₊ - m_y)² P₊ + (y_- - m_y)² P_-  (8)

En las ecuaciones (7) y (8) P₊ = P_- = ½ si la distribución probabilística de la variable x es simétrica. Estos conceptos pueden ser extendidos para funciones de “m” variables aleatorias, en cuyo caso el número de términos será 2^m y la probabilidad asociada con cada uno de ellos será P = 1/2^m suponiendo que las “m” variables aleatorias son independientes y que sus distribuciones probabilísticas son simétricas. Esta metodología puede también ser aplicada para variables aleatorias con distribuciones asimétricas y/o correlacionadas entre sí (Rosenblueth, 1975). El MEP tiene una importante ventaja sobre el MSMC puesto que requiere, por lo general, un número sustancialmente menor de evaluaciones numéricas de la respuesta del sistema; sin embargo, tiene como desventaja la necesidad de conocer previamente la distribución probabilística de dicha respuesta para evaluar la probabilidad de falla.

El MEP ha sido utilizado para analizar diversos problemas relacionados con la ingeniería civil (Melchers, 1999). Así, por ejemplo, Nguyen & Chowdhury (1985) desarrollaron una metodología basada en el MEP para evaluar el descenso del nivel freático causado por excavaciones y compararon los resultados obtenidos con aquellos obtenidos con el MSMC para variables aleatorias correlacionadas. Calabresi et al. (1988) usaron el MEP para evaluar los asentamientos de diques experimentales y compararon los resultados con los obtenidos con el Método de los Elementos Finitos. Li (1992) recomendó el uso de los estimadores puntuales para obtener los momentos estadísticos de funciones que no pueden ser expresadas matemáticamente, tales como los resultados obtenidos mediante el Método de los Elementos Finitos o el Método de las Diferencias Finitas. Finalmente, Marinilli (2009) propuso una metodología basada en el MEP para evaluar la respuesta sismorresistente de pórticos de concreto reforzado, prestando especial atención al comportamiento no lineal de los mismos y validando los resultados obtenidos con el MSMC.

Método de Simulación de Monte Carlo (MSMC)

El MSMC es un método numérico utilizado para resolver problemas mediante la simulación de variables aleatorias. Debido a que su implementación es relativamente simple, el MSMC ha sido utilizado ampliamente para abordar problemas relacionados con la ingeniería civil (Bejamin & Cornell, 1981; Ang & Tang, 1984). Más recientemente el MSMC ha sido utilizado para analizar la respuesta de estructuras de comportamiento elástico lineal o de comportamiento plástico bajo la acción de solicitaciones sísmicas; así por ejemplo Esteva et al. (2002) evaluaron los valores medios y las desviaciones estándar de diversas respuestas estructurales, Vukazich et al. (2002) calcularon la probabilidad de falla para diversas estructuras, Chen & Li (2004) estudiaron la confiabilidad del comportamiento no lineal de estructuras, Marubashi et al. (2004) estudiaron el efecto de la variabilidad de la resistencia de elementos estructurales sobre el comportamiento sismorresistente de estructuras, Biondini & Toniolo (2004) validaron criterios de diseño sismorresistente de estructuras aporticadas con los resultados obtenidos de ensayos seudoestáticos efectuados sobre estructuras a escala natural, Choi et al. (2007) indicaron que una ventaja básica de los métodos de muestreo es el uso directo de simulaciones numéricas para obtener las soluciones, o bien información probabilística, cuando las ecuaciones que gobiernan un problema no pueden ser resueltas fácilmente mediante procedimientos conocidos. Los autores discutieron sobre el uso, implementación y limitaciones del MSMC para la realización de análisis de confiabilidad estructural.

A continuación se presenta un esquema simplificado que permite identificar la organización general del método, suponiendo para ello la función que describe el comportamiento del sistema y = f(X) antes descrita:

i. Los valores de cada una de las variables aleatorias (X) que intervienen en el problema son generados en forma aleatoria.

ii. La respuesta del sistema (y = f(X)) es evaluada en forma determinista con los valores generados en el punto anterior.

iii. Los dos primeros pasos son repetidos hasta obtener un número estadísticamente representativo de valores de la respuesta del sistema.

iv. Se realiza un análisis estadístico para obtener los parámetros estadísticos y las distribuciones probabilísticas de la respuesta del sistema.

v. Se evalúa la probabilidad de falla (p_f) o la confiabilidad (1 - p_f) del sistema analizado.

La implementación detallada del MSMC puede encontrarse en referencias especializadas tales como Ang & Tang (1984) o Melchers (1999). Debido a que los resultados obtenidos con el MSMC se pueden contar entre las mejores aproximaciones disponibles de los “resultados reales”, esta técnica es comúnmente usada para validar las metodologías novedosas que son propuestas en la literatura técnica (Adhiakri & Friswell, 2004). Sin embargo, el MSMC tiene la desventaja de requerir usualmente un número elevado de simulaciones numéricas para obtener resultados confiables y por lo tanto puede resultar costoso desde el punto de vista computacional.

EJEMPLO DE APLICACIÓN

El desarrollo de un ejemplo de aplicación permite ilustrar la implementación de la metodología propuesta. En el ejemplo se evalúa la probabilidad de falla de una estructura cuando ésta es sometida a la acción de un movimiento sísmico. Todos los análisis que se presentan, tanto el análisis determinista como los análisis probabilísticos con MEP y MSMC, fueron realizados mediante un código computacional desarrollado por el autor en el ambiente Matlab (MathWorks 1999). El código permite obtener la respuesta de la estructura mediante análisis modal, realizando la integración en el tiempo de la respuesta para cada modo de vibración mediante el método de Newmark con aceleración lineal (Chopra, 2001).

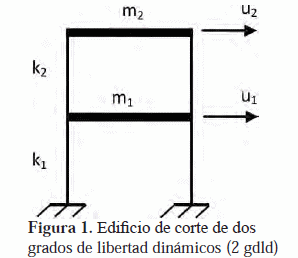
Descripción de la estructura La estructura es un pórtico de concreto reforzado, de dos pisos y discretizada como un edificio de corte de 2 gdld, tal como se ilustra en la figura 1. La altura de ambos entrepisos (h) es de 300 cm. Las matrices de masa y de rigidez de la estructura se muestran en la ecuación (9) y se supone una fracción de amortiguamiento modal ξ_i = 0,05 (Paz, 1992).

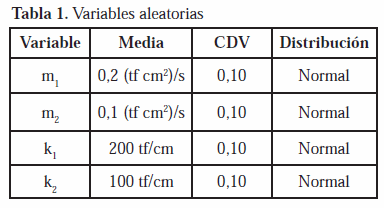
Donde m_i son las masas y k_i la rigideces laterales de cada piso tal como son identificadas en la figura 1. La tabla 1 contiene las medias y los coeficientes de variación (CDV) de las variables m₁, m₂, k₁ y k₂, consideradas para el desarrollo del ejemplo como variables aleatorias independientes con distribuciones normales.

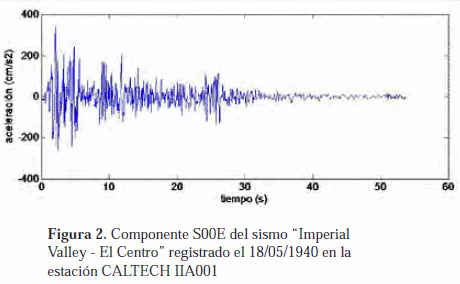
Movimiento sísmico

El movimiento sísmico considerado para el desarrollo del ejemplo se muestra en la figura 2 y corresponde a la componente S00E del sismo “Imperial Valley - El Centro”, registrado el 18/05/1940 en la estación CALTECH IIA001 y corregido por el NISEE de la Universidad de California en Berkeley, California. El registro sísmico posee una duración de 53,74s, un intervalo de digitalización de 0,02s y una aceleración máxima de 0,35g.

Análisis determinista

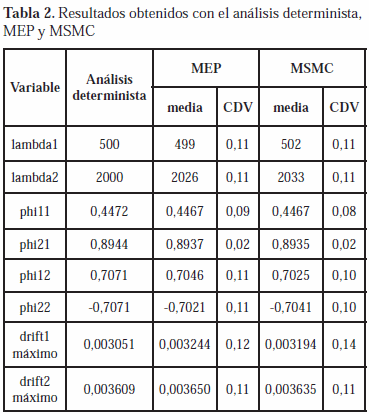
Para realizar el análisis determinista se usaron como valores de las variables m₁, m₂, k₁ y k₂ las medias aritméticas mostradas en la tabla 1. La solución del problema de autovalores y autovectores arrojó dos autovalores, identificados como lambda1 y lambda2, y dos autovectores identificados como Ф₁ y Ф₂. La ecuación (10) permite observar los elementos de las formas modales obtenidas, las cuales fueron normalizadas para que su módulo fuese la unidad. La tabla 2 contiene los autovalores y autovectores obtenidos de manera determinista.

Las respuestas estructurales consideradas fueron la distorsión del primer entrepiso (drift1) y la distorsión del segundo entrepiso (drift2). Las distorsiones de entrepiso fueron calculadas mediante la ecuación (11) donde u_i representa el desplazamiento de piso i, según se muestra en la figura 1, y h es la altura del entrepiso. El uso de la distorsión de entrepiso es conveniente puesto que es fácil de estimar y, más importante aún, se puede relacionar con diversos estados de desempeño y/o daño estructural (Ghobarah, 2004; COVENIN-1756, 2001). Las historias de las distorsiones de entrepiso obtenidas mediante el análisis determinista arrojaron los valores máximos que se muestran en la tabla 2.

drift1 u₁ ⁄ h drift2= (u₂ - u₁) ⁄ h     (11)

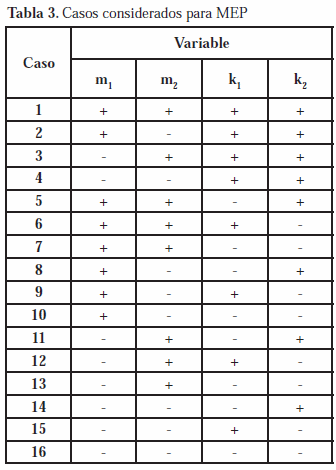
Método de los Estimadores Puntuales

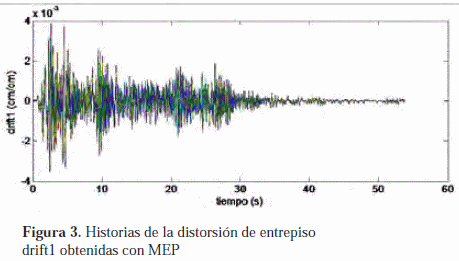
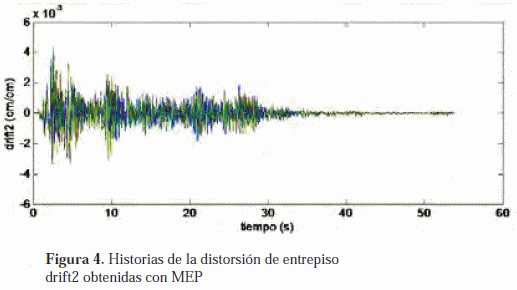
Para realizar el análisis probabilístico mediante MEP se realizó un total de dieciséis simulaciones puesto que fueron consideradas cuatro variables aleatorias (m₁, m₂, k₁ y k₂). En la tabla 3 se muestran los casos considerados, indicando para cada uno de ellos si a la media aritmética de cada variable aleatoria se le debe sumar (+) o restar (-) una desviación estándar para implementar el análisis con MEP. Los resultados obtenidos de la solución del problema de autovalores y autovectores se muestran en la tabla 2. Las figuras 3 y 4 contienen las dieciséis historias de distorsiones de entrepiso drift1 y drift2 obtenidas con MEP, respectivamente. Las medias y los CDV obtenidos para los valores máximos de distorsión de entrepiso se muestran también en la tabla 2.

Método de Simulación de Monte Carlo

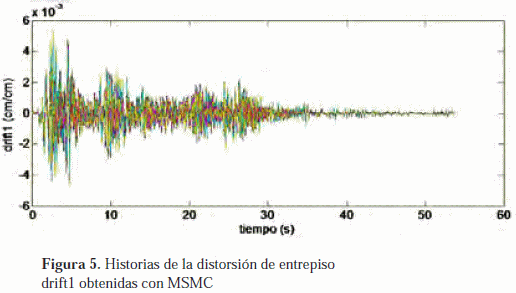
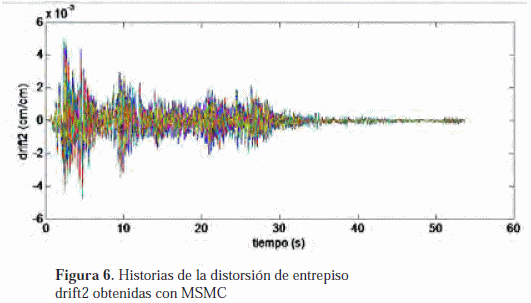
Para realizar el análisis probabilístico mediante MSMC se realizó un total de mil simulaciones con la finalidad de obtener un número estadísticamente significativo de resultados. Los resultados obtenidos de la solución del problema de autovalores y autovectores se muestran en la tabla 2. Las figuras 5 y 6 contienen las mil historias de distorsiones de entrepiso drift1 y drift2 obtenidas con MSMC, respectivamente. Las figuras 7 y 8 contienen los histogramas obtenidos para los valores máximos de las distorsiones de entrepiso drift1 y drift2, cuyas medias aritméticas y CDV son mostradas también en la tabla 2.

Probabilidad de falla

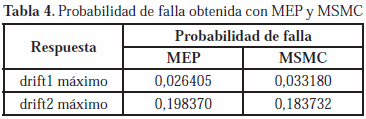
El criterio de falla establecido para fines de este ejemplo es que la estructura analizada sufra cualquier tipo de daño estructural bajo la acción de la componente S00E del sismo “Imperial Valley - El Centro” registrado el 18/05/1940. La ocurrencia de daño y el estado de daño estructural pueden ser relacionados con los niveles de deformación que ocurren en una estructura en particular; por ejemplo, Ghobarah (2004) indica que distorsiones de entrepiso del orden de 0,004 producen daño estructural ligero y reparable en pórticos dúctiles de concreto reforzado. Con base en los criterios expuestos la probabilidad de falla puede ser definida por la ecuación (12). La tabla 4 contiene las probabilidades de falla calculadas para MEP y MSMC suponiendo que las distribuciones probabilísticas de los valores máximos de drift1 y drif2 son normales.

pf = P[distorsiones de entrepiso ≥ 0,004]  (12)

Análisis de resultados

Las medias aritméticas de las distorsiones de entrepiso máximas obtenidas mediante el análisis probabilístico, tanto con MEP como con MSMC, son hasta 6,3% mayores que las distorsiones de entrepiso máximas obtenidas mediante el análisis determinista. Las distorsiones de entrepiso máximas drift1 y drift2 obtenidas mediante el análisis determinista son menores que el valor límite 0,004 establecido al definir el criterio de falla. Igual situación ocurre con las medias aritméticas obtenidas mediante el análisis probabilístico; sin embargo, al analizar las probabilidades de falla calculadas según la ecuación (12) se observa que existe una probabilidad de hasta 20% que la estructura analizada falle bajo la acción de la componente S00E del sismo “Imperial Valley - El Centro”. En contraste con esta última observación, los resultados del análisis determinista permitirían concluir que el comportamiento de la estructura sería satisfactorio.

Los resultados que se presentan en la tabla 2 permiten observar que los resultados obtenidos mediante la metodología propuesta, basada en el MEP, genera valores consistentes con aquellos obtenidos con el MSMC. Es importante resaltar que estos resultados se obtuvieron para MEP con menos del 2% del número de simulaciones realizadas con MSMC. Estos resultados permiten validar la metodología propuesta así como sus ventajas para fines prácticos.

CONCLUSIONES

Se ha propuesto una metodología basada en el Método de los Estimadores Puntuales, que puede ser usada en la práctica para realizar análisis probabilísticos simplificados de la respuesta de sistemas estructurales discretos de comportamiento elástico lineal bajo la acción de movimientos sísmicos. La metodología propuesta puede ser perfectamente adaptada para considerar variables aleatorias correlacionadas entre sí y con distribuciones probabilísticas distintas a la normal.

El desarrollo de un ejemplo de aplicación permitió ilustrar la implementación de la metodología propuesta. Los resultados obtenidos con el Método de Simulación de Monte Carlo permitieron validar dicha metodología así como destacar sus ventajas para fines prácticos.

Finalmente es interesante comentar que, a pesar de no haber sido tratado específicamente en este trabajo, la metodología propuesta puede ser empleada ventajosamente para elaborar las curvas de fragilidad requeridas para estimar el desempeño sismorresistente de estructuras, u otras edificaciones, ante diversos escenarios de amenaza en estudios de riesgo sísmico.

REFERENCIAS

1. Adhiakri, S. & Friswell, M. I. (2004). Random Eigenvalue Problems in Structural Dynamics. Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, California.        [ Links ]

2. Ang, A. & Tang, W. H. (1984). Probability Concepts in Engineering Planning and Design, Vol. II. John Wiley and Sons, New York.        [ Links ]

3. Benjamin, J. R. & Cornell, C. A. (1981). Probabilidad y Estadística en Ingeniería Civil. Nueva York, Mc Graw Hill.        [ Links ]

4. Biondini, F. & Toniolo, G. (2004). Validation of seismic design criteria for concrete frames based on Monte Carlo simulation and full-scale pseudo-dynamic tests. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B. C., paper 2581.        [ Links ]

5. Calabresi, G., Pardi, L., Rampello, S. (1988). Application of Statistics to the Geotechnical Modelling of Heterogeneous Soils. Symposium on Reliability- Based Design in Civil Engineering, Lausanne.        [ Links ]

6. Chen, J & Li, J. (2004). Seismic reliability assessment of nonlinear stochastic structures. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B. C., paper 3015.        [ Links ]

7. Choi, S-K., Grandhi, R. V., Canfield, R. A. (2007). Reliability-based Structural Design. London, Springer-Verlag.        [ Links ]

8. Chopra, A. K. (2001). Dynamics of Structures: theory and applications to earthquake engineering. New Jersey, Prentice Hall.        [ Links ]

9. Clough, R. W. & Penzien, J. (2003). Dynamics of Structures. Berkeley, Computers & Structures Inc.        [ Links ]

10. COVENIN-1756 (2001). Norma COVENIN 1756-2001. Edificaciones Sismorresistentes. Fondonorma, Caracas.

11. Esteva, L., Alamilla, J., Díaz-López, O. (2002). Failure Models, Significant Variables and Reference Systems in Reliability Based Seismic Design of Multistory Buildings. Proceedings of the Seventh U.S. National Conference on Earthquake Engineering, Boston, paper 158.        [ Links ]

12. Ghobarah, A. (2004). On drift limits associated with different damage levels. Proceedings of the International Workshop on Performed-Based Seismic Design, Bled, Slovenia.        [ Links ]

13. Guerra, A.C., Sánchez, M., Reyes, J.C. (2006). Análisis probabilístico del comportamiento dinámico de estructuras. Memo de Investigación ICYA 2006-35. Bogotá, Universidad de Los Andes.        [ Links ]

14. Li, K.S. (1992). Point-Estimate Method for Calculating Statistical Moments. J. of Eng. Mech., 118(7); 1506-1511.        [ Links ]

15. Marinilli, A. & Fuentes, T. (2010). Evaluación probabilística de la respuesta dinámica de sistemas de comportamiento elástico-lineal. Modelos Computacionales en Ingeniería. Desarrollos Novedosos y Aplicaciones. Sociedad Venezolana de Métodos Numéricos en Ingeniería, Caracas.         [ Links ]

16. Marinilli, A. (2009). Análisis probabilístico simplificado de pórticos de concreto reforzado ante acciones sísmicas. Boletín Técnico IMME. Vol. 47, No. 2, 27- 36.        [ Links ]

17. Marubashi, N., Umemura, H., Ichinose, T. (2004). Effects of strength variation on seismic response of structures. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B. C., paper 2253.        [ Links ]

18. Mathworks (1999). Matlab Version 5.3.0.10183(R11). The MathWorks Inc.        [ Links ]

19. Melchers, R. E. (1999). Structural Reliability Analysis and Prediction. Chichester, John Wiley & Sons.        [ Links ]

20. Nguyen, V. U. & Chowdhury, R. N. (1985). Simulation for risk analysis with correlated variables. Géotechnique, 35(1); 47-58.        [ Links ]

21. Paz, M. (1992). Dinámica Estructural. Teoría y Cálculo. Barcelona, Editorial Reverté S.A.        [ Links ]

22. Rosenblueth, E. (1975). Second-order probabilities approximations. Proc. Nat. Acad. Sci. USA, 72(10);3812-3814.        [ Links ]

23. Schuëller, G. I. (2001). Computational stochastic mechanics–recent advances. Computers and Structures, 79, 2225-2234.        [ Links ]

24. Vukazich, S., Marek, P., Fischer, O. (2002). Uncertainty Assessment by means of Simulation. Proceedings of the Seventh U.S. National Conference on Earthquake Engineering, Boston, paper 431.        [ Links ]