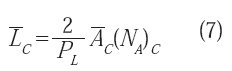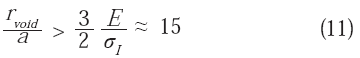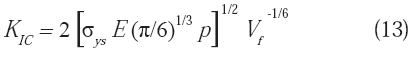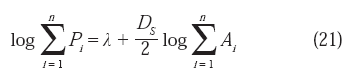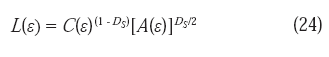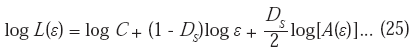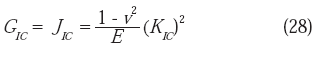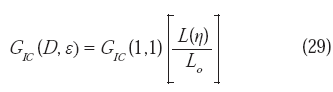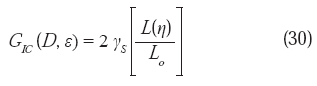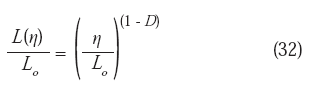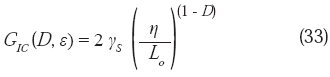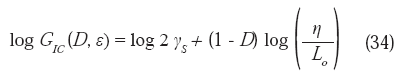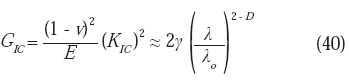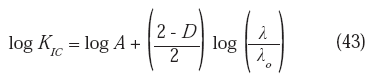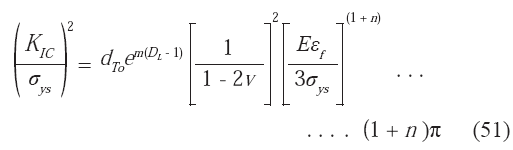Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Facultad de Ingeniería Universidad Central de Venezuela
Print version ISSN 0798-4065
Rev. Fac. Ing. UCV vol.26 no.4 Caracas Dec. 2011
Mecánica de fractura fractal: efectos a micro y nanoescala parte I: Tenacidad y mecanismos de fractura a microescala
Oswaldo Hilders
Centro de Investigación y Desarrollo de Aceros Inoxidables de la UCV (CINDACI). Escuela de Ingeniería Metalúrgica y Ciencia de los Materiales, Facultad de Ingeniería, Universidad Central de Venezuela. Apartado 47514, Caracas, 1041-A. Venezuela. e-mail: ohilders@hotmail.com
RESUMEN
Se analiza la naturaleza fractal de las superficies de fractura en aleaciones metálicas en general, combinando algunos resultados anteriores con los obtenidos en el presente trabajo para siete aleaciones de aluminio: cuatro de la serie 7000, dos de la serie 2000 y la aleación Al-0,57Si-2,03Ge; además de tres tipos de acero inoxidable, dos austenoferríticos: el
dúplex SAF 2205 y el superdúplex SAF 2507, así como el acero austenítico AISI 304. La relación entre los mecanismos de fractura, la dimensión fractal y las propiedades mecánicas, especialmente la tenacidad, se estudia en términos de algunos de los modelos empíricos y teóricos actuales; al igual que los métodos más utilizados para la caracterización fractal de superficies de fractura. Se discute el resultado general al observar que un incremento en la tenacidad se relaciona con una superficie de fractura más irregular y, por lo tanto, con un aumento de la dimensión fractal. Los valores experimentales de la dimensión fractal dependen del método empleado en su determinación, pero mantienen la misma tendencia general.Palabras clave: Dimensión fractal, Mecánica de fractura, Tenacidad, Tenacidad de fractura, Fractografía.
Fractal fracture mechanics micro and nanoscale effects part I: Toughness and microscale mechanisms of fracture
ABSTRACT
The fractal nature of fracture surfaces in metallic alloys is discussed on the basis of the present investigation and some previous results for seven aluminum alloys and three stainless steels. Four aluminum alloys were of the 7000-series; two of the 2000-series and the Al-0,57Si-2,03Ge alloy. Two stainless steels were austenoferritic: the duplex SAF 2205 and the superduplex SAF 2507. The other stainless steel was the austenitic 304 type. The relation between the fracture mechanisms, fractal dimension and mechanical properties, particularly toughness; is explained from some of the current empirical and theoretical models, whereas the main methods for fractal characterization of metallic fracture surfaces were reviewed. The results related with the observed changes in toughness, roughness and fractal dimension are discussed and it is shown that the higher the toughness the rougher the fracture surface, which is related with an increase in fractal dimension. Fractal dimension values depend on the method of experimental measurement, but show the same general trend.
Keywords: Fractal Dimension, Fracture Mechanics, Toughness, Fracture Toughness, Fractography.
Recibido: diciembre de 2010 Recibido en forma final revisado: junio de 2011
INTRODUCCIÓN
Los resultados obtenidos hasta el presente en el área de la caracterización fractal de aleaciones metálicas, son de una inmensa utilidad. Sin embargo, aún cuando la geometría fractal ha sido usada con una frecuencia cada vez mayor, mediante determinadas relaciones que involucran a ciertas propiedades mecánicas comunes (Afrin et al. 2008; Tanaka et al. 2006), varias dudas persisten en cuanto a la relación
básica entre la tenacidad, en general, y la dimensión fractal. Este tipo de relación reviste una gran importancia tecnolólógica, particularmente para las aleaciones metálicas, las cuales continúan predominando en muchas áreas, tales como en las industrias química, del petróleo, aeronáutica, nuclear y otras (Dabydeen, 2004).La tenacidad es una propiedad que resume la capacidad global de una aleación para su buen desempeño en servicio, porque combina las características asociadas con la ductilidad y con la resistencia; o, en otras palabras, está relacionada con la habilidad que posee un material para almacenar energía. En la práctica de la ingeniería, la idea que se asocia con esta habilidad para el almacenamiento de energía, ha sido expresada comúnmente de múltiples formas, aunque para la mayoría de las aplicaciones se utilizan principalmente alguna de las siguientes:
(a) (Fuerza/Área)(Longitud/Longitud), lo cual equivale a Energía/(Longitud)3, cuando la tenacidad es evaluada a través de la integración de la curva σ vs ε en un ensayo de tracción monótono:
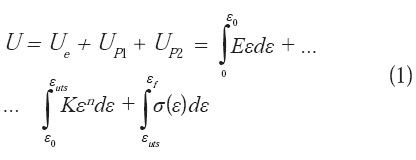
donde:
U es la energía total por unidad de volumen almacenada por el material o tenacidad; Ue es la energía elástica por unidad de volumen almacenada desde el comienzo del proceso de deformación hasta la deformación ε0 relacionada con el esfuerzo de fluencia; UP1 es la energía plástica por unidad de volumen almacenada durante el proceso de deformación entre ε0 y la deformación εuts, necesaria para alcanzar el esfuerzo real uniforme máximo; UP2 la energía plástica por unidad de volumen que se almacena durante el proceso de deformación entre εuts y la deformación real de fractura εf; E es el módulo de Young; ε es la deformación real; K es el llamado coeficiente de resistencia; n el coeficiente de endurecimiento por deformación, y σ(ε) es una función, generalmente no especificada, que relaciona al esfuerzo y la deformación reales, durante la etapa de deformación final comprendida entre εuts y la deformación real de fractura (Hosford, 2009).
(b) (FuerzaLongitud)/Área = Energía/(Longitud)2; es decir, cuando la tenacidad se evalúa a través del ensayo de impacto, por lo que la misma es denominada comúnmente tenacidad de impacto. Para este caso, debe cumplirse:
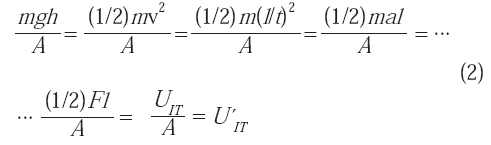
donde:
m es la masa del péndulo que administra el impacto a la muestra del material; g es la constante de aceleración de
la gravedad; h es la altura medida desde el punto donde el péndulo comienza a caer hasta el nivel donde se encuentra la muestra (es decir; mgh es la energía potencial disponible al inicio de la caída del péndulo); A es el área de sección de la muestra; v es la velocidad del péndulo (siendo mv2/2, la energía cinética correspondiente, la cual adquiere su valor máximo al momento del impacto con la muestra); l y t son correspondientemente, la longitud y el tiempo relacionados con el valor de v; a = l / t 2 es la aceleración; F es la fuerza respectiva, la cual alcanza de igual forma su mayor valor al entrar en contacto con la muestra; UI T = (1/2) Fl representa la energía total con la que se realiza el impacto (es decir, la energía potencial inicial, transformada en energía cinética al momento del impacto); y; finalmente, UI T representa la energía de impacto total, disponible por unidad de área.Sólo una fracción de
UI T conocida como tenacidad de impacto = U < UI T, genera cambios en el material. A su vez la mayor parte de U´ es utilizada en la formación de la superficie de fractura, mientras que la diferencia que resta es absorbida en un volumen limitado de la muestra que se sitúa en la zona adyacente a dicha superficie. Luego la tenacidad de impacto U queda, por lo tanto, definida en unidades de Energía/Área.(c) (Fuerza/Área)(Longitud)
1/2, lo cual resulta equivalente a: Fuerza/(Longitud)3/2 = Energía/(Longitud)2,5, cuando la tenacidad es medida mediante el denominado factor de intensidad de tensiones, llamado como veremos luego, bajo determinadas condiciones, tenacidad de fractura. En este caso: 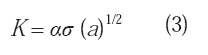
donde:
K es el factor de intensidad de tensiones; α es un parámetro adimensional que depende de la geometría de la muestra y de la forma en que ocurre la separación; σ es el esfuerzo aplicado y a es la longitud de una grieta que se puede extender hasta producir la fractura. Si la grieta se hace inestable y se extiende de acuerdo al modo I de ruptura o separación (tensión), se tiene:
![]()
donde:
K
C es el factor crítico de intensidad de tensiones en condiciones de esfuerzo plano. Pueden existir muchos valores de KC , dependiendo de σ y a. Si el espesor de la muestra aumenta hasta generar un estado de deformación plana, KC tendrá ahora un valor que permanecerá invariable e independiente de aumentos posteriores. Es este valor particular al que se le conoce como tenacidad de fractura, o también factor crítico de intensidad de tensiones en deformación plana KIC , y que puede definirse mediante: 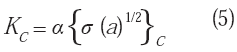
El subíndice c en el segundo miembro, representa el valor crítico del producto σ (a
)1/2. Puede demostrarse que existen muchas combinaciones de σ y a, para las cuales es posible en cada material, alcanzar un único valor de KIC (Barsom et al.1999). Por lo anterior, la tenacidad de fractura se define como: "La habilidad inherente de un material en estado de deformación plana, de resistir la propagación inestable de una grieta por tensión, siendo su valor numérico, el resultado de la combinación crítica de esfuerzo y longitud de grieta que generan ésta propagación". De acuerdo a Kobayashi (2004), esta propiedad también puede definirse como: "La resistencia que opone un material a la expansión irreversible de una grieta".Todas estas definiciones son de tipo operacional, e indican la importancia práctica de esta propiedad; lo que explica el mayor número de estudios realizados desde la perspectiva de la geometría fractal, que involucran a
KIC . Si analizamos las dimensiones de la tenacidad de fractura tenemos: 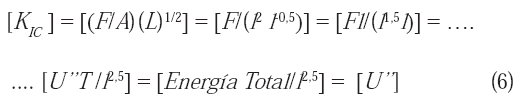
donde:
F es la fuerza o carga externa aplicada; A el área de sección transversal efectiva de la muestra utilizada; L representa la longitud de la grieta en cuestión; U"T es la energía total asociada con la expansión irreversible de la grieta, la cual no se mueve en dos dimensiones, sino de forma irregular, creando una superficie de dimensión 2,5 al salir del plano principal, y U" podría definirse como una "energía por unidad de área fractal" asociada a
KIC , debido a que la dimensión de la superficie creada por la grieta en su avance es fraccionaria, no correspondiendo a una superficie plana (dimensión 2) o al volumen (dimensión 3). En otras palabras, la superficie irregular creada por la grieta, tratará de ocupar parcialmente el volumen que la contiene. Aunque en general, los valores de U y U son de utilidad en la práctica de la ingeniería, especialmente U, sin embargo; la medida de U" (tenacidad de fractura), ha demostrado ser más importante. Las razones para ello serán evidentes al realizarse la discusión respectiva.Existen también otras medidas útiles de la tenacidad como, por ejemplo, la denominada integral J, la cual se utiliza con frecuencia (a través de su valor crítico JIC), para encontrar de forma indirecta el valor respectivo de KIC, en los casos donde éste resulta imposible de determinar de acuerdo a la norma respectiva. Aunque las unidades de la Integral J se expresan de la misma manera que la tenacidad de impacto [Energía/(Longitud)2]; sin embargo, su significado es muy diferente. Debido a que no será materia de discusión en este trabajo, su significado puede ser consultado en la literatura respectiva (Zehnder, 2008).
El objetivo del presente artículo, es el de discutir la relación que existe entre la tenacidad de los materiales metálicos, las características fractales de las superficies de fractura respectivas y sus efectos a escala micrométrica. La discusión estará basada en una serie de resultados previos en diversos tipos de acero y aleaciones de aluminio, así como en ciertos modelos propuestos en la literatura. De igual forma, se discutirán los principales métodos para la determinación de la dimensión fractal, así como la descripción de las superficies de fractura desde el punto de vista fractal.
PROCEDIMIENTO EXPERIMENTAL
Parte de los resultados presentados en este trabajo, han sido obtenidos previamente mediante la aplicación de diversas técnicas experimentales conocidas. Otros resultados de tipo complementario, se han obtenido específicamente para esta investigación, con el objeto de poder interpretar diferentes aspectos de la relación existente entre la dimensión fractal y la tenacidad. Los diferentes procedimientos experimentales relacionados con los primeros, serán mencionados y referenciados, mientras que los relacionados con los segundos serán objeto de una descripción más detallada. Entre los diferentes tipos de materiales metálicos que han sido estudiados con anterioridad y en el presente trabajo, pueden mencionarse: el acero inoxidable dúplex SAF 2205, fracturado en tensión a 25 ºC y envejecido por diferentes intervalos de tiempo a 475 ºC (Hilders et al. 2000-a; Hilders et al. 1999), el acero superdúplex SAF 2507, fracturado por impacto a 25 ºC y el acero inoxidable austenítico AISI 304, tratado a 850 ºC por 216 horas y fracturado por tensión a temperatura ambiente (Hilders et al. 1997-a; Hilders et al. 1998).
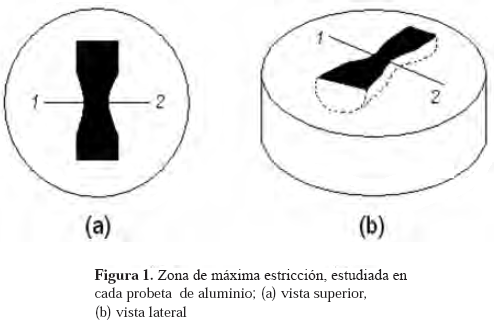
Por otra parte, 7 aleaciones de aluminio fueron estudiadas en la zona de máxima deformación por tensión a diferentes valores de alargamiento, antes de la fractura. Las distintas composiciones químicas, los tratamientos termomecánicos previos y los ensayos mecánicos, han sido descritos por Hilders (1998) y Hilders et al. (2002-a). Cuatro de las aleaciones son de la serie 7000 [7075/T651 (Zn/Mg = 2,27 y Zn/Mg = 2,82), 7050/T7451 y 7178/T651]; dos son de la serie 2000 (2024/T351 y 2090/T8) y la aleación Al-0,57Si2,03Ge. Los ensayos de tensión se realizaron a temperatura ambiente, a una velocidad de deformación de 10-3 seg -1, de manera interrumpida; es decir, deformando las probetas de las distintas aleaciones a valores progresivamente mayores sin llegar a la fractura. Para cada valor de deformación, la probeta respectiva se analizó en la zona de mayor estricción localizada, en forma tal que para cada aleación se utilizaron tantas probetas como deformaciones fueron realizadas. El estudio de la zona de mayor estricción se realizó luego de separar ésta de la probeta, mediante dos cortes transversales y un corte longitudinal, revelando así la zona que se analizó para la determinación del tamaño de las cavidades que se forman internamente y que darán origen a la superficie de fractura. Las cavidades se estudiaron por microscopía electrónica de barrido (MEB), luego de que las muestras fueran montadas en resina sintética autofraguante. En la figura 1 se observa un esquema del montaje referido, donde se ha señalado la zona de máxima estricción localizada (segmento 1-2).
La cuantificación del tamaño promedio de cavidad en las muestras de aluminio, se realizó de acuerdo a la relación para superficies metalográficas planas con elementos separados, de perímetro cerrado y con forma cóncava (con la tercera dimensión por debajo del plano metalográfico, tal como las cavidades):
donde:
L
C es el tamaño promedio de cavidad, AC el área promedio de cavidad, PL es el número de intersecciones o cortes con los perímetros o contornos de las cavidades, por unidad de longitud de las líneas de prueba (es decir, PL = P/L, siendo P el número de cortes y L la longitud total de todas las líneas de prueba trazadas en el área a analizar) y (NA)C se define como el número de cavidades por unidad de área analizada. El área promedio de cavidad y (NA)C se pueden expresar (DeHoff et al. 1968) mediante:y
donde:
(
AT) es el área total cubierta por las cavidades, (NT)C es el CC número total de cavidades y (AT)a es el área total que se está analizando. La sustitución de (8) y (9) en (7), permite obtener el tamaño promedio de cavidad, a partir de (2/PL) y la fracción de área (AT)C) ⁄(AT)a.RESULTADOS Y DISCUSIÓN
Mecanismos de fractura y dimensión fractal
En la figura 2 (Hilders et al. 2000-a), se observa una típica superficie de fractura de naturaleza dúctil, correspondiente al acero SAF 2205 ensayado en tensión a 25 ºC, luego de un tratamiento de envejecimiento a 475 ºC por 6,5 h. En la medida en que se desarrolla el proceso de deformación, las cavidades que se nuclean en la zona de máxima estricción, aumentan de tamaño progresivamente, uniéndose luego y formando una serie de paredes o ligamentos capaces de soportar el esfuerzo externo. Ahora bien, si el proceso de crecimiento de las cavidades no dependiera de su posición, entonces la dimensión fractal de la superficie asumiría un valor universal e independiente del material. En realidad, al unirse una cavidad con otras y formar pequeños ligamentos a nivel local, el aumento del esfuerzo sobre los mismos y por tanto, el desarrollo posterior de las cavidades, dependerá de su ubicación. Mandelbrot (1982), postuló este tipo de comportamiento, al describir por vez primera desde el punto de vista fractal, la fractura por impacto de un acero Maraging grado 300, encontrando una excelente correlación entre la tenacidad de impacto y la dimensión fractal.
La dimensión fractal no puede asumir un valor universal, porque, por ejemplo, en los materiales metálicos existe una distribución heterogénea de inclusiones, tanto en su tamaño como en su ubicación; lo que implica que las cavidades que se forman alrededor de aquéllas, crecerán a un ritmo que es una función de su tamaño inicial (que es el mismo tamaño de la inclusión) y de su posición. Como puede observarse en la Figura 2, existen tres tipos principales de accidentes en las superficies de fractura originadas por el mecanismo de coalescencia de cavidades: hoyuelos profundos donde estuvo alojada una inclusión (flechas verticales); hoyuelos superficiales en los que se puede observar el fondo de los mismos, y cuyo origen no necesariamente se explica por la presencia de inclusiones (flechas horizontales), y zonas donde se aprecia un proceso de deformación por desgarramiento (flechas oblicuas). Se ha comprobado que en las superficies de fractura, las características fractales son el resultado de la suma de muchos procesos básicos, de forma tal que cada tipo de característica topográfica contribuye, en el rango de escalas bajo consideración, a la relación que pueda existir entre las diferentes propiedades mecánicas de importancia y la dimensión fractal (Lung, 1998). En el caso específico de la fractura dúctil, los accidentes señalados en la figura 2, son los responsables de la gran absorción de energía que el material en cuestión mostró una vez fracturado. Cada clase o tipo de superficie de fractura (desde el punto de vista del mecanismo de separación), mostrará a su vez distintos tipos de accidentes topográficos, que constituyen una manera en la que puede inferirse la capacidad de absorción de energía por deformación. Distintos estudios han sido desarrollados en muchas clases de aleaciones metálicas, con la finalidad de establecer algunas relaciones de utilidad, entre varias de las propiedades más relevantes desde el punto de vista de la ingeniería, y la dimensión fractal: Colás (2001) en acero inoxidable AISI 316L; Afrin et al. (2008) en la aleación de magnesio AZ31B-H24; Li et al. (1995) en acero de muy bajo carbono (0,02%C en peso) y en acero 11%Cr-2%Ni (% en peso); Venkatesh et al. (2008) en una aleación Ti6Al-4V; entre otros.
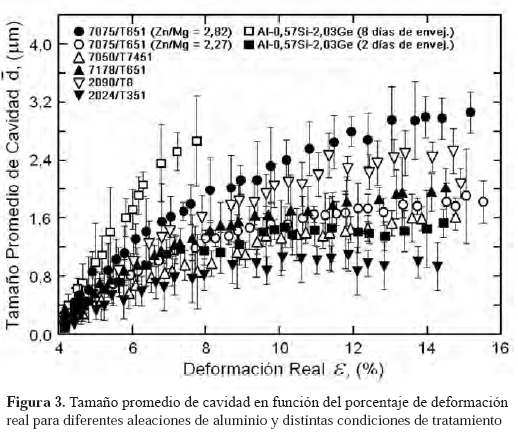
En la Figura 3 se pueden observar los diferentes resultados que corresponden a la evolución del tamaño de cavidad en la zona de máxima estricción localizada para las aleaciones de aluminio ya mencionadas, en función del porcentaje de deformación plástica.
Las muestras utilizadas se comenzaron a analizar desde un valor de deformación real de 4%, porque a valores menores no se pudo detectar la presencia de cavidades o no resultó fácil su determinación. Se observa que la tasa de variación del tamaño de cavidad con la deformación real, depende de la clase de aleación. De manera particular para la aleación 2024/T351, el tamaño promedio de cavidad aumenta a valores bajos de deformación, estabilizándose luego en unos 0,8 mm, a partir de un valor de deformación real de un 8%. Por otra parte, para la aleación 7075/T651 (Zn/Mg = 2,82), esta tasa de variación es mucho mayor, notándose que la estabilización ocurre aproximadamente a un valor de tamaño de cavidad de 3,0 mm, para una deformación real de un 13,5%. En la Figura 4 puede verse un ejemplo de las cavidades desarrolladas en esta aleación, en la zona de máxima estricción (tamaño promedio de cavidad = 2,9 μm; %ε = 12%). Aunque no resulta evidente en toda la zona
que se ha mostrado; sin embargo, el alargamiento de ciertas cavidades indica la dirección de deformación por tensión (dirección horizontal). Por el contrario, formando 90° con esta dirección pueden observarse claramente dos grietas en su etapa inicial de desarrollo. El crecimiento lateral de las cavidades en el centro de la zona de máxima estricción de la probeta correspondiente (cuello), origina este tipo de grietas y ocurre debido al campo de esfuerzos triaxiales desarrollados en esa región. La forma en que estas grietas se expanden hacia la superficie de la probeta, determinará la morfología final de la superficie de fractura; por lo tanto, las etapas de nucleación, crecimiento y coalescencia de cavidades, así como las inclusiones, impurezas, etc., a partir de las cuales aquéllas se forman, resultan de gran importancia al considerar los factores que influyen en los valores de la dimensión fractal determinados en la práctica.Broek (1973), al estudiar 13 aleaciones de aluminio con diferentes tipos y tamaños de partículas, aunque no pudo detectar la nucleación de cavidades, sin embargo encontró que las mismas crecían perpendicularmente a la dirección de aplicación del esfuerzo. Goods et al. (1979) han desarrollado un modelo, en el cual se propone que la deformación crítica para nuclear una cavidad con una partícula menor o igual a 1 μm, es:
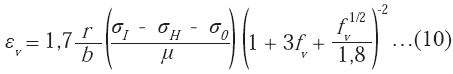
donde:
r es el radio de la partícula, b es el vector de Burgers,
σI es la resistencia interfacial, σH es la tensión hidrostática, σ0 es el esfuerzo de fluencia en tensión de un policristal, μ es el módulo de rigidez y fv la fracción volumétrica de partículas. Argon et al. (1975); por su parte, han encontrado que las cavidades se comienzan a formar cuando:donde:
rvoid es el radio de la cavidad, a es el parámetro de red y
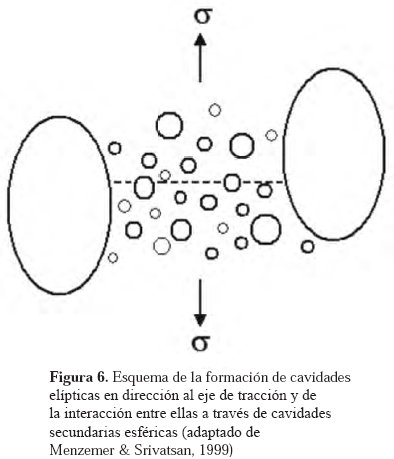
E es el módulo de Young. El criterio que expresa la relación (11) se cumple, siempre y cuando haya suficiente energía elástica almacenada como para crear la superficie libre de la cavidad. La situación que se presenta en el caso de la fractura dúctil, como puede verse, resulta bastante más compleja que en los otros mecanismos de separación; es decir, para los casos de clivaje, cuasiclivaje y separación intergranular, en los cuales la formación de la superficie de fractura respectiva, está acompañada de una tasa de liberación de energía elástica mayor, así como de una cantidad de energía almacenada por deformación plástica menor, por lo que la topografía resultante es menos tortuosa o irregular.En la Figura 5 se muestran cuatro casos particulares, para otras tantas aleaciones metálicas, que ejemplifican la naturaleza morfológica de las cavidades y su relación con el campo de esfuerzos externo, así como con la grieta principal o superficie de fractura. Para la aleación 7075/T651 (Zn/Mg = 2,82; figura 5-a), las cavidades desarrolladas en la zona de máxima estricción, están claramente orientadas en la dirección del esfuerzo axial (dirección vertical); es decir, se han alargado por efecto de la fluencia plástica en la mencionada dirección. Ya que inicialmente estas cavidades son aproximadamente esféricas, un alargamiento en la dirección del esfuerzo axial determina una morfología que puede considerarse como la de un elipsoide de revolución. En el caso presente las cavidades de la Figura 5-a están situadas a unos 20 μm de la superficie de fractura; pero en regiones alejadasde ésta; es decir, fuera de la zona de máxima estricción localizada, la morfología correspondiente vuelve a ser la esférica. La morfología descrita para las cavidades cercanas a la superficie de fractura, se hace más evidente al observar las Figuras 5-b, 5-c y 5-d. Puede observarse cómo una cavidad en el acero dúplex SAF 2205 fracturado por tensión (Figura 5-b), permanece asociado con la matriz, al no romperse el ligamento que lo está separando de la grieta principal. La morfología, en éste caso, es de naturaleza elipsoidal. Ya anteriormente Gurland & Plateau (1963), habían encontrado esta clase de morfología en aleaciones metálicas de diverso tipo. Broek (1974), ha descrito detalladamente el crecimiento de cavidades de tipo elipsoidal, particularmente para aleaciones de aluminio. Thomason (1985), en su modelo tridimensional para la fractura dúctil por crecimiento y coalescencia de cavidades, ha predicho el desarrollo de éste tipo de morfología para la etapa del crecimiento, mientras que Menzemer & Srivatsan (1999), han mostrado un excelente esquema de la formación de cavidades elípticas alargadas en la dirección de aplicación del esfuerzo uniaxial y la posterior nucleación de cavidades secundarias esféricas en la zona situada entre las primeras (ver esquema adaptado en la Figura 6). La interacción que tiene lugar de manera posterior entre las cavidades elípticas, ocurre a través de las cavidades secundarias, lo que determinaría la generación de grietas transversales, perpendiculares al esfuerzo de tracción, que darían orígen a la grieta principal.
Recientemente Garrison & Wojcieszynski (2009), han enfatizado la importancia de las inclusiones en la tenacidad de los aceros, mostrando que las cavidades nucleadas a partir de las inclusiones visibles, sumadas a las cavidades potencialmente nucleadas a partir de inclusiones, cubren un porcentaje de la superficie de fractura comprendido entre 36% y 64%, lo cual indica que la coalescencia o unión final de estas cavidades al conformar la grieta principal o superficie de fractura, deberá influir en la irregularidad de la misma. Esto puede explicarse a partir de las consideraciones de Chan & Davidson (1999), quienes han demostrado en una aleación Nb-13Cr-37Ti (% atómico) que la profundidad de las cavidades depende de si éstas se forman o no a partir de inclusiones. En este tipo de aleación, cuando la nucleación resulta de naturaleza homogénea, las cavidades son poco profundas, contribuyendo por lo tanto a la formación de una superficie de fractura menos rugosa. En la Figura 7 se pueden observar de manera esquemática, los casos que corresponden tanto a la nucleación heterogénea (a partir de inclusiones), como a la nucleación homogénea de cavidades. La rugosidad local asociada con esta morfología Rc , puede definirse sobre la base de los parámetros n y m, los cuales representan la profundidad y el diámetro de la cavidad respectivamente. Luego:
Rc = n/m (12)Cuando una cavidad tiende a ser plana, m sufre un aumento relativo respecto a n; es decir, para n → 0, la superficie de fractura en las adyacencias de una cavidad en particular, es de una baja rugosidad, como ocurre en el caso de las facetas de clivaje, donde los patrones de río, en principio, constituyen los únicos accidentes de importancia. Dado que los patrones de río representan un desnivel relativamente pequeño respecto al plano medio de fractura, en comparación al generado por una cavidad promedio, el grado de irregularidad de una superficie de fractura donde predomine el mecanismo de clivaje tiende a ser bajo, lo cual a su vez constituye una indicación de la baja tenacidad que puede asociarse al material.
Los patrones de río de la Figura 8-a, presentan un desnivel de aproximadamente 1 μm respecto al plano medio de fractura, en tanto que las cavidades nucleadas de manera heterogénea, típicas de una superficie de fractura dúctil como las de la Figura 8-b, muestran una profundidad promedio de unos 10 μm (desnivel igualmente relativo al plano medio de fractura). En el primer caso, la energía absorbida por impacto fue de 15,75 J y en el segundo, de 300 J; en correspondencia con los valores de la dimensión fractal, los cuales fueron 1,08 y 1,33 respectivamente.
Aunque no constituye el caso más común; sin embargo, las cavidades con un bajo indice de rugosidad local pueden desarrollarse con facilidad bajo ciertas condiciones, por lo que el grado de irregularidad de las mismas y, por lo tanto, la dimensión fractal, deberían resultar semejantes al caso de la fractura por clivaje con presencia predominante de patrones de río. Un caso interesante de este tipo de cavidad, es mostrado por Bauer & Wilsdorf (1973) en láminas delgadas de acero inoxidable 304, fracturado por tensión a temperatura ambiente. Los resultados obtenidos en este acero, constituyen una de las primeras evidencias de la nucleación de cavidades en ausencia de partículas de segunda fase, impurezas o inclusiones. Por su parte, Thompson (1983) en su análisis de la reducción de la ductilidad, ha demostrado que cuando esto ocurre y el mecanismo de coalescencia de cavidades permanece, entonces debería esperarse un aumento en la densidad efectiva de núcleos («efectiva» denota el hecho de que no todos los núcleos potenciales, como por ejemplo, las inclusiones; actúan como tales en la formación de cavidades). Este aumento implica una disminución del tamaño de cavidad. Thompson, además, define la micro-rugosidad de la superficie de fractura, en forma similar al concepto de rugosidad local introducido en el presente trabajo; sin embargo, no hace la distinción entre la formación de cavidades del modo homogéneo o del modo heterogéneo, lo cual es fundamental para la explicación de la obtención de valores similares de dimensión fractal, para mecanismos de fractura muy diferentes (como, por ejemplo, coalescencia de cavidades y clivaje).
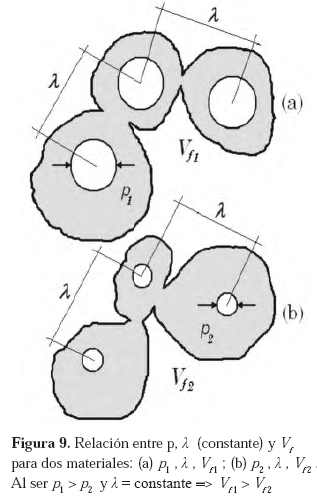
Siendo una propiedad más importante que la ductilidad, la tenacidad de fractura ha sido correlacionada en numerosos modelos con las propiedades mecánicas y las características microestructurales de las aleaciones metálicas, por lo cual el estudio de la morfología de las superficies de fractura, juega finalmente un papel relevante en los desarrollos que actualmente se realizan en el campo de la geometría fractal aplicada a la fractografía. Hahn & Rosenfield (1975), han desarrollado un importante modelo pára el cálculo de la tenacidad de fractura en aleaciones de aluminio cuyo comportamiento es de naturaleza dúctil, que se expresa en la forma:
donde:
σ
ys es el esfuerzo de fluencia, p es el tamaño promedio de las partículas que nuclean cavidades y Vf la fracción volumétrica de las mayores inclusiones de tamaño promedio p. Aunque existe una buena correlación de tipo experimental entre la tenacidad de fractura y Vf −1/6 (Reddy & Rajan, 2005); sin embargo, la ecuación (13) predice un aumento de KIC (en lugar de una disminución) al aumentar σys, manteniendo Vf y p constantes. De igual manera, como ha sido observado en diversas aleaciones de aluminio, si tanto el esfuerzo de fluencia como el espaciado entre inclusiones λ, son mantenidos constantes, una disminución de p determinará un aumento significativo de KIC , porque la correspondiente fracción volumétrica sería menor. La ecuación (13) predice un aumento de la tenacidad de fractura con el aumento de p, lo cual es evidentemente contradictorio, porque por otro lado predice correctamente que KIC es una función inversa de la fracción volumérica. En la Figura 9 se muestra un esquema de la relación entre p y Vf , para dos materiales, cuando el valor del espaciado entre inclusiones permanece constante. De acuerdo a la ecuación (13), el material representado en la figura 9-b sería el más tenaz (Vf 2< Vf 1 ), lo cual coincide con el comportamiento real observado, ¡pero simultáneamente sería el menos tenaz, ya que p2< p1!, lo cual no obedece al comportamiento real en la práctica.Lo anterior apenas ilustra lo complejas que pueden resultar las correlaciones entre las propiedades mecánicas (la tenacidad en particular) y los parámetros microestructurales de una determinada aleación. Ahora bien, en el caso de las superficies de fractura, las irregularidades de las mismas, las cuales constituyen un indicio de la plasticidad del material y que pueden ser cuantificadas mediante geometría fractal, son un puente para establecer la funcionalidad entre la tenacidad y la dimensión fractal. Es por ello que el desarrollo conjunto en los campos de la mecánica de fractura y la geometría fractal, ha tomado tanta importancia en las dos últimas décadas (Balankin, 1997; Cherepanov et al. 1995; Carpinteri et al. 2004; Wnuk & Yavary, 2005; Epstein & Sniatycki, 2006; entre otros). Adicionalmente, la aplicación de los conceptos de la geometría fractal no se ha limitado a las aleaciones metálicas o a los diferentes tipos de fractura. Dos ejemplos recientes, entre otros, ilustran la importancia que ha alcanzado esta nueva área de investigación: Konăs et al. (2009) han analizado la estructura fractal de la madera a escala microscópica, pro- poniendo que su microestructura en estado original contiene suficiente información acerca de la tenacidad, lo que podría permitir la determinación de esta propiedad sin la utilización de técnicas destructivas. Por su parte, Vallet et al. (2009), han desarrollado modelos para la deformación mecánica de diversos tipos de asperezas e irregularidades presentes en superficies rugosas en contacto, con el propósito de validar la utilización de superficies sintéticas, en lugar de las reales, que exhiban propiedades de naturaleza fractal.
Análisis Fractal de Superficies de Fractura
Resulta conveniente, en función de la utilidad de la relación entre la tenacidad y la dimensión fractal, establecer que si esta última se mide fuera del rango en el cual la superficie de fractura se comporta como un objeto fractal (en el sentido estadístico), entonces no será una propiedad sensible a los cambios experimentados por las propiedades mecánicas de interés. Por otra parte, para una mejor comprensión de los aspectos relacionados con la naturaleza fractal de las superficies de fractura, es necesario que la dimensión fractal o de similaridad D, sea definida.
Puede demostrarse (Mandelbrot, 1986) que para objetos de naturaleza regular y de dimensiones 1, 2 y 3 (en otras palabras, ubicados en el espacio euclídeo), el número N de partes similares en las cuales pueden dividirse, está dado por:
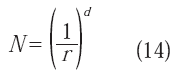
donde:
d es la dimensión euclídea ( 0, 1, 2, 3 ), y r es la longitud
fraccionaria de cada una de las partes en las que el objeto queda dividido. Si el objeto es una línea recta y N es 4, por ejemplo; entonces r = ¼ y d = 1. Si una superficie plana y cuadrada es dividida en N = 16 partes o elementos cuadrados, entonces r = ¼, ya que cada lado de cada elemento cuadrado, tiene una longitud que es ¼ de la longitud del lado del cuadrado mayor o superficie total; mientras que d = 2. De igual manera, un volumen en forma de cubo puede dividirse a su vez en 64 pequeños cubos, cada uno con una arista de longitud igual a ¼ de la arista del cubo mayor, por lo que N = 64, r = ¼ y d = 3. Debe notarse que estas relaciones no dependen del tamaño de la línea recta, de la superficie cuadrada o del volumen cúbico en cuestión.Es posible generalizar el concepto anterior para objetos D dimensionales; es decir, aquéllos cuya dimensión no es entera (euclídea), pero que sin embargo también se pueden dividir en un número N de pequeñas copias de sí mismos, cada una de las cuales está a una escala r respecto al tamaño original del objeto. Para estos casos, la ecuación (14) puede ser escrita, como ha sido establecido por Mandelbrot (1986) y Falkoner (2003) en la forma:
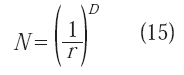
por lo que la dimensión fractal o de similaridad, estará dada mediante la relación:
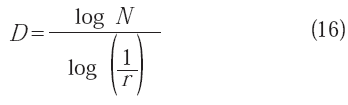
Esta dimensión no entera, mayor que 1 pero menor que 2, indica que una curva ocupa una superficie del plano (d = 2), mayor que la ocupada por una línea recta (d = 1). Para varios objetos fractales reales, diferentes valores, tanto de N como de r, pueden combinarse para originar un mismo valor de D, por lo que, para un valor definido de la dimensión fractal, la configuración física del objeto correspondiente no es única (Feder, 1988). Es por lo anterior que la dimensión fractal puede ser útil en la caracterización del cambio contínuo de una morfología o configuración inicial, pero no puede esperarse una correspondencia biunívoca entre D y las superficies de fractura de los materiales.
Debe resaltarse el hecho de que a menudo es necesario considerar los denominados "fractales multirango"; es decir, el comportamiento fractal en distintos intervalos de escala para un mismo material. Este tipo de fractales, no son necesariamente "fractales multiescala", aunque presenten intervalos de escala con solapamiento (Lung et al. 1996). Como ejemplo puede mencionarse el de un material que presente una separación totalmente transgranular en ciertas condiciones conocidas y separación intergranular en otras condiciones diferentes a las primeras. Si los niveles de tenacidad de fractura que corresponden a cada caso son muy diferentes, cada fractura tendrá su propio sistema auto-similar. Sin embargo en una misma superficie de fractura, resulta común que estos dos mecanismos de separación aparezcan mezclados, cuando los niveles de tenacidad de fractura sean muy semejantes para cada uno de estos mecanismos por separado. En este caso los sistemas individuales están mezclados, por lo que se formará un solo "sistema fractal auto-similar multi-escala" (Lung & March, 1999).
De igual forma debemos mencionar que en el tema de la descripción fractal de las superficies de fractura, aunque el interés inicial estuvo basado en estructuras de tipo o naturaleza auto-similar, sin embargo no existe una certeza total acerca del modelo que mejor las describe: el auto-similar o el auto-afín (Balankin et al. 2002; Hilders et al. 1998). Resulta importante resaltar el hecho de que, pese a los diferentes tipos de interrogantes que persisten en esta área, todo indica que la hipótesis fractal aplicada a los diferentes tipos de superficies de fractura, quedará bien establecida en los estudios que se realizan en múltiples clases de materiales, no solamente en aplicaciones propias de la ingeniería, sino de otras áreas afines.
Desde el año de 1982 se han propuesto una serie de técnicas para el estudio de superficies de fractura desde el punto de vista fractal. Entre otras se destacan: El método perfilométrico y el de las islas (Mandelbrot, 1982; Mandelbrot et al. 1984); el método del perímetro vs máximo diámetro (Mu et al. 1993); el método del cálculo directo del área de fractura (Falkoner, 2003); la utilización de la microscopía electrónica de efecto túnel (Morgan & Bonnell 1990); el uso de los histogramas de probabilidad (Malfy et al. 1992); la técnica de las variaciones (Dubuc et al. 1989); el estudio de las líneas de electrones secundarios de barrido (Huang et al. 1989); etc. La discusión siguiente estará basada únicamente en los dos primeros métodos, ya que estos han sido, con mucho, los más extensamente utilizados en los más diversos tipos de aleaciones metálicas.
Método Perfilométrico o de las Secciones Verticales
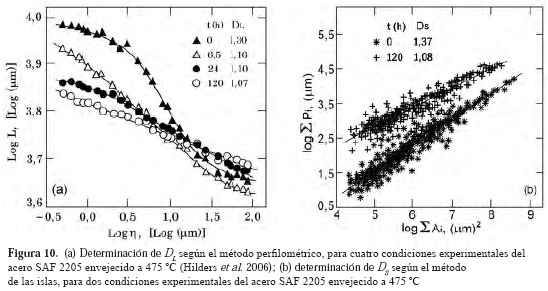
En este caso, el valor de la dimensión fractal DL, se deriva a partir del análisis de los perfiles de fractura que se obtienen mediante cortes perpendiculares al plano medio. Esta técnica implica la medición de la longitud del perfil L, como una función del tamaño de la unidad de medida η, utilizada para ello, como se observa en la figura 10-a (Hilders et al. 2006). Esta unidad de medida es de tipo o naturaleza absoluta, ya que la proyección del perfil (Lo), en el plano medio, es constante. Se ha demostrado que las curvas de la clase, log L vs log η, a menudo no presentan un comportamiento lineal para todo el rango de valores de η utilizados (Dauskardt et al. 1990), por lo que la dimensión fractal se determina en éstos casos, a partir de la zona rectilínea central. En la Figura 10-a, donde se representan 4 curvas correspondientes al mismo número de condiciones de envejecimiento a 475 ºC, del acero dúplex SAF 2205, se observa un alto grado de linealidad en tres de ellas, pero la curva para el acero en su condición original (0 h de envejecimiento), es de forma sigmoidal reversa, término utilizado para éstos casos por Lung & March (1999). La ecuación en la cual se basa este método (Dauskardt et al. 1990); viene dada por:
A partir de esta relación, es posible la evaluación de la di- mensión fractal DL, mediante:
![]()
Ha sido bien documentado (Dubuc et al. 1989); que para el caso de curvas fractales construidas de manera geométrica, la longitud obtenida del perfil no se encuentra limitada, observándose un comportamiento lineal para el rango completo de valores de la unidad de medida η. En los sistemas físicos; sin embargo, el comportamiento fractal está confinado a un intervalo restringido de valores de η. La explicación de este comportamiento, descansa en el argumento de que para valores bajos de η ocurre la ruptura de la linealidad, porque la estructura microscópica de los perfiles de fractura deja de ser auto-similar a la escala del micrón (meso-escala). De la misma forma, para valores altos de η ocurre una pérdida de linealidad, debido a que los perfiles comienzan a mostrarse homogéneos o, en otras palabras, el uso de altos valores de η implica en muchos tipos de perfiles de fractura, que los detalles más pequeños e irregulares sean obviados.
Método de las islas o de las secciones finas
La aplicación de este método permite la determinación de la dimensión fractal DS, a partir del análisis de secciones horizontales consecutivas, paralelas al plano medio de las superficies de fractura. En la medida de que las secciones progresan en profundidad, aparecen "islas" o zonas planas separadas entre sí, las cuales se unen al aumentar de tamaño. Este método genera patrones auto-similares, dado que todas las direcciones que yacen en las "islas" de cada sección son equivalentes, por lo que DS puede definirse sin ambigüedades. El fundamento teórico del método está basado en que el cociente:
no depende del tamaño de las islas o zonas metálicas planas de perímetro L y área A, pero sí del tamaño de la unidad de medida ε utilizada, porque tanto L como A también dependen. En la anterior ecuación, β es un parámetro que permanece constante para un valor fijo de ε. La dimensión fractal DS, puede entonces determinarse a partir de la relación anterior, mediante:
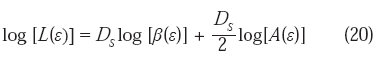
donde el término DS log [β(ε)] = λ(ε), permanece igualmente constante para valores fijos de ε. Debe aclararse que, en la práctica, cada dato experimental es el resultado de la suma de todos los perímetros y áreas que corresponden a una sección plana particular, por lo que la ecuación (20) puede reescribirse en la forma:
En esta ecuación ha quedado tácita la dependencia de ε, y la longitud de los perímetros ha sido sustituída por la letra genérica P, de manera que Pi y Ai denotan el perímetro y el área, respectivamente, de la i-ésima isla situada en la j-ésima sección metalográfica. Derivando la ecuación (21) respecto al log ΣPi, se obtiene:
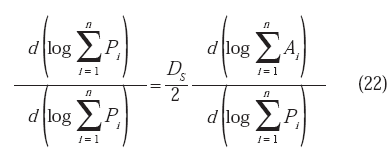
por lo que DS puede expresarse finalmente como:
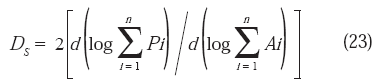
es decir;
DS se determina a partir de la pendiente de la curva log Σ Pi vs log Σ Ai. Los valores de Pi y de Ai deben obtenerse mediante el uso de una unidad de medida que sea lo suficientemente pequeña (ε para el perímetro y ε2 para el área). En la figura 10-b han sido representados los resultados que corresponden a las condiciones extremas de envejecimiento del acero SAF 2205, que ya han sido señaladas en la Figura 10-a (0 h y 120 h a 475 ºC). Estos resultados se obtuvieron mediante el método de las islas aplicado a varias superficies de fractura para cada condi- ción: 20 para 0 h y 15 para 120 h (para un total general de 230 y 175 secciones metalográficas correspondientemente). Los valores respectivos de la dimensión fractal DS, 1,37 y 1,08, aunque superiores a los obtenidos por el método perfilométrico, sin embargo guardan la misma relación, resultado que puede verse reforzado, por el hecho de que los datos experimentales son muy numerosos, dejando ver una inequívoca linealidad en cada caso. Estos resultados reafirman la tesis original de Mandelbrot (1982), cuando establece que: "Muchas superficies de fractura siguen el modelo fractal admirablemente bien. En metalurgia existen muy pocos gráficos que afecten a todos los datos dispo- nibles y a una gama muy amplia de tamaños, y que sean a su vez tan directos".Una variante de la ecuación (19) ha sido propuesta por Feder (1988), aunque su implementación práctica en la determinación de
DS, resulta idéntica a la planteada por la primera:donde:
C es una constante de proporcionalidad. El valor de DS es determinado para cualquier tamaño de ε lo suficientemente pequeño, a partir de la pendiente del ploteo log L vs log A:
Debe aclararse que en el método de las islas, la unidad utilizada para medir A y L (es decir; ε ), en general debe estar normalizada, para tomar en cuenta el tamaño de las diferentes zonas metálicas (o "islas"). Debido a que las morfologías de las islas pueden resultar muy diferentes en distintas secciones, o aún en una misma sección metalográfica, es difícil definir una medida que represente el tamaño. Para una forma simple, como la de un círculo, el tamaño quedaría definido como el diámetro, lo cual no se observa en la realidad; ni aún en forma aproximada. Si la
morfología pudiera mantenerse relativamente invariable, el parámetro ε igualmente permanecería constante, porque el mismo se define como el cociente de la unidad de medida absoluta η, entre el tamaño de la isla (Lo): ε = η / Lo; es decir, podrían elegirse los valores de η para cada isla, de acuerdo al valor respectivo de Lo, cumpliendo en esta forma con el requerimiento de la constancia de ε. Sin embargo, debido a la variación de la morfología, en la práctica generalmente se utilizan directamente las medidas de η (η : perímetro y η2 : área).
La adopción del mencionado método, permite la evaluación tanto de áreas como de perímetros, manteniendo el parámetro η constante. Sin embargo, si no se utiliza un valor de ε que sea lo suficientemente pequeño, entonces C podría no ser constante (ecuaciones 24 y 25).
Correlación Fenomenológica entre la Dimensión Fractal y la Tenacidad
Fractura frágil y cuasi-frágil
Basándose en el criterio de Irwin, Lung (1986) propuso un modelo fundamentado en los principios de la mecánica de fractura lineal elástica. En este modelo se considera que la tasa crítica de liberación de energía de deformación, o fuerza crítica para la extensión de una grieta, en el caso de la fractura frágil ideal
GIC , puede ser descrita mediante:donde:
D es la dimensión fractal de un perfil de fractura asociado con una superficie totalmente lisa y paralela al plano medio, ε = η / Lo es la unidad de medida normalizada, en este caso, para valores unitarios de η y de Lo: ε = 1/1 = 1, y γS es la energía superficial específica. De igual forma, en el caso de la fractura cuasi-frágil tenemos:
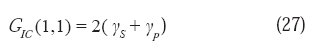
donde:
γ
p es la energía superficial necesaria para el avance inestable de una grieta en la zona plástica. Debe recordarse que la relación entre GIC , JIC y KIC (Broek, 2002), es:donde:
v es la relación de Poisson y E es el módulo de Young.
Para el caso de la fractura cuasi-frágil, se supone que la zona plástica en la punta de la grieta, es bastante pequeña comparada con el largo de la parte de la probeta que soportará la carga y que el espesor de la zona deformada es muy pequeño, porque el proceso de fluencia ocurre a baja escala.
Por otra parte, en el caso de la fractura frágil, debido al hecho de que la propagación de grietas ocurre de manera irregular, las áreas reales de las superficies de fractura, así como también las longitudes proyectadas en el plano medio, serán mayores que las obtenidas en las mediciones macroscópicas, por lo que en lugar del valor específico unitario respectivo para la dimensión fractal D = 1, y del correspondiente valor unitario para la unidad de medida normalizada ε (ecuación 26), tendremos:
donde:
D y ε son valores cualesquiera de la dimensión fractal y de la unidad de medida normalizada respectivamente, L(η) es la longitud de la grieta como una función de la unidad de medida, tal como se define en la ecuación (17) y Lo es la longitud de la proyección del perfil de fractura en el plano medio. Para un perfil de fractura plano (superficie de fractura lisa), la grieta tiene una longitud igual a su proyección, por lo que el cociente entre corchetes será igual a la unidad, lo cual corresponde al caso ideal de la fractura frágil. La ecuación (29) puede escribirse, tomando en cuenta la ecuación (26), como:
Ahora bien, dado que la ecuación (17) también puede escribirse en términos de ε(ε = η /Lo):
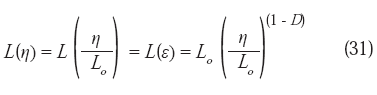
Entonces, la longitud total normalizada de un perfil de fractura, puede expresarse mediante la relación:
Luego, a partir de la ecuación (32), la ecuación (30) puede escribirse:
Tomando logaritmos a ambos lados, en esta última relación, tenemos:
La ecuación (33) y su forma logarítmica, la ecuación (34), revisten una gran importancia desde el punto de vista de la geometría fractal, la mecánica de fractura y la naturaleza de la relación entre la tenacidad y la dimensión fractal, en el caso de fluencia a pequeña escala.
A partir de la diferenciación de la ecuación (34), es posible demostrar que log
GIC (D,ε ) se encuentra relacionado positivamente con D: 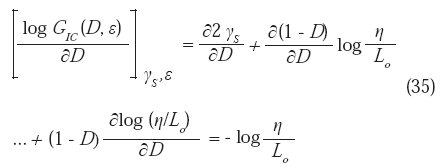
Dado que la unidad de medida η es siempre menor que Lo, entonces: log (η /Lo) < 0 y, por lo tanto: − log (η /Lo) > 0, quedando establecido que:
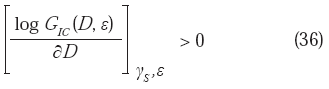
Esta conexión positiva entre
GIC y D, es extensiva a todos los parámetros críticos de la mecánica de fractura, que se utilizan regularmente como medida de la tenacidad. En este sentido, además de la ecuación (28), deberá tomarse en consideración para fluencia a baja escala, la ecuación encontrada por Shih (1981); a partir de las ecuaciones de campo de Rice & Rosengren (1968): ![]()
donde: δIC es el valor crítico de la abertura en la punta de la grieta y dn es un parámetro empírico de restricción plástica. Tanto δIC como JIC (este último definido anteriormente), se refie- ren a un estado de deformación plana.
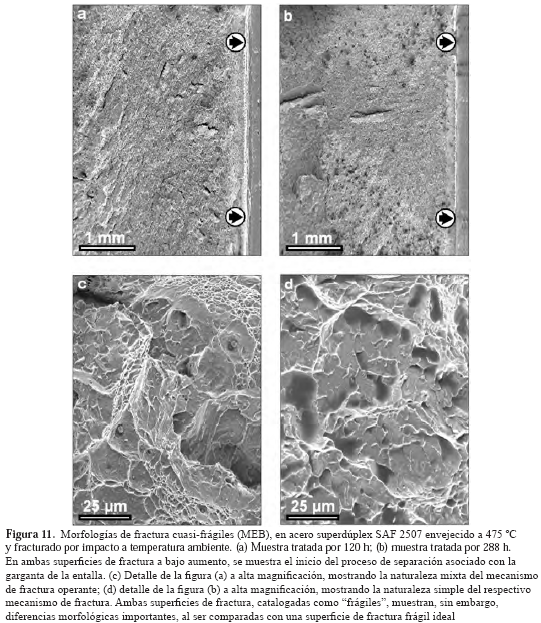
En la figura 11 se muestra una serie de fractografías a baja y alta magnificación, correspondientes a dos superficies de fractura por impacto del acero SAF 2507, envejecido a 475 ºC por 120 y 288 h. En las dos superficies resulta posible observar aspectos que comúnmente se asocian con el concepto de "material frágil", aunque sabemos que en los materiales en general, y en los de naturaleza metálica en particular, las superficies de fractura siempre presentan evidencia de plasticidad, por lo que la designación de este tipo de superficie de fractura como "cuasi-frágil", resulta más apropiado. Aún en el caso de monocristales (por ejemplo, de Zn), donde las superficies de fractura son sumamente lisas, resulta posible verificar la presencia de irregularidades, tales como las de los patrones de río (Russell & Lec 2005). Puede verse como a altas magnificaciones (Figuras 11-a y 11-b), no es fácil diferenciar el grado de plasticidad inherente a las superficies: en el caso de la Figura 11-a (120 h); un grado o nivel de irregularidad ligeramente mayor, se asocia con una energía de impacto de unos 94 J, mientras que para la superficie más lisa de la Figura 11-b (288 h), el nivel de energía respectivo que se encontró fue de 45 J. Las fractografías que corresponden a las Figuras 11-c y 11-d, (mayor magnificación), revelan igualmente superficies de fractura similares, donde el grado de irregularidad relativo es difícil de determinar de manera cualitativa, pese a la diferencia en los valores de energía absorbida. En el caso de la Figura 11-c (120 h); se observa un micromecanismo mixto de separación: cuasi-clivaje y coalescencia de cavidades, y en el caso de la Figura 11-d (288 h); es posible observar únicamente cuasi-clivaje. Esta diferencia, es relativamente fácil de detectar a simple vista, pudiendo ser asociada, en un principio, con la diferencia registrada en energía absorbida, pero difícilmente al grado de irregularidad. Por todo lo anterior, resulta evidente la importancia de una variable tal como la dimensión fractal en los estudios de tipo fractografico (cuantitativos), capaz de detectar en forma simultánea cambios en la irregularidad de las superficies de fractura y en la tenacidad de los materiales respectivos. Luego, desde este punto de vista, la desigualdad (36) resulta de una gran importancia para el entendimiento de las relaciones básicas entre la geometría fractal y la tenacidad. Cuando se presenta fluencia a gran escala, la situación es muy diferente, lo cual será discutido en los apartes siguientes.
Fractura Tenaz
Hemos considerado al término "fractura tenaz" como el que mejor se ajusta al contexto del presente trabajo; porque las aleaciones metálicas tenaces generalmente se comportan de una manera bastante dúctil, pero muchas aleaciones dúctiles no son altamente tenaces, por lo que el término alternativo muchas veces utilizado de "fractura dúctil", no es del todo apropiado para el caso donde se analiza la habilidad para el almacenamiento de energía.
Hoy en día no existe una certeza total acerca de la clase de relación entre D y las propiedades mecánicas, en el caso de materiales muy tenaces (fluencia a gran escala). Aunque la correlación positiva entre la tenacidad y D se ha aceptado, en principio, por la comunidad de la Ciencia de los Materiales, frecuentemente se han encontrado, especialmente en el caso de aleaciones tenaces, correlaciones de tipo negativo (Mandelbrot et al. 1984; Mu & Lung, 1988; Feder, 1988; entre otros). Una revisión crítica acerca de los múltiples factores que podrían determinar el tipo de correlación entre D, la tenacidad y otras propiedades mecánicas, ha sido presentada por Milman et al. (1994).
La correlación negativa entre D y la tenacidad, ha tratado de explicarse de varias maneras; entre otras, bajo el concepto de que cuando se emplean cantidades relativamente altas de energía en el trabajo realizado para extender una grieta, el proceso tiene lugar fundamentalmente por corte, determinando el desplazamiento de un gran número de dislocaciones en muy pocos planos (Williford, 1988), y generando una superficie de fractura muy lisa a nivel atómico, lo que produce un bajo valor de D. La principal crítica a este argumento, radica en el hecho de que una superficie de fractura lisa a nivel atómico, puede parecer rugosa a nivel micrométrico, en el cual usualmente se realizan la mayoría de las mediciones. Este incremento de D a nivel del micrón, se debe a las diferentes orientaciones de los planos cristalográficos en los distintos granos. En otras palabras, para un intervalo de valores de tenacidad altos, si evaluamos D a nivel atómico, su valor podría ser cada vez más bajo, para valores cada vez mayores de tenacidad en el referido intervalo (relación de tipo negativo), pero si D es evaluada a nivel micro, éste no sería necesariamente el resultado. Por otra parte, Milman et al. (1994); han demostrado en estos casos, que a escala nanométrica frecuentemente D resulta mayor.
Debe destacarse entonces que la escala experimental que se utilice en el análisis fractal, debe ser consistente con la escala del aspecto microestructural relacionado con la propiedad a estudiar. Balankin (1997), ha demostrado que la tenacidad de fractura macroscópica KIC , se relaciona con la tenacidad de fractura a nanoescala KnIC mediante:
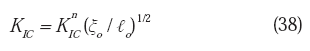
donde:
ξ
o es la longitud de correlación auto-afín ( ≈10-2 - 10-3 m ), y ℓo es la longitud límite microscópica ( ≈10-6 - 10-8 m), la cual coincide con el tamaño de la zona libre de dislocaciones en la punta de la grieta para materiales dúctiles (Cherepanov, 1994). La configuración y la dinámica de las dislocaciones, juegan un importante papel en la deformación plástica de las aleaciones metálicas, por lo que la aplicación del análisis fractal a escala nanométrica, debe ser de primera importancia en el estudio de la tenacidad y, en general, de las propiedades mecánicas. Infortunadamente, muy pocas investigaciones se han realizado a éstos niveles (Milman et al. 1994; Zaiser et al. 1999).Antes de discutir algunos modelos fractales específicos para fluencia a gran escala, es conveniente mencionar el criterio propuesto por Nagahama (1994), el cual se basa en conceptos fractales y en la condición crítica para la propagación de una grieta de Griffith-Orowan-Irwin. La aplicación de este criterio, permitiría establecer la naturaleza frágil o tenaz de una fractura. La condición crítica que se ha mencionado, establece que:
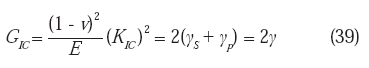
donde:
2
γ = 2(γS + γp) es la energía de superficie efectiva. Este modelo define un tamaño promedio de cavidad λ en la superficie de fractura, normalizado por el correspondiente tamaño promedio de cavidad en una superficie de fractura generada en condiciones de transición dúctil-frágil λo:donde:

es la energía de superficie fractal (siendo 2 < D < 3; válido para una superficie fractal, lo que sería análogo a 1 < D < 2 para una curva fractal). Si
GIC resulta mayor que la energía de superficie fractal, una grieta podrá entonces propagarse (condición crítica). Partiendo de la relación expresada a través de la ecuación (40), puede deducirse que: 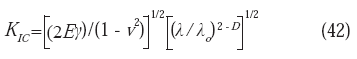
Tomando logaritmos en ambos miembros tenemos:
siendo A una constante igual a: [(2Eγ)/(1-v
)]1/2. La ecuación (43) puede ser re-escrita como: 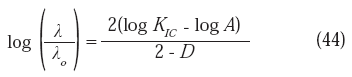
Dado que (2−D) < 0; si log (λ/ λo) es positivo (cavidades en la superficie de fractura mayores que las cavidades en la zona de transición), entonces logA > log KIC, es decir:
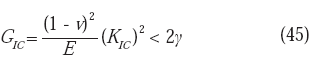
Si esta desigualdad se cumple, físicamente la grieta tenderá a frenarse, porque la fuerza crítica necesaria para la extensión de la misma (
GIC ), no será suficiente comparada con la energía de superficie mínima requerida (energía de superficie efectiva 2γ). En este caso, la fractura será de tipo tenaz. Por el contrario, si log (λ/ λo) es negativo (cavidades en la superficie de fractura menores que las cavidades en la zona de transición), entonces GIC > 2γ por lo que la grieta se extenderá rápidamente, generándose una fractura de naturaleza frágil. La ecuación (43) también puede escribirse: 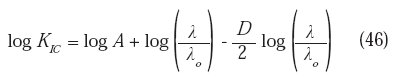
Ya que el cociente (λ/ λo) puede permanecer constante, tanto para una aleación, como para un sistema de aleaciones, la ecuación (46) puede ser escrita como:
log
KIC = a -bD (47)siendo respectivamente las constantes "a" y "b": log
A + log(λ/λo) y (1/2)log(λ/λo). La ecuación (47), expresa el hecho de que para un valor constante del cociente (λ/ λo), existe un rango de valores de D, y por lo tanto, de la tenacidad de fractura. La constancia del cociente (λ /λo) no está restringida obviamente, a valores únicos de λ o de λ o . La ecuación (47) permite el conocimiento de la naturaleza de la relación entre la tenacidad y D: de acuerdo a Nagahama, cuando "b" es positivo [ log (λ/ λo) > 0 ]; se obtiene una relación negativa entre KIC y D. En este caso, los resultados experimentales utilizados como ejemplo para esta clase de relación, involucran materiales con un comportamiento tenaz: acero 24SiMnCrNi2Mo, y acero 30CrMnSiNi2A (Mu & Lung, 1988). Por otra parte, cuando "b" es negativo [ log (λ /λo) < 0 ]; la relación encontrada entre D y la tenacidad, resulta positiva. Los dos materiales que han sido referenciados este caso, fueron de comportamiento típicamente frágil: Dióxido de Aluminio (Alúmina: Al2O3) y Dióxido de Silicio (Sílica: SiO2) (Nagahama, 1994).Si bien, el criterio anteriormente discutido es similar al de
Griffith-Orowan-Irwin, puede sin embargo ser interpretado como un criterio fractal generalizado, para fracturas tenaces o frágiles. Aunque es similar al criterio de Lung (1986), para el caso de materiales cuasi-frágiles, sin embargo, esclarece el papel del parámetro λ/ λo (ε en el modelo de Lung), al establecer la posible naturaleza de la diferencia entre las superficies frágiles y las tenaces, sobre la base del tamaño de las cavidades formadas. Finalmente, aunque este criterio explica algunas de las tendencias observadas, tanto en materiales frágiles como en materiales tenaces, falla en explicar las correlaciones de tipo positivo que se han encontrado experientalmente entre la tenacidad y D, en materiales cuyo comportamiento es básicamente tenaz.Es interesante notar que el cociente (
λ /λo), aunque refiere el valor relativo del tamaño de cavidad a un valor de transición, es en cierto modo semejante a la relación establecida para la rugosidad local Rc (ecuación 12). En el último caso, el grado de irregularidad queda referido a una cavidad individual, en tanto que en el primero se establece una comparación entre cavidades. Sin embargo, a diferencia de Rc, donde la tenacidad y D están relacionadas de una manera directa, en el criterio de Nagahama, cuando log (λ/ λo) > 0 (material tenaz), la relación entre D y la tenacidad es de naturaleza inversa.Ya ha sido suficientemente demostrado (Lung & Zhang 1989) que la relación negativa entre la tenacidad y D, se ha vinculalo con la utilización o uso de unidades de medida relativamente grandes, obviándose así los detalles más pequeños, lo cual se manifiesta en la obtención de la ya mencionada tendencia de tipo inverso. Para unidades de medida que sean lo suficientemente pequeñas, se observa una correlación positiva entre la tenacidad y la dimensión fractal. Recientemente Ravindran et al.(2009) han realizado un estudio de los procesos de crecimiento y coalescencia de cavidades en la aleación Al5052 a diferentes temperaturas de recocido, evaluando varias categorías de parámetros que se relacionan con dichas cavidades, mediante su correlación con diversas propiedades mecánicas, microestructura, etc., encontrando que el material cuyas cavidades presentaban una relación largo/ancho menor (equivalente a la relación n/m de la ecuación 12), mostraron un grado superior de conformabilidad. Aunque este resultado pareciera estar de acuerdo con el criterio utilizado por Nagahama, sin embargo deberíamos tener en cuenta, que el mejoramiento de la conformabilidad puede deberse, en un mayor grado, al % de recristalización.
Existen otros factores que deben tomarse en cuenta durante las mediciones cuantitativas realizadas en las superficies de fractura. Es importante, por ejemplo, determinar el tamaño de cavidad promedio, con un número significativo de ellas; es decir, las mismas no deben restringirse a una pequeña área. Solamente cuando el área es significativamente grande, el tamaño promedio de las cavidades converge hacia un valor real fijo. Hilders (1985), ha demostrado que para el acero inoxidable austenítico AISI 304, en condiciones de recocido y sensibilización, la tendencia a un valor promedio fijo ocurre alrededor de 10
3 cavidades. Sin embargo, el número de mediciones debe también mantenerse restringido a la zona de la superficie de fractura relevante para el caso en estudio. Debe enfatizarse el hecho de que la dispersión de los valores de D puede limitar la validez de los modelos que relacionan la tenacidad de fractura con la dimensión fractal. Esta dispersión se origina por el grado de complejidad del relieve de las superficies de fractura a lo largo de la muestra. Por lo anterior, resulta conveniente restringir las mediciones a la zona bajo estado de deformación plana, donde la dispersión es menor.Asimismo, resulta de gran importancia el considerar los diferentes tipos de mecanismos de fractura operantes durante la separación. Generalmente, los estudios que se realizan en diferentes sistemas de aleación metálicos, desde el punto de vista fractal, implican la presencia de un único mecanismo de separación: coalescencia de cavidades, clivaje, cuasi-clivaje o fractura intergranular. Es posible que al mezclar los valores de D, obtenidos en aleaciones donde opera un único mecanismo de separación, con los correspondientes a sistemas donde se han manifestado dos o más de estos mecanismos, se obtengan correlaciones erróneas entre
KIC y D. En éstos casos deben tenerse en cuenta las observaciones realizadas por Lung (1995), respecto a los así denominados "sistemas fractales multi-escala". Por otra parte, Dauskardt et al. (1990), han mostrado la alta especificidad de las características fractales respecto al mecanismo de fractura, al observar que algunos aspectos microestructurales típicos de los mecanismos locales de fractura, están relacionados con D. Un interesante estudio reciente en acero Ni-Cr (Dlouhý & Strnadel, 2008); muestra los efectos de la competencia entre los mecanismos de fractura transgranular (frágil) e intergranular (frágil) en el valor de la dimensión fractal. Los valores registrados para D se incrementan cuando el mecanismo de separación cambia de transgranular a intergranular, siendo el umbral de transición para la dimensión fractal de 1,12.En base a la micro-rugosidad local observada en una superficie de fractura tenaz y a la relación de Thompson & Ashby (1984) entre
JIC, algunos parámetros de la microestructura y propiedades mecánicas, Jiang et al. (1994) desarrollaron una relación positiva entre la dimensión fractal y la tenacidad, para el acero AISI 310. Esta relación se expresa mediante la ecuación: 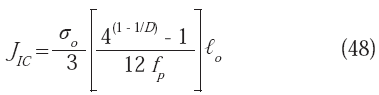
donde:
σ
o es la resistencia a la tracción del acero, fP es la fracción volumétrica de partículas iniciadoras de cavidades, y ℓo es la distancia característica. Los valores de D obtenidos fueron de 1,097 y 1,171, para el acero cargado con hidrógeno y en condición de recocido respectivamente. Aunque este estudio sólo reporta un único orden de magnitud para el rango de valores de η utilizado (método perfilométrico), el gráfico respectivo es rectilíneo, lo que confirma el comportamiento fractal de las superficies de fractura en dicho rango. La relación (48) indica que la integral J crítica disminuye al bajar el valor de D, hecho que concuerda con la observación experimental de la pérdida de tenacidad normalmente inducida por el hidrógeno, y con los resultados obtenidos de una dimensión fractal menor para este caso.Las principales críticas relacionadas con el modelo de Jiang et al. (1994), se relacionan, en primer lugar, con el hecho de que la ecuación (48) predice una tenacidad negativa, a menos que la fracción
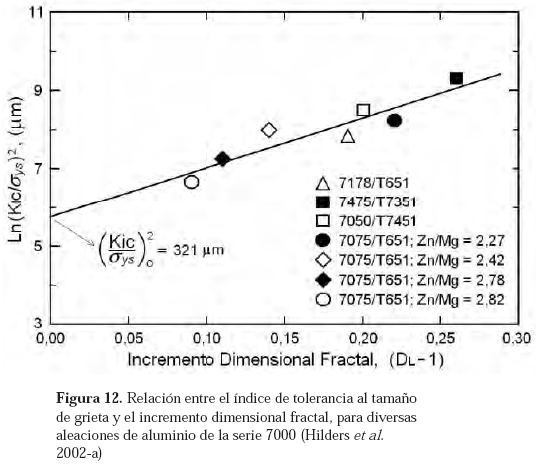
fP esté bastante por debajo del 1%, y en segundo lugar, de acuerdo a los autores, los valores de la rugosidad local M (M = h/w; equivalente a Rc = n/m) deberán estar comprendidos entre 0 y 0,5 para valores de D en el intervalo 1 < D < 2; sin embargo, Thompson et al. (1984), han reportado resultados experimentales para M, comprendidos entre 0,5 y 1; no existiendo razón física alguna, que prohiba que para la rugosidad local: M ≥ 1.Hilders et al. (2002-a) han propuesto una relación entre el índice de tolerancia al tamaño de grieta (medida de la tenacidad y el incremento dimensional fractal, en varias aleaciones de aluminio de la serie 7000. Mediante el método perfilométrico, se determinaron los valores de la dimensión fractal
DL (ecuación 17), obteniéndose la relación: 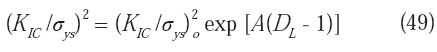
donde:
(KIC/
σys)2 es el índice de tolerancia al tamaño de grieta (en sunidades de longitud); (KIC/σys)20 es el índice respectivo en el espacio euclídeo (para una superficie de fractura plana, donde DL = 1) y A es una constante, definida como la pendiente d [Ln (KIC /σ ys)2] / d [(DL − 1)]; en la Figura 12. A partir de esta figura, puede determinarse el índice de tolerancia al tamaño de grieta en el espacio euclideo, el cual tiene un valor de unos 321 micrones. Este valor se relaciona con el tamaño que desarrolla una grieta en una superficie de fractura lisa, antes del momento crítico.
En la medida en que la rugosidad de la superficie de fractura se incrementa, se observa un aumento de la dimensión fractal, así como del índice de tolerancia al tamaño de grieta general. En otras palabras, para una superficie de fractura más irregular, el valor de (
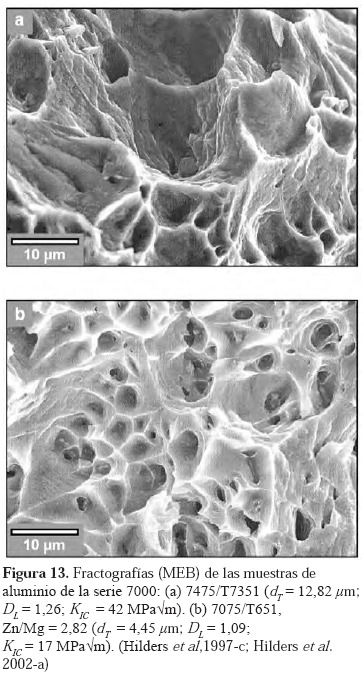
KIC /σ ys)2 aumenta, lo cual debe estar relacionado con el hecho de que para condiciones de mayor tenacidad, el tamaño que se debe alcanzar para que la grieta se propague, será mayor. Las condiciones crecientes de irregularidad superficial, se verificaron mediante la determinación del tamaño de cavidad dT , cuyos valores están relacionados directamente con DL.En la Figura 13 se observan dos zonas de las superficies de fractura que corresponden a las aleaciones: (a) 7475/T7351 y (b) 7075/T651 (Zn/Mg = 2,82). El tamaño de cavidad de la primera aleación, casi triplica al de la segunda; mientras que el valor de D para la primera, es respectivamente, un 13,5% mayor. Correspondientemente, el valor de KIC para la aleación (a) es de 42 MPa√m y para la aleació (b) 17 Mpa √m. Resulta evidente en las fractografías, la diferencia que existe, tanto en la profundidad como en el ancho (diámetro) de las cavidades, lo que denota un mayor grado de plasticidad y por lo tanto, de irregularidad, en la superficie de fractura que corresponde a la aleación (a).
Una relación específica entre el tamaño promedio de cavidad
dT y la dimensión fractal DL, ha sido encontrada para el acero SAF 2205, en diferentes condiciones de envejecimiento a 475 ºC (Hilders et al. 2006):dTo
espacio euclídeo y m se define como la tasa de variación del logaritmo natural de dT , respecto al incremento dimensional fractal (DL − 1), es decir: m = d [(Ln dT)] /d [(DL − 1)].La relación (50) ha sido utilizada por Hilders & Zambrano (2007) para el estimado de la tenacidad de fractura en el acero SAF 2205, incorporando el ya conocido índice de tolerancia . La ecuación resultante es:
donde:
n es el coeficiente de endurecimiento por deformación y
εf es la deformación de fractura en tensión. Los demás términos ya han sido definidos anteriormente. De acuerdo a la ecuación (51), puede verse que KIC es una función directa de DL y del tamaño de cavidad. Aunque existen muy pocos valores de KIC reportados en la literatura para esta aleación, los mismos están de acuerdo con los encontrados por Hilders & Zambrano (2007). Las variaciones en la tenacidad predicha por este modelo, tienen su orígen en los cambios de rugosidad de las superficies de fractura: mayores valores de KIC corresponden a rugosidades igualmente mayores (mayor área superficial).Para el mismo tipo de acero austenoferrítico grado 2205, de nombre comercial URANUS 45N (EURONORM: 1.4462-X2CrNiMoN 22.5.3), Spyra & Sozanska (2006) han realizado una serie de estudios fractográficos cuantitativos, en superficies de fractura obtenidas por agrietamiento por tensión en ambiente sulfuroso. Para el caso de una carga externa igual a (1,02)
σ yss, la dimensión fractal obtenida por el método de las secciones verticales, fue de 1,25; siendo la superficie de fractura de carácter mixto, con algunas zonas de naturaleza dúctil. En el caso de una carga externa de (0,97)σ ys, el valor respectivo de DL fue de 1,13; y la naturaleza de la superficie de fractura fue frágil. Infortunadamente, el trabajo en cuestión no muestra ninguna evidencia fractográfica de las zonas dúctiles con presencia de cavidades. Aunque no aparece reportada la tenacidad como tal, puede inferirse fácilmente que el material más tenaz deberá corresponder al que presenta el mayor valor de la dimensión fractal.Se ha demostrado a través de modelos computacionales de propagación de grietas en microestructuras reales en diversos tipos de acero (como, por ejemplo, en aceros para herramienta ledeburíticos) y ensayos virtuales en materiales diseñados artificialmente, que la tenacidad de fractura aumenta con el incremento de la dimensión fractal y la altura de los picos o zonas elevadas de los perfiles de fractura correspondientes (Mishnaevsky et al. 2003).
Aunque la tenacidad en general (y la tenacidad de fractura, en particular), es la propiedad mecánica de más importancia en los aspectos tecnológico y de ingeniería, en los diversos tipos de materiales (debido a que viene determinada, tanto por la resistencia como por la ductilidad); a menudo los materiales más dúctiles resultan igualmente los más tenaces. En particular, cuando hay predominio del modo I de separación, o de un estado de tensión axisimétrica, las cavidades sufrirán un alargamiento en una dirección perpendicular o cercanamente perpendicular, a la superficie de fractura. Si el material es tenaz y la deformación experimentada por el mismo resulta comparativamente grande, la relación entre la ductilidad y la dimensión fractal, será de tipo positivo, es decir; similar a la que guardan la tenacidad y D.
Hilders et al. (2002-b), han mostrado este tipo de relación (entre DL y la deformación real de fractura εf , e igualmente entre DL y el tamaño de cavidad dT), para 10 aleaciones de aluminio: las 7 ya nombradas, reportadas anteriormente por Hilders et al. (2002-a); más 2 adicionales: la 2090/T8 y la aleación Al-0,57Si-2,03Ge. En la figura 14, se observan las relaciones DL vs εf y dT vs εf para las 10 aleaciones en cuestión. Puede notarse que existe una proporcionalidad directa en ambas relaciones; lo que indica que tanto el crecimiento de las cavidades, como la rugosidad de las superficies de fractura, se incrementan al aumentar el grado de deformación. Aunque los datos experimentales no se agrupan alrededor de una recta única en cada caso sino que se distribuyen en sendas bandas de valores, la funcionalidad directa resulta inequívoca. También es posible deducir de la figura 14, que los tamaños de cavidad mayores, están asociados igualmente con una dimensión fractal mayor; lo cual se puede explicar sobre la base del incremento experimentado por el área de la superficie de fractura (cavidades mayores) y, por consiguiente, por el aumento de la tortuosidad de la misma. Balankin (1996), ha realizado un importante análisis, de cómo la rugosidad en las caras de una grieta, se traduce en el aumento del área de la superficie de fractura, demostrando cómo la energía liberada al propagarse ésta, se consume parcialmente en la formación de las nuevas superficies y el resto es disipado a los alrededores.
Resulta difícil admitir, en vista de los numerosos resultados publicados, que exista un índice de rugosidad único para todas las superficies de fractura (y por lo tanto un valor único de D). De acuerdo a Bouchaud et al. (1993); el exponente de rugosidad ζ , relacionado con la dimensió fractal a travé de la expresión: D = 3 - ζ (Mandelbrot, 1986); posee el valor constante de 0,8; tal como se observa en los resultados de los diferentes ensayos realizados en la aleación de aluminio 7475 con cuatro tratamientos témicos de diferente tipo (Bouchaud et al. 1990 y Bouchaud et al.1991). Esta universalidad de la dimensión fractal, impediría que los diferentes tipos de mecanismos de fractura, pudieran ser estudiados desde el punto de vista fractal y que D tuviese algú significado respecto a la morfologí. En la prática ha sido posible determinar, sin embargo, que la variación de D estápor encima del error experimental. Por ejemplo, para MgO, Si y Cu, se ha determinado que ζ = 0,6 ± 0,1 (Milman et al. 1993); a escala nanomérica, mediante el uso de microscopía electrónica de efecto túnel. Este valor, obviamente estámá alládel margen de error de los estudios hechos a nivel mesoscópico. Adicionalmente, es comú encontrar diferentes valores de ζ a distintas escalas en ciertos materiales (Dauskardt et al. 1990).
En la búsqueda de correlaciones que expliquen la naturaleza inversa entre D y la tenacidad ó D y la ductilidad, ciertos modelos basados en propiedades geométricas de objetos fractales, han sido propuestos. Independientemente de que estas relaciones no sean de tipo general; sin embargo, es posible que puedan ayudar a explicar porqué a altas deformaciones, cuando las componentes de corte comienzan a tener mayor importancia, las superficies de fractura tienden a ser más planas y por lo tanto, con un valor de D menor. Un modelo fractal basado en curvas de Koch autosimilares, ha sido propuesto por Hilders et al. (2000b) y Hilders et al. (2000-c). Dos curvas de esta clase: la curva triádica (Miloević et al. 2007) y la curva cuadrática tipo 2 (Ghosh et al. 2005), fueron utilizadas como perfiles de fractura artificiales o sintéticos. El modelo asume que las cavidades pueden nuclearse homogéneamente o heterogéneamente, adoptando la forma de un elipsoide de revolución.
Para un rango de deformaciones de fractura intermedio, el modelo explica algunas de las tendencias negativas encontradas en ciertos sistemas de aleación.
CONCLUSIONES
Por todo lo anterior podría inferirse que para cada material deberá existir una microestructura que genere una tenacidad óptima, la cual estará relacionada a un valor característico de la dimensión fractal. Esta constituye la idea principal en torno al uso de D como un parámetro de gran utilidad en la descripción y evaluación de la microestructura, así como en su caracterización. Luego, y de acuerdo con los objetivos que se han planteado, resulta posible establecer, en principio, una serie de conclusiones vinculadas con la relación existente entre la tenacidad y las características fractales de las superficies de fractura en las aleaciones de naturaleza metálica:
1. Se observó que un aumento de la tenacidad en las aleaciones estudiadas, se relaciona con una superficie de fractura más irregular y, por lo tanto, con un mayor valor de la dimensión fractal, lo cual ha sido comprobado por la mayoría de los modelos actuales, para éstas y otras muchas aleaciones de naturaleza metálica.
2. Las correlaciones negativas entre la dimensión fractal y la tenacidad, encontradas en algunas aleaciones de tipo metálico, son muy difíciles de justificar, porque estas dos propiedades se relacionan con la creación de una mayor superficie de fractura durante el acto final de separación.
3. Los valores de la dimensión fractal son dependientes del método empleado para su determinación: el perfolométrico o el de las islas (en el presente caso); aunque para diferentes condiciones experimentales en un mismo material, los valores de D mantienen una misma tendencia, la cual resultó independiente del método.
AGRADECIMIENTOS
A la Fundación Instituto de Mejoramiento Profesional del Colegio de Ingenieros de Venezuela, por el apoyo tanto técnico como financiero. De igual forma, el autor agradece al Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuela CDCH-UCV, el financiamiento recibido a través del proyecto PI 08-00-5904 2005, e igualmente a la Coordinación de Investigación de la Facultad de Ingeniería por el apoyo financiero recibido.
REFERENCIAS
1. Afrin, N., Chen, D.L., Cao, X., Jahasi, M. (2008). Microstructure and tensile properties of friction stir welded AZ31B magnesium alloy. Mater. Sci. Eng. A, 472, pp. 179-186. [ Links ]
2. argon, A.S., Im, J., sofoglu, R. (1975). Cavity formation from inclusions in ductile fracture. Metall. Mater. Trans. A, 6, pp. 825-837. [ Links ]
3. Balankin, A.S. (1996). Models of self-affine cracks in brittle and ductile materials. Phil. Mag. Lett., 74, pp. 415-422. [ Links ]
4. Balankin, A.S. (1997). Physics of fracture and mechanics of self-affine cracks. Eng. Fract. Mech., 57(2/3), pp. 135-203. [ Links ]
5. Balankin, A.S., Ivanova, V.S., Breusov, V.P. (2002). Cooperative effects in the kinetics of metal fracture and the spontaneous change in fractal dimensionality of dissipative structure during ductile-brittle transition. Sov. Phys. Dokl., 37(2); pp. 105-108. [ Links ]
6. Barsom, J.M. & Rolfe, S.T. (1999). Fracture and fatigue control in structures. 3rd Ed., ASTM International, Philadelphia, pp. 67-93. [ Links ]
7. Bauer, R. W. & Wilsdorf, H. G. F. (1973). Void initiation in ductile fracture. Scrip. Metall., 7, pp. 1213-1220. [ Links ]
8. Bouchaud, E., Lapasset, G., Planès, J. (1990). Fractal dimension of fractured surfaces: a universal value? Europhys. Lett., 13, pp. 73-79. [ Links ]
9. Bouchaud, E., Arcangelis, L., Lapasset, G., Planès, J. (1991). Les fractales dans la rupture des matériaux. La Recherche (Paris), 22, p. 808. [ Links ]
10. Bouchaud, E., Lapasset, G., Planès, J., Naveos, S. (1993). Statistics of branched fracture surfaces. Phys. Rev. B, 48, pp. 2917-2928. [ Links ]
11. Broek, D. (1973). The role of inclusions in ductile fracture and fracture toughness. Eng. Fract. Mech., 5(2), pp. 55-66. [ Links ]
12. Broek, D. (1974). Some contributions of electron fractography to the theory of fracture. Int. Met. Rev., 19, pp. 135-182. [ Links ]
13. Broek, D. (2002). Elementary engineering fracture mechanics, 4th Ed., Kluwer Academic Publishers, Boston, p. 24, and p. 419. [ Links ]
14. Carpinteri, A., Chiaia, B., Cornetti, P. (2004). A fractal theory for the mechanics of elastic materials. Mater. Sci. Eng. A, 365, pp. 235-240. [ Links ]
15. Chan, K. S. & Davidson, D. L. (1999). Evidence of void nucleation and growth on planar slip bands in a Nb- Cr-Ti alloy. Metall. Mater. Trans. A, 30, pp. 579-585. [ Links ]
16. Cherepanov, G.P. (1994). Nanofracture mechanics approach to dislocation generation and fracturing. App. Mech. Rev., 47, pp. 326-330. [ Links ]
17. Cherepanov, G.P., Balankin, A.S., Ivanova, V.S. (1995). Fractal fracture mechanics a review. Eng. Frac.Mech., 51(6), pp. 997-1033. [ Links ] 18. C
19. Dabydeen, S.R. (2004). UK steel industry & international trade, iUniverse Inc., Lincoln. [ Links ] 20. D 21. D 22. D 23. D
24. Epstein, M. & Śniatycki, J. (2006). Fractal mechanics. Physica D: Nonlinear Phenomena, 220(1), pp. 54-68. [ Links ] 25. F 26. F
27. Garrison, W. M. & Wojcieszynski, A. L. (2009). A discussion of the spacing of inclusions in the volume and of the spacing of inclusion nucleated voids on fracture surfaces of steels. Mater. Sci. Eng. A, 505, pp. 52-61. [ Links ] 28. G 29. G 30. G 31. Hahn, G.T. & Rosenfield, A.R. (1975). 32. Hilders, O.A. (1985). 33. Hilders, O.A., Berrío, L., Ramos, M., Peña, N. (1997-a). 34. Hilders, O.A. & Pilo, D. (1997-b). 35. Hilders, O.A. & Peña, N.D. (1997-c). 36. Hilders, O.A., Peña, N.D., Ramos, M., Berrío, L., Ichaso, A. (1998). 37. Hilders, O.A. (1998). 38. Hilders, O.A., Sáenz, L., Ramos, M., Peña, N.D. (1999). Effect of 475ºC embrittlement on fractal behavior and tensile properties of a duplex stainless steel. J. Mater. Eng. Perf., 8, pp. 87-90. [ Links ] 39. Hilders, O.A., Sáenz, L., Peña, N., Ramos, M., Quintero, A., Caballero, R., Berrío, L. (2000-a). 40. Hilders, O. A., Peña, N. D., Ramos, M., Berrío, L., Sáenz, L. (2000-b). 41. H 42. H 43. H 44. H 45. H 46. H 47. H 48. J 49. K 50. K 51. L 52. L 53. L 54. L 55. L 56. L 57. L 58. M 59. M 60. M 61. M 62. M 63. M 64. Milman, V.Y., Stelmashenko, N.A., Blumenfeld, R. (1994). Fracture surfaces: a critical review of fractal studies and a novel morphological analysis of scanning tunneling microscopy measurements. Prog. Mater. Sci., 38, pp. 425-474. [ Links ] 65. Miloević, N.T. & Ristanović, D. (2007). Fractal and nonfractal properties of triadic Koch curve. Chaos Solitons and Fractals, 34(4), pp. 1050-1059. [ Links ] 66. M 67. M 68. M 69. M 70. N 71. R 72. R 73. R 74. Russell, A. & Lee, K.L. (2005). Structure-property relations in nonferrous metals, 3rd Ed., Wiley-Interscience, Hoboken, p. 66. [ Links ] 75. S 76. Spyra, K. K. & Sozańska, M. (2006). 77. Tanaka, M., Kimura, Y., Kato, R., Taguchi, J., Oyama, N. (2006). 78. Thomason, P.F. (1985). 79. Thompson, A.W. (1983). 80. Thompson, A.W. & Ashby, M.F. (1984). 81. Vallet, C., Lasseux, D., Sainsot, P., Zahouani, H. (2009). Real versus synthesized fractal surfaces: contact mechanics and transport properties 82. Venkatesh, B., Chen, D.L., Bhole, S.D. (2008). 83. Williford, R.E. (1988). Multifractal fracture. Scrip. Metall. Mater., 22, pp. 1749-1754. [ Links ] 84. Wnuk, M.P. & Yavary, A. (2005). 85. Zaiser, M., Bay, K., Hähner, P. (1999). 86. Zehnder, A.T. (2008).