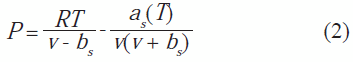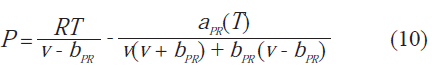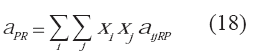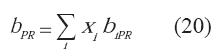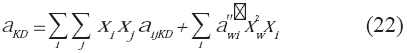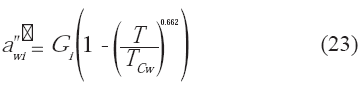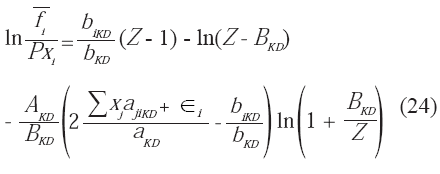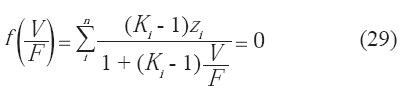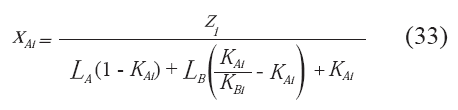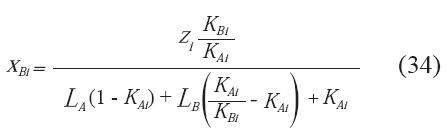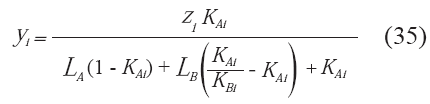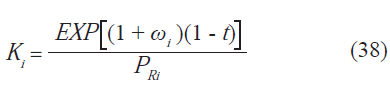Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Facultad de Ingeniería Universidad Central de Venezuela
Print version ISSN 0798-4065
Rev. Fac. Ing. UCV vol.26 no.4 Caracas Dec. 2011
Estimación de equilibrio de fases en tuberías de producción de gas natural a través del uso de ecuaciones cúbicas de estado
Flavio Marín1, Narciso Pérez2
1 Escuela de Ingeniería Química, Facultad de Ingeniería Universidad Central de Venezuela, Caracas 1020A, Venezuela. flaviocordero@gmail.com
2 Departamento de Procesos y Sistemas, Universidad Simón Bolívar, Caracas 89000, Venezuela. naperez@usb.ve
RESUMEN
El presente trabajo surge de la necesidad de estimar el perfil de condensado en tuberías de producción de gas natural, como parte del desarrollo de un paquete de simulación comercial que, empleando los modelos termodinámicos propuestos por Soave, Peng-Robinson y Kabaddi-Danner, estime las características de la formación de condensado y agua en las tuberías de producción de seis pozos de gas natural. Se diseñó un algoritmo de cálculo que permite estimar el perfil de condensado en segmentos de tubería utilizando el modelo de equilibrio Phi-Phi. Se desarrollaron las ecuaciones de balance de materia para equilibrio líquido-vapor (LV) y líquido-líquido-vapor (LLV), así como el uso de las ecuaciones cúbicas en la determinación de los coeficientes de fugacidad y las constantes de reparto de las sustancias, en las cuales los valores iniciales se estimaron a partir de la correlación de Wilson. Finalmente se compararon los resultados obtenidos respecto a datos de campo y se determinó que el error en el cálculo de la cantidad de condensado fue menor al 20% para el caso de equilibrio líquido-vapor y menores a 6% para el líquido-líquido-vapor. La diferencia entre los resultados obtenidos por cada ecuación cúbica de estado para todos los casos fue menor al 7%. La ecuación cúbica de estado de Kabaddi-Danner, utilizando el modelo de equilibrio trifásico, permite representar de manera confiable el equilibrio de fases en sistemas compuestos por mezclas de hidrocarburos de cadena simple y agua con características similares a las estudiadas en este trabajo.
Palabras clave: Ecuaciones de estado, Equilibrio de fases, Tuberías, Pozos de gas, Gas natural, Condensado.
Prediction of phase equilibrium in natural gas well tubing using cubic equations of state
ABSTRACT
This work arises from the need to estimate the condensate profile of a natural gas well tubing, as part of the development of a commercial simulation package, that employs the thermodynamic models proposed by Soave, Peng-Robinson and Kabaddi-Danner to estimate the condensate and condensed water formation in natural gas well tubing was studied. A calculation algorithm to estimate the condensate profile using tubing segments was designed using the Phi-Phi equilibrium model. The study included the development of the mass balance equations for vapor-liquid equilibrium (VL) and vapor-liquid-liquid equilibrium (VLL), and the use of cubic equations of state to determine the fugacity coefficients and the equilibrium constant of each substance; the Wilson equation was used to determine the initial values of the equilibrium constants. The obtained results using each cubic equation were compared with field data, it was determined that the error in the condensate estimation was less than 20% for vapor-liquid equilibrium and less than 6% for vapor-liquid-liquid equilibrium. The estimated error for the difference between the results obtained by each equation of state was less than 7%. The Kabaddi-Danner equation of state and the model of three-phase equilibrium represent with high reliability the phase equilibrium of single-chain hydrocarbons and water systems.
Keywords: Equations of state, Phase equilibrium, Tubing, Gas well, Natural gas, Condensate.
Recibido: diciembre de 2010 Recibido en forma final revisado: diciembre de 2011
INTRODUCCIÓN
El gas natural es una mezcla de hidrocarburos con impurezas. Los compuestos no-hidrocarbonados se dividen en dos grupos; los diluentes, que son aquellos compuestos que reducen el poder calorífico del gas, entre los que se encuentran nitrógeno (N
2), dióxido de carbono (CO2), vapor de agua (H2O); y los contaminantes, como el sulfuro de hidrógeno (H2S) y otros compuestos sulfurados. Debido a la presencia de agua e hidrocarburos de alto peso molecular, existe la posibilidad de formación de condensado en las tuberías de producción de gas natural (Kumar, 1987; Himmelblau, 1997).En los procesos en los cuales están involucradas dos fases, es necesario modelar cada una de ellas, determinar sus propiedades y las composiciones de las especies que conforman las mismas, a través de una ecuación, correlación o modelo matemático (Sandler, 1999). Una ecuación de estado debe poseer generalidad para modelar las fases líquida, vapor y gas, así como también debe ser una expresión que no genere dificultades de cálculo a nivel numérico o analítico al aplicarla (Smith et al. 2000; Sonntag & Van Wylen, 1971), las ecuaciones cúbicas de estado son una de las expresiones matemáticas que permiten describir el comportamiento termodinámico de una sustancia (Wankat, 1988).
EQUILIBRIO DE FASES
En un sistema compuesto por dos o más fases, se dice que las mismas están en equilibrio cuando la temperatura, la presión y los potenciales químicos entre las fases que conforman el sistema en estudio; es decir, que la fugacidad parcial de cada una de las especies, es igual fase a fase (Himmelblau, 1997; Smith et al. 2000).
ECUACIONES CÚBICAS DE ESTADO
La ecuación cúbica de estado (ECE) es una representación analítica del comportamiento volumétrico (PVT) sobre intervalos amplios de presión y temperatura. La primera de este tipo fue la introducida por J. D. van der Waals (ecuación 1) en 1873, la cual representa mejoras desde el punto de vista teórico de la ecuación de gas ideal.
En la ecuación 1, la expresión ubicada del lado derecho de la igualdad se divide en dos términos, el primero representa la presión de repulsión de las moléculas y el segundo término, la presión de atracción de las moléculas. Donde: a y b son constantes positivas, b intenta corregir el volumen ocupado por las moléculas, mientras que el término a, corrige las fuerzas de atracción intermoleculares. A partir de la ecuación propuesta por van der Waals, se han desarrollado otras expresiones cúbicas en el volumen que describen de forma más acertada el comportamiento PVT y el equilibrio de fases (Sonntag & Van Wylen, 1971; Peng et al
. 1975).Ecuación de Soave:
La ecuación introduce modificaciones al término relacionado con las interacciones intermoleculares de la ecuación original de Redlich-Kwong, con la finalidad de determinar de manera más acertada el valor de la presión de vapor de sustancias puras, así como también mejoras en la estimación de las propiedades en sistemas multicomponentes (Soave, 1972).
El modelo propone que el término de interacciones intermoleculares es función de las propiedades críticas, del factor acéntrico y de la temperatura. El factor de ajuste introducido se determinó aproximando las curvas de presión de vapor respecto a la raíz cúbica de temperatura reducida a una línea recta. Soave consideró como valores
experimentales de presión de vapor de las sustancias, los determinados a través de la ecuación de Antoine reportadas por la API (American Petroleum Institute).El modelo comprobó que el uso de las reglas de mezclado propuestas originalmente por Redlich-Kwong en mezclas multicomponentes generan resultados aceptables y fueron
consideradas adecuadas.De acuerdo con los resultados obtenidos por Soave, la ecuación cúbica de estado representa de manera adecuada el equilibrio de fases de sustancias no polares y la presión de vapor de sustancias puras incluyendo compuestos polares. El modelo propuesto por Soave corresponde con la ecuación 2.
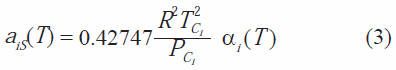
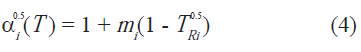
![]()
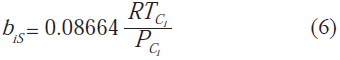
Se mantienen las reglas de mezclado propuestas en el
modelo de Redlich-Kwong y el coeficiente de fugacidad del modelo viene definido por la sigue expresión: 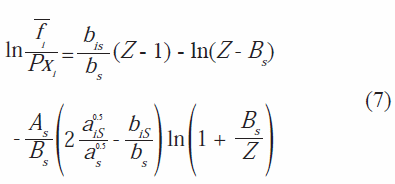


Ecuación de Peng-Robinson
Es un modelo semiempírico que modifica el término de presión de atracción de la ecuación de van der Waals con el fin de determinar con mayor precisión el valor de la densidad de la fase líquida y el valor de la presión de vapor de sustancias puras y mezclas multicomponentes (Peng & Robinson, 1975).
El modelo, al igual que el planteado por Soave, propone que el término de interacciones intermoleculares es función de las propiedades críticas, del factor acéntrico y de la temperatura. El factor de ajuste del modelo inicialmente se estimó como el valor numero necesario para que la ecuación propuesta pudiera calcular la presión de vapor y las condiciones de equilibrio de las sustancias reportadas en la literatura, utilizando el método iterativo de Newton con una tolerancia de 10-4. Los valores calculados se graficaron respecto a raíz cúbica de la temperatura reducida y se aproximaron las curvas a una línea recta.
La ecuación de estado de Peng-Robinson corresponde con la expresión de la ecuación 10:
donde:
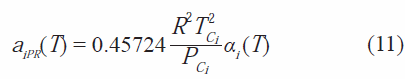
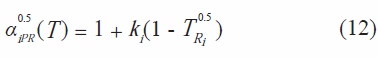
![]()
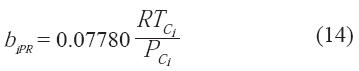
El coeficiente de fugacidad parcial del modelo viene definido por la ecuación 15.
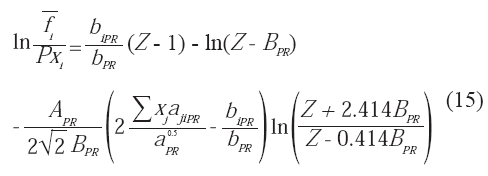
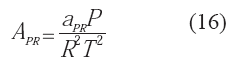
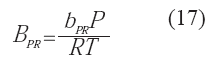
Los parámetros de mezcla utilizados en la expresión de fugacidad parcial corresponden con las reglas de mezclado indicadas por las ecuaciones 18, 19 y 20:
Ecuación de Kabaddi-Danner:
Presentan un modelo fundamentado en la ecuación propuesta por Soave, con modificaciones en las reglas de mezclado y en los parámetros de interacción binaria, con el fin de representar de manera más adecuada el equilibrio vapor líquido de sistemas compuestos por hidrocarburos y agua (Kabaddi & Danner, 1985). Debido a que las modificaciones se presentan exclusivamente en las reglas
de mezclado y en los parámetros de interacción, el uso de las ecuaciones de la 2 a la 6 son válidas, salvo para el agua, sustancia para la cual el parámetro α cambia a la expresió indicada en la ecuación 21:Las nuevas reglas de mezclado siguen las expresiones indicadas en 22 y 23:
Donde: Gi representa la contribución de los diferentes grupos que conforman la molécula de hidrocarburo "
i".Debido a las modificaciones en las reglas de mezclado, el coeficiente de fugacidad parcial se estima a través de la ecuación 24:
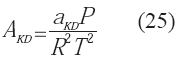
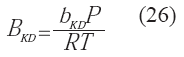
Si el compuesto "
i" es agua: 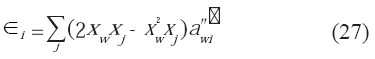
Si "
i" corresponde a hidrocarburo: 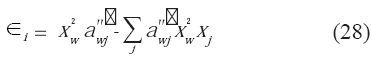
BALANCE DE MASA – ESTIMACIÓN DE LAS CONSTANTES DE REPARTO
Ecuaciones de Balance
Para determinar la proporción en la que los compuestos se reparten en cada una de las fases así como la cantidad de condensado formado respecto al total manejado por la tubería de producción, es necesario resolver el balance de masa global y el balance de masa por componente.
En el caso en que se realice el análisis para dos fases en equilibrio, comúnmente, el balance de masa es expresado a través de la ecuación Rachford-Rice (29) (Wankat, 1988), la cual se obtiene a través de la sustitución de las ecuaciones de balance de masa global y por componente.
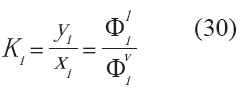
donde:
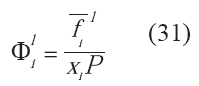
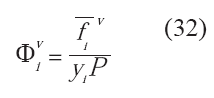
Para condiciones de presión, temperatura y composición definidas, la única variable a definir en la ecuación anterior es la fracción vaporizada, por lo que se requiere de un método numérico para determinarla. (Wankat, 1988; Carroll, 1990; Palke, 1996) El uso del método iterativo de Newton es ampliamente recomendado. La convergencia del mismo para esta ecuación es relativamente rápida; sin embargo, se recomienda acotar el valor de la relación de vaporización entre 0 y 1.
El análisis para sistemas de equilibrio líquido-líquidovapor es estrictamente análogo, se debe hacer el balance de masa por componente y el balance de masa global, donde para el caso de sistemas hidrocarburo agua, una de las fases líquidas corresponde a la fase rica en agua (A) y la fase rica en hidrocarburo (B). Al igual que en el equilibrio líquido vapor, se asume que la sumatoria de las composiciones de cada fase es igual a la unidad. Teniendo esto en cuenta, se debe satisfacer el sistema de ecuaciones compuesto por 33, 34, 35.
donde:
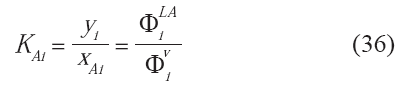
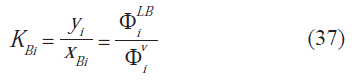
Una de las principales complicaciones que surgen durante el cálculo de equilibrio de fases, es la estimación de valores
iniciales de las constantes de reparto o constantes de distribución de las especies (Ki, KBi y KAi). Con el fin de estimar los valores semilla de las constantes de reparto, en el presente estudio se empleó la correlación Wilson (38), la cual es una aproximación analítica de la constante de distribución basada en la ecuación de Raoult (Al-Saygh et al. 2004).
Para el caso de equilibrio líquido-líquido-vapor, la ecuación 35 genera una buena estimación para los valores de KB. En el caso de la fase rica en agua, para estimar la constante de reparto de los hidrocarburos se recomienda utilizar la ecuación 39 (Peng & Robinson, 1976).
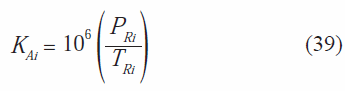
ALGORITMO DE CÁLCULO
El modelo de cálculo de equilibrio de fases, tanto líquidovapor como líquido-líquido-vapor se compiló en un lenguaje de programación de ambiente Windows, con el fin de ser integrado posteriormente a la herramienta de cálculo que se va a desarrollar. Los resultados obtenidos se reportaron y organizaron en una hoja de datos de Microsoft Excel ®
Para estimar el perfil de condensado en la tubería de producción de gas natural, se debe dividir la misma en segmentos de igual longitud. La presión y la temperatura de cada segmento corresponden al promedio de los valores de la entrada y la salida de cada uno, donde la temperatura y presión de entrada a cada segmento es la temperatura y
presión de salida del segmento precedente; el cálculo se realiza siguiendo el sentido del flujo del gas dentro de la tubería de producción.A partir del primer segmento, se determinar el valor de las
constantes de distribución o de equilibrio liquido-vapor/ liquido-liquido-vapor de cada uno de los componentes, empleando las ecuaciones 38 y 39, modelo bifásico y trifásico respectivamente. Para el caso de equilibrio bifásico, se estima la fracción vaporizada usando la ecuación 29 y se calcula la distribución de las especies en cada una de las fases. Para la estimación del equilibrio trifásico, se deber resolver el sistema de ecuaciones compuesto por las ecuaciones 33, 34 y 35 (Peng & Robinson, 1976). Posteriormente, se estima el factor de compresibilidad de cada fase, la fugacidad parcial de cada una de las especies, utilizando las ecuaciones cúbicas de estado (ecuaciones 2, 7, 10, 15 y 24) y se recalculan las constantes de reparto a través de las ecuaciones 30, 36 y 37. Se verifica que los valores calculados correspondan con los valores supuestos, en caso contrario se realiza nuevamente la estimación utilizando los valores calculados como valores iniciales.Una vez estimada la fracción de condensado y el equilibrio de fases, se repite el procedimiento anterior con el siguiente segmento de tubería, hasta completar la longitud del tubo.
RESULTADOS
Se calculó el perfil de condensado para seis tuberías verticales de producción de gas natural, utilizando las ecuaciones cúbicas de estado de Soave, Peng-Robinson y Kabaddi-Danner. El perfil de condensado generado por el modelo para la estimación de equilibrio de fase liquido vapor corresponde con el mostrado en la Figura 1.
Los datos estimados a partir de las ecuaciones cúbicas de estado utilizadas para representar el perfil de condensado a lo largo de la tubería de producción del pozo 1 reproducen con diferencias poco significativas el perfil de condensado reportado en los datos de campo. Para el resto de los pozos analizados en el presente trabajo, se obtiene resultados similares.
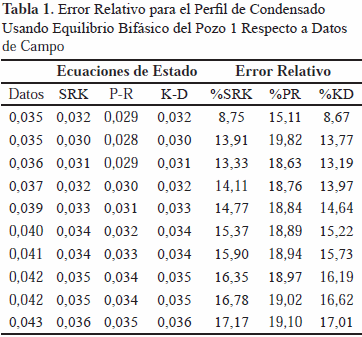
Se calcularon las desviaciones de los perfiles obtenidos respecto a los datos de campo. La máxima desviación relativa obtenida para el pozo 1 fue de 20% respecto a los valores de campo. Para el resto de los pozos analizados el comportamiento es similar al del pozo 1 y los porcentajes de desviación relativa son inferiores al 20%. En la Tabla 1 se presentan el error relativo porcentual para el pozo 1 caso bifásico.
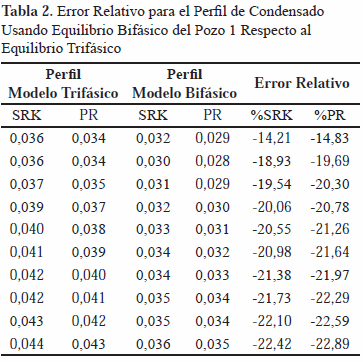
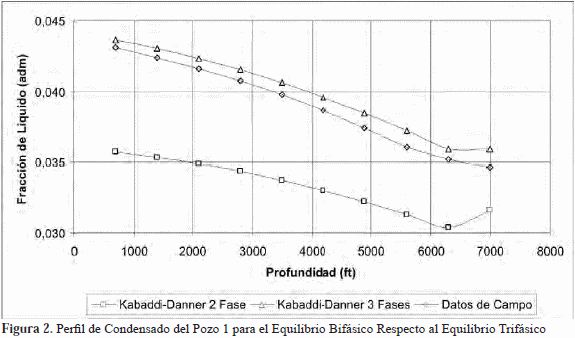
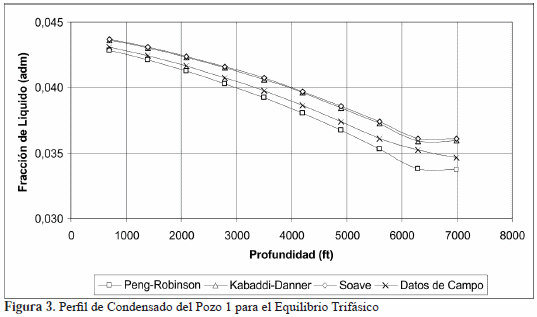
Esta diferencia es similar al obtenido al comparar los valores de fracción de condensado calculados a través del equilibrio bifásico respecto al trifásico. Se compararon los resultados y se determinó que la diferencia del uso de un método de cálculo respecto al otro es menor al 20% para los pozos analizados. En la tabla 2 se reportan las diferencias de las ecuaciones de estado de Soave y Peng-Robinson, para el pozo 1. Se obtuvieron resultados similares para la ecuación de estado de Kabaddi-Danner, los cuales se ilustran en la Figura 2. El perfil de condensado generado por el modelo para la estimación de equilibrio de fase trifásico, líquidolíquido-vapor, corresponde con el mostrado en la Figura 3.
El perfil de condensado a lo largo de la tubería de producción del pozo 1, estimado bajo el esquema de equilibrio líquidoliquido-vapor, presenta diferencias respecto a los datos de campo.
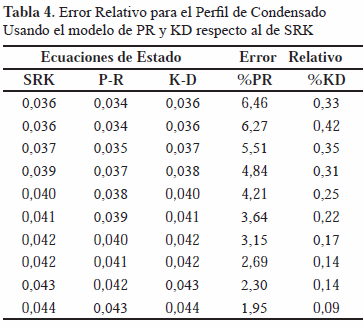
Las desviaciones obtenidas son menores al 5% respecto a los datos de campo para los modelos termodinámicos utilizados, tal y como se muestra en la tabla 3. Este comportamiento se reproduce en el resto de los pozos con porcentajes de desviación menor o igual al indicado. El modelo de equilibrio trifásico representa con confiabilidad el perfil de condensado de los datos de campo.
Se compararon los resultados obtenidos a través de los modelos de Peng-Robinson y Kabaddi-Danner respecto a la ecuación de estado de Soave. Los modelos describen la misma tendencia a lo largo del perfil de condensado. Se determinó que la máxima desviación presentada para la ecuación de Peng-Robinson es menor al 7%; mientras que para la ecuación de Kabaddi-Danner es inferior al 1% para los pozos analizados.
Las desviaciones de la ecuación de estado de Peng-Robinson respecto a la de Soave, se deben principalmente a las modificaciones realizadas por los autores al término de la presión de atracción de la ecuación de estado de van der Waals. Peng & Robinson (1975) entre sus resultados reportan que a condiciones de presión y temperatura superiores al punto crítico la ecuación de Soave presenta desviaciones entre el 7 y el 20%. En la tabla 4 se presentan los resultados para el pozo 1, los mismos se reproducen de manera similar en el resto de los pozos analizados en el presente trabajo.
CONCLUSIONES
La ecuación de estado presentada por Kabaddi-Danner utilizando el modelo de equilibrio trifásico (liquidoliquido-vapor) representa de manera mas adecuada el comportamiento de los pozos estudiados respecto a los datos de campo.
El modelo de cálculo propuesto para la estimación del perfil de condensado de acuerdo al equilibrio de fases líquido-liquido-vapor, reproduce de manera confiable el comportamiento de los pozos analizados. La máxima desviación obtenida para los pozos estudiados fue menor al 5%.
Las ecuaciones cúbicas de estado utilizadas en el presente estudio pueden estimar de manera confiable el perfil de condensado a lo largo de la tubería de producción de gas natural para los pozos analizados.
REFERENCIAS
1. Al-saygh, A., MoshFeghian, M., Maddox, R. (2004). Calculating and Applying K-Values. Oklahoma State University [Artículo en línea] Disponible: http://www.ripi.ir/en/congress12/calculating%20and%20applying.pdf. [ Links ]
2. Carroll, S. (1990). Multivariable Production Systems Optimization. Master Thesis Stanford University. Disponible: http://pangea.stanford.edu/ERE/research/suprid/reports/carrollms.pdf [Consulta: 2010, octubre 15]. [ Links ]
3. Himmelblau, D. (1997). Principios Básicos y Cálculos en Ingeniería Química. Naucalpan de Juárez, México: Prentice Hall. [ Links ]
4. Kabaddi, V. & danner, R. (1985). A Modified Soave Redlich-Kwong Equation of State for Water-Hydrocarbon Phase Equilibria Ind. Eng. Chem. Process Des. and Dev., 24(3), 537-541. [ Links ]
5. Kumar, S. (1987). Gas Production Engineering. Texas, Gulf Publishing Company. [ Links ]
6. PalKe, M. (1996). Nonlinear Optimization of Well Production Considering Gas Lift and Phase Behavior. Master Thesis Stanford University. Disponible: http://pangea.stanford.edu/ERE/research/suprid/reports/palke.pdf [Consulta: 2010, septiembre 25]. [ Links ]
7. Peng, D. & robinson, D. (1975). A New Two-Constant Equation of State Ind. Eng. Chem., Fundam., Vol. 15, No. 1. pp. 59-64. [ Links ]
8. Peng, D. & robinson, D. (1976). Two and Three Phase Equilibrium Calculations for Systems Containing Water. Canadian Journal of Chemical Engineering, 54, 595-599. [ Links ]
9. Sandler, S. (1999). Chemical and Engineering Thermodynamics. United States of America: Wiley International Edition. [ Links ]
10. Smith, J., Van Ness, H., Abbott, M. (2000). Introducción a la Termodinámica en la Ingeniería Química. México: McGrawHill. [ Links ]
11. Soave, G. (1972). Equilibrium Constants from a Modified Redlich-Kwong Equation of State. Chemical Engineering Science, 27, 1197-1203. [ Links ]
12. Sonntag, R. & Van Wylen, G. (1971). Introductions to Thermodynamics. United States of America: Wiley International Edition. [ Links ]
13. Wankat, P. (1988). Equilibrium Staged Separations. New Jersey, Prentice Hall. [ Links ]