Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Facultad de Ingeniería Universidad Central de Venezuela
versión impresa ISSN 0798-4065
Rev. Fac. Ing. UCV vol.27 no.1 Caracas mar. 2012
Estudio del equilibrio líquido-vapor en mezclas de hidrógenoe hidrocarburos con énfasis en procesos de hidrocraqueo
Luis Miguel Gomes 1, Alfredo Escalante 2, Alexis Bouza 3
1 Universidad Simón Bolívar, Ingeniería Química. E-mail: mickygomesdias@hotmail.com
2 Universidad Simón Bolívar, Departamento de Termodinámica. E-mail: escalantealf@gmail.com
3 Universidad Simón Bolívar, Departamento de Termodinámica. E-mail: abouza@usb.ve
RESUMEN
En el presente trabajo se realizó un estudio del equilibrio líquido vapor (ELV) utilizando las ecuaciones de estado (EOS) cúbicas de Peng-Robinson (PR) y Soave-Redlich-Kwong (SRK), con el particular énfasis en lograr representar de manera adecuada el equilibrio líquido vapor en mezclas de hidrógeno con hidrocarburos en un rango de temperatura y presión de interés para procesos de hidrocraqueo. Inicialmente se estudiaron diferentes modelos representativos encontrados en la literatura, basados en la modificación de parámetros tales como el "a
(T,w)" y/o el "b" (covolumen) de las EOS, y en el uso de correlaciones para el parámetro de interacción binaria entre el hidrógeno y el hidrocarburo. Posteriormente, se correlacionaron los parámetros de interacción binaria utilizando un total de 520 datos de solubilidad de hidrógeno en hidrocarburos que van desde n-hexano hasta n-hexatetracontano. Se obtuvo que al utilizar dos parámetros de interacción binaria (kij y EHj) que modifiquen los parámetros a(T,w) y b de las EOS, se logra una representación del equilibrio en estos sistemas con un error relativo no mayor a 3,3 % para la EOS de PR y no mayor a 3,6 % para la EOS de SRK. Las correlaciones obtenidas pueden ser utilizadas para predecir el ELV en sistemas con hidrógeno e hidrocarburos pesados presentes comúnmente en procesos de hidrocraqueo.Palabras clave: Equilibrio líquido vapor, EOS, Hidrógeno, Hidrocarburos, Hidrocraqueo.
VAPOR-LIQUID EQUILIBRIUM STUDY IN MIXTURES OF HYDROGEN AND HYDROCARBONS WITH EMPHASIS ON HYDROCRACKING PROCESSES
ABSTRACT
In this work, a study of the vapor-liquid equilibrium (ELV) in mixtures of hydrocarbons and hydrogen was made using the cubic equations of state (EOS) of Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK). The main objective is to predict accurately the vapor liquid equilibrium in mixtures of hydrocarbons and hydrogen in a range of temperature and pressures commonly used in hydrocracking processes. Initially, various models available in the literature are studied. These models are based in the modification of parametersof the equations of state such as "a
(T,w)" and/or the covolume"b", and in the use of correlations for the binary interaction parameters between hydrogen and hydrocarbons. Subsequently, the binary interaction parameters were correlated using 520 experimental points of solubility of hydrogen in hydrocarbons from n-hexane to n-hexatriacontane.The results obtained indicated that by adjusting two parameters, one for as a(T,w) and other for b,the equilibrium is represented with an average error of 3.3 % for the PREOS and 3.6 % for the SRK EOS. The correlations proposed can be used to predict ELV in systems containing hydrogen and heavy hydrocarbons usually present in hydrocracking processes.Keywords: Vapor-liquid equilibrium, EOS, Hydrogen, Hydrocarbons, Hydrocracking.
Recibido: mayo 2011 Revisado: diciembre 2011
INTRODUCCIÓN
El hidrocraqueo es un proceso de conversión comúnmente utilizado en la industria de la refinación del petróleo. En este proceso se utilizangeneralmente cargas pesadas que, a través de la rotura de enlaces carbono-carbono y la posterior o simultánea hidrogenación (de allí deriva su nombre), se convierten en moléculas más livianas y de mayor valor comercial (Scherzer & Gruia, 1996). El hidrocraqueo generalmente se lleva a cabo en un reactor de lecho fijo trifásico conocido como Trickle-Bed (TBR), el cual es cargado con el catalizador (fase sólida) y a través del cual pasa la carga de hidrocarburos y el hidrógeno requerido. La alimentación del proceso de hidrocraqueo suele ser gasóleos de vacío o residuos pesados provenientes de procesos como el Fluid Catalytic Cracking (FCC) y coquización. Los productos obtenidos pueden ser cortes tales como gas-oil, kerosenes, gasolinas, naftas livianas y hasta gases.
Las condiciones de operación típicas del hidrocraqueo oscilan entre 300 y 450 °C de temperatura y presiones entre 6 y 12 MPa (Scherzer & Gruia, 1996). A estas condiciones de operación, el equilibrio líquido-vapor (ELV) presenta grandes desviaciones de la idealidad. Las EOS cúbicas como las de Peng-Robinson (Peng & Robinson, 1976) y Soave- Redlich-Kwong (Soave, 1972) son una manera bastante eficaz de representar el ELV para mezclas de componentes. Sin embargo, es necesario contar con parámetros de interacción binaria adecuados o modificaciones a la ecuación de estado, si se quiere predecir adecuadamente el equilibrio entre los hidrocarburos y el hidrógeno en condiciones de elevadas temperaturas y presiones. Por lo tanto, sería de gran utilidad contar con un modelo que represente adecuadamente el equilibrio líquido-vapor encondiciones de operación cuando se modelan reactores de hidrocraqueo e hidrotratamiento.
Numerosos autores han realizado estudios del ELV en sistemas hidrógeno-hidrocarburos y han propuesto modificaciones a las EOS para representar adecuadamente la interacción entre los hidrocarburos y el hidrógeno. Estudios tales como los de Graboski et al. (1979) y Twu et al. (1999), han propuesto diferentes modificaciones al parámetro α; mientras que El-Twaty & Prausnitz (1979) modificaron el parámetro b (covolumen). Otras publicaciones, como las de Moysan et al. (1983), Valderrama et al. (1990) y Chenet al. (2009), han propuesto modificaciones para el parámetro a
(T,w), mediante correlaciones para el coeficiente de interacción binaria (kij), entre el hidrógeno y el hidrocarburo. Dichas correlaciones, están basadas en ajustes utilizando datos experimentales.En general, todos los estudios coinciden en que utilizar un coeficiente de interacción binaria adecuado es fundamental para predecir el ELV con bajos márgenes de error. En este trabajose realizó un análisis de algunas de las modificaciones propuestas para las EOS y de las correlaciones para los parámetros cruzados kij más representativos disponibles en la literatura, validándolas utilizando 520 datos experimentales de solubilidades de hidrógeno en hidrocarburos parafínicos que van desde n-hexano (n-C6) hasta n-hexatetracontano (n-C46). De igual manera, se realizó el ajuste de los parámetros de interacción binaria para todos los componentes utilizados tanto para la ecuación de Soave-Redlich-Kwong (SRK) como para la ecuación de Peng-Robinson (PR). El enfoque primordial es lograr representar el ELV con un error mínimo en el rango de presión y temperatura de interés para los procesos de hidrocraqueo.
ECUACIONES DE ESTADO
El estudio del equilibrio-líquido vapor se realizó utilizando principalmente las EOS de PR y SRK. Las modificaciones utilizadas son divididas en dos grupos: aquellas que simplemente dan una correlación para el cálculo de los coeficientes de interacción binarias para ambas EOS y otras que proponen la modificación de los parámetros a y/o b
de la EOS, bien sea a través de la modificación de la función α(T) o de la utilización de reglas de mezclado diferentes para el cálculo de los parámetros a y/o b.La EOS de PR es la siguiente (Peng & Robinson, 1976):
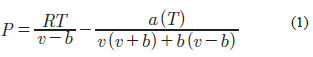
Con los parámetros para los componentes puros calculados de la siguiente manera
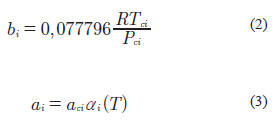
con:
![]()
![]()
donde:
![]()
La extensión para mezclas se realiza utilizando la siguiente expresión:
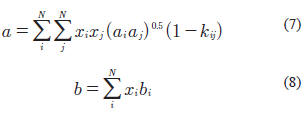
En el caso de la ecuación de estado de Redlich Kwong modificada por Soave la expresión es la siguiente (Soave, 1972).
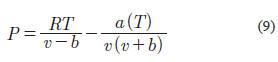
Para esta ecuación, las reglas de mezclado se mantienen de manera similar que para la ecuación de PR y las únicas expresiones que cambian son las que expresan los parámetros
a y b para cada componente, así como la expresión de m para cada componente. Las ecuaciones para el modelo de SRK son las siguientes: 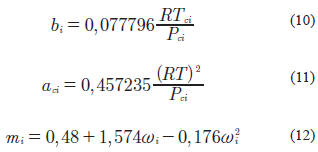
La capacidad de predecir el equilibrio a través de estas dos EOS ha sido justificada extensamente en la literatura (Grabowski & Daubert, 1979; Moysan et al. 1983; Valderrama et al. 1990). Sin embargo, cuando el sistema está constituido por especies con características químicas muy diferentes, la capacidad de predecir buenos valores con estas EOS cúbicas disminuye. Para subsanar dicho problema, se han propuesto diversas correlaciones para estimar los coeficientes de interacción binaria que mejor representen el equilibrio líquido vapor en sistemas que contienen hidrógeno e hidrocarburos. De igual manera, se han planteado variadas modificaciones a las reglas de mezclado existentes y expresiones diferentes para el cálculo de los parámetros ai ó mi.
Para la correcta aplicación de las EOS, es fundamental conocer las propiedades críticas de los compuestos presentes en el sistema. En el caso del hidrógeno, existen diferentes propiedades críticas reflejadas en la literatura unas llamadas "reales" y otras denominadas "efectivas". Las propiedades "reales" del hidrógeno son: ω= -0,216, Tc= 33,19 K y Pc=13,13 bar (Smith, 2003). Las propiedades "efectivas", también denominadas por otros autores como "clásicas", ω= 0, Tc= 41,67 K y Pc= 21,03 bar (API, 1977). Chueh & Prausnitz, (1967), por ejemplo, propusieron correlaciones para las propiedades críticas del hidrógeno en función de la temperatura:
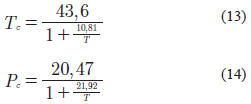
MODIFICACIONES DE LAS REGLAS DE MEZCLADO
El-Twaty & Prausnitz, (1979) propusieron una modificación a la expresión del covolumen. Según estos autores, al añadir un segundo coeficiente de interacción a la EOS, se disminuye el error de predicción y la dependencia de la ecuación con respecto al valor de
kij. Ellos proponen que pequeñas modificaciones en el factor b son más determinantes en el resultado que grandes variaciones del valor de a, producto de kij. La regla de mezclado propuesta fue: 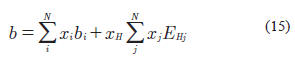
Con esta modificación de las reglas de mezclado, los autores buscaron evitar la necesidad de utilizar valores de kij sin sentido físico. Para las EOS cubicas, los parámetros de interacción binaria kij deben ser mayores que cero y menores que la unidad. Si se emplean valores fuera de este rango, el parámetro a de la ecuación de estado pasa a ser negativo (por definición debe ser positivo), ocasionando que el término atractivo de las EOS cambie de signo, lo cual carece totalmente de sentido físico.
Gray et al. (1983) propusieron un cambio en las reglas de mezclado y al igual que El-Twaty & Prausnitz, (1979), la modificación del parámetro b o covolumen de la ecuación de estado incluye un segundo coeficiente de interacción. Para ellos el b debe calcularse mediante la siguiente expresión:
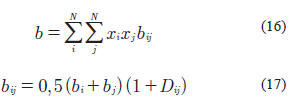
Wong & Sandler, (1992) plantearon una modificación para las reglas de mezclado para las EOS cúbicas. En esta ecuación existen 3 parámetros que se deben correlacionar: Los parámetros τij, τji y kij. Estos autores propusieron calcular los parámetros a y b, para mezclas, de la siguiente manera (Huang et al. 1994):
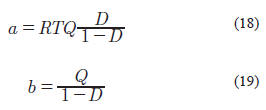
donde: Q y D se calculan con las siguientes ecuaciones:
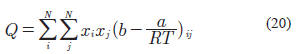
donde:
![]()
y
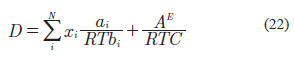
Para la ecuación de PR, C es igual a:
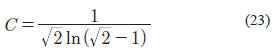
El segundo término de la expresión para calcular D, se obtiene de:
![]()
donde:
![]()
Para el autor, en sistemas compuestos por hidrógeno e hidrocarburos, aji es igual a 0,36. Otra regla de mezclado es la propuesta por Huron & Vidal (1979), expresada por Ioannidis & Knox (1999) de la siguiente manera:
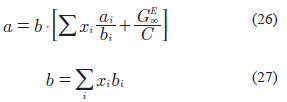
donde ai y bi representan los parámetros de la EOS de PR y C es la constante denotada anteriormente para la regla de mezclado de Wong y Sandler. El parámetro GE∞ se calcula a través de la ecuación:
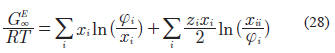
donde:
![]()
Con ![]() . Para una mezcla binara los valores de xij serán:
. Para una mezcla binara los valores de xij serán:
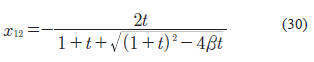
donde
![]()
Para los valores cruzados se tiene que:
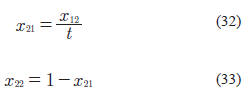
Los parámetros t y β están definidos como:
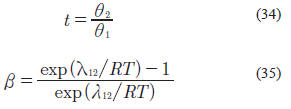
donde: θi se expresa de la siguiente manera:
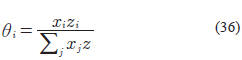
En este caso se tienen un total de cuatro parámetros de ajuste: los coeficientes ri y qi para el hidrocarburo, el Pij para el hidrógeno y el parámetro λ12.
MODIFICACIONES DE LOS PARÁMETROS DE LAS EOS
Graboski & Daubert (1979), propusieron una correlación para calcular el aH2, con el cual se podría asumir el kij=0 entre el hidrógeno y los hidrocarburos. La expresión propuesta fue la siguiente:
![]()
Sus resultados fueron producto de la regresión de datos de solubilidad de H
2 en varios alcanos. Esta correlación fue obtenida para aplicarla con la ecuación de estado de SRK. Estos mismos autores en 1978, reportaron una correlación para el cálculo de mi basados en una regresión de datos de presión de vapor para una gran cantidad de mezclas de hidrogeno con diversos hidrocarburos. La expresión reportada fue: ![]()
Esta correlación fue obtenida para aplicarla conjuntamente con la ecuación de estado de SRK en sistemas de hidrógeno e hidrocarburos únicamente.
El-Twaty & Prausnitz (1979), encontraron que el parámetro ai debía cambiar según las condiciones del sistema en los cuales se encontrara el ELV y que ese cambio dependía de la temperatura del sistema y de la temperatura crítica de los compuestos, para T > Tc la expresión de α será:
![]()
con mi obtenido de la expresión de Graboski & Daubert (1978). Para T < Tc se usa en cambio la misma ecuación propuesta por Soave (SRK) para calcular ai.
Twu et al. (1991) obtuvieron una expresión para calcular a través de tres parámetros (L, M y N), los cuales son únicos para cada componente. Los parámetros fueron calculados por regresión de las presiones de vapor para componentes puros. La expresión reportada por ellos fue:
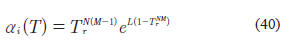
Dicha ecuación se aplica para la predicción de propiedades de mezclas de algunos hidrocarburos e hidrógeno a través de la ecuación de estado de SRK. Los valores reportados para algunos compuestos están expuestos en la siguiente Tabla:
Tabla 1. Parámetros para la función i apara algunos hidrocarburos (Twu et al. 1991)
| Compuesto | L | M | N |
| Metano | 0,106750 | 0,920161 | 3,09674 |
| n-butano | 0,308201 | 0,859571 | 2,0089 |
| n-hexano | 0,128223 | 0,893666 | 4,88241 |
| n-heptano | 0,206521 | 0,852664 | 3,32097 |
| n-octano | 0,363345 | 0,825314 | 2,32182 |
| n-decano | 0,316547 | 0,828468 | 2,90395 |
| Hidrogeno | 1,25282 | 13,269 | 0,04000 |
Twu et al. (1996) desarrollaron luego una función de i acon una estructura similar a la antes expuesta, pero aplicable exclusivamente a sistemas de hidrógeno-hidrocarburo, la cual presenta la siguiente forma, aplicable para la ecuación de estado de SRK.
![]()
CORRELACIONES PARA EL CÁLCULO DEL PARÁMETRO
kij ENTRE HIDRÓGENO E HIDROCARBUROSMoysan et al. (1983), desarrollaron una expresión para calcular los
kij como una función de las propiedades del hidrógeno. Esta correlación depende de la temperatura reducida y de a del hidrógeno. La expresión es: 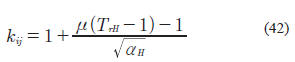
donde: el coeficiente μ depende de la ecuación de estado utilizada.
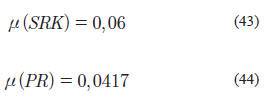
Los a
i son calculados con las expresiones originales propuestas por los autores de las EOS.Valderrama et al. (1990), propusieron otra expresión para la correlacionar el valor de
kij. En esta ocasión la expresión depende de las propiedades del hidrocarburo en lugar de las del hidrógeno. Su expresión es la siguiente: 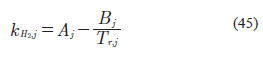
con:
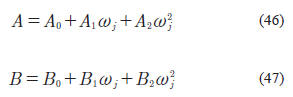
En la siguiente Tabla se presentan los valores de dichos coeficientes dependiendo de la ecuación de estado utilizada:
Tabla 2. Coeficientes Ai y Bi para las EOS cúbicas PR y SRK. (Valderrama et al. 1990)
| Ecuación | A 0 | A 1 | A 2 |
| Soave | 0,2759 | 0,8422 | 6,2969 |
| PR | 0,3063 | 0,7787 | 7,3040 |
| Ecuación | B 0 | B 1 | B 2 |
| Soave | 0,1674 | -0,5609 | 5,1627 |
| PR | 0,1815 | -0,7770 | 5,9287 |
Chen et al. (2009) estudiaron el ELV utilizando mezclas de cortes de hidrocarburos pesados y aromáticos con hidrógeno. Su estudio consistió en variar el contenido total de aromáticos en diversas muestras de hidrocarburos, con la cual obtuvieron una correlación entre la composición porcentual de aromáticos, la temperatura de ebullición y el
kij, dando como resultado la siguiente expresión: ![]()
donde:
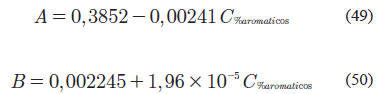
La correlación antes expresada, utiliza la temperatura en grados centígrados y además fue obtenida para ser utilizada en la EOS de PR.
Las diferentes modificaciones y correlaciones, antes mencionadas, fueron validadas con los datos experimentales disponibles en la literatura. En general, estos datos experimentales pueden encontrarse como solubilidad del hidrógeno en el hidrocarburo y están reportados a una determinada temperatura y presión. Todas las correlaciones y modificaciones reflejadas sobre las EOS cúbicas, fueron validadas con estos datos. Para su validación, se utilizó el criterio de punto de burbuja; determinando la presión y la composición del vapor a partir de la temperatura y composición del líquido. Los coeficientes presentes en cada modelo estudiado fueron ajustados de manera de cumplir con el error mínimo. Para cada sistema hidrogeno-hidrocarburo, se halló el error relativo promedio de las presiones de burbuja y la composición de vapor calculadas a través de los diversos modelos y se compararon con los valores experimentales a través de la siguiente expresión:
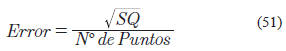
donde:
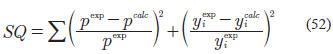
Estas expresiones para el error también fueron utilizadas para verificar la aplicabilidad de las correlaciones propuestas por Moysan et al. (1983), Valderrama et al. (1990) y Chen et al. (2009) para estimar el ELV entre hidrógeno e hidrocarburos pesados.
DATOS EXPERIMENTALES EN ELV ENTRE HIDRÓGENO E HIDROCARBUROS
Para validar los resultados, se contó con un total de 520 datos de solubilidad del hidrógeno en hidrocarburos de diferentes pesos moleculares a diferentes temperaturas y presiones. La siguiente Tabla muestra de manera resumida los componentes empleados, el número de puntos, los rangos de temperatura y presión y, por último, las referencias donde se encuentran disponibles.
Tabla 3. Resumen de datos experimentales disponibles
| HC | N° Ptos | Rangos de T y P | Referencias |
| n-C6 | 33 | T=344,1-410,9K P=1,2-15MPa | (Gao et al. 2001) |
| n-C7 | 12 | T=238,2-323,2K P=0,1MPa | (Cook et al. 1957) |
| i-C8 | 4 | T=248,2-308,2K P=0,1MPa | (Cook et al. 1957) |
| n-C8 | 4 | T=248,2-308,2K P=0,1MPa | (Cook et al. 1957) |
| n-C10 | 147 | T=283,2-583,5K P=1,2-25,5MPa | (Sebastian et al. 1980) (Florusse et al. 2003) (Park et al. 1995) |
| n-C12 | 24 | T=344,3-410,9K P=1,4-13MPa | (Gao et al. 1999) |
| n-C16 | 110 | T=298,1-448,2K P=1,1-15MPa | (Florusse et al. 2003) |
| n-C20 | 22 | T=323,2-423,2K P=2,2-13MPa | (Park et al. 1995) |
| n-C28 | 75 | T=348,2-447,3K P=2.8-13.1MPa | (Florusse et al. 2003) (Park et al. 1995) |
| n-C36 | 53 | T=357,5-447,4K P=1,3-16,7MPa | (Florusse et al. 2003) (Park et al. 1995) |
| n-C46 | 36 | T=372,5-447,5K P = 2,2-16MPa | (Florusse et al. 2003) |
RESULTADOS Y DISCUSIONES
Las presiones de burbuja reportadas en bibliografías previas, para diversos hidrocarburos, fueron utilizadas para validar las EOS, reglas de mezclado y demás correlaciones estudiadas. Los resultados obtenidos se encuentran reportados en la siguiente Tabla:
Tabla 4. Errores arrojados para los diferentes modelos estudiados
| Método | Error Promedio (%) | Error Máximo Obtenido (%) |
| Modificación de α del H2 (Grabowski & Daubert, 1979) | 6,26 | 13,02 |
| Modificación de b (El Twaty & Prausnitz, 1979) | 23,10 | 35,56 |
| Correlación kij para PR (Moysan et al. 1983) | 19,48 | 65,52 |
| Correlación kij para SRK (Moysan et al. 1983) | 19,21 | 91,88 |
| Modificación de Gray (Gray et al. 1983) | 16,42 | 41,29 |
| Correlación kij para SRK (Valderrama et al. 1990) | 34,51 | 73,86 |
| Correlación kij para PR (Valderrama et al. 1990) | 46,29 | 93,39 |
| Regla de Mezclado Wong- Sandler (Huang et al. 1994) | 3,54 | 7,75 |
| Modificación de α del Hidrógeno (Twu et al. 1999) | 17,56 | 89,64 |
| Regla de Mezclado Huron- Vidal (Ioannidis et al. 1999) | 7,69 | 11,80 |
| Correlación kij para PR (Chen et al. 2009) | 56,39 | 140,77 |
| Propiedades "efectivas" del H2 (Chueh & Prausnitz, 1967) | 54,47 | 98,68 |
Los errores reportados corresponden al error promedio tomando en cuenta todos los sistemas (primera columna) y al mayor error obtenido entre todos los sistemas hidrogeno-hidrocarburo.
Para poder analizar los resultados obtenidos se subdividirán en dos grupos. En primer lugar, se encuentran las correlaciones propuestaspara
kij por Moysan et al. (1983), Valderrama et al. (1990) y Chen et al. (2009). Estas correlaciones teóricamente pueden predecir el ELV a partir únicamente de algunas propiedades de los hidrocarburos y deberían ser capaces de arrojar buenas predicciones. Según la Tabla anterior, las correlaciones de Moysan et al. (1983), Valderrama et al. (1990) y Chen et al. (2009) arrojan un error promedio por encima de 19%.Una de las observaciones más importantes al utilizar estas correlaciones, es que en la mayoría de los casos el error aumenta con el número de carbonos presentes en el hidrocarburo, lo cual limita el rango de aplicación de estas correlaciones. Al consultar las referencias originales, se puede evidenciar que la mayoría de ellas fueron obtenidas a partir del estudio de mezclas de hidrógeno e hidrocarburos livianos, con un número de carbonos entres C
1 y C7. Al momento de intentar extrapolar estas correlaciones para compuestos más pesados (por ejemplo, n-C46), las correlaciones fallan y son incapaces de predecir adecuadamente el ELV.Algunas de las correlaciones estudiadas, tal y como la correlación de Chen et al. (2009), sólo reportan valores positivos de
kij, lo cual implica una disminución del parámetro a(T) en las EOS (sea PR o SRK). Al analizar el comportamiento de las EOS cúbicas en relación con los valores de presiones de burbuja predichos, se puede observar que para compuestos entre C6 y C20, las EOS estiman valores de presión de burbuja por encima de los experimentales, con lo cual al añadir un 0 < kij < 1 se disminuye el término atractivo de las EOS (parámetro a) y en su defecto se disminuye el error entre el valor de las presiones de burbuja calculadas con respecto a los valores experimentales, logrando así el ajuste necesario.Para compuestos pesados entre C
20 y C46 el comportamiento es completamente diferente. Las EOS cúbicas de SRK y PR predicen valores para las presiones calculadas menores a los valores experimentales por lo cual se hace imposible un ajuste de a(T) con un valor comprendido 0 < kij < 1. Al utilizar valores de kij ≤ 0 ó kij ≥ 1, el término a(T) carece de sentido físico puesto que se hace negativo; sin embargo, es la única forma de lograr elevar el valor de la presión de burbuja estimada y efectivamente minimizar la función de error. En ese sentido, las correlaciones que arrojan únicamente valores positivos para kij en todo su rango son incapaces de predecir el comportamiento real del equilibrio entre el hidrógeno y los diferentes hidrocarburos pesados.En un segundo grupo, se encuentran las modificaciones de los componentes de la EOS (parámetros como α) y de las reglas de mezclado para los parámetros
a y b. En este grupo se encuentran las modificaciones de Grabowski & Daubert (1979), El Twaty & Prausnitz, (1979), Gray et al. (1983) y Twuet al. (1996) para las EOS, así como las reglas de mezclado de Wong-Sandler y de Huron-Vidal. En este grupo se obtienen errores inferiores al grupo anterior, entre 3,5% y 16%, debido a que los parámetros se ajustaron con datos experimentales.El menor error (3,54%), se obtiene cuando se utiliza la regla de mezclado de Wong-Sandler. Este error es de esperarse ya que para esta regla de mezclado se realizó el ajuste de 3 parámetros característicos, permitiendo así mayores grados de libertad que contribuyen a disminuir el error total. El máximo error de este grupo lo representa la modificación de las propiedades críticas propuestas por Chueh & Prausnitz (1967) para el hidrógeno; esta modificación transforma las propiedades críticas (temperatura y presión) en una función de la temperatura además de asumir el factor acéntrico como cero. Debe señalarse que suponer que las propiedades críticas son función de la temperatura arroja una desviación importante en el momento de predecir el ELV, ya que ni realizando un ajuste del parámetro de interacción binaria
kij se logra obtener un error promedio significativamente menor.De igual manera cabe destacar que si bien utilizando las reglas de mezclado de Wong-Sandler o la de Huron-Vidal se obtienen errores muy bajos (3,54 y 7,7 %), el elevado número de parámetros de ajuste ocasiona que no puedan ser fácilmente utilizables.
De todos los resultados anteriores, se puede inferir que las correlaciones y modificaciones de EOS estudiadas no son capaces de predecir correctamente el ELV entre hidrógeno y compuestos pesados. Es de esperarse que al generar correlaciones para el
kij a partir de datos experimentales para hidrocarburos pesados, la predicción del equilibrio líquido-vapor tendrá un menor margen de error, siendo así de mayor utilidad en mezclas de hidrocarburos pesados e hidrógeno (típicas de procesos de hidrocraqueo) y a las condiciones típicas de estos procesos.Para generar estas correlaciones, lo primero que se estudió fue el efecto de variar el parámetro
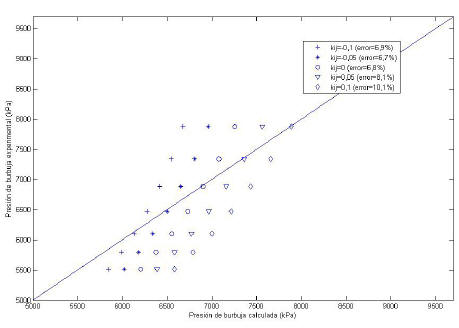
a(T) de las EOS cúbicas PR y SRK. Para ello, se aplicaron inicialmente las reglas de mezclado clásicas, las cuales contemplan un parámetro de interacción binaria kij. En la siguiente figura se muestra el comportamiento predictivo de las EOS, con respecto a las presiones de burbuja, al variar el valor de kij para el n-hexatriacontano.Figura 1. Presiones de burbuja reportadas y calculadas para el hexatriacontano, usando diversos valores de kij
En esta Figura se observa que al variar el parámetro de interacción
kij entre -0,1 y 0,1, los valores de las presiones de burbuja calculadas se desplazan de izquierda a derecha y el error oscila entre 6,7 y 10,1%. Esto indica que la modificación del parámetro de interacción binaria kij permite trasladar y rotar ligeramente las curvas; sin embargo, no es posible que los valores de las presiones de burbuja calculadas se igualen por completo a los valores experimentales o en su defecto se disminuya considerablemente el error utilizando algún valor de kij.Como la variación de
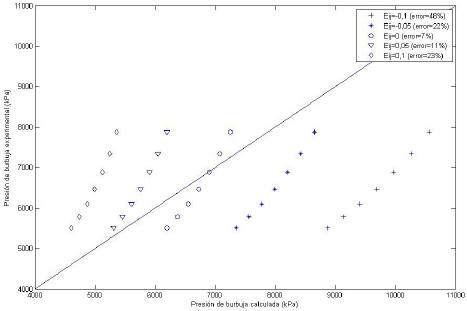
kij no produce el efecto deseado, se procedió a cambiar la regla de mezclado clásica para el covolumen, por la regla de mezclado propuesta por El- Twaty & Prausnitz, (1979) incluyéndose así un nuevo parámetro de interacción EHj. Para poder apreciar el efecto de cambiar el parámetro b, se asumió kij=0 y únicamente se modificó EHj. La siguiente Figura muestra el efecto de la variación antes mencionada:Figura 2. Presiones de burbuja reportadas y calculadas para el hexatriacontano, usando diversos valores de EHj para kij=0
El efecto de variar el parámetro
EHj se ve reflejado nuevamente en una traslación de las curvas de izquierda a derecha, y de un cambio en la pendiente de una manera mucho más importante que la obtenida al variar el parámetro kij. Variaciones entre -0,1 y 0,1 para el EHj hacen que el error oscile entre 7 y 48 %.Sobre la base de lo expuesto anteriormente, se puede inferir que no es posible realizar una buena representación de los datos experimentales utilizando únicamente un parámetro de ajuste, sea
EHj o kij. Si se realiza el ajuste de ambos parámetros, EHj y kij, el efecto obtenido es el siguiente: 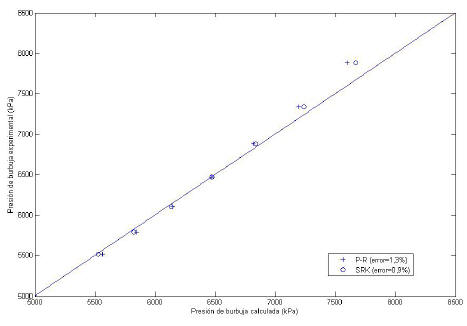
Figura 3. Presiones de burbuja reportadas y calculadas para el hexatriacontano, ajustando los valores de EHj y kij
De estos análisis se puede concluir que para poder correlacionar y predecir el ELV de mezclas compuestos pesados con hidrógeno de acuerdo con los datos experimentales, es necesario utilizar más de un parámetro de interacción, por lo cual se escogió utilizar la regla de mezclado para b
de El-Twaty & Prausnitz, (1979).Para obtener una correlación que se adapte, tanto para compuestos pesados como para livianos, se asumió que el
EHj y el kij son únicos para cada mezcla y son variables en función de alguna propiedad del sistema tal y como el peso molecular del hidrocarburo. Para este caso, el ajuste se realizó utilizando las propiedades reales del hidrógeno. La correlación obtenida, para ser utilizada con la EOS de PR, presenta la siguiente forma: 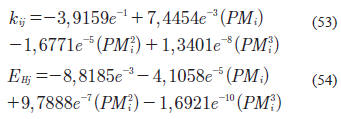
En el caso de la EOS de SRK, se obtuvieron las siguientes correlaciones para EHj y kij:
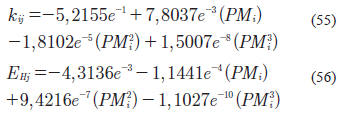
Al aplicar las correlaciones antes presentadas, se calcularon los errores totales utilizando todos los datos experimentales (primera columna) y posteriormente se calcularon los errores en el rango de temperaturas entre 300 y 450 °C y presión entre 6 y 12 MPa, típicos de los procesos de hidrocraqueo.
En la siguiente Tabla se expresan tanto los errores totales porcentuales así como los errores porcentuales para el rango de temperatura y presión de interés:
Tabla 5. Errores al validar la presión de burbuja calculada con la reportada
| Peng Robinson | ||
| Peso molecular | Error total (%) | Error en el rango de interés (%) |
| Hexano (C6) | 1,19 | 0,51 |
| Decano (C10) | 2,48 | 2,95 |
| Dodecano (C12) | 6,53 | 6,35 |
| Hexadecano (C16) | 1,29 | 1,21 |
| Eicosano (C20) | 1,18 | 0,76 |
| Octacosano (C28) | 6,41 | 7,37 |
| Hexatriacontano (C36) | 5,18 | 5,23 |
| Hexatetracontano (C46) | 1,49 | 1,19 |
| Promedios | 3,22 | 3,20 |
| Soave Redlich Kwong | ||
| Peso molecular | Error total (%) | Error en el rango de interés (%) |
| Hexano (C6) | 1,02 | 0,41 |
| Decano (C10) | 5,33 | 6,11 |
| Dodecano (C12) | 5,55 | 5,31 |
| Hexadecano (C16) | 1,24 | 1,09 |
| Eicosano (C20) | 1,13 | 0,66 |
| Octacosano (C28) | 7,43 | 8,38 |
| Hexatriacontano (C36) | 5,34 | 5,43 |
| Hexatetracontano (C46) | 1,25 | 0,96 |
| Promedios | 3,53 | 3,54 |
De la Tabla anterior, se obtiene en primer lugar que las correlaciones planteadas para el
EHj y el kij son capaces de predecir las propiedades de un ELV con un error promedio de 3,22% con la ecuación de PR y de 3,53% con la ecuación de SRK, para una variedad de componentes parafínicos desde C6 hasta C46. El máximo error reportado en todo el rango de presión y temperatura es de 6,53% para la ecuación de PR y de 7,43% para la EOS de SRK. Se puede observar que el error no aumenta con el peso molecular tal y como sucede para las correlaciones validadas de Moysan et al. (1983), Valderrama et al. (1990) y Chen et al. (2009). Este hecho se evidencia al observar el error para el C6 es bastante similar al error para el C46, 1,19% y 1,49% respectivamente, para la EOS de PR. Para SRK el comportamiento es similar (1,02% para C6o hexano, y 1,25% para C46hexatetracontano).Cuando se compara el error promedio obtenido en todo el rango de presiones y temperaturas, con el error obtenido en el rango de interés, se observa que el error porcentual promedio disminuye de 3,22% a 3,20% para el rango de hidrocraqueo utilizando la EOS de PR y aumenta de 3,53% a 3,54% para la EOS de SRK. Es válido señalar que esa disminución de 0,02% y el aumento de 0,01% no son significativos, por lo cual se puede decir que es indistinto el error obtenido al utilizar la correlación en el rango completo de temperatura y presión o al utilizarla sólo en el rango de los procesos de hidrocraqueo, a excepción de tres puntos donde el error varía significativamente (para los componentes C
6 y C20 donde disminuye de manera importante; y para C28 donde aumenta).Al comparar los resultados entre las ecuaciones de PR y SRK se observan errores similares entre sí, con la salvedad de que los errores para la EOS de SRK tienen un error promedio total ligeramente mayor al de la EOS de PR (3,22% para PR y 3,53% para SRK). De igual manera, el máximo error en el rango de temperatura y presión de procesos de hidrocraqueo es aproximadamente 1% mayor en SRK en relación con la ecuación de PR (7,37% para PR y 8,38% para SRK). Con estas ligeras diferencias entre los errores se podría afirmar que es prácticamente igual utilizar cualquiera de las dos EOS anteriores para predecir el equilibrio líquido-vapor en mezclas de hidrocarburos conhidrógeno, en el rango de pesos moleculares estudiados y a condiciones de temperatura y presión típicas de los procesos de hidrocraqueo.
VALIDACIÓN DE LAS CORRELACIONES PROPUESTAS
Para validar las correlaciones antes expuestas, a continuación se presentan las Figuras de presión de burbuja calculada en función de la presión experimental, para tres compuestos: el más liviano (n-hexano, con un peso molecular de 86,18 g/ gmol), uno intermedio (octacosano, con un peso molecular de 394,77g/gmol) y el más pesado (hexatetracontano, con un peso molecular de 646,75 g/gmol). Adicionalmente, se delimitaron los rangos de presión a los utilizados comúnmente en el proceso de hidrocraqueo para facilitar la visibilidad de los errores. Las Figuras son las siguientes:
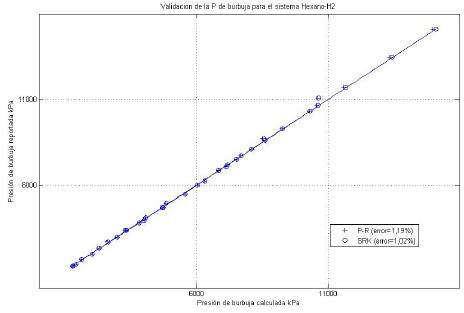
Figura 4. Validación de las correlaciones para el sistema hexano-H2 (C6)
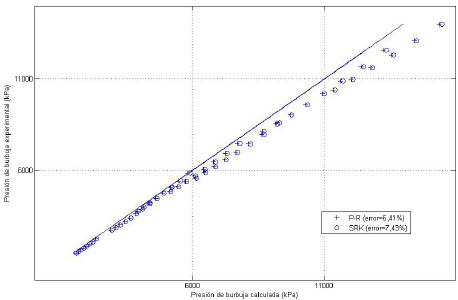
Figura 5. Validación de las correlaciones para el sistema octacosano-H2 (C28)
A partir de las Figuras anteriores, se puede observar que las correlaciones propuestas corrigen de manera exitosa las presiones de burbuja calculadas. En general, los valores de presiones de burbuja calculadas presentan una ligera desviación para presiones mayores a 12MPa; sin embargo, la misma es pequeña (9,67% para SRK y 8,89% para PR, para el octacosano C28). En el caso del hexano, el error promedio es de 1,19 y 1,02 % para PR y SRK respectivamente, lo que representa una considerable disminución del error respecto a la utilización de correlaciones disponibles reportadas en la literatura. Para el hexatetracontano igualmente el error promedio es bastante bajo, con un valor de 1,49 % para la ecuación de PR y 1,25 % para la ecuación de SRK.
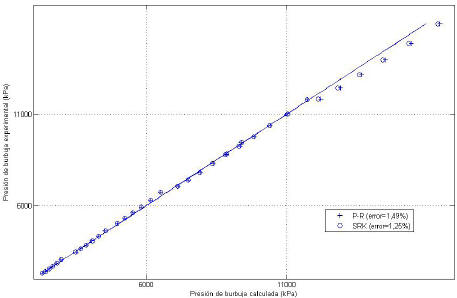
Figura 6. Validación de las correlaciones para el sistema hexatetracontano-H2 (C46)
En el caso del octacosano se puede observar que se mantiene una tendencia similar al hexano y al hexatriacontano aun cuando la desviación tiende a aumentar con la presión. Sin embargo, los errores promedio no son mayores al 7 % para el total de datos experimentales (6,41%) y apenas supera el 7% para el rango de temperatura y presión de las reacciones de hidrocraqueo (7,43 %).
Finalmente, puede afirmarse que las correlaciones propuestas son óptimas para predecir el equilibrio líquido vapor en mezclas de hidrocarburos con hidrógeno en el rango de temperatura de 280 a 550 K, de presión de 1 a 15 MPa y puede ser utilizada para compuestos que posean un peso molecular equivalente entre el valor del C
6 y el valor del C46.En los procesos de hidrocraqueo, generalmente se procesan componentes pesados tales como los gasóleos de vacío o residuos pesados cuyo peso molecular no es superior al del n-hexatriacontano, por lo que las correlaciones propuestas pueden ser útilmente aplicadas para predecir adecuadamente el equilibrio líquido vapor a las condiciones típicas de operación de estos procesos (temperaturas entre 300 y 450 °C y presión entre 6 y 12 MPa). El cálculo del equilibrio líquido vapor es una de las bases fundamentales cuando se quiere modelar algún proceso de separación, tal y como los separadores Flash, o un reactor químico bifásico (en el cual el ELV es un cálculo fundamental). Las correlaciones propuestas son sencillas y fácilmente acoplables con modelos y herramientas de cálculo más complicadas (simuladores comerciales, por ejemplo), y contribuyen a que el cálculo de dicho equilibrio se ajuste con un bajo margen de error a los valores experimentales, a las condiciones de T y P típicas de hidrocraqueo, disminuyendo así los márgenes de error al modelar estos procesos.
CONCLUSIONES
Se estudiaron diferentes modelos para el cálculo del equilibrio líquido-vapor en sistemas con hidrógeno e hidrocarburos. Los modelos están basados en modificaciones a las EOS cúbicas de PR y SRK bien sea a través del uso de una correlación para el parámetro de interacción binaria, de la modificación de algún otro parámetro de la ecuación o de la utilización de reglas de mezclado diferentes a las comúnmente utilizadas. Se encontró que en general todos los modelos estudiados reproducen con cierto margen de error el equilibrio; sin embargo, el error aumenta conforme los hidrocarburos se hacen más pesados.
Para poder correlacionar y predecir adecuadamente el equilibrio líquido-vapor, se determinó para ambas EOS estudiadas que utilizando dos parámetros, uno que modifique a y otro que modifique b, se logra predecir el equilibrio líquido vapor en mezclas de hidrocarburos con hidrógeno, obteniendo un error de 3,53 % en promedio para todos los componentes.
A partir de las correlaciones obtenidas puede predecirse el equilibrio líquido vapor utilizando las EOS de PRy de SRK con bajos márgenes de error para ambas ecuaciones, 3,22 % para la ecuación de PR y 3,53 % para la ecuación de SRK.
Para las correlaciones propuestas se determinó que representan, con un bajo margen de error, el equilibrio líquido vapor en los rangos de temperatura y presión de interés para el modelaje de procesos de hidrocraqueo.
REFERENCIAS
1.
American Petroleum Institute. (1977). Technical Data Book, Vols I y II, American Petroleum Institute, Washington DC. [ Links ]2. Chen, J., Wang, N., Mederos, F., Ancheyta, J. (2009). Vapor-liquid equilibrium study in trickle-bed reactor, Ind. Eng. Chem. Res., 48, pp. 1096-1106. [ Links ]
3. Chueh, P. L. & Prausnitz, J. M. (1967).Vapor-liquid equilibria at high pressures.Vapor-phase fugacity coefficients in nonpolar and quantum-gas mixtures.Ind. Eng. Chem. Fundam.,6, pp. 492. [ Links ]
4. Cook, M. W., Hanson, D. N., Alder, B. J. (1957). Solubility of hydrogen and deuterium in nonpolar solvents.J. ChemPhys 26, (4), pp 748. [ Links ]
5. El-Twaty, A. & Prausnitz, J. M. (1979). Correlation of k-factors for mixtures of hydrogen and heavy hydrocarbons. Chem. Eng. Science. 35, pp.1765-1768. [ Links ]
6. Florusse, L.J., Peters, C.J., Pámies, J.C., Vega, L.F. (2003). Solubility of hydrogen in heavy n-alkanes: experiments and SAFT modeling. AIChE Journal. 49, 12, pp. 3260. [ Links ]
7. Gao, W., Robinson, R.L., Gasem, K. (1999). High pressure solubility of hydrogen, nitrogen, and carbon monoxide in dodecane from 344 to 410 K at pressures to 13.2 MPa. J. Chem. Eng. Data. 44, pp. 130. [ Links ]
8. Gao, W., Robinson, R.L., Gasem, K. (2001). Solubilities of hydrogen in hexane and of carbon monoxide in cyclohexane at temperatures from 144.3 to 410.9 K and pressures to 15 MPa. J. Chem. Eng. Data. 46, pp. 609. [ Links ]
9. Graboski, M. & Daubert, T. (1978). A modified soave equation of state for phase equilibrium calculations.1. Hydrocarbonsystems. Ind. Eng. Chem. Process Des. Dev., 17, pp. 443. [ Links ]
10. Graboski, M. & Daubert, T. (1979). A modified soave equation of state for phase equilibrium calculations. 3. Systems containing hydrogen. Ind. Eng. Chem. Process Des.Dev. 18, (2). [ Links ]
11. Gray, R. D., Heidman, J. L., Hwang, S. C., Tsonopoulos, C. (1983). Industrial applications of cubic equations of state for vle calculations, with emphasis on h2 systems, Elsevier Science Publishers B.V, pp. 59-76. [ Links ]
12. Huang, H., Sandler, S.I., Orbey, H. (1994). Vapor-liquid equilibria of some hydrogen + hydrocarbon systems with the wong-sandler mixing rule. Fluid Phase Equilibria, 96, pp. 143. [ Links ]
13. Huron, M. J. & Vidal, J. (1979). New mixing rules in simple equations of state for representing vapour-liquid equilibria of strongly non-ideal mixtures. Fluid Phase Equilibria, 3, pp. 255. [ Links ]
14. Ioannidis, S. & Knox, D.E. (1999). Vapor-liquid equilibria predictions of hydrogen-hydrocarbon mixtures with the huron-vidal mixing rule. Fluid Phase Equilibria, 165, pp. 23. [ Links ]
15. Moysan, J., Huron, M., Paradowski, H., Vidal, J.(1983). Prediction of the solubility of hydrogen in hydrocarbon solvents through cubic equations of state. Chem. Eng. Science, 38 (7), pp.1085-1092. [ Links ]
16. Park, J., Robinson, R., Gasem, K. (1995). Solubilities of hydrogen in heavy normal paraffins at temperatures from 323.2 to 423.2 K and pressures to 17.4 MPa. J. Chem. Eng. Data, 40, pp. 241. [ Links ]
17. Peng, D. & Robinson (1976). A new two constant equation of state.Ind. Eng. Chem. Fundam.15; pp.49-54. [ Links ]
18. Scherzer, J. & Gruia, A. J. (1996). Hydrocracking science and technology. Marcel Dekker Inc. Primera Edición. [ Links ]
19. Sebastian, H., Simnick, J., Lin, H., Chao, K. (1980). Gas- Liquid equilibrium in the hydrogen + n-decane system at elevated temperatures and pressures. J. Chem. Eng. Data, pp. 68-70. [ Links ]
20. Smith, J.M. (2003). Introducción a la termodinámica en Ingeniería Química. Sexta edición. pp 705. [ Links ]
21. Soave, G. (1972). Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci., 27, pp. 1197. [ Links ]
22. Twu, C., Bluck, D., Cunningham J., Coon, J. (1991). A cubic equation of state with a new alpha function and a new mixing rule. Fluid Fase Equilib. 69, pp. 33-50. [ Links ]
23. Twu, C., Bluck, D., Cunningham J., Coon, J., Harvey, H. (1999). An Approach for the Application of Cubic Equation of Sate to Hydrogen-Hydrocarbon Systems. Ind. Eng Chem. Res, 35, pp. 905-910. [ Links ]
24. Valderrama, J., Cisternas, L.,Vergara, M., Bosse, M.(1990). Binary interaction parameters in cubic equations of State for hydrogen-hydrocarbon mixtures. Chem. Eng. Science, 45(1), pp. 49-54. [ Links ]
25. Wong, D. & Sandler, S. (1992). Theoretically correct new mixing rule for cubic equation of state. AIChe J., 38, pp. 671-680. [ Links ] LISTA DE SÍMBOLOS
| Símbolo | Significado |
| A | Parámetro dependiente del factor acéntrico, para el cálculo del coeficiente de interacción propuesto por Valderrama |
| A0 ,A1 y A2 | Parámetros dependientes de las EOS, para el cálculo del coeficiente de interacción propuesto por Valderrama. |
| aci | Parámetro de las EOS |
| AE | Parámetro de la regla de mezclado de Wong-Sandler |
| Símbolo | Significado |
| ai y aj | Parámetro de la regla de mezclado, para las EOS |
| αH2 | Parámetro de la ecuación de estado, dependiente de la temperatura para el hidrógeno |
| αi (T) | Parámetro de las EOS, dependiente de la temperatura |
| αji | Constante de la regla de mezclado de Wong-Sandle |
| B | Parámetro dependiente del factor acéntrico, para el cálculo del coeficiente de interacción propuesto por Valderrama |
| B0 ,B1 y B2 | Parámetros dependientes de las EOS, para el cálculo del coeficiente de interacción propuesto por Valderrama |
| b | Covolumen |
| bi | Parámetro de la regla de mezclado, para las ecuaciones de estado. |
| β | Parámetro de la regla de mezclado de Huron & Vidal |
| bij | Factor cruzado para el covolumen, según la regla de mezclado de Gray |
| C | Constante de la regla de mezclado de Wong-Sandler |
| C(% aromaticos) | Composición porcentual de aromáticos |
| D | Parámetro de la regla de mezclado de Wong-Sandler |
| Dij | Coeficiente de interacción binaria para el covolumen, según la regla de mezclado de Gray |
| Eij | Coeficiente de interacción binario, para el covolumen |
| φi | Parámetro de la regla de mezclado de Huron & Vidal |
| G∞E | Parámetro de la regla de mezclado de Huron & Vidal |
| Gij | Parámetro de la regla de mezclado de Wong-Sandler |
| kij | Coeficiente de interacción binaria |
| λ12 | Parámetro de ajuste (para el hidrocarburo y el hidrogeno) de la regla de mezclado de Huron & Vidal. |
| Símbolo | Significado |
| mi | Parámetro de la ecuación de estado, dependiente del factor acéntrico |
| P | Presión |
| Pcalc | Presión calculada por EOS |
| Pci | presión crítica del compuesto i |
| PMi | Peso molecular del hidrocarburo i |
| Pexp | Presión experimental o reportada en la bibliografía |
| Pij | Parámetro de la regla de mezclado de Huron y Vidal, es igual a q_i |
| Q | Parámetro de la regla de mezclado de Wong-Sandler |
| qi | Parámetro de ajuste para el hidrocarburo de la regla de mezclado de Huron & Vidal |
| R | Constante universal de los gases |
| T | Temperatura |
| τji y τij | Parámetro de la regla de mezclado propuesta por Wong-Sandler |
| Tbi | Temperatura de ebullición del compuesto i |
| t | Parámetro de la regla de mezclado de Huron y Vidal |
| θi | Parámetro de la regla de mezclado de Huron & Vidal, con respecto al compuesto i |
| Tri | Temperatura reducida del compuesto i, definida como Tr=T/Tci |
| v | Volumen molar |
| ωi | Factor acéntrico del compuesto i |
| xH | Composición molar de hidrogeno |
| xi y xj | Composición molar del compuesto i |
| xij y xij | Parámetros de la regla de mezclado de Huron & Vidal |
| yicalc | Composición molar en fase vapor del compuesto i, calculada por EOS |
| yiexp | Composición molar en fase vapor del compuesto i, experimental o reportada en la bibliografía |
| zi | Parámetro de la regla de mezclado de Huron & Vidal |