Criterio de convergencia en piezas plásticas inyectadas de poliestireno

María V. Candal¹, Héctor Rojas², Joel Campero³

1 Universidad Simón Bolívar, Departamento de Mecánica, Sección de Polímeros

2 Universidad Simón Bolívar, Laboratorio E, Sección de Polímeros

3 Universidad Simón Bolívar

Apartado 89000, Caracas 1080-A, Venezuela.  mcandal@usb.ve 

RESUMEN

El objetivo de este trabajo consistió en la evaluación del criterio de la convergencia como herramienta para la obtención de resultados más precisos en la simulación del proceso de inyección de piezas plásticas. Se alcanzó un espectro mayor de resultados comparados con los presentados en trabajo previos, se obtuvo el número de nodos óptimo para cada parámetro de proceso. Se seleccionaron diferentes concentradores de esfuerzos (triangular, rectangular, semicircular y circular) y se realizaron mallados de las piezas con diferente número de nodos alrededor de las entallas, se usaron de 10 a 80 nodos. Se procedió al estudio de los resultados disponibles en el programa simulador, con la finalidad de verificar la convergencia entre ellos. Se concluyó que los resultados de temperatura de desmoldeo, temperatura de la masa al final del llenado, temperatura de la pared del molde, flujo de calor en la pared del molde, porcentaje en peso y desplazamiento en la dirección "Y" convergen a medida de que se aumenta número de nodos, mientras que la temperatura del refrigerante y el número de Reynolds convergen sin necesidad de aumentar el número de nodos. Sin embargo, los resultados de diferencia de temperatura y desplazamiento en la dirección "Z" nunca presentan convergencia dentro del rango estudiado. Finalmente, existe una serie de resultados que, dependiendo del caso de estudio, convergen o no, entre los cuales se encuentran el porcentaje de rechupe, fuerza de cierre, presión al final del llenado, contracción volumétrica y desplazamiento en la dirección "X".

Palabras clave: Criterio de convergencia, Simulación, Nodos, Piezas plásticas, Herramientas CAD/CAE.

Convergence Criteria For Polystyrene Injection Plastic Parts

ABSTRACT

The main objective of this work involves the study and evaluation of the criteria of convergence as a significant and fundamental tool in simulations made in injected plastic parts. In the same way, it is intended to obtain a greater spectrum of results available at the time to carry out simulations different to present in the work previous, thus obtaining the optimal number of nodes for each of these can be established with greater ease. To achieve this, was selected in each form of stress concentrator (triangular, rectangular, semicircular and circular) the smaller geometry and were made mesh of the parts with different number of nodes around the notches, where the magnitudes employed were 10 to 80 nodes. Once have completed the simulations, all the results available on the simulator program employee were studied, in order to verify the presence of results that converge, results do not converge and what they do from the beginning. Finally, it was concluded that the results of bulk temperature, bulk temperature at end of filling, mold wall temperature, mold wall heat flux, percentage total weight and displacement in "Y" component present convergence when the nodes increment, while the coolant temperature and the coolant Reynolds number always converge. Moreover, the results of temperature difference and displacement in "Z" component, never presented convergence within the range studied. Finally, there are some results that depending on the case had or not convergence, among which are the sink index, clamp force, pressure at end of filling, volumetric shrinkage and displacement in "X" component.

Key words: Criteria of convergence, Simulation, Nodes, Plastics parts, CAD/CAE Tools.

Recibido: marzo 2009 Recibido en forma final revisado: febrero 2012

INTRODUCCIÓN

El moldeo por inyección es el principal proceso de transformación de plásticos encontrado en la industria. Este proceso es idealmente utilizado para elaborar piezas que requieran de una gran precisión dimensional, así como que tengan formas complejas (piezas electrónicas y médicas, partes para la industria automotriz, componentes para la construcción, entre otros) (Beaumont et al. 2002; Osswald et al. 2007).

Igualmente, se hace necesario mantener en consideración que el primer paso antes de la producción de cualquier pieza en particular, es el diseño de la misma, por lo que el proceso de diseño ingenieril toma una gran importancia en lo referente a la concepción de ideas destinadas a la consiguiente solución de problemas. El diseño de cualquier pieza plástica es un proceso de gran complejidad, en el cual la persona encargada de llevar a cabo el proceso debe conocer a cabalidad no sólo aquellos aspectos relacionados con las condiciones finales y operativas del producto, sino también estar al tanto de las particularidades de los materiales con los que trabaja, además de todos aquellos factores que de una u otra forma ejercen influencia sobre la pieza durante su proceso de transformación (Gordillo et al. 1997; Malloy, 1994; Sánchez et al. 1997).

Con la finalidad de llevar a cabo y facilitar la operación de todas las etapas del diseño, se han desarrollado nuevas tecnologías y programas computarizados. Esta serie de programas permite que se pueda trabajar simultáneamente en todas las etapas del proceso de diseño, a la vez de que ofrecen una gran facilidad y versatilidad para la resolución de problemas complejos con una muy buena precisión.

FUNDAMENTOS TEÓRICOS Y ANTECEDENTES

Proceso de inyección

Básicamente, éste es un proceso automatizado y continuo que es desarrollado a alta velocidad, con el que se pueden elaborar gran cantidad de piezas utilizando casi cualquier material (termoplástico, termoestable, elastómero).

El ciclo para este proceso de transformación da comienzo una vez cerrado el molde, seguido de la inyección del plástico fundido a la cavidad. Una vez la cavidad o las cavidades del molde son llenadas, es aplicada una presión de sostenimiento con el objetivo de compensar la contracción final de la pieza; simultáneamente el tornillo gira para cargar el material necesario para la próxima inyección. Por último, una vez enfriada la pieza, el molde se abre y ésta es expulsada (Vivancos et al. 1996). Se puede decir entonces que en términos muy generales este proceso se encuentra comprendido por dos grandes etapas principales, la primera que corresponde al fundido del material plástico en estado sólido, mezclado, presurización y flujo, todo lo cual ocurre en la unidad de moldeo de la máquina de inyección, mientras que en la segunda etapa el material se encuentra dentro del molde de inyección, en el cual será enfriado y tomará la forma final. Igualmente, es importante mencionar que de todas las variables involucradas en el proceso de inyección, las más importantes corresponden a la presión de inyección, presión sostenida, tiempo de presión sostenida, velocidad de inyección, temperatura del fundido y temperatura del molde (Beaumont et al. 2002; Osswald et al. 2007).

Herramientas CAD/CAE/CAM

Las herramientas computacionales se encuentran en la actualidad en una etapa de madurez, por lo que han abierto grandes posibilidades para el rediseño de piezas a la vez de que han contribuido a que los procedimientos de fabricación cambien radicalmente. Estas tecnologías pueden ser divididas en tres grandes grupos: diseño asistido por computadora (CAD), ingeniería asistida por computadora (CAE) y manufactura asistida por computadora (CAM), sin embargo es importante tener en cuenta que estos sistemas deben trabajar sinergísticamente para que los resultados sean los más óptimos. Seguidamente se presenta una descripción más detallada de cada uno de estos sistemas (Rojas & Salas, 1999; Vivancos et al. 1996):

• Diseño asistido por computadora: permite la creación y diseño de la pieza a través de la computadora, haciendo posible el análisis y verificación del mismo.

• Ingeniería asistida por computadora: por medio de ésta es posible realizar las simulaciones que reflejan el comportamiento del sistema en la realidad.

• Manufactura asistida por computadora: la principal función de esta herramienta es la búsqueda de la automatización en el proceso de manufactura de la pieza que se desee realizar, esto a través de la traducción de las especificaciones de diseño a especificaciones de producción.

Métodos numéricos

Entre las distintas formas de resolver sistemas de ecuaciones diferencias en los programas de simulación existentes, el método de diferencias finitas (MDF) es el más simple de todos. Éste consiste en una aproximación de derivadas parciales por expresiones algebraicas, envolviendo los

valores de la variable dependiente en un limitado número de puntos seleccionados. Como resultado de la aproximación, las ecuaciones diferenciales parciales que describen el problema son reemplazadas por un número finito de ecuaciones algebraicas, escritas en términos de los valores de la variable dependiente en los puntos seleccionados.

Sin embargo, es necesario tener en consideración que la resolución de un sistema de ecuaciones diferenciales por MDF presenta una serie de desventajas, entre las cuales se encuentran: la dificultad de satisfacer a plenitud las condiciones de borde y que la precisión de los resultados es pobre si no se trabaja con un número de elementos considerable. Debido a esto, el método de elementos finitos (MEF) es la herramienta dominante en esta área debido a la gran flexibilidad que ofrece al estudio de piezas con geometrías complicadas, las cuales son las que comúnmente son encontradas en los productos elaborados por moldeo por inyección (Chandrupatla & Belegundu, 2002; Reddy, 1993; Weaver & Johnston, 1984).

Antecedentes

De acuerdo a estudios realizados por Candal et al. (2007; 2005), los resultados obtenidos en simulaciones con mallas efectuadas en programas modeladores se ajustan de una manera eficiente a los obtenidos experimentalmente, debido a que estas mallas copian mejor todos los detalles existentes en la pieza, a la vez de que presentan la posibilidad de modificar el tamaño y la posición de los elementos empleados, mientras que las mallas elaboradas a través de herramientas MDF únicamente permiten la variación del número de elementos, haciendo imposible un análisis exhaustivo y localizado de las zonas con cambios en su área transversal, a menos de que no importe incrementar el tiempo de simulación. De igual forma, los sistemas con mallas realizadas bajo MEF exhiben una convergencia y tiempo de simulación más rápido que aquellos que han sido elaborados en algún software de simulación.

Adicionalmente y de acuerdo a estos mismos trabajos, es conocido con anterioridad que los resultados correspondientes a tiempo de llenado, tiempo de ciclo, esfuerzo de corte en la pared del molde antes del tiempo de llenado y esfuerzo promedio en cargas de servicio, presentan una convergencia efectiva.

En cuanto a la influencia de diferentes concentradores de esfuerzos (triangular, rectangular, medio círculo y circular) sobre las propiedades mecánicas de piezas plásticas inyectadas, Candal et al. (2007) encontraron que el factor Kt depende de los parámetros geométricos y de los esfuerzos que genera el concentrador.

Previo a esto, Candal et al. (2007; 2007; 2008a; 2008b) estudiaron el efecto de las variables del proceso de inyección sobre las propiedades mecánicas de piezas que presentan concentradores de esfuerzos triangulares. Se determinó que el factor Kt varía ligeramente, por el material utilizado, de conformidad con las condiciones del proceso (temperatura de fundido, presión sostenida, velocidad de inyección).

METODOLOGÍA

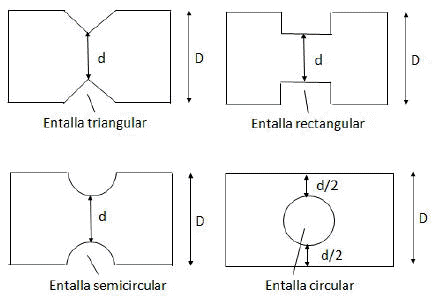
Para el desarrollo de este criterio, se seleccionó en cada forma de concentrador de esfuerzo estudiada (triangular, rectangular, semicircular y circular) (Figura 1) la geometría más pequeña (Candal et al. 2007 a y b), debido a que ésta debería corresponder a la más crítica en cada caso. A partir de esto, se realizaron mallados de las placas en cuestión con diferente número de nodos, en donde las magnitudes empleadas fueron 10 a 80 nodos.

Esta variación en el número de nodos fue llevada a cabo únicamente en las secciones correspondientes a las entallas, debido a que es en los alrededores a estas zonas en donde los cambios de flujo se suponen serán más importantes, y por lo tanto, en donde se requiere que el estudio sea más exacto. Este procedimiento se efectuó de acuerdo a lo establecido por Candal et al. (Candal et al. 2007a; Candal et al. 2007b ; Candal et al. 2005) y Villarroel et al. (2002) en su metodología. En la Figura 2 es presentado un ejemplo de placas con distinto número de nodos, en el cual es posible verificar las diferencias en la zona correspondiente a las entallas.

Figura 1. Formas de entallas estudiadas

De igual manera, al llevar a cabo el mallado de la pieza en el programa modelador empleado, únicamente es posible seleccionar elementos cuadrilaterales o triangulares, por lo que estos últimos fueron seleccionados debido a la capacidad de obtener el menor radio de aspecto posible, así como el mayor número de elementos por unidad de área. No obstante y a pesar de lo anteriormente descrito, en la actualidad existen plataformas computacionales más avanzadas y que permiten un control y manejo más eficiente del proceso de mallado mediante MEF.

La convergencia de resultados mediante el MEF, utilizando una configuración de refinamiento de la malla, es decir, incrementando el número de nodos o elementos, se denomina convergencia-h, mientras que el tipo de convergencia basado en el aumento del grado polinómico se llama convergencia-p. De esto es necesario destacar que el método empleado durante este trabajo fue el de la convergencia-h, debido a que las distintas placas presentan cambios abruptos en su geometría por lo que fue necesario el suministrar una malla más densa alrededor de esas zonas, con la finalidad de conseguir resultados más precisos (Candal et al. 2005; Reddy, 1993).

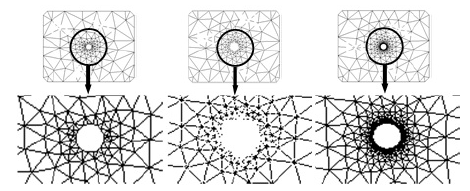
Figura 2. Distribución de los nodos en la entalla circular

Se realizó la simulación del proceso de inyección y del ensayo de tracción e un programa simulador del proceso de inyección, para todas las entallas. Se presenta en la Figura 3 solamente la representación del molde en el programa simulador para la entalla circular.

El material empleado para la simulación fue Poliestireno de Alto Impacto PS8720 de la casa comercial BASF (Módulo tensil 150 MPa, Esfuerzo tensil a la ruptura 22 MPa y Máximo esfuerzo de corte 0,24 MPa). De los resultados reportados por el programa, los que se tuvieron en consideración para evaluar este criterio fueron los de tiempo de llenado, tiempo de ciclo, esfuerzo de corte en la pared del molde antes del tiempo de llenado y esfuerzo promedio en cargas de servicio. Esto debido a que se conocía con antelación la efectiva convergencia de estos resultados, de acuerdo a estudios realizados por Candal et al. (2005; 2007 a y b), sin embargo, otros resultados fueron estudiados y analizados también, con la finalidad de verificar si en realidad existen resultados adicionales que convergen de la misma manera, además de encontrar aquellos que no convergen y cuáles convergen desde el principio.

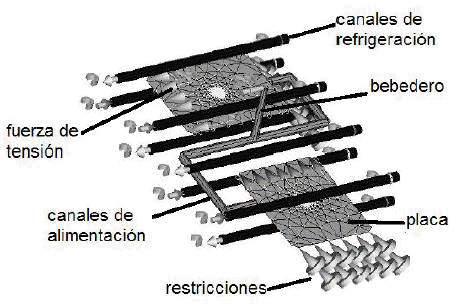
Figura 3. Representación del programa simulador para la entalla circular

RESULTADOS Y DISCUSIÓN

A través de la puesta en práctica de un criterio de convergencia, se intenta principalmente obtener resultados más precisos y ajustados a la realidad con cada simulación realizada (Reddy, 1993).

Adicionalmente, mediante la aplicación de este método, se pretende hallar el número de nodos óptimo a utilizar en un proceso determinado de simulación de una pieza. El número de nodos óptimo corresponderá al punto de la gráfica variable vs. Número de nodos, a partir del cual ya no existen variaciones significativas en los resultados.

De todos los posibles resultados disponibles luego de las simulaciones, fueron tomados en consideración para el establecimiento del criterio de convergencia los referidos a tiempo de llenado de la pieza dentro del molde, tiempo de ciclo y esfuerzo de corte en la pared del molde antes del tiempo de llenado. Estos resultados en particular fueron seleccionados de acuerdo al estudio previamente mencionado y elaborado por Candal et al. (Candal et al. 2005). También se utilizó el resultado pertinente a esfuerzo promedio en cargas de servicio (simulación del ensayo de tracción), debido a la gran relevancia que presenta para el presente estudio y en donde se verificará más adelante que es el resultado que más tarda en converger.

La Figura 4 corresponde a los gráficos de los resultados de la simulación empleados para el criterio de convergencia en función del número de nodos, para el caso de una placa con entalla del tipo semicircular. De aquí es posible observar que el primer resultado en converger es el de tiempo de ciclo, el cual lo hace para 20 nodos, seguidamente el resultado correspondiente al tiempo de llenado alcanza el punto de convergencia en mallas a partir de 40 nodos; sin embargo, tanto para el esfuerzo de corte en la pared del molde, como para el esfuerzo promedio en cargas de servicio es necesario que se cuente con al menos 50 nodos para que los valores puedan estabilizarse. Es por este motivo que las simulaciones realizadas en placas con concentrador de esfuerzos de tipo semicircular, fue obligatorio el mallado de cada una de ellas con 50 nodos alrededor de la discontinuidad.

El mismo procedimiento anterior fue seguido para las restantes geometrías de entallas estudiadas, para las cuales se obtuvo que el número de nodos óptimo para alcanzar la convergencia en concentradores circulares fue de 40 nodos, mientras que para entallas rectangulares y triangulares el número de nodos fue de 70 en ambos casos. Sólo se presentan los resultados para una de estas entallas por ser similares las formas de las gráficas (Figura 5).

Es importante señalar que se tuvo que mantener en consideración, el hecho de que al aumentarse el número de nodos en el mallado, igualmente se incrementa el tiempo necesario para llevar a cabo la simulación del proceso, tal como lo previera Villarroel et al. (2002). Por ello, como anteriormente fue expresado, se decidió realizar el estudio por convergencia-h, de manera que fuese posible la escogencia del número de elementos óptimo y con él realizar todas las simulaciones.

Adicionalmente, fueron estudiados otros resultados disponibles por el programa simulador para todas las formas de concentrador de esfuerzos estudiados, pero sólo se muestran las figuras para dos por ser similares, con el objeto de analizar la presencia o no de convergencia y de este modo poder ampliar el espectro de posibles resultados que se deben tomar en consideración al momento de aplicar esta metodología.

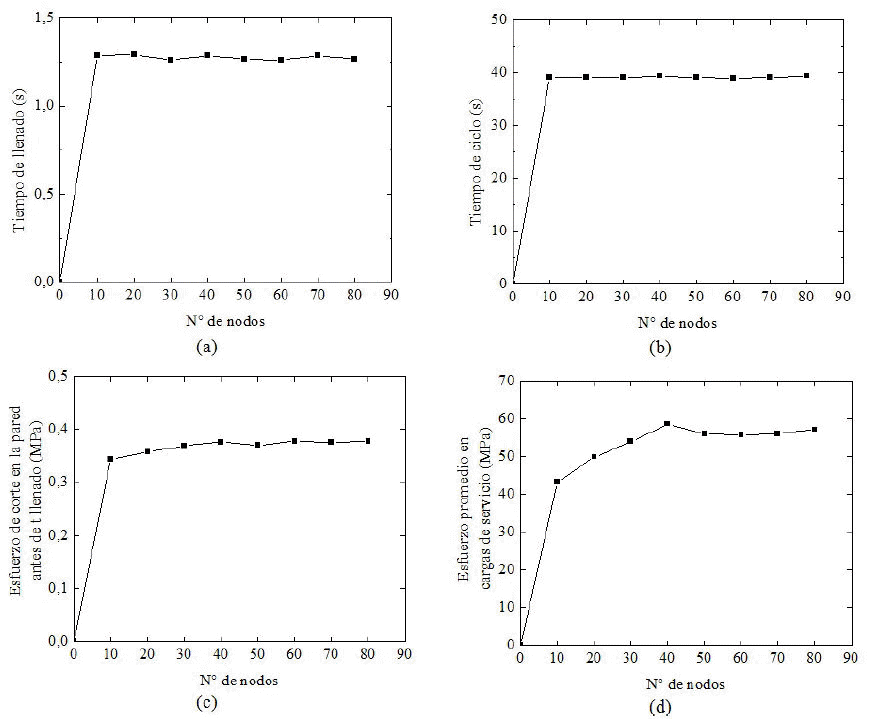
Figura 4. Criterios de convergencia para una placa con entalla semicircular. (a) Tiempo de llenado, (b) tiempo de ciclo, (c) esfuerzo de corte en la pared del molde antes del tiempo de llenado de la cavidad y (d) esfuerzo promedio en cargas de servicio

 

En la Tabla 1 se presentan todos los resultados adicionales estudiados para entallas semicirculares y triangulares, así como una descripción en cada caso de la convergencia o no descrita y bajo qué cantidad de nodos es establecida en el caso de ser posible, esto último dentro del rango de 10 a 80 nodos evaluados en las simulaciones realizadas.

A partir de esto, se puede afirmar que los resultados de temperatura de desmoldeo, temperatura de la masa al final del llenado, temperatura de la pared del molde, flujo de calor en la pared del molde, porcentaje en peso y desplazamiento en la dirección "Y" presentan convergencia en todos los casos, mientras que la temperatura del refrigerante y el número de Reynolds convergen desde el principio.

Figura 5. Criterios de convergencia para una placa con entalla rectangular. (a) Tiempo de llenado, (b) tiempo de ciclo, (c) esfuerzo de corte en la pared del molde antes del tiempo de llenado de la cavidad y (d) esfuerzo promedio en cargas de servicio

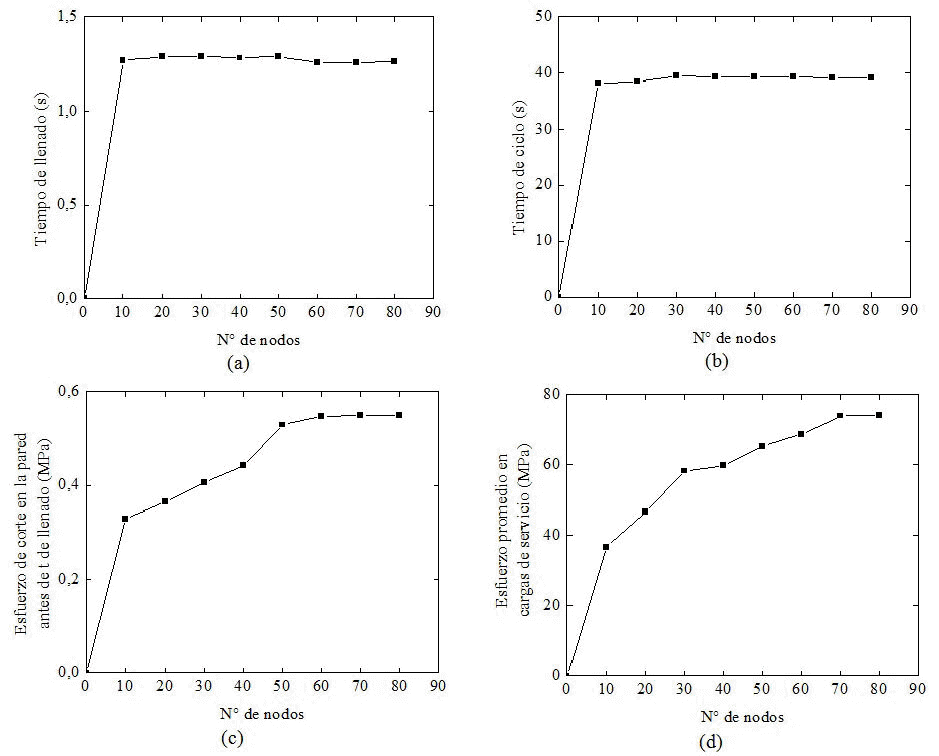
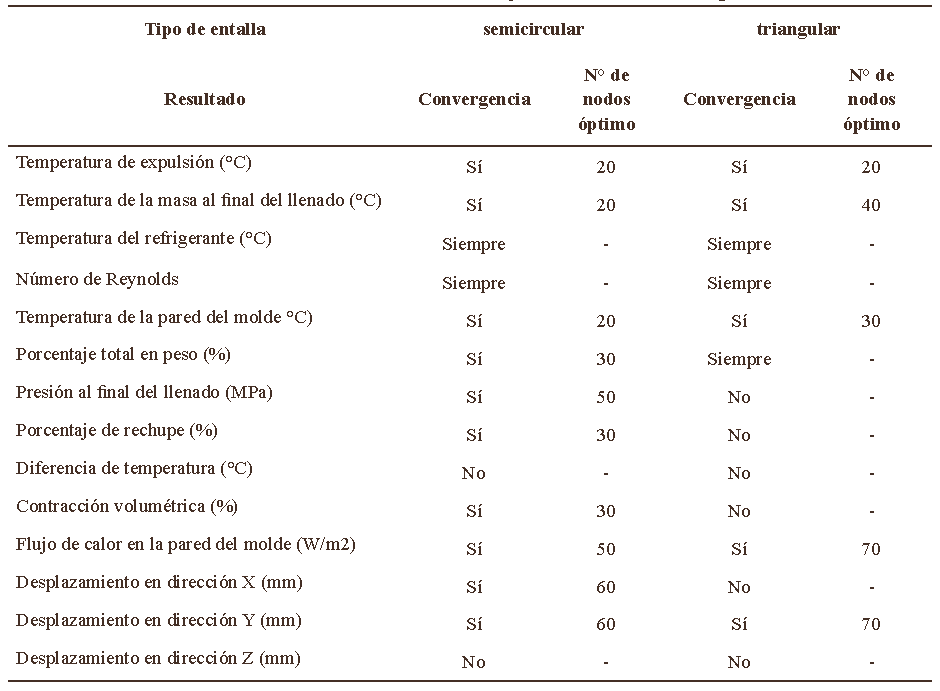
Tabla 1. Resultados adicionales estudiados para el criterio de la convergencia

Por otra parte, los resultados correspondientes a diferencia de temperatura y desplazamiento en la dirección "Z" nunca presentan convergencia dentro del rango estudiado. Por otro lado, existe una serie de resultados que dependiendo del caso de estudio exhiben o no convergencia, entre los cuales se encuentran el porcentaje de rechupe, fuerza de cierre, presión al final del llenado, contracción volumétrica y desplazamiento en la dirección "X" (Figuras 6 a 11).

Al analizar estos datos, es posible encontrar que aquellos resultados correspondientes a la fase de llenado de la pieza en la cavidad, no presentan ningún tipo de inconvenientes por lo que efectivamente pueden alcanzar la convergencia. No obstante, el problema es encontrado para los resultados vinculados con la fase de enfriamiento y contracción, además de la fuerza de cierre ejercida por la máquina de inyección. Esto es principalmente ocasionado a que las curvas P-v-T elaboradas para los distintos materiales disponibles en la base de datos del programa simulador, fueron realizadas bajo condiciones de compresión isotérmica y teniendo en cuenta únicamente a la temperatura del fundido y a la presión de inyección. En vista de esto, la velocidad de enfriamiento no fue tomada en consideración, por lo que los resultados obtenidos para el volumen específico en cada caso, no se corresponden a la realidad, lo cual puede ser evidenciado al observar la variación de las curvas de volumen específico en función de la presión y temperatura, para diferentes velocidades de enfriamiento, como las realizadas por Pantani & Titomanlio (2001), en donde éstas presentan grandes cambios en sus formas.

Desde el punto de vista ingenieril, la influencia de las condiciones del proceso y particularmente de la velocidad de enfriamiento, ejercen un notable peso sobre el volumen específico, el cual a su vez es una importante propiedad del material, ya que éste determina la posible contracción o alabeo final de la pieza. Para el caso de piezas con espesores variables, la aproximación realizada por el simulador variará fuertemente, no obstante, para piezas con espesores relativamente uniformes, como las empleadas en este estudio, la aproximación realizada no es tan incongruente, sin embargo, no es exacta y por ello se presentan los errores obtenidos y la no convergencia de estos resultados (Zuidema et al. 2001).

Figura 6. Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos semicirculares (a) Temperatura de desmoldeo, (b) Temperatura de la masa al final del llenado, (c) Fuerza de cierre, (d) Temperatura del refrigerante, (e) N° De Reynolds y (f) Temperatura de la pared del molde

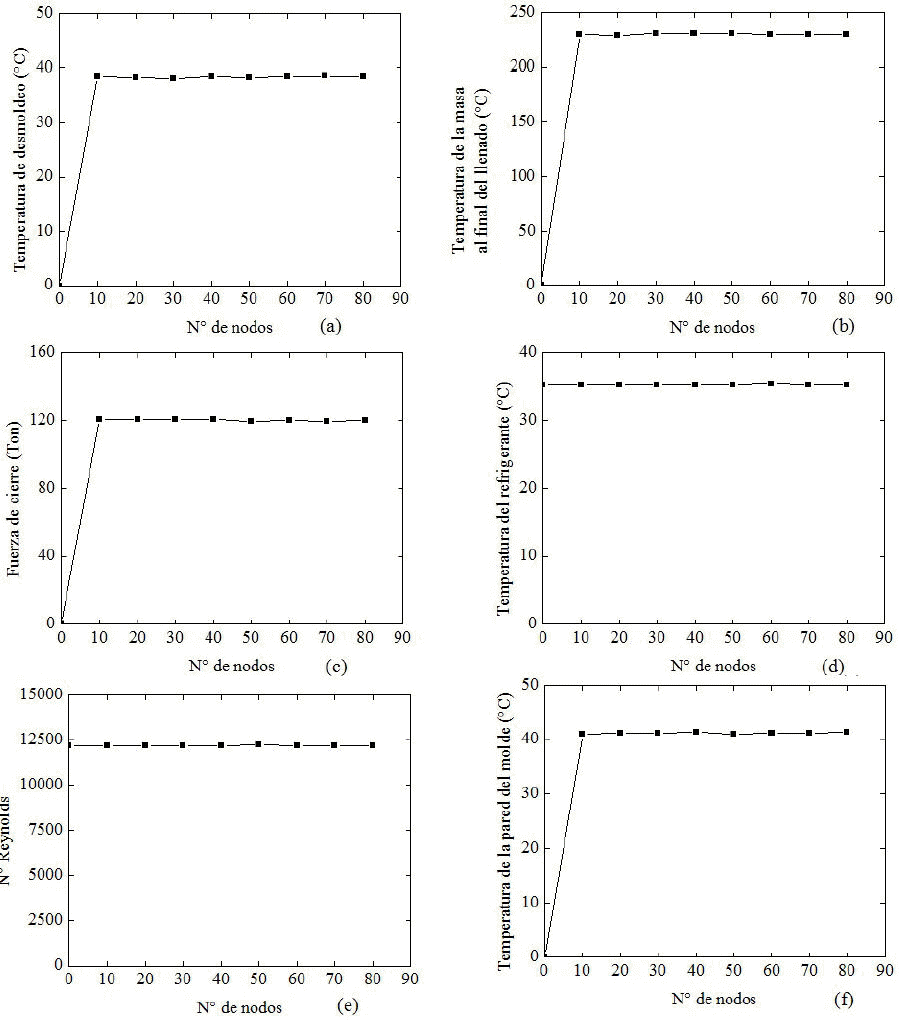
Figura 7. Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos semicirculares (a) Porcentaje total en peso, (b) Presión final del llenado, (c) Porcentaje de rechupe, (d) Diferencia de temperatura; (e) Contracción volumétrica y (f) Flujo de calor en la pared del molde

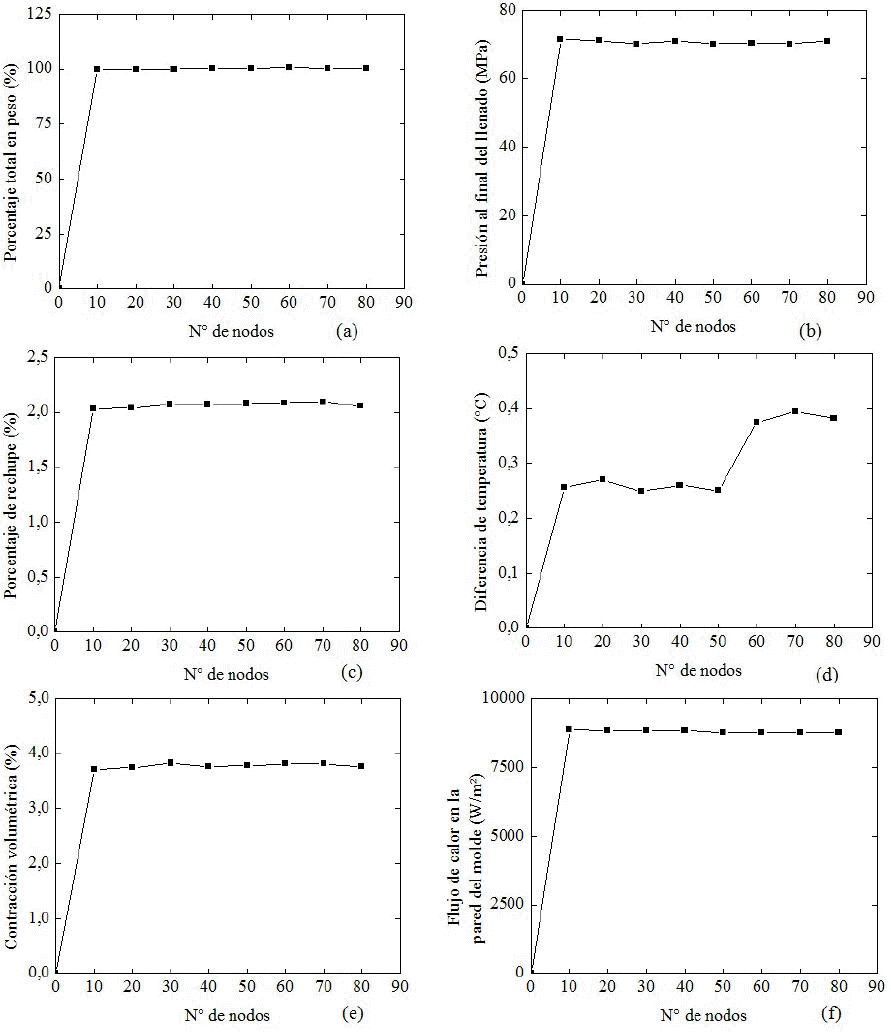
Figura 8. Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos semicirculares (a) Desplazamiento en "x", (b) Desplazamiento en "y" y (c) Desplazamiento en "z"

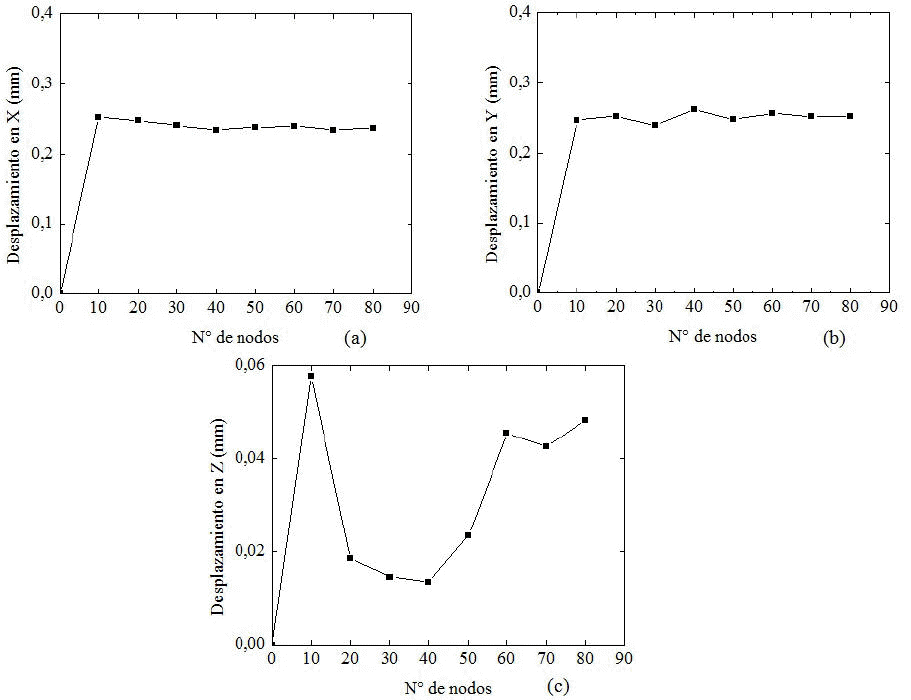
Figura 9. Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos triangulares (a) Temperatura de desmoldeo y (b) Temperatura de la masa al final del llenado

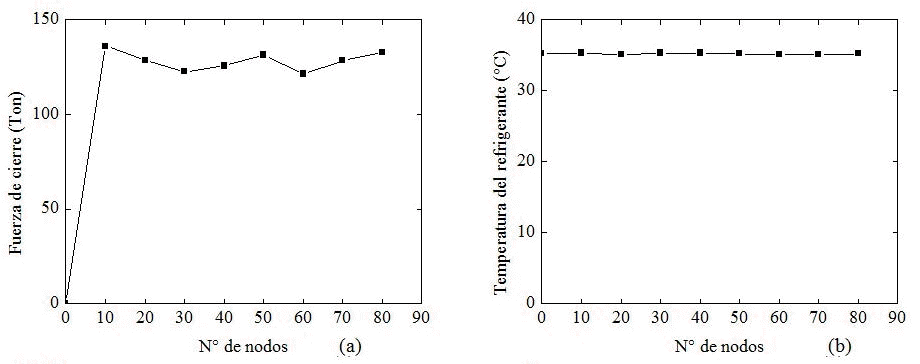
Figura 10. Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos triangulares (a) Fuerza de cierre, (b) Temperatura del refrigerante, (c) N° De Renolds, (d) Temperatura de la pared del molde, (e) Porcentaje total en peso y (f) Presión final del llenado

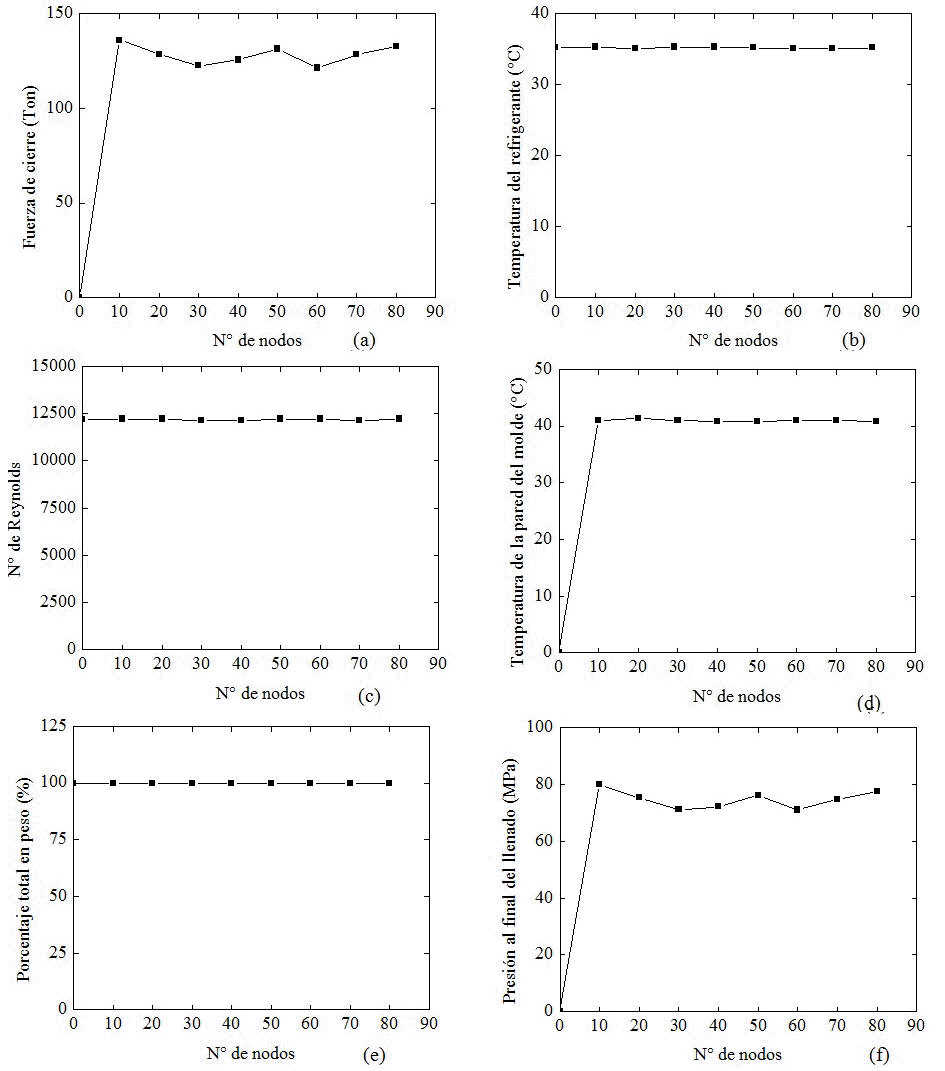
Figura 11. Otros resultados utilizados para el estudio del criterio de la convergencia en placas con concentradores de esfuerzos triangulares (a) Porcentaje de rechupe, (b) Desplazamiento en "x", (c) Desplazamiento en "y" y (d) Desplazamiento en "z"

CONCLUSIONES

• Es de vital importancia el establecimiento de un criterio para la convergencia en simulaciones realizadas mediante sistemas CAE, debido a que a través de éste será posible la obtención de resultados precisos y ajustados a la realidad.

• Resultados como la temperatura de desmoldeo, temperatura de la masa al final del llenado, temperatura de la pared del molde, flujo de calor en la pared del molde, porcentaje en peso y desplazamiento en la dirección "Y", presentaron rápida convergencia en ambos casos de estudio, mientras que la temperatura del líquido refrigerante y el número de Reynolds convergen desde el principio en todo el rango de elementos simulado.

• Los resultados correspondientes a diferencia de temperatura y desplazamiento en la dirección "Z" nunca presentaron convergencia dentro del rango estudiado, mientras que resultados como el porcentaje de rechupe, fuerza de cierre, presión al final de llenado, contracción volumétrica y desplazamiento en la dirección "X", convergen dependiendo del caso evaluado, esto debido al problema de sobreestimación de la contracción y fuerza de cierre presente en el programa empleado.

REFERENCIAS BIBLIOGRÁFICAS

1.Beaumont, J., Nagel, R., Sherman, R. (2002). Successful injection molding: process, design, and simulation. USA: Hanser Gardner Publications. 127-150.         [ Links ]

2.Candal, M. V., Campero J., Rojas, H. (2007). Effect of four stress concentrators over the mechanical properties of injected plastic parts, SPE’s ANTEC Proceedings, s/p.        [ Links ]

3.Candal, M. V., Morales, R. A., Gorrin, K. (2007). Influence of the elements number of a mesh over the simulations results, Journal of Plastics Technology, July, 1-8.         [ Links ]

4.Candal, M. V., Morales, R., González, O. (2005). Effect of the finite element meshing for designing plastic pieces, Polymer-Plastics Technology and Engineering, 44 (8-9), 1573-1590.         [ Links ]

5.Candal, M. V., Jiménez, J., Rojas, H. (2007). Methodology for the study of the stress concentrators in plastic parts, Polymer-Plastics Technology and Engineering, 46 (10), 991-999.         [ Links ]

6.Candal, M. V., Rojas, H., Jiménez, J. (2007). Influence of a triangular stress concentrator on the mechanical properties of plastic parts, SPE’s ANTEC proceedings, s/p.         [ Links ]

7.Candal, M. V., Rojas, H., Jiménez, J. (2008). Determination of Kt curves for plastic parts with a triangular stress concentrator, Polymer-Plastics Technology and Engineering, 47 (1-3), 82-88.         [ Links ]

8.Candal, M. V., Rojas, H., Jiménez, J. (2008). Effect of the injection molding process conditions over the determination of Kt curves for plastic parts, Polymer- Plastics Technology and Engineering, 47 (1-3), 89-95.         [ Links ]

9.Chandrupatla, T. & Belegundu, A. (2002). Introduction to finite elements in engineering. USA: Prentice Hall. 1- 10         [ Links ]

10.Gordillo, A., Sánchez, M., Martínez, A. (Abril-Mayo 1997). Simulación del proceso de inyección en el diseño de piezas de plástico. Plásticos Universales. Recuperado de: http://www.plastunivers.com/Tecnica/Hemeroteca/ArticuloCompleto.asp?ID=5035 .         [ Links ]

11.Malloy, R. (1994). Plastic part design for injection molding. USA: Hanser Gardner Publications. 1-50         [ Links ]

12.Osswald, T., Turng, L., Gramann, P. (2007). Injection molding handbook. USA: Hanser Gardner Publications. 541-564.         [ Links ]

13.Pantani, R. & Titomanlio, G. (2001). Description of PvT behavior of an industrial polypropylene–EPR copolymer in process conditions, Journal of Applied Polymer Science, 81 (2), 267-278.         [ Links ]

14.Reddy, J. (1993). An introduction to the finite element method. (2th Ed.). USA: McGraw-Hill. 12-29         [ Links ]

15.Rojas, O. & Salas, J. (1999). Producción automatizada sistemas CAD/CAE/CAM. Industrial Data. Recuperado de:http://sisbib.unmsm.edu.pe/bibvirtual/Publicaciones/indata/v02_n1/produccion.htm .         [ Links ]

16.Sánchez, M., Gordillo, A., Martínez, A. (Febrero- Marzo 1997). Diseño optimizado de piezas de plásticos. Plásticos Universales. Recuperado de: http://www.plastunivers.com/Tecnica/Hemeroteca/ArticuloCompleto.asp?ID=4808 .         [ Links ]

17.Villarroel, S., Morales, R., Sánchez, A. (2002). Effect of the mesh number elements in the simulation results of normalized test specimens injection molded, SPE’s ANTEC Proceedings s/p.         [ Links ]

18.Vivancos, J., Fenollosa, F., Costa, L. (1996). Tendencias actuales de los sistemas CAD/CAE/CAM. Universidad Politécnica de Cataluña. Recuperado de: http://www.teleworkspain.com/Art019.htm .         [ Links ]

19.Weaver, W. & Johnson, P. (1984). Finite elements for structural analysis. USA: Prentice-Hall, Inc. 5-23         [ Links ]

20.Zuidema, H., Peters, G. W., Meijer, H. E. (2001). Influence of cooling rate on PvT-data of semicrystalline polymers, Journal of Applied Polymer Science, 82, 1170-1186.        [ Links ]