Efecto de la vaporización de la carga en reactores de hidrotratamiento

Alejandro Sabbagh, Ronald Chacón, Alexis Bouza

Departamento de Termodinámica y Fenómenos de Transferencia. Universidad Simón Bolívar

e-mail: alejandro.sabbagh@gmail.com e-mail: ronaldchj1@gmail.com e-mail: abouza@usb.ve

RESUMEN

Las reacciones de hidrotratamiento constituyen uno de los principales procesos en refinación, es por tal motivo que en la búsqueda para obtener un mayor entendimiento de estos procesos se procederá a incluir la vaporización de la carga y la reacción en la fase gas. Estas consideraciones conllevan a modelos de cálculo mucho más complejos, pero mucho más ajustados a lo que ocurre realmente durante el proceso de hidrotratamiento. Los resultados obtenidos en este trabajo, muestran un efecto competitivo entre la disminución de la concentración y el aumento del tiempo de residencia en la conversión, efectos de la vaporización; de igual forma se puede observar, a través de un error promedio global, con respecto a una serie de datos experimentales, que el sistema que considera la vaporización de la carga y la reacción en las dos fases se ajusta mucho mejor, con un error global de 4,80%, mientras que sistema no considera la vaporización presentó un error de 5,22%. Partiendo del análisis comparativo entre las resistencias a la transferencia de masa y las resistencias de reacción química, se concluyó que los efectos de la transferencia de masa están ausentes en el reactor y en las condiciones de operación donde se obtuvieron los datos experimentales.

Palabras clave: Hidrotratamiento, Gasóleo de vacío, Equilibrio líquido-vapor, Modelaje y reactor.

Effect of feed vaporization in hydrotreating reactions

ABSTRACT

Hydrotreating reactions are one of the main refining processes. In this paper, in order to reach a greater understanding of these processes, the vaporization of the feedstock and the reaction in the gas phase are considered. These factors lead to a more complex calculation model, but much more alike to what really happens during the hydrotreating process. Results from this study show a competitive effect between the decrease in concentration and increased residence time over conversion, as the effect of vaporization. The global average error compared to experimental data showed that the system with vaporization and the reaction in both phases fits much better, with an overall error of 4.80%, while the system with vaporization and the reaction only in the liquid phase obtained an overall error of 5.22%. Starting from the comparative study among the resistances to mass transfer and the resistances of the chemical reaction, it is possible to conclude that there are no mass transfer effects in the reactor, at the operating conditions where experimental data were obtained.

Keywords: Hydrotreating, Vacuum gas oil, Vapor-liquid equilibrium, Modeling and reactor.

Recibido: mayo 2011 Recibido en forma final revisado: noviembre 2013

INTRODUCCIÓN

Los procesos de hidrotratamiento son utilizados en la industria de la refinación para retirar contaminantes tales como azufre y nitrógeno (Jiménez et al. 2007), los cuales se remueven a través de reacciones de hidrodesulfuración e hidrodesnitrogenación, respectivamente.

El estudio de las reacciones de hidrotratamiento de cortes pesados, como los gasóleos de vacío (VGO), ha adquirido gran importancia debido al aumento de las restricciones ambientales que limitan la concentración de contaminantes en los combustibles, tales como la gasolina y el diesel. Por ejemplo, para el año 2010 la Unión Europea, limitó la concentración de azufre a un máximo de 10 wt ppm (López & Dassori, 2001), lo que ha convertido a este proceso en uno de los aspectos centrales de la refinación (Korsten & Hoffmann, 1996).

Es por tal razón que diversos autores han buscado modelar y simular estas reacciones bajo diferentes suposiciones; por ejemplo, Gopalan (1998), Yang et al. (2005), Marafi et al. (2003) modelaron reactores de flujo pistón para reacciones de hidrodesulfuración e hidrodesnitrogenación en fase gas o líquida.

Otros autores, como Botchwey et al. (2003), Jiménez et al. (2007), Korsten & Hoffman (1996) y López & Dassori (2001), modelaron las reacciones de hidrotratamiento en reactores Trickle-Bed, presentando resistencia a la transferencia de masa en diferentes interfases dependiendo de las suposiciones realizadas por cada uno de los autores. Todos estos trabajos tienen una suposición en común, considerar que la carga no se vaporiza. Sin embargo, los trabajos realizados por Akgerman et al. (1985), LaVope & Satterfield (1988), Kocis & Ho (1986) y Gauthier et al. (2007) introducen la vaporización al balance de masa del reactor. Adicionalmente, Reinhoudt et al. (2001) y Thybaut et al. (2006) plantean que las reacciones de hidrotratamiento e hidrocraqueo se pueden llevar a cabo tanto en la fase gas como en la fase líquida. Sin embargo, no se encontraron trabajos previos en los cuales se evalúe la vaporización y la reacción en fase gas y fase líquida simultáneamente.

A pesar de que desde 1985, se plantea que en las condiciones de operación industrial de las reacciones de hidrotratamiento se puede llegar a alcanzar hasta un 50% de vaporización (Akgerman et al. 1985), la mayoría de los trabajos realizados sobre procesos de hidrotratamiento toman la suposición de que la carga no se vaporiza. Es por tal razón que se estudiara el efecto de la vaporización de la carga en reacciones de hidrotratamiento.

MODELO CINÉTICO

Los modelos cinéticos utilizados en este trabajo, son los planteados por Korten & Hofmann (1996) y López & Dassori (2001). Dichos modelos son:

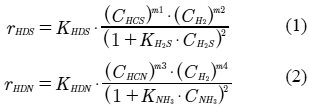
donde: K_HDS es la constante de velocidad de reacción para la Hidrodesulfuración, K_H2S es la constante de adsorción de sulfuro de hidrógeno, C_HCS es la concentración molar del hidrocarburo azufrado, C_H2 es la concentración molar de hidrógeno y C_H2S es la concentración molar de sulfuro de hidrógeno. De forma similar, se tiene que K_HDN es la constante de velocidad de reacción para la Hidrodesnitrogenación, K_NH3 la constante de adsorción del amoníaco, C_HCN es la concentración molar del hidrocarburo nitrogenado y C_NH3 es la concentración molar de amoniaco.

Las constantes de velocidad de reacción y de adsorción se rigen por la ecuación de Arrhenius (López & Dassori, 2001), respectivamente.

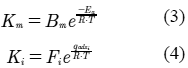
donde: K_m es la constante de velocidad de velocidad de reacción, bien sea para hidrdesulfuración o hidrodesnitrogenación, B_m es el factor de frecuencia asociado con la velocidad de reacción y E_a es la energía de activación. Así mismo, K_i es la constante de adsorción del compuesto i, F_i es el factor de frecuencia asociado con la constante de adsorción y qadsi es el calor molar de adsorción.

Finalmente, se tiene que los modelos cinéticos seleccionados para llevar a cabo este trabajo se utilizarán tanto para modelar la reacción en la fase gas como en la fase líquida, siendo las concentraciones participantes en la reacción, la concentración de cada uno de los elementos en la fase correspondiente. Esto basado en los trabajos realizados por Reinhoudt et al. (2001) y Thybaut et al. (2006). Estos trabajos utilizan el mismo modelo cinético para evaluar reacciones de hidrotratamiento e hidrocraqueo en fase líquida y en fase gas.

REACTOR DE FLUJO PISTÓN IDEAL (FPI)

El balance de masa en la fase gas para el sistema que no considera vaporización y para el que considera la vaporización de la carga pero que la reacción sólo se lleva a cabo en la fase líquida, es:

donde: F_i^G representa el flujo molar del compuesto i en el gas y V el volumen del lecho catalítico. Para el sistema que considera la vaporización de la carga y la reacción en ambas fases el balance de masa para cada componente queda:

donde: ρ_b representa la densidad del lecho catalítico, ν_i el coeficiente estequiométrico del compuesto i y r_c la velocidad de la reacción.

El balance de masa para la fase líquida y para los tres casos que se evaluarán en este trabajo, queda:

donde: F_i^L representa el flujo molar del compuesto i en el líquido.

REACTOR DE FLUJO PISTÓN IDEAL CON TRANSFERENCIA DE MASA (FPITM)

Para el caso en el cual no se considera la vaporización de la carga se tiene que para los componentes gaseosos que participan en la reacción: hidrógeno, amoníaco y sulfuro de hidrógeno, el balance de masa queda:

donde: K_ia_S^L representa el coeficiente de transferencia de masa por unidad de área, U_G la velocidad lineal del gas, P_i la presión parcial del compuesto i, H_i la constante de Henry del compuesto i, R la constante universal de los gases, T la temperatura, z la longitud del reactor y C_i^L es la concentración molar del compuesto i en la fase líquida.

Para el caso que considera la vaporización de los hidrocarburos, pero la reacción sólo se lleva a cabo en la fase líquida, se tienen que considerar, aparte de los componentes gaseosos, el compuesto azufrado, el compuesto nitrogenado y el hidrocarburo puro en el balance de masa.

Para el caso con vaporización de la carga y reacción en las dos fases, las ecuaciones del balance de masa deben considerar la transferencia de masa de la fase gas a la fase sólida. Por lo que las ecuaciones de balance de masa quedan:

donde: K_ia_S^G representa el coeficiente de transferencia de masa entre el gas y la superficie del sólido, C_i^G la concentración molar del compuesto i en el gas y C_i^S la concentración molar del compuesto i en la superficie del sólido.

Los componentes transferidos entre la fase gas y la superficie del catalizador son producidos o consumidos por la reacción química, por lo tanto:

Para el caso en el cual no se considera la vaporización de la carga tenemos que para los componentes gaseosos que participan en la reacción: hidrógeno, amoníaco y sulfuro de hidrógeno, el balance de masa tiene que considerar los términos de transferencia en la inter-fase líquido-gas:

Mientras que el componente azufrado y nitrogenado sólo tienen que considerar la transferencia en la interfase líquido-sólido:

Para los casos que consideran la vaporización de la carga, el balance de masa de los componentes azufrados y nitrogenados deben incluir los términos de transferencia de masa entre la interfase líquido-gas.

Los componentes transferidos entre la fase líquida y la superficie del catalizador son producidos o consumidos por la reacción química, por lo tanto:

EFECTO DE LA VAPORIZACIÓN DE LA CARGA MODELAJE MATEMÁTICO

La vaporización y condensación de forma general, afecta la concentración de las especies, lo que afecta la conversión. Para introducir la vaporización en el modelaje del reactor, se puede suponer que el equilibrio entre el gas y el líquido está establecido en toda la superficie del lecho catalítico. Adicionalmente, se supone que cuando no existe vaporización el catalizador está completamente mojado por el líquido y que cuando existe vaporización, el catalizador se encuentra mojado sólo por la fracción líquida de los hidrocarburos.

Con base en esa suposición, es apropiado utilizar un modelo de equilibrio instantáneo (flash), para determinar la fracción molar de las especies.

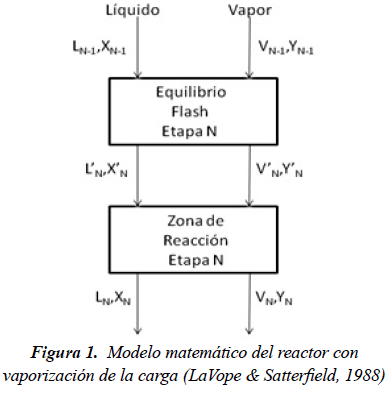
Matemáticamente, el reactor se modela como N etapas en serie, en la cual cada etapa contiene una etapa de equilibrio flash, y una sección diferencial del reactor. En la Figura 1 podemos observar un esquema del modelo matemático (LaVope & Satterfield, 1988).

Al suponer que en cada punto del reactor se tiene que el gas y el líquido están en equilibrio, entonces parte de la carga se vaporiza.

Los trabajos realizados por Kocis & Ho (1986) y Gauthier et al. (2007), plantean un tiempo de residencia real, en función del flujo volumétrico de líquido real y la vaporización, el cual se puede expresar como (Gauthier et al. 2007):

donde: Q_f^t representa el flujo volumétrico y f la fracción vaporizada.

Expresando la velocidad espacial del líquido como el inverso del tiempo de residencia, se llega a la expresión planteada por Kocis & Ho (1986):

donde: LHSV_e es la velocidad espacial efectiva del líquido y LHSV es la velocidad espacial del líquido.

El término f_s, que represente la fracción vaporizada, se calcula como:

donde: f_HC⁰ es el flujo molar de hidrocarburo total que entra al reactor y f_HC, es el flujo molar de hidrocarburo en la fase gas.

REACTOR FLUJO PISTON IDEAL (FPI)

Por lo que la ecuación para modelar el balance de masa en la fase líquida para un reactor FPI queda:

Partiendo de que el factor (1-f_s) representa la fracción no vaporizada y que, como se mencionó anteriormente, fs corresponde con la fracción vaporizada, el balance de masa para la reacción en fase gas se puede expresar como se muestra a continuación:

REACTOR FLUJO PISTÓN CON TRANASFERENCIA DE MASA (FPITM)

Para el reactor flujo pistón ideal con transferencia de masa, el balance de masa para la fase líquida queda:

Mientras que para el gas, el balance queda:

COEFICIENTES DE TRANSFERENCIA DE MASA

El coeficiente de transferencia de masa en la interfase líquido-gas, puede ser determinado a partir de la correlación de Goto & Smith (1975):

donde: D_i^L es la difusividad del compuesto i en el líquido, μ_L es la viscosidad dinámica del líquido, ρ_L es la densidad del líquido y G_L es el flujo másico del líquido.

La ecuación de Van Krevelen-Krekels (Froment & Bischoff, 1990) permite calcular la transferencia de masa entre la inter-fase líquido-sólido para un régimen de baja interacción:

DENSIDAD

Para obtener la densidad del líquido en las condiciones de operación, se dispone de la correlación de Standing-Katz, en la cual se parte de la densidad en una condición estándar y se le agrega algebraicamente, el efecto de la temperatura y de la presión sobre esta variable (Ahmed, 1989):

La dependencia de la presión puede ser calculada como:

La dependencia de la temperatura puede ser calculada como:

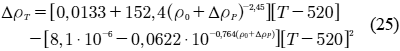
donde: ρ₀ es la densidad del líquido a condiciones estándar, P es la presión y T es la temperatura.

En el cálculo de la densidad, se tiene que introducir la temperatura en [°R], la presión en [psia] y la densidad del líquido a condiciones estándar en [lb/ft³].

VISCOCIDAD DINÁMICA

Para calcular la viscosidad dinámica de una mezcla de hidrocarburos se puede utilizar la correlación de Glaso (Ahmed, 1989):

Donde la temperatura se debe introducir en [°R] y donde el superíndice [a] se calcula como:

Por último, los grados API se calculan como:

DIFUSIVIDAD

La difusividad del compuesto i gaseoso, en un hidrocarburo líquido se puede calcular a través de la correlación de Tyn- Calus, la cual asume dilución infinita (Reid et al. 1987). La temperatura se debe introducir en [K]:

VOLUMEN MOLAR

Para calcular el volumen molar del compuesto i se puede utilizar la siguiente ecuación en función del volumen molar crítico (Perry & Green, 1997):

Los volúmenes molares críticos de los gases están tabulados, como el hidrógeno, sulfuro de hidrógeno y amoníaco. Para el solvente, el hidrocarburo, el compuesto azufrado y nitrogenado, el volumen molar crítico puede ser determinado a partir de la correlación de Riazi-Daubert (Ahmed, 1989):

donde: T_MeABP es la temperatura promedio de ebullición del líquido en [°R] y PM es su peso molecular.

CONSTANTE DE HENRY

El equilibrio gas-líquido puede ser descrito a través de la Ley de Henry. En este caso, la constante de Henry para el hidrógeno, el sulfuro de hidrógeno y el amoníaco se puede calcular en función del volumen molar del compuesto i, la solubilidad del compuesto i en el líquido y la densidad del líquido a las condiciones de operación:

donde: γ_i es la solubilidad de compuesto i en el líquido.

SOLUBILIDAD DEL HIDRÓGENO

La solubilidad del hidrógeno en el líquido es calculada a través de la correlación derivada por Korsten & Hoffmann (1996):

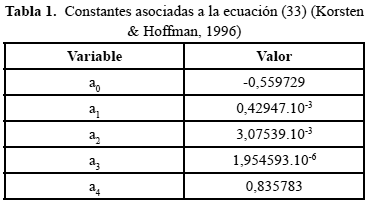
Las constantes necesarias para resolver la ecuación (33) se pueden observar en la Tabla 1.

SOLUBILIDAD DEL SULFURO DE HIDRÓGENO

La solubilidad del sulfuro de hidrógeno se puede calcular con una correlación obtenida a partir de los datos experimentales de Yokoyama et al. (1993), en los cuales se presentan datos de solubilidad de sulfuro de hidrógeno en varios hidrocarburos como isooctano, n-decano, n-tridecano, n-hexadecano y escualano, en un rango de temperatura entre 323 K y 523 K y presiones por debajo de 1,6 MPa:

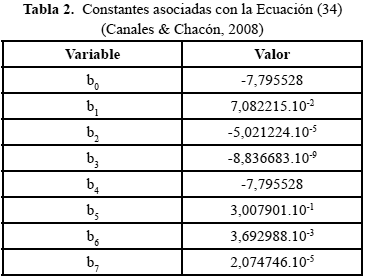
Las constantes necesarias para resolver la Ecuación (34) se pueden observar en la Tabla 2.

SOLUBILIDAD DEL AMONÍACO

La solubilidad del amoníaco se calcula según la correlación presentada por Korsten & Hoffmann (1996) y utilizada por López & Dassori (2001):

Donde la temperatura se debe introducir en [K].

CONSTANTES DE EQUILIBRIO DEL HIDROCARBURO

Para lograr estimar las constantes de equilibrio del hidrocarburo, así como del compuesto azufrado y nitrogenado, se utilizó la siguiente ecuación planteada por Riazi (2005), en la cual la temperatura de introduce en [K]:

donde: P_Ci es la presión crítica, T_Ci es la temperatura crítica y ω_i es el factor acéntrico.

Las constates de equilibrio se relacionan con las constantes de Henry de la siguiente forma:

donde: C_t es la concentración molar total del líquido, yi es la fracción molar del compuesto i en el gas y x_i es la fracción molar del compuesto i en el líquido.

METODOLOGÍA

El procedimiento de cálculo consistió en determinar las constantes termodinámicas e hidrodinámicas. Con estas constantes se procedió a calcular los diferentes sistemas de ecuaciones diferenciales utilizando el método numérico Runge–Kutta 4 (RK4).

Para el modelo de reactor de flujo pistón ideal, el procedimiento de cálculo consistió en plantear un equilibrio líquido vapor previo a cada paso del método numérico. Para el sistema sin vaporización, se suponían que los hidrocarburos eran no volátiles, de forma que el equilibrio líquido vapor permitía determinar la transferencia de los gases, hidrógeno, sulfuro de hidrógeno y amoníaco entre el líquido y el gas. Para los dos casos en los que se consideraba la vaporización de la carga se procedió a plantear que todos los compuestos, tanto los hidrocarburos como los gases, presentaban equilibrio entre el líquido y el vapor.

Para el modelo de reactor flujo pistón ideal con transferencia de masa, se utilizó el mismo método numérico, RK4, para el cálculo del sistema de ecuaciones diferenciales. La metodología para los casos que consideraban la vaporización de la carga fue similar a la implementada en el reactor de FPI, como lo plantean LaVope y Satterfield (1988) se suponía que en toda la superficie del catalizador se alcanzaba el equilibrio entre las dos fases. Para el sistema que suponía que la carga era no volátil, la transferencia entre las dos fases estaba determinada por los términos de resistencia a la transferencia de masa presentes en el balance de masa del reactor.

AJUSTE DE LOS PARÁMETROS CINÉTICOS

Los parámetros cinéticos que se ajustaron fueron las constantes de velocidad de reacción, para HDS y HDN, y de adsorción, para el H₂S y el NH₃. Para realizar el ajuste de las constantes cinética se utilizó el paquete de Optimetool de Matlab R2007b^®, utilizando como función objetivo la que se muestra a continuación:

donde: CS_cal y CS_exp representan la concentración de compuestos azufrados calculada y experimental, respectivamente. De igual manera, CN_cal y CN_exp son la concentración de compuestos nitrogenados calculada y experimental, respectivamente. Los datos experimentales que se utilizaron en la función objetivo, fueron los publicados por (Botchwey et al. 2003), que corresponden a un gasóleo derivado de un bitumen de Athabasca, con un rango de puntos de ebullición de 340 a 550 °C.

RESULTADOS Y DISCUSIÓN PERFILES DE CONCENTRACIÓN

Los perfiles de concentración, tanto para los casos evaluados con el modelo de reactor de flujo pistón ideal como para los casos evaluados con el modelo de reactor flujo pistón ideal con transferencia de masa, se generaron con las constantes cinéticas ajustadas para el sistema sin vaporización, de forma de que se observe el efecto de suponer esta simplificación. Al considerar la vaporización de la carga, se presenta un efecto competitivo sobre la conversión. Al haber vaporización, la concentración de los reactivos disminuye, por lo que la conversión también lo hace, mientras que al disminuir el flujo de líquido se produce un aumento en el tiempo de residencia, lo que aumenta la conversión.

Para estudiar cuál de estos efectos es más influyente, se mostrarán los perfiles de concentración así como los errores que se obtienen al evaluar cada uno de los tres casos, con las constantes ajustadas al sistema sin vaporización, como ya se dijo, para que se pueda observar las consecuencias de tomar esta simplificación.

RESULTADOS PARA EL REACTOR DE FLUJO PISTÓN IDEAL

A continuación (Figura 2-9), se muestran los perfiles de concentración y de presión para los componentes participantes en la reacción.

Para efectos de los gráficos que se exhibirán, se utiliza la siguiente nomenclatura:

SV: Sistema sin vaporización

CV: Sistema con vaporización

CVR: Sistema con vaporización y reacción en las dos fases.

Las condiciones de operación a las cuales se evaluaron los sistemas para generar los perfiles de concentración y de presión se muestran en la Tabla 3.

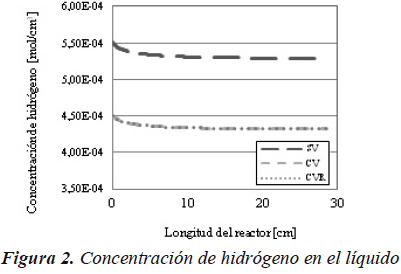
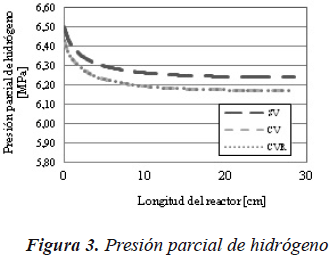
En la Figura 3, se muestra que al considerar la vaporización, la presión parcial del hidrógeno disminuye, por lo que la concentración en el líquido es menor, como se puede observar en la Figura 2.

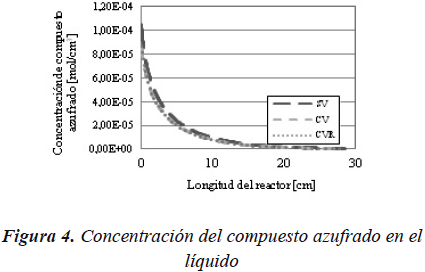
En la Figura 4, se observa cómo al considerar la vaporización disminuye la concentración de compuesto azufrado.

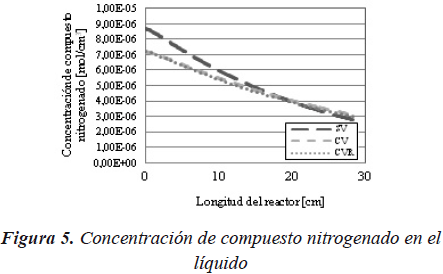
En la Figura 5, se observa el mismo efecto dado que la concentración del compuesto nitrogenado disminuye al considerar la vaporización al sistema.

Por lo tanto se puede decir que al introducir el equilibrio líquido vapor del compuesto azufrado y del compuesto nitrogenado en el sistema, se produce una disminución en las concentraciones de los reactantes, por lo que la conversión alcanzada para el caso con vaporización, es menor.

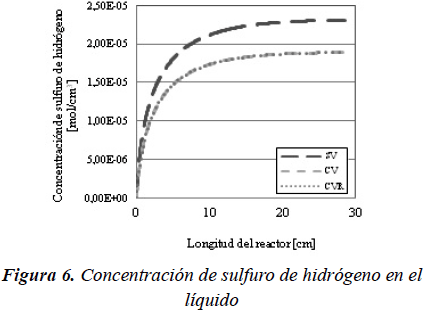
En lo que respecta al sulfuro de hidrógeno, se puede observar como su concentración aumenta a lo largo del reactor (Figura 6) y que es superior para el sistema sin vaporización ya que para los casos en que se considera la vaporización, la presencia de hidrocarburos en la fase gas diluye su fracción molar.

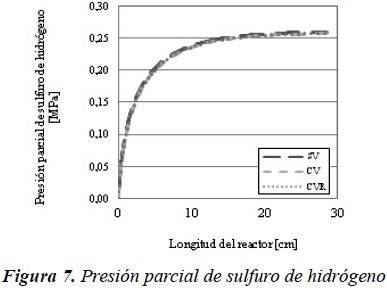
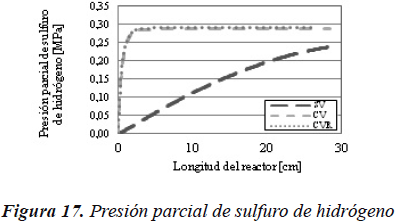
Por lo tanto y como se observa en la Figura 7, la presión parcial de sulfuro de hidrógeno para el caso sin vaporización es superior que para los casos en donde se considera la vaporización.

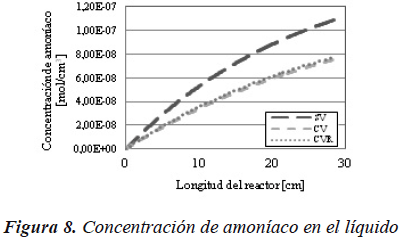
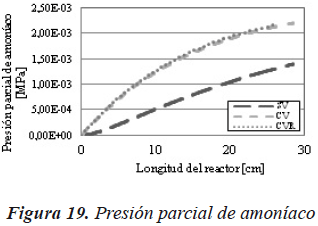
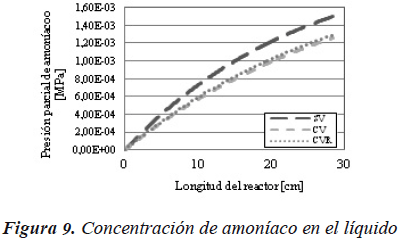
El mismo efecto se puede observar en las Figuras 8 y 9, donde la presión parcial y la concentración de amoníaco en el sistema sin vaporización, es superior al de los otros dos casos.

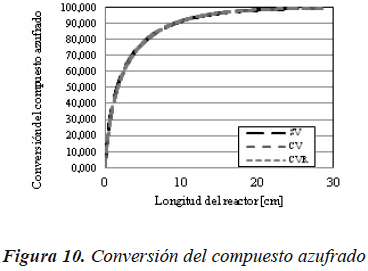
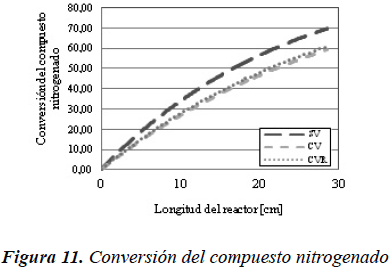
Las consecuencias de la disminución de la concentración se pueden observar en las Figuras 10 y 11, en las cuales se muestra la conversión tanto en la reacción de hidrodesulfuración como en la de hidrodesnitrogenación, para cada uno de los tres casos evaluados con el modelo de reactor de flujo pistón ideal.

RESULTADOS PARA EL MODELO DE REACTOR DE FLUJO PISTÓN IDEAL CON TRANSFERENCIA DE MASA

A continuación, se mostrarán los perfiles de concentración y de presión a lo largo del reactor para cada uno de los componentes que participan en la reacción. Estos perfiles se generaron a las mismas condiciones de operación que los perfiles obtenidos a través del modelo de reactor de flujo pistón ideal, las condiciones de operación se pueden observar en la Tabla 3.

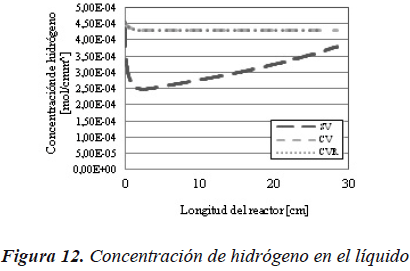
De la Figura 12 hasta la Figura 19, se muestran los perfiles de concentración y de presión para los componentes participantes en la reacción a través del modelo de flujo pistón ideal con transferencia de masa.

En la Figura 12, en la curva para el caso SV, se puede observar que primero presenta una pendiente negativa, que posteriormente asciende. Esto se debe a que en el primer intervalo, la velocidad de reacción es superior a la velocidad de transferencia de masa, mientras que para la sección de la curva con pendiente positiva, la velocidad de transferencia de masa es superior que la velocidad de reacción.

De igual forma podemos ver cómo al suponer que los casos con vaporización están en equilibrio de fases a lo largo de todo el reactor, la concentración de hidrógeno es siempre superior, a diferencia que para el reactor de flujo pistón ideal.

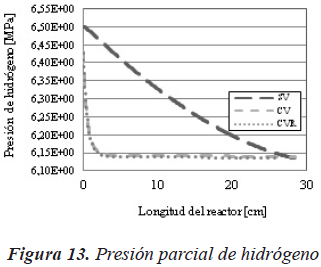
En la Figura 13 se muestra como al incluir la resistencia a la transferencia de masa, la presión parcial de hidrógeno disminuye prácticamente de forma lineal, mientras que para los casos en donde se considera la vaporización esta disminuye abruptamente.

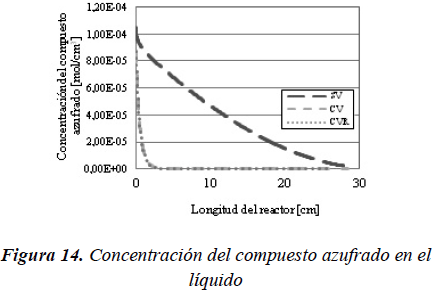
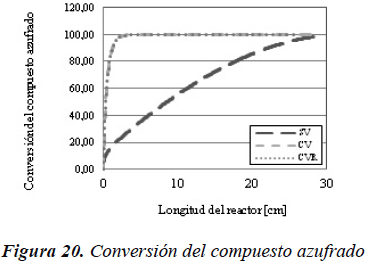
En la Figura 14 se observa como disminuye la concentración del compuesto azufrado a lo largo de todo el reactor, con lo cual se puede afirmar, tal y como se evidencia en la Figura 20, que al incluir la vaporización en el modelo se alcanzan mayores conversiones que cuando no se considera, lo que concuerda con los resultados obtenidos por Akgerman et al. (1985) y Chen et al. (2011). Además, cuando no existe vaporización la cantidad total de compuesto azufrado está completamente ubicada en el líquido, mientras que cuando existe la posibilidad de vaporización, la cantidad total del compuesto distribuye entre el líquido y el vapor.

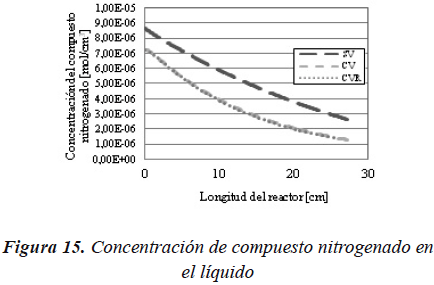
Para el compuesto nitrogenado (Figura 15) se observa el mismo efecto que para el compuesto azufrado.

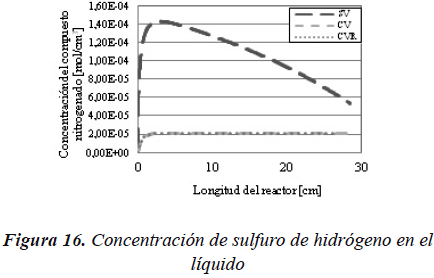
En la Figura 16 se muestra la concentración de sulfuro de hidrógeno para los tres sistemas, a lo largo de todo el reactor. En la cual, la concentración de sulfuro de hidrógeno en el líquido es superior para el caso SV que para los dos casos con vaporización.

Podemos observar en la Figura 17 como cambia el perfil de presión parcial de sulfuro de hidrógeno, a lo largo de todo el reactor.

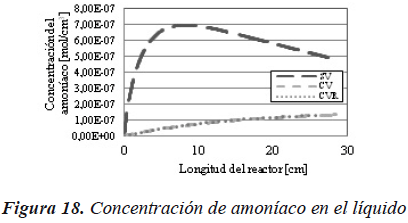
Para el amoníaco (Figura 18 y Figura 19) se puede observar el mismo efecto que para el sulfuro de hidrógeno.

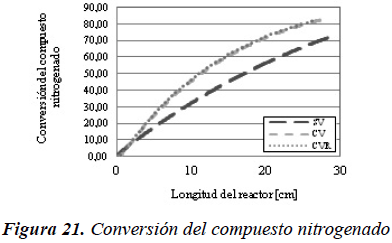
En el modelo de reactor flujo pistón ideal con transferencia de masa, a diferencia del reactor de flujo pistón ideal, se muestra una diferencia considerable en lo que respecta a la tendencia de las curvas entre los casos que consideran vaporización y el caso que no considera la vaporización. Adicionalmente, se pueden observar comportamientos opuestos entre los dos tipos de reactor, para el modelo FPI la conversión tiende a disminuir al introducir la vaporización, mientras que en el modelo FPITM aumenta. Este comportamiento se muestra en las Figuras 20 y 21.

Como se pudo observar en las Figuras 12 hasta la Figura 19, esta diferencia considerable se debe a que en los casos que consideran vaporización, se introduce la suposición de que en todo punto del catalizador está presente el equilibrio, por lo que, a pesar que las concentraciones de los compuestos azufrados y nitrogenados son ligeramente menores en el líquido, la concentración de hidrógeno en el líquido es mucho mayor.

EFECTO DEL AUMENTO DEL TIEMPO DE RESIDENCIA POR EFECTO DE LA VAPORIZACIÓN

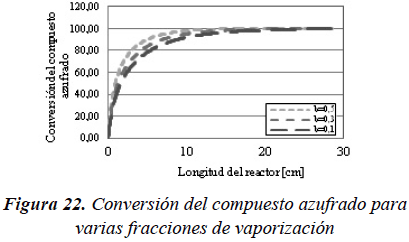
Para evaluar como es el cambio en la conversión por efecto del aumento de tiempo de residencia, y observar este efecto, se procedió a modificar la fracción de la carga vaporizada para las mismas condiciones de operación a través del modelo de reactor FPI, considerando vaporización y la posibilidad de reacción en las dos fases. En las Figuras 22 y 23 se observa como a medida que aumenta la fracción vaporizada, la conversión alcanzada es mayor.

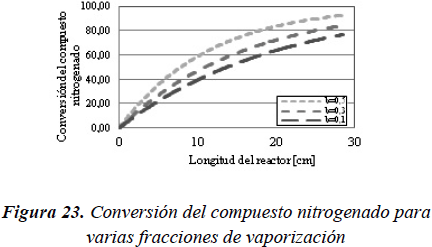
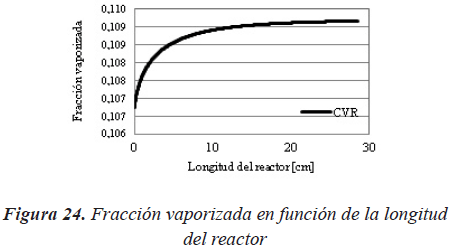
Como se puede observar en la Figura 22 y 23, al aumentar la fracción vaporizada de la carga, pero manteniendo las mismas condiciones de operación, la conversión alcanzada en el reactor aumenta. Sin embargo, como se supuso que los reactores se comportaban de forma isotérmica (condición de obtención de los datos experimentales), se puede observar en la Figura 24 que la vaporización se produce principalmente a la entrada del reactor y que, a pesar que a lo largo del reactor va aumentando la fracción vaporizada, esta es prácticamente despreciable con respecto a la vaporización alcanzada en la entrada del mismo.

Por tal razón se puede llegar a pensar que al considerar un modelo de reactor adiabático, en vez de uno isotérmico, el efecto de la vaporización se haría más considerable.

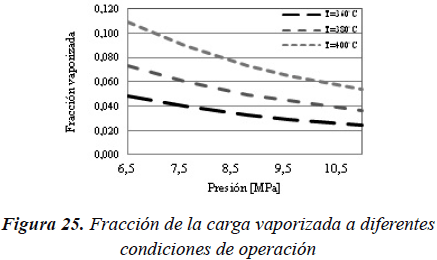
Por último en la Figura 25, observaremos cómo cambia la fracción vaporizada a la entrada del reactor en función de las condiciones de operación.

Se hace evidente que la vaporización es directamente proporcional a la temperatura e inversamente proporcional a la presión.

COMPARACION DE LOS ERRORES PARA CADA SISTEMA CON LAS CONSTANTES AJUSTADAS

Finalmente, buscaremos comparar como se ajusta cada modelo a los datos experimentales utilizados. Para esto procederemos a utilizar las constantes cinéticas que se determinaron para cada uno de los casos y comparar los errores globales promedio que se obtiene para cada uno de ellos.

Para el modelo de reactor de flujo pistón ideal, se muestra en la Tabla 4, los valores obtenidos para el error global. En la Tabla 5 se muestra los valores obtenidos para el error global para el modelo de reactor de flujo pistón ideal con transferencia de masa.

Como se puede observar las tablas anteriores, el caso que considera la vaporización de la carga y la reacción en las dos fases, es el que mejor se ajusta a los datos experimentales en los dos modelos de reactores.

Adicionalmente, comparando las Tablas 4 y 5 se puede ver que a pesar que el modelo del reactor FPITM es mucho más complejo que el modelo de FPI, la diferencia entre los errores globales es pequeña. Esto permite presumir que los efectos de la resistencia a la transferencia de masa están ausentes en el montaje experimental de donde se obtuvieron los datos.

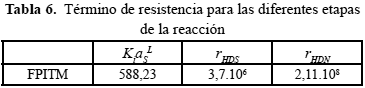
En la Tabla 6, se muestra una comparación entre la resistencia a la transferencia de masa y la de reacción química.

Como se observa en la Tabla 6, la resistencia a la transferencia de masa es prácticamente despreciable comparada a las resistencias de la reacción química.

CONCLUSIONES

Se determinó que los cambios que se producen en las concentraciones por efecto de la vaporización, con respecto al sistema sin vaporización, tienen una mayor influencia sobre la conversión alcanzada que el aumento en el tiempo de residencia.

A través del modelo de reactor de FPI se pudo identificar como al incluir la vaporización de la carga, se produce una disminución en las concentraciones, con respecto al sistema sin vaporización, lo que conlleva a que las conversiones alcanzadas sean menores para los casos con vaporización. A través del modelo de reactor FPITM se pudo observar que las conversiones alcanzadas en los casos con vaporización fueron mayores que en los casos sin vaporización. En este caso, al suponer el equilibrio de fases en toda la superficie del catalizador, para introducir la vaporización, si bien disminuye un poco la concentración del compuesto azufrado y del compuesto nitrogenado, aumenta considerable la concentración del hidrógeno en el líquido.

A mayor vaporización, mayor tiempo de residencia, por lo que se alcanzan mayores conversiones.

Para un reactor isotérmico se obtuvo que la vaporización ocurre principalmente en la entrada del mismo y que es directamente proporcional a la temperatura e inversamente proporcional a la presión.

El caso que considera la vaporización y la posibilidad de reacción en las dos fases, es el que mejor se ajusta a los datos experimentales. En tal sentido, el modelo de FPITM arrojó un error global 4,0% y el modelo de FPI un 4,23%. Por lo tanto, se puede decir que si bien la introducción del equilibrio líquido vapor y la posibilidad de reacción en fase gas en un modelo de reactor FPITM conlleva una mayor dificultad, el error promedio global obtenidos es menor que en los demás casos.

Por último, tenemos que a las condiciones en que se obtuvieron los datos experimentales, el paso que gobierna el proceso es la velocidad de reacción, por lo que los efectos de la velocidad de transferencia de masa son casi despreciables.

Letras latinas

a Constante de la ec. (26)

b Relación entre la constante de adsorción y la de desorción

B_m Factor de frecuencia asociado a la velocidad de reacción [(cm³/gcat s) m1(cm³/mol)m² para HDS y (cm³/gcats)m3(cm³/mol)m4 para HDN]

C_i Concentración molar de i [mol/cm³]

D Difusividad [cm²/s]

E_a Energía de activación [J/mol]

f_S Fracción vaporizada

f₀^HC Flujo molar de hidrocarburo que entra al reactor [mol/s]

f_HC Flujo de molar de hidrcarburo en el gas [mol/s]

F_i Flujo molar de i [mol/s]

F_i Factor de frecuencia asociado a la constante de adsorción [cm³/mol]

G Flujo másico por unidad de área [g/cm2s]

H Constante de Henry [Mpa cm³/mol]

K Constante de equilibrio líquido-gas

Ka_S Coeficiente de transferencia de masa externo por unidad de área [s-1]

K_i Constante de adsorción del compuesto [cm³/mol]

K_m Constante de velocidad de la reacción [cm/s]

m Orden de reacción global

P Presión [MPa]

PM Peso molecular

q_adsi Calor molar de adsorción (J/mol)

Q_t^f Flujo volumétrico [cm³/s]

r Velocidad de reacción [mol/s]

R Constante universal de los gases

S Superficie específica del catalizador

T Temperatura [K]

U Velocidad lineal (cm/s)

v_i Volumen molar del compuesto i (cm³/mol)

v_ic Volumen molar crítico del compuesto i (cm³/mol)

v_L Volumen molar del líquido (cm³/mol)

V Volumen del lecho catalítico (cm³)

X Fracción molar del líquido

Y Fracción molar de los gases

Letras latinas

Z Fracción molar

z Longitud del reactor [cm]

Letras griegas

ρ Densidad [lb/ft³]

μ Viscosidad dinámica [mPa s]

γ Solubilidad del compuesto i en el líquido [Nl H₂/kg_crudo]

φ Relación Hidrógeno/Carga [ml/ml]

Subíndices

b Lecho catalítico

c Crítico

G Gas

H₂ Hidrógeno

H₂S Sulfuro de hidrógeno

HC Hidrocarburo

HCN Hidrocarburo nitrogenado

HCS Hidrocarburo azufrado

HDN Hidrodesnitrogenación

HDS Hidrodesulfuración

i Componente i

L Líquido

NH₃ Amoníaco

REFERENCIAS BIBLIOGRÁFICAS

1. Ahmed, T. (1989). Hydrocarbon phase behavior. Gulf Publishing, Houston.        [ Links ]

2. Akgerman, A., Collins, G. M., Hook, D. (1985). Effect of feed volatility on conversion in trickle bed reactors. Ind. Eng. Chem. Fundamen., 24(3), 398–401.        [ Links ]

3. Botchwey, C., Dalai, A. K., Adjaye, J. (2003). Product selectivity during hydrotreating and mild hydrocracking of bitumen-derived gas oil. Energy Fuels, 17(5), 1372– 1381.        [ Links ]

4. Chacon, R., Canale, A., Bouza, A., Sanchez, Y. (2012). Modeling of a three-phase reactor for bitumen-derived gas oil hydrotreating. Brasilian J. of Chem. Eng., 29(1), 135-146.        [ Links ]

5. Chen, J., Mulgundmath, V., Wang, N. (2011). Accounting for vapor−liquid equilibrium in the modeling and simulation of a commercial hydrotreating reactor. Ind. Eng. Chem. Res., 50(3), 1571–1579.        [ Links ]

6. Froment, G. F. & Bischoff, K. B. (1990). Chemical Reactor Analysis and Design. 2nd ed., Wiley, New York.        [ Links ]

7. Gauthier, T., Héraud, J.P., Kressmann, S., Verstraete, J. (2007). Impact of vaporization in a residue hydroconversion process. Chem. Eng. Science., 62(18- 20), 5409–5417.        [ Links ]

8. Gopolan, U. (1998). Hidrogenation of pyridine over alumina supported platinum catalysis. Tesis de Mestría no publicada, Universidad de Ottawa, 1-27.        [ Links ]

9. Goto, S. & Smith, J. M. (1975). Trickled-bed Reactor Performance: I. Holdup and mass transfer effects. AIChE J., 21(4), 706-713.        [ Links ]

10. Jiméneza, F., Kafarova , V., Nuñez, M. (2007). Modeling of industrial reactor for hydrotreating of vacuum gas oils simultaneous hydrodesulfurization, hydrodenitrogenation and hydrodearomatization reactions. Chem. Eng. J., 134(1-3), 200–208.        [ Links ]

11. Kocis, G.R. & Ho, T.C. (1986). Effects of liquid evaporation on the performance of Trickle-Bed reactors. Chem. Eng. Sci., (64), pp. 288-291.        [ Links ]

12. Korsten, H. & Hoffmann, U. (1996). Three-phase reactor model for hydrotreating in pilot trickle-bed reactors. AIChE J., 42(5), pp. 1350-1360.        [ Links ]

13. La Vope, V. & Satterfield, C.N. (1988). Some effects of vapor-liquid equilibria on performance of a trickle-bed reactors. Chem. Eng. Sci., 43(8), pp. 2175-2180.        [ Links ]

14. López, R. & Dassori, C.G. (2001). Mathematical modeling of a vgo hydrotreating reactor” Society of Petroleum Engineering Inc., SPE69499, 1-16.        [ Links ]

15. Marafi, A., Fukase, S., Al-Marri, M., Stanislaus, A. (2003). A comparative study of the effect of catalyst type on hydrotreating kinetics of Kuwaiti atmospheric residue. Energy Fuels, 17(3), 661-668.        [ Links ]

16. Perry, R. H. & Green, D. (1984). Perry’s Chemical Engineers’ Handbook. 6th ed, McGraw-Hill, New York.        [ Links ]

17. Reid, R. C., Prausnitz, J. M., Poiling, B. E. (1987). The Properties of Gases & Liquids. 4th ed, McGraw-Hill, New York.        [ Links ]

18. Reinhoudt, H.R., Boons, C.H.M., Langeveld, A.D., Veen, J.A.R., Sie, S.T., Moulijin, J.A. (2001). On the difference between gas- and liquid-phase hydrotreating test reactions. Applied Catalysis A: General, 207(1-2), 25-36.        [ Links ]

19. Riazi, M.R. (2005). Characterization and Properties of Petroleum Fractions, ASTM, Filadelfía, pp 287.        [ Links ]

20. Thybaut, J.W., Laxmi, C.S., Marin, G.B. (2006). Bridging the gap between liquid and vapor phase hydrocracking. Catalysis Today, 111(1-2), 94–102.        [ Links ]

21. Yang, C., Dua, F., Zhenga, H., Chunbg, K.H. (2005). Hydroconversion characteristics and kinetics of residue narrow fractions. Fuel, 84(6), 675–684.        [ Links ]

22. Yokoyama, C., Usui, A., Takahashi, S. (1993). Solubility of hydrogen sulfide in isooctane, n-decane, n-tridecane, n-hexadecane and squalane at temperaturas from 323 to 523 K and pressures up to 1.6 MPa. Fluid Phase Equilibria, 85, 257-269.        [ Links ]