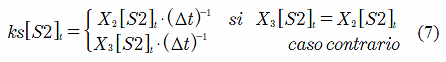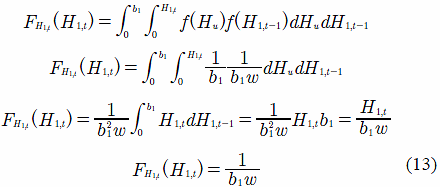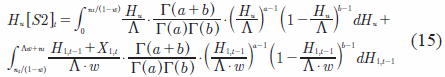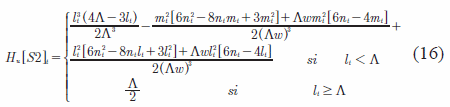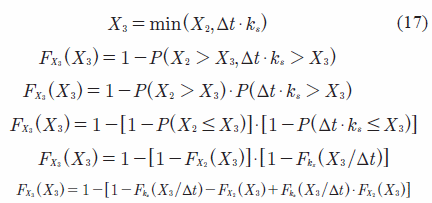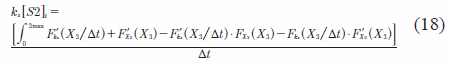Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Facultad de Ingeniería Universidad Central de Venezuela
versão impressa ISSN 0798-4065
Rev. Fac. Ing. UCV vol.29 no.4 Caracas dez. 2014
Ecuaciones de parámetros variables para escalar el proceso de infiltración en la mesoescala
Miguel Ignacio Barrios Peña
Facultad de Ingeniería Forestal. Universidad del Tolima. e-mail: mibarrios@ut.edu.co
RESUMEN
Los efectos de escala espacial y la representación de la heterogeneidad son complicados de abordar en Hidrología debido a que los procesos hidrológicos no son lineales. Como consecuencia de ello, los modelos hidrológicos utilizan parámetros efectivos que tratan de ser representativos de la escala de modelación. Sin embargo, los parámetros efectivos no logran solucionar de manera satisfactoria los problemas de escala espacial. Ante la necesidad de proponer parametrizaciones que reduzcan las dependencias de escala, este artículo presenta el desarrollo de ecuaciones de escalado analíticas que permiten calcular parámetros efectivos hidráulicos del suelo cuyos valores cambian en función del estado de humedad y las variables de entrada, en el contexto de la representación del proceso de infiltración de agua en el suelo. El funcionamiento de las ecuaciones de escalado en un experimento sintético de simulación, ha permitido comprobar una disminución del efecto de escala espacial al transferir la información de la heterogeneidad espacial desde la microescala a la mesoescala y demuestra el potencial de la aplicación del concepto de parámetros efectivos variables.
Palabras clave: Escalado, Parámetros efectivos, Efectos de escala, Hidrología, Infiltración.
Variable parameter equations to scale infiltration process at the mesoscale
ABSTRACT
Spatial scale effects and heterogeneity representation are complex issues in Hydrology, particularly due to the non-linearity of the hydrological processes. Therefore, hydrological models use effective parameters, which are representative values at the specific modeling scale. However, the effective parameters are not able to successfully fix the spatial scale problems. Given the need to propose parameterizations reducing scale dependencies, this paper presents the development of analytical scaling equations to estimate soil water effective parameters, which depends on state and input variables in the context of the representation of soil water infiltration process. The performance of the scaling equations using a synthetic simulation shows that the use of non-stationary effective parameters helps to reduce the spatial scale effect in non-linear processes driven by flow and storage thresholds from microscale to mesoscale.
Keywords: Scaling, Effective parameters, Scale effects, Hydrology, Infiltration.
Recibido: febrero 2012 Recibido en forma final revisado: julio 2014
INTRODUCCIÓN
Es fundamental entender y conocer la dinámica de los procesos hidrológicos que ocurren en las cuencas hidrográficas para valorar a priori los efectos de las potenciales acciones de manejo y contribuir al soporte de la toma de decisiones de gestión. La dinámica no lineal de los sistemas hidrológicos, implica que los modelos sean válidos a una escala particular y surjan efectos de escala cuando se utilizan en escalas diferentes. La existencia de estos efectos de escala hace que la capacidad predictiva de los modelos esté limitada por la dificultad de identificar los parámetros de manera precisa y la aparición de errores estructurales en la conceptualización de los modelos hidrológicos.
Wolock & Price (1994) encontraron que las predicciones hechas con TOPMODEL son muy sensibles al valor medio del índice topográfico de humedad, el cual cambia significativamente al variar la escala y la resolución del modelo de elevación digital, por lo que la disminución de estos efectos de escala influye la eficiencia del modelo y por ende en las conclusiones del proceso de validación del mismo. Zhang & Montgomery (1994) compararon el efecto de varios tamaños de celda (2-, 4-, 10-, 30-, y 90- m) en la simulación de hidrogramas, y obtuvieron que un tamaño de celda de 10 m reduce los errores de simulación en contraste con los tamaños de 30- y 90-m. De acuerdo con Kuo et al. (1999), la resolución de la información topográfica tiene un efecto relevante en la calidad de las simulaciones hidrológicas, puesto que la parametrización de los procesos hidrológicos está controlada por la primera y segunda derivadas de la altitud (pendiente y curvatura del terreno, respectivamente). De acuerdo con Beven (1995), el uso de parámetros promedios no es adecuado para resolver este efecto espacial, por lo que se ha hecho común emplear parámetros efectivos para "corregir" los efectos de escala y errores en la conceptualización del modelo; estos valores efectivos se obtienen a través de calibración a partir de series de datos históricos (Todini, 2011). Sin embargo, los parámetros efectivos son difíciles de estimar, dependen del tamaño de tormenta (Binley et al. 1989), la escala (Vázquez et al. 2002) y no remedian de manera adecuada el efecto de la variabilidad en la subcelda (Beven, 1989). Por ello, es necesario el desarrollo de nuevos conocimientos relacionados con la no estacionalidad de los parámetros efectivos (Barrios & Francés, 2011; Di Baldassarre & Uhlenbrook, 2012) y la formulación de nuevos enfoques para tratar las macro no linealidades (Todini, 2011).
Según Blöschl & Zehe (2005), en hidrología se identifican tres fuentes de no linealidad: ecuaciones con términos de segundo orden o superiores, ecuaciones con estructura lineal pero con parámetros no lineales y ecuaciones que representan umbrales de flujo o almacenamiento. La existencia de estas no linealidades dificulta la formulación de operadores de escalado y la identificación de parámetros a diferentes escalas, por lo que en este artículo se presentan ecuaciones analíticas que calculan parámetros hidrológicos variables para tratar el efecto de escala espacial debido a la heterogeneidad de los parámetros y dos tipos de no linealidad, sin considerar la interacción horizontal de los procesos. La principal virtud de utilizar parámetros hidrológicos variables es que transfieren la variabilidad desde la microescala (S1) hacia la mesoescala (S2) (Barrios, 2011). La microescala se refiere al soporte mínimo en el cual se consideran válidas las ecuaciones de un proceso y la mesoescala es una escala mayor en la cual se emplean parámetros efectivos. En este trabajo el término subcelda hace referencia a la resolución espacial de la microescala contenida dentro de una unidad de modelación con extensión igual a la mesoescala.
El principal objetivo de este trabajo es formular ecuaciones que permitan calcular parámetros efectivos variables para un modelo con no linealidades definidas por umbrales de flujo y capacidad de almacenamiento, y comprobar su funcionamiento mediante un experimento sintético. Para tal fin, se utilizó la conceptualización de la infiltración del modelo hidrológico distribuido TETIS (Vélez, 2001; Francés et al. 2002), y la verificación de las ecuaciones analíticas de parámetros variables se realizó mediante simulaciones de Monte Carlo. La motivación de la investigación es demostrar que la utilización de parámetros variables para escalar un proceso no lineal en la mesoescala, puede constituirse en un enfoque potencial para el desarrollo de nuevas vías para tratar el efecto de escala. El lector debe comprender que no es esperable una aplicación inmediata de las ecuaciones de escalado analizadas en este artículo a un caso práctico de modelación hidrológica.
MÉTODOS
Proceso no lineal
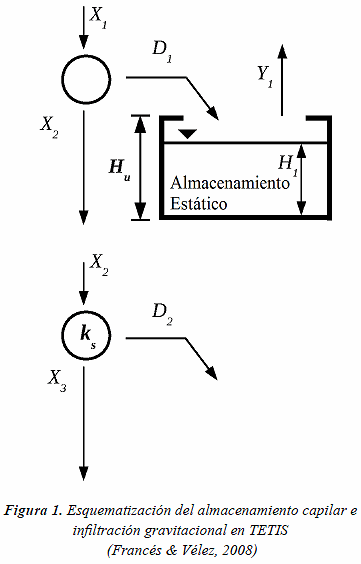
Se empleó la conceptualización del proceso de infiltración del modelo hidrológico distribuido TETIS (Francés et al. 2007), cuyo proceso está controlado por dos tipos de no linealidad: un umbral de flujo a partir del cual ocurre el almacenamiento superficial de agua y un umbral de almacenamiento a partir del cual cesa la infiltración capilar. La infiltración en TETIS está compuesta por la infiltración capilar y la infiltración gravitacional. La primera está representada en el tanque de almacenamiento estático (Figura 1), en el cual se almacena el agua capilar más las abstracciones iniciales y posee un umbral denominado "capacidad de almacenamiento estático" . La cantidad de agua que ingresa al sistema es almacenada en el suelo mientras no se alcance la capacidad, y la cantidad de agua excedente se expresa de manera discreta así:
donde: H1,t-1 es la cantidad de agua almacenada en el tanque de almacenamiento estático al inicio del intervalo de tiempo t. Según la expresión (1), la capacidad de infiltración es ilimitada mientras no se alcance la capacidad de campo, y la infiltración capilar es:
![]()
La infiltración gravitacional tiene la siguiente expresión:
![]()
donde: ks es la conductividad hidráulica saturada.
Sin pérdida de generalidad, en el análisis no se incluye la intercepción, y la evapotranspiración se considera como una reducción de la entrada en el modelo. Para estudiar la aplicabilidad del concepto de "parámetros efectivos variables en S2", se consideró la heterogeneidad espacial de los parámetros capacidad de almacenamiento estático Hu y conductividad hidráulica saturada ks en S1.
Escalas espaciales y representación de la heterogeneidad
Para realizar la simulación numérica se definió una microescala de 1 m y una mesoescala de 100 m. Es importante notar que para este trabajo el tamaño de la microescala (S1) es importante en términos relativos con respecto al tamaño de la mesoescala (S2) y no en términos absolutos. El valor de microescala igual a 1 m y mesoescala igual a 100 m han sido seleccionados para trabajar con un reducido orden de magnitud, por lo que es importante la relación S1/S2 y no los valores S1 y S2 por separado. Por ello, la microescala no es importante en términos absolutos y debe quedar claro que la conceptualización de TETIS no corresponde a soportes de 1*1 m2, pero a efectos de este estudio se ha utilizado dicho soporte por comodidad de trabajar con valores pequeños sin incidencia en la forma y estructura de las ecuaciones analíticas derivadas. Las ecuaciones planteadas no son sensibles al aumento del orden de magnitud, por lo que la microescala podría ser entendida igual a 20 m (orden de magnitud conceptualización TETIS) y la mesoescala igual a 2000 m (escala de modelación para acoplar el modelo hidrológico con otros tipos de modelos, como los modelos climáticos regionales o globales). El artículo presentado busca constatar la utilidad de emplear parámetros variables para escalar ecuaciones no lineales de tipo umbral, incluso el efecto de la macro-heterogeneidad. Por ello, se ha utilizado el modelo TETIS como un medio para constatar la aplicabilidad de un concepto y no como un fin.
La heterogeneidad de los parámetros hidrológicos se representó a través de una función de densidad de probabilidad Beta para la capacidad de almacenamiento estático y lognormal para la conductividad hidráulica saturada (Vauclin et al. 1994; Oldenborger et al. 2003; Gupta et al. 2006; Ceddia et al. 2009):
![]()
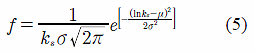
Cálculo de parámetros hidrológicos variables
Barrios & Francés (2012) propusieron una formulación inversa para parametrizar el efecto de agregar espacialmente el proceso no lineal estudiado en este artículo, encontrando parámetros efectivos variables como operador de escalado. Sin embargo, la aplicación de dicha formulación inversa implica resolver las ecuaciones del flujo en la microescala y posteriormente agregar los flujos linealmente:
En este trabajo se presenta el cálculo analítico de los parámetros variables Hu y ks en la mesoescala utilizando el método "de dos pasos" para calcular funciones de distribución derivadas. En dicho método se calcula la función de distribución de probabilidad acumulada de la función inversa del flujo y luego por diferenciación se calcula la función de densidad. El desempeño de las ecuaciones de escalado analíticas se evaluó a través de la comparación de la respuesta hidrológica usando estas ecuaciones en la mesoescala y la respuesta hidrológica de la microescala agregada, utilizando simulación de Monte Carlo en el software MATLAB versión R2010b con un código programado por el autor y ejecutado en ambiente Windows en un computador de escritorio con 8 GB de memoria RAM y un procesador Intel core QUAD de 3.2 ghz de velocidad. Las características de dicha simulación se describen en la Tabla 1.
RESULTADOS
Ecuaciones analíticas de parámetros variables: caso de Hu
De acuerdo con la formulación inversa del parámetro Hu en la mesoescala, representada por la Ecuación (6), su valor es equivalente al estado de humedad al final del intervalo. H1,t Por lo tanto, el valor de Hu[S2] coincide con el primer momento de la distribución de H1,t. Dadas las ecuaciones del excedente de precipitación X2,t y humedad al final del intervalo H1,t:
y reemplazando la Ecuación (8) en (9) se tiene que la humedad al final del intervalo es:
La Ecuación (10) puede expresarse así:
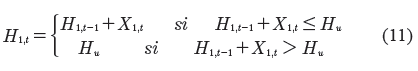
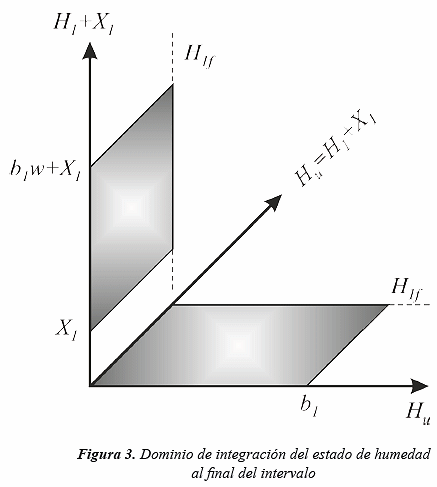
Si H1,t-1 + X1,t > Hu, y se considera que H1 y Hu son variables aleatorias asumiendo que Hu tiene una distribución uniforme U(0,b1) (lo cual se hace para simplificar cálculos y luego se cambia a una distribución beta) y H1,t-1= w·Hu, con w constante en el intervalo [0,1], entonces la función de distribución de H1,t queda definida por la siguiente ecuación (de acuerdo con la convolución en la Figura. 3):
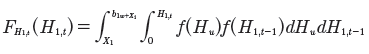
Reemplazando las funciones de densidad de H1,t-1 y Hu en la ecuación anterior se tiene que:
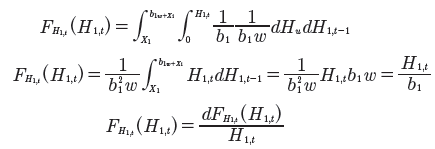
Como era de esperar, la Ecuación (12) demuestra que la función de densidad de H1,t es igual a la función de densidad de Hu cuando H1,t-1+X1,t > Hu. La función de distribución y densidad de H1,t para el caso en que H1,t-1+X1,t ≤ Hu está dada por:
De acuerdo con la Ecuación (13), la función de densidad de H1,t es igual a la función de densidad de H1 al inicio del intervalo cuando H1,t-1+X1,t ≤ Hu.
Teniendo en cuenta las anteriores consideraciones, ahora se asume que Hu sigue una distribución beta [Beta(a,b)]·Λ, donde Λ es el factor de escala de la distribución y a y b son los parámetros de la distribución. A partir de las Ecuaciones (12) y (13), es inmediato que la función de densidad de H1,t queda expresada así:
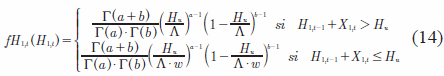
Los límites de integración para calcular el primer momento son:
El mínimo valor que puede tomar la variable aleatoria: 0
El valor en que H1,t-1+X1,t = Hu: nt/(1-w).
El valor máximo que puede tomar H1,t-1+X1,t: Λ·w + nt.
El primer momento de la función de densidad de H1,t está dado por:
La solución particular de la Ecuación (15) para el caso en que los parámetros y sean iguales a 2 es:
donde:
nt = nt-1+X1,t
lt = nt/(1-w)
mt = Λw + nt
Ecuaciones analíticas de parámetros variables: caso de ks
El valor del parámetro ks en la mesoescala es equivalente al primer momento de la función de distribución de X3, como se muestra en la Ecuación (7). Para una función de variables aleatorias como la representada por la Ecuación (17), su función de distribución de probabilidad y su función de densidad se deducen así:
El parámetro efectivo ks[S2] en la mesoescala se ha definido como variable y, de acuerdo con la solución del problema inverso presentado en la Ecuación (7), este es igual a:
Las funciones ![]() se presentan en el apéndice A.
se presentan en el apéndice A.
Verificación numérica por simulaciones de Monte Carlo
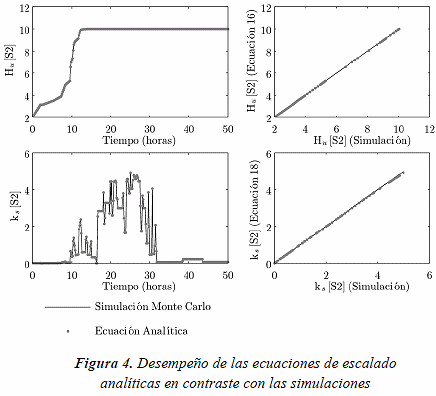
Los resultados de las simulaciones numéricas muestran que existe una coincidencia aceptable entre los valores de los parámetros efectivos variables calculados mediante las Ecuaciones (16) y (18), y los valores calculados a través de la simulación de Monte Carlo (Figura 4), con valores de la raíz cuadrada del error cuadrático medio (RMSE) de 0,0019 y 0,2843 respectivamente. Para el caso de la Ecuación (16) la solución es analítica, mientras que la Ecuación (18) se resolvió a través de integración numérica utilizando el método trapezoidal (Yang et al. 2005).
DISCUSIÓN
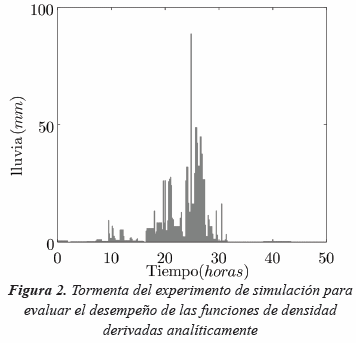
El evento que se ha seleccionado para realizar la simulación tiene características de simulación continua, ya que inicia en los primeros minutos con lluvia, luego hay un periodo seco hasta las 8 h y luego hacia las 15 h hay otro periodo seco. Esto permite inferir que las ecuaciones analíticas propuestas funcionan igualmente para simulación continua que para eventos. El hecho de no realizar una simulación con una serie más larga se justifica en el elevado costo computacional que implicaría realizarla manteniendo una discretización temporal pequeña.
Las ecuaciones analíticas encontradas son válidas únicamente para los parámetros hidráulicos que se ajusten a las funciones de distribución asumidas (Beta para Hu, lognormal para ks) y sin autocorrelación espacial. Si dichos parámetros siguen otra función de distribución, deberán derivarse nuevamente las ecuaciones de escalado de parámetros variables. En hidrología e hidrogeología es muy frecuente encontrar que la conductividad hidráulica saturada se ajusta a una función de distribución lognormal (Vauclin et al. 1994; Oldenborger et al. 2003; Gupta et al. 2006; Ceddia et al. 2009), y es poco común que se ajuste a otra función de distribución. Para el caso de la capacidad de almacenamiento capilar, hay mayor variedad de modelos a los que se ajusta esta variable en diferentes casos, pero la característica fundamental es que es una función de distribución acotada (no asintótica en las colas). Se ha seleccionado la distribución Beta, ya que es una distribución acotada y tiene la ventaja de que puede tomar diversas formas dependiendo de los valores de sus parámetros, además algunos trabajos han encontrado un buen ajuste de la capacidad de almacenamiento capilar a una distribución Beta (Ceddia et al. 2009).
El cálculo analítico de funciones de distribución derivadas con variables aleatorias dependientes tiene un alto nivel de dificultad (Hilhorst, 2009), y el grado de complejidad se incrementa cuando el número de variables aleatorias dependientes es significativamente grande, pues cada variable estaría condicionada a muchas otras variables y los cálculos analíticos serían inabordables. Este es un tema de investigación abierto en el campo de la estadística matemática, puesto que no existen teoremas centrales de límite para dar solución a este tipo de problemas (Papoulis, 2002; Doukhan et al. 2010).
Las Ecuaciones (15) y (18) fueron derivadas para condiciones en que la autocorrelación espacial de y sea cero. Aun en esta condición dichas ecuaciones son de naturaleza compleja y requieren la utilización de métodos numéricos para su solución y su aplicación, en la práctica resulta ser muy difícil de implementar. Sin embargo, con el experimento sintético presentado en este trabajo, se demuestra el potencial de utilizar ecuaciones de escalado con parámetros efectivos variables para corregir el efecto de escala espacial desde la microescala hacia la mesoescala.
Intentar la incorporación de dependencia espacial en el cálculo de las ecuaciones de parámetros efectivos variables hace que el problema sea inmanejable, dada la no linealidad de las ecuaciones del proceso analizado (Valdés, 2011). Por esto, es necesario explorar otras opciones para el desarrollo de ecuaciones de escalado, como la formulación de ecuaciones empíricas a partir de simulaciones de Monte Carlo, como las presentadas por Barrios (2011), o ecuaciones fundamentadas en técnicas de Machine Learning.
CONCLUSIONES
Los efectos de escala espacial están controlados por la naturaleza heterogénea de las características ambientales de los sistemas hidrológicos, la variabilidad de los procesos involucrados en un amplio rango de escalas espacio-temporales y las no linealidades de dichos procesos. Con este trabajo se ha demostrado que la utilización de ecuaciones de escalado de parámetros efectivos variables puede contribuir a disminuir el efecto de escala espacial en procesos no lineales definidos por umbrales de flujo y almacenamiento. Ya que el valor del parámetro efectivo captura el efecto de heterogenenidad espacial del proceso en la microescala como consecuencia de que sus valores cambian en función del estado de humedad del sistema y las características de heterogeneidad a nivel de subcelda. Esta propiedad funciona de manera similar a la relación conceptual de los parámetros de la ecuación de Richards, los cuales cambian en función del estado de humedad de la matriz de suelo y sus propiedades físicas.
Dada la dificultad de su derivación analítica, las ecuaciones propuestas para calcular parámetros efectivos variables no incluyen la autocorrelación espacial de los parámetros en la microescala, ni la interacción horizontal de los procesos. Por lo tanto, es importante en trabajos futuros formular operadores de escalado de acuerdo con otras técnicas estadísticas que permitan incluir estas propiedades y aplicarlos en cuencas reales.
AGRADECIMIENTOS
El autor agradece el apoyo económico de la Universidad del Tolima para realizar la presente investigación, según lo establecido en el acuerdo 011 de 2006 del Consejo Superior de dicha institución.
REFERENCIAS
1. Barrios, M. (2011). Estudio del efecto de escala espacial en un modelo hidrológico distribuido. Tesis Doctoral. Universitat Poltècnica de València. Valencia, España. [ Links ]
2. Barrios, M. & Francés, F. (2011). Application of scaling equations to deal with the spatial aggregation effect on watershed hydrological modelling. En: SCARCE 2nd ANNUAL CONFERENCE: Integrated modelling and monitoring at different river basin scales. Madrid, España.
3. Barrios, M. & Francés, F. (2012). Spatial scale effect on the upper soil effective parameters of a distributed hydrological model. Hydrological Processes, 26 (7), 1022-1033. doi: 10.1002/hyp.8193.
4. Beven, K. (1989). Changing ideas in hydrology The case of physically-based models. Journal of Hydrology, 105(1-2), 157-172. doi: 10.1016/0022-1694(89)90101- 7.
5. Beven, K. (1995). Linking parameters across scales: subgrid parameterizations and scale dependent hydrological models. Hydrological Processes, 9(5-6), 507-525. doi: 10.1002/hyp.3360090504.
6. Binley, A., Beven, K., Elgy, J. (1989). A physically based model of heterogeneous hillslopes 2. Effective Hydraulic conductivities. Water Resour. Res., 25(6), 1227-1233.
7. Blöschl, G. & Zehe, E. (2005). On hydrological predictability. Hydrological Processes, 19(19), 3923-3929.
8. Ceddia, M. B., Vieira, S. R., Oliveira-Villela, A. L., dos- Santos-Mota, L., Cunha-dos-Anjos, L. H., Fonseca-de-Carvalho, D. F. (2009). Topography and spatial variability of soil physical properties. Scientia Agricola, 66(3), 338-352.
9. Di Baldassarre, G. & Uhlenbrook, S. (2012). Is the current flood of data enough? A treatise on research needs to improve flood modelling. Hydrological Processes, 26(1), 153-158. doi: 10.1002/hyp.8226.
10. Doukhan, G. L., Lang, G., Surgailis, D., Teyssiere, G. (2010). Dependence in probability and statistics (lecture notes in statistics). Berlin: Springer.
11. Francés, F., Vélez, J. I., Vélez, J. J. (2007). Split-parameter structure for the automatic calibration of distributed hydrological models. Journal of Hydrology, 332(1-2), 226-240.
12. Francés, F. & Vélez, J. J. (2008). Descripción del modelo conceptual distribuido de simulación hidrológica TETIS V.7.3.
13. Francés, F., Vélez, J. J., Vélez, J. I., Puricelli, M. (2002). Distributed modelling of large basins for a real time flood forecasting system in Spain. En: Second Federal Interagency Hydrologic Modeling Conference. Las Vegas, EE. UU.
14. Gupta, N., Rudra, R. P., Parkin, G. (2006). Analysis of spatial variability of hydraulic conductivity at field scale. Canadian Biosystems Engineering, 48, 1.55-1.62.
15. Hilhorst, H. J. (2009). Central limit theorems for correlated variables: some critical remarks. Brazilian Journal of Physics, 39(2A), 371-380.
16. Kuo W.-L., Steenhuis, T. S., McCulloch, C. E., Mohler, C. L., Weinstein, D. A., DeGloria, S. D., Swaney, D. P. (1999). Effect of grid size on runoff and soil moisture for a variable-source-area hydrology model. Water Resour. Res., 35(11), 3419-3428. doi: 10.1029/1999wr900183.
17. Oldenborger, G. A., Schincariol, R. A., Mansinha, L. (2003). Radar determination of the spatial structure of hydraulic conductivity. Ground Water, 41(1), 24-32.
18. Papoulis, A. (2002). Probability, random variables and stochastic processes. Nueva York: McGraw-Hill.
19. Todini, E. (2011). History and perspectives of hydrological catchment modelling. Hydrology Research, 42(2-3), 73- 85. doi: 1O.2166/nh .20 11.096.
20. Valdés, J. B. (2011). Comunicación personal. Valencia, España.
21. Vauclin, M., Elrick, D. E., Thony, J. L., Vachaud, G., Revol, P., Ruelle, P. (1994). Hydraulic conductivity measurements of the spatial variability of a loamy soil. Soil Technology, 7(3), 181-195. doi: 10.1016/0933- 3630(94)90020-5.
22. Vázquez, R. F., Feyen, L., Feyen, J. (2002). Effect of grid size on effective parameters and model performance of the MIKE-SHE code. Hydrological Processes, 16(2), 355-372.
23. Vélez, J. I. (2001). Desarrollo de un modelo hidrológico conceptual y distribuido orientado a la simulación de las crecidas. Tesis Doctoral. Universidad Politécnica de Valencia. Valencia, España.
24. Wolock, D. M. & Price, C. V. (1994). Effects of digital elevation model map scale and data resolution on a topography-based watershed model. Water Resour. Res., 30(11), 3041-3052. doi: 10.1029/94wr01971.
25. Yang, W. Y., Cao, W., Chung, T., Morris, J. (2005). Applied numerical mehods using MATLAB. New Jersey: Wiley- Interscience.
26. Zhang, W. & Montgomery, D. R. (1994). Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour. Res., 30(4), 1019-1028. doi: 10.1029/93wr03553.