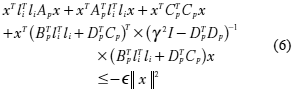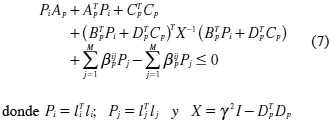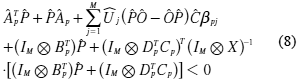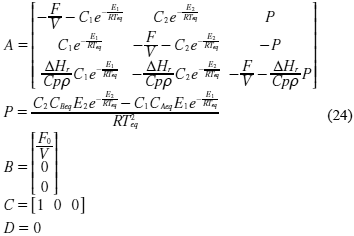Análisis de sensibilidad de un algoritmo de estimación de la norma inducida L₂ para sistemas conmutados lineales

Juan Pablo Requez¹, Miguel Strefezza², Gustavo Sánchez² y Ernesto Granado²

¹ Universidad Centroccidental Lisandro Alvarado. Departamento de Agroindustriales. Barquisimeto, Venezuela. e-mail: jprequez@ucla.edu.ve

² Universidad Simón Bolívar. Departamento de Procesos y Sistemas. Sartenejas, Venezuela.

e-mail: strefeza@usb.ve, gsanchez@usb.ve, granado@usb.ve

RESUMEN

Este artículo presenta un análisis experimental de la sensibilidad de un algoritmo de estimación de la norma inducida L₂ especialmente diseñado para sistemas lineales conmutados. En particular, se analiza el efecto observado sobre el comportamiento del algoritmo con respecto a variaciones en el número de subfunciones, en el número de modos conmutados y en parámetros físicos característicos de cada modo. Para el análisis se seleccionaron tres modelos de prueba con diferentes grados de complejidad. Los resultados obtenidos permiten avanzar en la comprensión de dos aspectos fundamentales del algoritmo: la selección de un número de subfunciones adecuado y el significado físico de la cota de aproximación obtenida.

Palabras clave: Análisis de Sensibilidad, Norma Inducida L₂, Sistemas Conmutados Lineales. Desigualdades Matriciales Lineales y Bilineales, Norma H_¥.

Sensitivity analysis of an induced L₂ norm estimation algorithm for linear switched systems

ABSTRACT

This paper present an experimental sensitivity analysis for a L₂-induced gain estimation algorithm designed for linear switched systems, which studies the observed effect in the numerical approximation with respect to variations on the number of sub-functions and switched modes used and the effect of the physical parameters in each mode. The analysis is done by studying three test models with different complexity degrees. The results obtained allow one to go a step ahead in the comprehension of two fundamental features of the algorithm: the right selection of the subfunction numbers and the meaning of the approximated L₂-induced gain value obtained.

Keywords: Sensitivity Analysis, L₂-Induced gain, Switched Linear Systems, Linear and Bilinear Matrix Inequalities, H_¥ Norm.

Recibido: octubre 2013 Recibido en forma final revisado: diciembre 2014

INTRODUCCIÓN

Una amplia variedad de sistemas dinámicos pueden ser descritos mediante una combinación de lógica de eventos y ecuaciones diferenciales. Considere por ejemplo la caja de velocidades de un vehículo, la cual alterna entre distintas posiciones generadas por un evento (el cambio de la posición de la palanca realizado por el conductor) que genera saltos o discontinuidades en la dinámica de funcionamiento del vehículo.

Al evento que consiste en la transición entre dos modos de funcionamiento diferentes (es decir, entre dos ecuaciones diferenciales diferentes para describirlo) se le denomina conmutación. Las características propias de los sistemas conmutados han sido bastante estudiadas y se cuenta con una amplia literatura sobre el tema (Hirata y Hespanha, 2009, pág. 1), (Hirata y Hespanha, 2010a), (Dayawansa y Martin, 1999), (Branicky, 1994) y (Sun y Ge, 2005). En particular, se ha puesto énfasis en la estimación de la norma inducida L₂ para este tipo de sistemas, lo cual resulta de mucha utilidad en problemas de control robusto y otras aplicaciones (Alves, Kirata, y Strefezza, 2011) y (Qiu, Feng, y Yang, 2009).

Dado un sistema conmutado, el valor de su norma L₂ puede calcularse de manera aproximada mediante diversos procedimientos numéricos. Por ejemplo, en (Alves, Kirata, y Strefezza, 2011) se propuso un método de estimación basado en la solución de ecuaciones de Hamilton-Jacobi- Bellman (HJB). Dicho método requiere especificar, entre otros parámetros, un número entero M que determina el número de inecuaciones bilineales que deben resolverse de manera simultánea. Uno de los objetivos del presente trabajo consiste precisamente en analizar, a través del análisis experimental, la influencia del valor M sobre los resultados y el comportamiento del algoritmo. Este análisis aporta entendimiento sobre el funcionamiento de este algoritmo y su aplicación sobre algunos sistemas de manera que, en un problema en particular, pudiera permitir la selección de un número de subfunciones adecuado, conduciendo a una medida aceptable del tiempo de cálculo involucrado. Note que este tipo de análisis se conoce en la literatura como análisis de sensibilidad y en general tiene como finalidad la evaluación del efecto que generan las variaciones en un determinado parámetro sobre una variable de interés generada por el mismo algoritmo.

Un segundo objetivo planteado en el trabajo consiste en establecer una comparación entre el valor L₂ estimado para el sistema conmutado con respecto al valor correspondiente a cada modo de manera separada, lo que aporta conocimiento acerca de la relación existente entre los modos de funcionamiento por separado e integrados de un sistema conmutado.

También se propone analizar el efecto de las variaciones en los parámetros característicos de cada modo, lo que permite avanzar en la interpretación física de la aproximación y obtener orientación al momento de formular especificaciones de diseño para un eventual controlador del sistema conmutado.

La información que se presenta en este documento está estructurada como se explica a continuación: en la sección II se describen algunos conceptos generales relacionados con sistemas lineales conmutados y se presenta de manera detallada el algoritmo de estimación considerado para el estudio. En la sección III se describe la metodología utilizada y los modelos dinámicos de prueba seleccionados para generar los resultados numéricos. En la sección IV se realiza una discusión de los resultados obtenidos. Finalmente, en la sección V se incluyen las conclusiones del trabajo.

SISTEMAS LINEALES CONMUTADOS

En esta sección se presenta una introducción general sobre los sistemas conmutados y se desarrolla el algoritmo de estimación de la norma inducida L₂, incluyendo las condiciones necesarias para dicho cálculo.

Sistema Conmutado Lineal

Un sistema conmutado lineal puede ser descrito por un conjunto de ecuaciones de estado de la forma

donde s Î S es una señal de conmutación continua y constante a trozos con

S = {s : [0,¥) ® Ã}             (2)

la cual selecciona valores de las matrices (A_P, B_p, C_p, D_p) dentro de una familia parametrizada como

{(A_P, B_p, C_p, D_p) | p Î Ã}     (3)

donde à es un conjunto compacto de índices. Tal como es usual x Î Rⁿ representa al vector de estados, y Î R^k al vector de salidas controladas y u Î R^m al vector de entradas manipuladas del sistema.

Clases de señales conmutadas

Se denota S a la clase conformada por las señales de conmutación constantes y continuas a trozos (Hirata y Hespanha, 2009). A continuación se establecen algunas propiedades importantes de regularidad en S. Dado un subconjunto S’ de S y para constantes b > a ≥ 0, se denota S’ [a,b) a la restricción para todas las señales de conmutación s Î S’ al intervalo [a,b).

Invariancia ante desplazamientos temporales

Sea S’ Ì S y t > 0. A partir del conjunto de S’ [t,∞), se puede definir otro conjunto Σ_t S’ [t,∞) = {σ|σ(ρ) = μ(ρ+t) μ Î S’ (t,∞), ρ ≥ 0}. Se dice entonces que S’ es invariante ante desplazamientos temporales si S’ = Σ_t S’ [t,∞) para todo t > 0.

Cerradura bajo concatenación

Sea S’ Ì S y t > 0. Supóngase que s Î S' [0,t) y m Î S' [t,¥). Defina la señal

y el conjunto S' [0,t) Å S' [t,¥) = {s Å m | s Î S' [0,t),m Î S' [t,¥)}.

Se dice que S’ es cerrado bajo concatenación si S' = S' [0,t) Å S' [t,¥) para todo t > 0.

Señal conmutada regular

Sea S’ Ì S. Se dice que S’ es regular si:

1. Para todo p Î P, la señal conmutada constante s^p (t) = p pertenece a S’.

2. La clase de señal conmutada S’ es invariante ante desplazamientos temporales.

3. La clase de señal conmutada S’ es cerrada bajo concatenación.

Ganancia inducida L₂

Se dice que el sistema descrito por (1) tiene ganancia inducida, L₂ ≤ g Î R, g > 0, uniformemente sobre S’ Ì S si y sólo si para todo T Î R, T > 0, todo s Î S’ y todo u Î L₂^m, se cumple, considerando x(0) = 0:

Cálculo aproximado de L₂

En Hirata y Hespanha (2010b) se proponen las condiciones necesarias y sufcientes para que un sistema conmutado sea exponencialmente estable y admita una ganancia inducida L₂ ≤ g: Sea S’ un subconjunto de S regular y g > 0. Suponga que existe al menos un índice q Î P tal que el par (C_q, A_q) sea observable. Entonces los siguientes enunciados son equivalentes:

1. El sistema (1) es exponencialmente estable sobre S’ y tiene una ganancia L₂ inducida menor que γ uniformemente sobre S’.

2. La constante positiva g satisface g²I - D_p^T D_p > 0 para todo p Î P. Además existe una constante e > 0 y una función V: Rⁿ ® R estrictamente convexa, cero a cero, homogénea de grado 2, la cual, para todo x Î Rⁿ excepto en un conjunto de puntos de medida cero donde V(x) no es diferenciable, satisface:

3. La constante positiva g satisface g²I - D_p^T D_p > 0 para todo p Î P y existe una constante e > 0 y un subconjunto compacto K Ì R^nxn de matrices definidas positivas tales que la función cuadrática continua a trozos V(x) = max_QÎK x^T Qx satisface (5) para todo p Î Ã y para todo x Î Rⁿ excepto en un conjunto de puntos de medida cero donde V(x) no es diferenciable.

4. La constante positiva g satisface g²I - D_p^T D_p > 0 para todo p Î P y existe una constante e > 0, un entero M que satisface M ≥ n y un conjunto de vectores l_i Î Rⁿ, i = 1...M tal que la matriz L º [ℓ₁...ℓ_M]^T Î R^Mxn tiene rango completo y la función cuadrática continua a trazos V(x) = max_i=1,...,M (l_i^Tx)² satisface (5) para todo p Î Ã y para todo x Î Rⁿ excepto en un conjunto de puntos de medida cero donde V(x) no es diferenciable.

Por otra parte, note que la ecuación (5) puede ser reescrita como se indica a continuación, sujeto a (l_i^Tx)² > (l_j^Tx)² para todo j = 1,...,M

Si se escoge cualquier p Î Ã, i = 1,...,M, y considerando números reales b^ij_p > 0,  j = 1,...,M, la ecuación (6) puede escribirse nuevamente como (7)

Algoritmo para el cálculo aproximado de L₂

En Alves, Kirata, & Strefezza (2011) los autores demuestran que la ecuación (7) es equivalente a:

donde

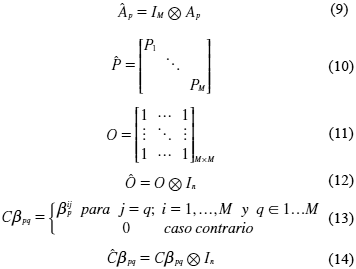
El operador Ä, representa al operador de multiplicación de Kronecker. Mediante el Teorema del Complemento de Schur, la ecuación (8) se plantea en términos de Inecuaciones Matriciales Lineales (en inglés, LMIs) como

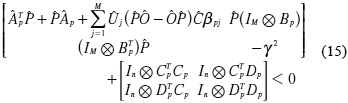
Defínase ahora

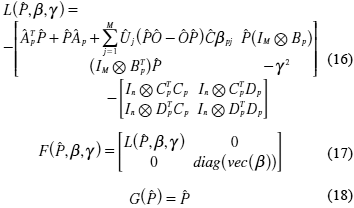
donde, por simplicidad β^ij_p = β y diag(vec(β)) denotan una matriz diagonal con los elementos de β como su diagonal principal. Denote entonces F1 a la función F para β constante y F2 a la misma F para constante. El algoritmo de estimación propuesto por (Alves, Kirata, & Strefezza, 2011) consta de los siguientes pasos:

1. Inicialización: Escoger los valores de β como valores positivos aleatorios de donde se obtiene la estimación inicial β₀. Escoger el número de subfunciones M ≥ n o M = 1.

2. Resolver

Minimizar g

Sujeto a F1 (, β₀, g) ≥ 0; G() ≥ 0

de donde se obtiene ₀

3. Resolver

Minimizar g

Sujeto a F2 (₀, β, g) ≥ 0

de donde se obtiene β₀

4. Repetir

Minimizar g

Sujeto a F1 (, β₀, g) ≥ 0; F2 (₀, β, g) ≥ 0; G() ≥ 0

de donde se obtiene y β, luego se sustituye ₀ = , β₀ = β hasta convergencia de g con la precisión deseada.

De esta forma se concluye la introducción de los conceptos más importantes con respecto a los sistemas conmutados y al algoritmo de estimación de la norma inducida L₂ para este tipo de sistemas, el cual será considerado en las siguientes secciones.

METODOLOGÍA

A continuación se describe la metodología utilizada para conducir el estudio de sensibilidad. Se eligieron 3 modelos de los cuales el primero fue previamente estudiado en Alves, Kirata, y Strefezza, (2011) y constituye el punto de partida del presente trabajo. El segundo fue tomado de Benzaouia (2009) y consiste en un sistema de dos modos de conmutación, de complejidad similar al primero. El tercero consiste en un modelo de reactor no isotérmico, en el cual se desarrolla una reacción química reversible, caracterizado por 3 modos de conmutación, lo que requiere mayor esfuerzo numérico respecto a los anteriores.

Sistema de prueba 1

Consiste en un modelo para el sistema de amortiguación de un vehículo, instalado en el banco de pruebas del Laboratorio de Dinámica de Máquinas de la Universidad Simón Bolívar, Venezuela. El sistema se caracteriza por dos modos de funcionamiento descritos por los modos mostrados a continuación.

Modo 1

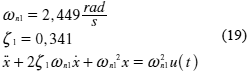
Modo 2

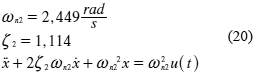
En términos de ecuaciones de estado, el modelo puede representarse como:

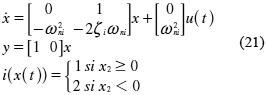
Sistema de prueba 2

Este modelo de segundo orden con una sola entrada y una sola salida posee dos modos de funcionamiento (Benzaouia, 2009). El sistema puede modelarse con la representación de espacio de estados que se presenta a continuación:

Modo 1

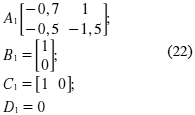
Modo 2

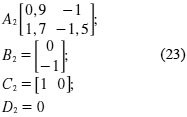
Sistema de Prueba 3

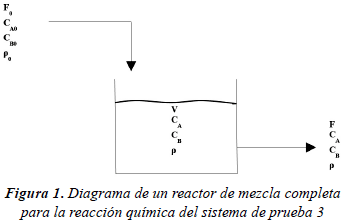
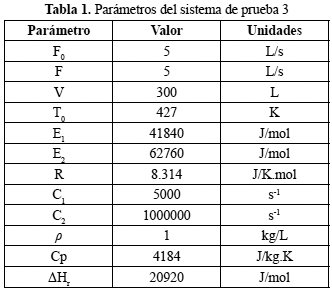
El tercer modelo consiste en un reactor no isotérmico presentado en Willis (2000) en el cual se produce reacción química reversible A « B ) que sucede a razón k₁ en el sentido directo y a razón k₂ en el sentido inverso. La reacción directa es exotérmica y libera un calor ΔHr. Un diagrama simplificado del proceso se muestra en la figura 1. En la ecuación (24) se presenta el modelo lineal y los valores correspondientes de los parámetros utilizados se presentan en la tabla 1.

Las variables de estado son x₁ = C_A, x₂ = C_B y x₃ = T, que representan a las concentraciones y la temperatura del fluido dentro del reactor respectivamente. La variable de entrada u = T₀ representa la temperatura del flujo de alimentación. Los valores en el punto de operación se denotan como (25)

El sistema puede conmutar a tres modos posibles, a saber:

Modo 1: ū < 430,77 K

Modo 2:  ū > 433,31

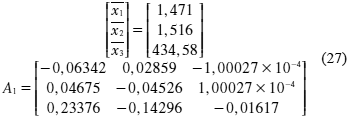
Modo 3: 430,77 ≤ ū ≤ 433,31

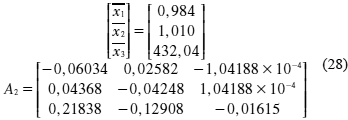
Procedimiento

Para analizar el efecto de variaciones en el número de subfunciones M se realizaron varias ejecuciones del algoritmo descrito en la sección II, parte E, tomando valores de M = 1, 2, 3, 4 y 5.Seobservaron 100 iteraciones de cada ejecución considerando los sistemas de prueba 1 y 3.

Para determinar la influencia de los parámetros físicos sobre la estimación L₂, en el caso del sistema de prueba 1 se modificaron los valores de ωn y ζn con un incremento y una disminución de 50% respecto a los valores iniciales.

RESULTADOS

En esta sección se describen los resultados obtenidos al ejecutar las pruebas descritas en la sección anterior.

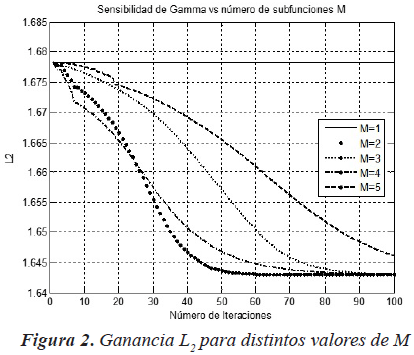
Sensibilidad del algoritmo con respecto al número de subfunciones M

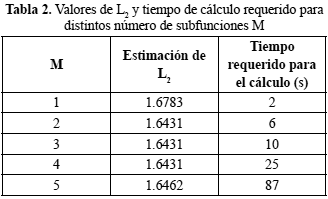
En la figura 2 se puede observar que el valor obtenido para M=1 es superior en todos los casos al obtenido para M>1, lo que es de esperarse pues corresponde al caso trivial de una sola ecuación de Ricatti. Nótese que al aumentar el valor de M disminuye la rapidez de la convergencia del método numérico, aunque se converge al mismo valor final. Es decir que, en los experimentos realizados, un valor de M>3 no aporta mejoras en el resultado numérico. Por el contrario, se produce un incremento el tiempo de procesamiento de los datos como se puede ver en la tabla 2. A medida que se incrementa M, existe una complejidad del cálculo superior lo que hace que el tiempo aproximadamente se duplique para un incremento de M en una unidad. El tiempo reportado en la tabla 1 está en segundos y se utilizó un procesador Intel Centrino de doble núcleo, con 1.6GHz de frecuencia y una memoria RAM instalada de 3GB sobre el sistema operativo Windows 7.

Resultados de L₂ para funcionamiento no conmutado

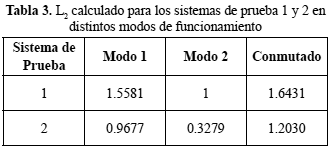
En una segunda etapa se determinó el valor de L₂ para cada sistema de prueba considerando cada uno de sus modos de manera aislada, valor que corresponde simplemente a la norma H_¥ del sistema considerado. Para los sistemas de prueba 1 y 2 se observa que la estimación L₂ para el sistema conmutado es mayor que la norma H∞ de cada uno de sus modos de funcionamiento por separado, es decir

L_2conmutado > L_2modoi

donde i corresponde al modo de funcionamiento. Estos resultados pueden observarse en la tabla 3.

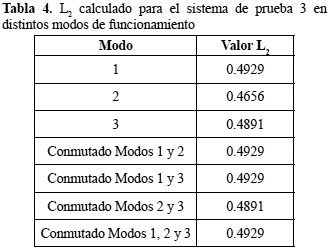
En el caso del sistema de prueba 3, se crearon tres reglas de conmutación que corresponderían a las combinaciones de dos modos entre tres posibles y una regla de conmutación que permite que el sistema trabaje en los tres modos posibles de funcionamiento. Usando estas reglas de conmutación, se observa nuevamente que la estimación L₂ es mayor o igual que el mayor valor de L₂ en cada modo de funcionamiento por separado. Estos resultados se pueden observarse en la tabla 4.

Efectos de los parámetros del sistema

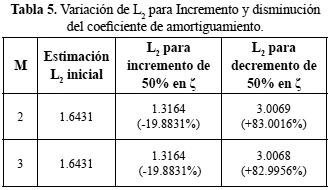
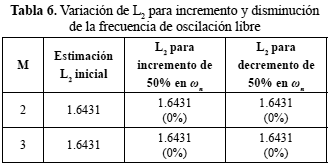
En esta etapa se simularon variaciones en los parámetros físicos que describen al sistema conmutado. La variación de estos coeficientes, como es de esperarse, tiene influencia sobre el valor de L₂ obtenido para el sistema conmutado. Esta variación es prácticamente despreciable en el caso de incrementos en la frecuencia natural de oscilación (ω_n) pero muy notable en el caso de incrementos y disminuciones del coeficiente de amortiguamiento (ζ). Esto se interpreta por la manera como el sistema “disipa” energía: la disipación se está relacionada fundamentalmente con la capacidad de amortiguamiento del resorte, mientras que la frecuencia de oscilación no se relaciona con la posibilidad de atenuar la transferencia de energía en el sistema, lo cual se ilustra mediante los resultados presentados en las tabla 5 y tabla 6.

CONCLUSIONES

En este artículo se presentó un análisis experimental de la sensibilidad del algoritmo de estimación de la norma inducida L₂, propuesto por Alves, Kirata, y Strefezza (2011). En particular se analizó el efecto de las variaciones en el número de subfunciones M, en el número de modos conmutados y en los parámetros físicos característicos de cada modo.

Con respecto al parámetro M los resultados parecen confirmar que el método numérico requiere el uso del menor valor posible para este parámetro. Un incremento M aumenta el tiempo de ejecución y no produce mejoras apreciables en el valor de convergencia.

Igualmente, se constató que el valor estimado para el sistema conmutado es consistentemente mayor que los valores determinados para cada uno de los modos de funcionamiento del sistema de manera aislada. Por otra parte, también se constató mediante la variación de los parámetros físicos del modelo de prueba 1 que el valor estimado de L₂ está relacionado con la capacidad de disipación de energía del sistema físico (amortiguamiento).

REFERENCIAS

1. Alves, J. R., Kirata, K. y Strefezza, M. (2011). Método numérico para estimar la ganancia L₂ inducida en sistemas conmutados lineales. Proyecto de grado no publicado, Universidad Simón Bolívar, Venezuela.        [ Links ]

2. Benzaouia, A. (2009). Stabilization of saturated switching systems. En J. Kleban, Switched Systems (pág. 1 a 35). Vukovar: In-Teh.        [ Links ]

3. Branicky, M. S. (1994). Stability of Switched and Hybrid Systems. Proceedings of the 33rd Conference on Decision and Control. Lake Buena Vista.        [ Links ]

4. Dayawansa, W. P. y Martin, C. F. (1999). A converse Lyapunov Theorem for a Class of Dynamical Systems Which Undergow Swithnig. IEEE Transactions on Automatic Control, 44(4), 751-760.        [ Links ]

5. Hirata, K. y Hespanha, J. (2009). L₂-induced Gain Analysis for a class of Switched Systems. Joint 48th IEEE conference on Decision and Control and 28th Chinese Control Conference. Shanghai.        [ Links ]

6. Hirata, K. y Hespanha, J. P. (2010a). L₂-induced Gain Analysis of Switched Linear Systems via Finitely Parametrized Storage Functions. Proceedings of the 2010 American Control Conference. Baltimore.        [ Links ]

7. Hirata, K. y Hespanha, J. P. (2010b). L₂-induced Gains of Switched Systems and Classes of Switching Signals. 49th IEEE Conference of Decision and Control. Atlanta.        [ Links ]

8. Qiu, J., Feng, G. y Yang, L. (2009). Robust H-Infinity static output feedback control of discrete-time switched polytopic linear systems with average dwell-time. Science in China Series F: Information Sciences, 52(11), 2019-2031.        [ Links ]

9. Sun, Z. y Ge, S. S. (2005). Analysis and synthesis of switched linear control systems. Automatica, 41, 181- 195.        [ Links ]

10. Willis, M. J. (1 de Marzo de 2000). Newcastle University, School of Chemical Engineering and Advanced Materials. Recuperado el 10 de Enero de 2013, de http://lorien.ncl.ac.uk/ming/control/gen/cstr.pdf        [ Links ]