Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de la Facultad de Ingeniería Universidad Central de Venezuela
versión impresa ISSN 0798-4065
Rev. Fac. Ing. UCV vol.30 no.1 Caracas mar. 2015
Diseño de una metodología que permita mejorar los portafolios de proyectos de inversión en un sistema eléctrico de potencia
Daniel Manfre 1 y Ebert Brea 2
1 Universidad Central de Venezuela. Escuela de Ingeniería Eléctrica. e-mail: daniman28@gmail.com
2 Universidad Central de Venezuela. Escuela de Ingeniería Eléctrica. e-mail: ebert.brea@ucv.ve
RESUMEN
Un Portafolio de Proyectos de Inversión en un Sistema Eléctrico de Potencia (PPISEP) es considerado en este artículo como un conjunto de proyectos de ampliación de la capacidad instalada de un Sistema Eléctrico de Potencia (SEP). Estos proyectos de ampliación pueden consistir en incrementos de las capacidades de las plantas generadoras o de las líneas de transmisión del SEP. El presente artículo desarrolla una metodología que permite mejorar estos PPISEP. Ésta consiste en estimar el momento en el cual los proyectos de inversión deben llevarse a cabo, y la cantidad de energía activa promedio que cada proyecto de inversión debe introducir al SEP, con el fin de mejorar el equilibrio económico de la empresa eléctrica y disminuir el consumo pronosticado no cubierto de energía activa promedio. Debido a que la mejora del PPISEP entra dentro de un problema de optimización, el presente artículo hace uso de la técnica de optimización Algoritmo Simplex Entero Mixto (ASEM) para plantear la resolución de este problema. La metodología desarrollada en este artículo utiliza la simulación por Monte Carlo para modelar las aleatoriedades del SEP. Dicha metodología es presentada en forma de pseudocódigo y ésta es implementada en un ejemplo numérico, cuyos resultados son analizados mediante algunas herramientas estadísticas.
Palabras Clave: planificación de la expansión de los sistemas eléctricos de potencia, optimización mediante la simulación, método de Monte Carlo, optimización entera mixta, teoría de grafos.
Design of a methodology to improve the investment project portfolios in an electric power system
ABSTRACT
An Investment Project Portfolio in an Electric Power System (IPPEPS) is considered in this article as a set of enhancement projects to increase the installed capacity of an Electric Power System (EPS). These enhancement projects can consist of the installed capacity of power plants or transmission lines of the EPS. This paper develops a methodology to improve the IPPEPS. This consists in estimating the time where the investment projects should be carried out, and the amount of average active energy that each investment project must enter to the EPS, in order to improve the economic balance of the electric utility and decrease the forecasted not covered consumption of average active energy. Since the improvement of the IPPEPS falls into an optimization problem, this paper uses the Integer Mixed Simplex Algorithm (IMSA) to solve this problem. The methodology developed in this article uses Monte Carlo simulation to model the randomness of the EPS. This methodology is formulated in pseudocodes and is implemented in a numeric example whose results are analyzed by some statistical tools.
Keywords: expansion planning of electric power systems, optimization by simulation, Monte Carlo method, mixed integer optimization, graph theory.
Recibido: marzo 2014 Recibido en forma final revisado: diciembre 2014
INTRODUCCIÓN
El presente artículo tiene como alcance el diseño de una metodología que permita mejorar los Portafolios de Proyectos de Inversión en un Sistema Eléctrico de Potencia (PPISEP) al determinar cuándo los proyectos de inversión se deben comenzar a construir y qué cantidad de energía activa promedio introduce cada proyecto de inversión al SEP. Esta mejora busca incrementar el balance económico de la empresa eléctrica y disminuir el consumo pronosticado no cubierto de energía activa promedio. Los proyectos de ampliación que componen los PPISEP pueden ser proyectos de generación (incrementos de la capacidad instalada de las plantas generadoras) o proyectos de transmisión (incrementos de la capacidad instalada de las líneas de transmisión). Mediante el uso de la teoría de grafos, el SEP es considerado como un modelo de repartición de energía activa promedio, por intervalos de tiempo, desde los generadores hasta las cargas mediante líneas de transmisión. Además de la teoría de grafos, la propuesta metodológica expuesta en este artículo tiene como fundamentos teóricos la teoría de simulación por Monte Carlo, la optimización mediante la simulación, la planificación de la expansión de los SEP, así como varios conceptos de ingeniería económica, algoritmia y estadística. La simulación por Monte Carlo tiene un papel sumamente importante en esta investigación puesto que permitió considerar y analizar las aleatoriedades en el consumo de energía del SEP y en las capacidades de transmisión de energía de las líneas de transmisión.
Existe una gran diversidad de estudios que han empleado la simulación por Monte Carlo para realizar análisis relacionados con los SEP. Uno de estos estudios es el análisis de riesgo de la planificación de la expansión de los sistemas hidroeléctricos de potencia presentado por Hreinsson et al., (2003). Este trabajo se basa en la simulación por Monte Carlo para resolver el problema de selección y secuencia de proyectos hidroeléctricos sujetos a diferentes tipos de riesgo e incertidumbre. Tales incertidumbres están asociadas al crecimiento futuro de la demanda, a los costos de los proyectos y a la capacidad de éstos, la cual está vinculada a datos hidrológicos aleatorios. Por otra parte, el trabajo de Su et al., (1997) presenta un enfoque de la optimización de la planificación de la expansión de los sistemas eléctricos de potencia, en el cual hace uso de las técnicas de simulación por Monte Carlo para simular el estado (en funcionamiento o inactivo) de los generadores y de las líneas de transmisión. La expansión del sistema eléctrico de potencia es considerada como la adición de nuevas líneas de transmisión y/o generadores en un año específico. Para resolver el problema de optimización, este trabajo hace uso de algoritmos genéticos.
Así como el estudio de Su et al., (1997) hace uso de los algoritmos genéticos para resolver el problema de optimización, el presente artículo utiliza otro algoritmo heurístico de optimización denominado Algoritmo Simplex Entero Mixto (ASEM), el cual fue desarrollado recientemente por Brea (2013), y del concepto general de la optimización por camino de muestra para desarrollar un método distinto de mejora del PPISEP.
El presente artículo está estructurado en diez secciones. La sección II sintetiza algunas definiciones relacionadas con la temática abordada. El problema de mejora del PPISEP es planteado en la sección III. La sección IV define las técnicas de optimización empleadas. La sección V replantea el problema presentado en la sección III con el fin de poder utilizar el algoritmo de optimización ASEM. La sección VI describe el algoritmo general de solución del problema planteado en la sección V en forma de pseudocódigos, presentando de esta manera la propuesta metodológica para determinar la mejora de un PPISEP. La sección VII presenta la implementación de un ejemplo numérico en el cual se hace uso de la propuesta metodológica diseñada. Los resultados del ejemplo numérico son presentados y analizados en la sección VIII y IX respectivamente. Finalmente, las conclusiones del presente artículo se desarrollan en la sección X.
CONSIDERACIONES DEL MODELO Y DEFINICIONES PRELIMINARES
Los SEP considerados en este artículo son representados como modelos de repartición de energía activa promedio, por intervalos de tiempo, desde los generadores hasta las cargas mediante líneas de transmisión de energía. En estos modelos se considera que los generadores tienen asociados capacidades energéticas nominales, mientras que las líneas de transmisión, sujetas a fallas aleatorias, tienen asociadas capacidades energéticas nominales máximas. Dichas fallas aleatorias son representadas como una disminución aleatoria en la capacidad de transmisión de energía activa promedio de las líneas de transmisión. Por otra parte, en estos modelos se establece la existencia de tres tipos de cargas o consumidores: residenciales, comerciales e industriales, cada uno con un consumo energético aleatorio en el tiempo diferente. Como se puede observar, en el modelo desarrollado en el presente artículo las capacidades de los generadores y líneas de transmisión, así como el consumo energético, no son estudiadas en unidades de potencia sino en unidades de energía activa promedio. Finalmente, para estudiar un modelo más sencillo, se considera un solo conjunto de transformadores, ubicado entre los generadores y las cargas.
La Red o Dígrafo ponderado R que representa al SEP consta de un conjunto de Nodos Iniciales, Intermedios y Terminales, además de un Nodo Fuente y un Nodo Hundido.
Cada i-ésimo Nodo de la Red R es clasificado de la siguiente manera:
Nodo Fuente, si i = 1;
Nodo Inicial, si i Î {2,3,...,Ng+1};
Nodo Intermedio, si i Î {Ng+2,Ng+3,...,Ng+Nt+1};
Nodo Terminal, si i Î {Ng+Nt+2,Ng+Nt+3,...,Ng+Nt+Nc+1};
Nodo Hundido, si i = Ng + Nt + Nc + 2,
donde Ng, Nt y Nc representan respectivamente el número y la ubicación de generadores, subestaciones o puntos de transformación y cargas presentes en el SEP, los cuales son iguales al número de Nodos Iniciales, Intermedios y Terminales respectivamente de la Red R. Adicionalmente, la Red R consta de un conjunto de arcos que representan los generadores, las líneas de transmisión y las cargas del SEP. Cada generador tiene asociado dos tipos de arcos de generación de igual ubicación en la Red R: un arco cuyo valor hace referencia a la capacidad nominal de generación de energía activa promedio por intervalo de tiempo (arco nominal de generación) y otro arco cuyo valor hace referencia a la energía efectivamente producida por el generador en cada período (arco efectivo de generación). Por otra parte, cada línea de transmisión de energía tiene asociada tres tipos de arcos de transmisión de igual ubicación en la Red R: un arco cuyo valor hace referencia a la capacidad nominal máxima de transmisión por intervalo de tiempo (arco nominal máximo de transmisión), otro arco cuyo valor significa la capacidad nominal de transmisión por intervalo de tiempo (arco nominal de transmisión), el cual considera el efecto de las fallas aleatorias asociadas a dicha línea de transmisión como una disminución en su capacidad de transmisión y, un último arco cuyo valor hace referencia a la energía activa promedio que efectivamente fluye por la línea de transmisión en cada intervalo de tiempo (arco efectivo de transmisión). Finalmente, cada carga tiene asociada dos tipos de arcos de consumo de igual ubicación en la Red R: un arco cuyo valor hace referencia al consumo pronosticado o proyectado de energía activa promedio por intervalo de tiempo del consumidor respectivo (arco nominal de consumo) y otro arco cuyo valor significa la energía activa promedio efectivamente entregada al consumidor (arco efectivo de consumo).
A continuación se presenta un conjunto de definiciones relacionadas con la temática abordada. En estas definiciones y en las demás secciones del presente artículo se hace uso de la nomenclatura descrita en el Anexo 1.
Definición 1 (t-ésimo intervalo de tiempo) Se dice que un t-ésimo intervalo de tiempo de duración t es el lapso comprendido entre los instantes tt y (t+1)t, y su suma representa el Horizonte de Planificación Hp; es decir,
![]()
donde ![]() Î N es el número máximo de intervalos tiempo t que comprende el Horizonte de Planificación Hp.
Î N es el número máximo de intervalos tiempo t que comprende el Horizonte de Planificación Hp.
Definición 2 (q-ésimo proyecto de inversión en un SEP) Un q-ésimo proyecto de inversión a ser ejecutado sobre un SEP representado por la Red R, viene descrito por su clase o tipo tp[q] (proyecto de generación o de transmisión); el arco nominal a[q] = (Ni[q],Nf[q]) de la Red R al cual va a modificar, donde Ni[q] = 1, Nf[q] Î {2,3,...,Ng+1} si es un proyecto de generación o Ni[q] Î {2,3,...,Ng+Nt+1}, Nf[q] Î {Ng+2,Ng+3,...,Ng+Nt+Nc+1} si es un proyecto de transmisión; la cantidad de energía activa promedio ep[q] Î R que le añade al valor del arco nominal a[q]; y el intervalo de tiempo ti[q] Î Z en el cual se inicia su construcción. El costo asociado al q-ésimo proyecto de inversión es directamente proporcional a la cantidad de energía activa promedio ep[q]. Por otra parte, los intervalos de tiempo o la tardanza que se presenta entre el intervalo de tiempo ti[q] y la puesta en marcha o ejecución del q-ésimo proyecto de inversión es igual al próximo entero por encima de un valor directamente proporcional a la energía activa promedio ep[q].
Definición 3 (PPISEP) Un g-ésimo Portafolio de Proyectos de Inversión en un Sistema Eléctrico de Potencia (PPISEP) es un conjunto finito Pg de q-ésimos proyectos de inversión, de acuerdo a la Definición 2. Según las definiciones y notaciones empleadas previamente, un Pg puede ser expresado en términos matemáticos como:
Pg = [tp,Ni,Nf,ep,ti]nx5' (2)
donde:
n: cantidad total de proyectos de inversión,
tp = (tp1,tp2,...tpn)t: tipos o clases de cada uno de los proyectos de inversión (proyectos de generación o de transmisión),
Ni = (Ni1,Ni2,...Nin)t Î {1,2,...,Ng+Nt+1}n: Nodos de Cola de los arcos nominales de la Red R que son alterados por cada uno de los proyectos de inversión,
Nf = (Nf1,Nf2,...Nfn)t Î {2,3,...,Ng+Nt+Nc+1}n: Nodos de Cabeza de los arcos nominales de la Red R que son alterados por cada uno de los proyectos de inversión,
ep = (ep1,ep2,...epn)t Î Rn: energías activas promedio que introducen cada uno de los proyectos de inversión a la Red R,
ti = (ti1,ti2,...tin)t Î Zn: intervalos de tiempo en los cuales se inicia la construcción de cada uno de los proyectos de inversión.
Definición 4 (Demanda insatisfecha del SEP) Para el presente artículo la demanda insatisfecha viene representada por la diferencia entre la energía activa promedio efectivamente entregada a los consumidores menos el consumo de energía activa promedio proyectado o pronosticado de éstos. Considerando la representación del SEP como una Red R, la diferencia de los valores de los arcos efectivos de consumo respecto a los valores de los arcos nominales de consumo representa la demanda insatisfecha. Para poder representar el efecto que la demanda insatisfecha tiene sobre la empresa eléctrica, su valor debe ser convertido en dinero mediante el uso de factores de penalización de demanda insatisfecha. Cada tipo de consumidor tiene asociado su respectivo factor de penalización de demanda insatisfecha. Para cada intervalo de tiempo se debe calcular el valor de demanda insatisfecha de cada consumidor (en términos de dinero) para luego sumarlos y, de esta manera, obtener el valor de demanda insatisfecha total (en términos de dinero) de cada intervalo de tiempo. Los valores de demanda insatisfecha total (en términos de dinero) de cada intervalo de tiempo deben ser llevados a valor presente (usando tasas fijas de interés y de inflación promedio por intervalo de tiempo) donde pueden ser sumados y, de esta forma obtener el valor de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación.
Definición 5 (Balance económico de la empresa eléctrica) La evaluación del balance económico de la empresa eléctrica consiste en determinar los ingresos menos los egresos de la misma durante el Horizonte de Planificación establecido. Los ingresos para cada intervalo de tiempo se obtienen mediante tarifas aplicadas a la energía activa promedio efectivamente entregada en cada intervalo de tiempo a los consumidores (valores de los arcos efectivos de consumo), donde cada tipo de consumidor tiene su tarifa respectiva. Por su parte, los egresos para cada intervalo de tiempo se obtienen mediante la adición de los costos de los proyectos de inversión, los costos variables y los costos fijos. Los costos de los proyectos de inversión se consideran dependientes de manera lineal de la cantidad de energía activa promedio que éstos introducen al SEP y son considerados únicamente en el intervalo de tiempo de inicio de su construcción. Por otra parte, los costos variables dependen de la energía activa efectivamente generada por el SEP y están presentes en cada intervalo de tiempo. Considerando la representación del SEP como una Red R, el cálculo de los costos variables para cada intervalo de tiempo se obtiene mediante la suma de la aplicación de un costo por unidad de energía activa generada a cada uno de los valores de los arcos efectivos de generación. Por último, los costos fijos, los cuales representan los costos de operación y mantenimiento, los compromisos adquiridos y los cargos por depreciación son constantes y están presentes en cada intervalo de tiempo del Horizonte de Planificación. Luego de determinar los ingresos y los egresos en cada uno de los intervalos de tiempo que componen el Horizonte de Planificación, se debe realizar una suma aritmética de los mismos en valor presente, utilizando tasas fijas de interés mínimas atractivas e inflación promedio por intervalo de tiempo, obteniéndose de esta manera el valor del balance económico de la empresa eléctrica para el Horizonte de Planificación.
EL PROBLEMA
Sean ep Î Rn el conjunto de n variables reales independientes que representan las energías activas promedio que introducen a la Red R cada uno de los proyectos de inversión de un PPISEP, y ti Î Zn el conjunto de n variables enteras independientes que representan los intervalos de tiempo en los cuales se inicia la construcción de cada uno de los proyectos de inversión del PPISEP. Sean además Bp el valor promedio de las muestras de balance económico de la empresa eléctrica para el Horizonte de Planificación Hp, y Dp el valor promedio de las muestras de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación Hp, siendo este último menor o igual a cero. Entonces, el presente problema de optimización mediante la simulación puede ser expresado de la siguiente manera:
![]()
sujeto a:
![]()
donde x1 Î (0,1), x2 Î (0,1) son los factores de ponderación, tales que x1 + x2 = 1, Rd es el presupuesto que se dispone en valor presente para los proyectos de inversión,(![]() ep[q])|p es el costo de inversión del q-ésimo proyecto de inversión referido a su valor presente, siendo
ep[q])|p es el costo de inversión del q-ésimo proyecto de inversión referido a su valor presente, siendo ![]() el costo por unidad de energía activa promedio que introduce el proyecto de inversión y,
el costo por unidad de energía activa promedio que introduce el proyecto de inversión y, ![]() =
=![]() si el q-ésimo proyecto de inversión es de generación o
si el q-ésimo proyecto de inversión es de generación o ![]() =
=![]() si el q-ésimo proyecto de inversión es de transmisión;
si el q-ésimo proyecto de inversión es de transmisión;
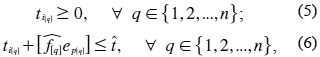
donde ti[q] + [![]() ep[q]] es el intervalo de tiempo de puesta en marcha o ejecución del q-ésimo proyecto de inversión, siendo
ep[q]] es el intervalo de tiempo de puesta en marcha o ejecución del q-ésimo proyecto de inversión, siendo ![]() un factor que multiplica la energía activa promedio que introduce el proyecto de inversión y,
un factor que multiplica la energía activa promedio que introduce el proyecto de inversión y, ![]() =
=![]() si el q-ésimo proyecto de inversión es de generación o
si el q-ésimo proyecto de inversión es de generación o ![]() =
=![]() si el q-ésimo proyecto de inversión es de transmisión. El operador [·] es utilizado para aproximar el resultado a su próximo superior entero;
si el q-ésimo proyecto de inversión es de transmisión. El operador [·] es utilizado para aproximar el resultado a su próximo superior entero;
ep[q] ≥ 0, " q Î {1,2,...,n}, (7)
Como se puede observar, las variables de decisión del presente problema de optimización son las energías activas promedio ep que introducen cada uno de los proyectos de inversión a la Red R (conjunto de variables reales independientes) y los intervalos de tiempos ti en los cuales dichos proyectos se empiezan a construir (conjunto de variables enteras independientes).
TÉCNICAS DE OPTIMIZACIÓN EMPLEADAS
Algoritmo Simplex Entero Mixto - Una de las técnicas de optimización utilizadas para la resolución del problema antes planteado es el Algoritmo Simplex Entero Mixto (ASEM) puesto que éste permite considerar el campo numérico entero del intervalo de tiempo de inicio de construcción y el campo numérico real de la cantidad de energía activa promedio de cada uno de los proyectos de inversión que constituyen el PPISEP. El ASEM, denominado de esta manera por el autor Brea (2013), es una extensión del método algorítmico simplex de Nelder Mead (Nelder et al.,1965) para la identificación de al menos un óptimo local, cuando es usado en problemas no lineales enteros mixtos irrestrictos. El ASEM se basa en una doble estructura de símpleces, la cual está compuesta de una estructura simplex real de dimensión n (simplex real), y otra estructura simplex entera de igual dimensión n (simplex entero). Las operaciones propuestas originalmente por Nelder et al., (1965) son ejecutadas sobre el simplex real mientras que otro grupo de nuevas operaciones desarrolladas por Brea (2013) son empleadas en el simplex entero. Este conjunto de nuevas operaciones junto con las operaciones originales del método de Nelder Mead garantizan que en cada iteración del ASEM se arroje un nuevo punto de prueba definido en el campo numérico de dimensión 2n enteros mixtos Rn x Zn, con el fin de garantizar la identificación del óptimo local entero mixto, sin convertir las variables enteras en variables reales. Es muy importante destacar que debido a que el ASEM es un algoritmo de minimización, el problema de la mejora del PPISEP debe ser replanteado como un problema de minimización.
Optimización por camino de muestras - La otra técnica o estrategia de optimización empleada para la resolución del problema antes planteado es la optimización por camino de muestras. En la optimización por camino de muestras el valor esperado de la función objetivo se calcula mediante el valor promedio de una muestra relativamente grande de observaciones en cada punto (camino de muestras) (Carson et al., 1997), (Azadivar, 1999), para luego hacer uso de métodos deterministas de programación no lineal (Carson et al., 1997). De esta manera, esta técnica de optimización permite considerar las incertidumbres aleatorias asociadas a la función objetivo del Problema.
El presente artículo utiliza el ASEM como método determinista de programación no lineal en la optimización por camino de muestras, de esta forma se considera la naturaleza entera-mixta del problema y las incertidumbres asociadas al mismo.
REPLANTEAMIENTO DEL PROBLEMA
Con el propósito de redefinir el problema como un problema de minimización irrestricto y, de esta manera poder utilizar el algoritmo de optimización ASEM, la ecuación (3) es replanteada de la siguiente manera:
![]()
y cada una de las restricciones expresadas en las ecuaciones (4), (5), (6) y (7) es replanteada como una función de penalización:
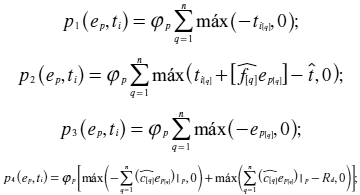
donde jp es el coeficiente de las funciones de penalización.
Considerando las funciones de penalización antes señaladas, el problema de optimización mediante la simulación se puede redefinir de la siguiente manera:
![]()
MODELO COMPUTACIONAL PARA RESOLVER EL PROBLEMA PLANTEADO
A continuación se presentan los algoritmos, procedimientos y funciones que conforman el modelo computacional diseñado para resolver el Problema anteriormente planteado.
Algoritmo 1. Metodología que permite mejorar los Portafolios de Proyectos de Inversión en un Sistema Eléctrico de Potencia (PPISEP). Este es el algoritmo principal, en el cual se presentan las instrucciones necesarias para emplear la metodología.

Como se puede observar, el Algoritmo 1 agrupa en un solo vector v0 ÎRn x Zn las cantidades iniciales de energía activa promedio y de intervalo de tiempo de inicio de construcción de cada uno de los proyectos inversión que componen el PPISEP inicial, y establece una matriz Z donde se representan todas las características fijas de cada uno de dichos proyectos de inversión. El vector v0 representa el vector inicial del algoritmo de optimización ASEM, el cual comienza a generar vectores v hasta determinar un vector final vf ÎRn x Zn que genera una disminución notoria en el valor de su función objetivo. Este último vector representa la energía activa promedio y el intervalo de tiempo de inicio de construcción de cada uno de los proyectos de inversión que conforman el PPISEP mejorado.
Algoritmo 2. Metodología que permite evaluar la expansión de un Sistema Eléctrico de Potencia (SEP). Este algoritmo constituye la función objetivo del algoritmo de optimización ASEM puesto que permite evaluar un PPISEP.

En este último algoritmo existen dos ciclos iterativos principales, el primero calcula la cantidad de muestras que se deseen y el segundo simula el paso de los intervalos de tiempo durante el Horizonte de Planificación considerado. A continuación se explican los procedimientos que componen este algoritmo.
Procedimiento 1. Construcción de la Matriz de Proyectos.
Mediante este procedimiento se construye una Matriz W en la que se guarda toda la información asociada a cada uno de los proyectos de inversión que componen al PPISEP que desea ser evaluado. El vector nulo de dimensión n es representado mediante la notación 0n.

Procedimiento 2. Asignación de los valores de los arcos nominales de consumo ![]() de la Red R.
de la Red R.
De acuerdo a los tipos de clientes tih presentes en los Nodos Terminales de la Red R con sus respectivas distribuciones de probabilidad tipo triangular, se determinan los valores de los arcos nominales de consumo ![]() para el intervalo de tiempo considerado.
para el intervalo de tiempo considerado.

Procedimiento 3. Adición de los costos de proyectos de inversión.

Procedimiento 4. Modificación de los valores de los arcos nominales de generación ![]() y de los arcos nominales máximos de transmisión
y de los arcos nominales máximos de transmisión ![]() de la Red R debido a la entrada en funcionamiento de los proyectos de inversión.
de la Red R debido a la entrada en funcionamiento de los proyectos de inversión.

Procedimiento 5. Determinación de los valores de los arcos nominales de transmisión ![]() de la Red R.
de la Red R.
Mediante este procedimiento se calculan los valores de los arcos nominales de transmisión ![]() de la Red R para el intervalo de tiempo considerado como una disminución aleatoria de los valores de los arcos nominales máximos de transmisión
de la Red R para el intervalo de tiempo considerado como una disminución aleatoria de los valores de los arcos nominales máximos de transmisión ![]() , mediante el uso de una distribución de probabilidad tipo triangular. En los procedimientos siguientes se emplea la notación S(i) para representar los Nodos sucesores al Nodo i y, la notación P(i) para representar los Nodos predecesores al Nodo i (Strang, 2005).
, mediante el uso de una distribución de probabilidad tipo triangular. En los procedimientos siguientes se emplea la notación S(i) para representar los Nodos sucesores al Nodo i y, la notación P(i) para representar los Nodos predecesores al Nodo i (Strang, 2005).

Procedimiento 6. Determinación de los valores de los arcos efectivos xij de la Red R. Mediante este procedimiento se resuelve el problema de flujo máximo (también denominado despacho óptimo de energía activa promedio) de la Red R, obteniéndose los valores de todos los arcos efectivos xij para el intervalo de tiempo considerado. Dicho problema es resuelto mediante programación lineal puesto que tanto la función objetivo como las restricciones del problema son expresiones lineales.

Procedimiento 7. Contabilización de los ingresos. Mediante el uso de las tarifas ktipo y de la energía efectivamente entregada a cada uno de los consumidores, este procedimiento permite determinar los ingresos de la empresa eléctrica para el intervalo de tiempo considerado.

Procedimiento 8. Contabilización de los egresos.
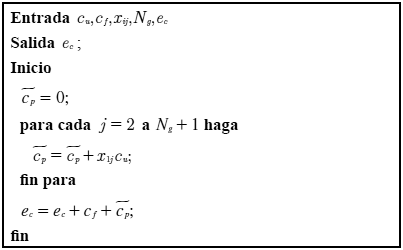
Procedimiento 9. Cálculo del balance económico en valor presente. Mediante el método de valor presente (Sullivan et al., 2004), este procedimiento determina el balance económico de la empresa eléctrica para el intervalo de tiempo considerado.
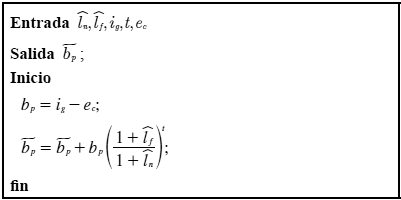
Procedimiento 10. Cálculo de la demanda insatisfecha total en valor presente. Mediante el método de valor presente (Sullivan et al., 2004), este procedimiento determina la demanda insatisfecha total (en términos de dinero) para el intervalo de tiempo considerado.

Procedimiento 11. Cálculo de los valores promedio de balance económico y de demanda insatisfecha.
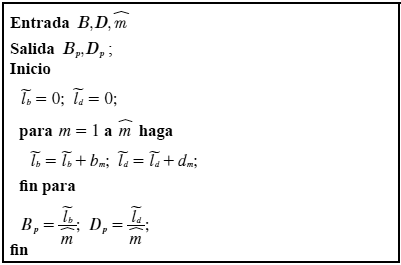
Procedimiento 12. Cálculo de los valores de las funciones de penalización. Este procedimiento permite evaluar cada una de las funciones de penalización asociadas al PPISEP que desee ser evaluado.
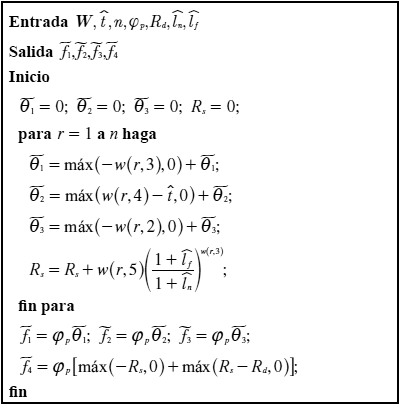
Función 1. Generador de distribución triangular a partir de una uniforme.

IMPLEMENTACIÓN DEL EJEMPLO NUMÉRICO
Descripción del sistema eléctrico de potencia (SEP) -
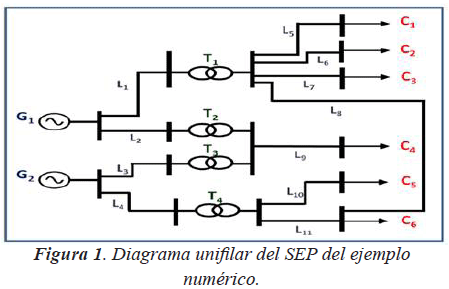
El ejemplo numérico considerado se basa en un Sistema Eléctrico de Potencia (SEP) cuyo diagrama unifilar se presenta en la figura 1. Como se puede observar en la figura, se tienen dos generadores, once líneas de transmisión y seis cargas en el SEP considerado para el ejemplo numérico. Para el presente ejemplo numérico, los intervalos de tiempo fueron establecidos de una duración igual a dos años.
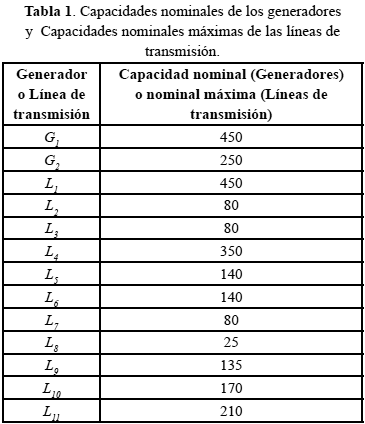
En la tabla 1 se muestran las capacidades nominales de generación de energía de los generadores G1 y G2 y las capacidades nominales máximas de transmisión de energía de las líneas de transmisión L1 a L11 del SEP considerado. En cuanto a las líneas de transmisión, se estableció que éstas podían tener una capacidad nominal típica o más probable igual al 90% de su capacidad nominal máxima y una capacidad nominal mínima igual al 80% de su capacidad nominal máxima, es decir, mínfalla = 0,8; modfalla = 0,9; máxfalla = 1. Finalmente, a cada una de las cargas C1, C2 y C3 se le asignó un cliente residencial, mientras que a cada una de las cargas C4 y C5 se le asignó un cliente comercial y a la carga C6 se le asignó un cliente industrial.
Descripción del PPISEP - Para el presente ejemplo numérico se estableció estudiar el SEP antes descrito durante un Horizonte de Planificación Hp de veinte años, compuesto de 10 intervalos de tiempo de 2 años de duración (![]() = 10, t= 2 años).
= 10, t= 2 años).
Dentro de este Horizonte de Planificación, se consideró el siguiente PPISEP inicial de tres proyectos inversión (n3=):
Proyecto de transmisión N°1: incremento de la capacidad nominal máxima de transmisión de energía activa promedio por intervalo de la línea de transmisión de energía L7 en 10 unidades de energía. Intervalo de tiempo de inicio de su construcción: N°2 (cuarto año).
Proyecto de transmisión N°2: construcción de una nueva línea de transmisión de energía que conecte el transformador T1 con la Carga C4 y cuya capacidad nominal máxima de transmisión de energía activa promedio por intervalo de tiempo es de 10 unidades de energía. Intervalo de tiempo de inicio de su construcción: N°2 (cuarto año).
Proyecto de generación N°1: incremento de la capacidad nominal de generación de energía activa promedio por intervalo de tiempo del Generador G2 en 10 unidades de energía. Intervalo de tiempo de inicio de su construcción: N°2 (cuarto año).
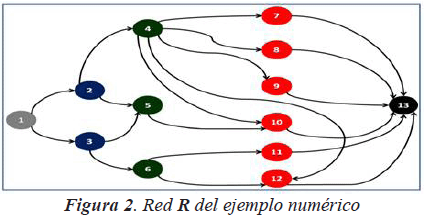
Construcción de la Red R - La representación del SEP como una Red R, considerando el PPISEP inicial antes descrito, se muestra en la figura 2. Como se puede observar en la Red R de la figura 2, se tienen dos Nodos Iniciales (Nodos 2 y 3), tres Nodos Intermedios (Nodos 4, 5 y 6) y seis Nodos Terminales (Nodos 7, 8, 9, 10, 11 y 12), debido a la presencia de dos generadores, tres puntos de transformación y seis cargas en el SEP, respectivamente (ver figura 1). Además de los Nodos antes mencionados, en la Red R de la figura 2 se presentan el Nodo Fuente (Nodo 1) y el Nodo Hundido (Nodo 13). Todos estos Nodos se encuentran enumerados tal como se explicó anteriormente.
Por otra parte, en la Red R considerada se tienen dos arcos de generación (arcos que unen al Nodo Fuente con los Nodos Iniciales), doce arcos de transmisión (arcos que unen a los Nodos Iniciales con los Nodos Intermedios y arcos que unen a los Nodos Intermedios con los Nodos Terminales) y seis arcos de consumo (arcos que unen a los Nodos Terminales con el Nodo Hundido).
Todos estos arcos presentan una dirección establecida desde el Nodo Fuente hasta el Nodo Hundido. Ahora bien, el arco de la Red R que une al Nodo Intermedio 4 con el Nodo Terminal 10 no representa alguna línea de transmisión en el diagrama unifilar del SEP mostrado en la figura 1. Esto se debe a que dicho arco hace referencia a la nueva línea de transmisión que puede introducir el proyecto de transmisión N°2.
PPISEP inicial en términos matemáticos - Es importante destacar que para definir un proyecto de generación, se seleccionó la variable tp = 1, mientras que para definir un proyecto de transmisión, se seleccionó la variable tp = 2. De acuerdo con la descripción expuesta en la definición 3, a continuación se presenta el PPISEP inicial:

Escenarios estudiados - La metodología fue implementada en dos escenarios de consumo pronosticado en alza de energía activa promedio en el tiempo por parte de los clientes presentes en el SEP, los cuales difieren únicamente en los valores de las tasas de interés atractiva e inflación promedio por intervalo de tiempo. El primer escenario toma en consideración una tasa de interés atractiva por intervalo de tiempo (![]() ) igual a 17% y una tasa de inflación promedio por intervalo de tiempo (
) igual a 17% y una tasa de inflación promedio por intervalo de tiempo (![]() ) igual a 10 %, mientras que en el segundo escenario se considera una tasa de interés atractiva por intervalo de tiempo (
) igual a 10 %, mientras que en el segundo escenario se considera una tasa de interés atractiva por intervalo de tiempo (![]() ) igual a 10% y una tasa de inflación promedio por intervalo de tiempo (
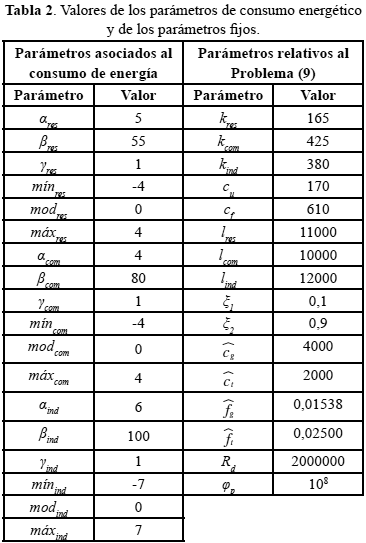
) igual a 10% y una tasa de inflación promedio por intervalo de tiempo (![]() ) igual a 17 %. En la tabla 2 se presentan los valores de los parámetros atipo, btipo, gtipo, míntipo, modtipo y máxtipo para cada tipo de consumidor (residencial, comercial e industrial) y los valores fijos de los parámetros restantes.
) igual a 17 %. En la tabla 2 se presentan los valores de los parámetros atipo, btipo, gtipo, míntipo, modtipo y máxtipo para cada tipo de consumidor (residencial, comercial e industrial) y los valores fijos de los parámetros restantes.
El ejemplo numérico fue programado en MATLAB 7 ®, estableciendo un total de 30 muestras (![]() =30) o ejecuciones del modelo de simulación para obtener los valores de la función objetivo del ASEM en cada punto. El número de muestras o ejecuciones del modelo de simulación fue establecido en 30 para obtener una mínima muestra significativa de valores en cada punto de evaluación del ASEM que permitiera obtener la mejora del PPISEP inicial en un tiempo razonable. Por último, para el algoritmo ASEM se consideró como criterio de parada un número máximo de etapas igual a 12, estableciendo de esta manera que los valores que brinda el ASEM de tiempo de inicio de construcción y de cantidad de energía activa promedio que introduce cada proyecto de inversión del PPISEP considerado constituyen unos valores mejores a los iniciales mas no los valores óptimos. A medida que se considere un número mayor de etapas del ASEM, los valores obtenidos estarán más cercanos a los valores óptimos.
=30) o ejecuciones del modelo de simulación para obtener los valores de la función objetivo del ASEM en cada punto. El número de muestras o ejecuciones del modelo de simulación fue establecido en 30 para obtener una mínima muestra significativa de valores en cada punto de evaluación del ASEM que permitiera obtener la mejora del PPISEP inicial en un tiempo razonable. Por último, para el algoritmo ASEM se consideró como criterio de parada un número máximo de etapas igual a 12, estableciendo de esta manera que los valores que brinda el ASEM de tiempo de inicio de construcción y de cantidad de energía activa promedio que introduce cada proyecto de inversión del PPISEP considerado constituyen unos valores mejores a los iniciales mas no los valores óptimos. A medida que se considere un número mayor de etapas del ASEM, los valores obtenidos estarán más cercanos a los valores óptimos.
RESULTADOS DEL EJEMPLO NUMÉRICO
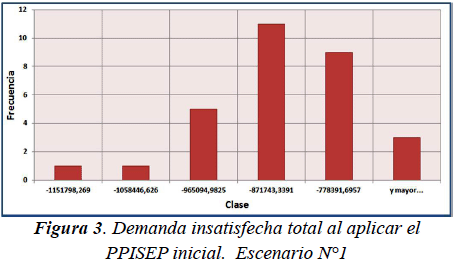
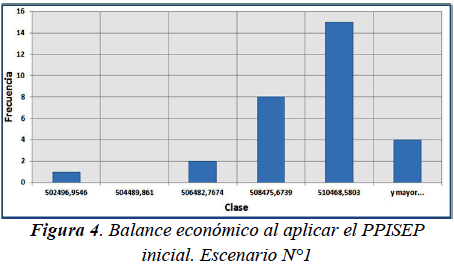
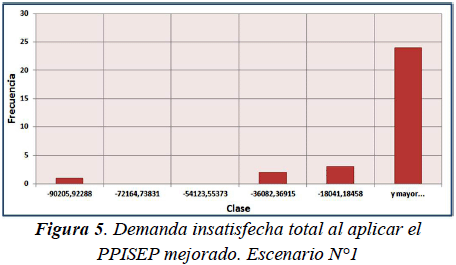
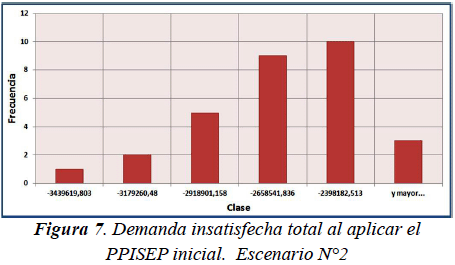
A continuación, para cada escenario planteado, se presenta la evaluación mediante un histograma de la demanda insatisfecha total (en términos de dinero) y del balance económico de la empresa eléctrica para el Horizonte de Planificación al aplicar tanto el PPISEP inicial como el PPISEP mejorado (considerando los valores de las componentes del vector de la etapa 12 arrojado por el ASEM). Tales histogramas (ver figuras 3 a 10) se basan en un total de 30 muestras o ejecuciones del ASEM para el PPISEP inicial como para el PPISEP mejorado. Para cada medición asociada a algún histograma se presenta el intervalo de confianza al 95% de la media poblacional. Es relevante comentar que para el cálculo de la media muestral se hace uso de la varianza muestral s2 como estimador puntual de la varianza poblacional σ2.
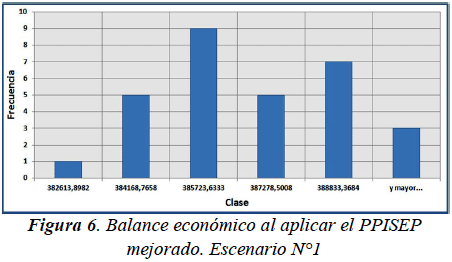
Escenario N°1. Consumo en alza. Interés mayor que inflación.
Al evaluar el rendimiento del PPISEP inicial se obtuvo un intervalo de confianza al 95% para la media de la demanda insatisfecha total (en términos de dinero) μd igual a: -935962,82 ≤ μd ≤ -860796,7742 y un intervalo de confianza al 95% para la media del balance económico μb igual a: 507973,82 ≤ μb ≤ 509406,7842. Las figuras 3 y 4 presentan los histogramas de este escenario con el PPISEP inicial.
El PPISEP mejorado arrojado por el ASEM en la etapa 12 luego de 1024 evaluaciones de la función objetivo es el siguiente:

Al evaluar el rendimiento del PPISEP mejorado se obtuvo un intervalo de confianza al 95% para la media de la demanda insatisfecha total (en términos de dinero) μd igual a: -18017,25506 ≤ μd ≤ -3782,208917 y un intervalo de confianza al 95% para la media del balance económico μb igual a: 385369,923 ≤ μb ≤ 386862,6541 Las figuras 5 y 6 presentan los histogramas de este escenario con el PPISEP mejorado.
Escenario N°2. Consumo en alza. Inflación mayor que interés.
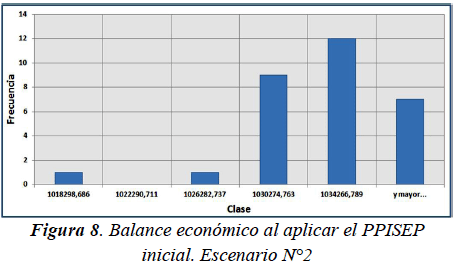
Al evaluar el rendimiento del PPISEP inicial se obtuvo un intervalo de confianza al 95% para la media de la demanda insatisfecha total (en términos de dinero) μd igual a: -2843822,939 ≤ μd ≤ -2629141,657 y un intervalo de confianza al 95% para la media del balance económico μb igual a: 1029475,9 ≤ μb ≤ 1032349,327. Las figuras 7 y 8 presentan los histogramas de este escenario con el PPISEP inicial.
El PPISEP mejorado arrojado por el ASEM en la etapa 12, luego de 1424 evaluaciones de la función objetivo, es el siguiente:
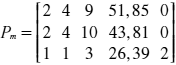
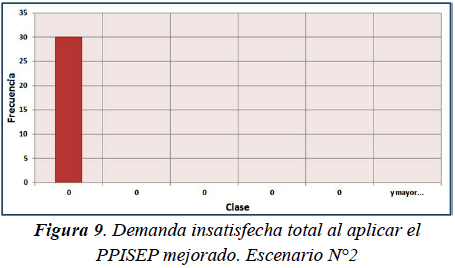
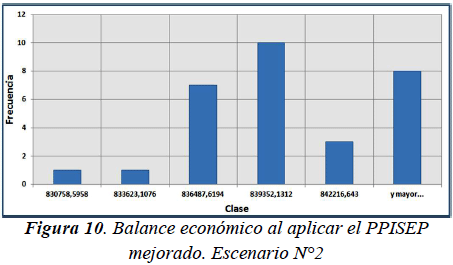
Al evaluar el rendimiento del PPISEP mejorado se obtuvo un intervalo de confianza al 95% para la media del balance económico μb igual a: 837336,4542 ≤ μb ≤ 840096,5465 y una media de demanda insatisfecha total (en términos de dinero) μd igual a cero. Las figuras 9 y 10 presentan los histogramas de este escenario con el PPISEP mejorado.
ANÁLISIS DE RESULTADOS
En el escenario N°1 se puede constatar que las muestras obtenidas al evaluar el PPISEP mejorado presentan valores absolutos de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación notablemente menores a los valores obtenidos al evaluar el PPISEP inicial (véanse los histogramas de las figuras 3 y 5). Por otra parte, las muestras asociadas al PPISEP mejorado presentan valores de balance económico de la empresa eléctrica para el Horizonte de Planificación levemente superiores a los valores obtenidos al evaluar el PPISEP inicial (véanse los histogramas de las figuras 4 y 6). Este último resultado era de esperar, puesto que en la estrategia de optimización se estableció una mayor importancia a la disminución del valor negativo de la demanda insatisfecha que al aumento del balance económico x2 > x1. En cuanto a los intervalos de confianza, resulta interesante comentar la notable amplitud del intervalo asociado a la media de la demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación obtenida al evaluar el PPISEP mejorado. Esta amplitud se debe a la gran diferencia entre los valores de las muestras obtenidas al evaluar el PPISEP mejorado puesto que existen muestras (la mayoría) con magnitudes muy pequeñas de demanda insatisfecha total, mientras que se tienen otras muestras con valores de demanda insatisfecha total de mayor magnitud. Para el escenario N°2 se puede observar que las muestras obtenidas al evaluar el PPISEP mejorado presentan valores nulos de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación, lo cual representa una absoluta mejora en comparación con los valores obtenidos al evaluar el PPISEP inicial (véanse los histogramas de las figuras 7 y 9). Al igual que en el escenario anterior, debido a los valores considerados de x1 y de x2, las muestras asociadas al PPISEP mejorado presentan valores de balance económico de la empresa eléctrica para el Horizonte de Planificación levemente superiores a los valores obtenidos al evaluar el PPISEP inicial (véanse los histogramas de las figuras 8 y 10). Si se detalla el PPISEP mejorado obtenido en este escenario con el obtenido en el escenario anterior, se puede constatar que los intervalos de tiempo de inicio de construcción de los proyectos de inversión del PPISEP mejorado del escenario N°2 son menores a los del PPISEP mejorado del escenario N°1. Este resultado era de esperar puesto que al presentarse una tasa promedio de inflación superior a la tasa de interés, invertir antes resulta más rentable económicamente.
CONCLUSIONES
La propuesta metodológica desarrollada constituye un aporte inédito dentro del campo de la planificación de la expansión de los SEP. Partiendo de un PPISEP inicial y haciendo uso de la técnica de optimización ASEM, esta metodología identifica unos valores mejores de tiempo de inicio de construcción (variable entera) y de energía activa promedio introducida al SEP (variable real) de cada uno de los proyectos de inversión que componen el PPISEP. Éstos constituyen una disminución del consumo pronosticado no cubierto de energía activa promedio y un incremento del balance económico de la empresa eléctrica. Por otra parte, mediante el uso de la simulación por Monte Carlo, la metodología diseñada considera las incertidumbres aleatorias asociadas al consumo energético y las fallas en las líneas de transmisión del SEP. Finalmente, la virtud más importante de la propuesta metodológica desarrollada es la de permitir considerar diferentes topologías de SEP y distintos tipos de PPISEP, con diferente cantidad y tipos de proyectos de inversión. Aun cuando en el presente artículo se muestra un SEP simplificado para ilustrar la metodología desarrollada, el modelo computacional expuesto permite considerar diversas topologías radiales de SEP. Es relevante destacar que aun cuando no se toma en cuenta la ampliación de la capacidad energética de los transformadores en la metodología descrita, los mismos pueden ser considerados como arcos de transmisión cuyos valores representan las capacidades de transmisión de energía activa promedio de los transformadores.
ANEXO 1. NOMENCLATURA
m, t, r: contador de muestras, de intervalos de tiempo y de proyectos de inversión respectivamente;
i: contador de los Nodos de Cola de los arcos de la Red R;
j: contador de Nodos de Cabeza de los arcos de la Red R;
k: contador de Nodos de Cola y Nodos de Cabeza de los arcos de la Red R;
bm, dm: balance económico de la empresa eléctrica y demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación Hp en valor presente de la muestra m;
![]() : sumador de balance económico de la empresa eléctrica y sumador de demanda insatisfecha total (en términos de dinero) en valor presente de cada muestra m;
: sumador de balance económico de la empresa eléctrica y sumador de demanda insatisfecha total (en términos de dinero) en valor presente de cada muestra m;
![]() : arco nominal de generación de la Red R cuyo Nodo de Cola es el Nodo 1 (Nodo Fuente) y cuyo Nodo de Cabeza es el j-ésimo Nodo Inicial, es decir, tiene una dirección asignada hacia el Nodo Inicial, y su valor representa la capacidad nominal de generación de energía activa promedio en el intervalo de tiempo t del generador asociado al j-ésimo Nodo Inicial, "j Î {2, 3,...,Ng + 1}. Si alguno de estos arcos es añadido a la Red R por parte de algún proyecto de generación, su valor debe ser inicialmente igual a cero hasta que dicho proyecto de generación comience a ejecutarse, momento en el cual pasa a ser igual a la energía activa promedio que introduce el proyecto de generación;
: arco nominal de generación de la Red R cuyo Nodo de Cola es el Nodo 1 (Nodo Fuente) y cuyo Nodo de Cabeza es el j-ésimo Nodo Inicial, es decir, tiene una dirección asignada hacia el Nodo Inicial, y su valor representa la capacidad nominal de generación de energía activa promedio en el intervalo de tiempo t del generador asociado al j-ésimo Nodo Inicial, "j Î {2, 3,...,Ng + 1}. Si alguno de estos arcos es añadido a la Red R por parte de algún proyecto de generación, su valor debe ser inicialmente igual a cero hasta que dicho proyecto de generación comience a ejecutarse, momento en el cual pasa a ser igual a la energía activa promedio que introduce el proyecto de generación;
![]() : arco nominal máximo de transmisión de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Inicial o el i-ésimo Nodo Intermedio y cuyo Nodo de Cabeza es el j-ésimo Nodo Intermedio o el j-ésimo Nodo Terminal, y su valor representa la capacidad nominal máxima de transmisión de energía activa promedio en el intervalo de tiempo t de la línea de transmisión ubicada entre dichos Nodos (sin considerar las fallas aleatorias asociadas a dicha línea en el intervalo de tiempo t), "i Î {2, 3,...,Ng + Nt + 1}, "j Î {Ng + 2, Ng + 3,...,Ng + Nt + Nc + 1}. Si alguno de estos arcos es añadido a la Red R por parte de algún proyecto de transmisión, su valor debe ser inicialmente igual a cero hasta que dicho proyecto de transmisión comience a ejecutarse, momento en el cual pasa a ser igual a la energía activa promedio que introduce el proyecto de transmisión.
: arco nominal máximo de transmisión de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Inicial o el i-ésimo Nodo Intermedio y cuyo Nodo de Cabeza es el j-ésimo Nodo Intermedio o el j-ésimo Nodo Terminal, y su valor representa la capacidad nominal máxima de transmisión de energía activa promedio en el intervalo de tiempo t de la línea de transmisión ubicada entre dichos Nodos (sin considerar las fallas aleatorias asociadas a dicha línea en el intervalo de tiempo t), "i Î {2, 3,...,Ng + Nt + 1}, "j Î {Ng + 2, Ng + 3,...,Ng + Nt + Nc + 1}. Si alguno de estos arcos es añadido a la Red R por parte de algún proyecto de transmisión, su valor debe ser inicialmente igual a cero hasta que dicho proyecto de transmisión comience a ejecutarse, momento en el cual pasa a ser igual a la energía activa promedio que introduce el proyecto de transmisión.
![]() : arco nominal de transmisión de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Inicial o el i-ésimo Nodo Intermedio y cuyo Nodo de Cabeza es el j-ésimo Nodo Intermedio o el j-ésimo Nodo Terminal, y su valor representa la capacidad nominal de transmisión de energía activa promedio en el intervalo de tiempo t de la línea de transmisión ubicada entre dichos Nodos (considerando las fallas aleatorias asociadas a dicha línea en el intervalo de tiempo t), "i Î {2, 3,...,Ng + Nt + 1}, "j Î {Ng + 2, Ng + 3,...,Ng + Nt + Nc + 1};
: arco nominal de transmisión de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Inicial o el i-ésimo Nodo Intermedio y cuyo Nodo de Cabeza es el j-ésimo Nodo Intermedio o el j-ésimo Nodo Terminal, y su valor representa la capacidad nominal de transmisión de energía activa promedio en el intervalo de tiempo t de la línea de transmisión ubicada entre dichos Nodos (considerando las fallas aleatorias asociadas a dicha línea en el intervalo de tiempo t), "i Î {2, 3,...,Ng + Nt + 1}, "j Î {Ng + 2, Ng + 3,...,Ng + Nt + Nc + 1};
![]() : arco nominal de consumo de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Terminal y cuyo Nodo de Cabeza es el Nodo h = Ng + Nt + Nc + 2 (Nodo Hundido), y su valor representa el consumo pronosticado de energía activa promedio en el intervalo de tiempo t de la carga asociada al i-ésimo Nodo Terminal, "i Î {Ng + Nt + 2, Ng + Nt + 3,...,Ng + Nt + Nc + 1}.
: arco nominal de consumo de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Terminal y cuyo Nodo de Cabeza es el Nodo h = Ng + Nt + Nc + 2 (Nodo Hundido), y su valor representa el consumo pronosticado de energía activa promedio en el intervalo de tiempo t de la carga asociada al i-ésimo Nodo Terminal, "i Î {Ng + Nt + 2, Ng + Nt + 3,...,Ng + Nt + Nc + 1}.
xij: arco efectivo de generación, transmisión o consumo de la Red R cuyo valor representa el mayor flujo de energía activa promedio (energía efectiva) entre el i-ésimo Nodo y el j-ésimo Nodo en cada intervalo de tiempo t, "i Î {1, 2,...,Ng + Nt + Nc + 1}, "j Î {2, 3,...,Ng + Nt + Nc + 2};
itipo: sumador de los ingresos obtenidos por la empresa eléctrica, de acuerdo al tipo de consumidor, en cada intervalo de tiempo t;
ig: ingresos totales obtenidos por la empresa eléctrica en cada intervalo de tiempo t;
![]() : sumador de los costos variables (costos que varían de acuerdo a la energía activa promedio generada por intervalo de tiempo) que tiene la empresa eléctrica en cada intervalo de tiempo t;
: sumador de los costos variables (costos que varían de acuerdo a la energía activa promedio generada por intervalo de tiempo) que tiene la empresa eléctrica en cada intervalo de tiempo t;
ec: sumador de los egresos de la empresa eléctrica en cada intervalo de tiempo t. Dichos egresos abarcan los costos fijos y los costos variables en el intervalo de tiempo t, además de los costos de los proyectos de inversión, en el caso de que éstos inicien su construcción en el intervalo de tiempo t;
bp, dp: balance económico de la empresa eléctrica y demanda insatisfecha total (en términos de dinero) en cada intervalo de tiempo t;
dtipo: sumador de demanda insatisfecha (en términos de dinero), de acuerdo al tipo de consumidor, en cada intervalo de tiempo t;
![]() : sumador de balance económico de la empresa eléctrica y sumador de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación Hp en valor presente de cada muestra m;
: sumador de balance económico de la empresa eléctrica y sumador de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación Hp en valor presente de cada muestra m;
Bp: promedio de los valores de balance económico de la empresa eléctrica para el Horizonte de Planificación Hp en valor presente obtenidos en cada una de las muestras m;
Dp: promedio de los valores de demanda insatisfecha total (en términos de dinero) para el Horizonte de Planificación Hp en valor presente obtenidos en cada una de las muestras m;
![]() : sumadores asociados a las funciones de penalización;
: sumadores asociados a las funciones de penalización;
![]() : funciones de penalización.
: funciones de penalización.
Ng, Nt, Nc: número de Nodos Iniciales, Nodos Intermedios y Nodos Terminales de la Red R respectivamente. Para el caso de Ng y Nt, dicho número considera la posible adición de generadores o líneas de transmisión al SEP por parte de algún proyecto de inversión;
G1j: arco inicial de generación de la Red R cuyo Nodo de Cola es el Nodo 1 (Nodo Fuente) y cuyo Nodo de Cabeza es el j-ésimo Nodo Inicial, y su valor representa la capacidad nominal inicial de generación de energía activa promedio en el intervalo de tiempo t del generador asociado al j-ésimo Nodo Inicial, "j Î {2, 3,...,Ng + 1}. Si alguno de estos arcos es añadido a la Red R por parte de algún proyecto de generación, su valor debe ser igual a cero;
Tij: arco inicial de transmisión de la Red R cuyo Nodo de Cola es el i-ésimo Nodo Inicial o el i-ésimo Nodo Intermedio y cuyo Nodo de Cabeza es el j-ésimo Nodo Intermedio o el j-ésimo Nodo Terminal, y su valor representa la capacidad nominal inicial máxima de transmisión de energía activa promedio en el intervalo de tiempo t de la línea de transmisión ubicada entre dichos Nodos, "i Î {2, 3,...,Ng + Nt + 1}, "j Î {Ng + 2, Ng + 3,...,Ng + Nt + Nc + 1}. Si alguno de estos arcos es añadido a la Red R por parte de algún proyecto de transmisión, su valor debe ser igual a cero;
![]() : número total de muestras del modelo de simulación;
: número total de muestras del modelo de simulación;
![]() : número de intervalos de tiempo que conforman el Horizonte de Planificación Hp;
: número de intervalos de tiempo que conforman el Horizonte de Planificación Hp;
n: número total de proyectos que componen el PPISEP;
tih: tipo de cliente asociado a cada Nodo Terminal i de la Red R, "i Î {Ng + Nt + 2, Ng + Nt + 3,...,Ng + Nt + Nc + 1};
atipo, βtipo, gtipo: parámetros que definen la tendencia del consumo pronosticado de un tipo de consumidor;
míntipo, modtipo, máxtipo: parámetros que definen la distribución de probabilidad tipo triangular (valor mínimo, moda y valor máximo) asociada al consumo pronosticado de un tipo de consumidor;
mínfalla, modfalla, máxfalla: parámetros que definen la distribución de probabilidad tipo triangular (valor mínimo, moda y valor máximo) asociada al cálculo de las capacidades nominales de las líneas de transmisión de energía (valores de los arcos ![]() );
);
ktipo: tarifa a la cual se factura la energía efectivamente entregada a los consumidores (valores de los arcos efectivos de consumo) según el tipo de consumidor;
cu: costo por unidad de energía activa promedio generada (valores de los arcos efectivos de generación) que tiene la empresa eléctrica;
cf: costo fijo de cada intervalo de tiempo que tiene la empresa eléctrica;
ltipo: factor de penalización de demanda insatisfecha según el tipo de consumidor;
x1, x2: factor de ponderación de Bp y Dp;
![]() ,
,![]() : tasa de interés mínima atractiva y tasa de inflación por intervalo de tiempo;
: tasa de interés mínima atractiva y tasa de inflación por intervalo de tiempo;
REFERENCIAS
1. Azadivar F. (1999). Simulation Optimization Methodologies. Proceedings of the 1999 Winter Simulation Conference, pp. 93 - 100. [ Links ]
2. Brea E. (2013). Una extensión del método de Nelder Mead a problemas de optimización no lineales enteros mixtos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, vol. 29, no. 3, July- September 2013, Pages 163-174, ISSN_0213-1315, http://dx.doi.org/10.1016/j.rimni.2013.06.005 [ Links ]
3. Carson Y. & Maria A. (1997). Simulation Optimization: Methods and Applications. Proceedings of the 1997 Winter Simulation Conference, pp. 118 - 126. [ Links ]
4. Hreinsson E. & Jónasson K. (2003). Monte Carlo based risk analysis in Hydroelectric Power System Expansion Planning in the presence of uncertainty in project cost and capacity. 38th International Universities Power Engineering Conference (UPEC), University of Thessaloniki, septiembre 2003. [ Links ]
5. Nelder J. & Mead R. (1965). A simplex method for function minimization. The Computer Journal, vol. 7, pp. 308 - 313. [ Links ]
6. Strang G. (2005). Linear Algebra and its Applications. India: 4ta ed. Brooks Cole. 128 - 140. [ Links ]
7. Su C. & Lii G. (1997). Power System Capacity Expansion Planning Using Monte Carlo Simulation and Genetic Algorithm. MODSIM 1997 International Congress on Modelling and Simulation. Modelling and Simulation Society of Australia and New Zealand, pp. 1450 - 1455, diciembre 1997. [ Links ]
8. Sullivan W., Wicks E., Luxhoj J. (2004). Ingeniería Económica de DeGarmo (12). México: Editorial Pearson Educación. 70 - 148. [ Links ]