LA DINÁMICA P2MA UNA OPCIÓN DIDÁCTICA FRENTE A LA

ENSEÑANZA TRADICIONAL DE LA MATEMÁTICA

Fredy E. González

(UPEL-IPEMAR)

fgonzalez@ipmar.upel.edu.ve

Fredy E. González

Doctor en Educación (énfasis en Educación Matemática). Dirige el Núcleo de Investigación en Educación Matemática "Dr. Emilio Medina". Universidad Pedagógica Experimental Libertador (Núcleo Maracay). Autor de numerosas publicaciones en el área de la enseñanza de la matemática. Ponente y conferencista en eventos nacionales e internacionales. Profesor acreditado por el Sistema PPI-Fonacit. Correo electrónico: fgonzalez@ipmar.upel.edu.ve

RESUMEN

En el presente trabajo se expone una proposición didáctica, derivada de una investigación realizada por el autor con un grupo de estudiantes del área de Matemática; el punto de partida se ubica en la confirmación de las insuficiencias que presenta el proceso tradicional de enseñanza y aprendizaje de esta ciencia lo cual constituye un contexto que justifica la necesidad de que sean formulados nuevos modelos didácticos orientados a superar las limitaciones y fallas que se observan en la forma como habitualmente se trabaja la matemática escolar. Este artículo comienza con una revisión de los aspectos ontológicos, epistemológicos y pedagógicos de la visión que tradicionalmente se tiene de la enseñanza de la Matemática; luego, se delínea una perspectiva socio-cognitiva del aprendizaje, que se asocia con la insurgencia de nuevas opciones para la adquisición de saberes matemáticos. Con base en lo anterior, se propone la Dinámica P²MA (Profesor-Problema, Matemática, Alumno) como una manera diferente de desarrollar el proceso de enseñanza y aprendizaje de la Matemática. Esta propuesta se basa en: (a) resolución de problemas; (b) toma de conciencia, por parte del alumno, de su propio accionar cognitivo, llevado a cabo durante la actividad resolutoria; y, (c) consideración de la Matemática como una forma especial de pensamiento y el aula de clases como una Comunidad Matemática en cuyo contexto se llevan a cabo procesos de producción y socialización del conocimiento matemático.

Palabras clave: educación matemática; resolución de problemas; metacognición; tareas intelectualmente exigentes.

THE DYNAMIC P2MA AS AN ALTERNATIVE FOR THE MATHEMATIC TEACHING AND LEARNING PROCESS

ABSTRACT

This paper presents a didactic proposal coming from a piece of research performed by this author and a group of mathematic student teachers. The limitations of the traditional mathematic teaching and learning process becomes the context for creating new didactic models. This paper presents a review of the ontological, pedagogical and epistemological perspectives held by traditional mathematic teaching. It also presents a socio cognitive perspective of learning, associated with emergent ideas on mathematic learning. From there, this author propose the dynamic P²MA (teacher, problem, mathematic, student) as an alternative for the mathematic teaching and learning process. This proposal is based in: (a) problem solving, (b) pupil development of consciousness from his own cognitive behavior, and (c) mathematic as a special way of thinking in class, as a community for producing and socializing mathematical knowledge.

Key words: mathematic education, mathematic teaching, problem solving, metacognition, intellectually demanding tasks.

Introducción

El nivel de competencia Matemática que exhiben los ciudadanos de los países latinoamericanos ha sido objeto de cuestionamiento reiterado; este asunto está asociado con los más diversos factores; de allí que, con cierta frecuencia, se llevan a cabo procesos de reformas con la expectativa de que dicha situación mejore; no obstante, ello no ocurre en los niveles esperados. De modo que el mejoramiento de la calidad del conocimiento matemático de nuestros ciudadanos sigue siendo una materia pendiente para todos los miembros de la comunidad latinoamericana de educadores matemáticos. Éste es el contexto en el que el autor del presente trabajo ofrece una proposición didáctica que aspira superar las limitaciones observadas en el proceso que tradicionalmente se ha venido siguiendo para la enseñanza de la Matemática en Venezuela, cuyas características, en mayor o menor medida, son replicadas en el resto de los países de la región latinoamericana.

En la primera parte se hace una revisión de los aspectos ontológicos, epistemológicos y pedagógicos que subyacen en el modelo que predomina en la enseñanza tradicional de la Matemática; aquí se explicita la concepción acerca de la disciplina que implícitamente es sustentada por los profesores; luego, se esboza la visión que se tiene acerca del aprendizaje y la consecuente posición que el maestro asume en su función pedagógica. También se hace referencia a otros eventos claves del trabajo en el aula de clases de Matemática, como la evaluación, por ejemplo.

Seguidamente, se esboza la perspectiva socio-cognitiva del aprendizaje, la cual se asume como un contexto propiciatorio de la emergencia de nuevas perspectivas en relación con la adquisición de los saberes matemáticos. Es con base en esto último que el autor propone la Dinámica P²MA, como un modo diferente de desarrollar el proceso de enseñanza y aprendizaje de la Matemática, cuya implementación se orienta a superar las insuficiencias, anomalías e inadecuaciones que tradicionalmente han predominado en dicho proceso.

Las insuficiencias del proceso tradicional de enseñanza y aprendizaje de la Matemática

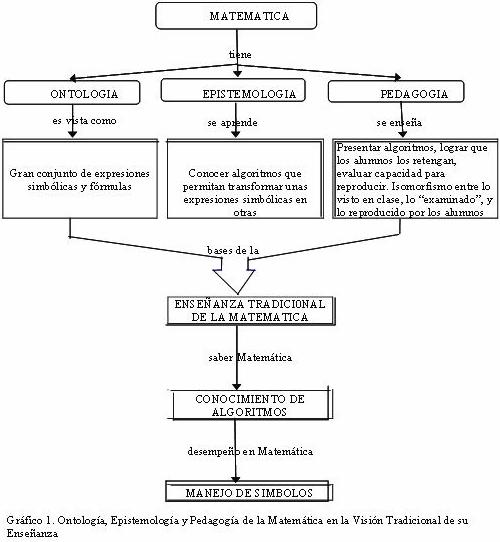
Una revisión de los aspectos ontológicos, epistemológicos y pedagógicos de la visión que tradicionalmente se tiene de la enseñanza de la Matemática hace posible la identificación de sus insuficiencias. En efecto, tradicionalmente, la Matemática es vista como un gran conjunto de expresiones simbólicas y fórmulas (ontología), cuyo aprendizaje consiste en el re-conocimiento de algoritmos que permitan transformar unas expresiones simbólicas en otras (epistemología) y, por tanto, el papel del enseñante se limita a presentar esos algoritmos, lograr que los alumnos los retengan y evaluar la capacidad de éstos para reproducirlos (Gómez, 1995). Se trata de lograr un isomorfismo entre "lo visto" en clases, lo "evaluado" en los exámenes y lo "reproducido-devuelto" por los alumnos; es la rutina de "teoría-ejemplos-ejercicios" que se basa en "transmitir información para que el estudiante la registre y sea capaz de repetirla" (pedagogía); a esto se reduce la enseñanza tradicional de la Matemática, la cual "campea" en los espacios académicos universitarios venezolanos, "es portada" en los libros de texto que se utilizan habitualmente, y se ve "legitimada" por los profesores, quienes la reproducen en su acción docente cotidiana, en un proceso de consagración y reconfirmación del modo como a ellos les fue enseñada-expuesta la Matemática. Se trata de una "visión reproductivista" del proceso de enseñanza y aprendizaje de la Matemática en la que de ésta se tiene una visión estática (se la mira como ciencia hecha), el docente es sólo un "expositor-mostrador-exhibidor" de un "producto acabado", el alumno es un "consumidor-receptor" pasivo de ese producto, y en el trabajo en el aula impera la cultura del "silencio discente" bajo el imperio de la "oralidad docente" (Esté, 1994), en un contexto donde la Matemática se transmite como dogma (Gutiérrez Borovia, 1994).

Puede decirse, entonces, que la enseñanza tradicional de la Matemática se inserta en el paradigma de la "transmisión pasiva"; en este caso, la dinámica de la interacción profesor-alumno en el aula de clase se orienta hacia la transmisión de información y conocimientos matemáticos desde el docente -quien los posee- hasta los alumnos -ayunos de tales conocimientos- quienes actúan como receptores que, mediante la imitación de lo exhibido por el docente y la reiteración de lo que éste hace, tratan de reproducir lo que les fue impartido-dado-transmitido por el profesor (Contreras, 1995).

La intencionalidad de este enfoque presupone una in-competencia del alumno; éste, por sí mismo, no es capaz de acceder al conocimiento. Es preciso brindárselo desde afuera, donde se ubica el docente, quien opera como un proveedor de estímulos: conocimientos que han de "ponerse en la cabeza" de los estudiantes, quienes han de reaccionar ante tales estímulos mediante una respuesta que es valorada y, en consecuencia, reforzada o rechazada por el docente, según sea o no isomórfica con un patrón esperado previamente establecido.

Una representación de la ontología, la epistemología y la pedagogía de la visión tradicional del proceso de enseñanza y aprendizaje de la Matemática se muestra en el Gráfico 1.

Algunos modelos representativos del proceso de enseñanza y aprendizaje de la Matemática

En el caso de la Dinámica P²MA, se está en presencia de la propuesta de un "mentefacto" heurístico para orientar la enseñanza y el aprendizaje de la Matemática. Este modelo amplía la literatura venezolana relacionada con propuestas didácticas para orientar los procesos de enseñanza y aprendizaje de la Matemática; entre ellas, cabe desatacar las presentadas por Nava y Escalona (1995), Morales y Mora (1995), Coello (1995), y Monagas (1996).

El trabajo de Nava y Escalona (1995) surgió a partir de un diagnóstico que les permitió detectar el uso de métodos tradicionales y poco productivos para enseñar Matemática en instituciones educativas de sectores urbanos del Estado Zulia (Venezuela); las autoras consideraron que tan improductivas rutinas estaban asociadas con las orientaciones para el trabajo escolar contenidas en los textos usados por los docentes: lo que los maestros hacen es lo que le indican los libros que hagan; entonces, su quehacer didáctico se modificará si se produce un material que le proponga a los maestros que hagan cosas cualitativamente mejores y distintas a las que hacen rutinariamente. Con base en esta hipótesis propusieron un modelo que destaca el uso de material didáctico impreso a fin de "atender a los contenidos, a las necesidades de los alumnos y docentes, y a los procesos de enseñanza y aprendizaje con su evaluación" (p. 6); así que, en la perspectiva de las nociones de la Ingeniería Didáctica que estas autoras asumen, el modelo que ellas proponen enfatiza sobre los procesos vinculados con el aspecto instruccional, centrado en el trabajo docente, dentro de la relación enseñanza-aprendizaje.

En cuanto al trabajo de Morales y Mora (1995) puede señalarse que el mismo constituye una experiencia didáctica para enseñar Matemática a nivel superior basada en la estrategia metodológica denominada PROPÓSITO-META-OBJETIVO, que desarrollaron María Itriago y Cipriano Cruz en 1992. El punto de partida de Morales y Mora fue su inconformidad con la "didáctica convencional" (p. 132) usada por los docentes de Matemática de la Universidad Nacional Experimental de Guayana (Venezuela) la cual generaba en los alumnos "apatía, sorna o temor por la actividad académica" (p. 132); la metodología elaborada por Itriago y Cruz y, luego, aplicada por Morales y Mora (1995), contempla cuatro fases: "motivación, ejecución, retroalimentación y complementaria" (p. 131) relacionadas dinámicamente; la primera aspira lograr un clima motivacional favorable en el aula, la fase II enfatiza el trabajo del alumno teniendo en cuenta las características del objetivo a lograr; la fase III se orienta hacia el reconocimiento por parte del alumno del aprendizaje que ha logrado; y, por último, la fase IV es para complementar los conocimientos adquiridos por el alumno.

La estrategia se centra en el trabajo que el alumno ejecuta en la clase en torno al contenido matemático correspondiente, y a la forma como el docente dirige las sesiones de trabajo. De tal manera que la estrategia PMO se basa en el desarrollo del contenido programático, por parte de los alumnos, en un clima de aula agradable, no coercitivo ni penalizante, que ofrece al alumno más oportunidades de intervención activa que en la clase tradicional expositiva centrada en el docente.

A partir de lo anterior se puede inferir que la estrategia PMO enfatiza el aspecto gerencial del trabajo de aula, privilegiando al contenido aun cuando propicia un mayor número de interacciones directas entre este contenido y los alumnos; en este caso el docente actúa como un gerente del tiempo, de los recursos didácticos disponibles en la sesión de trabajo y de las interacciones que se dan entre los alumnos.

El trabajo de Coello (1995) se refiere a la utilización del Modelaje Matemático como estrategia para la transferencia de conocimientos matemáticos a situaciones concretas; este autor presentaba a sus alumnos diferentes situaciones problemáticas que ellos debían modelar Matemáticamente, es decir, traducir a términos matemáticos situaciones del mundo real, formulando ecuaciones para relacionar la mayor cantidad de variables que intervienen en la situación dada, con lo cual se procura que los estudiantes revisen sus conocimientos previos, obtengan la información necesaria, y le den significado al conocimiento matemático. Finalmente, Monagas (1996) se pronuncia por el uso de modelos como herramienta didáctica en la educación Matemática pero no explicita cómo hacerlo.

Coello (1995) enfatiza el Modelaje Matemático desde una perspectiva de transferencia de conocimientos, con el propósito de superar el aprendizaje memorístico y no significativo de la Matemática; Monagas (1996) propone el uso de Modelos Matemáticos como herramienta didáctica con el fin de superar las deficiencias observadas en la presentación (por parte del docente) y en la adquisición (por parte de los alumnos) de los conceptos matemáticos básicos; Morales y Mora (1995), en cambio, privilegian el trabajo de los alumnos en clase, en torno al contenido matemático, adoptando un enfoque de enseñanza activa con base en su inconformidad con la didáctica convencional empleada para enseñar Matemática en el nivel de Educación Superior; finalmente, Nava y Escalona (1995) le dan relevancia al uso de material didáctico impreso, incorporando indicaciones para los docentes acerca de cómo gerenciar el trabajo de aula, y asumen los principios de la Ingeniería Didáctica como una opción para superar los métodos tradicionales y poco productivos empleados para enseñar Matemática.

La perspectiva socio-cognitiva del aprendizaje y la insurgencia de nuevas opciones para la adquisición de saberes matemáticos

En la visión tradicional del proceso de enseñanza y aprendizaje de la Matemática, el énfasis está colocado sobre el contenido, entendiéndose que éste refiere a conocimientos socialmente validados y aceptados; en este caso, la Matemática es reducida a ese contenido del cual el alumno, en su estructura cognitiva, debe incorporar una réplica; para ello debe adoptar un postura contemplativa y asistir a las exposiciones orales y visuales que hace el docente, el original que ha de ser copiado; el alumno atiende (oye, ve), imita (reproduce) y corrige (elimina), por indicación del docente, aquello que no se corresponde con el original mostrado. Esto lleva implícita una noción de aprendizaje repetitivo (mecánico) logrado por recepción en el que no ha habido lugar para el ejercicio de procesos superiores de pensamiento, sencillamente porque éstos han sido ignorados.

Desde las ciencias cognitivas, se han formulado otras maneras de abordar el funcionamiento cognitivo humano (Corral, 1991) que aluden a los procesos que una persona activa para percibir los influjos del medio, y transformarlos, reducirlos, elaborarlos, almacenarlos, recuperarlos y usarlos en la realización de tareas intelectuales.

El estudio de la cognición humana se interesa, pues, por averiguar cuáles son los mecanismos psicológicos internos que explican sus variaciones, sin embargo, la cognición humana no es un asunto exclusivamente individual; al contrario, a ella se le atribuye un carácter activo y socialmente determinado, ubicando así los procesos de adquisición del conocimiento en una perspectiva sociohistórico-cultural (Perelstein de Braslavsky, 1995) que concibe diferencias entre los procesos psicológicos elementales, de origen biológico, y los procesos psicológicos superiores, de origen social. Así, el esquema conductista clásico: E (estímulo excitante) -R (respuesta, reacción) es complementado por las ciencias cognitivas al integrar un tercer término constituido por "procesos internos de transformación" (Perelstein de Braslavsky, 1995; p. 307) que median entre el estímulo (E) y la Respuesta (R).

El enfoque socio-histórico-cultural, citado anteriormente, enriquece aún más el esquema cuando, entre los estímulos excitantes de la acción humana, privilegia los estímulos sociales que provienen de la misma persona y de las otras con quienes interacciona; entonces, en una relación dialéctica, tales estímulos a la vez que fundamentan la conciencia social son el origen social de la conciencia (Perelstein de Braslavsky, 1995; p. 308), y de los procesos superiores del pensamiento.

Sobre esta base es posible concebir el proceso de enseñanza y aprendizaje que ocurre en el aula de clases de matemática como un conjunto de acciones comunicativas múltiples, protagonizadas por el docente y los alumnos a través de relaciones sociales, basadas en reglas convenidas explícita o implícitamente, las cuales se integran en un amplio sistema que incluye tanto los vínculos entre la clase, la escuela y la sociedad, como las relaciones de los participantes (docentes y alumnos) con el saber y la cultura.

De este modo, la clase se asume como un contexto cultural en donde se dan procesos de creación, re-creación y negociación de significados asociados con los saberes constitutivos de la Matemática escolar; y, al aula se la mira como "unidad ecológica" (Ojalvo, 1994) cuyo estudio reclama la utilización de métodos tales como observación participante, etnografía, y análisis del contenido de documentos escritos por docente y alumnos, entre otros.

Se tiene entonces que la clase de Matemática es un proceso complejo de comunicación, es decir, de común-acción, que comprende: intercambio de información, interacción, influencia, percepción y comprensión mutua entre docente y alumno; todo lo cual requiere de la creación de una positiva atmósfera grupal, favorecedora de la expresión individual de cada uno de los participantes, a los fines de promover un mayor conocimiento de sí mismos, mediante estrategias que propicien la autorreflexión, la autovaloración y el autoperfeccionamiento, asuntos éstos respectivamente vinculados con la metacognición, el autoconcepto matemático y general, y la posibilidad de aprender a aprender.

La clase de Matemática, al suponer la formación de reuniones entre dos personas por lo menos, constituye una ocasión social (Goffman, referido en Bateson et. al., 1991), que da lugar a situaciones sociales que, a su vez, generan actividades en las que los alumnos se implican, es decir, mantienen en ella cierta atención intelectual y afectiva que reclama la movilización de sus recursos psicológicos, entre los que se incluyen procesos superiores de pensamiento.

Desde esta perspectiva, la competencia Matemática se expresa no sólo en el manejo de algoritmos y otros procedimientos de cálculo sino, fundamentalmente, en un elevado nivel de conciencia en torno a cuándo, dónde, sobre qué y de qué forma usar los saberes matemáticos, tanto en ambientes escolares como fuera de ellos. La formación y desarrollo de esta competencia tiene lugar mediante la inmersión del alumno en un contexto matemáticamente rico y enriquecedor; rico, porque considera que la Matemática es un "proceso social" (Vasco, 1994); y este carácter se refleja en las aulas de clase de Matemática, debido a los esfuerzos que hace el docente por crear escenarios que estén próximos a lo que es el quehacer matemático real, es decir, aquél que llevan a cabo quienes producen el saber matemático, sin menospreciar con ello el "relativismo cultural" (D’Ambrosio, 1993) presente en esa producción; y enriquecedor porque al alumno le proporciona oportunidades para la realización de actividades propias del quehacer matemático.

Por otro lado, es necesario acotar que el desarrollo de la competencia matemática se da en un proceso interpersonal e intrapersonal; lo primero alude a los vínculos que el alumno establece tanto con sus compañeros, en relaciones de aprendizaje colaborativo, como con el docente, cuando éste ejerce el rol de mediador; lo segundo se asocia con el desarrollo de capacidades para controlar y autorregular los procesos de conocimientos propios (actividad metacognitiva).

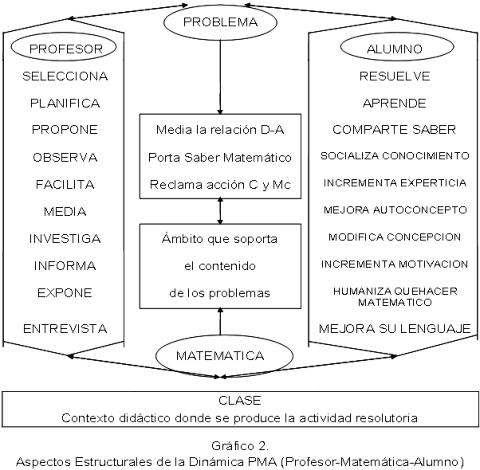
Con base en lo anterior, se propone la Dinámica P²MA (Profesor-Problema-Matemática- Alumno) como una manera diferente de desarrollar el proceso de enseñanza y aprendizaje de la Matemática: (a) basándolo en la resolución de problemas; (b) enfatizando la toma de conciencia, por parte del alumno, de su propio accionar cognitivo, llevado a cabo durante la actividad resolutoria; y, (c) considerando la Matemática como una forma especial de pensamiento y al aula de clases como una comunidad matemática en cuyo contexto se llevan a cabo procesos de producción y socialización del conocimiento matemático. Los elementos estructurales de la Dinámica P²MA se visualizan en el Gráfico 2.

Desde el punto de vista conceptual, puede decirse que la Dinámica P²MA (Profesor-Problema, Matemática-Alumno) (Gráfico 2), consiste en un conjunto de apreciaciones relacionadas con las implicaciones del proceso de resolución de problemas en el contexto de un aula de clases concebida como comunidad matemática.

En la Dinámica P²MA, el profesor es asumido como un facilitador, mediador de procesos de pensamiento e investigador; asume un papel protagónico preponderante, pero propiciador del desempeño cognitivo de los alumnos, mediante el planteamiento de problemas, asumidos éstos como tareas intelectualmente exigentes (González, 1997).

La Matemática vista, simultáneamente, como modalidad específica de pensamiento y código lingüístico común que posibilita los intercambios comunicativos, es el saber incluido en el enunciado de los problemas; así que, es en el contexto de esta disciplina donde adquiere sentido y significado la actividad resolutoria de los problemas, los cuales son concebidos como portadores de saber matemático, que median la relación entre el docente y los alumnos, y reclaman de éstos un accionar cognitivo y metacognitivo, intensamente comprometido desde el punto de vista afectivo.

El alumno, concebido como estudioso de su accionar cognitivo, coloca la actividad resolutoria propia como objeto de reflexión, logrando con ello aprender sobre el proceso de resolución en sí, sobre el área de conocimiento matemático a la que se refiere el contenido del problema, y acerca de sí mismos como resolvedor de problema.

El aula constituye un contexto, matemáticamente rico y enriquecedor, debido a que es el lugar de encuentro del profesor con los alumnos quienes, como miembros de una comunidad matemática, interactúan entre sí, haciendo que la clase sea un escenario para compartir saberes y socializar conocimiento matemático.

La Dinámica P2MA como modelo didáctico

En el diseño de la Dinámica P²MA se adoptaron los planteamientos de Cañal y Porlán (1987) para quienes un modelo didáctico constituye "una construcción teórico-formal que, basada en supuestos científicos e ideológicos, pretende interpretar la realidad escolar y dirigirla hacia determinados fines" (p. 92); en consecuencia, desde un modelo didáctico se han de responder las siguientes interrogantes: (a) ¿cómo se conceptualiza el aula?, (b) ¿cuáles son los fines educativos hacia donde se orienta el quehacer didáctico?, (c) ¿sobre cuáles principios didácticos se sustenta la práctica escolar? (Cañal y Porlán,1987).

El Modelo Didáctico propuesto por Cañal y Porlán (1987), asumido como una herramienta simbólica de intermediación susceptible de ser aplicada al estudio de las peculiaridades de los procesos de apropiación -aprendizaje- y comunicación -enseñanza- de saberes matemáticos asociados con la resolución de problemas en un contexto didáctico) sirvió de base para la construcción la Dinámica P²MA, la cual cumple las funciones "sustitutivo-heurística, aproximativa y extrapolativo-pronosticadora" que Omelianovsky, Novik, Ruzavin y otros (1981, p. 313) asignan a los modelos.

La construcción de la Dinámica P²MAexigió: (a) el establecimiento de fundamentos científicos e ideológicos del proceso de enseñanza y aprendizaje de la Matemática; (b) la definición de los fines a lograr mediante este proceso, en términos de aptitudes y valores por desarrollar en los aprendices; (c) la postulación de principios didácticos pertinentes; (d) la conceptualización del quehacer de aula; y, (e) la caracterización de la práctica escolar que en esta última se realiza.

La Dinámica P²MA, concebida como modelo didáctico, parafraseando a Omelianovsky, et al. (1981), constituye un ‘objeto sustituto’ relativamente independiente de los procesos que están siendo modelados, pero que es utilizable como una segunda realidad por medio de la cual se interpreta lo que acontece en el contexto del aula de Matemática.

A continuación se desarrolla cada uno de los elementos estructurales de la Dinámica P²MA, concebida como modelo didáctico en la perspectiva de Cañal y Porlán (1987).

Fundamentos científicos e ideológicos de la Dinámica P2MA

1. Concepción acerca del quehacer en el aula

Se asume que la vida en el aula es interpretable en términos de intercambios socioculturales protagonizados por los alumnos y el profesor quienes son considerados como procesadores activos de información y elaboradores de comportamientos que presentan las siguientes características: (a) se manifiestan en términos de roles y agrupamientos que se constituyen como plataforma sobre la que se sustenta el intercambio educativo entre alumnos y docente (relaciones sociales); (b) se derivan de las relaciones de poder que marcan la dinámica del control de las acciones que protagonizan en el aula sus principales actores (docente y alumnos); y (c) se expresan a través de los intercambios comunicativos de diversa naturaleza que se dan en el aula (explícitos, no explícitos, verbales, simbólicos, etc.) tanto entre las personas que participan en el proceso como entre éstas y los elementos materiales y ambientales (Cañal y Porlán, 1987, p. 93).

2. Caracterización de la clase

Se asume la clase como una situación social (Castillo, 1984) y al grupo integrado por quienes participan en ella como un sistema social donde docente y alumno se influencian recíprocamente con las acciones que protagonizan en el contexto de una institución, cuya organización contribuye a "crear un clima de intercambio, generar roles y patrones de conducta individual, grupal y colectiva, y desarrollar una cultura peculiar" (Pérez Gómez, 1994, p. 89).

3. Visión del aprendizaje

Se privilegia una visión constructivista del aprendizaje de acuerdo con la cual, este último es siempre "una reconstrucción interior y subjetiva" (Flórez Ochoa, 1994; p. 244); en este sentido, se tiene que: (a) aprender una disciplina determinada implica apropiarse de los modos expertos de organizar, representar y utilizar los conceptos y procedimientos que le son propios; (b) los problemas de aprendizaje pueden ser concebidos como deficiencias en el funcionamiento cognitivo (procesos de pensamiento asociados con la percepción, transformación y generación de información) y en el funcionamiento metacognitivo (procesos de pensamiento orientados hacia el control, regulación y supervisión de la actividad cognitiva propia); (c) el aprendiz es un constructor activo de su propio conocimiento; y (d) el aprendiz, como procesador activo de información, es capaz de dar sentido y significado a lo que aprende; por ello, las acciones del docente y las incidencias y pormenores del proceso instruccional afectan la ejecución del aprendiz sólo en la medida en que inciden sobre los mecanismos (procesos de pensamiento) que utiliza para procesar información.

4. Concepción acerca de la Matemática

Se asume que la Matemática constituye "un cuerpo de conocimientos no terminados, una disciplina en constante expansión, tanto en resultados particulares como en métodos y principios generales" (Santos Trigo, 1996, p. 14). y que "evoluciona a través de un proceso humano y creativo de generación de ideas, relacionado con un proceso social de negociación de significados, simbolización, refutación y formalización" (D’Ambrosio, 1993, p. 35), todo lo cual subsidia la idea de que la Matemática es "una ciencia por hacer, una ciencia viva que cada estudiante reinventa y cada época reconstruye" (Prada, 1979, pp. 9-10).

5. Concepciones acerca de la enseñanza y el aprendizaje de la Matemática

El planteamiento anterior acerca de la Matemática genera sendas concepciones en torno a sus procesos de enseñanza y de aprendizaje; en cuanto a la primera, se concibe, parafraseando a Pérez Gómez (1994, p.81), como un proceso que propicia la transformación del pensamiento matemático y de las actitudes y comportamientos de los alumnos hacia la Matemática, mediante su inmersión en un "microcosmos de la cultura Matemática" (Schoenfeld, citado por Santos Trigo, 1996, p. 4); de acuerdo con Schoenfeld (1985, pp. 87-88), puede decirse que tal microcosmos se crea si se constituye, en el aula de clases, un conjunto de situaciones que propicien la activación en el estudiante de procesos propios del pensamiento matemático, a fin de que pueda construir, desarrollar y profundizar su propio conocimiento; de este modo, resulta posible hacer Matemática, es decir, "resolver problemas, abstraer, inventar, probar y encontrar el sentido a las ideas matemáticas" (Santos Trigo, 1996, p. 2), o sea, poner en práctica procesos propios del accionar matemático tales como inferir, transformar, representar, generalizar, abstraer, entre otros (Serrano Gómez, 1995).

Del mismo modo, a partir de la visión de la Matemática como una ciencia por hacer, se deriva una concepción del aprendizaje de esta disciplina de acuerdo con la cual aprender Matemática consiste en apropiarse de los procesos que le son propios a esta disciplina e incrementar la experticia personal en el manejo de los mismos.

6. Concepción acerca del desempeño en Matemática

El desempeño en Matemática es interpretado desde un punto de vista cognitivo; en este sentido, se le considera asociado con la activación, por parte del aprendiz, de procesos intelectuales de orden superior demandados por las tareas propias de esta disciplina (especialmente por la resolución de problemas) y con la toma de conciencia en cuanto a dichos procesos, lo cual se manifiesta como el reconocimiento consciente de las formas, modalidades y procedimientos que utiliza para abordar las tareas y el control, regulación y supervisión que ejerce sobre su accionar cognitivo propio.

7. Enfoque del proceso de resolución de problemas

Los problemas se enfocan desde la perspectiva de quien intenta resolverlos, considerando predominantemente las demandas cognitivas que se le plantean al resolvedor en cada una de las fases en las que se puede organizar el desarrollo del proceso de resolución; el énfasis se coloca sobre los mecanismos cognitivos internos que los resolutores utilizan para realizar la búsqueda de la solución a un problema.

8. Relaciones entre Matemática y resolución de problemas

En correspondencia con la idea de que "aprender Matemática significa que el estudiante identifique, seleccione, y use estrategias comúnmente usadas por los matemáticos al resolver problemas" (Santos Trigo, 1996, p. 30), y de que "los problemas constituyen el corazón de la Matemática" (Halmos, 1980), se asume que la resolución de problemas es la tarea básica que el estudiante debe acometer a los fines de que pueda desarrollar estrategias y habilidades propias del quehacer matemático; en este sentido se supone que: (a) la resolución de problemas matemáticos en el aula propicia en los estudiantes una mejor comprensión acerca de la naturaleza de la Matemática y de las actividades que llevan a cabo los matemáticos; (b) las estrategias generales para la resolución de problemas aprendidas en las clases de Matemática pueden ser transferidas y aplicadas en otras situaciones; (c) como actividad fascinante, participar en la resolución de problemas incrementa la motivación hacia el estudio de la Matemática.

Por otro lado, el logro de esta triple finalidad (comprensiva, de transferibilidad y motivacional) plantea la necesidad de adoptar una perspectiva dual (psico-sociológica) del proceso de resolución de problemas, tomando en consideración las condiciones subjetivas del resolvedor en conjunción con el contexto social en el que se presenta la situación problemática; lo psicológico se asocia con lo individual y hace alusión al estado interior (cogniciones, metacogniciones y afectos) de quien intenta resolver el problema, y lo sociológico se vincula con el conjunto de intercambios y negociaciones que se producen entre quien propone el problema (el docente) y quienes intentan resolverlo (los estudiantes) cuando el proceso de búsqueda de la solución se da en el marco de la situación didáctica constituida por la clase de Matemática.

9. Teleología de la Dinámica P²MA

Con la implantación de la Dinámica P²MA se pretende que los estudiantes: (a) incrementen su conocimiento y experticia en el uso de herramientas de pensamiento formal e informal; (b) aumenten sus conocimientos acerca de la cognición en general y la suya propia en particular; y, (c) hagan uso eficiente y efectivo de sus recursos cognitivos propios.

10. Explicitación de las características del discurso matemático

En el aula de clases, la Matemática aparece como un discurso1 contentivo de los signos específicos que la comunidad matemática ha establecido para comunicar sus significados; dichos signos se superponen con los códigos del lenguaje natural propio de los aprendices (resolvedores de problemas); en el caso de los problemas matemáticos, éstos se convierten en portadores de saber matemático que el resolvedor debe descodificar y, con base en sus propios esquemas lingüísticos y cognitivos, manejarse a partir de las funciones comunicativas del discurso matemático, entre las cuales cabe mencionar las siguientes: (a) construcción de razonamientos para sustentar las demostraciones, (b) interpretación de relaciones, y (c) elaboración de pruebas y argumentos convincentes.

Fines educativos de la Dinámica P2MA

Los fines hacia los que se orienta la Dinámica P²MA tienen que ver con el desarrollo de valoraciones positivas hacia la Matemática por parte de los aprendices así como el fortalecimiento de su autoconcepto matemático, de su capacidad para hacer Matemática y para elaborar razonamientos y comunicar ideas propias de esta disciplina; en este sentido, se espera que los estudiantes que participen en procesos de enseñanza y aprendizaje llevados a cabo conforme al modelo didáctico explicitado en la Dinámica P²MA desarrollen: (a) una valorización positiva de la Matemática; (b) una razonable confianza en su aptitud propia para desempeñar tareas específicas del quehacer matemático; (c) capacidad para resolver problemas matemáticos; (d) habilidad para comunicarse matemáticamente; (e) pericia en el desarrollo de razonamientos matemáticos.

Principios didácticos de la Dinámica P2MA

Esquema conceptual para interpretar el quehacer en el aula

Las actividades, tareas e interacciones que se producen en las aulas de clase de Matemática se asocian con las interrelaciones que se generan entre los elementos de la tríada constituida por el profesor (P); los aprendices (A); y el saber matemático (M); tales interrelaciones se relativizan en función de las ideas que los actores sustentan en torno a la enseñanza, el aprendizaje y el conocimiento matemático (Llinares, 1994; p. 253); de manera que los modos como el docente desarrolla su gestión didáctica en el aula están vinculados con las perspectivas que él adopta en relación con el papel que desempeña el aprendiz en el proceso de su propio aprendizaje y con la naturaleza del conocimiento matemático; dichas perspectivas subyacen en las decisiones que el docente toma antes, durante y después de su desempeño en el aula.

En efecto, sobre la base de una visión que atribuye un carácter activo del aprendiz en la construcción del conocimiento matemático escolar, el docente fundamenta la organización social del aula, es decir, las modalidades según las cuales se lleva a cabo el trabajo en el aula. De esta forma, la organización social del aula se expresa en modalidades de trabajo que tienen que ver con las interacciones sociales generadas a partir de las maneras como los alumnos acometerán las tareas; éstas son un medio a través del cual se aspira lograr un objetivo (fin) determinado y, a la vez, constituyen oportunidades para que los alumnos construyan conocimiento matemático (Llinares, 1994; p. 275).

Las tareas generan actividades, es decir, acciones cognitivas, afectivas y psicomotrices asociadas con la tarea que los alumnos llevan a cabo de manera individual (cada alumno por separado), grupal (organizados en equipos de no más de cuatro integrantes), o colectivamente (todo el grupo de alumnos abocados simultáneamente a una misma tarea).

Además de asociarse con las modalidades de trabajo que se implementarán para llevar a cabo las tareas, la Organización Social del Aula genera la definición, tanto para el docente como para los alumnos, de roles diferenciados que demarcan sus respectivas responsabilidades en el contexto del trabajo escolar antes, durante y después de la clase concebida ésta como un escenario espacio-temporal donde se manifiestan las actividades asociadas con las tareas propuestas.

La clase: contexto propiciador del accionar cognitivo del alumno

En la Dinámica P²MA, el aula es concebida como un contexto donde un conjunto de actores sociales (docente y alumnos) protagonizan una serie de intercambios comunicativos mediante los cuales negocian significados idiosincrásicos en torno a un saber específico: la Matemática; el contenido de esta disciplina constituye el medio que hace posible la acción comunicativa entre los protagonistas del hecho didáctico.

La clase se concibe como el escenario donde se llevan a cabo las tareas que dan lugar a las acciones cognitivas y metacognitivas de los aprendices. Por tanto, ella se corresponde con la dinámica planteada por las interacciones entre los protagonistas, el medio disciplinario que propicia el intercambio (Matemática), y el contexto donde aquellas ocurren. Tales interacciones están orientadas hacia el logro de objetivos socialmente valiosos y ocurren durante lapsos o períodos temporales especificados. Teniendo en cuenta esto, en la clase pueden destacarse dos dimensiones: la organizativo-epistemológica y la temporal.

La primera se refiere a las modalidades de interacción social que adoptan los protagonistas durante sus intercambios, lo cual se vincula con las suposiciones, explícitas e implícitas, en torno a las formas como se produce el saber; desde este punto de vista, se concibe a la clase como una SITUACIÓN SOCIAL (Castillo, 1984, pp.7-19), protagonizada por ACTORES (docente y alumnos) comprometidos en la realización de una TAREA INTELECTUALMENTE EXIGENTE (resolver problemas) que demanda la activación de PROCESOS DE PENSAMIENTO (cognitivos y metacognitivos); así que la clase es una situación académica e institucional que, en un determinado escenario geográfico (aula) y temporal (horario) congrega a un docente y a un grupo de alumnos para que, mediante la realización actividades académicas específicas (resolver problemas), interactúen (i.e. generan intercambios comunicativos de variados tipos), mediados por el contenido de una determinada área del saber (Matemática), a los fines de lograr ciertos propósitos académicos (objetivos).

La dimensión temporal de la clase puede ser esquematizada en una secuencia de momentos diferenciados pero integrados: Apertura, Desarrollo y Cierre, a lo largo de los cuales transcurren las interacciones protagonizadas por el docente y los alumnos. La apertura es el momento durante el cual se predispone positivamente a los alumnos, de manera que éstos deseen acometer con agrado las tareas; la responsabilidad principal de este momento la tiene el docente quien, para lograr el clima propicio para el trabajo, puede compartir información, comentar generalidades o formular instrucciones. Luego de la apertura viene el desarrollo, lapso éste durante el cual los alumnos y el docente se comprometen en la realización de la tarea y luego comparten, analizan y reflexionan acerca de las incidencias y pormenores de la misma. Finalmente, está el cierre, el cual es un tiempo para consolidar saberes y extenderlos más allá de lo aprendido en el aula.

En resumen, la clase es una noción temporo-espacial, un lugar y un tiempo de encuentro durante el cual unos actores protagonizan diversas acciones que dan lugar a variados tipos de productos, y, además, generan intercambios y negociaciones con significado, propósito, fin y sentido diferenciado según la posición que ocupa el actor en el contexto de la situación social en la cual participa. Lo característico de la clase es que: (a) demarca un espacio temporal; (b) congrega a los protagonistas durante lapsos precisados; (c) denota la situación donde se generan las acciones principales objeto de estudio; (d) constituye el momento para propiciar la oportunidad de que los estudiantes lleven a cabo la tarea de resolver problemas; (e) configura un escenario que permite: aportar y recabar información, aplicar instrumentos de recolección de datos, realizar las entrevistas, entregar material instruccional (guías), y realizar la mediación cognitiva socializada.

Modelo conceptual sobre el aula

El aula de clase como comunidad matemática

El aula constituye un espacio de escenificación de situaciones sociales protagonizadas por actores que desempeñan roles con los que ejecutan variados intercambios (comunicativos, culturales) a nivel sociosimbólico (Córdova, 1990; p. 22); con ello se hace posible compartir las representaciones que los actores tienen acerca de la Matemática y de los significados que ellos le atribuyen al quehacer que en torno a este saber se desarrolla en el contexto escolar. Además, puede concebirse como un lugar de encuentro donde convergen personas con historias de vida diferentes (Córdova, 1990) que se comprometen en la realización de tareas orientadas hacia el logro de objetivos comunes. Finalmente, el aula es un ambiente propicio para la ejercitación de un discurso que viabiliza la posibilidad de compartir saberes; de esta manera, el aula se constituye en un espacio para la comunicación.

Estos rasgos aluden a elementos vinculantes entre los protagonistas que permiten visualizar al aula de Matemática como una comunidad. En efecto, los protagonistas del quehacer en el aula, es decir, el docente y los alumnos, se vinculan mediante los signos propios del discurso matemático, a partir del cual generan intercambios de variada índole que se orientan hacia el logro de objetivos comunes socialmente validados; todo ello constituye la base para establecer al aula como comunidad.

Cabe señalar que, por lo prolongado del lapso de trabajo (un semestre o un año escolar), es posible que el grupo constituido por el docente y los alumnos interrelacionen de forma duradera alrededor de diversas tareas tendentes al logro de los objetivos educativos (Peleteiro, 1995; p. 34); de este modo es posible caracterizar al aula como un escenario propiciador de encuentros entre unos protagonistas comprometidos en la realización de quehaceres propios de la Matemática, vinculados entre sí por medio del ejercicio de acciones intelectuales demandadas por la necesidad de resolver problemas de esta disciplina.

Aunque tales acciones, esencialmente, correspondan a la utilización de recursos cognitivos de cada uno de los individuos, al realizarse en forma socializada, es decir, conjuntamente con los demás y con la mediación del docente en el contexto del aula, es posible que esta última se transforme en una verdadera comunidad matemática, es decir, un ámbito social cuyos "habitantes" están comprometidos, individual y colectivamente, con el ejercicio de tareas propias del quehacer matemático. Así, cuando las acciones didácticas se llevan a cabo de esta manera, el aula se convierte en una microsociedad generadora de saber matemático.

La práctica escolar en la Dinámica P2MA

Producción de saberes y socialización de conocimientos matemáticos

La práctica escolar de la Dinámica P²MA se sustenta sobre la base de la producción de saberes matemáticos y la socialización de los conocimientos alcanzados en el aula de Matemática. Dicha producción se realiza en conexión con los esfuerzos (individuales, en pareja, en pequeño grupo, y en grupo total) para encontrar la solución de algún problema matemático; la actividad resolutoria genera la posibilidad de "hacer Matemática"; es decir, la necesidad de hacer esfuerzos cognitivos asociados con la ejecución de acciones propias del quehacer matemático (inducir, deducir, inferir, conjeturar, demostrar, despejar, formular, simbolizar, graficar, visualizar, etc.); es en la mente de quien realiza la tarea donde se produce dicho "hacer"; el docente media en el proceso (dando información, llamando la atención, estructurando situaciones, reforzando acciones adecuadas, etc.), y el alumno lo manifiesta a través de sus expresiones, orales o escritas, las cuales pueden ser concebidas como la concretización del mencionado "hacer".

La socialización, por su parte, ocurre cuando los alumnos intercambian ideas, inquietudes, y opiniones generadas por ellos a partir de la actividad resolutoria ejecutada por cada uno; este proceso procura la concientización de elementos propios de la actividad resolutoria de los problemas que apuntan hacia la transferencia y la generalización.

La socialización, mediada por el facilitador, se inicia después del trabajo individual o de un pequeño número de integrantes, cuando se reconstituye el grupo total con el propósito de crear un escenario en el que los participantes puedan compartir sus experiencias y vivencias individuales; el proceso implica el reconocimiento de las actitudes asumidas durante la actividad resolutoria, así como la toma de conciencia por parte de cada resolutor, acerca de sus propias debilidades y fortalezas como resolvedor de problemas, en procura de elementos que posibiliten la transferencia y la generalización; de este modo la resolución de problemas se convierte en una auténtica experiencia de aprendizaje, lo cual amerita tanto la reflexión concurrente acerca del proceso (la que se lleva a cabo en el momento mismo en el que se está realizando la actividad de búsqueda de solución), como la reflexión retrospectiva (aquella que se efectúa después que el problema haya sido resuelto, o intercalada en momentos culminantes del proceso). Este segundo tipo de reflexión permite: (a) concientizar vivencias, (b) consolidar saberes, (c) reforzar el autoconcepto matemático, y (d) reconocer patrones, esquemas y/o automatismos de acción.

Así que la socialización del conocimiento constituye un proceso de mediación cognitiva que tiene como "materia prima" la actividad resolutoria de problemas desplegada durante el trabajo individual, en parejas o en pequeños grupos; con base en las "ideas, criterios, y opiniones" que los alumnos emiten acerca de su actividad resolutoria propia, el docente contribuye a la construcción de un discurso interpretativo, que explica lo acontecido, le da sentido, y lo relativiza, mediante referencias a las situaciones comunicadas por los participantes.

La Pedagogía de la comprensión

Una proposición pedagógica pertinente para la Dinámica P²MA es la Pedagogía para la Comprensión (Villegas, 2003, pp. 387-418); la cual se sustenta sobre diez principios que, al ser aplicados al caso de la educación Matemática, se manifestarían del modo siguiente:

• Los protagonistas de un encuentro edumático han de sumergirse (tanto dentro como fuera del aula) en experiencias sociales alrededor del conocimiento matemático de tal modo que puedan apropiarse idiosincrática, experiencial y vivencialmente de los contenidos conceptuales, procedimentales y actitudinales, propios de esta disciplina cuyo aprendizaje esté previsto en los planes y programas de estudio de Matemática (La inmersión como estrategia).
  

• En la presentación del conocimiento matemático se debe utilizar una multiplicidad de modalidades de presentación (gráficos, dibujos, tablas, maquetas, modelos, esquemas, entre otros); así mismo, siempre que sea posible, se deben usar las diferentes variantes del lenguaje matemático (geométrico, algebraico, analítico, probabilístico, etc.) de modo tal que se "estimulen las visiones múltiples que son posibles" en relación con los contenidos matemáticos (La variedad como oportunidad; Villegas, 2003, p. 398).
  

• Ha de reconocerse que, en algunos casos, el conocimiento previo que el alumno posee "puede convertirse en obstáculo ante su eventual discrepancia con el nuevo conocimiento que se desea enseñarle" (ob. cit., 399); un ejemplo de esto se presenta cuando el alumno ha de enfrentarse por vez primera con la aritmética transfinita en la cual la idea según la cual el cardinal de un subconjunto es igual al del superconjunto que lo contiene se contradice con la idea habitual de que el todo es más que las partes (El conocimiento como problema; Villegas, 2003, p. 399).
  

• La adquisición de conocimientos matemáticos (conceptuales, procedimentales y actitudinales) exige "el desarrollo de estrategias que utilicen a la investigación como el contexto natural de las experiencias didácticas" (La Investigación como proceso; Villegas, 2003, p. 401). Este principio resulta especialmente apropiado para la Dinámica P²MA puesto que la búsqueda de solución a los problemas matemáticos puede convertirse en una enriquecedora experiencia indagatoria que puede propiciar acercamientos afectivos de carácter positivo hacia la Matemática, sobre todo cuando se utilizan problemas de una complejidad adecuada al nivel de conocimientos y expectativas de los alumnos.
  

• En el aula de clases, el profesor, más que respuestas, lo que debe plantear son preguntas; éstas constituyen:

Una invitación a la movilización del pensamiento, la creación y la imaginación de quien es su receptor. La pregunta emerge ante la insatisfacción por la expresión del objeto, ella se activa ante la necesidad de llenar vacíos o suprimir incoherencias en la información que se tienen o que había sido útil anteriormente... la pregunta es una fuente potencial de saber (La Pregunta como método; Villegas, 2003, pp. 404-405).

• Tomando en cuenta que una verdad matemática se establece sobre la base de argumentos debidamente fundamentados, en los encuentros edumáticos se deben propiciar oportunidades para que el alumno argumente razonadamente sus decisiones; esta habilidad argumentativa tendrá una interesante proyección en su formación como ciudadano puesto que se hará consciente de la necesidad de superar la arbitrariedad y el capricho en los planteamientos, valorando el consenso y el acuerdo entre iguales (El argumento como respuesta; Villegas, 2003, p. 408).
  

• El aula de clases de Matemática debe ser asumida no sólo como una comunidad productora de saberes matemáticos, sino también como un espacio para la formación de ciudadanos; en este sentido, los encuentros edumáticos propios de la Dinámica P²MA deben: (a) darse en un clima donde se respeten los pensamientos y las ideas de cada quien; (b) propiciar el uso de la comunicación para la generación de opciones de solución a los conflictos que puedan suscitarse; (c) brindar oportunidades para que todos los actores puedan expresarse; (d) valorar por igual tanto los derechos colectivos como los individuales; (e) estimular el reconocimiento del sentido de lo colectivo (El consenso como alternativa; Villegas, 2003, p. 411).
  

• Con la finalidad de superar el predominio, en el aula de clases de Matemática, de la visión reproductivista estimuladora del apuntismo (réplica fidedigna, sin reflexión, de lo que dice y escribe el profesor), la Dinámica P²MA suscribe el uso del diario, un recurso donde el alumno registra, pormenorizada y sistemáticamente "todas las situaciones que acontecen tanto a nivel interno de su persona durante el curso de la asignatura como desde la dinámica de la clase" (p. 412); este diario es una fuente privilegiada para tomar conciencia acerca de los progresos propios así como también en relación con las dificultades que se han encontrado a lo largo del proceso de estudio y apropiación del conocimiento matemático (El diario como recurso; Villegas, 2003, p. 412).
  

• Del lenguaje matemático se ha dicho que tiene un carácter imperativo y que las verdades matemáticas son inapelables ("dos más dos son cuatro aquí y en la Conchinchina"); esto tiene una incidencia en los modos como se establecen las relaciones sociales dentro del aula de clases de Matemática y, por ello, en ocasiones, el docente ejerce un férreo control sobre lo que allí acontece; la Pedagogía de la Comprensión (Villegas, 2003) reivindica la "evolución en el comportamiento de los sujetos protagónicos, docente y alumnos, en relación directa con el control que ejerza cada uno sobre el hecho escolar u objeto de conocimiento" (p. 415); para ello, propicia la transferencia del control desde el docente hacia el alumno, procurando que éste se responsabilice de su propio aprendizaje: "a través de una práctica guiada, el alumno va progresivamente asumiendo el control del proceso en el aula" (p. 416) "basándose en el incremento de sus propios conocimientos acerca del contenido tratado" (El control como significado; Villegas, 2003, p. 414).
  

• La finalidad esencial de todo proceso de enseñanza de la Matemática es que el alumno aprenda; esto implica una apropiación idiosincrásica del conocimiento que se pretende enseñar, lo cual se manifiesta a través de la comprensión, entendida ésta como: (a) identificación del objeto de conocimiento matemático; (b) captación de su sentido y naturaleza en el contexto de la estructura matemática de la que forma parte; (c) autointerrogatorio (actividad metacognitiva), es decir, reconocimiento del grado de dominio que se tiene en relación con el objeto matemático que está siendo estudiado; (d) valoración de los medios de que se dispone para aproximarse y o adentrarse en el objeto de estudio (conciencia de los conocimientos previos que se poseen o que se requieren); (e) identificación de inconsistencia, es decir, reconocimiento de situaciones anómalas en relación con conocimientos anteriormente adquiridos; (f) valoración positiva del objeto de estudio (reconociendo utilidad y pertinencia); (g) negociación de significados, es decir, comunicación con los pares (La comprensión como abstracción en la construcción del conocimiento; Villegas, 2003, p. 336)

Conclusiones

Como puede inferirse, la Dinámica P²MA es una propuesta que antagoniza diametralmente con la visión tradicional de la enseñanza de la Matemática; ontológicamente ésta es asumida como una ciencia por hacer, no consumada y abierta, en constante crecimiento, a la vez que se la conceptúa como una manera especial de pensar que se manifiesta como saber incluido en el enunciado de los problemas.

En cuanto a los procesos de producción del saber matemático, dimensión ésta que alude a la epistemología de la disciplina, se concibe que la adquisición de este conocimiento constituye un proceso socialmente situado que, por ende, obliga a la aplicación de enfoques didácticos en escenarios matemáticamente ricos y enriquecedores.

Las dimensiones ontológica y epistemológica de la Matemática en la Dinámica P²MA encuentran al aula como espacio para la conciliación donde se genera una pedagogía expresada en acciones comunicativas múltiples que transportan significados negociales en el marco cultural de la clase; estas tres dimensiones sustentan una nueva noción de lo que significa Saber Matemática que supera la visión tradicional (que reduce dicho saber al sólo manejo de algoritmos), ampliándola hacia la toma de conciencia en cuanto a cuándo, dónde, sobre qué y cómo usar los saberes; de modo que se produce una re-conceptualización del desempeño en Matemática, asumiéndolo como la pericia en la ejecución de los procesos propios del quehacer matemático. Estos aspectos de la Dinámica P²MA, descritos en los párrafos anteriores, se visualizan en el Gráfico 3.

La Dinámica P²MAsuscribe, integra y trasciende lo fundamental de las experiencias y propuestas referidas en el marco teórico, asentándolas sólidamente sobre una base multidisciplinaria que armoniza cuestiones ontológicas, epistemológicas y pedagógicas, y colocando el acento en el desarrollo del alumno, concibiéndolo como totalidad indivisible en cuyo desempeño expresa un accionar múltiple en el que concilia sus cogniciones y metacogniciones con sus saberes y afectos.

En síntesis, la Dinámica P²MA es la respuesta que el autor presenta como opción para superar las insuficiencias, anomalías e inadecuaciones de la visión que tradicionalmente se tiene del proceso de enseñanza y aprendizaje de la Matemática, proponiendo asentarlo sobre la base del funcionamiento cognitivo del estudiante; tal propuesta se manifiesta como un modelo didáctico representativo de los procesos de enseñanza y aprendizaje de la Matemática, considerando a estos últimos como el sistema objeto al cual se refiere el modelo; en cuya configuración se muestran los elementos que permiten dar cuenta de: (a) las concepciones subyacentes que se asumen en torno al quehacer escolar; (b) la teleología que se suscribe en el modelo, es decir, los fines hacia los cuales se dirige dicho quehacer; y (c) los principios didácticos sobre los cuales este último se asienta.

Prospectiva

La Dinámica P²MAse ofrece como una proposición cuya implantación podría ayudar a mejorar la calidad de la enseñanza y aprendizaje de la Matemática; esta promesa sólo podrá ser confirmada mediante su puesta en práctica en escenarios reales, concretos, con espíritu de indagación crítico y reflexivo.

Referencias

1. Bateson, G., Bindwhistell, R. L., Goffman, E. y otros (1991). La Nueva Comunicación. En Investigaciones Sobre la Vida Institucional y Pública, 1991 (Parte 4., 287-298). Barcelona (España): Kairós.         [ Links ]

2. Cañal, P. y Porlán, R. (1987). Investigando la realidad próxima: un modelo didáctico alternativo. Enseñanza de las ciencias 5(2), 89-96.         [ Links ]

3. Castillo, V. de. (1984). Situaciones sociales y observación participante. Paradigma V(1, 2 y 3), 7 – 19.         [ Links ]

4. Coello, Y. (1995). Modelo matemático como estrategia metodológica para transferir el conocimiento matemático a situaciones concretas. Acontecer Educativo, 11, 12-15.         [ Links ]

5. Contreras, I. (1995). De la enseñanza a la mediación pedagógica: ¿cambio de paradigma o cambio de nombre?. Revista Educación 19(2), 5-15.         [ Links ]

6. Corral, R. (1991). La Psicología Cognitiva Contemporánea y la Educación. Revista Cubana de Educación Superior XI(1-2), 29-33.         [ Links ]

7. Córdova, V. (1990). Historias de Vida: una metodología alternativa para las ciencias sociales. Caracas: Fondo Editorial Tropykos.         [ Links ]

8. D’Ambrosio, B. (1993). Formaçao de Professores de Matemática para O Século XXI: O Grande Desafio. PROPOSIÇOES 4(1[10]), 35- 41         [ Links ]

9. Esté, A. (1994). El Aula Punitiva (Vol. I). Caracas: Co-edición del Fondo Editorial Tropykos y el Equipo TEBAS.         [ Links ]

10. Flórez Ochoa, R. (1994). Hacia una pedagogía del conocimiento. Santa Fe de Bogotá: Mc Graw Hill.         [ Links ]

11. Gómez, P. (1995). Riesgos de la innovación curricular en Matemática. Colombia. Ciencia y Tecnología 14(4, Oct./Dic.), 25-35.         [ Links ]

12. González, F. (1998, Jan/Jun). Metacognición y tareas intelectualmente exigentes: el caso de la resolución de problemas matemáticos. ZETETIKÉ, 6(9), 59-88.         [ Links ]

13. Gutiérrez Borobia, L. (1994). La Matemática escolarizada: ¿la ciencia convertida en dogma? un estudio etnográfico realizado en aulas universitarias. Tesis doctoral no publicada. Universidad Nacional Experimental Simón Rodríguez, Caracas.         [ Links ]

14. Halmos, P. (1980). The Heart of Mathematics. The American Mathematical Monthly, 87(7), 519 – 524.         [ Links ]

15. Llinares, S. (1994). La enseñanza de la Matemática: perspectivas, tareas y organización de la actividad. En L. Santaló, S. Llinares, V. Sánchez y otros (Comps.). La Enseñanza de la Matemática en la Educación Secundaria(parte II, Cap. 4, pp. 249-295). Madrid: Ediciones RIALP, S. A.         [ Links ]

16. Medina, A. (1994). Aportaciones del enfoque vygostkyano a la tecnología educativa. Tecnología y Comunicación Educativas, 9(24, jul./sep.), 83-96.         [ Links ]

17. Monagas, O. (1996). Modelos como herramienta didáctica en la educación Matemática. Paradigma XIV al XVII, (1-2), 270-287.         [ Links ]

18. Morales, J. V. y Mora, A. O. (1995). Estrategia didáctica basada en la solución de problemas: una experiencia didáctica en Matemáticas superiores. Acción Pedagógica, 4(1 y 2).         [ Links ]

19. Nava, F. y Escalona, Ma. (1995). Resultados de una propuesta didáctica para Matemáticas. Encuentro educacional 2(1), 03-13.         [ Links ]

20. Ojalvo, V. (1994). La Comunicación en el Aula: su investigación y entrenamiento. Revista Cubana de Educación Superior 14(1), 29-34.         [ Links ]

21. Omelianosvsky, M., Novik, Y., Ruzavin, G. y otros. (1981). La Modelación y el Conocimiento Científico. En La Dialética y los Métodos Científicos Generales de Investigación (Tomo I, Cap. VI, pp. 311-315). La Habana: Editorial de Ciencias Sociales.         [ Links ]

22. Peleteiro, I. (1995). Cómo educar e investigar fuera del ámbito escolar: un modelo pedagógico alternativo. Caracas: Ediciones de la Unidad de Publicaciones del Instituto Pedagógico de Caracas.         [ Links ]

23. Perelstein de Braslavsky, B. (1995). La lengua escrita y los procesos de adquisición de conocimientos en una concepción sociohistórico-cultural. Revista Brasileira de Estudios Pedagógicos 76(182/183), 305-325.         [ Links ]

24. Pérez Gómez, A. (1994). Enseñanza para la comprensión. En J. Gimeno Sacristán y A. Pérez Gómez (comps.). Comprender y transformar la enseñanza: Cap. IV. El modelo ecológico de análisis de aula (3ª. ed., pp.78-144). Madrid: Ediciones Morata, S. L.         [ Links ]

25. Prada, M. (1979). Matemática Moderna: nuevo modo de pensar y arte nuevo para transmitirla. En Equipo de didáctica de las Matemáticas del I.E.P.S. Matemáticas: un nuevo modo de pensar. Madrid: Narcea, S. A.         [ Links ]

26. Santos Trigo, M. (1996). Principios y métodos de la resolución de problemas en el aprendizaje de la Matemática. México: Grupo Editorial Iberoamérica.         [ Links ]

27. Schoenfeld, A. (1985). Matematical problem solving. San Diego, CA.: Academic Press, Inc.         [ Links ]

28. Serrano Gómez, I. (1995) [Reseña del libro Learning and Doing Mathematics de J. H. Mason], Epsilon, 33, 301-302.         [ Links ]

29. Vasco, C. (1994, Mayo). La educación Matemática: una disciplina en formación. Matemáticas: Enseñanza universitaria, 3(2), 59-75.         [ Links ]

30. Villegas, M. (2003). La Construcción del conocimiento por parte de estudiantes de Educación Superior: un caso con alumnos del Instituto Pedagógico de Maracay. Tesis doctoral no publicada, Universidad de Carabobo. Valencia.         [ Links ]

Gráficos

 

 

 

 

 

Notas

¹ El vocablo mentefacto es referido por D’Ambrosio (1993) éste, a su vez, remite a Ch. Lumsden y E. Wilson, dos investigadores de la Universidad de Harvard quienes, en su obra Mente y Cultura publicada en 1981, utilizan la expresión mentifacts para hacer referencia a constructos mentales que no tienen correpondencia directa con objetos, personas o eventos reales. Sin embargo, en este estudio, la noción de mentefacto se ubica en la perspectiva de los planteamientos acerca de las mediaciones simbólicas formulados por Vygotsky quien, por analogía con las herramientas físicas (artefactos) que se interponen entre el hombre y la naturaleza mediando su conducta sobre el medio y los objetos, considera a los símbolos (entre los que han de incluirse los modelos) como “instrumentos esencialmente psicológicos que median y regulan nuestra propia actividad intelectual” (Vygotsky, 1979; citado en Medina, 1994; p. 86)