Modelo teórico de asignación óptica del recurso hídrico en la frontera Guajira Colombo-Venezuela

 

José Miguel Sánchez

Economista (Universidad de Los Andes, ULA, Venezuela); M. Sc. en Economía del Medio Ambiente y de los Recursos Naturales (Universidad de Los Andes, UNIANDES, Bogotá); profesor agregado de las cátedras de Macroeconomía y Ecología de la Escuela de Economía, Facultad de Ciencias Económicas y Sociales de la ULA; investigador del Grupo Redes y del Grupo de Investigación Sobre Agricultura, Gerencia y Ambiente (GISAGA)  de la Facultad de Ciencias Económicas y Sociales de la ULA, en temas sobre economía y ambiente; actualmente, Director del Instituto de Investigaciones Económicas y Sociales de la Facultad de Ciencias Económicas y Sociales de la ULA. Dirección postal: Núcleo La Liria, Edif. G, 3º piso, IIES. Mérida 5101, Venezuela. Teléfono: 58-274-2401081. E-mail: josems@ula.ve

 

Resumen

La cuenca del río Carraipía-Paraguachón es una zona fronteriza comprendida entre las fronteras de Venezuela y Colombia, un área de gran importancia económica para ambos países. Esta zona se caracteriza por condiciones climáticas que producen efectos negativos tales como inundaciones en una época del año, así como las sequías en otras épocas. En este escenario el autor plantea diversas medidas aplicables para obtener el mayor provecho del recurso hídrico y procurar su conservación. Dentro de los objetivos está la determinación de las características operacionales óptimas en la asignación del recurso hídrico de un embalse, para los dos países. Para lograr este objetivo la metodología planteada hace referencia a la utilización de un modelo de optimización dinámica (aplicando la teoría de Control Óptimo), que puede ser empleado para identificar los planes de manejo que mejor se ajusten a los objetivos de la sociedad.

Palabras clave: recursos hídricos, asignación, control óptimo, Colombia, Venezuela.

 

Abstract

The Carraipía-Paraguachón River basin is an area between the Venezuelan and Colombian borders, a zone of great economic importance for both countries. This area is characterized by climatic conditions that produce negative effects such as flooding during part of the year as well as droughts in others. In this scenario, the author proposes diverse measures to obtain greater water resources and achieve its conservation. Within these objectives is the determination of the optimum operational characteristics in assigning water resources to a reservoir for the two countries.  To achieve this objective, the proposed methodology makes reference to using a dynamic optimization model (applying Optimum Control Theory) that can be employed to identify management plans that better adjust to society’s objectives.

Key words:  water resources, assignment, optimum control, Colombia, Venezuela.

 

Résumé

Le bassin de la rivière du Carraipía-Paraguachón est une zone de frontière entre la Colombie et le Venezuela qui a une grande importance pour ces deux pays. Du point de vue climatique, cette zone a un comportement négatif  lorsqu’elle présente de périodes des inondations et de sécheresse, au cours de l’année. En tenant compte de ces caractéristiques-ci, l’auteur examine diverses mesures adéquates pour mieux utiliser les ressources hydriques et pour promouvoir leur conservation.  Parmi les objectifs, l’auteur cherche à déterminer les conditions optimales pour assigner la ressource hydrique afin de construire  un barrage pouvant servir aux deux pays. Pour traiter cet objectif l’auteur emploi une méthode ou modèle d’optimisation dynamique, en appliquant la théorie du contrôle optimal.

Mots-clés : ressources hydriques, contrôle optimal, Colombie, Venezuela.

 

Recibido: 01-02-2002 Aceptado: 07-07-2004

 

 

Justificación

 

La cuenca del río Carraipía-Paraguachón presenta unas condiciones climáticas que la hacen propensa a sufrir fuertes y prolongados períodos de sequía a lo largo del año lo que resulta en graves problemas de suministro de agua para el consumo de la población asentada en la zona así como la dotación para actividades como el riego de cultivos. Por otro lado, durante  la época lluviosa ocurren grandes inundaciones especialmente en la parte baja de la cuenca que corresponde al territorio venezolano. Como solución simultánea a estos problemas, a mediados de la década de los noventa y en el marco de la Comisión Binacional, se propuso la construcción del embalse “La Chingolita” ubicado en la parte alta de la Cuenca al sur del corregimiento Carraipía, territorio colombiano. Dicho embalse tendría como objetivos el almacenamiento del agua en los períodos lluviosos para suministrarla en forma continua durante la época de verano así como el control de inundaciones en la cuenca baja. Dichos objetivos, a la luz de la realidad reciente, es decir, ante el agravamiento de los problemas de sequías e inundaciones a lo largo de los años mantienen su pertinencia.

 

Según lo anterior, surge la inquietud de determinar las características operacionales óptimas del embalse en función de los objetivos para la sociedad y la economía de ambos países. Para su solución se plantea un problema de optimización dinámica del recurso agua para Colombia individualmente y luego, para ambos países, lo que permitirá comparar ambos casos. La solución a dicho problema generará la utilización óptima del recurso disponible en el embalse tanto para el objetivo de asegurar los requerimientos de agua para la población del territorio colombiano como para el control de inundaciones y la demanda de agua para consumo humano en territorio venezolano. El desarrollo de la metodología se basa en el trabajo de Sánchez (1998) al cual se le ha aplicado un nuevo enfoque que ha permitido encontrar unas nuevas e importantes relaciones entre las variables objeto de estudio.

 

Se considera urgente propiciar el establecimiento de estrategias y programas para la cuenca que garanticen el proceso de desarrollo y el bienestar económico y social de la población de la región. En tal sentido, se presentan en el diagnóstico alternativas de proyectos para los cuales se deben profundizar los estudios correspondientes a las fases de su evaluación técnica-económica.

 

A raíz de la preocupación de los dos países por el manejo de los recursos de la cuenca del río Carraipía-Paraguachón, se han plasmado varios acuerdos binacionales que han fijado las bases para adelantar proyectos conjuntos en materia de cuencas hidrográficas. Los objetivos de estos proyectos buscan beneficiar a la comunidad asentada en la región fronteriza. En virtud del “Acta de Entendimiento” del 5 de octubre de 1989, en el año 1991, se presentó el “Estudio Conjunto del Aprovechamiento de los Recursos Hídricos de la cuenca del río Carraipía-Paraguachón”. En dicha Acta se señala la preocupación de los dos países  por la escasez del recurso hídrico en La Guajira  y la necesidad de la formulación de proyectos, enmarcados en planes regionales, que permitan el aprovechamiento óptimo y la conservación del recurso. Dentro de estos proyectos se encuentra el plan de construcción del embalse “La Chingolita” al cual haremos mención más concretamente y cuyo Estudio de Factibilidad se presentó en el año 1994.

 

1.  Introducción

 

La cuenca hidrográfica del río Carraipía-Paraguachón se encuentra localizada en territorio venezolano, en el Municipio Guajira del Distrito Páez del Estado Zulia y en territorio colombiano en el Municipio Maicao del Departamento de La Guajira. Comprende una amplia zona de 560 Km2 de los cuales 320 Km2 corresponden a Colombia y 240 Km2 a Venezuela. El conocimiento del recurso hídrico de la cuenca del Río Carraipía-Paraguachón reviste vital importancia, ya que éste está relacionado con los desarrollos de las diversas actividades económicas que se efectúan en la frontera colombo-venezolana. De aquí la necesidad de realizar la evaluación del aprovechamiento hídrico y conocer su comportamiento con relación a los requerimientos de agua en el área de estudio por parte de Colombia y Venezuela. Este conocimiento permitirá visualizar las alternativas de abastecimiento de agua para eliminar o mitigar los déficit y los posibles conflictos que se pudieran originar.

 

2.  Objetivos

 

a.  Plantear un modelo de optimización dinámica que, bajo ciertas condiciones, solucione el problema de manejo del recurso para satisfacer la demanda de agua para consumo humano y para uso agrícola de la población asentada en la cuenca, así como el control de inundaciones en la cuenca baja.

 

b.  Compatibilizar los beneficios económicos y sociales de los dos países en un escenario integracionista que supone la administración conjunta del recurso entre ambos países, definiendo así el manejo óptimo del embalse con relación a ello.

 

3.  Metodología

 

Los planes de manejo, en general, envuelven la selección de muchas variables de diseño y operación. Sin embargo, nos restringimos a la variable operacional más relevante en función de nuestros objetivos que es la cantidad del recurso extraída del embalse en un instante del tiempo.

 

En los modelos matemáticos usados para describir sistemas de recursos hídricos esas variables son llamadas variables de decisión cuyos valores, óptimos a través del tiempo, deben ser determinados. La magnitud de cada variable de decisión puede afectar los costos y los beneficios asociados a un plan particular.

 

Suponiendo que hay P planes, cada uno designado con la letra p. Para cada plan existe un valor de la variable de decisión q. El objetivo de este análisis va a ser encontrar para Colombia y Venezuela el plan particular p, definido por el valor de la variable de decisión q_p, que maximice los beneficios netos del plan. Este objetivo puede ser expresado matemáticamente como:

 

max_p=1,....,p BN(q_p)

 

Si, paralelamente, se considera que la cantidad de agua (q) puede ser asignada a dos usos, el problema será determinar para Colombia y Venezuela la asignación qj a cada uso j que maximice sus beneficios netos totales.

 

En este caso, las dos variables de asignación qj son variables desconocidas. El valor que estas variables pueden asumir está restringido entre 0 (una asignación negativa es imposible) y valores cuyas sumas q_h(t) + q_a(t) no excedan la oferta de agua disponible (q) en un momento determinado donde q_h(t) es la cantidad de agua asignada para consumo humano y q_a(t) para uso agrícola, en un momento t. Las restricciones pueden ser escritas como:

 

q_h(t) + q_a(t) ≤ q(t),

 

q_h(t), q_a(t)≥ 0.

 

Estas ecuaciones de restricción junto con la función objetivo definen, a grosso modo, el problema de cada escenario.

 

1.1.  El modelo

 

El siguiente modelo ilustra un embalse simple que tiene i(t) flujos de entrada y q(t) salidas en cada instante. En problemas como el que nos ocupa la secuencia de flujos de entrada se asume como conocida y se determina la secuencia de flujos de salida. Suponiendo conocida la capacidad de almacenamiento del embalse K, el problema de operación del embalse envuelve la producción de una secuencia de salidas q(t) que maximizan los beneficios totales netos. Suponemos que los beneficios netos en cada período t pueden ser definidos como una función de las salidas q(t), y puede ser denotado por BN[q(t)]. Asumimos que esa función de beneficios netos por cada período t será la misma. Podría plantearse a los beneficios netos, también, como una función del stock del recurso almacenada en el embalse en cada momento t. Los beneficios asociados al almacenamiento son un componente importante para la modelación de los beneficios por control de inundaciones: El agua almacenada tendrá un efecto negativo para este objetivo pues al entrar la época de lluvias mientras más agua almacenada tenga el embalse, menor será su capacidad de controlar los flujos de inundación que puedan ocurrir. Lo ideal sería que el embalse mantuviese una alta capacidad de almacenamiento para poder acumular el agua cuando hay peligro de que se generen inundaciones en la cuenca baja, por tanto, mientras mayor sea el agua almacenada mayores serán los daños por inundaciones, cuando estamos en la época de lluvias, y menores serán los beneficios económicos para la población de esa región. Cuando estamos en la época de sequía el stock de agua contenida en el embalse también tendrá un efecto negativo sobre los beneficios del grupo de intereses de la cuenca baja pues, como es lógico, mientras más agua se almacene menor agua quedará disponible para los requerimientos de la población que se encuentra en la parte baja de la cuenca. Para los intereses de la población de la cuenca media y alta se podría asumir que el stock de agua almacenado tiene unos beneficios asociados a los objetivos de previsión para la escasez de agua en la época de sequía, la conservación de especies, recreación. Sin embargo, y para darle más simplicidad, nuestro modelo considera los beneficios como una función de las salidas.  Es decir, se estudiaran los beneficios por consumo humano y uso agrícola del recurso para la población asentada en la cuenca alta y media y, por otro lado, los beneficios por consumo humano y control de inundaciones en la cuenca baja.

 

Los beneficios asociados con las salidas del agua son más sencillos de entender y, como se ha comentado anteriormente, están relacionados con la asignación del recurso para satisfacer los requerimientos de consumo directo y producción agrícola en la cuenca alta. También corresponden a las salidas de agua que van corriente abajo y se emplean para atender la demanda de agua de la población asentada en la cuenca baja así como influye en los problemas de inundaciones que se generan.

  

1.1.1. Manejo óptimo del embalse para Colombia

 

Para determinar los beneficios económicos asociados a la operación del embalse en Colombia se supone que hay funciones de demanda de agua lineales para consumo humano (q_hc) y para uso agrícola (q_ac). Las funciones inversas de demanda en cada caso son:  

 

 P_hc = a-bq_hc.  (1)

 

P_ac = c-dq_ac (2)

                                     

Donde p_hc y p_ac son los precios por consumo de agua para uso humano y uso agrícola en Colombia, respectivamente y a, b, c, d > 0². Para determinar los beneficios totales derivados del consumo de agua en cada caso integramos la correspondiente función inversa de demanda de la siguiente manera:         

                    

Beneficios por consumo humano:

                  

 

 

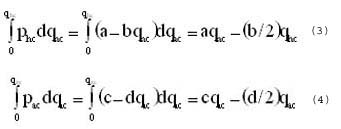
Un supuesto adicional está relacionado con la condición de eficiencia marginal en la asignación de un recurso entre diferentes alternativas. Se tiene que phc = pac, condición que establece que para el regulador del recurso el beneficio marginal por la asignación para el consumo humano debe ser igual al beneficio marginal para uso agrícola. Si fuese de otra manera, la asignación del recurso se realizaría en su totalidad para uno de los dos usos, aquel que marginalmente le proporcione más beneficios al regulador del embalse. Este es un supuesto fuerte pues en un ejercicio intertemporal como el que tenemos, esta condición no es necesaria, sin embargo, es considerada a objeto de poder relacionar qhc y qac, entonces:

 

 P_hc ⁼P_ac^=P(t)  (5)

                     

 a-bq_hc=c-dq_ac  (6) 

            

Luego:

 

     q_hc = (dq_ac+a-c)/b  (7) 

  

 q_ac=(bq_hc+c-a)/d  (8)

 

La cantidad de agua total extraída para Colombia es la suma de la cantidad asignada a consumo humano más uso agrícola q_c = q_hc + q_ac, entonces, usando las anteriores expresiones:

                                   

q_c =q_hc + (bqhc +(bq_hc+c-a)/d  (9) 

 

 

Luego:                       

            q_hc = (dq_c +a-c)/(b+d)  (10)

 

Igualmente se tiene que:

 

             q_c 0 (dq_ac +a-c)/b+a_ac  (11)

 

Luego

 

q_ac = (bq_c +c-a)/(b+d)  (12)

 

Para efectos de simplificar el ejercicio llamamos    A = (b+d) > 0 y B = (a - c)/(b+d) para el cual suponemos que B > 0, es decir, a > c, lo que constituye un supuesto no muy restrictivo si consideramos que “a”, el precio para el cual se hace cero la demanda de agua para consumo humano, debe ser superior a “c” el equivalente para uso agrícola. Es decir, teóricamente la demanda de agua para consumo se debe anular a un precio superior al precio que se anula la demanda del recurso para uso agrícola. Según lo anterior, podemos rescribir (10) y (12) de la siguiente manera:

 

qhc = dqc / A + B   (10.a)

 

qac = bqc / A-B  (12.a)

 

Empleando estas expresiones se podrá obtener otra para la suma de los beneficios por la utilización del agua para consumo humano y uso agrícola:

 

(dq_c / A)(a-bB) + (bqc / A)(c+dB) - (q_c² /2A²)(bd² + db²) + B (a-c-dB/2)              (13)

 

Para simplificar se llama E = a - bB ; F = c + dB;    G = bd2 + db2 > 0; H = B(a - c - dB/2) pudiéndose demostrar que E, F, H > 0 (si se hace el supuesto que B > 0). Se puede entonces tener la siguiente expresión para la suma de los beneficios:

 

 

 

donde I = dE + bF > 0.

 

Adicionalmente, se debe considerar los costos sociales en que se incurre cuando la cantidad del recurso asignada a los diferentes usos es menor que la cantidad de agua demandada. Si se fija  qhc y qac las cantidades de agua demandadas para consumo humano y uso agrícola, respectivamente. Se define una función de costos sociales por consumo de agua insatisfecho de la siguiente manera:

 

 

     

de donde resulta que  ¶f1/¶q_c ≤ 0  lo que es evidente ya que se supone que los incrementos en q_c significan aumentos en q_hc y q_ac. Entonces, al incrementarse la cantidad de agua asignada a ambos usos se espera que los costos sociales por consumo insatisfecho desciendan.

 

Igualmente, una función de costos sociales por requerimientos agrícolas no satisfechos:

 

     (16)

             

de donde resulta que ¶f2/¶q_c ≤ 0  lo que es también evidente ya que, igualmente, suponemos que los aumentos en qc significan incrementos en qhc y qac.

 

En tercer lugar, se debe considerar los costos de asignación o explotación del recurso los cuales se asumen como una función de q_c y donde suponemos que: ¶C / ¶q_c > 0 y ¶²C / ¶q_C²≥0  , es decir, se asume una función de costos cuasi-convexa con respecto a la utilización del recurso. Este tipo de función de costos es tradicionalmente supuesta para casos similares de manejo de recursos hídricos (Brown-Deacon, 1972). Es decir, se tendrá:

 

Costos de abastecimiento = C(q_c)          (17)

 

La función de costos por consumo humano no cubierto en Colombia que está planteada en la ecuación (15) puede ser representada por la función ¦₁ de la figura 1 (anexo). La figura indica que hay una relación inversa entre el nivel del recurso asignado a Colombia (q_c) y el valor monetario de los costos por consumo humano no cubiertos en ese país. Existe un nivel de q_c al que se llama q_c1 que es el nivel de asignación tan alto como para que la función de costos ¦₁ se haga cero._ Es decir, la asignación q_c1 es aquella para la cual q_hc = q_hc  y, por tanto, los costos por consumo humano insatisfecho son nulos. A medida que q_c se acerca a los valores mínimos (qc ® 0 ) dichos costos toman valores monetarios muy altos (¦₁ ® ∞ ) indicando la disposición a pagar por unidad adicional del recurso (no está de más recordar que un incremento (disminución) en q_c implica aumentos (caídas) en q_hc y q_ac).

 

Hay una relación inversa entre el nivel de q_c y el valor monetario de los costos por uso agrícola no cubiertos en Colombia (¦₂ )  representado por la ecuación (16). El nivel de q_c al cual dichos costos se anulan es q_c2 (para el cual q_ac = q_ac )  el cual es mayor que q_c1 puesto que los requerimientos de agua para uso agrícola son mucho mayores que los requerimientos para consumo humano. Cuando se supone que el nivel del recurso asignado a Colombia se acerca a cero, la función de costos ¦2  tiende a un valor teórico determinado que nos señala cual es el costo agrícola en que se incurre cuando no se asigna el recurso a la producción agrícola (puesto que si, q_c ® 0 , q_ac ® 0 también), por tanto, es el costo agrícola máximo (MC). 

 

A partir de la figura 1 se puede derivar la representación gráfica de los costos marginales por consumo humano y uso agrícola insatisfechos en Colombia, ¶¦₁ / ¶q_c  y ¶¦₂ / ¶q_c  respectivamente. Dicha representación está constituida por la figura 2 la cual  se obtuvo graficando la pendiente de ¦_{1 y} ¦₂ para los diferentes valores de q_c. Con el empleo de la figura 2 se puede determinar el comportamiento de los costos marginales ¶¦₁ / ¶q_c  y ¶¦₂ / ¶q_c en relación con la variable de decisión q_c. A medida que q_c aumenta, ambas funciones de costo marginal se incrementan pues toman valores negativos cercanos a cero. Lo contrario ocurre para caídas en q_c pues, teóricamente, a medida que q_c ®0 tendremos que ¶¦₁ / ¶q_c ® mínimo costo marginal agrícola (mcm) y ¶¦₁ / ¶q_c ®- ∞ . En síntesis, tenemos una relación directa entre,  ¶¦₁ / ¶q_c., ¶¦₂ / ¶q_c.

 

Según los supuestos que hemos formulado sobre los costos de abastecimiento, existe una relación directa entre q_c y el nivel de dichos costos. La relación está descrita por una función cuasi-convexa que nos indica que mientras más agua es asignada a Colombia los costos de suministrar o abastecer del recurso aumenta a una tasa creciente. La figura 3 (ver anexo) nos representa los costos marginales de abastecimiento ( ¶C / ¶q_c ) en la que podemos observar que mientras q_c se acerca a los valores teóricamente mínimos q_c ® 0  tendremos que ¶C  / ¶q_c ® 0. Por lo contrario, cuando q_c ® ∞ ,  ¶C  / ¶q_c ® ∞ es decir, hay una relación directa entre ¶C  / ¶q_c y q_c.

  

 

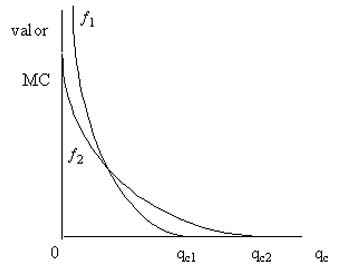
Figura No. 1

Costos por consumo humano (f1) y uso agrícola (f2) insatisfechos

 

 

 

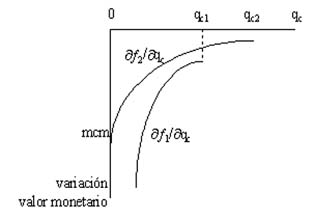
 Figura No. 2 Costos marginales por consumo humano (¶f₁/¶q_c)

 y uso agrícola (¶f₂/¶q_c) insatisfechos

 

 

 

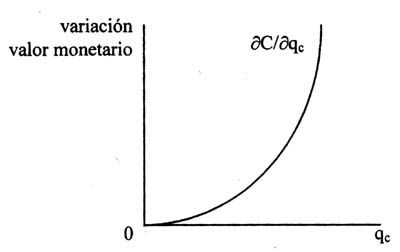
  Figura No. 3  Costos marginales de abastecimiento (¶C/¶q_c)

 

Según todo lo anterior, el problema de control óptico es maximizar:

 

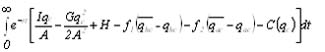       (18)

Sujeta a:

¶S/¶t = i(t) - q_c - qr_c  (19)

 

Donde en la expresión (19),  es la variación del stock del recurso en el tiempo, qrc es el caudal remanente para Colombia, lo que se evidencia en el diagrama de distribución de caudales (Figura 4 anexa) en el que qb es el caudal base. Entonces, el Hamiltoniano H  es  y escrito como:

 

 

 

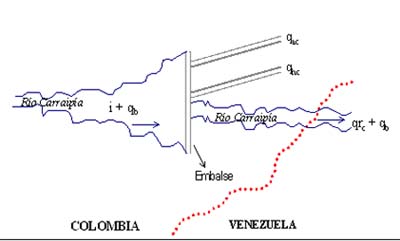
Figura No. 4 Diagrama de Distribución de Caudales

 

Si m = e^rt l  el Hamiltoniano de valor corriente es:

 

^H_c = Iq_c / A - Gq₂ / 2A² + H - f₁(.) - f₂(.) -C (q_c) + m (1-q_c -qr_c)  (21)

 

y  las siguientes ecuaciones deben ser satisfechas:  

     

       ¶Hc/ ¶q_c =  (22)

 

     =I/A - Gq_c / A² - ¶¦₁ / ¶q_c - ¶¦₂ / ¶q_c - ¶C/ ¶q_c - m (1 + ¶qr_c / ¶q_c)=0

 

-¶Hc / ¶S = -rm + ¶m / ¶t = 0³        (23)

 

 ¶Hc/ ¶m = ¶S/ ¶t = i(t) - q_c -qr_c = 0   (24)  

 

La primera condición óptima (22) señala que el uso del recurso en el momento t está en el nivel donde la suma  del costo de abastecimiento y el costo de uso son iguales al beneficio marginal del consumo. El beneficio marginal del consumo es, también, igual al precio óptimo:

 

I / A- Gq_c / A²-¶f₁ / ¶q_c -¶f₂ / ¶q_c  = ¶C / ¶q_{c +} m  ( 1 + ¶q_rc / ¶q_c ) = P(t)  (25)

 

Las condiciones (23) y (24) son las ecuaciones de movimiento del stock del recurso y del precio sombra. La tasa de cambio del costo de uso en el tiempo se puede obtener a partir de (23):    

 

 

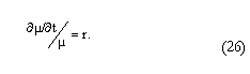
La anterior condición señala que el costo de uso o el precio sombra del recurso antes de su utilización crece a la misma tasa de descuento, r.

 

La derivada de P(t) con respecto a t proporciona la ecuación de movimiento del precio del recurso:

 

 

 

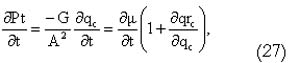
A partir de la cual, considerando que ¶m/¶t = rm , se obtiene:

 

 

 

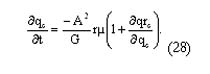
A partir de la ecuación (25) se tiene que  m = (P(t) - ¶C / ¶q_c) / (1 + ¶qr_c / ¶q_c). Usando la anterior expresión y dividiendo la ecuación (28) entre q_c se tiene que:

 

 

 

es la ecuación de movimiento del recurso, es decir, la ecuación que determina el comportamiento óptimo del uso del recurso en el tiempo para el manejo del embalse en Colombia. Se puede demostrar que:

 

 

 

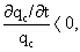
Por tanto, un aumento en la tasa de descuento, r, hará que el uso óptimo del recurso decline más rápido en el tiempo y, mientras la tasa de declinación en el uso óptimo del recurso en el tiempo decline más rápido, mayor será el uso del recurso en los primeros períodos. Similar consecuencia tendrá sobre el manejo del recurso un aumento de la diferencia (P(t) - ¶C/¶q_c), lo cual es evidente pues indica que el administrador del recurso preferirá asegurarse los beneficios de su explotación más pronto a medida que el beneficio marginal neto de los costos de abastecimiento sea mayor.

 

Como se puede demostrar y se desprende del trabajo de Sánchez (1998), la expresión (29) es equivalente a:

 

 

 

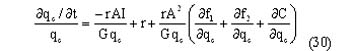
que es la misma ecuación de movimiento del recurso en su uso óptimo, pero en función de otras variables, también de interés en este trabajo.

 

3.1.2.   Manejo óptimo del embalse para Colombia y Venezuela

 

En esta sección se plantea el manejo óptimo del embalse ampliando el problema a la consideración de los dos países como afectados por la operación y distribución del recurso. Los supuestos básicos del modelo inicial, presentado en la sección precedente, se mantienen lo que quiere decir que el problema a abordar enseguida implica sólo la agregación o adición del caso venezolano a las mismas condiciones que sirven de marco al problema de control en Colombia. Se está asumiendo, simplemente, un escenario integracionista entre ambos países en el que la optimización del uso del recurso considera los problemas de cada país de manera conjunta.

 

Como se ha señalado anteriormente, las condiciones básicas que rodean el problema de control en Venezuela, son que este país se encuentra ubicado en la parte baja de la cuenca, además, que la propiedad y el manejo del embalse están en manos de Colombia por lo que debemos asumir que se está planteando un problema en el que las decisiones de manejo del recurso están bajo la jurisdicción de uno de los dos afectados. Con la adición al  problema de la realidad venezolana, se añade, paralelamente, un problema que no se consideró en el caso anterior dadas las características de la cuenca y de las cuales es redundante retomar; dicho problema es el de control de inundaciones en la cuenca baja del Río Carraipía-Paraguachón.

 

Como se desprende del Estudio Conjunto del Aprovechamiento Integral y Conservación de los Recursos Hídricos del Río Carraipía-Paraguachón del Comité Técnico Binacional (1991) cerca de 13.000 Ha de la cuenca baja (28% del total) son tierras no aptas para cultivos. De éstas últimas una proporción (aproximadamente 478 Ha)  tienen “alta o moderada limitación para cultivos por la presencia de sales e inundaciones ocasionales que impiden un mejoramiento de las tierras para cualquier sistema de manejo”⁴ . Es así como se supone para nuestro modelo de control que existen unos costos por inundaciones que están representados por el rendimiento económico agrícola que se deja de percibir debido a la presencia de este problema. Se supone, por cuestión de simplicidad, que todo caudal por encima del caudal base (q_b) genera inundaciones por lo que el rendimiento agrícola no obtenido depende directamente del caudal remanente en Venezuela (qr_v), donde este caudal remanente es simplemente la diferencia entre el remanente en Colombia y la utilización del recurso para consumo humano en Venezuela (q_hv), es decir:

           

 qr_v = qr_c - q_hv.                (31)

 

Luego, los costos por inundaciones se establecen de la siguiente manera: una función f(qrv) que es el área con potencialidad agrícola que es inundada, donde ¶f/¶qrv > 0, multiplicada por el valor económico marginal de la producción agrícola (K3), es decir, los costos por inundaciones son equivalentes a:

 

K₃¦(qr_v).                      (32)

 

Suponemos que ¶qrv/¶q_c < 0 siendo, entonces ¶f/¶q_c < 0⁵ donde ¶f/¶qc = ¶f/¶qr_v.¶qr_v/¶q_c < 0.Para determinar los beneficios económicos asociados a la operación del embalse en ambos países, suponemos que la función de demanda de agua para consumo humano en Venezuela (q_hv) es una función lineal (al igual que las funciones de demanda de agua para Colombia) y cuya función inversa viene representada por:

 

P_hv = d - fq_hv,       (33)

 

Donde phv es el precio por consumo de agua para uso humano en Venezuela y d, f> 0. Para  determinar los beneficios totales derivados del consumo de agua integramos la correspondiente función inversa de demanda.

 

Si phv y phc son los precios por consumo de agua en Venezuela y Colombia respectivamente y “e” denota la relación de precios de bienes y  servicios  no  transables  en los dos países⁵, debe tenerse que phv = phc/e entonces, según (33) y (1):

 

p_hv = d - fq_hv = (a - bq_hc)/e.        (34)

 

Según las condiciones del problema anterior: qh_c = dq_c/A + B. Sustituyendo esta expresión en la anterior se podrá encontrar la relación entre p_hv y q_c (la variable de control):

 

 Phv = [a - b(dq_{c /} A + B)] / e = (aA - bdq_{c -} bAB) / eA ( 35 )

 

Entonces, la renta total por consumo de agua en Venezuela es:

 

 

                                                                                                         

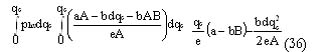
Para obtener la renta agregada total para ambos países se necesita, primero, homologar la expresión (36) con su contraparte que considera el caso colombiano (expresión (13)). Para ello se multiplica (36) por la relación de precios, e, obteniendo, de esa forma, la siguiente expresión:

 

En segundo lugar, se suma al término referente a la renta total o sumatoria de los beneficios por consumo y uso agrícola del agua para Colombia la expresión (36.a) que considera el caso venezolano:

 

Jq_c - Kq_c² / 2 + H                (37)

 

Similarmente a lo hecho en el problema anterior, se deben considerar los costos sociales en que se incurre cuando la cantidad del recurso asignada al consumo es menor que la cantidad demandada. En primer lugar, se debe obtener una expresión para q_hv = ¦(q_c), la cual se obtuvo a partir de p_hv = d - ¦q_hv  = (a - bq_hc)/e de donde se tiene que: 

 

qhv = ( bqhc + ed - a ) / e f            (38)

                                  

Luego, sustituyendo qhc = dqc/A + B en la expresión anterior se obtiene, luego de algunas manipulaciones algebraicas:

 

q_hv = ( bdq_c + bAB + eAd - aA ) / Aef      (39)

 

Para simplificar el ejercicio se llamará L = bd/Aef > 0 y M = (bB + ed - a)/ef; se puede renombrar (39) de la siguiente manera:

 

 q_hv = M - Lq_c.   (39.a)

                        _     

Si se fija como q_hv la cantidad de agua demandada para consumo de la población asentada en la cuenca baja. Se define una función de costos sociales por consumo insatisfecho de la siguiente manera:

                                         _                            _                                        _    

¦₄ ( q_hv -q_hv ) = ¦₄ ) (q_hv - M + Lq_c ) si q_hv < q_hv,      (40)

 

donde ¶¦₄/¶q_c ≥ 0, lo que es muy evidente, pues al incrementarse la cantidad de agua asignada a consumo y uso agrícola en Colombia, se espera que los costos sociales por consumo insatisfecho en Venezuela aumenten pues el recurso remanente en Colombia (qr_c) será menor para un “i” constante.

 

En la expresión (39.a) se tiene que ¶q_hv/¶q_c = -L < 0,  lo que concuerda con nuestros supuestos pues al incrementarse q_c debe disminuir q_hv aumentando los requerimientos no satisfechos en Venezuela, ¦₄,(q_hv - q_hv ) e incrementando los costos sociales por consumo insatisfecho en este país, luego ¶¦₄/¶q_c ≥ 0.

 

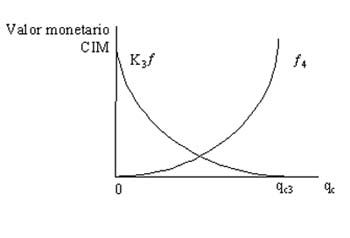
 Figura No. 5 Costos por inundaciones (K ₃ f ) y por consumo

humano insatisfecho (f₄)   en Venezuela

 

Según los supuestos que se han formulado con anterioridad, los costos por inundaciones que se establecieron en la ecuación (32) tienen una relación inversa con qc puesto que, mientras más agua se asigne a Colombia, menos problemas de inundaciones hay en Venezuela. Existirá, entonces, un nivel de qc tan alto que hará reducir a cero los beneficios agrícolas no obtenidos (costos) debido a la presencia de inundaciones en tierras aptas para cultivos en la cuenca baja. Dicho nivel de asignación es designado por q_c3. Mientras menos agua se asigne a la cuenca, alta y media, los problemas de inundaciones en la parte baja son mayores por lo que existirá un costo de inundaciones máximo (CIM) cuando qc sea nulo. El comportamiento de los costos por inundaciones (K₃f) y por consumo humano insatisfecho f₄ es representado por la figura 5 (ver anexo). El comportamiento de f₄ refleja el supuesto de que a medida que qc crece, habrá menos recurso remanente para Venezuela y, por tanto, los costos f4 serán mayores. En la figura 5 se ha optado por representar el caso en que M = (q_hv), es decir, de la ecuación (40) se puede deducir que cuando q_c = 0 y M = (q_hv), los costos f₄ serán nulos; entonces f4 debe partir del origen.

 

En la figura 6 se muestra la representación de los costos marginales por inundaciones (K₃¶f/¶q_c) y por consumo humano insatisfecho en Venezuela (¶f₄/¶q_c) en función de q_c. La derivación de esta gráfica fue hecha de manera similar a la figura 4.

 

 

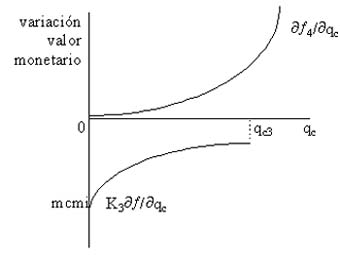
Figura No. 6 Costos marginales por inundaciones (K3¶f/¶qc) y por consumo

 humano insatisfecho (¶ f4/¶qc) en Venezuela

 

 

De manera similar a lo que se concluyó con la figura 5, se puede decir que las funciones derivadas en la figura 6  muestran una relación directa entre   k₃¶¦/¶q_c, ¶f₄/¶q_c y q_c . Para disminuciones en q_c que se supone que se acercan a cero (qc ® 0) se tendrá que ¶f4/¶qc ®  0 y  k₃¶f/¶q_c ® mínimo costo marginal por inundaciones (mcmi).

 

Y a medida que q_c aumenta,  ¶f₄/¶q_c ® ∞ y k₃¶f/¶q_c  ® 0.

 

Procediendo de manera similar a lo hecho con la expresión (36), se debe multiplicar las expresiones (32) y  (40) por la relación de precios (e) a objeto de homologar las expresiones que entran en la función objetivo considerada en el análisis.

 

(40) por la relación de precios (e) a objeto de homologar las expresiones que entran en nuestra función objetivo.

 

Según todo lo anterior, el problema de control óptimo es maximizar:

 

 

 

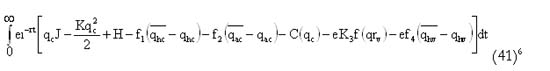
sujeto a:

 

¶ S/¶t = i (t) - q_c q_{hv -} qr_{v =} i (t) - qe -qr_c           (42)

 

En la expresión anterior ¶S/¶t equivale a la variación del stock del recurso en el tiempo, qrv es el caudal remanente para Venezuela a partir del diagrama de distribución de caudales Figura 7 en el que q_b es el caudal base. Entonces, el Hamiltoniano es representado por H y escrito como:

                                             _                     _                                                   _

 H= e₁^-rt[jqc-Kq_c2/2 + H - f1 (qhc - qc ) - f2 (qac - qac ) - C /qc) - eK₃ f(qr_v) -ef₄ (qhv - qhv ) ] +l (i - qc - qhv -qr_v )  (43) 

 

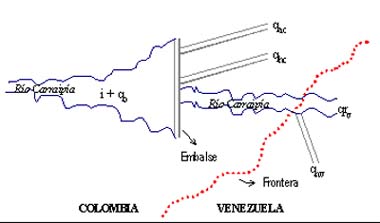
Figura No. 7 Diagrama de Distribución de Caudales

 

 

Si m = e₁^rtl, el Hamiltoniano de valor corriente es:

 

Hc=                                                        (44)

= Jc - Kqc / 2 + H -f ₁(.) - C(q_c) - eK₃ f(.) +m (i-q_c-q_hv-qr_v)  

 

Siguiendo un procedimiento similar al desarrollado en la sección anterior se obtiene la siguiente relación:

 

que es la ecuación que gobierna el comportamiento óptimo del uso del recurso en el tiempo para el manejo del embalse en Colombia y Venezuela, conjuntamente. Dicha expresión, como se puede demostrar y se desprende del trabajo de Sánchez (1998), es equivalente a:

 

 

 

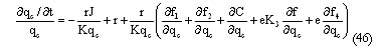
3.2 Comparación entre las tasas de utilización del recurso en ambos escenarios

 

El desarrollo del modelo de asignación óptima del recurso hídrico del embalse al que se ha hecho referencia ha permitido llegar a determinar expresiones para la senda de explotación de dicho recurso bajo los dos escenarios estudiados. En primera instancia, se considera el caso de la utilización del recurso hídrico suponiendo la optimización de los beneficios netos por el uso del agua para Colombia como la función objetivo. Con el empleo de algunos supuestos simplificadores se determinó la senda óptima de utilización del recurso a través del tiempo en las expresiones (29) y (30).

 

De manera similar, se abordó el problema de optimización del uso del agua para el caso en que se supone una función objetivo que integra los beneficios netos de los dos países, Colombia y Venezuela, considerando, de esa forma, un escenario conjunto. De la misma manera en que se hizo para el caso inicial, y con el apoyo de algunos supuestos, se obtuvo la senda óptima de utilización temporal del recurso en las expresiones (45) y (46). Estas ecuaciones, al igual que las anteriores, nos muestran que mayores tasas de descuento social tienden a conllevar una utilización más rápida del recurso. Altas tasas de descuento significan que el “administrador” del recurso prefiere asegurarse los beneficios de la utilización ahora, en lugar de esperar a más tarde.

 

Un descuento positivo del futuro incentiva una explotación más rápida de los recursos naturales.

 

Según las igualdades (29) y (45), a mayor diferencia entre P(t) y ¶C/¶qc el recurso se utiliza de manera más acelerada a través del tiempo pues mayor beneficio marginal, descontando los costos de abastecimiento, se obtendrá con la explotación del mismo.

 

En las expresiones (30) y (46), se observa la relación positiva entre los costos marginales por consumo humano (en ambos escenarios) y uso agrícola insatisfechos    (¶f₁/¶q_c , ¶f₂ /¶q_c, e¶f₄ /¶q_c) con la tasa de explotación del recurso a través del tiempo   lo cual es cierto sabiendo que el cociente r/K > 0. Esta relación es también cierta cuando consideramos el caso de la utilización óptima del recurso para Colombia individualmente puesto que el cociente rA2 /G > 0. Es decir, a medida que dichos costos aumentan, la explotación óptima del recurso declina más lentamente en el tiempo recordando que,  . Esta relación señala que el regulador del recurso prefiere utilizarlo más lentamente a medida que los costos marginales por consumo humano y uso agrícola insatisfecho son mayores (se acercan a cero (0) en el caso de Colombia y tiende a + ∞  en el caso de Venezuela) siendo menores los costos totales sociales en Colombia y mayores en Venezuela. Hay que considerar que cuando se plantea un escenario conjunto para el manejo del recurso hídrico entre los dos países, Venezuela y Colombia, el modelo toma en una sola función objetivo los beneficios y costos de los dos países. Por tanto resulta que, si por ejemplo se incrementan exógenamente los costos marginales (y los totales) por consumo insatisfecho en Venezuela, la senda óptima de utilización del recurso en Colombia se hace más lenta. Lo anterior es evidente por la razón que se acaba de exponer en cuanto a la agregación de los beneficios y costos de Venezuela al suponer el uso conjunto del recurso hídrico.

 

De manera similar hay una relación positiva entre los costos marginales por inundaciones en Venezuela   (eK₃¶f /¶q_c ) y la utilización óptima del recurso a través del tiempo. Es decir, a medida que los costos marginales por inundaciones son mayores (menores los totales) la política óptima a seguir será explotar el recurso menos intensivamente en el tiempo, cuando estamos en el escenario conjunto. O sea, si se tiene que, por ejemplo, q_c aumenta en nuestra política óptima el caudal remanente  en Venezuela (qr_v) será menor lo que conlleva a unos costos marginales por inundaciones mayores según nuestro supuesto de que el caudal remanente (por encima del caudal base) es el que genera problemas de inundaciones en la cuenca baja. En ese caso, la política óptima, como es obvio, será explotar el recurso menos intensivamente al agregarse el efecto tanto de eK₃¶f /¶q_c como de los demás costos marginales en ambos países.

 

 Al incrementarse los costos marginales de abastecimiento del recurso éste se utilizará menos intensivamente en el tiempo, es decir, que el uso óptimo del recurso en el tiempo declina menos rápido tal como se desprende de las ecuaciones (30) y (46). Lo mismo ocurriría para incrementos en la relación de precios (e) en caso de que |K₃¶¦ /¶q_c|<¶f₄ /¶q_c puesto que ello implica que habrá una relación positiva entre el término “e” y la tasa de explotación óptima del escenario conjunto. Por tanto, para empeoramientos en la relación de intercambio de Venezuela y, en consecuencia, mejoramientos en la relación para Colombia que se traducen en incrementos de e, la tasa óptima de utilización del recurso en el escenario conjunto aumentará. Lo anterior indica que, en ese caso, la utilización del recurso será menos intensiva en el escenario conjunto que en el escenario individual ya que Lo contrario ocurre para incrementos en “e” cuando se tiene que |K₃¶f /¶q_c| > ¶f₄ /¶q_c puesto que en ese caso habrá una relación inversa entre “e” y  . Cuando se tiene que |K₃¶f /¶q_c| = ¶f₄/¶q_c las variaciones en la relación “e” no tendrán incidencia sobre la tasa de utilización óptima en el escenario conjunto.

 

Se puede demostrar que, usando las ecuaciones (29) y (45), la diferencia entre las tasas de utilización del recurso entre el caso en que se considera la optimización para Colombia de manera individual y el escenario en que consideramos los dos países de manera conjunta, está dada por:

 

 

 

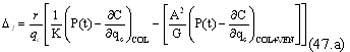
Por otra parte, empleando las expresiones (30) y (46), se tiene que:

 

 

 

A partir de las ecuaciones (47.a) y (47.b), se pueden determinar las condiciones bajo las cuales la diferencia entre la senda de utilización del recurso en Colombia y en el escenario conjunto, D1,es mayor, igual o menor a cero. Como se puede comprobar, dichas condiciones se pueden resumir en:

 

 

 

 

 

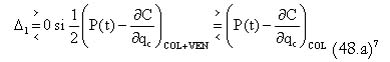
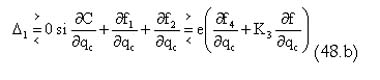
Según la condición (48.a), el caso en el que Δ₁ > 0     (Δ₁ = 0) implica que la diferencia entre P(t), el beneficio marginal del consumo, y ¶C/¶q_c, el costo marginal de abastecimiento del recurso en el escenario individual, es menor (igual) a la misma diferencia en el escenario conjunto dividida entre dos, es decir, el beneficio marginal del consumo descontando los costos marginales de abastecimiento para cada país. En ese caso, el uso óptimo del recurso en el escenario conjunto declina más (igual de) rápido en el tiempo que el uso óptimo del escenario individual. Puesto que, por definición, P(t) - ¶C/¶q_c = costo de uso o precio sombra del stock del recurso, según la condición (48.a), Δ₁ > 0 si ½(precio sombra)^col+ven > (precio sombra)col lo cual implica que (precio sombra)col+ven > (precio sombra)col. Lo anterior  lleva a que, dado un nivel inicial del stock del recurso, a una tasa de declinación más rápida en el uso del recurso sobre el tiempo, mayor será el uso del recurso en los primeros momentos. Como resultado menor va a ser la cantidad del recurso remanente haciendo que su valor económico, su precio sombra en el escenario conjunto, sea mayor. Todo lo contrario si Δ₁ < 0.

 

La condición (48.b) indica que Δ₁ > 0 ( Δ₁ = 0) si la diferencia entre los costos marginales de abastecimiento y los costos marginales por consumo y uso agrícola insatisfechos en Colombia es mayor (igual) a la diferencia entre los costos marginales por consumo insatisfecho y por inundaciones en Venezuela. En ese caso, la tasa óptima de utilización del recurso en Colombia, individualmente, declinará menos (igual de) rápido que la tasa óptima del escenario conjunto, dejando un mayor caudal remanente para la cuenca baja. Por tanto, para que ello ocurra, se debe tener que en el margen, los costos de abastecimiento descontados los costos por demandas insatisfechas en Colombia, superen (igualen) a los costos por consumo insatisfecho menos los costos de inundaciones en Venezuela. Lo anterior es evidente pues señala que el “administrador” del recurso utilizará el mismo de una manera menos intensiva, en el escenario individual, si en el margen el costo “neto” de abastecer el recurso para Colombia resulta ser mayor que el costo “neto” de su escasez en Venezuela.

 

En el caso del manejo conjunto del recurso, la explotación se haría más intensiva en el tiempo pues no sólo se consideran los costos “netos” del abastecimiento sino los costos “netos” de su escasez en Venezuela (que son bajos cuando aumentan los problemas de inundaciones). En el caso de que Δ₁  < 0, la explotación óptima del recurso individualmente es más intensiva pues, en el margen, los costos “netos” del abastecimiento en Colombia son menores a los costos “netos” de su escasez en Venezuela. Por tanto, en el escenario conjunto, la explotación del recurso es menos intensiva (dejando un mayor remanente del recurso para la cuenca baja) pues el modelo considera los costos sociales por demanda insatisfecha en Venezuela.

 

El anterior análisis lleva a plantearse las tendencias subyacentes en el manejo del recurso cuando el “administrador” del mismo se enfrenta a dos condiciones exógenas al modelo pues dependen de las características climáticas de la cuenca. Dichas condiciones, como se ha señalado en el planteamiento del problema, están dadas por la alternación de períodos de sequía y períodos lluviosos a lo largo del año. Sólo se puede hablar de tendencias al comparar la mayor o menor intensidad del manejo del recurso hídrico en cada escenario pues, como se ha planteado arriba, las condiciones (48.a) y (48.b) dependen de la magnitud de los parámetros e y K y de un conjunto de variables (como los costos marginales de abastecimiento, etc.). Dichas magnitudes son dinámicas y, con sus modificaciones, pueden alterar completamente los resultados. Por tanto resulta difícil determinar, a ciencia cierta, cual escenario es más intensivo en el uso del recurso. Sin embargo, se puede señalar que:

 

•  En época de lluvias, los costos por inundaciones son el problema predominante haciendo que la explotación conjunta tienda a ser más intensiva que la individual (Δ₁  > 0). Como es evidente cuando el modelo considera en el escenario conjunto dichos costos, el recurso debe ser explotado más intensivamente en la cuenca alta y media reduciendo el caudal remanente para la cuenca baja.

 

•  En época de sequía son los costos por consumo insatisfecho los que predominan haciendo que, como es de esperar, la explotación individual tienda a ser más intensiva que la conjunta (D1 < 0), lo cual también es un resultado esperado.

 

 

Conclusiones y recomendaciones

 

La sensibilidad de la tasa de explotación del recurso ante cambios en los costos de Colombia será menor cuando se supone un escenario integracionista, esto nos sugiere la existencia de efectos negativos para Colombia al producirse un proceso de explotación del recurso hídrico con Venezuela. Es decir, bajo los supuestos que hemos mencionado, para Colombia plantearse un escenario conjunto en el uso del recurso significa, por ejemplo, que la explotación óptima del agua será menos intensiva en el tiempo si los costos totales por consumo insatisfecho aumentan (los marginales disminuyen). Lo mismo ocurriría para disminuciones en los costos marginales de abastecimiento y/o de uso agrícola insatisfecho. Lo anterior indica la existencia de efectos negativos para Colombia en el marco integracionista pues se está “ponderando” con menor peso cualquier cambio en los costos en la cuenca alta y media. En ese sentido, bajo los supuestos señalados, los resultados del modelo de optimización llevan a establecer como no recomendable para Colombia la integración en el uso del recurso hídrico si sólo se considera la menor sensibilidad de la tasa de explotación del agua frente a las variaciones en los costos de la cuenca alta y media.         

 

Se espera para ambos países aumentos en los costos por consumo insatisfecho (disminución de los costos marginales en Colombia) debido a la menor “oferta” del recurso que puede ocurrir una vez el embalse entre en operación pero se presente, por ejemplo, una sequía mayor de lo normal. En cuanto a Venezuela, el impacto de emplearse por parte de Colombia un proceso conjunto de explotación del agua significa que las variaciones en los costos marginales de inundaciones y de consumo humano insatisfecho en la cuenca baja van a incidir en la tasa de explotación del recurso. En ese caso un aumento en los costos marginales por consumo humano insatisfecho en la cuenca baja debido a, por ejemplo, un aumento poblacional en Venezuela significaría que el agua se explote menos intensivamente en Colombia. El efecto es que en el escenario integrado, habrá más recurso hídrico disponible para los requerimientos de la población residente en Venezuela. Debe recordarse que, debido al efecto de la variación en los costos marginales en la cuenca alta cuando el recurso es escaso, es más probable que la tasa de explotación óptima del recurso de manera individual sea más intensiva que la conjunta. Se tendrá, entonces, que para Venezuela una explotación conjunta del agua regulada por el embalse es conveniente cuando el recurso disponible esté en disminución puesto que habrá más posibilidad de acceso al mismo. Hay que hacer la salvedad del caso en que se estén presentando problemas de inundaciones en cuya situación la explotación conjunta tiende a ser más intensiva que la individual por lo que el caudal remanente para Venezuela es menor, aminorando así los problemas de inundaciones. 

 

En cualquiera de las dos condiciones exógenas (inundaciones o sequía), los resultados del modelo sugieren entonces efectos positivos para Venezuela al plantearse un manejo conjunto del recurso hídrico. Lo anterior unido a las consideraciones acerca del efecto del escenario integracionista en Colombia, conduce a plantear como necesario para Venezuela el lograr acuerdos binacionales para el uso conjunto del recurso hídrico. En cuanto a Colombia, se podría plantear asumir un escenario de manejo integrado a cambio de obtener, por parte de Venezuela, ayuda financiera, asistencia técnica, etc. para la conservación de la cuenca y el funcionamiento del Embalse.

 

Notas 

 

 

Referencias bibliográficas

 

1. BROWN, J. R. G.; Deacon, R. 1972. “Optimization of a single-cell aquifer”. En: Water Resources Research, 8: 557-564.        [ Links ]

 

2. BURT, O. 1967. “Temporal allocation of groundwater”. En: Water Resources Research, 3: 45-56.        [ Links ]

 

3. CARLSON, Gerald; Zilberman, David; Miranowski, John. 1993. Agriculture and Natural Resources Economics.        [ Links ]

 

4. CHIANG, Alpha C. 1987. Métodos Fundamentales de Economía Matemática. Tercera edición. México: Mc Graw Hill.

 

5. COMITÉ TÉCNICO BINACIONAL (COLOMBIA-VENEZUELA). 1991. Estudio Conjunto del Aprovechamiento Integral y Conservación de los Recursos Hídricos del Río Carraipía-Paraguachón.         [ Links ]

 

6. CONRAD, Jon; Clark, Colin. 1987. Natural Resource Economics-Notes and Problems. Cambridge: Cambridge University Press.

 

7. CORPORACIÓN AUTÓNOMA REGIONAL DE LA GUAJIRA (CORPOGUAJIRA). 1995. Aprovechamiento Integral y Conservación de los Recursos Hídricos del Río Carraipía-Paraguachón. Colombia: Corpoguajira.

 

8. CORPORACIÓN AUTÓNOMA REGIONAL DE LA GUAJIRA (CORPOGUAJIRA). 1994. Estudio de Factibilidad Embalse La Chingolita. Colombia: Corpoguajira.

 

9. DEEB, Alejandro. 1975. Comparison of Decision-Making Structures for Decentralized Water Resource Allocation. Massachusetts: Harvard University.

 

10. GIBBONS, Robert. 1993. Un Primer Curso de Teoría de Juegos. Barcelona (España): Antoni Bosh Editor.

 

11. GISSER, M.; Sánchez, D.A. 1980. “Competition versus optimal control in groundwater pumping”. En: Water Resources Research, 16(4): 638-642.        [ Links ]

 

12. KNAPP, K. C. and E. Feirnerman. 1985. “The optimal steady-state in groundwater management”. En: Water Resources Research, 21(6): 967-975.

 

13. SÁNCHEZ, José M. 1998. Modelo de Asignación Óptima del Recurso Hídrico en un Escenario Binacional. Trabajo de grado para optar al título de Joint Master in Environmental Economics and Natural Resources (UNIANDES-University of Maryland). Bogotá: UNIANDES, CEDE.