Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Bioagro
versión impresa ISSN 1316-3361
Bioagro v.17 n.1 Barquisimeto ene. 2005
OPTIMIZACIÓN DE LA MADURACIÓN DEL CAMBUR CV. MANZANO (Musa sp. (L.) AAB) PARA USO INDUSTRIAL
Tonny García1
1 Dpto. de Ecología y Control de Calidad. Decanato de Agronomía, Universidad Centroccidental "Lisandro Alvarado". Apdo. 400. Barquisimeto. Venezuela.
RESUMEN
El proceso de maduración del cambur cv. Manzano para uso industrial se optimizó aplicando la metodología de superficie de respuesta, mediante un diseño compuesto central ortogonal (DCCO) para tres factores (temperatura, dosis de ethephon y tiempo de almacenamiento), con ocho tratamientos en la porción cúbica, seis en la estrella y seis repeticiones del punto central, con una distancia axial a de 1,525 unidades, para un total de quince tratamientos, en tres repeticiones del ensayo, Las respuestas cuantificadas fueron pH, acidez titulable y contenido de sólidos solubles (SST). Los rangos de trabajo de las variables independientes fueron 18-28 ± 1ºC de temperatura; 1000-3000 mg∙L-1 de ethephon; 24 a 144 h de almacenamiento. Con base al análisis matemático el mínimo de pH (4,25) se alcanzó con 25,7 °C, 2081 mg∙L-1 de ethephon y 118 h de almacenamiento. No se pudo establecer el punto crítico para la acidez titulable y SST ya que se obtuvieron máximos matemáticos con valores fuera de la región experimental.
Palabras clave adicionales: Poscosecha, banano, almacenamiento
ABSTRACT
Optimization of banana cv. Manzano (Musa sp. (L.) AAB) ripening for industrial use
The ripening process of the banana cv. Manzano for industrial use was optimized using response surface methodology with an orthogonal central composite design (OCCD) of three factors (temperature, ethephon dosage, and storage time), with eigth treatments in the cubic portion, six in the star position, and six replications of the central point, with axial statistics a of 1.525, for a total of 15 treatments with three replications of the assay. The quantified responses were pH, acidity, and total soluble solids (TSS). The working ranges of the independent variables were 18-28 ºC ± 1 ºC for temperature; 1000-3000 mg∙L ethephon; 24 to 144 h of storage. Based on mathematical analysis, the minimum pH (4.25) was reached at 25.7 ˚C, 2081 mg∙L-1 of ethephon, and 118 h of storage time. No critical points were established for the acidity and TSS because mathematical maxima were obtained out of the experimental region.
Additional key words: Postharvest, banana, storage
Recibido: Mayo 6, 2004 Aceptado: Abril 8, 2005
INTRODUCCIÓN
Las investigaciones en inducción de maduración de frutos climatéricos como el cambur cv. Manzano reportados por la literatura se refieren a la maduración del fruto para consumo fresco (Flores, 2000), siendo escasos los estudios realizados bajo diseños estadísticos que faciliten optimizar el proceso, y que le permitan a la industria disponer de herramientas de predicción de condiciones óptimas de maduración para satisfacer las exigencias de calidad de procesamiento como son: tiempos cortos de maduración de frutos fisiológicamente maduros, alto contenido de sólidos solubles totales (SST), alta acidez y bajo pH (Rosales et al., 1999; Ávila y Fuentes, 2004).
Las condiciones de calidad de la materia prima son críticas en la producción de pulpa de frutas industrializadas, ya que ésta debe ser estándar, homogénea y continua en el tiempo; durante su producción y así mantener su calidad de mercado (denominación de origen). Por ello, las empresas industriales han instalado cámaras de maduración refrigeradas, con el objetivo de comprar frutos fisiológicamente maduros, que puedan madurarse hasta las condiciones óptimas requeridas. Aún con estas consideraciones, en estas empresas persiste el problema ya que los ensayos de prueba y error o algunos diseños básicos usados no permiten modelar y predecir dichas condiciones.
Las encuestas a nivel industrial del porqué esto persiste, reportan que se debe a la falta de soporte técnico en cuanto a diseño y análisis experimental aplicado, y si existe no conoce, y/o no maneja programas estadísticos.
En la industria, en general, la metodología de superficie de respuesta (MSR) ha estado utilizándose cada vez más; sin embargo, en la agroindustria de la poscosecha de vegetales, se han estado aplicando incipientemente diseños o arreglos factoriales, los cuales permiten modelar, pero tienen la desventaja de que el número de tratamientos aumenta considerablemente cuando se incrementan los factores y más aún cuando se aumentan los niveles de éstos, llegando incluso a imposibilitar el desarrollo de la investigación, ya que se hacen muy costosos en economía y tiempo. (Saguy, 1982; Montgomery, 1991; Chacín, 2000).
Dadas las consideraciones y problemas anteriormente encontrados a nivel industrial, los objetivos de esta investigación fueron la aplicación del diseño y análisis de metodología de superficie de respuesta en la optimización del proceso de maduración del cambur cv. Manzano ante diferentes niveles de temperatura, tiempo de almacenamiento y dosis del regulador de crecimiento ethephon bajo condiciones controladas.
MATERIALES Y MÉTODOS
El material vegetal utilizado fueron tres racimos de cambures cv. Manzano, en madurez fisiológica, cosechados en el sector La Palma, municipio San Carlos, estado Cojedes. Los frutos sanos recolectados manualmente se transportaron al Laboratorio de Ingeniería y Tecnología de Alimentos de la Universidad Nacional Experimental de los Llanos Ezequiel Zamora, en la ciudad de San Carlos. A los racimos les fueron descartados un par de manos de cada extremo, dejando para el ensayo las del centro; estos últimos fueron preenfriados con agua a 25 °C por 24 horas para extraer el calor de campo.
Trascurrido el pre-enfriamiento los dedos de cambur se lavaron con agua fresca y se procedió a aplicar los 15 tratamientos (Cuadro 1), según lo establecido en la matriz de diseño (Cuadro 2). La unidad experimental fue un dedo de cambur, cada tratamiento se midió por triplicado, aunque en cada caja de cada tratamiento se colocaron 10 dedos para extraer muestras aleatorias. El experimento se repitió completamente en el tiempo, uno cada 30 días.
Cuadro 1. Niveles codificados y naturales de las cinco dosis de cada tratamiento de los tres factores experimentales
| Factores experimentales | Niveles codificados/naturales | ||||
| -α -1,5225 | -1 | 0 | +1 | +α +1,5225 | |
| X1=Temperatura (°C) | 18 | 19,72 | 23 | 26,28 | 28 |
| X2=Ethephon (mg∙L-1) | 1000 | 1344 | 2000 | 2656 | 3000 |
| X3=Tiempo de almacen. (h) | 24 | 45 | 84 | 123 | 144 |
El producto comercial Ethrel (ácido 2-cloro etilfosfónico) cuyo i.a. es el ethephon, se diluyó en agua en dosis según cada tratamiento (Cuadro 1) agregando surfactante y regulando el pH de la solución a 5,5 para permitir la liberación lenta del etileno; luego se sumergieron los cambures por un minuto, se extrajeron y se colocaron en cajas de cartón distribuidas en los niveles de tratamientos (cinco cavas). Las condiciones de saneamiento de gases de almacenamiento se mantuvieron con un flujo de aire fresco de 1,28 m∙s-1, manteniéndo una humedad relativa de 87 ± 2%.
Una vez transcurrido el tiempo de almacenamiento indicado en la matriz de diseño, se tomaron tres dedos al azar, a los cuales se les determinó pH, acidez y sólidos solubles totales (SST) de la pulpa.
Los SST se determinaron según la norma COVENIN (1977) para frutas. El pH y la acidez titulable total se determinaron según Merck (1972).
El diseño estadístico fue un compuesto central ortogonal (DCCO), completamente repetido, para tres factores de estudio, a cinco niveles cada uno; con ocho tratamientos en la porción cúbica, seis en la porción estrella y seis repeticiones del punto central, para un total de quince tratamientos; la distancia axial para la ortogonalidad fue a = 1,525.
El rango de las dosis para la temperatura se definió entre 18 a 28 ± 1 °C, ethephon de 1000 a 3000 mg∙L-1 y el tiempo de almacenamiento de 24 a 144 h. La conversión de los niveles codificados (-α -1 0 +1 +α) a niveles naturales, se calculó por interpolación utilizando α de 1,525; sin embargo, el valor natural del punto central no fue la media aritmética entre las dosis extremas de máxima y mínima (Cuadro 1).
Cuadro 2. Matriz de respuestas según diseño de tratamientos DCCO para tres factores a cinco niveles cada uno, con 2k = 8, 2k = 6 y n0 = 6; con α para ortogonalidad de 1,525
| Respuestas | Factores de estudio | |||||||||
| pH | Acidez titulable (ml NaoH 0,01N) | SST (%) | Temperatura (°C) | Ethephon (mg∙L-1) | Tiempo (h) | |||||
| Trat. Rep. | Código | Natural | Código | Natural | Código | Natural | ||||
| 1 | 1 | 6,00 | 4,80 | 3,00 | -1 | 19,72 | -1 | 1344 | -1 | 45 |
| 2 | 1 | 5,65 | 4,80 | 6,80 | -1 | 19,72 | -1 | 1344 | +1 | 123 |
| 3 | 1 | 6,15 | 4,80 | 3,60 | -1 | 19,72 | +1 | 2656 | -1 | 45 |
| 4 | 1 | 5,90 | 5,50 | 6,00 | -1 | 19,72 | +1 | 2656 | +1 | 123 |
| 5 | 1 | 6,00 | 4,60 | 4,20 | +1 | 26,28 | -1 | 1344 | -1 | 45 |
| 6 | 1 | 4,55 | 11,80 | 19,00 | +1 | 26,28 | -1 | 1344 | +1 | 123 |
| 7 | 1 | 6,00 | 4,80 | 5,00 | +1 | 26,28 | +1 | 2656 | -1 | 45 |
| 8 | 1 | 4,55 | 11,60 | 19,00 | +1 | 26,28 | +1 | 2656 | +1 | 123 |
| 9 | 1 | 5,80 | 4,60 | 4,20 | - α | 18,00 | 0 | 2000 | 0 | 84 |
| 10 | 1 | 4,70 | 9,30 | 18,00 | + α | 28,00 | 0 | 2000 | 0 | 84 |
| 11 | 1 | 4,90 | 8,80 | 9,90 | 0 | 23,00 | - α | 1000 | 0 | 84 |
| 12 | 1 | 4,60 | 9,90 | 15,00 | 0 | 23,00 | + α | 3000 | 0 | 84 |
| 13 | 1 | 6,20 | 4,00 | 1,80 | 0 | 23,00 | 0 | 2000 | - α | 24 |
| 14 | 1 | 4,60 | 15,30 | 21,60 | 0 | 23,00 | 0 | 2000 | + α | 144 |
| 15 | 1 | 4,65 | 8,90 | 12,00 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 1 | 4,75 | 8,30 | 9,60 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 1 | 4,50 | 11,10 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 1 | 4,60 | 10,60 | 15,00 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 1 | 4,60 | 10,80 | 16,60 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 1 | 4,60 | 10,60 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 1 | 2 | 6,15 | 5,10 | 3,00 | -1 | 19,72 | -1 | 1344 | -1 | 45 |
| 2 | 2 | 5,80 | 4,80 | 6,00 | -1 | 19,72 | -1 | 1344 | +1 | 123 |
| 3 | 2 | 6,10 | 4,30 | 3,00 | -1 | 19,72 | +1 | 2656 | -1 | 45 |
| 4 | 2 | 5,80 | 4,70 | 6,00 | -1 | 19,72 | +1 | 2656 | +1 | 123 |
| 5 | 2 | 6,15 | 5,10 | 3,60 | +1 | 26,28 | -1 | 1344 | -1 | 45 |
| 6 | 2 | 4,55 | 13,00 | 19,80 | +1 | 26,28 | -1 | 1344 | +1 | 123 |
| 7 | 2 | 6,00 | 4,70 | 4,80 | +1 | 26,28 | +1 | 2656 | -1 | 45 |
| 8 | 2 | 4,55 | 13,70 | 21,00 | +1 | 26,28 | +1 | 2656 | +1 | 123 |
| 9 | 2 | 5,95 | 4,60 | 3,90 | - α | 18,00 | 0 | 2000 | 0 | 84 |
| 10 | 2 | 4,70 | 10,60 | 21,00 | + α | 28,00 | 0 | 2000 | 0 | 84 |
| 11 | 2 | 4,70 | 10,60 | 9,65 | 0 | 23,00 | - α | 1000 | 0 | 84 |
| 12 | 2 | 4,60 | 11,20 | 16,20 | 0 | 23,00 | + α | 3000 | 0 | 84 |
| 13 | 2 | 6,10 | 3,90 | 1,80 | 0 | 23,00 | 0 | 2000 | - α | 24 |
| 14 | 2 | 4,60 | 15,20 | 21,60 | 0 | 23,00 | 0 | 2000 | + α | 144 |
| 15 | 2 | 4,60 | 10,40 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 2 | 4,75 | 8,70 | 10,20 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 2 | 4,55 | 11,10 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 2 | 4,60 | 12,40 | 15,00 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 2 | 4,65 | 10,10 | 12,00 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 2 | 4,60 | 11,10 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 1 | 3 | 6,00 | 4,80 | 3,00 | -1 | 19,72 | -1 | 1344 | -1 | 45 |
| 2 | 3 | 5,70 | 4,60 | 6,60 | -1 | 19,72 | -1 | 1344 | +1 | 123 |
| 3 | 3 | 6,20 | 5,00 | 3,60 | -1 | 19,72 | +1 | 2656 | -1 | 45 |
| 4 | 3 | 5,90 | 5,50 | 6,00 | -1 | 19,72 | +1 | 2656 | +1 | 123 |
| 5 | 3 | 6,05 | 4,35 | 3,60 | +1 | 26,28 | -1 | 1344 | -1 | 45 |
| 6 | 3 | 4,55 | 12,70 | 19,80 | +1 | 26,28 | -1 | 1344 | +1 | 123 |
| 7 | 3 | 6,00 | 5,00 | 5,80 | +1 | 26,28 | +1 | 2656 | -1 | 45 |
| 8 | 3 | 4,55 | 16,00 | 20,80 | +1 | 26,28 | +1 | 2656 | +1 | 123 |
| 9 | 3 | 5,95 | 4,70 | 3,90 | - α | 18,00 | 0 | 2000 | 0 | 84 |
| 10 | 3 | 4,70 | 11,00 | 20,80 | + α | 28,00 | 0 | 2000 | 0 | 84 |
| 11 | 3 | 4,90 | 10,00 | 9,40 | 0 | 23,00 | - α | 1000 | 0 | 84 |
| 12 | 3 | 4,60 | 10,70 | 16,80 | 0 | 23,00 | + α | 3000 | 0 | 84 |
| 13 | 3 | 6,10 | 3,90 | 1,80 | 0 | 23,00 | 0 | 2000 | - α | 24 |
| 14 | 3 | 4,60 | 16,10 | 22,80 | 0 | 23,00 | 0 | 2000 | + α | 144 |
| 15 | 3 | 4,75 | 9,10 | 10,80 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 3 | 4,75 | 8,70 | 40,80 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 3 | 4,75 | 7,80 | 10,20 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 3 | 4,55 | 10,60 | 15,00 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 3 | 4,60 | 10,40 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
| 15 | 3 | 4,65 | 10,30 | 14,40 | 0 | 23,00 | 0 | 2000 | 0 | 84 |
Los análisis estadísticos se realizaron con los programas SAS v.08, Statistica v.06 y JMP v. 04. El SAS se utilizó en la determinación de las sumas de cuadrados de las fuentes de variación para contrastar la calidad de los coeficientes regresores del modelo (Jennrich y Sampson, 1976). El programa Statistica se utilizó para obtener los coeficientes regresores del modelo cuadrático, las pruebas de t de student, así como la representación gráfica de éstos, en superficies de respuestas tridimensionales.
El JMP se utilizó para el proceso de optimización, aplicando procedimientos de perfiles de respuestas múltiples bidimensionales por superposición de las gráficas de contornos (Derringer y Suich, 1980).
En las pruebas de inferencia para determinar la significancia estadística se utilizó la prueba de F.
RESULTADOS Y DISCUSIÓN
Optimización para respuestas individuales
El Cuadro 2 muestra la matriz con el vector de tratamientos, repeticiones, los vectores para las respuestas medidas y la matriz de diseño de tratamientos con valores codificados y valores naturales.
Análisis preliminar de las correlaciones canónicas y predictibilidad
El Cuadro 3 muestra la matriz de correlación aumentada para la respuesta pH donde se observa que no existe correlación entre las variables predictoras, indicando que no hay dependencia lineal y se descarta la multicolinealidad.
Cuadro 3. Matriz de correlación para el modelo poblacional fijado para la respuesta pH (Y), acidez titulable (Z) y SST (W)
| Y | Z | W | X1 | X2 | X3 | X11 | X22 | X33 | X12 | X13 | X23 | |
| Y | 1,000 | |||||||||||
| Z | -0,920 | 1,000 | ||||||||||
| W | -0,902 | 0,960 | 1,000 | |||||||||
| X1 | -0,416 | 0,453 | 0,533 | 1,000 | ||||||||
| X2 | -0,016 | 0,054 | 0,116 | -0,000 | 1,000 | |||||||
| X3 | -0,557 | 0,636 | 0,666 | 0,000 | 0,000 | 1,000 | ||||||
| X11 | 0,415 | -0,351 | -0,171 | 0,000 | 0,000 | -0,000 | 1,000 | |||||
| X22 | 0,142 | -0,100 | -0,129 | -0,000 | 0,000 | -0,000 | 0,000 | 1,000 | ||||
| X33 | 0,446 | -0,139 | -0,171 | 0,000 | -0,000 | -0,000 | -0,005 | -0,005 | 1,000 | |||
| X12 | -0,038 | 0,026 | 0,027 | 0,000 | 0,000 | -0,000 | 0,000 | 0,000 | 0,000 | 1,000 | ||
| X13 | -0,280 | 0,376 | 0,306 | -0,000 | 0,000 | 0,000 | -0,000 | -0,000 | -0,000 | -0,000 | 1,000 | |
| X23 | 0,014 | 0,042 | -0,019 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 1,000 |
Otra observación importante es que existe alta correlación entre el pH y la acidez (ρ = -0,92) y entre el pH y los SST (ρ = -0,902). Esto indica que en la práctica se podrían predecir los cambios de la acidez titulable y de los SST con sólo determinar el pH (acidez iónica). Además se podría estimar la acidez en función de los sólidos solubles totales (ρ = +0,96).
Análisis de las raíces latentes (l ij) y vectores latentes (g 0j) para pH, acidez titulable total y sólidos solubles totales
pH: Se detectó que las variables del modelo con baja correlación con la respuesta pH fueron: X2 (ethephon), su término cuadrático X22 y las interacciones X12 y X23. Estas bajas correlaciones indican la potencialidad de reducir los componentes del modelo; sin embargo, esto requeriría un estudio previo de las raíces latentes y los vectores propios; aplicando análisis multivariado de componentes de varianza (Cuadro 4) a la matriz "X" centrada y escalada.
El Cuadro 4 muestra que únicamente el componente susceptible de extraer del modelo pH seria el factor X23, ya que presenta un valor propio o raíz latente baja (0,02164), lo que indica que este factor presenta una dependencia lineal con las otras variables predictoras; y si se extrae, el modelo explicaría el 99,78 % de la varianza total. El predictor más influyente es X1 (temperatura), con 19,76%; los demás explican en proporciones similares de ±10%.
Cuadro 4. Raíces latentes (l ij) y vectores latentes (g 0j) para la respuesta pH.
| Valor propio l ij | Varianza total % | Y g yj | X1 g 1j | X2 g 2j | X3 g 3j | X11 g 11j | X22 g 22j | X33 g 33j | X12 g 12j | X13 g 13j | X23 g 23j | |
| 1 | 1,9758 | 19,76 | 0,71 | -0,00 | -0,00 | 0,00 | -0,00 | -0,00 | -0,00 | -0,00 | -0,00 | -0,71 |
| 2 | 1,0068 | 10,07 | -0,30 | 0,02 | 0,10 | -0,81 | 0,01 | -0,00 | -0,17 | -0,14 | -0,33 | -0,30 |
| 3 | 1,0000 | 10,00 | -0,01 | 0,001 | -0,02 | -0,19 | -0,01 | -0,14 | 0,97 | -0,01 | -0,01 | -0,01 |
| 4 | 1,0000 | 10,00 | -0,40 | 0,02 | -0,02 | 0,46 | -0,02 | 0,45 | 0,14 | -0,19 | -0,44 | -0,40 |
| 5 | 1,0000 | 10,00 | 0,30 | -0,52 | 0,00 | 0,00 | 0,00 | -0,00 | -0,00 | -0,69 | -0,29 | 0,30 |
| 6 | 1,0000 | 10,00 | 0,10 | -0,50 | -0,00 | -0,00 | -0,00 | 0,00 | 0,00 | 0,68 | -0,51 | 0,10 |
| 7 | 1,0000 | 10,00 | 0,32 | 0,69 | -0,00 | 0,00 | -0,00 | -0,00 | 0,00 | -0,00 | -0,56 | 0,32 |
| 8 | 0,9998 | 9,99 | -0,03 | 0,00 | 0,94 | 0,15 | 0,21 | -0,20 | 0,02 | -0,01 | -0,03 | -0,03 |
| 9 | 0,9957 | 9,96 | -0,20 | 0,01 | -0,23 | 0,25 | -0,06 | -0,86 | -0,09 | -0,09 | -0,22 | -0,20 |
| 10 | 0,0216 | 0,22 | 0,01 | -0,00 | 0,22 | 0,00 | -0,98 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 |
Para la singularidad de la matriz de diseño "X" y la capacidad de predicción del modelo se examinaron las raíces latentes con sus correspondientes vectores latentes, según Webster et al. (1974). Se observa que la raíz latente 10, l 10 = 0,0216 < 0,05 y el vector propio g yj =0,009 < 0,01, indican que la interacción X23, causa problemas de singularidad por tanto es susceptible de extraerlo del modelo.
El resto de las raíces latentes fueron altas indicando una alta predictibilidad del modelo, aun con algunos valores bajos de su respectivo vector latente (g yj).
Acidez titulable total y SST: Al analizar las raíces y vectores latentes se encontró que los factores X2, X22, X33, X12 y X23 tuvieron baja correlación con la respuesta acidez titulable; teniendo la mayor correlación el factor X3 (ρ = 0,636) seguido de X1 (ρ = 0,453), y la interacción X13, estimándose que el componente más susceptible de ser extraído del modelo de acidez titulable fue X23, ya que presentó un valor propio o raíz latente baja (0,046467). Esto indica que este factor presenta una dependencia lineal con las otras variables predoctoras, y si se extrae, el modelo explicaría el 99,54 % de la varianza total. Así mismo, se estableció que el componente que más influyó fue X1 (temperatura), con 19,53%; los demás explicarían en proporciones similares de ±10%.
La raíz latente 10, l 10= 0,046 < 0,05 y el vector propio g yj = 0,031 > 0,01 indican que la interacción X23 no causa problemas de singularidad, por tanto es susceptible de dejarla participar en el modelo. El resto de las raíces latentes fueron altas, lo que indica la alta predictibilidad del modelo, aun con algunos valores bajos de su respectivo vector latente (g yj).
Con respecto al estudio de las raíces y vectores latentes sobre el modelo para sólidos solubles se determinó que el componente susceptible de extraer del modelo de SST fue X23, ya que presenta un valor propio bajo (l 10=0,045548). Esto indica que este factor presenta una dependencia lineal con las otras variables predoctoras, y si se extrae, el modelo explicaría el 99,54 % de la varianza total. El componente que más influyó fue X1 (temperatura) con 19,54%; los demás explicarían en proporciones similares de ±10%.
La raíz latente 10, l 10 = 0,0455 < 0,05 y el vector propio g yj = 0,014 > 0,01, indica que la interacción X23, no causa problemas de singularidad y que puede permitirse su participación en el modelo. El resto de las raíces latentes fueron altas, lo que indica una alta predictibilidad del modelo, tal como en el caso de la acidez.
Análisis de la varianza para el modelo poblacional fijado
El análisis de las fuentes de variación para las respuestas pH, acidez titulable y SST se muestra en el Cuadro 5. Se observa una alta significancia de los tratamientos y la regresión fue altamente significativa con R2 de 95,53%, 87,80% y 89,85%, respectivamente. Sin embargo, la falta de ajuste en la respuesta pH fue significativa, indicativo de que podrían probarse otros modelos. A pesar de ello, debe observarse que quizás el problema estuvo en el bajo valor del cuadrado medio del error experimental, por lo que se continuó el análisis con los modelos fijados. El coeficiente de variación para las respuestas pH, acidez titulable y sólidos solubles fue de 1,37, 8,56 y 5,67%, respectivamente, ubicándose dentro de los rangos deseables (Chacín, 1998).
Cuadro 5. Probabilidad de significancia de las fuentes de variación del ANAVAR para las respuesta pH, acidez titulable total y sólidos solubles totales, para el modelo cuadrático poblacional del ensayo completamente repetido
| Fuente de variación | pH | Acidez titulable total | SST |
| Tratamientos | 0,00000 ** | 0,00000 ** | 0,00000 ** |
| Regresión | 0,00000 ** | 0,00000 ** | 0,00000 ** |
| 1er Orden | 0,00000 ** | 0,00233 ** | 0,00000 ** |
| X1 ( °C) | 0,00000 ** | 0,00000 ** | 0,00001 ** |
| X2 ( mg× L-1) | 0,02038 * | 0,40986 ns | 0,00000 ** |
| X3 ( h) | 0,00000 ** | 0,00000 ** | 0,00000 ** |
| 2do Orden | 0,00000 ** | 0,00000 ** | 0,00620 ** |
| X12 | 0,00000 ** | 0,00000 ** | 0,02523 * |
| X22 | 0,00000 ** | 0,01553 * | 0,06197 ns |
| X32 | 0,00000 ** | 0,00777 ** | 0,022212 * |
| Interacciones | 0,00000 ** | 0,00000 ** | 0,00000 ** |
| X1 ´ X2 | 0,00853 ** | 0,24019 ns | 0,65030 ns |
| X1 ´ X3 | 0,00000 ** | 0,00000 ** | 0,00677 ** |
| X2 ´ X3 | 0,32290 ns | 0,72113 ns | 0,65030 ns |
| Falta de ajuste | 0,00000 ** | 0,07300 ns | 0,05222 ns |
| Repetición | 0,67278 ns | 0,22991 ns | 0,52974 ns |
| R2 (%) | 95,53 | 87,80 | 89,85 |
Los efectos cuadráticos puros fueron altamente significativos, indicando que hubo efecto de curvatura. La única interacción significativa fue la de X1 x X3 (temperatura x tiempo de almacenamiento). La no significancia de las repeticiones demuestra que hubo un buen control local del error experimental, por lo que se consideró hacer el análisis con las medias de las respuestas.
Estimación de los parámetros para los modelos poblacionales fijados
El Cuadro 6 muestra las estimaciones de los coeficientes regresores del modelo poblacional fijado para las respuestas pH, acidez titulable total y SST estándar y su significancia "t" para cada uno de los parámetros.
Cuadro 6. Coeficientes regresores del modelo poblacional fijado para pH, acidez titulable y SST
| pH | Acidez titulable total | SST |
| 24,58 ** |
|
|
| -14900E-4** |
|
|
| 352E-4** |
|
|
| -8,60E-4ns |
|
|
| 0,003E-4* |
|
|
| -44,8E-4ns |
|
|
| 2,64E-4** |
|
|
| -0,2E-5ns |
|
|
| -23,1E-4** |
|
|
| 0,006E-4ns |
|
|
ns = no significativo; * significativo al 5%; ** significativo al 1%
Se observa que el beta regresor de los factores X2 y X3 no fue significativo y su signo negativo indica que por cada unidad de cambio que incremente este factor, la respuesta pH disminuye en 8,6E-4 y 44,8E-4 unidades, respectivamente.
Para las interacciones, el único beta significativo fue el de X1 x X3, lo que indica los cambios de la interacción entre los factores temperatura y tiempo de almacenamiento son importantes, haciendo disminuir la respuesta pH en 0,00231 unidades por cada unidad de incremento de la interacción. Los coeficientes regresores con signo negativo para la acidez titulable indican que por cada incremento unitario de esta fuente de variación disminuye la acidez titulable de la pulpa del cambur. Los incrementos del factor X1 (temperatura) y X2 (ethephon), hacen incrementar la acidez, siendo la temperatura el factor más importante. Este comportamiento fue similar al encontrado en los coeficientes regresores de la variable SST.
Análisis canónico de la superficie de respuesta pH, acidez titulable y SST
En el análisis canónico (Cuadro 7) para la respuesta pH se observa que todos los valores propios fueron positivos, indicando que el punto estacionario es un mínimo. El valor propio más alto (1,265461) está asociado con X3 y el próximo más alto (0,569826) está asociado con X1. El tercer valor propio está asociado con X2. Los dos últimos valores propios asociados con X1 y X2, fueron relativamente más bajos que el primero, indicando que la superficie de respuesta fue poco sensible a cambios en estos factores; por ello podría decirse que el factor que más influye en los cambios de pH es el tiempo de almacenamiento, lo que coincide con lo detectado en el anavar (Cuadro 4).
Cuadro 7. Vectores propios y valores propios para pH, acidez titulable y SST
| Respuestas | Valores propios | Vectores propios | ||
| X1 | X2 | X3 | ||
|
| 1,265461 | -0,670144 | 0,045988 | 0,740806 |
| 0,569826 | 0,736314 | -0,084591 | 0,671332 | |
| 0,300914 | 0,093539 | 0,995354 | 0,022827 | |
|
| -0,010734 | 0,514436 | 0,252687 | 0,819454 |
| -1,026690 | -0,079979 | 0,965572 | -0,247535 | |
| -5,077403 | 0,853791 | -0,061802 | -0,516935 | |
|
| -1,411406 | 0,711407 | 0,028692 | 0,702194 |
| -3,714564 | 0,107709 | 0,982910 | -0,149284 | |
| -8,215703 | -0,694477 | 0,181835 | 0,696159 | |
El valor crítico o punto estacionario predicho de pH = 4,25 se encuentra dentro de la región experimental, con una combinación de X1=25,65 °C, X2=2081,79 mg× L-1 de ethephon y X3=118,08 horas de almacenamiento.
El signo positivo del vector propio más alto (+0,740806) indica que el vector propio asociado estuvo en dirección de cascada ascendente desde el punto estacionario. Los vectores propios asociados con bajos valores propios indican que hubo una relativa tendencia a que la sábana o superficie tienda a ser asintótica cuando se aleja del centro del diseño, lo que significa que existe un fuerte efecto de curvatura en los bordes de la región experimental.
El punto estacionario o valor crítico para la respuesta acidez titulable correspondió a valores extremadamente altos (se obtuvo un máximo matemático) ubicados fuera de la región experimental y muy alejado del centro del diseño, lo que tecnológicamente sería imposible de alcanzar en una pulpa de fruta. Es por ello que en este caso interesa cuantificar las respuestas máximas operativas y no máximos matemáticos, los cuales se encuentran en las orillas del diseño. Todos los valores propios fueron negativos señalando que el punto estacionario es un máximo. El signo positivo del vector propio más alto (+0,819454) indica que el vector propio asociado va en dirección de cascada ascendente desde el punto estacionario. Los vectores propios asociados con pequeños valores propios indican que hay relativa tendencia a que la sábana o superficie tienda a ser asintótica cuando se aleja del centro del diseño, lo que quiere decir que hay fuerte efecto de curvatura en las orillas de la región experimental.
Con relación al punto estacionario de SST ocurrió una situación similar. Todos los valores propios fueron negativos, indicando que el punto estacionario es un máximo. El signo positivo del vector propio más alto (+0,711407) indica que el vector propio asociado va en dirección de cascada ascendente desde el punto estacionario tal como se explicó para el caso de la acidez titulable.
Estimados Ridge de máxima respuesta para el pH
El Cuadro 8 muestra el radio codificado de pH, el cual es la distancia desde el origen (radio cero), y muestra la respuesta predicha y el error estándar. Este último da una medida de la credibilidad relativa de predicción, que como se observa se incrementa rápidamente cuando el radio Ridge se desplaza hacia las orillas o perímetro del diseño, lo que refleja la inherente dificultad de hacer predicciones en esta zona.
Cuadro 8. Respuesta Ridge máxima para el radio experimental codificado de pH
| Radio codificado | Respuesta estimada | Error estándar | Factores experimentales | ||
| X1 | X2 | X3 | |||
| 0,0 | 4,59837 | 0,0364 | 23,000 | 2000,00 | 84,00 |
| 0,1 | 4,51468 | 0,0362 | 23,308 | 2002.83 | 84,71 |
| 0,2 | 4,44274 | 0,0366 | 23,633 | 2006,94 | 93,28 |
| 0,3 | 4,38240 | 0,0364 | 23,967 | 2012,69 | 97,73 |
| 0,4 | 4,33360 | 0,0365 | 24,308 | 2020,55 | 102,10 |
| 0,5 | 4,29640 | 0,0374 | 24,655 | 2031,08 | 106,40 |
| 0,6 | 4,27050 | 0,0394 | 25,005 | 2045,01 | 110,64 |
| 0,7 | 4,25590 | 0,0430 | 25,357 | 2063,55 | 114,81 |
| 0,8 | 4,25270 | 0,0484 | 25,709 | 2087,92 | 118,91 |
| 0,9 | 4,26060 | 0,0551 | 26,060 | 2120,11 | 122,93 |
| 1,0 | 4,27940 | 0,0645 | 26,407 | 2162,67 | 126,81 |
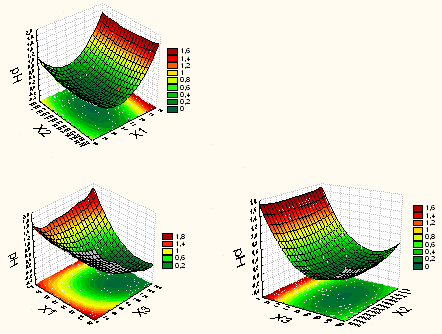
La Figura 1 del modelo ilustra la variabilidad predicha de la respuesta pH, donde se observa que la forma de la superficie se corresponde con lo mostrado por el análisis canónico, percibiéndose un punto estacionario dentro de la región experimental, así como un efecto de curvatura y una relativa tendencia en los perímetros a ser zonas aplanadas.
Estimados Ridge de máxima respuesta para la acidez titulable
El radio codificado de la acidez titulable (Cuadro 9) muestra la respuesta predicha y el error estándar.
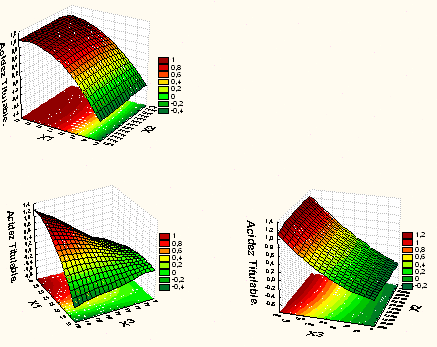
La variabilidad predicha (Figura 2) se corresponde con lo mostrado por el análisis canónico, donde se percibe un punto estacionario fuera de la región experimental, así como un efecto de curvatura y una relativa tendencia en uno de los perímetros a ser zonas aplanadas.
Cuadro 9. Respuesta Ridge máximo para el radio experimental codificado de la acidez titulable
| Radio codificado | Respuesta estimada | Error estándar | Valores de los factores experimentales | ||
| X1 | X2 | X3 | |||
| 0,0 | 10,2783 | 0,3153 | 23,000 | 2000,00 | 84,00 |
| 0,1 | 10,7974 | 0,3145 | 23,285 | 2007,69 | 88,91 |
| 0,2 | 11,3167 | 0,3125 | 23,564 | 2016,97 | 93,86 |
| 0,3 | 11,8363 | 0,3109 | 23,839 | 2027,68 | 98,83 |
| 0,4 | 12,3564 | 0,3123 | 24,112 | 2039,60 | 103,81 |
| 0,5 | 12,8769 | 0,3201 | 24,383 | 2052,64 | 108,80 |
| 0,6 | 13,3983 | 0,3383 | 24,652 | 2066,66 | 113,78 |
| 0,7 | 13,9202 | 0,3700 | 24,920 | 2081,56 | 118,77 |
| 0,8 | 14,4430 | 0,4173 | 25,187 | 2097,25 | 123,70 |
| 0,9 | 14,9665 | 0,4804 | 25,454 | 5113,65 | 128,75 |
| 1,0 | 15,4909 | 0,5590 | 25,720 | 2130,68 | 133,73 |
Figura 1. Representación gráfica de superficie y de contornos para la respuesta pH
Estimados Ridge de máxima respuesta para los SST
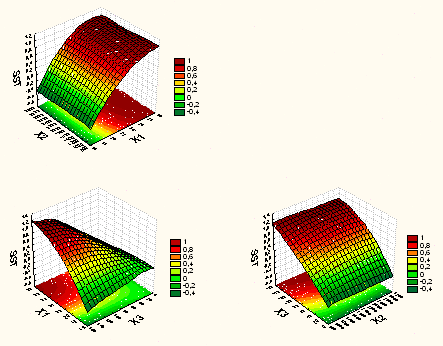
El radio codificado (Cuadro 10) muestra la respuesta predicha y el error estándar. La variabilidad predicha (Figura 3) se corresponde con lo mostrado por el análisis canónico, donde se percibe un punto estacionario fuera de la región experimental como es el caso de la acidez titulable.
Figura 2. Representación gráfica de superficie y de contornos para la respuesta acidez titulable total
Cuadro 10. Estimados Ridge de máxima respuesta para los SST
| Radio codificado | Respuesta estimada | Error estándar | Valores de los factores experimentales | ||
| X1 | X2 | X3 | |||
| 0,0 | 15,2510 | 1,0597 | 23,00 | 2000,00 | 84,00 |
| 0,1 | 16,2955 | 1,0566 | 23,30 | 2010,51 | 88,72 |
| 0,2 | 17,3090 | 1,0488 | 23,61 | 2020,11 | 93,34 |
| 0,3 | 18,2924 | 1,0411 | 23,94 | 2028,99 | 97,89 |
| 0,4 | 19,2460 | 1,0417 | 24,27 | 2037,27 | 102,38 |
| 0,5 | 20,1703 | 1,0619 | 24,60 | 2045,04 | 106,82 |
| 0,6 | 21,0654 | 1,1144 | 24,94 | 2052,38 | 111,24 |
| 0,7 | 21,9316 | 1,2104 | 25,28 | 2059,36 | 115,62 |
| 0,8 | 22,7690 | 1,3571 | 25,62 | 2066,01 | 119,98 |
| 0,9 | 23,5776 | 1,5564 | 25,97 | 2072,38 | 124,33 |
| 1,0 | 24,3576 | 1,8069 | 26,31 | 2078,50 | 128,65 |
Figura 3. Representación gráfica de superficie y de contornos para la variable SST
CONCLUSIONES Y RECOMENDACIONES
En la optimización de la madurez de Musa sp. AAB, el valor crítico para el pH fue 4,25 para una temperatura de 25,65 ºC, 2081 mg·L-1 de ethephon y 118 horas de almacenamiento.
No se pudo establecer valor crítico para la acidez titulable y SST ya que los puntos correspondieron a máximos matemáticos, ambos fuera de la región experimental.
Los modelos matemáticos desarrollados para cada variable fueron los siguientes, donde X1 es la temperatura, X2 la dosis de ethephon y X3 el tiempo de almacenamiento:
pH = 24,717 - 1,487X1 - 0,001067X2 - 0,004087X3 + 0,034998X12 +
3,5 E-7X22 + 2,61 E-4 X32 - 0,002296 X1*X3;
Acidez = - 63,285 + 6,048X1 + 4,084 E-3 X2 - 0,248 X3 - 0,150 X12 +
1,445E-6X22-4,11E-4X32+0,016X1*X3;
SST = -64,498+4,950X1+8,774E-3X2-0,242X3-0,129 X12 -
2,474 E-6 X22 - 9,05 E-4 X32 + 0,024 X1*X3.
LITERATURA CITADA
1. Ávila. E. y A. Fuentes. 2004. Simulación de la pérdida de vapor de agua y cambios de color en cambur cv. Manzano (Musa apple spp.) durante la maduración en atmósfera modificada, utilizando metodología de superficie de respuesta. Revista de ciencia y Tecnología Agrollania 1(1): 29-44. [ Links ]
2. Chacín, F. 1998. Comparaciones teóricas y prácticas y análisis en tiempo y/o espacio de los diseños de superficie de respuesta. Revista de la Facultad de Agronomía (UCV). Alcance 54. [ Links ]
3. Chacín, F. 2000. Diseño y análisis de experimentos. Ediciones del Vicerrectorado Académico. Facultad de Agronomía. Universidad Central de Venezuela (UCV). [ Links ]
4. COVENIN. 1977. Frutas y productos derivados. Determinación de sólidos solubles. Ministerio de Fomento, Venezuela. Norma 924. [ Links ]
5. Derringer, G., y R. Suich. 1980. Simultaneous optimization of several response variables. Journal of Quality Technology (12): 214-219. [ Links ]
6. Flores, A. 2000. Manejo post cosecha de fruta y hortalizas en Venezuela. Experiencias y Recomendaciones. Fusagri. Caracas. 320 p. [ Links ]
7. Jennrich, R. y P. Sampson. 1976. Newton-Raphson and related algorithms for maximum likelihood variance component estimation. Technometrics 18: 11-17. [ Links ]
8. Merk. 1972. Manual Técnico. Merk Darmstadst Alemania. [ Links ]
9. Montgomery, D. 1991. Diseño y análisis de experimentos. Grupo editorial Iberoamérica. Belmont, California. [ Links ]
10. Saguy, I. 1982. Optimization theory, techniques and their implementation in food industry. Food technology (7): 87 [ Links ]