Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Bioagro
versión impresa ISSN 1316-3361
Bioagro v.20 n.2 Barquisimeto ago. 2008
Estimación de evapotranspiración de referencia a nivel mensual en venezuela. ¿Cuál método utilizar?
Ricardo Trezza(1)
(1) Dpto. de Ingeniería, Núcleo Universitario Rafael Rangel, Universidad de los Andes. Trujillo. Venezuela. e-mail: rtrezza@ula.ve
RESUMEN
La determinación de las necesidades de riego de los cultivos se basa en la estimación precisa de la evapotranspiración de referencia (ETo) de cada zona en particular, y a su vez, las posibles alternativas para la estimación están sujetas a la limitación de la información meteorológica existente en cada país. En este trabajo se analizaron varias metodologías disponibles para realizar estimaciones de ETo a nivel mensual en Venezuela a partir de la información de estaciones meteorológicas ubicadas en diferentes regiones del país. Se encontró que los procedimientos más aplicables para estas condiciones climáticas son los incluidos en la publicación de la FAO-56, especialmente el método de FAO Penman-Monteith. La ecuación de Thornthwaite no resultó apropiada, ni tampoco las ecuaciones de la publicación FAO-24 como son la de Radiación y la de Penman-modificada, debido a que sobrestiman considerablemente los valores de ETo. El método de Blaney-Criddle puede aplicarse en zonas de baja altitud cuando sólo se cuente con datos de temperatura media del aire. El método de Hargreaves presentó potencial para su aplicación debido a que sólo utiliza información de temperatura máxima y mínima del aire, aunque requiere del cálculo de parámetros de ajuste climático para cada zona.
Palabras clave adicionales: FAO-56, FAO-24, Penman-Monteith, Hargreaves
ABSTRACT
Estimation of monthly reference evapotranspiration in Venezuela: Which method to be used?
The calculation of crop water needs is based on accurate estimate of reference evapotranspiration (ETo) for each particular zone, and in turn, the possible alternatives for estimations are subject to the limitation of meteorological information in each country. The purpose of this work was to analyze several available methodologies for the estimation of monthly reference evapotranspiration in Venezuela using meteorological data from different weather stations located in the country. It was found that the methodologies included in the publication FAO-56, particularly the Penman-Monteith, are the most applicable for the climatic conditions of the country. The Thornthwaite equation was not appropriate, nor the equations of the publication of FAO-24 such as Radiation and modified Penman, because they notably overestimate ETo. The method of Blaney-Criddle could be considered for low altitude regions when just mean air temperature data are available. The FAO-56 Hargreaves method has a potential for application due to it just needs minimum and maximum air temperature data, although requires the calculation of adjusting parameters for each region.
Additional key words: FAO-56, FAO-24, Penman-Monteith, Hargreaves
Recibido: Junio 29, 2007 Aceptado: Marzo 3, 2008
INTRODUCCIÓN
Uno de los componentes más importantes y más difíciles de cuantificar en el balance hídrico lo representa la evaporación que ocurre en superficies húmedas y cuerpos de agua y la transpiración que ocurre a partir de la vegetación natural y los cultivos. Se denomina evapotranspiración (ET) a la suma de la evaporación y la transpiración.
La evapotranspiración que ocurre a partir de una superficie con vegetación es función de las condiciones meteorológicas del área, así como de las características anatómicas y fisiológicas de la vegetación (Allen et al., 1994). Debido a que las características de la vegetación que afectan el proceso de evapotranspiración tienen una gran variabilidad de una especie a otra, ha existido la tendencia a tratar la evapotranspiración con base en una superficie específica o de referencia, lo que permite evaluar la ET considerando solamente las variables meteorológicas del área en estudio. Por lo tanto, la denominada evapotranspiración de referencia viene a representar un índice climático asociado al área en estudio, lo que la hace útil para la evaluación de las condiciones de humedad de un área determinada, en equilibrio con su clima.
En Venezuela ha existido cierta dificultad a la hora de evaluar el componente de evapotranspiración en el balance hídrico, debido a la escasez de registros meteorológicos representativos de diversas zonas del país y la poca información sobre las metodologías más convenientes a utilizar para cada región geográfica. Es por ello que se requiere de estudios donde se analicen las posibles alternativas de estimación de la ET, sujetas a la limitación de información meteorológica existente en el país.
La ET representativa de una región geográfica puede ser expresada como evapotranspiración potencial (ETp), o como evapotranspiración del cultivo de referencia (ETo), la forma utilizada en la actualidad. La Sociedad Americana de Ingenieros Civiles (ASCE, 1990) define la ETp como la tasa de evapotranspiración que ocurre a partir del conjunto de suelo húmedo y plantas, cuando no existen limitaciones de agua, y representa la evapotranspiración máxima que podría ocurrir a partir de una superficie cubierta con vegetación. Por su parte, el concepto de ETo fue desarrollado con el objeto de reemplazar de manera práctica al término de evapotranspiración potencial y se define como la tasa de evapotranspiración de una superficie extensa de gramíneas verdes, de 8 a 15 cm de altura, uniforme, en crecimiento activo, que sombrean completamente el suelo y que no tiene limitaciones de agua (Doorenbos y Pruitt, 1975). Posteriormente, se hizo más preciso el concepto y se definió como la tasa de evapotranspiración de una superficie extensa y uniforme de gramíneas en crecimiento activo y sin limitaciones de agua, con 12 cm de altura, un valor fijo de resistencia de la superficie de 70 s·m-1 y un albedo de 0,23 (Allen et al., 1998).
Al momento de seleccionar una ecuación para estimar la ETo se debe tomar en consideración la necesidad de calibrar y verificar los distintos procedimientos, antes de proceder a aplicarlos a un área en particular. Según Grassi (1993) el hecho de que prácticamente todos los procedimientos han sido desarrollados y verificados en países de clima templado (con pocas excepciones, entre ellas, la fórmula de García y López, 1970) hace riesgosa su aplicación a condiciones vecinas a los trópicos, donde actualmente se llevan a cabo importantes programas de aprovechamiento de recursos de aguas y tierras.
Doorenbos y Pruitt (1975) mencionan que a menudo se hace necesario aplicar fórmulas estimativas de la evapotranspiración en condiciones climáticas y agronómicas muy distintas de aquellas para las cuales fueron inicialmente concebidas. Por lo tanto, resulta muy importante someter a prueba la exactitud de las fórmulas antes de utilizarlas en un nuevo conjunto de condiciones. El objetivo de este trabajo fue el de comparar algunos de los principales métodos existentes para estimar la evapotranspiración y evaluar su aplicabilidad a las condiciones de Venezuela.
MATERIALES Y MÉTODOS
Se evaluaron los siguientes métodos de estimación de la evapotranspiración potencial (ETp) y la evapotranspiración de referencia (ETo):
Método de Thornthwaite (TW)
Es un método utilizado para estimar la ETp. La ecuación es expresada por la siguiente ecuación (Guevara, 2003):
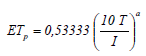
donde ETp es la evapotranspiración potencial [mm·d-1]; T es la temperatura media mensual [oC]; I es un índice de calor anual, calculado como la suma de los doce índices mensuales i. Los índices i para cada mes y el valor de a se calculan como:
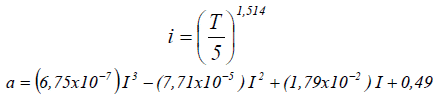
Los procedimientos para el cálculo de ETo fueron el de Penman-modificado, el de Blaney-Criddle y el de Radiación, todos incluidos en la publicación FAO-24 (Doorenbos y Pruitt, 1975), así como el método de FAO Penman-Monteith y el de Hargreaves, ambos incluidos en la publicación FAO-56 (Allen et al., 1998).
Método de Penman modificado (Pmod)
La ecuación modificada de Penman incluye una función del viento y el uso de un factor de ajuste c basado en condiciones climáticas locales. La ecuación es la siguiente:
donde ETo es la evapotranspiración del cultivo de referencia [mm·d-1]; Rn es la radiación neta en la superficie del cultivo [mm·d-1]; esat es la presión de vapor a saturación [kPa], correspondiente a la temperatura del aire; eact es la presión real de vapor [kPa]; D es la pendiente de la curva de presión de vapor a saturacion [kPa·oC-1]; g es la constante psicrométrica [kPa·oC-1], Wf es la función del viento, y c es un factor de ajuste.
Método de Blaney-Criddle (BC)
La ecuación es la siguiente:
Et0 = a + b * f y f = p(0,46T + 8,13)
donde ETo es la evapotranspiración del cultivo de referencia [mm·d-1]; T es la temperatura media del aire [oC]. Los valores de a, b y p son incluidos en la publicación FAO-24 (Doorenbos y Pruitt, 1975) para distintas condiciones de humedad relativa, fracción de insolación y velocidad del viento.
Método de la Radiación (Rad)
El método de la radiación es expresado a través de la siguiente ecuación:
Et0 = a + b *
donde ETo es la evapotranspiración del cultivo de referencia [mm·d-1]; Rs es la radiación solar expresada en equivalente de evaporación [mm·d-1]; W es un índice de ponderación que depende de la temperatura y de la altitud; a y b son coeficientes de regresión que dependen de la radiación solar, humedad relativa y velocidad del viento, según se incluye en la publicación FAO-24 (Doorenbos y Pruitt, 1975). En este caso, los datos de radiación fueron estimados a partir de la información de insolación disponible.
Método de FAO Penman-Monteith (PM)
Es en la actualidad el método más aceptado por la comunidad científica para la estimación de la evapotranspiración de los cultivos y es expresado a través de la siguiente ecuación:
donde ETo es la evapotranspiración del cultivo de referencia [mm·d-1]; Rn es la radiación neta en la superficie del cultivo [MJ·m-2·d–1]; G es el flujo de calor en el suelo [MJ·m-2·d–1]; T es la temperatura media del aire [oC]; u2 es la velocidad del viento [m·s-1]; esat es la presión de vapor a saturación [kPa], correspondiente a la temperatura del aire T; eact es la presión real del vapor [kPa]; D es la pendiente de la curva de presión de vapor a saturacion [kPa·oC-1] y g es la constante psicrométrica [kPa·oC-1].
Método de Hargreaves (HG)
Es un método sencillo debido a que utiliza principalmente información de temperatura máxima y mínima, y se aplica a través de la siguiente ecuación:
ETo = 0,0023 * Ra * (T + 17,8) (Tmax -Tmin)0,5
donde ETo es la evapotranspiración del cultivo de referencia [mm·d-1]; Ra es la radiación extraterrestre [mm·d-1] que depende de la latitud y el mes del año; T, Tmax y Tmin representan el valor medio, máximo y mínimo de la temperatura del aire [oC], respectivamente.
Adicionalmente, se adaptó la ecuación de Hargreaves a condiciones locales correlacionando sus resultados con los obtenidos con la ecuación de PM (Allen et al., 1998) y se determinaron coeficientes empíricos para obtener una ecuación ajustada de Hargreaves de la siguiente manera:
donde ETo(HG_corr) es la evapotranspiración del cultivo de referencia calculada a través de la ecuación ajustada de Hargreaves; a y b son los coeficientes de la regresión, y ETo (HG) es la correspondiente ETo calculada con la ecuación original de Hargreaves.
Para la aplicación de los distintos métodos se utilizó la información meteorológica incluida en la publicación FAO 49 que incluye datos recopilados hasta el año 1993 para distintas estaciones en Venezuela (FAO, 1994) para períodos de por lo menos 10 años de registro. Las estaciones meteorológicas evaluadas se presentan en el Cuadro 1.
Cuadro 1. Estaciones climáticas venezolanas consideradas para el análisis
| Estación | Altitud (msnm) | Latitud Norte (grados) | Longitud Oeste (grados) |
| Barquisimeto | 590 | 10,04 | 69,18 |
| Calabozo | 106 | 8,56 | 67,24 |
| Caracas | 835 | 10,30 | 66,53 |
| Ciudad Bolívar | 43 | 8,09 | 63,33 |
| Coro | 16 | 11,25 | 69,41 |
| Maracaibo | 40 | 10,39 | 71,36 |
| Maracay | 437 | 10,15 | 67,39 |
| Mérida | 1495 | 8,36 | 71,09 |
| Mucuchíes | 2980 | 8,44 | 70,55 |
| Puerto Ayacucho | 73 | 5,36 | 67,30 |
| San Antonio | 378 | 7,51 | 72,27 |
| San Fernando de Apure | 47 | 7,54 | 67,25 |
| Turén | 215 | 9,15 | 69,04 |
| Valencia | 463 | 10,10 | 68,00 |
| Yaritagua | 320 | 10,03 | 69,03 |
Fuente: FAO (1994)
Las diferencias porcentuales mensuales entre los valores de evapotranspiración obtenidos con cada método y los obtenidos a través del método PM (considerando éste como el más fiable de acuerdo con los estudios de Allen et al. (1998) y EWRI-ASCE (2005)) fueron promediadas para así obtener diferencias porcentuales promedio anuales.
RESULTADOS Y DISCUSIÓN
En el Cuadro 2 se presentan las diferencias porcentuales promedio anuales entre los valores de evapotranspiración obtenidos con cada método y los obtenidos a través de PM.
Cuadro 2. Diferencias promedio anuales (%) entre los valores de ETo con relación a PM para las diferentes estaciones climáticas
| Estación | PM | HG | Pmod | Rad | BC | TW |
| Barquisimeto | 0 | 16 | 20 | 19 | -4 | -9 |
| Calabozo | 0 | -38 | 22 | 16 | -8 | 21 |
| Caracas | 0 | 21 | 18 | 26 | -2 | -22 |
| Ciudad Bolívar | 0 | 6 | 22 | 11 | 3 | 25 |
| Coro | 0 | 8 | 23 | 12 | 4 | 19 |
| Maracaibo | 0 | 6 | 23 | 10 | 3 | 24 |
| Maracay | 0 | 16 | 18 | 19 | -5 | -8 |
| Mucuchíes | 0 | 16 | 14 | 24 | -26 | -40 |
| Mérida | 0 | 19 | 13 | 23 | -15 | -28 |
| Puerto Ayacucho | 0 | 29 | 14 | 11 | -6 | 32 |
| San Antonio | 0 | 18 | 20 | 11 | 3 | 17 |
| San Fernando de Apure | 0 | 10 | 19 | 12 | -6 | 14 |
| Turén | 0 | 17 | 19 | 12 | 6 | 14 |
| Valencia | 0 | 31 | 15 | 17 | 4 | 8 |
| Yaritagua | 0 | 24 | 16 | 16 | 5 | 8 |
Los valores positivos significan que el método tiende a sobrestimar y los negativos a subestimar la ET
Se observa que los valores de ETo calculados a través de HG presentaron una diferencia porcentual considerable (en un rango de 31 a -38 %) lo cual indica que la ecuación necesita de ajustes climáticos antes de ser aplicada en determinada área.
Con relación a la fórmula Rad, se produjeron sobrestimaciones del valor de ETo entre 10 y 26 %, aunque se debe hacer notar que para los cálculos se utilizaron datos de insolación para estimar los valores propios de radiación solar.
La fórmula BC produjo resultados
satisfactorios en la mayoría de las estaciones consideradas (exceptuando las estaciones andinas de Mérida y Mucuchíes) por lo que podría considerarse como una alternativa viable en los casos de escasez de información meteorológica adecuada. La diferencia entre los resultados obtenidos con el método BC y los correspondientes a PM fueron menores a 8 %. Es de destacar que el procedimiento requirió de mediciones o estimaciones adecuadas de humedad relativa mínima e insolación para llegar a este nivel de precisión.
La ecuación de Thornthwaite tendió a subestimar sensiblemente los valores de ETo en las estaciones ubicadas en las zonas andinas, en Mérida con 28 % y en Mucuchíes con 40 %. En las otras estaciones la tendencia de la ecuación de TW fue de sobrestimar los valores de ETo en porcentajes que variaron entre 8 y 32 %. Se debe destacar que Thornthwaite correlacionó valores de temperatura media mensual con valores de evapotranspiración calculados mediante estudios de balance hídrico realizados en valles del centro-este de los Estados Unidos, un área esencialmente húmeda. Por lo tanto, los valores obtenidos con la mencionada fórmula son representativos de las áreas donde fueron derivados (ASCE, 1990).
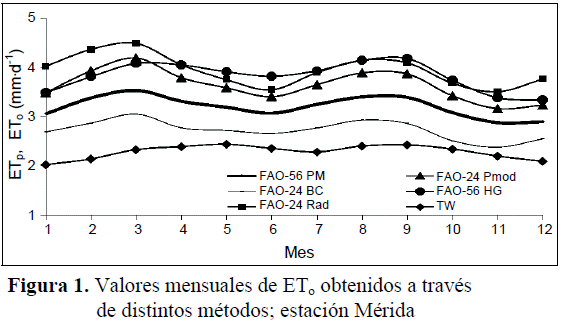
En zonas donde la temperatura media del aire no responda proporcionalmente a los cambios de otros parámetros, las fórmulas basadas principalmente en temperatura media, tales como BC y TW no son indicadas. Este es el caso de las zonas andinas (estaciones de Mérida y Mucuchíes) donde la estimación de la ETo es bastante delicada debido a que las temperaturas medias del aire son relativamente bajas a pesar de los altos niveles de radiación y la influencia de la velocidad del viento. Por ello los métodos basados en la temperatura media del aire producen una subestimación de la ETo (Figura 1).
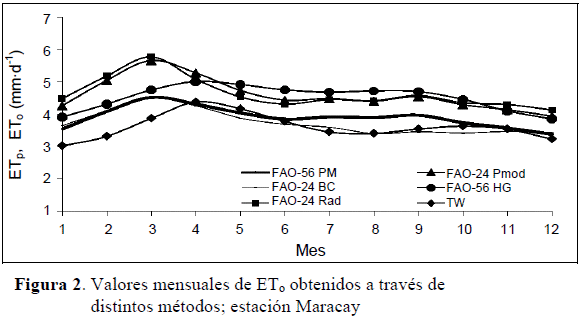
En las Figuras 1 y 2 se presenta la variación de los valores mensuales de ETo para dos estaciones contrastantes (Mérida y Maracay). Se puede observar que la diferencia entre los distintos métodos fue variable, siendo mayor en Mérida que en Maracay. En la estación andina de Mérida los métodos fuertemente basados en temperatura media (TW y BC) subestimaron los valores calculados a través de PM, situación que no se observa tan claramente en la estación Maracay. Esto se debe principalmente al hecho de que en las zonas andinas (de elevada altitud) las temperaturas medias pueden permanecer bajas a pesar de los altos niveles de radiación solar.
En ambos casos, la utilización de los métodos de Pmod, Rad y HG produjeron sobrestimaciones de los valores de ETo calculados a través de PM.
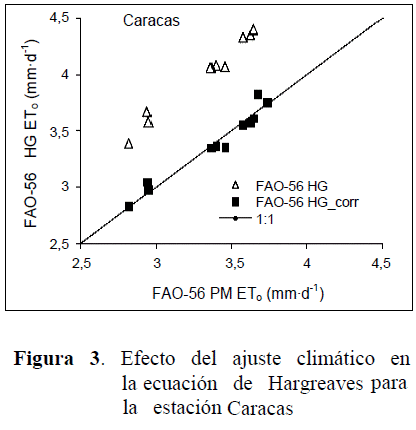
Con relación al ajuste de la ecuación de Hargreaves y tomado como ejemplo a la estación de Caracas, se encontró que la asociación entre los valores de ETo obtenidos por PM y los obtenidos por HG presentó un alto coeficiente de determinación (R2 = 0,976). La ecuación de regresión obtenida fue la siguiente:
ETo PM = 0,7748*ETo HG+0,20165
por lo que la ecuación HG fue ajustada como:
ETo (HG_corr)= 0,7748 [0,0023*Ra*(T+17,8)(Tmax-Tmin)0,5]+0,20165 de esta manera, la diferencia porcentual promedio anual se redujo desde 21 % hasta apenas 1,5 % cuando se utilizó la ecuación ajustada de Hargreaves. En la Figura 3 se puede observar el efecto del ajuste de la ecuación de Hargreaves para la estación de Caracas.
En la mayoría de las estaciones se logró un valor de R2 bastante aceptable (>0,80) y una reducción considerable de la diferencia porcentual con respecto a PM, lo que permite indicar que el ajuste fue satisfactorio para el uso de la ecuación de Hargreaves.
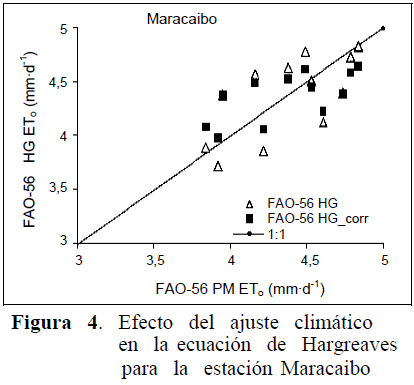
En la estación de Maracaibo el ajuste de la ecuación de Hargreaves no produjo reducciones significativas en los errores debido a la poca correlación entre los valores de HG y PM (Figura 4). En la estación de Calabozo no se presentó correlación alguna entre PM y HG, atribuido a la poca diferencia entre los valores de temperatura máxima y mínima reportados por la FAO (1994) para esta estación, valores que deberían ser revisados. Por esta razón, se debe destacar que toda la información a utilizar para estimar ETo por cualquier método debe ser sometida inicialmente a un análisis de integridad (Allen et al., 1998) para comprobar que dicha información meteorológica es totalmente confiable.
CONCLUSIONES
El uso de la fórmula de FAO-56 Penman-Monteith, la más aceptada en la actualidad, está limitada sólo a algunas regiones del país, donde exista toda la información meteorológica requerida por el método.
La ecuación de Thornthwaite no es apropiada para el cálculo de evapotranspiración de referencia a ser utilizada en balances hídricos regionales y estimación de demandas de agua en Venezuela, principalmente en zonas andinas. Tampoco se recomiendan las ecuaciones de Penman-modificado y Radiación de la FAO-24 debido a que tienden a sobrestimar considerablemente los valores de ETo.
Con respecto a la ecuación de Blaney-Criddle de la FAO-24 se pudo comprobar que la misma podría considerarse como una alternativa en los casos donde sólo se cuente con temperatura media del aire, no conociéndose los valores máximos y mínimos de temperatura. Esta ecuación no debería utilizarse en zonas altas (como en Mérida y Mucuchíes) donde la temperatura media del aire es relativamente baja comparada con los altos niveles de radiación solar. En estos casos podría utilizarse la ecuación ajustada de Hargreaves que involucra la diferencia entre las temperaturas máximas y mínimas del aire u oscilación térmica, el cual es un parámetro que responde a esos altos niveles de radiación.
La ecuación de Hargreaves ajustada permitió obtener resultados satisfactorios, siendo su principal ventaja la de requerir sólo de datos de temperatura máxima y mínima del aire, información disponible en gran cantidad de estaciones meteorológicas del país.
LITERATURA CITADA
1. Allen, R.G., M. Smith, A. Perrier y L.S. Pereira. 1994. An update for the calculation of reference evapotranspiration. Boletín de la Comisión Internacional de Riego y Drenaje (ICID) 43: 35-92. [ Links ]
2. Allen, R.G., L.S. Pereira, D. Raes y M. Smith. 1998. Crop evapotranspiration. Serie de Riego y Drenaje, FAO-56. Roma. 301 p. [ Links ]
3. ASCE (American Society of Civil Engineers). 1990. Evapotranspiration and irrigation water requirements. ASCE Report 70. New York. 216 p. [ Links ]
4. Doorenbos, J. y W.O. Pruitt. 1975. Guidelines for prediction of crop water requirements. Serie de Riego y Drenaje, FAO-24. Roma. 144 p. [ Links ]
5. EWRI-ASCE (Environmental and Water Resource Institute). 2005. The ASCE standardized reference evapotranspiration equation. ASCE. 216 p. [ Links ]
6. FAO (Food and Agriculture Organization). 1994. Climwat for Cropwat: a climatic database for irrigation planning and management. Grupo de Agrometeorología, FAO-49. Roma. 120 p. [ Links ]
7. García, J. y J. López. 1970. Fórmula para el cálculo de la evapotranspiración potencial adaptada al trópico. Agronomía Tropical 20(5): 335-345. [ Links ]
8. Grassi, C.J. 1993. Fundamentos de riego. CIDIAT. Mérida, Venezuela. 325 p. [ Links ]
9. Guevara, J.M. 2003. Métodos de estimación y ajuste de datos climáticos. Publicaciones de la Universidad Central de Venezuela. Caracas. 128 p. [ Links ]