Determinación de componentes de la varianza y parámetros genéticos en una población segregante de maíz tropical

Rubén Silva-Díaz¹, Pedro García-Mendoza², Diego Faleiro-Silva³ y Cláudio Lopes de Souza⁴

¹ Instituto Nacional de Investigaciones Agrícolas, INIA-CENIAP, Maracay, Aragua, Venezuela. e-mail: rjsilva@inia.gob.ve, rubenjsilvad@gmail.com (autor de correspondencia)

² Instituto Nacional de Investigaciones Agrícolas, INIA-Portuguesa, Araure, Portuguesa. Venezuela. e-mail: pgarcia@inia.gob.ve

³ Syngenta Semillas Ltda., Uberlândia, Minas Gerais, Brasil. diego_velasquez.silva@syngenta.com.

⁴ USP, Escuela Superior de Agricultura Luiz de Queiroz, Piracicaba, São Paulo, Brasil. e-mail: clsouza@usp.br

Resumen

La estimación de componentes de la varianza y parámetros genéticos es útil para direccionar el proceso de selección en programas de mejoramiento. La presente investigación fue realizada para estimar los componentes de la varianza genética, el grado medio de dominancia y la heredabilidad para producción de granos y caracteres de la planta, en una población de maíz (Zea mays L.) tropical formada a partir de dos líneas genéticamente divergentes. Cien progenies de retrocruzamientos fueron evaluadas en diversos ambientes en el municipio Piracicaba, SP, Brasil, en las temporadas agrícolas 2008-2009 y 2009-2010, bajo un diseño α-látice 15 x 20 en esquema factorial con dos repeticiones por ambiente. Los estimados de la varianza aditiva, de dominancia y de la interacción aditiva por ambiente fueron significativamente diferentes de cero (P≤0,05) para todos los caracteres estudiados. Los estimados de la varianza aditiva fueron superiores a los de la varianza de dominancia, y explicaron de 70 a 94 % de la varianza genética total. El grado medio de dominancia osciló de 0,35 (acame de raíz y tallo) a 0,93 (floración masculina y femenina), indicando dominancia parcial de los genes que gobiernan las características estudiadas. La heredabilidad a nivel de medias, para todos los caracteres, mostró valores altos, oscilando de 0,58  a 0,96  obteniendo la producción de granos un valor de 0,94. Los altos valores de los coeficientes de heredabilidad implican la posibilidad de una efectiva selección para el mejoramiento genético del rendimiento en grano y caracteres de la planta en la población estudiada.

Palabras clave adicionales: Grado medio de dominancia,heredabilidad,producción de grano, varianza genética, Zea mays

Estimation of variance components and genetics parameters in a segregating population of tropical maize

ABSTRACT

The estimation of variance components and genetic parameters is useful for directing the selection process in breeding programs. The present investigation was carried out to estimate the components of the genetic variance, average degree of dominance and the heritability for the yield grain and plant traits, in a tropical maize (Zea mays L.) population formed from two lines genetically divergent. One hundred progenies from backcrossing were evaluated in different environments in the municipality Piracicaba, SP, Brazil, in the 2008-2009 and 2009-2010 growing seasons, through an α-lattice design on a factorial scheme with two replications per environment. Estimates of the additive variance, dominance and the additive by environments interaction were significantly different from zero (P≤0.05) for all traits. Estimates of additive variance were significantly (P≤0.05) higher than those of dominance variance for all traits, explaining from 70 to 94% of the total genetic variance. The average degree of dominance ranged from 0.35 (root and stalk lodging) to 0.93 (days to anthesis and days to silk emergence), indicating partial dominance of genes that govern the traits studied. The heritability, at a mean level for all traits, showed high values, ranging from0.58 to 0.96, with a value of 0.94 for the grain yield. The high value of the heritability coefficients implies the possibility of an effective selection for the genetic improvement of grain yield and plant characteristics in the population studied.

Additional key words: Degree of dominance, genetic variance, heritability, yield grain, Zea mays

Recibido: Febrero 21, 2017 Aceptado: Octubre 9, 2017

Introducción

La variabilidad genética es indispensable en poblaciones segregantes cuando se quiere tener éxito en programas de mejoramiento genético de plantas, ya que el progreso de la selección depende de la cantidad de la variabilidad genética presente en la población y de las magnitudes relativas de sus componentes, los cuales junto a la interacción genotipo por ambientes, indican al fitomejorador si el germoplasma a utilizar posee suficiente variabilidad genética, qué método de selección es el más adecuado para un mejor aprovechamiento de esa variabilidad, si el método de selección escogido también es apropiado para mejorar otras características de distinta importancia y, en qué medida debe ser probado el germoplasma (en función de años, localidades y repeticiones) para identificar los genotipos superiores (Bernardo, 2002).

Ahora bien, la genética de cualquier caracter métrico se basa en el estudio de la variación de éste y en su partición en componentes atribuibles a diferentes causas. La variación de un caracter se mide y expresa a través de la varianza (Abbott y Pistorale, 2010). Los componentes que integran la varianza fenotípica son la varianza genética, la varianza ambiental y la varianza de la interacción genotipo-ambiente. Falconer (1989) señala que la varianza genética se compone de varianza aditiva (varianza de los valores reproductivos), varianza dominante (ó de dominancia, producto de la interacción entre alelos del mismo gen) y varianza de interacción (o epistática, producto de las interacciones entre alelos de genes diferentes).

La información proveniente de los componentes de la varianza genética y de los parámetros genéticos (heredabilidad, grado medio de dominancia y correlación genética aditiva) son esenciales para hacer inferencias a cerca de los beneficios que pueden obtenerse con la selección (Sobierajski et al., 2006). La varianza aditiva es la más importante, ya que es la que se hereda de los padres a su descendencia, determinante de las propiedades genéticas de la población y de la respuesta positiva a la selección; así la existencia de varianza aditiva se constituye en un indicativo de la facilidad de identificación de genotipos genéticamente superiores, los cuales proporcionaran ganancias más ventajosas en razón de su selección.

La existencia de varianza aditiva es deseable en programas de selección recurrente que tienen por objetivo la acumulación de genes favorables para mejorar la población per se. La varianza atribuida a las desviaciones de dominancia, cuando constituye una fracción importante de la varianza genética, es un indicador de las dificultades en el proceso de selección tanto en términos de identificación de genotipos con mayor concentración de alelos favorables como en la cantidad del avance obtenido por la selección y recombinación de individuos electos. La existencia de varianza atribuida a la dominancia es deseable en programas que tienen por objetivo la exploración del vigor manifestado en combinaciones híbridas (Cruz et al., 2004).

La heredabilidad es un parámetro genético importante pues expresa la proporción de la varianza fenotípica que es debida al efecto promedio de los genes, lo cual establece el grado de parecido entre parientes (Falconer, 1989), o sea, el grado en que los fenotipos de los individuos son determinados por los genes heredados de los progenitores a sus descendientes.

La heredabilidad tiene función predictiva, ya que suministra información sobre la cantidad a la cual un determinado caracter morfo-genético puede ser transmitido a sucesivas generaciones. La función más importante de la heredabilidad en estudios genéticos de caracteres cuantitativos es su rol predictivo para indicar la confiabilidad del valor fenotípico como guía del valor reproductivo. Caracteres con heredabilidad alta pueden fácilmente ser fijados por selección simple resultando en elevada ganancia genética. Sin embargo se ha señalado que esa heredabilidad sola no tiene uso práctico sin avance genético.

En tal sentido, el presente trabajo tuvo por objetivo estimar los componentes de la varianza genética, el grado medio de dominancia y la heredabilidad para la producción de granos y caracteres de la planta en una población de maíz (Zea mays L.) tropical formada a partir de dos líneas genéticamente divergentes con el fin de diseñar estrategias de mejoramiento a aplicar en la misma.

Materiales y métodos

La población utilizada en este estudio fue obtenida del cruzamiento entre las líneas endogámicas L-08-05F y L-38-05D, las cuales son divergentes para caracteres de importancia agronómica, pertenecen a grupos heteróticos distintos y tienen alta capacidad específica de combinación para producción de granos y prolificidad. La línea L-08-05F fue desarrollada de la población IG-1 de granos duros y coloración anaranjada (Santos et al., 2005) mientras que la L-38-05D fue derivada de un híbrido simple utilizado como progenitor femenino del híbrido doble BR-201 de granos dentados y coloración amarilla (Aguiar et al., 2003).

Plantas F₁ provenientes del cruzamiento entre ambas líneas fueron autofecundadas originando plantas F₂ que nuevamente fueron autofecundadas dando origen a progenies F_2:3. Cien progenies F_2:3 (usadas como hembras) fueron retrocruzadas con cada línea parental y con la F₁ en tres campos de despanojamiento, aislados, y produjeron 300 progenies de retrocruzamientos (G_RC1 = F_2:3 x L-08-05F; G_RC2 = F_2:3 x L-38-05D; G_RC3  = F_2:3 x F₁), según el diseño genético triple test cross descrito por Kearsey y Jink (1968). Se utilizaron progenies F_2:3, en vez de plantas F₂, debido a la mayor facilidad para obtener las progenies de retrocruzamiento vía despanojado en campos aislados y, de esa manera, obtener semillas suficientes de las mismas para su evaluación en experimentos, en diversas localidades y años. La constitución gamética de cada progenie F_2:3 es, en promedio, la misma de la planta F₂ que le dio origen. De esa forma, el retrocruzamiento de una F_2:3 con un progenitor es genéticamente igual al retrocruzamiento de la planta F₂ que la originó retrocruzada al mismo progenitor.

Durante los años 2008 y 2009 en el municipio Piracicaba, SP, Brasil, se evaluaron las 300 progenies de retrocruzamientos en tres localidades diferentes (dos localidades en la estación experimental Anhembi, 22°50’S; 48°01’W, y otra en la estación experimental Caterpillar, 22°43’S; 47°36’W, del Departamento de Genética de la Escuela Superior de Agricultura “Luiz de Queiroz” de la Universidad de Sao Paulo (USP), y en dos épocas de siembra (temporada habitual de siembra comercial del cultivo en la localidad y 30 días después). La combinación de años, localidades y épocas de siembra se consideró como un ambiente distinto, totalizando 11 ambientes en razón que en el año 2009 se sembró un solo experimento en la localidad de AnhembiII. El manejo agronómico de los experimentos fue el recomendado para el cultivo en cada localidad.

El diseño experimental utilizado fue el alfa látice 15 x 20 en esquema factorial con dos repeticiones por ambiente. Cada parcela estuvo constituida por una hilera de 4 m, con espaciamiento de 0,8 m entre parcelas y 0,2 m entre plantas para una densidad aproximada de 62.500 plantas∙ha^-1.

Los caracteres evaluados y utilizados para el análisis fueron la producción de granos (PG) ajustado al 15 % de humedad y expresado en  Mg∙ha^-1; porcentaje de acame de raíz y de tallo (ART) determinado como el número total de plantas de la parcela que presentaron ángulo de inclinación superior a 30° más el total de plantas con el tallo quebrado por debajo de la primera mazorca, floración masculina (FM) y femenina (FF) como los días transcurridos desde la siembra hasta que el 50 % de las plantas presentó anteras y estilos-estigmas visibles, respectivamente; intervalo entre florecimientos (IF) obtenido de la diferencia entre FF y FM; altura de planta (AP) y de inserción de la mazorca (AM) determinadas de cinco plantas en competencia completa y medidas desde la superficie del suelo hasta la altura de la hoja bandera y de la inserción de la primera mazorca, respectivamente, y la posición relativa de la mazorca (PRM) como el cociente AM/AP. Para obtener un mejor ajuste a la distribución normal el caracter ART fue transformado utilizando , en que x es el porcentaje de plantas de la parcela acamadas de raíz y/o de tallo. Los caracteres PG y ART fueron ajustados por el número total de plantas de la parcela para el análisis de covarianza (Vencovsky y Barriga, 1992). Los caracteres PG y ART fueron evaluados en los 11 ambientes, y los demás caracteres en 10 ambientes.

Todos los análisis fueron realizados por medio del programa computacional SAS versión 8.2 (Cary, NC, USA,). Antes de efectuarlos se probó la distribución normal y la homogeneidad de las varianzas de los residuos a través de las pruebas de Shapiro-Wilk y de Bartlett, respectivamente.

Para cada localidad se realizó un análisis de varianza individual. Los análisis de varianza conjunta fueron realizados utilizando las medias ajustadas de las progenies de retrocruzamientos y los cuadrados medios de los errores efectivos de cada experimento, usando el modelo:

donde Y_ijklm: se refiere al valor observado de la i-ésima progenie, en la j-ésima repetición, en el k-ésimo bloque, en la l-ésima generación de retrocruzamientos del m-ésimo ambiente; µ: es el efecto de la media general; p_i: es el efecto aleatorio de las progenies (i = 100); e_m: es el efecto aleatorio del ambiente (m = 11); r_j: es el efecto aleatorio de repetición dentro de ambientes (j = 2); b_k(jm): es el efecto aleatorio de bloques dentro de repetición dentro de ambiente (k = 20); (pe)_im: es el efecto aleatorio de la interacción entre las progenies con ambientes; g_l: es el efecto fijo de la generaciones de retrocruzamientos (l = 3); (pg)_il: es el efecto aleatorio de la interacción entre las progenies con la generación de retrocruzamientos; (ge)_lm: es el efecto aleatorio de la interacción entre las generaciones de retrocruzamientos con los ambientes; (pge)_ilm: es el efecto aleatorio de la interacción entre las progenies con las generaciones de retrocruzamientos con el ambiente y : es el error medio efectivo.

La  fuente generaciones de retrocruzamiento fue considerada de efectos fijos y todas las demás aleatorias. La prueba de F aproximada por Satterthwaite  (1946) fue utilizada para probar la fuente de variación generación de retrocruzamientos y sus respectivos desdoblamientos.

Estimados de componentes de la varianza y parámetros genéticos: En el análisis de la varianza conjunta del diseño triple test cross se descomponen las fuentes generaciones de retrocruzamientos (G_RC), generaciones de retrocruzamientos por ambientes (G_RC x E), progenies por generaciones de retrocruzamientos (P x G_RC) y progenies por generaciones de retrocruzamientos por ambientes (G_RC x P x E) en dos contrastes ortogonales (C₁ = G_RC1 vs G_RC2) y C₂ = G_RC1 + G_RC2 – 2G_RC3), utilizándose el segundo contraste (C₂) para probar la epistasis (Silva et al., 2017); sin embargo, las fuentes de variación P x C₁ y P x C₁ x E permiten probar los efectos de la desviación de dominancia y la interacción de ésta por ambientes, respectivamente.

Los componentes de la varianza para cada caracter fueron estimados según los cuadrados medios esperados de la varianza conjunta, siguiendo la metodología propuesta por Searle et al. (1992). Los componentes de varianzas fueron estimados por medio de las ecuaciones siguientes:

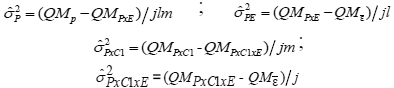
donde  son los estimados de la varianza genética entre progenies, de la interacción de la varianza entre progenies por ambientes, de la interacción de la varianza entre progenies por el contraste 1 y de la interacción de la varianza entre progenies por el contraste 1 por ambientes, respectivamente; QM_P, QM_PxE, QM_PxC1, QM_PxC1xE y  son los cuadrados medios de progenies, de la interacción progenies por ambientes, de la interacción progenies por el contraste 1, de la interacción de progenies por el contraste 1 por ambientes y del cuadrado medio del error medio efectivo, respectivamente; j, l y m son el número de repeticiones j = 2, generaciones de retrocruzamientos (l = 3) y los ambientes (m = 10 u 11), respectivamente. Los estimados de la varianza aditiva (), de dominancia () y sus interacciones con ambientes ( y ) fueron estimadas según Comstock y Robinson (1952), a través de las siguientes ecuaciones:

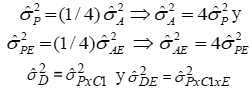
Se estimaron los coeficientes de heredabilidad tanto al nivel de medias de medios hermanos () como al nivel de plantas F₂ en sentido amplio () y restringido (), a través de las ecuaciones siguientes:

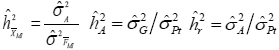
donde:  es el estimado de la varianza fenotípica en base a la media de progenies, estimada mediante la siguiente ecuación: , siendo  el estimado de la varianza genética obtenido por la suma de las varianzas aditiva y de dominancia, y  es el estimado de la varianza fenotípica al nivel de planta, obtenida de la siguiente forma: .

El grado medio de dominancia () fue estimado como:

Los intervalos de confianza para los estimados de los componentes de la varianza y del grado medio de dominancia al 0,95 de probabilidad fueron calculados siguiendo los procedimientos sugeridos por Burdick y Graybill (1992). La precisión de los estimados para los coeficientes de heredabilidad al nivel de medias de progenies y, al nivel de plantas, tanto en sentido restringido como en el amplio, fue obtenida siguiendo los procedimientos presentados por Knapp et al. (1985) y Falconer (1989), respectivamente. Los intervalos de confianza fueron utilizados en la comparación entre las medias generales y los estimados de los componentes de varianza de los caracteres evaluados. Dos medias o estimados de componentes de varianza fueron considerados diferentes entre sí (P≤0,05), solamente cuando una media ó estimado no estuviese dentro del intervalo de confianza del otro y viceversa.

Resultados y discusión

Las pruebas estadísticas para verificar si los datos cumplen con los supuestos del análisis de la varianzas fueron no significativas para todos los caracteres evaluados, por lo tanto, se infiere que hubo homocedasticidad de la varianza y distribución normal de los residuos.

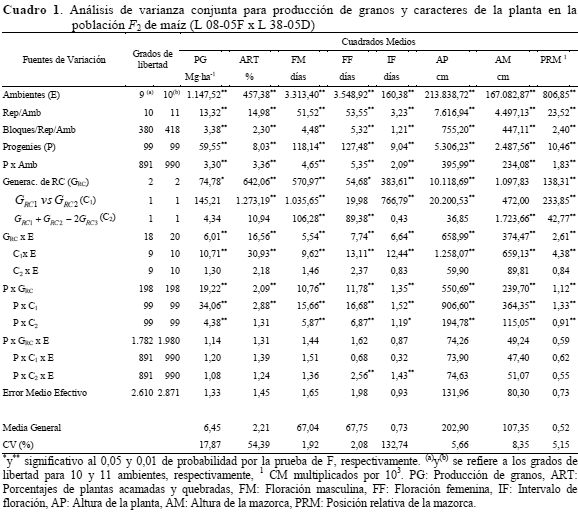
Análisis de varianza conjunta: El análisis de varianza combinado detectó diferencias significativas (P≤0,01) para ambientes, progenies y para las interacciones entre progenies por ambientes y progenies por generaciones de retrocruzamientos, para todos los caracteres. Tales resultados indicaron, respectivamente, la presencia de variabilidad entre los ambientes de evaluación, variabilidad genética entre las progenies, y que las progenies presentaron comportamiento diferencial tanto entre los ambientes de evaluación como entre las generaciones de retrocruzamientos (Cuadro 1).

Se detectaron diferencias significativas (P≤0,01/0,05) entre generaciones de retrocruza-mientos para todos los caracteres, excepto para AM (Cuadro 1). El contraste G_RC1 vs G_RC2 mostró diferencias entre las medias de las generaciones de retrocruzamientos uno y dos para los caracteres ART, FM, IF, AP y PRM (Cuadro 1). El contraste G_RC1 + G_RC2 - 2G_RC3 mostró diferencias entre la media de los dos progenitores y la media de la F₁ para los caracteres FM, FF, AM y PRM.

Las generaciones de retrocruzamientos a través de los ambientes presentaron diferencias significativas para todos los caracteres, por lo que el comportamiento de las mismas no fue constante en los diferentes ambientes de evaluación. El contraste G_RC1 vs G_RC2 mostró diferencias entre las medias de las generaciones de retrocruzamientos uno y dos a través de los ambientes para todos los caracteres. Los contrastes G_RC1 vs G_RC2 y G_RC1 + G_RC2- 2G_RC3 mostraron diferencias significativas entre las medias de las generaciones de retrocruzamientos uno y dos y entre la suma de éstas medias con la de la F1 a través de las progenies para todos los caracteres, excepto para ART en la interacción G_RC1 + G_RC2 - 2G_RC3 x progenies. Solamente la interacción triple (P x C2 x E) mostró diferencias significativas (P≤0,01), indicando que la interacción (P x C2) no se mantuvo constante en los diversos ambientes (Cuadro 1).

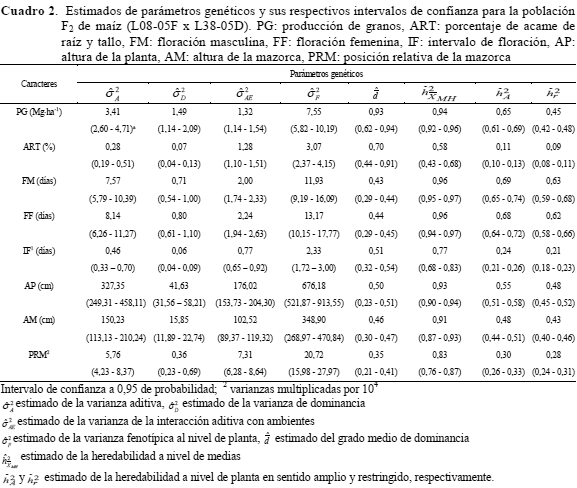
Estimados de componentes de la varianza y parámetros genéticos: El Cuadro 2 muestra estimados de componentes de varianza, de la interacción de componentes de varianza con ambientes, del grado medio de dominancia y de la heredabilidad. Los estimados de la varianza aditiva, de dominancia y de la interacción aditiva por ambientes fueron significativamente diferentes de cero para todos los caracteres estudiados. Los estimados de la varianza de dominancia por ambientes no son presentados en el Cuadro 2 ya que los mismos arrojaron valores negativos. Este resultado era esperado ya que la interacción P x C₁ x E, en el análisis de la varianza conjunta, fue no significativa para todos los caracteres. Silva y Hallauer (1975) relatan que, por definición, la varianza es cero o mayor que cero y, por lo tanto, estimados negativos deben representar el valor cero, o ellas reflejan alguna deficiencia del modelo.

Los estimados de la varianza aditiva y de la varianza aditiva por ambientes fueron significativamente mayores que los de dominancia (Cuadro 2), para todos los caracteres, excepto para producción de granos donde la varianza de dominancia fue mayor que la varianza aditiva por ambientes, no obstante, esa diferencia es no significativa ya que los intervalos de confianza de la varianza de dominancia y de la varianza aditiva por ambientes se sobreponen indicando similar importancia de estas varianzas (Cuadro 2). La varianza aditiva explicó gran proporción de la varianza genética total, oscilando de 69,59 % (PG) hasta 94, 12 % (PRM) de la misma.

Los estimados de la varianza aditiva fueron de magnitudes superiores a los de la varianza aditiva por ambientes para los caracteres PG, FM, FF, AP y AM, ocurriendo lo contrario para ART, IF y PRM (Cuadro 2), confirmando la importancia del ambiente en la expresión de esos tres caracteres. De igual forma, Lamkey et al. (1995) y Wolf et al. (2000) reportaron interacción de los efectos aditivos con los ambientes, en maíz.

Producción de granos. El estimado de la varianza aditiva para producción de granos fue de 3,41 (Cuadro 2), más del doble del estimado de la varianza de dominancia y al de la interacción de la varianza aditiva por ambientes (Cuadro2).

Magnitudes de estimados de varianza aditiva superiores a los de dominancia para producción de granos en maíz fueron reportadas por Hallauer et al. (2010), quienes encontraron para diversas poblaciones que la varianza aditiva es responsable por 61,2% de la varianza genética, en cuanto la de dominancia por 32,8%. Otros trabajos también han informado esa misma tendencia para producción de granos (Malvar et al., 1996; Singh y Gupta 2008; Bello y Olaoye, 2009) y, para peso de la mazorca Raposo y Ramalho (2004).

El estimado del grado medio de dominancia fue de 0,93; valor que sugiere la presencia de dominancia parcial de los genes que gobiernan ese caracter (Cuadro 2), o sea, los efectos aditivos tuvieron mayor importancia que los de dominancia en la expresión del caracter. El intervalo de confianza del grado medio de dominancia no englobó el valor 1,00 indicando que tanto los efectos aditivos como los de dominancia son importantes en el control genético de la producción de granos, pero con la predominancia de los efectos aditivos.

En trabajos previos se ha reportado dominancia parcial en el grado medio de dominancia para ese caracter (Lima et al., 2006; Hallauer et al., 2010), aunque otros autores han reportado estimados del grado medio de dominancia superiores a 1,00, lo que indica sobredominancia (Han y Hallauer, 1989; Silva et al., 2004). Sin embargo, según Comstock y Robinson (1952), las poblaciones F₂ presentan elevado desequilibrio de ligamiento, lo cual puede causar sesgos en los estimados de la varianza aditiva y de dominancia, haciendo que, en esas poblaciones, los estimados de la varianza de dominancia sean sobreestimadas y los de la varianza aditiva subestimadas ó sobreestimadas, en presencia de la fase de repulsión ó de asociación, respectivamente.

Los estimados de los componentes de la varianza, de la heredabilidad y del grado medio de dominancia presentados en este trabajo fueron obtenidos a partir de una población F₂, por lo que los mismos pudieran estar sesgados, debido a la covarianza entre el efecto de los locus, en desequilibrio de ligamiento, que controlan la producción de granos. Otros trabajos en maíz han reportado una disminución en el estimado del grado medio de dominancia en el transcurrir de las generaciones de recombinación (Han y Hallauer, 1989; Dudley, 1994), corroborando la hipótesis de Comstock y Robinson (1952).

Los estimados del coeficiente de heredabilidad para producción de granos, en base a la media de progenies y de plantas individuales tanto en sentido restringido como amplio, difirieron significativamente de cero (P≤0,05). El estimado del coeficiente de heredabilidad, en sentido restringido, presentó un valor de 0,45 (Cuadro 2), sugiriendo que el 45 % de la variabilidad fenotípica mostrada en las progenies de retrocruzamientos es debida a la varianza aditiva. Marker (2006) relató estimados del coeficiente de heredabilidad en sentido restringido de 0,52 y 0,53 en dos poblaciones de maíz, en cuanto Badu-Apraku et al. (2004) reportaron valor de 0,72 en el estimado de este parámetro.

Los estimados del coeficiente de heredabilidad al nivel de plantas en sentido amplio y al nivel de medias de progenies fueron de 0,94 y 0,65 (Cuadro 2), respectivamente, los cuales, según Stansfield (1974), son considerados altos. Valores altos del coeficiente de heredabilidad para PG también fueron reportados por Lima et al. (2006), Câmara et al. (2007) y Belicuas (2009). Por el contrario, Beyene et al. (2016) reportaron estimados de heredabilidad de bajo a medio en 9 de 10 poblaciones biparentales de maíz tropical evaluadas en ambientes de buena condición de humedad, mientras que bajo condiciones de estrés de sequía los estimados fueron ligeramente inferiores.

El caracter producción de granos, a pesar de tener herencia de tipo poligénica o compleja, en este estudio mostró coeficientes de heredabilidad altos y medios, indicando la factibilidad de identificar y seleccionar genotipos de superior comportamiento y heredar a sus descendientes genes favorables para la producción de grano. No obstante, el alto valor del estimado del coeficiente de heredabilidad en base a medias de progenies de medios hermanos puede deberse a que las progenies fueron evaluadas en gran cantidad de ambientes (once), con dos repeticiones por ambiente, lo que reduce las varianzas de la interacción progenies con ambientes y la del error experimental.

Caracteres de la planta. Para los caracteres de la planta (ART, FM, FF, IF, AP, AM y PRM) los estimados de la varianza aditiva fueron superiores a los de dominancia (Cuadro 2). Resultados similares han sido reportados para esos caracteres (Cockerham y Zeng, 1996; Singh y Gupta, 2008). Las magnitudes de los estimados de la varianza aditiva presentaron valores desde cuatro (ART) hasta 16 (PRM) veces superiores a los de dominancia, representando el estimado de la varianza aditiva para ART y PRM 80,00 y 94,1 %, respectivamente, de la varianza genética total.

Los estimados de la varianza aditiva para los caracteres altura y floración de la planta fueron desde 46,5 hasta 278,5 % superiores, respectivamente, a los estimados de la interacción entre la varianza aditiva y los ambientes; sin embargo, se obtuvo lo contrario para PRM, IF y ART; el estimado de la interacción entre la varianza aditiva y los ambientes, para esos caracteres, fue superior en 26,9; 67,4 y 357,1%, respectivamente, a los estimados de la varianza aditiva. Así, los efectos de la interacción entre la varianza aditiva y los ambientes son expresivos en el control genético del ART, IF y PRM, hecho corroborado por el bajo valor del estimado del coeficiente de heredabilidad de esos caracteres a nivel de plantas.

El grado medio de dominancia para los caracteres de la planta varió de 0,35 para PRM a 0,70 para ART (Cuadro 2); para ningún caracter el intervalo de confianza incluyó el valor 1,00, indicando la presencia de dominancia parcial de los genes involucrados en el control genético del acame, floración y altura de la planta. Se verificó, por consiguiente, que tanto los efectos aditivos como los de dominancia fueron importantes en la herencia de los caracteres de la planta, pero con predominancia de los efectos aditivos. Los resultados del grado medio de dominancia obtenidos en este estudio para los diversos caracteres de la planta son semejantes a los reportados en otros trabajos (Sughroue y Hallauer, 1997; Silva et al., 2004).

Los estimados del coeficiente de heredabilidad a nivel de plantas en sentido amplio y restringido presentaron valores medios para FM, FF, AP y AM y valores bajos para ART, IF y PRM (Cuadro 2). Para cada caracter, esos estimados tuvieron magnitudes semejantes, lo que también evidencia la mayor importancia de los efectos aditivos sobre los de dominancia.

Los estimados del coeficiente de heredabilidad a nivel de medias fueron altos para todos los caracteres de la planta, variando de 0,77 para IF a 0,96 para FM y FF, con excepción de ART, que presentó un valor moderado (0,58) (Cuadro 2). Los mayores valores de heredabilidad fueron obtenidos por caracteres de floración en comparación a los demás caracteres; resultados similares, en maíz, fueron obtenidos por Môro (2011) y Silva et al. (2004).

Para FF y AP, en condiciones de buena humedad del suelo, Beyene et al. (2016) encontraron estimados similares a los reportados en este trabajo, pero en condiciones de estrés de sequía, reportaron estimados de heredabilidad de bajos a medios en 10 poblaciones biparentales de maíz tropical, situación que era de esperarse pues la tolerancia a la sequía en maíz es una característica poligénica, típicamente tiene baja heredabilidad y está caracterizada por alta interacción genotipo x ambiente (Almeida et al., 2013).

Las altas magnitudes del coeficiente de heredabilidad, a nivel de medias, obtenidas en este trabajo pueden ser debidas a la variabilidad genética entre las progenies y al elevado número de ambientes de evaluación, lo que reduce la participación de la varianza de la interacción progenies por ambientes y del error experimental en el estimado de la varianza fenotípica.

Conclusiones

Las magnitudes de los estimados de los componentes de la varianza genética en las variables de producción de granos y caracteres de la planta, así como del grado medio de dominancia indican que los efectos aditivos tuvieron mayor importancia que los de dominancia en la expresión de esos caracteres.

Los estimados de los coeficientes de heredabilidad en sentido amplio y restringido, en la mayoría de los caracteres, estuvieron próximos, indicando que, probablemente, la mayor parte de la varianza genética es de naturaleza aditiva, por lo que métodos de selección simple como la selección familiar pueden conducir a ganancias genéticas satisfactorias.

Los altos valores de los coeficientes de heredabilidad implican la posibilidad de una efectiva selección para el mejoramiento genético del rendimiento en grano y caracteres de la planta.

LITERATURA CITADA

1. Abbott, L. y S. Pistorale. 2010. Determinación de componentes de la varianza y heredabilidad en cebadilla criolla (Bromus catharticus Vahl.). Agriscientia 27(2): 115-123.        [ Links ]

2. Abou-Deif, M. 2007. Estimation of gene effects on some agronomic characters in five hybrids and six populations of maize (Zea mays L.). World Journal of Agricultural Science 3(1): 86-90.        [ Links ]

3. Aguiar, A., L. Carlini-Garcia, A. Resende, M. Santos, A. García y C. de Souza. 2003. Combining ability of inbred lines of maize and stability of their respective single-crosses. Scientia Agrícola 60(1): 83-89.        [ Links ]

4. Almeida, G., D. Makumbi, C. Magorokosho, S. Nair, A. Borem, J. Ribaut et al. 2013. QTL mapping in three tropical maize populations reveals a set of constitutive and adaptive genomic regions for drought tolerance. Theor. Appl. Genet. 126(3): 583-600.        [ Links ]

5. Alves, G., M. Ramalho y C. de Souza. 2002. Alterações nas propriedades genéticas da população CMS-39 submetidas a seleção massal para prolificidade. Revista Brasileira de Milho e Sorgo 1(3): 89-101.        [ Links ]

6. Badu-Apraku, B., M. Fakorede, A. Menkir, A. Kamara y A. Adam. 2004. Effects of drought screening methodology on genetic variances and covariances in Pool 16 DT maize population. Journal of Agricultural Science 142(4): 445-452.        [ Links ]

7. Belicuas, P. 2009. Estudo da herança dos caracteres stay-green, produção e seus componentes emmilho utilizando o delineamento III e mapeamento de QTL. Escola Superior de Agricultura Luiz de Queiroz, Universidade de São Paulo, Piracicaba, SP. 97 p.        [ Links ]

8. Bello, O. y G. Olaoye. 2009. Combining ability for maize grain yield and other agronomic characters in a typical southern guinea savanna ecology of Nigeria. African Journal of Biotechnology 8(11): 2518-2522.        [ Links ]

9. Bernardo, R. 2002. Breeding for Quantitative Traits in Plants. Stemma Press. Woodbury, MN, USA. 369 p.        [ Links ]

10. Beyene, Y., K. Semagn, S. Mugo, B. Prasanna, A. Tarekegne, J. Gakunga et al. 2016. Performance and grain yield stability of maize populations developed using marker-assisted recurrent selection and pedigree selection procedures. Euphytica 208(2): 285-297.        [ Links ]

11. Bocanski, J., Z. Sreckov, A. Nastasic, M. Ivanovic, I. Djalovic y M. Vukosavljev. 2010. Mode of inheritance and combining abilities for kernel row number, kernel number for per row and grain yield in maize (Zea mays L.). Genetika 42(1): 167-176.        [ Links ]

12. Burdick, R. y F. Graybill. 1992. Confidence Intervals on Variance Components. Marcel Dekker. New York.        [ Links ]

13. Câmara, T., G. Alves, M. Santos, J. Moreira, y C. de Souza. 2007. Parámetros genéticos de caracteres relacionados à tolerância à deficiência hídrica emmilho tropical. Bragantia 66(4): 595-603.        [ Links ]

14. Ceballos, H., S. Pandey, L. Narro y J. Pérez- Velázquez. 1998. Additive, dominant, and epistatic effects for maize grain yield in acid and non-acid soils. Theoretical and Applied Genetics 96(5): 662-668.        [ Links ]

15. Cockerham, C. y Z. Zeng. 1996. Design III with marker loci. Genetics 143(3): 1437-1456.        [ Links ]

16. Comstock, R. y H. Robinson. 1952. Estimation of average dominance of genes. In: J. Gowen (ed.). Heterosis. Iowa State College Press. Ames, Iowa. pp. 494-516.        [ Links ]

17. Cruz, C., A. Regazzi y P. Carneiro. 2004. Modelos biométricos aplicados aomelhoramento genético. Ed. Universidade Federal de Viçosa. Viçosa, Minas Gerais, Brasil. 390 p.        [ Links ]

18. Dudley, J. 1994. Linkage desequilibrium in crosses between Illinois maize strains divergently selected for protein percentage. Theoretical Applied of Genetics 87(8): 1016- 1020.        [ Links ]

19. Falconer, A. 1989. Introduction to Quantitative Genetics. Longman, New York.        [ Links ]

20. Hallauer, A., M. Carena y J. Miranda-Filho. 2010. Quantitative Genetics in Maize Breeding. Third edition. Iowa State University Press. Ames, Iowa.        [ Links ]

21. Han, G. y A. Hallauer. 1989. Estimates of genetic variability in maize F2 populations. Journal of Iowa Academy Science 96(1): 14-19.        [ Links ]

22. Kearsey, M. y J. Jinks. 1968. A general method of detecting additive, dominance and epistatic variation for metrical traits. Heredity 23(3): 403-409.        [ Links ]

23. Knapp, S., W. Stroup y W. Ross. 1985. Exact confidence intervals for heredity on a progeny mean basis. Crop Sci. 25(1): 192-194.        [ Links ]

24. Lamkey, K., B. Schinicker y A. Melchinger. 1995. Epistasis in an elite maize hybrid and choice of generation for inbred line development. Crop Sci. 35(5): 1271-1281.        [ Links ]

25. Lima, M., C. de Souza, D. Bento, A. de Souza y L. Carlini-García. 2006. Mapping QTL for grain yield and plant traits in a tropical maize population. Molecular breeding 17:227-239.        [ Links ]

26. Malvar, R., A. Ordás, P. Revilla y M. Cartea. 1996. Estimates of genetic variances in two spanish populations of maize. Crop Sci. 36(2): 291-295.        [ Links ]

27. Marker, S. 2006. Genetic analysis of yield and other characters in two populations of maize (Zea mays). The Indian Journal of Agricultural Science 79(8): 512-514.        [ Links ]

28. Môro, G.2011, Uso da seleção genômica e fenotípica emlinhagens para a predição de teste crossesemmilho. Tese, Escola Superior de Agricultura Luiz de Queiroz, Universidade de São Paulo. 116.        [ Links ]

29. Raposo, F. y M. Ramalho. 2004. Componentes de variância genética de populações derivadas de híbridos simples de milho. Revista Brasileira de Milho e Sorgo 3(3): 402-413.        [ Links ]

30. Santos, M., G. Môro, A. Aguiar y C. de Souza. 2005. Responses to reciprocal recurrent selection and changes in genetic variability in IG-1 and IG-2 maize populations. Genetics and Molecular Biology 28(4): 781-788.        [ Links ]

31. Satterthwaite, F. 1946. An approximate distribution of estimates of variance components. Biom. Bull. 2(6): 110-114.        [ Links ]

32. Searle, R., G. Casella y C. McCulloch. 1992. Variance components. Wiley. New York.        [ Links ]

33. Silva, A., C. de Souza, A. Aguiar y A. Souza. 2004. Estimates of genetic variance and level of dominance in a tropical maize population. I. Grain yield and plant traits. Maydica 49: 65-71.        [ Links ]

34. Silva, J. y A. Hallauer. 1975. Estimation of epistatic variance in Iowa stiff stalk synthetic maize. J. of Heredity 66(5): 290-296.        [ Links ]

35. Silva, R., P. García, D. Silva y C. de Souza. 2017. Epistasis para producción de granos y caracteres de la planta en una población de maíz tropical. Bioagro 29(2): 83-94.        [ Links ]

36. Singh, S. y B. Gupta. 2008. Triple test cross analysis to detect of epistasis for morphophysiological traits related to drought tolerance and yield components in maize (Zea mays L.). Journal of Research 7(2): 202-209.        [ Links ]

37. Sobierajski, G., P. Kageyama y A. Sebbenn. 2006. Estimates of genetic parameters in Mimosa scabrella populations by random and mixed reproduction models. Crop Breeding and Applied Biotechnology 6: 47-54.        [ Links ]

38. Stansfield, W. 1974. Genética. São Paulo: McGraw-Hill do Brasil.        [ Links ]

39. Sughroue, J. y A. Hallauer. 1997. Analysis of the diallel mating design for maize inbred lines. Crop Sci. 37(2): 400-405.        [ Links ]

40. Vencovsky, R y P.Barriga. 1992. Genética Biométrica Aplicada ao Fitomelhoramento. Sociedade Brasileira de Genética. Ribeirão Preto, Sao Paolo. 496 p.        [ Links ]

41. Wolf, D., L. Peternelli y A. Hallauer. 2000. Estimates of geneticvariance in an F2 maizepopulation. J. of Heredity 91(5): 384-391.        [ Links ]

42. Zdunic, Z., A. Mijic, K. Dugalic, D. Simic, J. Brkic y A. Marjanovic-Jeromela. 2008. Genetic analysis of grain yield and starch content in nine maize populations. Turk. J. of Agric. and Forestry 32(6): 495-500.        [ Links ]