La transferencia de Hohmann y la propiedad de consumo equivalente de combustible.

Moreno Vega ,Valery;  Aeyels Dirk

 MSc. Valery Moreno Vega: Profesor Asistente en el Dpto. de Automática y Computación de la Facultad de Ingeniería Eléctrica del Instituto Superior Politécnico “José Antonio Echeverría, calle 114 entre 119 y 127, Nº 11901, La Habana, Cuba, Telef. 537-2602055, fax 537-2677129, correo electrónico  valery@electrica.cujae.edu.cu

Dr. Dirk Aeyels: Profesor Titular en la Facultad de Ciencias Aplicadas de la Universidad de Gantes, Bélgica, Telef. 32 (0) 9.264.58.40, correo electrónico dirk.aeyels@ugent.be.

Resumen: La astronáutica como tecnología ha evolucionado mucho en los últimos 50 años, pero a pesar de eso, es una de las tecnologías que demanda una búsqueda constante de nuevas soluciones. Uno de los temas subyacentes de las investigaciones espaciales es la búsqueda de soluciones rápidas para casos de fallas (planes de contingencia) y de soluciones alternativas para la evaluación de diferentes momentos del desarrollo de una misión [1]. Durante el desarrollo de una misión se efectúan diferentes maniobras que tienen como objetivo guiar al vehículo espacial desde el punto de partida al destino siguiendo una trayectoria previamente planificada. La más común de esas transferencias se conoce como transferencia de tipo Hohmann  y está demostrado que, bajo ciertas condiciones, es óptima con relación al consumo de combustible. En este artículo se reporta que partiendo de un análisis de este tipo de transferencias, se puede demostrar la existencia de órbitas Keplerianas con la propiedad, definida aquí, de “consumo equivalente de combustible”. La condición para la existencia de este tipo de órbitas se expresa en términos de un radio crítico. La aplicabilidad de este hallazgo para el diseño de planes de contingencia y soluciones alternativas, se muestra aquí por medio de dos ejemplos.

Palabras Claves: Modelo de los dos cuerpos/ Órbitas equivalente/ Órbitas Keplerianas/ Planes de contingencia/ Transferencia Hohmann.

The Hohmann transfer and the equivalent fuel consumption property.

Abstract: Despite of the great evolution of  the astronautic as a technology in the last 50 years, it remains as one of the fields that demands a constant search of new solutions. One of the underlying topics of the space research efforts is to look for quick solutions in case of unforeseen situations arrives (contingency plans) and of the alternative solutions to be evaluated in different phases of the mission deployment [1]. There exists different kind of maneuvers during the development of a mission, always performed with the objective of guiding the spacecraft from its initial location to its final location following a prescribed trajectory. The well known Hohmann transfer is the most used, and it has been proved that, under certain conditions, it is optimal with respect to the fuel consumption. In this paper we report on the existence of orbits with equivalent fuel consumption when a maneuver is performed between Keplerian orbits. The condition for the existence of these orbits is given in terms of a critical radius. The applicability of this finding for designing contingency plans is illustrated by means of two examples.

Keywords: Contingency Plans/ Equivalent Orbits/ Hohmann Transfers/ Keplerian Orbits/ Two Body Model.

Finalizado el 2004/01/28  Recibido el 2004/02/10  Aceptado el 2004/11/22

I. INTRODUCCIÓN

En el espacio, para producir un movimiento en el vehículo que cambie su curso, o la órbita sobre la cual se mueve, se necesita modificar su velocidad (aceleración). Esto se realiza mediante impulsos discretos, o sea, se encienden los motores por un tiempo determinado, para frenar o acelerar el vehículo. Esto provoca un desvío en la trayectoria del vehículo. A estas fases se les conoce por el nombre de maniobras impulsivas, pues el cambio en la velocidad se modela mediante una función impulsiva aplicada a los motores de la nave [2].

La búsqueda de trayectorias óptimas y de planes de contingencia es una de las tareas que siempre están presentes en problemas de diseño de misiones espaciales. Las trayectorias óptimas reducen los gastos de combustible de la misión ([3], [4], [5],[6],[7] ,[8]), y por tanto, su costo, mientras que un conjunto de soluciones alternativas subóptimas o  planes de contingencia reducen el riesgo que tiene toda misión de fallar  [1]. La capacidad potencial de DV (cambio en velocidad producido por las maniobras, una medida del consumo de combustible) de las misiones, por lo general, incluye algunas estimaciones del combustible adicional que podría necesitarse en caso de ocurrencia de fallas.

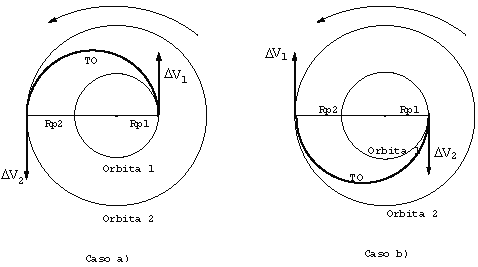
Las órbitas Keplerianas son aquellos tipos de órbitas que se obtienen al resolver el problema de los dos cuerpos en movimiento en el espacio exterior [2] y pueden ser, circulares, elípticas, parábolas o hipérbolas (se dicen que son cónicas pues todas se derivan de una sección cónica).  Estas órbitas son las que describen el movimiento de los vehículos espaciales, cuando se trabaja con el modelo de los dos cuerpos, que es, por demás el modelo más utilizado en el diseño de misiones espaciales. Para el estudio de las transferencias óptimas entre órbitas Keplerianas utilizando maniobras impulsivas puede hacerce referencia a un grupo de artículos y libros como los sugeridos en ([7], [8], [9], [10]). Ha sido demostrado (ver por ejemplo, [7], [9]) que bajo, ciertas condiciones, la transferencia de Hohmann es óptima con respecto al consumo de combustible. La transferencia de Hohmann es muy efectiva y consiste en mover un vehículo espacial de una órbita a otra, por medio de un movimiento que le hace describir una elipse, aplicándose para ello dos impulsos, uno para sacar a la nave de su órbita y otro para insertarla en la nueva (ver Figura 1). En [7] Lawden demostró que si la razón entre los radios de las dos órbitas circulares involucradas en la transferencia excede el valor de 15.6, entonces la transferencia de Hohmann no es óptima (más recientemente esta relación se fijó en 15.58 en [9]). Si esta condición se satisface, entonces la transferencia de 3 impulsos (una composición de dos transferencias de Hohmann), puede considerarse una mejor solución. En este artículo se demuestra como el valor 15.58 de la razón entre los radios de las órbitas juega un papel crítico e importante en un contexto diferente, o sea, se proporciona otra interpretación para este valor. Se muestra la existencia de pares de órbitas desde las cuales maniobras o transferencias impulsivas de tipo Hohmann pueden implementarse para alcanzar una órbita final, consumiendo la misma cantidad de combustible. También se incluye en el artículo la relación entre esta propiedad y la búsqueda de soluciones alternativas y planes de contingencia en el diseño de misiones espaciales.

Figura 1- Transferencia de Hohmann. Los DV son los impulsos, TO  es la órbita de transferencia (semi elipse), Rp1 y Rp2 son respectivamente los radios de las órbitas 1 y 2 involucradas en la transferencia.

II. DESARROLLO.

1. Resultados teóricos.

A menudo a las órbitas descritas por el movimiento de las naves espaciales se les denomina órbitas de parqueo, pues el vehículo espacial, sin la presencia de algún cambio de velocidad, se mantiene, en lo esencial, en ellas. En el movimiento de dichas naves y en general de cualquier cuerpo celestial, influyen varios astros. Con el objetivo de determinar hasta donde puede llegar la influencia de cada uno de ellos sin que pueda despreciarse, se define el concepto de Esfera de Influencia, formulado hace más de 100 años por Laplace [9]. Si la influencia sobre un vehículo espacial proviene de un solo cuerpo celestial, a ese cuerpo se le llama cuerpo central (CC). Estos dos conceptos se utilizarán en el artículo. El resto de las secciones del artículo se organizan como sigue: a continuación se formaliza mediante un teorema, el concepto de radio crítico que será utilizado en la sección 1.2. Para definir la propiedad de consumo equivalente de combustible entre órbitas de parqueo. A partir de la definición de órbitas equivalentes de la sección 1.2 en la sección 1.3 se reflexiona sobre algunos aspectos importantes de las órbitas equivalentes. En dicha sección además se brinda la forma de calcularlas. Para resaltar e ilustrar claramente la validez práctica y las ventajas del uso de estas órbitas equivalentes, y su relación con los planes de contingencia y las soluciones alternativas, se han incluido dentro de la sección 3 dos ejemplos. Las conclusiones se ofrecen en la sección III.

1.1  El Radio Crítico de las Transferencias.

Se supone que un vehículo se encuentra moviéndose en una órbita de parqueo (PO) de radio R. se supone además, que se considera una transferencia a otra PO de radio R_{órbita_final} y que R > R_{órbita_final},  perteneciendo ambas órbitas a la esfera  de influencia del  cuerpo central  (CBSOI) que influye sobre el vehículo.

Teorema 1: Bajo la hipótesis de que una órbita Y con Ry=15.5819* R_{órbita_final} pertenece a la  CBSOI, una transferencia desde la órbita Y de radio Ry a una PO de radio R_{órbita_final} se corresponde con un máximo consumo de combustible. A esta órbita se le llamará la órbita critica y a su radio, el radio critico.

Demostración:

La expresión general para la transferencia de tipo Hohmann de un vehículo espacial entre dos órbitas es:

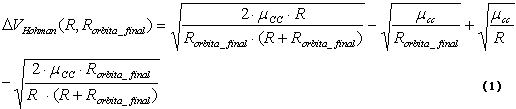
En la expresión anterior R es el radio de la órbita desde la cual se inicia la transferencia de Hohmann y R_{órbita_final} es la órbita donde llega el vehículo después de terminada la transferencia. La constante m es el parámetro gravitatorio específico del cuerpo central que domina el espacio en el cual se efectúa la transferencia.

Para demostrar que existe una órbita de parqueo entre la órbita de radio R_CBSOI y R_{órbita_final} , desde la cual la transferencia de Hohmann se realiza a un costo máximo en términos de combustible, se deben encontrar los extremos de (1) y verificar si constituyen un máximo, un mínimo o ninguno de ellos.  Considerando las siguientes notaciones:

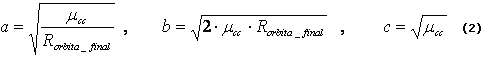
y la función real  f: Â⁺ ® Â⁺

f (R) = DV_hohmann(R,R_{orbita_final})            (3)

Sustituyendo (2) en (1) y ésta en (3) se obtiene:

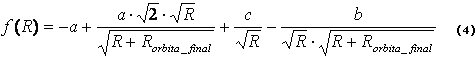
Derivando con relación a R se obtiene:

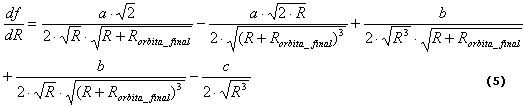
La condición necesaria para la existencia de extremos es precisamente igualar la primera derivada de f  (ecuación (5)) a cero. Después de un número de pasos se obtiene que las raíces de son las raíces de la ecuación cúbica polinómica:

R³ - 15 · R² · R_{orbita_final} - 9 · R · R²_{orbita_final}  - R³_{orbita_final}  = 0    (6)

Resolviendo (6) para R se encuentran tres raíces reales, a saber:

R_{orbita_final}   , R₂ = -04.4340∙R_{orbita_final}   , R₃ = -1480∙R_{orbita_final}

R₁ es la única solución válida de las raíces de (6) pues es la que pertenece a Â⁺, el dominio de R. La segunda derivada de (4), , evaluada para R₁ es negativa y por tanto la función f  tiene un máximo para R₁, que es precisamente el valor de Ry definido en el enunciado del teorema.

En (9) se obtiene la misma ecuación cúbica obtenida en la demostración del teorema. En ese caso, para determinar el valor de R para el cual la transferencia bielíptica requiere menos combustible que la transferencia de Hohmann. Notese que no se reclama originalidad con respecto al valor de 15.58; en cambio, se formaliza un nuevo concepto, el de radio crítico para proporcionar una nueva interpretación a este valor y obtener nuevos resultados, expresados en lo que aquí se definirá por primera vez como la propiedad de consumo equivalente de combustible y de órbitas equivalentes.

1.2  Las órbitas equivalentes.

La siguiente conclusión se deriva del teorema anterior:

Corolario 1:  Si R_CBSOI > Ry entonces existe una cantidad infinita de pares de PO desde las cuales un vehículo puede enviarse a una órbita de parqueo final dentro del sistema con el mismo costo en términos de consumo de combustible. Estos pares de órbitas se dicen que satisfacen la propiedad de “consumo equivalente de combustible'' (EFC). Cada par de órbitas satisfaciendo la propiedad EFC se dice que es un par de órbitas equivalentes.

El Corolario 1 se puede derivar de observar que puesto que la función continua  f tiene un máximo dentro del intervalo [R_{órbita_final},R_CBSOI] ,entonces órbitas con radios R_i y R_j (R_i Î [R_{órbita_final},Ry[ y R_j Î ]Ry,R_CBSOI]) satisfacen f(R_i)=f(R_j) (R_j debe escogerse de forma que f(R_j)³  f(R_CBSOI)).

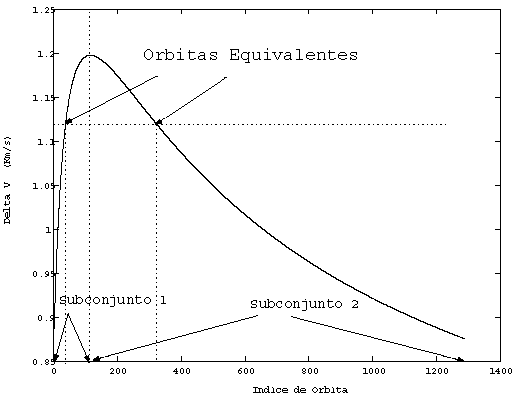
En la Figura 2 se muestra un ejemplo de dos órbitas que cumplen con la propiedad de “consumo equivalente de combustible”.

Figura 2- Un ejemplo de dos órbitas que satisfacen la propiedad de  "consumo equivalente de combustible". 

1.3  Algunos aspectos importantes sobre las órbitas equivalentes.

Obsérvese que el concepto de órbitas equivalentes se relaciona con transferencias, y por lo tanto, una órbita puede tener su equivalente o no dependiendo de la órbita hacia la cual se realizará la transferencia, o sea, la existencia de la órbita crítica Y dentro de la esfera de influencia del cuerpo central (CBSOI) depende del valor de R_{órbita_final}.

El concepto de órbitas equivalentes se puede también generalizar para más de una transferencia. Se puede demostrar que, si se considera una secuencia de transferencias comenzando en una órbita inicial de radio R_{órbita_inicial} tal que Ry < R_{órbita_inicial}  £ R_CBSOI, existirán pares de órbitas con radios R_xi Î [R_{órbita_final},Ry[ y R_yj Î]Ry,R_{órbita_inicial}] satisfaciendo:

f (R_xi) + DV_Hohmann (R_{orbita_inicial}, R_xi) = f (R_yj) + DV_Hohmann (R_{orbita_inicial}, R_yj)    (7)

Los caminos o trayectorias R_{órbita_inicial} ® R_xi ® R_{órbita_final} y R_{órbita_inicial} ® R_yj ® R_{órbita_final}  tendrán asociado el mismo consumo de combustible.

Si existen órbitas equivalentes, entonces el conjunto de todas las órbitas de parqueo dentro de la CBSOI pueden dividirse en dos subconjuntos definidos a partir del radio crítico: los miembros del primer subconjunto son las órbitas cuyos radios son menores que el radio crítico y los miembros del segundo, las órbitas con radios mayores que dicho radio crítico. En la Figura 2 se representan estos conjuntos tomándose como cuerpo central a la Luna y estando la órbita final (que define el valor de R_{órbita_final}) a 45km sobre la superficie lunar. Además, el DV se calculó considerando una órbita inicial  con radio igual al de la esfera de influencia de la Luna (R_CBSOI=66183 Km) ([9]) mientras que los radios de las órbitas de parqueo (en Km) se calcularon utilizando la ecuación R_i=50*i-5 evaluada para los índices de órbita i de la figura (desde 1 hasta 1280). 

Conociendo las órbitas equivalentes se pueden manejar mejor las restricciones típicas de un problema de diseño de trayectorias para un vehículo espacial. Por ejemplo, si se toma el primer subconjunto de la Figura 2, y se supone que para una misión particular el vehículo no puede ser transferido hacia ninguna de las órbitas que integran dicho subconjunto, entonces se puede pensar en utilizar la propiedad de consumo equivalente de combustible, para seleccionar un grupo de órbitas "equivalentes" pertenecientes al segundo subconjunto de dicha figura (en la próxima sección se ilustra con un ejemplo numérico) pues, como ya se demostró, la transferencia desde órbitas equivalentes a una órbita final se efectúa consumiendo la misma cantidad de combustible.

Para encontrar el radio R_e de la órbita equivalente a la órbita de parqueo de radio R₁, y conocido además el valor de  R_{órbita_final}, se debe resolver la siguiente ecuación para R_e:

f (R_e) = f (R₁)        (8)

y verificar si la condición R_e < R_CBSOI se satisface. Se  elaboró una rutina para MatLab 6.1 que resuelve numéricamente  la ecuación. Dicha rutina se encuentra disponible sobre la base de una solicitud.

2. Ejemplos.

A continuación se presentan algunos ejemplos que ilustran el uso de los resultados reportados por primera vez aquí sobre las órbitas equivalentes y su utilidad para la solución de problemas típicos encontrados en el diseño de trayectorias para misiones espaciales, como pueden ser, el manejo de restricciones, la búsqueda de soluciones alternativas y de planes de contingencia.

2.1 Manejo de restricciones y soluciones alternativas.

Considérese el siguiente problema:

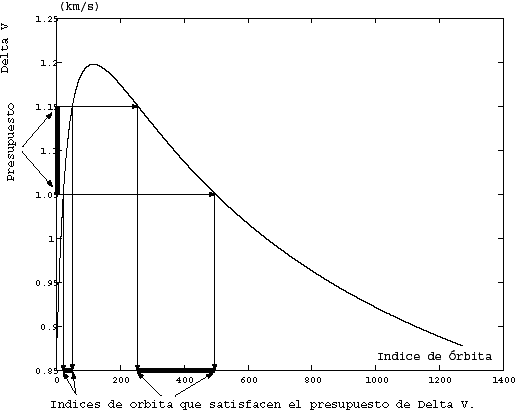
Encuentrar el conjunto de órbitas de parqueo lunares (MPO) hacia el cual debe ir un satélite lanzado desde la Tierra debe ir si el presupuesto disponible expresado en DV para el subsistema Esfera de Influencia de la Luna-Luna  de la misión satisface 1.05 km/s £ presupuesto DV £ 1.15 km/s.

El problema aquí es encontrar el conjunto de todas las órbitas de parqueo lunares MPO_i,  dada una restricción en el presupuesto de consumo de combustible. Además se quiere saber el conjunto de órbitas, o sea, que si hay más de una satisfaciendo la restricción de presupuesto, entonces también debe formar parte del conjunto. Conociendo el presupuesto en DV se pueden evaluar las transferencias de Hohmann (vea ecuación (1)) desde la órbita final en la Luna hasta la órbita crítica Y, y extraer el conjunto de MPO para la cual las restricciones en el presupuesto se satisfacen. Además de esas órbitas aplicando después la ecuación (8) se pueden obtener las “órbitas equivalentes” de las primeras encontradas y con eso se completaría la respuesta. Nótese que si no se hace uso del concepto de órbitas equivalentes habría que haber evaluado la ecuación (1) desde la órbita final en la Luna hasta la órbita que se encuentra en el límite de la esfera de influencia lunar, o sea, todas las posibles órbitas, lo cual demoraría enormemente la búsqueda de la solución, pudiendo ser incluso inviable si se necesita la respuesta rápidamente o si en lugar de ser la Luna se considera otro planeta (la Tierra) mayor en masa que la Luna y con una Esfera de Influencia mucho mayor.

La solución, representada gráficamente, se muestra en la Figura 3. Dicha solución es el conjunto de órbitas de parqueo cuyos índices  pertenecen a uno de los conjuntos w={21,...,49} y c={253,...,495}. El camino que el satélite debe seguir después de su entrada en la Esfera de Influencia de la Luna es para este ejemplo: MPO_i ®MFLO (denota aquí a  la órbita final en la Luna) con i Πw È c. Se elaboró una rutina con Matlab 6.1 que ayuda a encontrar  soluciones alternativas de este tipo, que está disponible a solicitud.

Figura 3- Solución al problema presentado en el Ejemplo 1.

2.2  Solución óptima. Caso crítico cuando solo esta solución es la adecuada para continuar la misión.

Introducción del Problema:

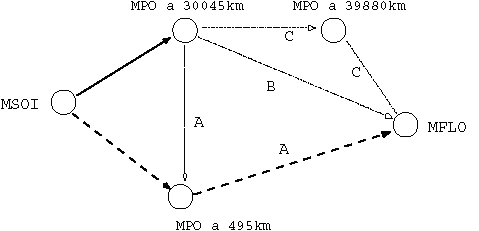
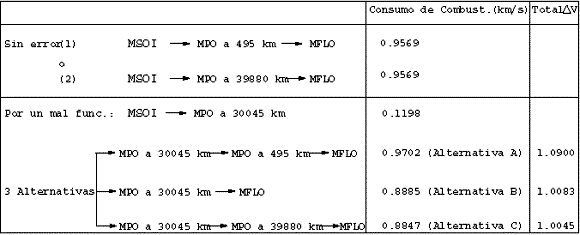
Un vehículo ha sido enviado a la Luna con propósitos de investigación. La misión se encuentra en progreso y el vehículo ha completado exitosamente la primera parte de la misión: ha arribado a la esfera de influencia de la Luna (órbita de Conexión) y ha comenzado una maniobra que lo ubicará dentro del subsistema de la Luna. Para la segunda fase, asumiendo que no se producen errores, se ha considerado un presupuesto en DV de 0.9569 km/s durante la fase de diseño de la misión. También se ha tenido en cuenta que el vehículo arribe a alguna MPO (órbita de parqueo lunar) para permitir procedimientos de comprobación, circularización de la órbita, etc. antes de dirigirse a la órbita final de parqueo (45 Km sobre la superficie lunar). El camino Órbita de Conexión ® MFLO no es deseado para la misión. Con estos señalamientos en mente se puede calcular ([2],[9]) que el vehículo debe arribar a una MPO localizada a 495 Km sobre la superficie lunar y después de un corto tiempo, dirigirse a la órbita final de parqueo (MFLO). Esta trayectoria planificada se dibuja con líneas de puntos en la Figura 4. El consumo estimado de combustible en función de DV se muestra en la Figura 5.

Figura 4- La línea discontinua es la trayectoria original. El resto son las alternativas.

Figura 5- DV necesarios para efectuar las transferencias representadas en la Figura 4.

Debido a un mal funcionamiento, un motor de impulso se ha puesto en marcha, causando que el vehículo permanezca  en movimiento en una MPO localizada a 30045km de la Luna. El objetivo principal es ubicar el vehículo en su posición final de alunizaje, por tanto, el problema aquí es encontrar una solución apropiada para que la misión pueda continuar, asumiendo de ser necesario que los procedimientos de comprobación, circularización, etc. pueden realizarse en la órbita actual. En otras palabras, se debe encontrar un nuevo camino (optimizado en relación con el combustible a gastar) desde la posición actual hasta la MFLO y ver después si la disponibilidad de combustible es suficiente para continuar la misión.

Discusión de la Solución:

El procedimiento estándar ([8]) es reinsertar el vehículo en el camino calculado durante la fase de diseño de la misión (vea Figura 4, Alternativa A). Esto significa que se debe realizar una maniobra que sea capaz de enviar el vehículo hacia la MPO a 495km de la superficie lunar mediante el uso de transferencias de Hohmann o alguna otra operación de corrección del rumbo para poder regresar al camino original. Sin embargo, además de la determinación de las posibles maniobras a realizarse y de cual de ellas es la apropiada (por medio de la evaluación de muchas de ellas), debe considerarse que el presupuesto de combustible en DV es limitado. Una dificultad adicional aparece si se consideran misiones con restricciones adicionales de tiempo de vuelo. También es usual (si no hay muchas restricciones en el tiempo de búsqueda de una nueva solución) considerar la continuación de la misión desde el punto donde se encuentra la nave actualmente (Alternativa B).

Para la búsqueda de la solución, sin embargo, y a la luz de lo reportado en este artículo sobre las órbitas equivalentes, se puede considerar otra posible solución, la llamada Alternativa C. Esta solución toma en cuenta la "órbita equivalente" de la MPO a 495km con relación a la órbita final de alunizaje. La idea fundamental detrás de esta alternativa es que el consumo de propelente es el mismo desde dichas órbitas, y quizás en las nuevas condiciones cueste menos ir desde la actual a la equivalente de la original, y de ahí al destino final. Incluso si se aplicó el concepto de órbitas equivalentes descrito aquí durante la fase de diseño,  se debió descartar una de las órbitas, pues tienen el mismo consumo de combustible (y por tanto hay dos trayectorias que presentan el mismo gasto escogiéndose una), pero debe tenerse en cuenta si algo incorrecto sucede durante el desarrollo de la misión. En este ejemplo, y aplicando (8), se encuentra que esta órbita equivalente se localiza a 39880km de la superficie lunar.

Conclusiones del Ejemplo:

Los valores de DV calculados para las tres opciones así como el valor inicial de consumo de combustible, se muestran en la Figura 5. La mejor solución es precisamente ir a la “órbita equivalente” (MPO a 39880km) y desde esa órbita a la MFLO. La peor solución es reinsertarse en la trayectoria anterior (esta trayectoria no tenía por qué ser óptima), o sea, la Alternativa A. Si el DV adicional incluido a bordo del vehículo no excede los 51 m/s (diferencia en DV cuando no se producen errores y el total para la Alternativa B) entonces la única solución posible es la Alternativa C. Nótese en la Figura 5 que para el caso en que no se produzcan errores  se tienen dos posibles soluciones óptimas: (1) y (2). Si el programa original hubiera sido el  (2), entonces la mejor solución después de haberse producido la falla y el desvió de la trayectoria, hubiera sido precisamente reinsertar al vehículo en la trayectoria (2) (en este caso la Alternativa C).

III.  CONCLUSIONES.

1) La propiedad de consumo equivalente de combustible, se reporta por primera vez en este trabajo sobre la base de un radio crítico que depende de varios factores, entre los cuales está la órbita final de la transferencia.

2) El uso de las órbitas equivalentes contribuye a disminuir el riesgo que toda misión tiene de no culminar satisfactoriamente.

3) También se muestra como se pueden brindar soluciones alternativas en menor tiempo, pues el número de cálculos se reduce.

4) Los resultados ayudan a brindar mayor autonomía en el espacio para los satélites y vehículos

5) El procedimiento de búsqueda de las soluciones alternativas, que se basa en la búsqueda de órbitas equivalentes, se puede programar e incluir en los programas de contingencia de las naves espaciales.

6) El método además brinda una solución directa y que consume muy poco tiempo de cálculo, por lo que puede ser utilizado como procedimiento en misiones tripuladas.

IV. REFERENCIAS

1) Koon, W.S. et all. “The Genesis Trajectory and Heteroclinic Connections”, AAS/AIAA Astrodynamics Specialist Conference, 1999. pp. 451-457,         [ Links ]

2) Sidi, M.J. “Spacecraft Dynamics & Control: A practical Engineering Approach”. Cambridge Aerospace Series 7, Cambridge University Press, 1997.        [ Links ]

3) Howell, K.C. et al. “Application of Dynamical Systems Theory to Trajectory Design for a Libration Point Mission”, The Journal of the Astronautical Sciences, Abril-Junio 1997.45(2), pp. 161-178,         [ Links ]

4) Lo, M.W et al. “Genesis Mission Design”, The Journal of the Astronautical Sciences, January – March 2001 49(1), pp. 169-184.        [ Links ]

5) Serban, R. et al. “Halo Orbit Mission Correction Maneuvers Using Optimal Control”, Automatica, April 2002 38(4), pp.571-583.        [ Links ]

6) Bate, R.R et all. “Fundamentals of Astrodynamics”, New York, Dover, 1971.        [ Links ]

7) Lawden, D.F. “Optimal Trajectories for Space Navigation”, London, Butterworths, 1963.        [ Links ]

8) Bryson, A.E., Ho, Y.C. “Applied Optimal Control”, Washington DC, Hemisphere, 1975.        [ Links ]

9) Prussing, J.E., Conway B.A. “Orbital Mechanics”, Oxford University Press, 1993, pp. 99-118.        [ Links ]

10) Hoelker, R.F., Silber, R. “The Bi-Elliptic Transfer Between Circular Coplanar Orbits”, Army ballistic Missile Agency, Redstone Arsenal, Ala. Report No. DA-TM-2-59, 1959.        [ Links ]