Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Universidad, Ciencia y Tecnología
Print version ISSN 1316-4821On-line version ISSN 2542-3401
uct vol.9 no.33 Puerto Ordaz Mar. 2005
Generalización del Algoritmo de Trazado de rayos de Monte Carlo Modificado para el Cálculo de la Respuesta al Impulso de Canales Ópticos Infrarrojos en Interiores.
Biosca Rojas, Dioén; López Presmanes, Jorge Luís
MSc. Dioén Biosca Rojas: Profesor Auxiliar del Dpto. de Telecomunicaciones, Facultad de Ingeniería Eléctrica, Instituto Superior Politécnico José Antonio Echeverría (ISPJAE), Calle 114, Nº 11901 e/ 119 y 127, Marianao, CP 19390, Ciudad Habana, Cuba, teléfono (537) 8303674, correo electrónico dioenbiosca@yahoo.com. y bios@reduniv.edu.cu.
Dr. Jorge Luis López Presmanes: Profesor Titular en el mismo Departamento, correo electrónico pres@reduniv.edu.cu
Resumen: En el presente trabajo se propone un nuevo modelo para el cálculo de la respuesta al impulso de canales ópticos inalámbricos en interiores. La inclusión de las Funciones de Distribución de Reflectancia Bidireccional sobre el esquema de trazado de rayos de Monte Carlo modificado permite una modelación mas precisa de las características de reflectividad de las distintas superficies reflectoras existentes en el canal, convirtiendo el algoritmo de Monte Carlo original en una herramienta de modelación mucho más general que sus antecesoras. La incorporación de las mencionadas funciones de reflectancia es posible gracias a la obtención del coeficiente de reflexión direccional-hemisférico para diversos modelos de reflectores, elemento que se muestra en el desarrollo del trabajo así como las vías para obtener las direcciones de los rayos reflejados a partir de tomar la función de reflectancia del material como una función de distribución de probabilidad. Se incluyen adicionalmente consideraciones de eficiencia y convergencia del nuevo algoritmo propuesto. Además, se presentan varios resultados de simulación obtenidos con el nuevo algoritmo en comparación con los resultados reportados por otros autores sobre un grupo de configuraciones típicas, tanto para reflectores Lambertianos como de Phong, los cuales permiten la validación del algoritmo presentado.
Palabras Clave: Algoritmo de trazado de rayos / Canales ópticos infrarrojos / Enlaces Ópticos Inalámbricos / Monte Carlo/ Respuesta al Impulso.
Generalization of Monte Carlo Ray-Tracing Algorithm for the Calculation of the Impulse Response on Indoor Wireless Infrared Channels
Abstract: In this paper a new model for the calculation of the impulse response on indoor wireless infrared channels is proposed. The use of Bidirectional Reflectance Distribution Functions on a modified Monte Carlo ray-tracing algorithm allows a better modeling of the reflection properties of the different reflecting surfaces present in the channel, transforming the original Monte Carlo scheme in a more general and accurate simulation tool. The work with reflectance functions is possible because of the derivation of the directional-hemispherical reflection coefficient as a function of reflectors material for different types of reflectors. This aspect is shown along the paper as well as the ways for obtaining reflected rays directions by sampling the reflectors reflectance function as a probability distribution function. Some considerations about efficiency and convergence of the new proposed algorithm are included. Also, some simulations results on typical reported configurations are presented and discussed as particular cases for the new formulation. The comparison of this results with the results reported by other authors for the same configurations is used for validating the new algorithm just presented.
Keywords: Impulse Response / Monte Carlo / Ray-Tracing Algorithm / Wireless Infrared Chanels / Wireless Optical Links.
Finalizado el 2003/08/01 Recibido el 2003/08/23 Aceptado el 2004/12/15.
I. Introducción.
Para el estudio y caracterización del canal infrarrojo inalámbrico en interiores se han propuesto típicamente modelos [1-4] que asumen las superficies reflectoras como difusores ideales de Lambert. Este supuesto, aunque contribuye a una simplificación importante de los algoritmos de cálculo de la respuesta al impulso del canal, constituye una limitación de los modelos tradicionales ya que existen, en los entornos más comunes, innumerables materiales y superficies que exhiben comportamientos de reflectividad que nada tienen que ver con el de un difusor ideal (ej. fórmica, madera barnizada, plásticos, vidrio, etc.).
En [5] se sugiere por primera vez el empleo del modelo de reflector de Phong, que permite simular superficies con componentes especulares significativas, obteniéndose una diferencia de aproximadamente 5dB en la estimación de la potencia óptica recibida, al comparar los resultados obtenidos, asumiendo que la superficie reflectora sigue el modelo de Phong o el de Lambert respectivamente. Este hecho deja en evidencia la importancia de considerar en la simulación modelos más específicos de reflectividad para cada superficie. El modelo de Phong se usa posteriormente también en [6].
A partir del éxito relativamente reciente del empleo de las funciones de distribución de reflectancia bidireccional (BRDF) en la síntesis artificial de imágenes por computadora [7,8], particularmente en la recreación de escenas del mundo real con un alto nivel de realismo, se decide incorporar estas funciones al análisis de los canales ópticos inalámbricos en interiores para la modelación de las propiedades de los distintos materiales reflectores.
El esquema de simulación escogido para la incorporación de los elementos de generalización dados por la inclusión de las BRDF es el del algoritmo de trazado de rayos de Monte Carlo modificado, fundamentalmente por su alta eficiencia de cálculo y su naturaleza (el trazado de rayos), que permite la modelación de forma natural de fenómenos ópticos como la reflexión, la refracción y la difusión o scattering. En dicho esquema se incorpora de forma novedosa, entre otros aspectos, el uso del coeficiente de reflectividad direccional-hemisférico, que depende de la BRDF del material, para la actualización de la potencia de los rayos reflejados durante el proceso de cálculo. Más adelante se ofrecen ejemplos del cálculo de este coeficiente para tres tipos de reflectores. Este elemento permite la modelación de virtualmente cualquier patrón de reflectividad posible a encontrar según el tipo de superficies típicas de los diversos entornos interiores, convirtiendo el algoritmo inicial en una herramienta mucho más general y exacta.
El trabajo está organizado de la siguiente forma: En la Sección 1 se expone la estructura básica del algoritmo original de trazado de rayos de Monte Carlo modificado, sobre el que se incorporan posteriormente en la Sección 2 los nuevos elementos de generalización. En la Sección 3 se ofrecen las expresiones para la obtención de las direcciones de los rayos reflejados cuando se utilizan diversos modelos de BRDF para los reflectores. Más adelante en la Sección 4 podrá encontrarse la estructura del nuevo algoritmo general propuesto mientras que en las secciones siguientes, 5 y 6, se ofrecen algunas consideraciones sobre la eficiencia del método, su convergencia y aspectos relativos a su validación.
II. DESARROLLO
1.- Trazado de Rayos de Monte Carlo Modificado Estándar: El algoritmo de trazado de rayos de Monte Carlo modificado original consta de tres etapas: la generación de los rayos, el procesado de las reflexiones y el cálculo de la respuesta al impulso del canal [2]. El emisor se considera que sigue un patrón de emisión de Lambert generalizado o de tipo cosn, aunque en principio otros tipos de emisores pueden ser incluidos también. La técnica para el trazado de rayos siguiendo un patrón de emisión de este tipo puede encontrarse en [3]. El receptor está determinado por su área fotosensible (Ar) y su campo de vista (FOV). El trabajo con elementos ópticos de concentración y lentes tanto para los emisores como para los receptores puede encontrarse en [9].
Los rayos son generados desde la posición del emisor, siguiendo una distribución de probabilidad derivada a partir del patrón de emisión: cuando un rayo incide sobre un obstáculo éste se convierte en un nuevo emisor y se genera un nuevo rayo, en este caso reflejado, calculando siempre en cada reflexión la contribución de potencia sobre el receptor. El proceso continua hasta que el rayo haya experimentado el número máximo de rebotes a analizar o su tiempo de vuelo sobrepase la duración de la ventana de tiempo especificada de inicio para la respuesta al impulso a calcular. La estructura básica del algoritmo original de trazado de rayos de Monte Carlo [4] se presenta en la Tabla I.
Tabla I. Estructura del algoritmo de Monte Carlo modificado básico
| Begin 1. Generar nuevo rayo (t=0, P=1) 2. Lazo while t<tMAX - Propagar rayo hasta el primer obstáculo (t = t + d/c) - Reducir potencia del rayo usando el coeficiente de reflexión (P=rP) - Calcular la contribución desde ese punto al receptor - Generar rayo desde el nuevo punto End 3. Repetir pasos 1 y 2 para un número de rayos NR, hasta que la varianza de la respuesta al impulso obtenida sea aceptable End |
En la etapa correspondiente al procesado de las reflexiones, los obstáculos son descritos típicamente por un coeficiente de reflexión r, lo cual es un planteamiento válido sólo para el caso de reflectores de Lambert. En [6] se brindan adicionalmente algunas expresiones para la inclusión de reflectores de Phong.
2. Nuevos Elementos en la Formulación: En una aproximación más realista del fenómeno, la luz es reflejada por las superficies cuyas propiedades de reflectividad son descritas utilizando la llamada Función de Distribución de Reflectancia Bidireccional (BRDF), la que se define como la razón entre la radiancia reflejada con respecto a la irradiancia según [7]:
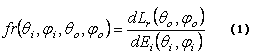
donde
qi, ji: son los ángulos de elevación y azimut de la radiación incidente
q0, j0: son los ángulos de elevación y azimut de la radiación reflejada
Esta es la relación más importante para la representación de las propiedades de reflectividad de las superficies. Las dependencias de la BRDF con la longitud de onda y la polarización de la radiación se han omitido, en aras de la simplicidad, pero pueden ser incorporadas si es necesario. Este tipo de funciones, que incluye además del modelo de reflectividad de Lambert muchos otros incluso para reflectores anisotrópicos, ha sido empleados recientemente con éxito en el campo de los gráficos por computadora, particularmente en la síntesis artificial de imágenes de gran realismo, utilizando también técnicas de trazado de rayos.
Los detalles acerca de la definición y propiedades de las funciones de reflectancia bidireccional pueden encontrarse en [7].
A la cantidad que expresa la razón entre el flujo incidente desde una dirección determinada y el flujo total reflejado integrado en todas las direcciones posibles de reflexión, se le llama Reflectancia Direccional-Hemisférica rdH, que en términos de la BRDF del reflector es [7]:
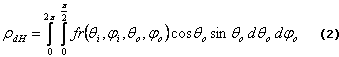
2.1 Modelo de BRDF de Lambert: En el caso de la reflexión difusa ideal, la radiación se refleja con igual probabilidad en todas direcciones, independientemente de la dirección de la radiación incidente. Por este motivo la BRDF de un difusor ideal se toma constante y:
rdH = p frLambert (3)
2.2 Modelo de BRDF de Phong Modificado: En 1994 Lafortune presentó el modelo de Phong modificado, una versión físicamente realizable del modelo original, su BRDF es [8]:
![]()
y su Reflectancia Hemisférica es:
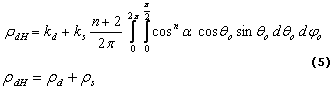
donde kd y ks son los coeficientes de reflectancia difuso y especular respectivamente. Se garantiza la conservación de la energía siempre que kd + ks ≤ 1.
2.3 Modelo Anisotrópico de BRDF de Ward: El modelo anisotrópico de BRDF presentado por Ward en 1992 [10] es:
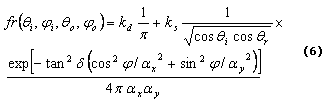
donde; ax y ay son las desviaciones estándar de las irregularidades de la superficie en las direcciones ![]() y ŷ respectivamente; d y j son los ángulos de elevación y azimut del vector mitad
y ŷ respectivamente; d y j son los ángulos de elevación y azimut del vector mitad ![]() entre las direcciones de incidencia y de reflexión.
entre las direcciones de incidencia y de reflexión.
3. Muestreo de las Direcciones de los Rayos Reflejados.
Toda vez que un rayo incidente intercepta la superficie de un reflector, ocurre la dispersión de la radiación que sigue un patrón dictado por la BRDF de la superficie.
El tipo de reflexión que se modelará debe determinarse previamente utilizando la técnica de la ruleta rusa: una primera variable aleatoria ξ, uniformemente distribuida en el intervalo [0, 1], se muestrea y se realiza en consecuencia una de las siguientes acciones:
0 ≤ ξ < ρd el rayo se refleja de forma difusa
ρd ≤ ξ < ρd + ρs el rayo se refleja muestreando el lóbulo especular
ρd + ρs ≤ ξ ≤ 1 el rayo es absorbido
En función del resultado de esta primera prueba, siempre que el rayo no sea absorbido, se obtiene la dirección del rayo reflejado muestreando la BRDF del material reflector de la siguiente forma.
3.1 Muestreo de la Componente Difusa.
La dirección de reflexión de un rayo sobre una superficie que se comporta como un difusor ideal, o de Lambert con n=1, puede obtenerse utilizando la función densidad de probabilidad:
![]()
Utilizando dos números aleatorios x1 y x2 uniformemente distribuidos en el intervalo [0, 1], la dirección resultante puede especificarse en términos de (q, f) según:
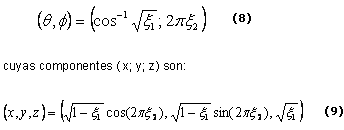
3.2 Muestreo de la BRDF del Modelo de Phong Modificado.
La manera más efectiva de muestrear una BRDF compuesta como la de Phong es separando la componente difusa de la especular. La componente difusa se muestrea de acuerdo a (9) utilizando la distribución coseno. La componente especular debe muestrearse de acuerdo al factor cosn q utilizando la función de densidad [8]:
![]()
que es una generalización de la anterior distribución. La dirección de reflexión resultante en términos de (q, f) es:
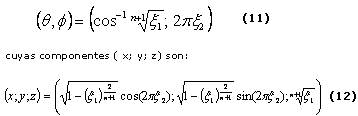
3.3 Muestreo de la BRDF del Modelo de Anisotrópico de Ward.
El modelo anisotrópico de Ward puede ser muestreado asignando [7]:
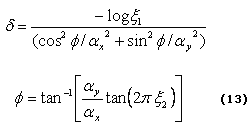
donde ξ1 y ξ2 son aleatorios, uniformemente distribuidos en el intervalo [0, 1], y (d, f) es la dirección del vector bisector entre las direcciones de incidencia y reflexión definidas para el modelo de Ward. En el caso del muestreo de modelos de BRDF de mayor complejidad se pueden emplear técnicas de muestreo por rechazo descritas en [7].
4. Generalización del Algoritmo de Trazado de rayos de Monte Carlo Modificado.
En esta nueva aproximación se asume que el emisor posee una potencia total Ps, del cual se trazan NR rayos, cada uno con una potencia asociada de Ps/NR.
La componente de línea de visibilidad directa de la respuesta al impuso corresponde a la potencia recibida por la componente LOS, que se calcula idénticamente al caso del planteamiento de Barry en [1]:
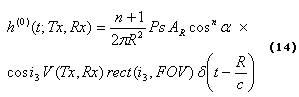
La reducción de la potencia de los rayos reflejados se hace mediante el empleo del término de reflectancia apropiado y las direcciones de reflexión que se utilizan se obtienen muestreando adecuadamente las BRDF de los diferentes materiales reflectores. En cada reflexión se calcula el aporte de potencia que las BRDF producen sobre el receptor, que es:
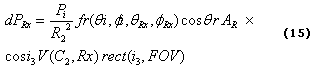
donde Pi es la potencia óptica del rayo incidente, fr es la BRDF del reflector evaluada para las direcciones de incidencia (qi,ji) y del receptor (qRx,jRx). V(Rx) es un término asociado a la visibilidad existente entre cada reflector y el receptor, R es la distancia entre los reflectores y el receptor y f es el ángulo entre la normal al receptor y la dirección del rayo incidente.
La respuesta al impulso para un número infinito k de rebotes según el método de trazado de rayos de Monte Carlo modificado viene dada por:
![]()
Donde los aportes dPRx(t) individuales se calculan para cada uno de los NR rayos lanzados en cada uno de los k rebotes que se desee tener en cuenta en la respuesta al impulso a estimar; estos aportes se van almacenando en los intervalos de tiempo correspondientes a sus demoras asociadas dentro del histograma de potencia recibida vs. Tiempo, que es la respuesta al impulso. La estructura del nuevo algoritmo propuesto puede apreciarse en la Tabla II.
Tabla II. Estructura del algoritmo de Monte Carlo modificado generalizado
| Begin 1. Generar un nuevo rayo (t=0, P=PS/NR) 2. Lazo while t<tMAX - Propagar rayo hasta el primer obstáculo (t = t + d/c) - Seleccionar tipo de reflexión usando Ruleta Rusa en función del tipo de BRDF. i. 0 ≤ ξ < ρd, rayo reflejado de forma difusa ii. ρd ≤ ξ < ρd + ρs, rayo reflejado muestreando el lóbulo especular iii. ρd + ρs ≤ ξ ≤ 1, rayo absorbido - Reducir la potencia del rayo reflejado usando el término de reflectancia apropiado i. Lambert: P = ρdH P (usando la reflectancia direccional-hemisférica) ii. Modelos compuestos: P = ρ P (usando la reflectancia difusa ρd o especular ρs, en dependencia del resultado arrojado por la prueba de la Ruleta Rusa ) - Calcular la contribución al receptor - Generar dirección del rayo reflejado muestreando la BRDF del reflector. End 3. Repetir pasos 1 y 2 para un número de rayos NR, hasta que la varianza de la respuesta al impulso obtenida sea aceptable End |
5. Consideraciones de Eficiencia y Convergencia del Algoritmo Propuesto.
La eficiencia de los esquemas de simulación se estima a partir de la cantidad de operaciones básicas de cálculo requeridas para modelar una configuración dada. La misma depende de los parámetros propios de cada esquema de simulación. En el caso del algoritmo recursivo de Barry [1], se llevan a cabo Nck operaciones elementales de cálculo, donde Nc es el número de celdas en que se discretiza el entorno y k es el número máximo de rebotes a incluir en el cálculo de la respuesta al impulso. Los algoritmos de trazado de rayos implementados iterativamente como el propuesto por López-Hernández et. al. [6] realizan N.k operaciones básicas, donde N es el número de rayos que se trazan. El algoritmo propuesto corresponde a esta última clasificación y tiene por tanto la misma eficiencia.
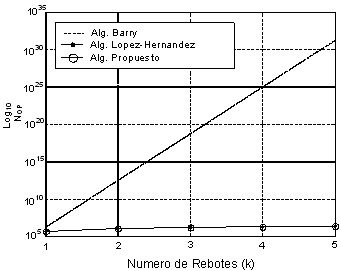
En la Figura 1 se presenta una comparación de la eficiencia de los métodos basados en el trazado de rayos con respecto al método clásico de Barry. En la misma se representa el logaritmo del número de operaciones básicas realizadas vs. el número de rebotes k a tener en cuenta en el cálculo de la respuesta al impulso.
Figura 1. Logaritmo del número de operaciones elementales de cálculo en función del número de rebotes para diferentes algoritmos de simulación
Se ha tomado como referencia para la comparación los datos reportados en [6]: 1735000 celdas de 1cm2 para el algoritmo de Barry y 500000 rayos para los algoritmos de trazado de rayos sobre una habitación vacía de 7.5x5.5x3.5 m. Puede apreciarse fácilmente la superioridad en la eficiencia de cálculo de los esquemas de trazado de rayos de Monte Carlo modificado.
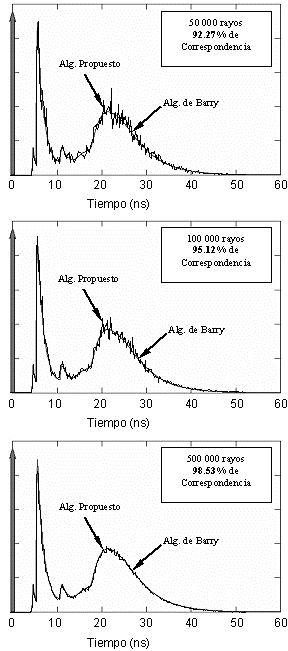
Para esta misma habitación, que corresponde a la configuración B reportada en [1], se ha hecho un análisis de la convergencia del método propuesto en función del número de rayos lanzados, tomando como referencia el resultado reportado en [1]. En la Figura 2 puede apreciarse como converge la respuesta al impulso obtenida con el método propuesto, a medida que aumenta la cantidad de rayos lanzados, obteniéndose una correspondencia de aproximadamente 98.5% entre ambos resultados cuando se trazan 500000 rayos. Los parámetros utilizados en la simulación de esta configuración B, así como los de otras dos que se emplean en comparaciones más adelante se encuentran en la Tabla III.
Figura 2. Convergencia del algoritmo propuesto para la configuración B de [1] con el aumento del número de rayos trazados.
Tabla III. Datos de las configuraciones reportadas en [1] usadas para la validación del algoritmo propuesto.
| Configuraciones Reportadas | |||
| Parámetro | A | B | C |
| Habitación Largo (x) Ancho (y) Altura (z) ρ norte ρ sur ρ este ρ oeste ρ techo ρ piso |
5 m 5 m 3 m 0.8 0.8 0.8 0.8 0.8 0.3 |
7.5 m 5.5 m 3.5 m 0.3 0.56 0.3 0.12 0.69 0.09 |
7.5 m 5.5 m 3.5 m 0.58 0.56 0.3 0.12 0.69 0.09 |
| Emisor Modo (n) x y z Elevación Azimut |
1 2.5 2.5 3 -90° 0° |
1 2.0 4.0 3.3 -90° 0° |
1 5.0 1.0 3.3 -70° 10° |
| Receptor Área FOV x y z Elevación Azimut |
1 cm2 85° 0.5 m 1.0 m 0 m 90° 0° |
1 cm2 70° 6.6 m 2.8 m 0.8 m 90° 0° |
1cm2 70° 2.0 m 4.0 m 0.8 m 90° 0° |
| Resolución | 0.2 ns | 0.2 ns | 0.2 ns |
6 . Validación del Algoritmo Propuesto.
El procedimiento utilizado para la validación del algoritmo propuesto es el mismo empleado en [5,6]. El estudio se basa en el modelo de propagación de reflexión simple y el emisor y el receptor se asumen en un mismo plano, apuntando verticalmente hacia arriba, que pueden moverse sobre una línea recta a lo largo del eje x.
La Tabla IV muestra los parámetros utilizados en la simulación, que corresponden con los mismos de [6] excepto para el techo en el que se usan los valores ajustados del modelo de BRDF de Phong que usa el nuevo algoritmo.
Tabla IV. Parámetros del nuevo modelo para la simulación.
| Parámetro | Valor | |
| Techo (BRDF de Phong) | kd ks n | 0.3 0.012 97 |
| Emisor | ángulo 1/2 elevación azimut | 1º 0º 0º |
| Receptor | Área FOV elevación azimut | 1cm2 85º 0º 0º |
| Resolución | Δt rebotes | 0.2ns 1 |
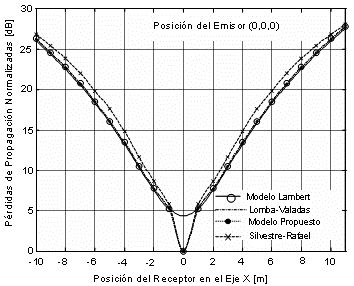
La Figura 3 muestra los resultados del cálculo de las pérdidas de propagación obtenidos originalmente por Lomba et. al. [5] para una posición del emisor de (0, 0, 0), desplazando el receptor a lo largo de uno de los ejes coordenados. Los resultados de [6] y los obtenidos con el algoritmo presentado se muestran también.
Figura 3. Pérdidas de propagación considerando los modelos de Lambert y Phong para diferentes algoritmos de simulación.
Las curvas representadas permiten la comparación de los valores de atenuación obtenidos, cuando se asume para el techo los modelos de reflectividad de Lambert y de Phong respectivamente.
Cuando el receptor se ubica en la dirección de reflexión especular con respecto al transmisor, se aprecia una diferencia de aproximadamente 5dB en los valores de atenuación que se obtienen al suponer un modelo o el otro. Esto se debe a que el modelo de Lambert no es capaz de simular correctamente la componente especular de reflexión de algunos materiales. Este hecho fundamenta la importancia de la utilización de los modelos de reflectividad específicos de cada material para una estimación más precisa de los parámetros de los enlaces IR en interiores.
Ambos resultados, los de [6] y los obtenidos con el nuevo modelo, corresponden razonablemente bien con los datos originales reportados en [5], reproduciendo la diferencia de 5dB a la que se hacía referencia anteriormente. Puede verificarse un mejor ajuste a los datos originales de [5] para el caso del modelo propuesto empleando las BRDF con respecto a los reportados en [6]. La correspondencia que se aprecia en la Figura 3 demuestra la validez del nuevo algoritmo, al tiempo que se comparan sus resultados, sobre la misma configuración, con los obtenidos por dos esquemas diferentes de dos autores distintos, un esquema similar basado en trazado de rayos [6] y el otro [5] que utiliza una técnica similar a la de Barry [1] discretizando las diversas superficies reflectoras.
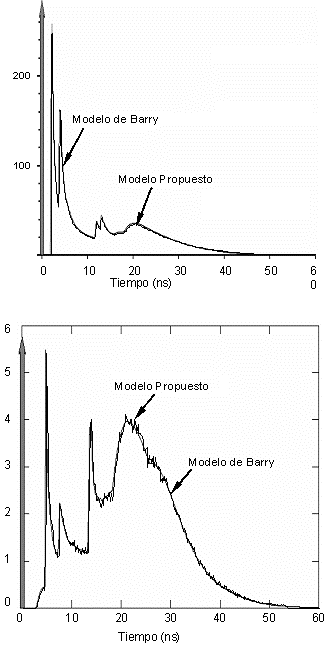
Los resultados obtenidos con el nuevo modelo corresponden también casi idénticamente con otros casos de simulación reportados en [1], en los que se utilizan únicamente reflectores de Lambert. La Figura 4 muestra la correspondencia entre las respuestas al impulso obtenidas para las configuraciones A y C de [1] y las obtenidas con el nuevo modelo propuesto para trazados de 500000 rayos. Los parámetros utilizados en la simulación se aprecian en la Tabla III.
Figura 4. Correspondencia de los resultados de simulación obtenidos con el nuevo algoritmo para las configuraciones A y C de [1].
El algoritmo presentado constituye una generalización de los esquemas de trazado de rayos de Monte Carlo anteriores, puesto que puede incorporar en principio cualquier comportamiento de reflectividad que esté caracterizado analíticamente por una función BRDF, incluyendo por primera vez patrones de tipo anisotrópico, como es el caso del modelo de Ward si fuera necesario.
Esto constituye un elemento de generalización que no poseen comúnmente los esquemas de modelación hasta ahora conocidos. La formulación matemática presentada deja abierta la posibilidad de incorporación de nuevos modelos de BRDF que no hayan sido desarrollados aún, siempre que sean descritos analíticamente.
A pesar de haber sido seleccionado para la generalización un esquema de simulación basado en trazado de rayos, los elementos relativos al uso de las BRDF pueden ser incluidos igualmente en esquemas de simulación discretos como el de Barry [1].
III. CONCLUSIONES.
1. El elemento clave en la implementación del nuevo modelo, empleando un esquema de trazado de rayos por Monte Carlo modificado, lo constituye la utilización del coeficiente de reflexión direccional-hemisférico.
2. Este parámetro permite la actualización de la potencia de los rayos reflejados, en función de la BRDF del material reflector a medida que los mismos van pasando de rebote en rebote en su trayectoria de propagación.
3. Otro aspecto importante a destacar es que la utilización de las funciones BRDF, como funciones de distribución de probabilidad para la determinación de las direcciones de los rayos reflejados, permite una modelación más realista del fenómeno físico de la reflexión que ocurre sobre materiales con comportamientos de reflectividad no Lambertianos, aspecto que incide directamente en la obtención de resultados de simulación más precisos.
4. Ambos aspectos anteriores dotan al nuevo esquema propuesto de una gran versatilidad y generalidad que lo hace superior a los esquemas de modelación hasta ahora reportados.
5. El algoritmo propuesto es validado utilizando como referencia de comparación resultados reportados por otros autores [1-6] para el caso de reflectores tanto Lambertianos como de Phong.
6. Los resultados obtenidos muestran una adecuada correspondencia con los reportados originalmente en todos los casos.
7. En la comparación con los resultados ofrecidos en [6], para reflectores no Lambertianos, el nuevo modelo produce incluso resultados de mayor exactitud en el ajuste.
8. Por las razones anteriormente expuestas se considera que el nuevo algoritmo presentado puede constituir una herramienta útil para la estimación más precisa de los parámetros de los enlaces infrarrojos inalámbricos en interiores.
IV. REFERENCIAS.
1) Barry, J.R., et al., Simulation of Multipath Impulse Response for Indoor Wireless Optical Channels, IEEE J. Select. Areas Comm., 1993, Vol.11, pp. 367-379. [ Links ]
2) López-Hernández, F.J., Pérez-Jiménez, R., and SANTAMARÍA, A.: Monte Carlo Calculation of Impulse Response on Diffuse IR Wireless Indoor Channels, Electronic Letters, 1998, Vol. 34, No.12, pp. 1260-1262. [ Links ]
3) López-Hernández, F.J., Pérez-Jiménez, R., and SANTAMARÍA, A.: Modified Monte Carlo Scheme for High-Efficiency Simulation of the Impulse Response on Diffuse IR Wireless Indoor Channels, Electronic Letters, 1998, Vol. 34, No.19, pp. 1819-1820. [ Links ]
4) López-Hernández, F.J., Pérez-Jiménez, R., and SANTAMARÍA, A.: Ray-Tracing Algorithms for Fast Calculation of the Channel Iimpulse Response on Diffuse IR-Wireless Indoor Channels, Opt. Eng., 2000, Vol. 39, No. 10, pp. 2775-2780. [ Links ]
5) Lomba, C.R., Valadas, R.T., and OLIVEIRA-DUARTE, A.M.: Experimental Characterization and Modeling of the Reflection of Infrared Signals on Indoor Surfaces, Proc. Inst. Elect. Eng., 1998, Vol. 45, pp. 191-197. [ Links ]
6) Rodríguez, S., et al., Reflection Model for Calculation of the Impulse Response on IR-Wireless Indoor Channels Using Ray-Tracing Algorithm, Microw. Opt. Tech. Letters, 2002, Vol. 32, No. 4, pp. 296-300. [ Links ]
7) Shirley, P.: Physically Based Lighting Calculations for Computer Graphics, Doctoral Thesis, University of Illinois, November 1990, pp.21-30. http://www.cs.utah.edu/~shirley/papers/dissertation.pdf [ Links ]
8) Lafortune, E.P., And Willems, Y.D.: Using the Modified Phong Reflectance Model for Physically Based Rendering, Report CW 197, Dept. of Computer Science, K.U. Leuven, November 1994, pp. 2-4. [ Links ]
9) Rodríguez Pérez, S., et al., Concentrator and Lens Models for Calculating the Impulse Response on IR-Wireless Indoor Channels Using a Ray-Tracing Algorithm, Microw. and Opt. Tech. Letters, 2003, Vol. 36, No.4, pp. 262-267. [ Links ]
10) Ward, G. J.. Measuring and Modeling Anisotropic Reflection.. In Proceedings of the 19th annual conference on Computer Graphics and Interactive Techniques (SIGGRAPH), July 1992. pp. 265–272. [ Links ]