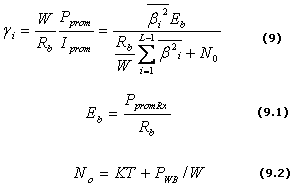Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Universidad, Ciencia y Tecnología
Print version ISSN 1316-4821On-line version ISSN 2542-3401
uct vol.9 no.33 Puerto Ordaz Mar. 2005
PREDICCIÓN DE PARÁMETROS DE CALIDAD DE LAS REDES INALÁMBRICAS 802.11
Alí Ajib, Bashar; Cabarrouy Fernández-Fontecha, Sergio Lázaro; García Simón, Amado Ignacio
Ing. Bachar Alí Ajib: Doctorante en el Dpto. de Telecomunicaciones del ISPJAE, Calle 9 Nº 616, Playa, La Habana, Cuba, Telef. 53-(7)2091300, correo electrónico bacharajib@yahoo.com.
Dr. Sergio Lázaro Cabarrouy Fernández-Fontecha: Especialista en Diseño y Construcción de Equipos Electrónicos en el Dpto. de Inversiones, Universidad de Pinar del Río, San Juan Nº 148, Pinar del Río, Cuba, Telf. 53(82)753522, correo electrónico sergio@vrect.upr.edu.cu.
Dr. Amado Ignacio García Simón: Jefe del Dpto. de Telecomunicaciones en el ISPJAE, 114 final, Marianao, La Habana, Cuba, Telef. 53(7)2607814, correo electrónico amado@electrica.ispjae.edu.cu .
RESUMEN: En este trabajo se propone un procedimiento para la predicción de la cobertura y la tasa efectiva de transferencia de datos para transmisiones en espectro ensanchado en sus variantes de secuencia directa y salto de frecuencia, para cualquier edificación, a partir la predicción de la potencia recibida, la dispersión de retardo y el desvanecimiento rápido, usando una base de datos arquitectónica. Para ello se utiliza un modelo de trazado de rayos complementado con redes neuronales del tipo perceptrón multicapa. El procedimiento de predicción expuesto aquí fue aplicado con éxito en redes 802.11b en interiores, lográndose errores menores de 3dB en la predicción.
Palabras clave: 802.11/ Parámetros de calidad/ Predicción de cobertura de redes/ Propagación radioeléctrica en interiores/ Redes Inalámbricas/ Redes neuronales/ Tasa efectiva de transferencia de datos.
QUALITY PARAMETERS PREDICTION OF CORDLESS NETWORKS 802.11
Summary: In this paper a model to predict covering area and data through-put for direct sequence and frequency hopping spread spectrum systems, is described Previously is ipredicted the receive power, delay spread, and fast fading, using an architectonical database. With that purpose a ray-tracing model, with multilayer perceptron neural network complementation, is proposed. This model was applied to indoor 802.11 networks, where errors less than 1.3m, for covering area, and 14% for data through-pat are achived.
Key words: Cordless Networks/ Effective Rate of Data Transfer/ 802.11/ Indoor Radioelectrical Propagation/ Networks Coverage/ Neuronal Networks/ Quality Parameters.
Finalizado el 2004/01/20 Recibido el 2004/02/12 Aceptado el 2004/09/21.
I. Introducción
En los últimos años se ha visto una explosión en los servicios de telecomunicaciones inalámbricas que ha sobrepasado a los servicios fijos y se pronostica que sigan creciendo. Existe una serie de estándares de redes inalámbricas con una creciente penetración en el mercado que se está extendiendo rápidamente también en Cuba, como es el caso de 802.11. No existen herramientas de diseño para estas redes en interiores que sean universalmente aceptadas y que sirvan a los ingenieros para predecir el mejor lugar para situar las estaciones y puntos de acceso, de manera que se logre un óptimo aprovechamiento del equipamiento. Las estaciones y los puntos de acceso se sitúan intuitivamente y si en algún sitio no hay cobertura o la tasa de transferencia es baja, simplemente se cambia para otro lugar. Muchos montajes se hacen por ensayo y error.
Los procedimientos que se proponen más abajo para estimar la zona de cobertura y la tasa efectiva de transferencia de datos, se basan en una predicción previa hecha por trazado de rayos, en la que se tuvo en cuenta sólo las trayectorias que alcanzan al receptor tras un rebote en los obstáculos del entorno. Los datos obtenidos por trazado de rayos arrojan una primera aproximación al valor de la potencia recibida y la dispersión de retardo, que son corregidos luego utilizando redes neuronales del tipo perceptrón multicapa. Éstas a su vez utilizan parámetros numéricos obtenidos del análisis geométrico del entorno [1]. El modelo de trazado de rayos es una variante del conocido método de las imágenes [2] y se reporta ampliamente en [3]. Por su parte, la profundidad promedio del desvanecimiento rápido, necesario para la estimación de la zona de cobertura, se predice utilizando sólo redes neuronales, sin que intervenga para nada el algoritmo de trazado de rayos.
La utilización de redes neuronales para corregir el error que se comete al obviar las trayectorias que sufren más de un rebote, representa un ahorro considerable en el tiempo de cómputo y el error se reduce a menos 2.5 dB. [4], [5].
II. DESARROLLO
1. Modelo de trazado de rayos
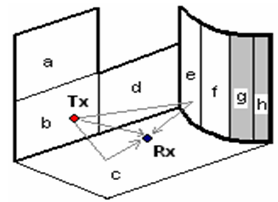
Primeramente es necesario discretizar la base de datos del entorno. Esto se realiza dividiendo todas las paredes, techo y piso de la edificación en rectángulos, llamados facetas, de modo que una pared curva o irregular puede simplificarse en un conjunto de facetas de distinto tamaño, mientras que una pared rectangular puede contener una sola faceta. De cada faceta se almacena en una base de datos las coordenadas de sus vértices, las atenuaciones de reflexión y transmisión, el índice de refracción, o sus parámetros de propagación radioeléctrica, conductividad, permitividad y permeabilidad s, er y mr. Ver la Figura 1.
Figura 1. Ejemplo de la división en facetas de varias paredes de una edificación. Las facetas sombreadas no tienen visibilidad directa con el transmisor y el receptor. Además de la trayectoria directa, se representan otras dos que experimentan un rebote.
La potencia recibida y la dispersión de retardo se obtienen a partir de encontrar el aporte de campo eléctrico de cada trayectoria considerada. Para el k-ésimo rayo (trayectoria) la señal en el receptor puede escribirse como:
![]()
Donde: ![]() (2) es la multiplicación de todos los factores de atenuación debido a los n rebotes o cruces a través de obstáculos; wo: es la frecuencia de la señal; q es el cambio de fase originado en los rebotes o paso a través de obstáculos; b = 2p/l; y l es la longitud del trayecto.
(2) es la multiplicación de todos los factores de atenuación debido a los n rebotes o cruces a través de obstáculos; wo: es la frecuencia de la señal; q es el cambio de fase originado en los rebotes o paso a través de obstáculos; b = 2p/l; y l es la longitud del trayecto.
Y la señal resultante será: ![]()
Por su parte, la dispersión de retardo puede calcularse como:
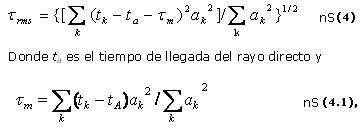
es el tiempo promedio de llegada de los rayos relativo a tA.
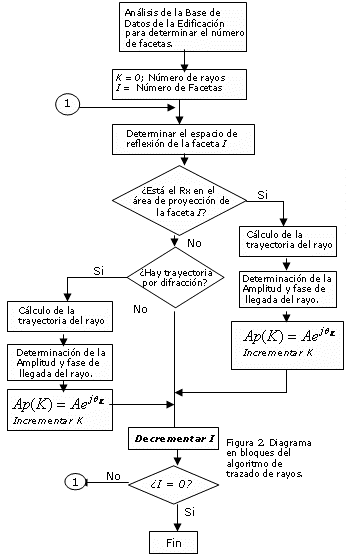
El inverso del valor de trms constituye un criterio muy aceptado para el máximo ancho de banda del canal para el cual la interferencia intersímbolo pueda despreciarse. [6] En la Figura 2 se muestra un diagrama de bloques del algoritmo de trazado de rayos.
Figura 2. Diagrama de bloques del algoritmo de trazado de rayos.
2. Redes neuronales artificiales
Se usan perceptrones de tres capas, entrenados con el algoritmo Backpropagation en su variante de Levemberg-Mcquart [7]. La conexión entre capas es total. Las funciones de activación son sigmoides tangenciales en todos los casos, excepto en la última capa en la que es la función identidad.
2.1. Corrección de la predicción por trazado de rayos
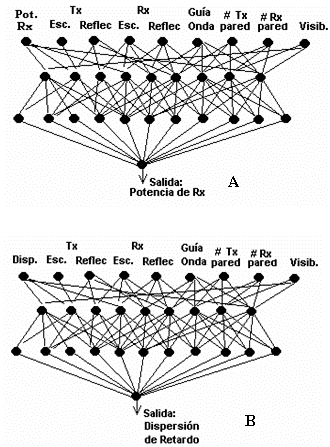
La Figura 3 muestra una representación de los perceptrones multicapa que corrigen la predicción de la potencia recibida y la dispersión de retardo.
Figura 3. Redes neuronales utilizadas como correctoras de la predicción trazado de rayos. A) Corrector de la potencia recibida. B) Corrector de la dispersión de retardo. Las capas están totalmente conectadas entre sí, aquí se han obviado algunas sinapsis para evitar oscuridad en el esquema.
Los parámetros de entrada de estas redes, además del valor correspondiente a corregir, son:
- Visibilidad: parámetro cuantitativo que vale 1 en caso de visibilidad directa, 0.75 en caso de que transmisor y receptor estén en habitaciones contiguas, 0.5 en caso de que haya dos paredes entre éstos, y 0.25 en otro caso. [8] Wölfle, Lands torfer, y otros del IHF de la Universidad de Stuttgart han propuesto varios modelos de predicción de parámetros del canal radioeléctrico utilizando redes neuronales, en los cuales se utilizan a su vez parámetros numéricos que dependen de la arquitectura del entorno, y cuya idoneidad demostraron empíricamente
- Coeficientes de reflexión y escudos locales: Parámetros que miden la influencia de las facetas con visibilidad directa al transmisor y al receptor, en cuanto a las trayectorias que llegan al segundo tras experimentar al menos un rebote [8].
- Número de facetas con visibilidad directa al transmisor y al receptor, normalizados respecto a número total de facetas de la base de datos procesada [9]. Los resultados del entrenamiento de las redes neuronales, así como los de las demostraciones empíricas de idoneidad de los parámetros de entrada están aquí ampliamente reportados, lo cual no es posible hacer en este artículo por razones de espacio.
- Coeficiente del efecto de guía de ondas: En ocasiones la señal atraviesa pasillos o habitaciones alargadas, en las que sufre varias reflexiones hasta llegar al receptor. En este caso los obstáculos se comportan como una guía que facilita la llegada de varios aportes multitrayecto al receptor. Su valor se acerca a uno cuando la trayectoria principal atraviesa un pasillo largo y estrecho y a cero cuando atraviesa habitaciones cuadradas o circulares.
2.2. Predicción de la profundidad del desvanecimiento
Una primera aproximación de la magnitud del desvanecimiento es la desviación típica del valor de la potencia recibida [10]. En el modelo considerado se utilizó redes neuronales para estimar este valor, luego del entrenamiento de dichas redes con valores de desviación estándar de potencia recibida obtenidos en campañas de medición [11]. Si P es una variable aleatoria, puede considerarse que el 95% de sus valores cumple |P - Pprom|≤2D, donde Pprom es la media de P, en virtud de una de las interpretaciones numéricas de la definición de desviación típica. De esta manera aproximadamente el 47% de los valores de P serán menores que Pprom., y otro 47%, mayores. El desvanecimiento ocurre cuando la potencia recibida es menor que la potencia promedio.
Durante las mediciones se comprobó que la desviación estándar de la potencia recibida aumenta cuando aumenta el número y la movilidad de las personas y los obstáculos en el entorno. Esto hizo que se definieran dos parámetros cualitativos que permitiesen tener en cuenta esta dependencia en el perceptron multicapa y así hacer más precisa la predicción. De esta manera se definió:
Coeficiente de concurrencia de personas: Es la tangente hiperbólica del cociente entre el número de personas promedio que circulan o permanecen en un entorno, y el área de dicho entorno: tanh(Número de Personas/Área(m2)) El coeficiente es adimensional por definición y da la idea de cuán transitado está el entorno. La tangente hiperbólica se usa como elemento normalizador. En la práctica el cociente nunca es mayor de 10. Se considera que las personas influyen cuando se encuentran dentro de las habitaciones del transmisor o del receptor, o cuando están en habitaciones contiguas, cuyas paredes sirvan de reflectores, o sean atravesadas por los rayos que alcanzan al receptor antes del tercer rebote.
Coeficiente de movilidad de las personas: Es cuantitativo y responde a la mera observación de los entornos universitarios aunque puede ser extensible a cualquiera. Se tendrá: (Ver Tabla I)
Tabla I. Valores del coeficiente propuesto para la caracterización de la movilidad del entorno. Estos valores fueron escogidos en ese rango, por razón de normalización, y los extremos cercanos a 0 y 1, se han reservado para futuras transformaciones del modelo.
| Valor del Coeficiente | Circunstancias de Validez |
| 0.2 | Movilidad escasa o nula de las personas, por ejemplo, en un local vacío, o donde las personas permanecen sentadas, como en una sala de juntas o un aula mientras se imparte una clase. |
| 0.5 | Movilidad baja, por ejemplo, en una oficina o taller, donde las personas permanecen sentadas en sus puestos de trabajo y se mueven escasamente hacia otros puestos de trabajo o en los pasillos. Un número reducido de personas, respecto al total, se mueven con frecuencia. |
| 0.7 | Movilidad alta, por ejemplo, el pasillo de una escuela en un cambio de turno de clase, una bolsa de valores, o un banco. |
La utilidad de estas definiciones se prueba luego mediante los resultados obtenidos al entrenar las redes neuronales que los utilizarán, así como al aplicarlas a la predicción del desvanecimiento.
Algunos de los parámetros de entrada a la red ya fueron descritos, aquí se utilizan además:
- Distancia entre el transmisor y el receptor: proporcional al desvanecimiento rápido, según se reporta en [12]. Aquí se usa su valor normalizado respecto a la distancia más grande que haya en la base de datos.
- Movilidad y concurrencia de personas, que fueron antes definidos.
La idoneidad de estos parámetros fue probada experimentalmente mediante sucesivos entrenamientos de redes neuronales con y sin los parámetros. La inclusión de los mismos mejora ostensiblemente la precisión y generalidad de las redes neuronales obtenidas.[13]
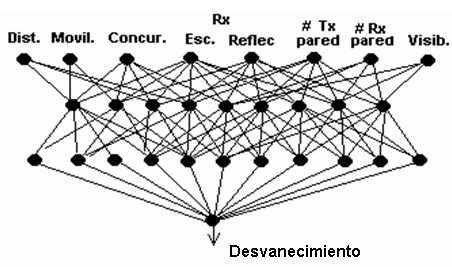
En la Figura 4, se muestra la red neuronal utilizada para la predicción de la profundidad del desvanecimiento rápido. El entrenamiento de las redes neuronales se realizó sobre una base de datos de 1870 vectores, obtenidos a partir de mediciones realizadas en 17 entornos interiores diferentes, en edificios hechos de hormigón armado y ladrillos de altura entre uno y siete pisos, situados en la ciudad de Pinar del Río, Cuba. Dichas mediciones se realizaron utilizando el software de prueba de tarjetas de red 802.11 de EnteraSysÒ [14].
Figura 4. Esquema de la Red Neuronal que predice la profundidad promedio del desvanecimiento rápido. Es un clásico perceptrón multicapas con 8 neuronas de entrada, 11 intermedias y una de salida.
Una red neuronal es adecuada para trabajar en determinado punto de un entorno cuando los parámetros de compatibilidad de dicho punto están en el rango de estos mismos parámetros en el entorno en que fue entrenada la red. En el fichero que contiene los datos de arquitectura y funcionamiento de una red neuronal, se incluyen dichos parámetros de compatibilidad, propios del entorno y algunas especificaciones del entrenamiento de las redes neuronales. Estos son:
- Rango de la razón entre conductividad, frecuencia angular y permeabilidad (s/we).
- Rango de las potencias de transmisión usadas en el entrenamiento.
- Rango de la distancia transmisor-receptor.
- Rango del número de facetas con visibilidad directa al transmisor y al receptor.
- Número de pisos del edificio.
2.3. Predicción de los parámetros de calidad
Para el montaje de cualquier una red inalámbrica en interiores interesa garantizar la cobertura del sistema en todo el edificio, al mismo tiempo que se logre que la conexión de los terminales satisfaga unos requerimientos de rapidez y de estabilidad. A continuación se proponen métodos para estimar la zona de cobertura y la tasa efectiva de transferencia de datos (throug-put), teniendo en cuenta la potencia recibida, la dispersión de retardo y el desvanecimiento rápido.
2.4. Cobertura
Se considera que un punto del entorno está dentro de la zona de cobertura si cumple:
PRx >SRx D (dB) (5).
Donde PRx es la potencia recibida, SRx es la potencia definida como sensibilidad del receptor, y D es el desvanecimiento rápido.
3. Tasa Efectiva de Transferencia de Datos
En ausencia de errores de transmisión, la tasa efectiva de transferencia de datos (through-put) se obtiene restando a la velocidad nominal, la velocidad equivalente de los bits de control que no aportan información. En las condiciones reales de un canal inalámbrico, hay que tener en cuenta además la razón de tramas perdidas, a partir de la probabilidad de error calculada en el punto que se evalúa, partiendo de los parámetros del canal predichos antes. [15] Cuando la probabilidad de error es apreciable, muchas de las tramas se pierden, en el caso de los sistemas ARQ, o simplemente se reciben con errores que no pueden ser corregidos por los códigos convolucionales que implementan sistemas FEC. Las retransmisiones de las tramas o las pérdidas de datos se traducen a las capas superiores de los protocolos de transmisión, en una disminución de la tasa efectiva de transferencia de datos La probabilidad de error en el bit puede encontrarse mediante:
Pe = P(g) (6)
Donde P(.·) es la función de probabilidad de error de acuerdo al método de modulación empleado [16], y g es la relación señal/perturbación.
El problema se reduce entonces a encontrar g , en el caso del presente trabajo, para las dos variantes del espectro ensanchado.
3.1. Tasa Efectiva de Transferencia de Datos para sistemas en Secuencia Directa (DS)
Para determinar el impacto del multitrayecto y el ruido en la recepción, se supone que se tiene L trayectos definidos, cada uno con una amplitud bi, que son en general variables aleatorias independientes entres sí.
La energía recibida por bit debido al i-ésimo trayecto es ![]() , donde Eb es la energía por bit de la señal transmitida y
, donde Eb es la energía por bit de la señal transmitida y ![]() el valor medio cuadrático de la amplitud del i-ésimo rayo. La potencia promedio recibida de éste será:
el valor medio cuadrático de la amplitud del i-ésimo rayo. La potencia promedio recibida de éste será:
![]()
Donde Rb es la velocidad de transmisión de la información. La suma de la interferencia de los L-1 rayos y el ruido será:
![]()
Donde No es la densidad espectral de ruido unilateral y W el ancho de banda del receptor. De esta manera, la relación señal a ruido por bit será:
Donde Pprom-Rx es la potencia promedio recibida, K la constante de Boltzman y T la temperatura en grados Kelvin. Rb es la velocidad de transmisión, W, el ancho de banda del canal y PWB la potencia de una fuente interferente de ruido de banda ancha que ocupa todo el canal y que sea necesario considerar.
El algoritmo de trazado de rayos que se corrió antes, devuelve la amplitud y fase de los rayos directo, difractados en esquinas y obstáculos y los que son reflejados una vez. Como el algoritmo no tiene en cuenta la variación temporal de la amplitud y la fase, es obligatoria la aproximación de que ![]() , donde Ai2 es la amplitud del i-ésimo rayo considerado en el algoritmo. Este juego de valores de señal recibida, pueden asumirse como muestras de la función de respuesta al impulso h(t), no estando equiespaciadas, y cuya función de distribución de llegada no se conoce de antemano.
, donde Ai2 es la amplitud del i-ésimo rayo considerado en el algoritmo. Este juego de valores de señal recibida, pueden asumirse como muestras de la función de respuesta al impulso h(t), no estando equiespaciadas, y cuya función de distribución de llegada no se conoce de antemano.
Como se utiliza trazado de rayos corregido mediante redes neuronales, se obtiene un estimado de la dispersión de retardo con exactitud equivalente a la anterior, con menos tiempo de cómputo, pero también con menos muestras de h(t). El valor de la dispersión de retardo corregida es en todos los casos mayor que la que se obtiene a partir de los aportes calculados teniendo en cuenta sólo un rebote, por lo que es necesario completar con muestras calculadas. Esto se hace utilizando una aproximación que asegure que el cálculo de la probabilidad de error será hecho por exceso para cualquier distribución estadística que sigan las muestras. De esa manera se rellena el intervalo que representa la dispersión de retardo con muestras equiespaciadas, con amplitud constante, y con fases aleatoriamente distribuidas de 0 a 2p. La amplitud es el promedio de la amplitud de las muestras reales. Se elige la distribución aleatoria de fases porque es una buena aproximación [17]. El error de los algoritmos de trazado de rayo está entre 6 dB y 8dB, cuando no se tiene en cuenta más que un rebote a la hora de encontrar las trayectorias de la onda que van del transmisor al receptor. Las muestras iguales y equiespaciadas fueron elegidas usando una simplificación sugerida en, [18] para el cálculo y asegurar que éste se realiza por exceso. El valor escogido fue el promedio de la amplitud de las muestras obtenidas con trazado de rayos, mientras que la separación relativa entre una y otra muestra de relleno fue escogida como el promedio de las diferencias de llegada entre las muestras consecutivas. La validez de estas consideraciones, para arrojar un cálculo por exceso del número de rayos y del peso relativo de sus amplitudes, se corroboró experimentalmente.
Si el valor de la dispersión de retardo estimada fuese mayor que el tiempo de chip, entonces se completa con muestras hasta dicho tiempo de chip, ya que en aplicaciones DS se produce un truncamiento de la respuesta impulsiva del canal [19] a un ancho igual al tiempo de chip, quedando el ancho de banda de coherencia igual al inverso de dicho tiempo. Ver la Figura 5.
Figura 5. El ancho temporal estimado para h(t) se rellena con muestras equiespaciadas, un tiempo igual al promedio de intervalos de llegada, una amplitud igual al promedio de las amplitudes, y la fase aleatoria y uniformemente distribuida entre 0 y 2p.
En resumen, se utiliza la ecuación (9) para encontrar la relación señal perturbación en el bit, y luego se sustituye en la ecuación (6), teniendo en cuenta la función P(·) adecuada para el tipo de modulación empleada en el sistema. Una parte de las muestras para evaluar la ecuación (9) es obtenida mediante trazado de rayos, la otra mediante operaciones de promedio y aleatorización.
A partir de conocer la probabilidad de error en el bit, la probabilidad de que se pierda una trama será:
Pe-trama = NPe-bit (10)
Donde N es el número de bits de la trama, Pe-bit es la probabilidad de error en el bit. Aquí se ha considerado que la ocurrencia de error en los bits de la trama es independiente entre sí y por tanto la probabilidad de un error en el conjunto de bits es la suma de las probabilidades individuales. También se asume que cualquier error en un bit es detectado.
Para calcular la tasa efectiva de transferencia de datos se tiene que el número de bits de información que se transfiere en un segundo, en ausencia de errores es:
![]()
Donde R es la velocidad de transmisión del sistema, N es el número de bits de las tramas de datos, y Nútil, el número de bits de información dentro de dicha trama. El número ![]() es mayor de 0.8 en los estándares de redes inalámbricas estudiados. Vale señalar que en este cálculo no se tienen en cuenta las tramas de sincronización o mantenimiento que forman parte de los protocolos de comunicación de todos estos sistemas, las cuales muchas veces se intercalan de forma irregular, y según las circunstancias específicas de funcionamiento del sistema, entre las tramas de datos.
es mayor de 0.8 en los estándares de redes inalámbricas estudiados. Vale señalar que en este cálculo no se tienen en cuenta las tramas de sincronización o mantenimiento que forman parte de los protocolos de comunicación de todos estos sistemas, las cuales muchas veces se intercalan de forma irregular, y según las circunstancias específicas de funcionamiento del sistema, entre las tramas de datos.
En presencia de errores, la tasa de transferencia efectiva será:
![]()
De esa manera, conocida Pe-bit en cada punto, a partir de los datos del entorno y la ubicación de los terminales en éste, se puede estimar la razón efectiva de transferencia de datos de cualquier sistema cuyo comportamiento se desea evaluar en dicho entorno.
3.2. Tasa Efectiva de Transferencia de Datos para sistemas en Salto de Frecuencia (FH)
FH es también resistente al desvanecimiento selectivo, pero el análisis es diferente. En este caso es mejor realizarlo en el dominio de la frecuencia. Las irregularidades en el tiempo de llegada y la amplitud de los rayos, que llegan al receptor en el dominio del tiempo, se traducen en desvanecimientos selectivos en el dominio de la frecuencia. Estos desvanecimientos normalmente afectan a unos saltos y a otros no. Así que es necesario analizar cada salto, y luego combinar las probabilidades de error obtenidas en cada uno de los casos, teniendo en cuenta que lo que ocurre en un salto es independiente de lo que puede ocurrir en otro. La probabilidad total será la suma de las probabilidades individuales multiplicadas cada una por la fracción del tiempo total en que ocurre el salto correspondiente. Como el carácter pseudoaleatorio del código generador asegura que cada salto ocurra el mismo número de veces que los demás, se puede escribir:
![]()
Donde Pi es la probabilidad del i-ésimo salto. Obsérvese que si los valores de Pi fueran iguales para todos los saltos, la probabilidad de error del sistema en salto de frecuencia es Pe-FH = Pi, que coincide en el caso de ausencia del desvanecimiento selectivo.
El problema se centra entonces en encontrar los valores de Pi para los diferentes saltos, que no es complicado porque el comportamiento del canal en un salto es equivalente al del canal en banda estrecha, en ausencia de espectro ensanchado [20]. Entonces Pi = P(gi) (14), donde P(·) es la ecuación de probabilidad de error correspondiente al método de modulación que se usa, y gi es la relación señal perturbación en el intervalo de frecuencias correspondiente al salto.
Por esta vía es sencillo calcular la probabilidad de error si se cuenta con una expresión o juego de valores exactos de la respuesta de frecuencia del canal. Como se cuenta sólo con una parte de estas muestras, entonces se simplifica el problema de la manera siguiente:
Se considerará que gi = Eb /No - D, siendo Eb la energía del bit calculada a partir de la potencia promedio recibida, No la potencia unitaria de ruido blanco (o de banda ancha) presente en el canal, calculados ambos según las ecuaciones (9.1) y (9.2), y D, la caída relativa de la respuesta de frecuencia, respecto al valor promedio de ésta para todo el espectro. Para obtener un estimado de esa respuesta de frecuencia H(fi) se halla la Transformada Rápida de Fourier (FFT) de la versión discreta y aproximada de h(ti) que se tiene a través de las muestras obtenidas mediante trazado de rayos, descritos antes.
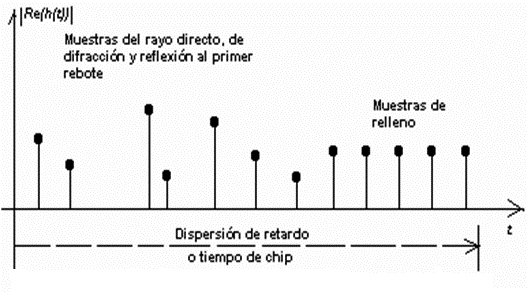
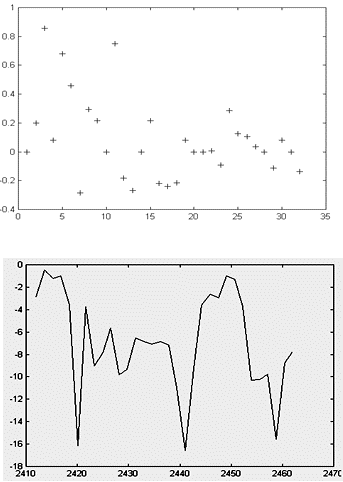
Para aplicar la FFT (utilizando el algoritmo Radix-2) es necesario que el número de muestras sea una potencia de dos, así que en la mayoría de los casos el predictor debe completar con ceros consecutivos y equidistantes. Los algoritmos FFT trabajan con juegos de muestras equidistantes en el tiempo, (las muestras de h(ti) no lo son en absoluto). Por esta razón es necesario realizar otra aproximación que consiste en subdividir el eje del tiempo en intervalos regulares pequeños respecto a la distancia en el tiempo entre cualesquiera dos muestras consecutivas. Luego se traslada la posición de las muestras en el tiempo, hacia el valor más cercano de los pequeños intervalos en que se ha dividido el eje. Los lapsos que queden vacíos serán completados con ceros. Mientras más pequeño sea el ancho de los intervalos escogidos, menor será la deformación de la función H(fi). Utilizando intervalos 4 veces más pequeños que el menor de los intervalos entre muestras, se obtuvo buenos resultados. Ver la Figura 6.
Figura 6. A la izquierda: juego de 32 muestras obtenidas a partir de 25 muestras de h(ti) obtenidas a su vez por trazado de rayos en la segunda planta del edificio docente de la UPR. A la derecha: estimado de la función H(fi) obtenida por FFT, en la banda FCC de 802.11.
4. Resultados
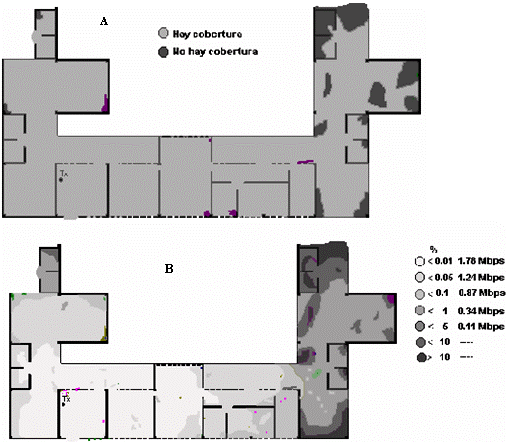
En la Figura 7 se muestran los resultados de la predicción de la cobertura y la tasa efectiva de transferencia en el entorno del edificio de oficinas de administración de la UPR. El error cuadrático medio de la distancia de cobertura respecto al transmisor es de 1.3 metros, por exceso, como era de esperar al considerar como margen de potencia al desvanecimiento rápido promedio. El error cuadrático medio de la razón de tramas perdidas (tasa de transferencia), respecto a las mediciones, es del 14%, también por exceso, dadas las aproximaciones realizadas.
Figura 7 A) Predicción de la Zona de Cobertura en la primera planta del edificio de oficinas de administración la UPR, de un sistema 802.11 a 11 Mbps. B) Predicción
El modelo se implementó en una aplicación para Windows que ha sido probada en 25 edificaciones diferentes, con buenos resultados. En 17 de éstas se comprobó su funcionamiento con datos provenientes de mediciones realizadas con este objetivo, que no fueron utilizadas para entrenar redes neuronales. El modelo fue implementado en una aplicación para WindowsÒ.
El error cometido por el predictor está en el rango señalado anteriormente, mientras se tenga el cuidado de aplicar las redes neuronales adecuadas para corregir en cada punto del entorno, realizando la correspondiente comprobación de compatibilidad para cualquier punto que se desee predecir.
La precisión del modelo varía, siendo menor en los puntos del entorno que están separados del transmisor por varias paredes. El aumento relativo de este error se estimó en 0.17 dB por habitación de separación del receptor.
5. Discusión de los resultados
Estos resultados demuestran la conveniencia de los métodos y lo adecuado de las aproximaciones realizadas. Los tiempos de cómputo están en el orden de los reportados en [5] para predictores de trazado de rayos que tienen en cuenta un solo rebote, mientras que la precisión está en el orden de los que tienen en cuenta hasta 3 rebotes. Se corrobora también la idoneidad de la combinación de los métodos de trazado de rayos y los perceptrones multicapa.
El problema de la ambigüedad en el rango de validez de los perceptrones multicapa [21] es resuelto aquí estableciendo unos parámetros de compatibilidad de la red a partir de características del entorno y el régimen en que fue entrenada la red [22]. Esto permitió estimar los rangos de error en la predicción. La precisión de las predicciones de potencia recibida y dispersión de retardo, están en el orden de lo reportado en varias fuentes [23], [24], [25], [26], [27].
III. Conclusiones
1. Se ha presentado un modelo para la predicción del área de cobertura y la tasa efectiva de transferencia máxima para sistemas en espectro que usen secuencia directa y salto de frecuencia.
2. El modelo fue puesto a punto para las frecuencias y las especificaciones de las redes 802.11b, en el interior de edificaciones.
3. Los resultados obtenidos permiten utilizarlo como herramienta de ingeniería en la planificación y explotación de dichas redes.
IV. Referencias
1) Wölfle., G.; Landstorfer., F. M. Dominant Paths for the Field Strength Prediction, in 48th IEEE Interna-tional Conference on Vehicular Technology (VTC), Ottawa, Optical Models, May 1998.pp. 552–556. [ Links ]
2) Pahalavan., Kaveh.; Levesque., Allen H. Wireless Information Networks. New York, John Wiley and Sons. 1995. pp 213-254. [ Links ]
3) Cabarrouy., Sergio L.; Fals, Juan; Yáñez., René.; Marante, Francisco. Modelación del canal radioeléctrico en interiores utilizando trazado de rayos y las redes neuronales artificiales. Universidad, Ciencia y Tecnología. Vol. 7 , Nº 27, Sept. 2003, pp 145-155. [ Links ]
4) Fortune S.J., Gay D.M., Kernighan B.W., Landron O., Valenzuela R.A. and Wright M.H., "WiSE Design of Indoor Wireless System: Practical Computation and Optimization," IEEE Computational Science & Engineering, Vol. 2, No. 1, Spring 1995, pp. 58-68. [ Links ]
5) Valenzuela R. A., Chizhik D., Ling J., "Measured and Predicted Correlation Between Local Average Power and Small Scale Fading in Indoor Wireless Communications Channels", IEEE Vehicular Technology Conference, Ottawa, May 1998. [ Links ]
6) Hashemi, H., The Indoor Propagation Chanel Proc IEEE, Vol 81, Nº 7, London, July 1993, [ Links ]
7) Hernández Montero, Fidel Ernesto. Aplicación de redes neuronales artificiales a la cancelación de ruidos. Tesis para optar por el título de Master en Sistemas Digitales. ISPJAE, La Habana, 2000. [ Links ]
8) Op. Cit Ref 1 [ Links ]
9) Op. Cit, Ref 3, pp 67-71 [ Links ]
10) Cabarrouy., Sergio L. Contribución al estudio de la propagación radioeléctrica en espectro ensanchado para el interior de edificaciones. Tesis Doctoral. La Habana, julio de 2003. pp 77-78. [ Links ]
11) Valido, I, et al. Estadística Elemental. EMPES, La Habana, enero de 2002. Capítulo 2, pp. 34-56. [ Links ]
12) Valenzuela R. A., Chizhik D., Ling J., "Measured and Predicted Correlation Between Local Average Power and Small Scale Fading in Indoor Wireless Communications Channels", IEEE Vehicular Technology Conference, Ottawa, May 1998. [ Links ]
13) Op. Cit, Ref 3, pp. 271-276 [ Links ]
14) EnteraSys NetworksÔ, RoamAbout 802.11 PC-Card Reference Guide. Fichero PDF. CDROM que acompaña al producto. Noviembre de 2000. [ Links ]
15) Op.cit. Ref 3, pp 71-72 [ Links ]
16) Op. Cit. Ref 2, pp 114-120. [ Links ]
17) Valenzuela., Reinaldo. Fortune., Steven.; Ling., Jonathan. Indoor Propagation Prediction Accuracy and Speed Versus Number of Reflections in Image-Based 3D Tracing. May, 1999. [ Links ]
18) Op.cit. Ref 2. [ Links ]
19) Vento Alvarez, José Raúl. Contribución al estudio de las comunicaciones ópticas en Espectro Ensanchado. Tesis Doctoral en la Universidad Politécnica de Madrid. julio 1998. Págs., 41-62. [ Links ]
20) Op. Cit. Ref 2, pp 150-257. [ Links ]
21) Op. Cit. Ref 18. [ Links ]
22) Op.cit. Ref 7. [ Links ]
23) D. Erricolo et al., "Measurements on Scaled Models of Urban Environments and Comparisons with Tracing Propagation Simulation," IEEE Trans. Antennas and Propagation, vol. 50, May 2002. pp. 727-735. [ Links ]
24) Wertz., P.; Wölfle, G.; Hoppe, R.; Zimmerman, D.; Landstorfer, F. M. Enhaced Localization Technique within Urban and Indoor Environments based on Accurate and Fast Propagation Models. COST 273 TD, 2002. [ Links ]
25) Fals Ramírez., Juan.; Marante Rizo., Francisco. Radiopropagación en interiores de edificaciones. Ponencia al Congreso Internacional de Telemática, CITEL 2000, La Habana. Diciembre de 2000. [ Links ]
26) Klepal, M. – Pechaz, P.: "Wide-band indoor propagation prediction by Motif model," In: 10th Aachen Symposium on Signal Theory - Algorithms and Software for Mobile Communications - Aachen, Germany. September 2001, [ Links ]
27) Rappaport., T. S.; Seidel., S. Y. "Multipath propagation models for in-bulding communications,""in Proc. IEEE Fifth Int. Conf. Mobile Radio and Personal Commun. Warick, Dec. 1989. pp. 69-74. [ Links ]