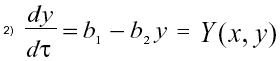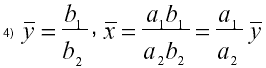UN ESTUDIO SIMPLIFICADO DE LA EVOLUCIÓN DE LA LEMNA SP

Ortega, Horacio

MSc. Horacio Ortega: Profesor Asociado en el Dpto. de Ciencias Básicas, de la Universidad Nacional Experimental Politécnica Antonio José de Sucre, (UNEXPO) Vicerrectorado Luís Caballero Mejías, Los Chaguaramos, Caracas 1041-A, Telf. 0212-69613337, correo electrónico palacu49@hotmail.com.

Resumen: Se utiliza un sistema de ecuaciones diferenciales acopladas para describir el comportamiento de una planta de la familia de las lemnáceas en un medio al que fluyen continuamente nutrientes (contaminantes) en dos condiciones diferentes. Tanto los resultados analíticos como los numéricos muestran que la persistencia de la lemna está asociada al proceso de eutrofización de masas de agua, y que debería tomarse medidas para combatir la contaminación de los medios acuáticos.

Palabras clave: Eutrofización/ Evolución de la Lemna SP/ Valores críticos / Saturación/ Ciclos/ Valores de equilibrio.

A SIMPLIFIED STUDY OF THE LEMNA SP EVOLUTION

Abstract: A system of differential equations is used in order to study the behaviour of a lemnaceae plant in a medium with continuous flow of nutrients (polluents) in two different conditions. Our analytical and numerical results both show that lemna persistence is related to the eutrophization processes in water reservoirs, and that care should be taken for fighting pollution of fresh water reservoirs.

Keywords: Eutrophization/ Critical Values/ Lemmna SP Evolution / Saturation/ Cycles/ Equilibrium Values.

Finalizado 2004/09/25   Recibido el 2004/10/29   Aceptado el 2005/03/07.

I. INTRODUCCIÓN

Durante el primer semestre de 2004 una mancha de lemna sp cubrió una fracción importante del lago de Maracaibo. Este lago tiene una superficie aproximada de 13.300 Km2, y guarda un volumen de 280 millones de m3, en proceso de eutrofización. La lemna o lenteja de agua es una planta del orden de las aráceas, familia lemnáceae, con cinco géneros y 38 especies [1]. En este orden se encuentran las plantas con flores más pequeñas que existen. Muchas especies dan la impresión visual de ser pequeñas hojas o virutas verdes [1,2]. Generalmente habitan en climas tropicales y subtropicales, en aguas dulces y tranquilas, y están ampliamente representadas en Venezuela [2]. Se nutren de residuos fosforados y nitrogenados que contaminan las aguas y que retiran de estas de manera continua [3, 4 ,5 ,6]. Producen gran cantidad de biomasa, proteínas incluidas, por lo cual podrían aprovecharse como alternativa importante en nutrición animal [7, 8, 9]. Son sensibles a ciertos venenos, y metales tóxicos [10, 11] y se utilizan rutinariamente en ensayos como DGIT (Duckweed Growth Inhibitor Test) para medir el grado de contaminación de reservorios de agua dulce, o de sedimentos y la presencia en ellos de compuestos químicos determinados [12,13]. Por la magnitud de la invasión, ocurrida al lago más grande de Suramérica, pareció de interés intentar predecir el comportamiento de la lemna mediante un modelo simplificado. En este artículo se plantea en primer lugar un conjunto de ecuaciones diferenciales asociado a la lemna y se considera la estabilidad de sus puntos de equilibrio. A continuación se presentan y discuten los resultados de diversas integraciones numéricas del sistema y posteriormente se establecen las conclusiones. Los detalles matemáticos se han agrupado en el apéndice.

II. DESARROLLO

1. Sistema:

Se utiliza un conjunto de dos ecuaciones diferenciales acopladas para describir el sistema. Se designará a la lemna por la variable x, al nutriente por la variable y. El tiempo será escrito como t. Cada ecuación se discute por separado a continuación. La lenteja crece por interacción con el nutriente, a razón axy, donde x es el coeficiente dinámico (variable) que rige dicha interacción. Sin embargo, si el sistema está eutrofizado, es decir, si la concentración del nutriente supera un valor crítico de saturación y_s, el crecimiento de la lemna se restringe (de hecho su razón de crecimiento se hace negativa). Esto ocurre también si la concentración del nutriente es inferior a otro valor crítico de sustentación y_s. (los nutrientes no alcanzan a suplir los requerimientos metabólicos de la planta) nuevamente, la razón de crecimiento de la lemna se hace negativa

Se puede tener en cuenta estas condiciones si se define una función de modulación b como sigue:

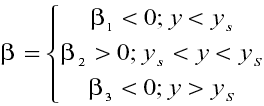
Si se define a₁ º b (nótese que a₁ puede ser positivo o negativo) entonces la razón temporal de cambio de la lemna por interacción con el nutriente es a₁xy. El crecimiento de la planta no es indefinido, sino que disminuye por superpoblación o hacinamiento a razón -a₂x² , con a₂ como el coeficiente dinámico correspondiente. Por lo tanto la evolución temporal de la lemna está dado por:

El nutriente es vaciado al medio ambiente a razón de b₁ por unidad de tiempo y permanece en él un tiempo b₂^-1 . La ecuación diferencial asociada al nutriente es:

Es pertinente observar que la evolución temporal de y es independiente del resto del sistema, por lo tanto la solución de (2) es y(t) = b₁b₂^-1 [1 - exp(-b₂t)], lo cual significa que el nutriente tiende asintóticamente a su valor límite . Adicionalmente, si , es decir, de no haber variación en la concentración del nutriente, entonces y(t) = b₁b₂^-1, constante y el sistema se reduce a una ecuación logística para x, tradicionalmente usada en estudios de crecimiento poblacional [14]. Finalmente, las trayectorias en el plano de fase (trazadas a partir de son horizontales en x = 0, así que esta recta es una separatriz y el sistema no puede abandonar el primer cuadrante cuando se encuentra dentro de él.

2. Puntos de equilibrio y su estabilidad:

El presente sistema posee dos puntos de equilibrio, el primero de ellos que se denomina punto nulo porque en él no existe la lemna:

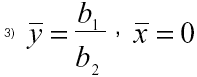
El siguiente punto de equilibrio, al cual se llamará punto general, viene dado por:

(este punto no existe si el sistema está eutrofizado, o en condiciones de ausencia de nutrientes, es decir si a₁ < 0

El sistema posee tres situaciones importantes diferentes a tratar:

I) Sistema no eutrofizado y_s < y < y_S (a₁ > 0) En este caso los autovalores asociados al punto nulo son l₀₁ =< 0 y l₀₂ > 0 y este punto de equilibrio es inestable (punto de ensilladura). En el punto de equilibrio general, l_G1 =< 0 y l_G2 < 0 por lo tanto el punto de equilibrio general es estable siempre que existe (nodo estable).

II) Sistema eutrofizado, y > y_S (a₁ < 0) En este caso los autovalores asociados al punto de equilibrio son ambos negativos, y se tiene un nodo estable. No existen puntos de equilibrio adicionales para este sistema.

III) Sistema en deficiencia de nutrientes, y < y_s (a₁ < 0) Esta situación repite simplemente la situación anterior y no se discutirá en detalle.

3. Resultados.

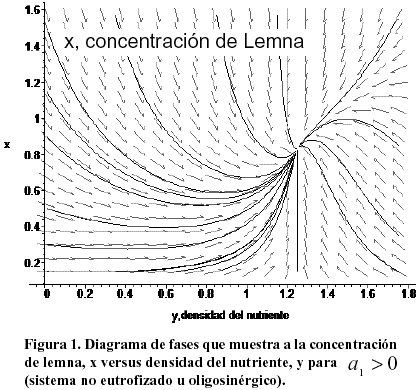
A continuación se muestra algunas simulaciones efectuadas al usar los comandos WithDEtools y DEplot de la versión 8 de MAPLE (Universidad de Waterloo, Canadá). La Figura 1 muestra simultáneamente la evolución temporal de las variables x (lemna) versus y (nutriente) para un sistema no eutrofizado. El sentido temporal está indicado por las flechas. A partir de cualquier concentración inicial de ambas variables el sistema evoluciona hacia su punto de equilibrio estable.

El flujo del sistema en el tiempo se indica por las flechas. El sistema se dirige hacia el punto de equilibrio estable. También se muestra el punto de equilibrio inestable en forma de un pequeño círculo vacío a mitad del eje y por el cual eventualmente pasan algunas trayectorias para migrar a continuación hacia el punto estable. La población de lenteja crece hasta estabilizarse saturando toda la región donde existe nutriente. Para ésta y para las Figuras 2 y 3 se tomó a₁ =1, a₂=1.5, b₁=1, b₂ =0.8. Con estos valores el punto de equilibrio general viene dado por x @ 0.83 y @ 1.25. Nótese que el valor no nulo de equilibrio de x puede hacerse arbitrariamente pequeño si se detiene la acumulación de nutrientes (b₁®0) o si se interrumpe la interacción de la lenteja con su fuente alimenticia (a₁®0)

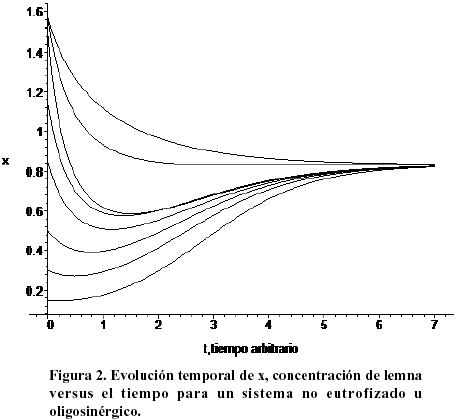
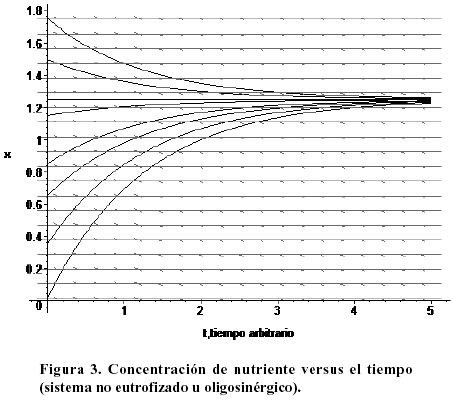
La Figura 2 muestra la evolución temporal de la lemna para diferentes condiciones iniciales por encima o por debajo de la concentración de equilibrio. Nótese que la lemna tiende hacia su población de saturación independientemente de cual haya sido su concentración inicial.

Independientemente de la concentración inicial de lemna, el sistema evoluciona asintóticamente hacia su valor de equilibrio estable. Esto implica que la lemna crecerá hasta ocupar eventualmente toda la región donde existe nutrientes. La Figura 3 muestra la evolución temporal del nutriente (contaminante) para el mismo sistema no eutrofizado de la figura anterior. Es claro el comportamiento asintótico del sistema. Igualmente se aprecia que la saturación se alcanza mientras se mantenga el flujo (b₁ > 0), independientemente de la concentración inicial del sistema.

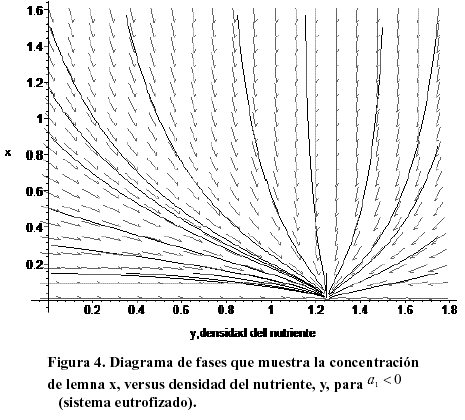
También los contaminantes terminan por ocupar toda la región disponible para su difusión independientemente de cual sea su concentración inicial. Es por tanto importante controlar el influjo del nutriente al medio, y posteriormente, su eliminación de él. Ambos objetivos sólo pueden alcanzarse a largo plazo. La Figura 4 muestra el diagrama de fases correspondiente a un sistema eutrofizado (a₁ < 0). El sentido de evolución temporal está indicado por las flechas. El sistema tiene un único punto de equilibrio (nulo, estable), y hacia él evoluciona a partir de cualquier concentración inicial.

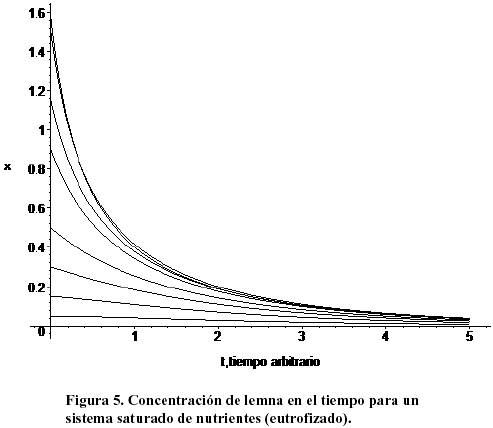
La población de lenteja eventualmente desaparece, pero el contaminante permanece en su valor de saturación. Esta situación de extinción de una especie que habita un medio (usualmente de todas) por polución incontrolada, se observa frecuentemente en la práctica. Los valores usados en ésta y en la siguiente simulación fueron a₁ =-0.5, a₂=1.5, b₁=1, b₂ =0.8. La Figura 5 muestra la evolución temporal de la lemna para el mismo sistema eutrofizado de la figura anterior. La población de planta desciende lentamente (asintóticamente) hacia el punto nulo.

La población de lemna tiende asintóticamente a cero independientemente de la concentración inicial. Es claro que el sistema no es viable y que el exceso de polución conducirá a la extinción de los organismos que habiten en el medio y se nutran de él.

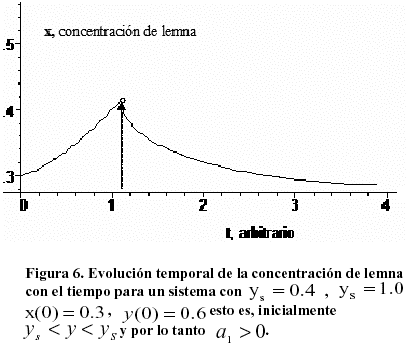
Una situación más próxima a lo que ocurre en la realidad se obtiene recordando que la evolución del nutriente es independiente del resto del sistema. El valor instantáneo de y(t) es importante, pero también la relación de orden existente entre el valor límite hacia el cual se dirije el nutriente, y los valores críticos y_s y y_S , los cuales pueden rebasados o no por la variable y(t), haciendo cambiar (o no) el flujo temporal del sistema. Esto se ejemplifica en la Figura 6, que muestra la dependencia de x, lemna con el tiempo. En esta Figura el sistema inicialmente es no eutrofizado (a₁ > 0) y la población de lemna crece, pero el flujo continuo de nutrientes hace crecer y hasta que y(t) = y_S. En ese momento a₁ < 0 y el proceso de crecimiento se invierte. Ciclos de crecimiento y decrecimiento alternos se observan frecuentemente en la práctica.

Para la simulación se tomó a₁ =1, a₂=1.5, b₁=1, b₂ =0.8. Al principio x(t) crece. y(t) crece continuamente y en t @ 1.2 alcanza el valor 1.0, crítico de eutrofización. Entonces a₁ se hace negativo, y(t) se dirige hacia su valor de saturación, pero x(t) decrece hacia cero. Para las nuevas simulaciones se tomó a₁ =-0.5, a₂=1.5, b₁=1, b₂ =0.8. En la figura se indica el punto donde ocurre el cambio de comportamiento del sistema.

4. Discusión

4.1. Puesto que la lemna ocupará toda la región donde existe nutrientes, es necesario evitar que éstos se sigan acumulando. El punto de equilibrio puede hacerse arbitrariamente pequeño haciendo b₁=0 en las ecuaciones (2) y (4). Esto equivale a detener el flujo del nutriente (contaminante) al medio, en el supuesto de que este demora un tiempo finito t ≈ b₂^-1 en desaparecer, bien sea por degradación, dilución o migración. Nótese además que si b₁ es pequeño, también lo es el valor límite y podría tenerse que y(t) < y_s a partir de cierto momento. Entonces el sistema evolucionará hacia su punto nulo, es decir, remitirá espontáneamente. Adicionalmente si se efectúa una extracción controlada de lemna del medio (y por lo tanto del nutriente que ésta ha fijado en sus frondas como proteína), puede llegarse a una situación en la cual y por lo tanto de persistencia indefinida de la planta en el medio aun cuando se la está utilizando como fuente de nutrientes.

4.2. La planta elimina los contaminantes del medio [3-6], con tal de que ella misma sea retirada del agua. Entonces podría utilizarse la lemna en condiciones controladas para mantener la calidad de las aguas.

4.3. Es sabido que la lenteja produce una importante cantidad de biomasa [7-9]. Así que queda planteada la alternativa de utilizarla como fuente básica para explotación comercial en piscicultura, en cría aviar, y en la producción de abonos. Sin embargo como en ella pueden acumularse metales pesados [10,11] habría que verificar los contenidos de dichos metales antes de utilizar la planta en producción de nutrientes de consumo humano.

4.4. Se conoce que la lenteja es susceptible a la acción de ciertos tóxicos, así como de algicidas y herbicidas [10,11] los cuales podrían usarse para su control. Sin embargo no es prudente agravar un problema de contaminación de un medio añadiendo una sustancia nociva más, la cual puede permanecer en solución durante tiempo indefinido.

4.5. Igualmente la sensibilidad de la lemna a ciertas toxinas permite su utilización en ensayos para verificar la presencia en el agua de ellas [12,13].

4.6. Aún queda disponible el uso de la variable a₁, que puede hacerse igual a cero (y por lo tanto la población de lemna es cero, ver la ecuación (4)) si se consigue anular la interacción de la lemna con el nutriente. Esto puede conseguirse trivialmente si se retira a toda la planta del agua.

III. CONCLUSIONES

1) La población de lemna puede invadir, saturar y permanecer en regiones donde existe nutrientes por períodos largos de tiempo. 2) Puede usarse la lemna como indicador de la calidad de las aguas, y también como elemento purificador de ellas. 3) La lemna produce gran cantidad de proteínas de potencial uso para producir nutrientes para uso animal o humano, previa verificación del contenido de toxinas que puedan contener. 4) Pareciera que la presencia de la lemna implica más ventajas que perjuicios, por lo tanto sólo depende del ingenio e iniciativa humanas el hacer uso provechoso de este vegetal.

IV. REFERENCIAS

1) Armstrong, W. Wayne’s Word Lemnaceae On-Line: 27 de Julio de 2004, http:waynesword.palomar.edu.1wayindx.htm (12 June 2001).        [ Links ]

2) Velázquez, J. Plantas acuáticas de Venezuela. Caracas, Universidad Central de Venezuela, CDCH, 1994, pp. 830-839.        [ Links ]

3) Cedergreen, N & Vindbaek, T. Nitrogen Uptake by Floating Macrophyte Lemna Minor. New Phytologist, 155:285-292, 2002.        [ Links ]

4) Oscarson, P. et al . Growth and Nitrate Uptake Properties of Plants Grown at Different Relative Rates of Nitrogen Supply. II. Activity and Affinity of the Nitrate Uptake Ssystem in Pisum and Lemna in Relation to Nitrogen Activity and Nitrogen Demand. Plant Cell and Environment, 12:787-794, 1989.effluent using duckweed.        [ Links ]

5) Reddy, K & De Busk, W. Nutrient Removal Potential of Selected Aquatic Macrophytes. 14: 459-462, 1985.        [ Links ]

6) Sutton, D. & Ornes, H. Phosphorus Removal from Static Sewage Effluent Using Duckweed. Journal of Environment Quality, 4:367-370, 1975.        [ Links ]

7) Oron, G. et al. Performance of the Duckweed Species Lemna Gibba on Municipal Wastewater for Effluent Renovation and Protein Production. Biotechnology and Bioengineering, 29:258-268, 1987.        [ Links ]

8) Rusoff, L. et al. Duckweed (Lemnaceae family): a Potential Source of Proteins and Aminoacids. Journal of Agricolal food Chemistry, 25: 848-850, 1980.        [ Links ]

9) Hillman, W. & Dudley, C. The Uses of Duckweed. American Sciencist, 66:442-481, 1978.        [ Links ]

10) Jain, S. et al. Azolla Pinnata and Lemna Minor L. for Removal of Lead and Zinc from Polluted Water, Water Research, 24: 177-183, 1990.        [ Links ]

11) Nasu, Y. et al. Comparative Studies on the Absorption of Cadmium and Cooper in Lemna Paucicostata. Environment Pollution A, 32:201-209, 1983.        [ Links ]

12) Lazorchak et al. A Sediment Toxicity Method Using Lemna Minor, Duckweed. Society of Environment Toxicology and Chemistry, Nashville, USA, 12-14 de Noviembre de 2000.        [ Links ]

13) Rowe et al. The Use of an Alga (Chlorella Pyrenoidosa) and a Duckweed (Lemna Perpusilla) as Test Organisms for Toxicity Bioassays of Spent Bleaching Liquors and their Components. Environment Pollution A, 27: 289-296, 1982.        [ Links ]

14) Krebs, C. Ecology, 4ª ed., New York, Harper-Collins College Publishers, 1994, 203-208.        [ Links ]

15) Jordan, D. & Smith, P. Non Linear Ordinary Differential Equations, London, Oxford University Press, 1976, 43-52.        [ Links ]

16) Elgoltz, L. Ecuaciones Diferenciales y Cálculo Variacional. Moscú, Editorial MIR, 2ª ed., 1977, pp. 232-234.        [ Links ]

V. APÉNDICE

Para analizar la estabilidad asintótica del sistema se utiliza linearización [15]. La matriz de Jacobi es

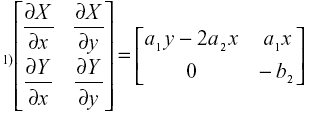
El signo de los autovalores, l, en cada punto de equilibrio puede hallarse por simple inspección o usando el criterio de Routh-Hurwitz [16]. En el punto de equilibrio nulo, los autovalores son:

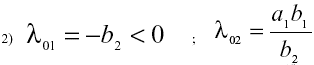
En el punto de equilibrio general, los autovalores son:

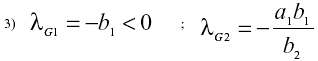
Se tratará sólo dos situaciones:

I) Sistema no eutrofizado a₁ > 0   y_s < y < y_S En este caso los autovalores asociados al punto nulo son l₀₁ =< 0 y l₀₂ > 0 Este punto de equilibrio es inestable punto de ensilladura). En el punto de equilibrio general, l_G1 =< 0 y l_G2 < 0 por lo tanto este punto de equilibrio es estable (nodo estable).

II) Sistema eutrofizado a₁ < 0, (y > y_S) .En este caso los autovalores asociados al punto de equilibrio son ambos negativos y se tiene un nodo estable. No existen puntos de equilibrio adicionales para este sistema.