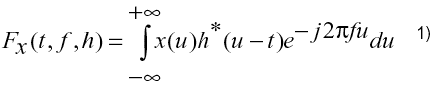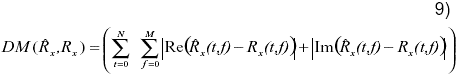CLASIFICACIÓN DE SEÑALES ELECTROCARDIOGRÁFICAS CONTAMINADAS CON RUIDO MEDIANTE REPRESENTACIONES TIEMPOFRECUENCIA

Mendoza Reyes, Miguel A.;  Lorenzo Ginori, Juan V.;  Taboada Crispí, Alberto

MSc. Miguel Arturo Mendoza Reyes,  Dr. Juan Valentín Lorenzo Ginori y Dr. Alberto Taboada Crispí: Profesores en el Centro de Estudios de Electrónica y Tecnologías de la Información, Facultad de Ingeniería Eléctrica, Universidad Central de Las Villas, Villa Clara, Cuba, carretera a Canajuaní, km 5 1/2 , Santa Clara, Villa Clara, Cuba, Telef. (53) 42-281157, correo electrónicos mendoza@uclv.edu.cu, juanl@uclv.edu.cu y ataboada@uclv.edu.cu respectivamente.

Resumen: El análisis de señales electrocardiográficas (ECG) constituye un elemento importante en la realización de diferentes tareas de diagnóstico automatizado, mediante algoritmos de computación. Un objetivo importante dentro de este análisis es la clasificación de formas de onda, para lo cual han sido utilizados diferentes algoritmos de procesamiento de la señal ECG en los dominios del tiempo y de la frecuencia. La naturaleza no estacionaria de la señal ECG ha motivado también la aplicación de técnicas tales como las Representaciones Tiempo-Frecuencia (RTF). El presente trabajo tiene como objetivos comparar el comportamiento de diferentes RTF en la clasificación de complejos QRS electrocardiográficos en presencia de ruido, e introducir un método de clasificación basado en el empleo de valores complejos para una RTF específica, la Transformada de Fourier Local. Se analizaron comparativamente los resultados de la aplicación del nuevo método con respecto a otro anterior introducido por los autores, también basado en RTF. Se determinó la efectividad del método evaluando el empleo de diferentes medidas de distancia entre los latidos contaminados con ruido y patrones de referencia utilizados para la clasificación. Se logró un desempeño superior durante la clasificación, para los tipos de ruido considerados, al emplear descriptores complejos en el dominio tiempo-frecuencia.

Palabras clave: Clasificación de latidos/ ECG/ Representaciones tiempo-frecuencia/ Señales electrocardiográficas.

ELECTROCARDIOGRAPHIC SIGNAL CLASSIFICATION USING TIME-FREQUENCY REPRESENTATIONS

Summary: The analysis of electrocardiographic (ECG) signals constitutes an important element in the completion of different tasks for automated diagnosis, by means of computational algorithms. Classification of waveforms is an important objective within this analysis, for which various ECG processing algorithms in the time and frequency domains have been used. The non-stationary nature of the ECG signal has motivated also the application of techniques such as the time-frequency representations (TFR). The objectives of this work are to compare, different alternatives for the application of TFR to the classification of noisy QRS, and to introduce a classification method based in the use of complex values for a specific TFR, the Short Time Fourier Transform. The results of the application of this method are analyzed in comparison to a previous method introduced by the authors, also based in the use of TFR. The effectiveness of this method to classify noisy beats was determined by evaluating the use of various distance measures between beats contaminated with noise and reference patterns used for classification. A better performance was obtained during classification, for the noise types considered, when complex descriptors in the time-frequency domain were used.

Key words: Beat Classification/ Electrocardiographic Siguals/ ECG/ Time-Frequency Representations.

Finalizado el 2004/10/20   Recibido el 2004/11/21   Aceptado el 2005/03/07.

I. INTRODUCCIÓN

El diseño de sistemas para la monitorización de la señal electrocardiográfica (ECG) ha sido objeto de numerosas investigaciones en las últimas décadas. Muchas de estas investigaciones abordan la problemática de la clasificación de la señal ECG, debido a la importancia que tiene ella en el estudio de las enfermedades del corazón [1, 2, 3]. Un ejemplo representativo lo constituyen las unidades de cuidados intensivos, donde la detección y clasificación precisa de la señal ECG resulta de vital importancia [1, 4, 5]. Específicamente, la clasificación de latidos es un procedimiento habitual en la mayoría de los sistemas de monitoreo dedicados a la adquisición y el procesamiento de la señal ECG [6, 7]. La información obtenida permite el conocimiento o estimación del estado de funcionamiento del miocardio y la previsión de situaciones que pueden poner en peligro la vida del paciente.

Varios métodos han sido descritos para la clasificación de latidos cardíacos. Un grupo de estos emplea la información de la señal ECG y además otros descriptores en el dominio del tiempo, como los valores de amplitud, la altura de las ondas y los valores de las muestras [1, 2, 3, 8, 9]. Otros, utilizan parámetros como la frecuencia, la fase y las características de sus componentes [10, 11, 12, 13]. Estos últimos persiguen incorporar nueva información para elevar los índices de clasificación correcta e incrementar la inmunidad al ruido. Entre estos métodos se destacan los basados en las Representaciones Tiempo-Frecuencia (RTF), en las cuales la energía asociada a la señal se representa mediante una función de densidad en el plano tiempo-frecuencia (t-f).

Una de las características deseadas de los procedimientos de clasificación es su inmunidad al ruido. Este puede aparecer en forma de interferencia de las líneas de potencia y de ruidos electroquirúrgico, de respiración, electromiográfico y otros [8]. La magnitud de la mayoría de los ruidos que afectan a la señal ECG debido a las condiciones del entorno, puede ser reducida mediante el cumplimiento de ciertos requisitos en las instalaciones clínicas o realizando correctamente el procedimiento de adquisición. Para otros ruidos fisiológicos, como los debidos a movimientos del paciente, la respiración y las contracciones musculares, no siempre se puede lograr esta reducción. La adquisición de la señal ECG durante largos períodos de tiempo también aumenta la probabilidad de que sea afectada por tales eventos. Esta situación demanda el empleo de descriptores con una alta inmunidad al ruido fisiológico en los sistemas para la clasificación de la señal ECG [8, 9].

El presente trabajo ha tenido dos objetivos principales: en primer lugar comparar el comportamiento de diferentes RTF en la clasificación de complejos QRS electrocardiográficos en presencia de ruido, y en segundo lugar, con una RTF específica, seleccionada a partir de los resultados de esta comparación -la Transformada de Fourier Local-, introducir un método de clasificación basado en el empleo de valores complejos.

Para alcanzar los objetivos trazados se diseñaron y realizaron experimentos de computación en los cuales se contaminó con diferentes tipos de ruido un conjunto de formas de onda de la señal ECG especialmente seleccionadas para este fin, se calcularon las RTF de las señales originales y ruidosas, y se realizó un proceso de clasificación basado en el empleo de diferentes distancias, realizando un análisis comparativo. Finalmente, se formuló y evaluó el método de clasificación basado en los valores complejos de la Transformada de Fourier Local.

II. DESARROLLO

1. Fundamentos teóricos sobre Representaciones Tiempo-Frecuencia

Para dar respuesta al primero de los objetivos planteados, se utilizaron diferentes RTF para describir la señal ECG en el plano t-f. La primera de ellas fue la Transformada de Fourier Local o de Tiempo Corto (Short-Time Fourier Transform o STFT). Esta se determina según la ecuación (1), tomando una porción o “ventana” de la señal a procesar x(u) alrededor de un instante de tiempo t, determinando la transformada de Fourier correspondiente y repitiendo el proceso mediante desplazamientos de la ventana para instantes sucesivos de tiempo.

En esta expresión, el significado de las variables es

t: tiempo

u: variable auxiliar

f: frecuencia

x(t): señal en el tiempo

h(t): función de ventana

La STFT tiene como desventajas relativas, la contradicción existente entre la resolución en los dominios del tiempo y de la frecuencia, y la fuerte dependencia con respecto a la relación entre el tipo de ventana y las características de la señal x(u) que tienen los resultados de la representación. No obstante, la STFT tiene a su favor la simplicidad de su implementación y una buena supresión de los llamados términos cruzados [14, 15, 16], lo cual determinó en este trabajo el empleo de los valores complejos de la STFT como rasgos a utilizar en el proceso de clasificación de formas de onda en la señal ECG.

En las RTF cuadráticas o bilineales se distribuye la energía de la señal en función de las variables tiempo y frecuencia [17, 18]. Existen diferentes RTF que cumplen con diferentes propiedades tales como que las mismas sean covariantes con la traslación en el tiempo y en la frecuencia, y otras. Una generalización de las mismas condujo a la formulación de la expresión de la llamada clase de Cohen de las RTF [19] que se expresa como

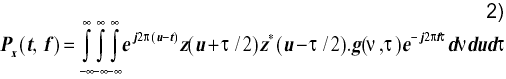
La función g(n,t) es denominada kernel o función de parametrización y define las características de una distribución en particular. La señal z(u) es la señal analítica asociada a la señal original x(u) y t es el desplazamiento en el tiempo.

Una de las RTF cuadráticas más utilizadas es la de Wigner-Ville (WV), para la cual la función de parametrización es g(n,t)=1, siendo su expresión

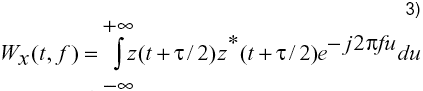
Las RTF cuadráticas presentan la desventaja de que en ellas aparecen valores en zonas del plano t-f en las que realmente no existe energía; estos son los llamados términos cruzados o crossterms. Una característica importante de cualquier RTF es su relativa inmunidad a la aparición de dichos términos [14]. Existen diferentes vías para reducir la influencia de los términos cruzados, ejemplo de las cuales son las RTF ‘pseudo-’ y ‘suavizadas’ o smoothed . Otros ejemplos pueden encontrarse en [20 y 21].

La distribución de Choi y Williams, (CW), es una RTF con una intensidad disminuida de los términos cruzados, al utilizar en (2) una función de parametrización exponencial dada por

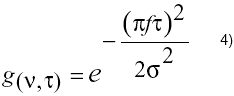
La distribución resultante tiene la forma siguiente:

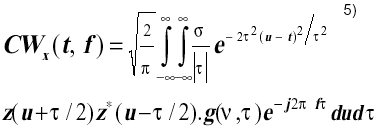
En la clasificación de complejos QRS contaminados con ruido, se analizó en este trabajo el efecto de utilizar dos distancias (Euclidiana y de Chebyshev) así como distintos niveles de umbral en las RTF. Los resultados fueron expresados en términos de tablas y gráficos que muestran estimados de los porcentajes de clasificación correcta para las señales contaminadas con ruido.

La novedad científica introducida en este trabajo, relacionada con el segundo objetivo, consistió en emplear los valores complejos obtenidos para la STFT, demostrándose mediante experimentos de simulación la efectividad de este enfoque.

2. Materiales y Métodos

2.1. Clasificación de complejos QRS utilizando Representaciones Tiempo-Frecuencia

Para investigar experimentalmente el comportamiento del método de clasificación de complejos QRS a partir de las RTF empleadas, se utilizaron como patrones de referencia seis segmentos seleccionados de la base MIT/BIH [22], correspondientes a igual número de complejos QRS morfológicamente diferentes, que según el criterio de especialistas médicos son representativos de algunas de las anomalías más frecuentes en el funcionamiento del corazón [8]. La frecuencia de muestreo de las señales fue cambiada de 360 Hz a 500 Hz con el objetivo de alcanzar una mayor precisión en la localización de las marcas fiduciales (posiciones temporales de las ondas R).

Para la realización de los experimentos se utilizó la versión 6.5 (release 13) de MATLAB® con las herramientas del “Time- Frequency Toolbox” 17), que contiene programas para el cálculo de un gran número de RTF y de funciones auxiliares. Se empleó una computadora personal Pentium IV a 3 GHz y con 512 Mb de RAM.

En lo que sigue se describen los experimentos de computación realizados, para analizar comparativamente el comportamiento de un conjunto de RTF durante la clasificación de patrones QRS electrocardiográficos contaminados con ruido.

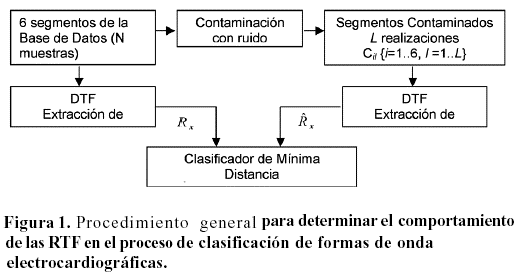
A partir de cada uno de los seis patrones antes referidos, que es a los efectos de esta investigación representativo de una clase diferente, se formaron L=37 realizaciones de segmentos contaminados con ruido. Tanto los segmentos de referencia como los contaminados se transformaron para obtener sus RTF, de las que se extrajeron los rasgos, Rx, que fueron utilizados para determinar y comparar las distancias entre los patrones contaminados y cada uno de los 6 patrones de referencia. Se asignó al segmento contaminado la clase asociada al patrón de referencia correspondiente a la menor distancia. Para la validación de los resultados se utilizó el método propuesto en [8]. El procedimiento general se describe en la Figura 1.

Las RTF empleadas para realizar el estudio de los patrones seleccionados fueron la STFT, la distribución CW, la WV y sus variantes Pseudo (PWV) y Suavizada-Pseudo (SPWV), por ser estas las más representativas al utilizar estas herramientas. Las ventanas de suavizamiento utilizadas se muestran en la Tabla I.

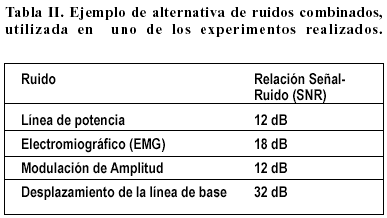
Para estudiar el efecto de la presencia ruidos sobre las RTF se realizaron las variantes de los experimentos descritos en [8]. En ellas se adicionaron varios tipos de ruido y sus combinaciones a los patrones originales, y se estudió la degradación producida en el dominio t-f. La Tabla II muestra un ejemplo de combinación de ruidos utilizada en los experimentos de simulación. Las relaciones señal a ruido para los diferentes tipos de ruido se determinaron independientemente, y luego los ruidos contaminantes se sumaron a la señal original.

En la determinación de las RTF de los complejos ECG, se probaron experimentalmente diferentes tipos y duraciones de ventanas así como diferentes kernels. Se tomaron como indicadores de la calidad de las RTF obtenidas el nivel de los términos cruzados y la concentración de la energía de la distribución.

Para utilizar las RTF en la clasificación se emplearon los estimados de la energía en cada punto del plano t-f, los estimados de la potencia instantánea y de la densidad espectral de energía, así como los máximos locales. Se seleccionaron aquellas características que efectivamente permitían la diferenciación entre las clases que se deseaba clasificar. Este proceso de extracción de características constituye un paso indispensable en la clasificación paramétrica de patrones, dada la necesidad de reducir al mínimo necesario la cantidad de parámetros que se utilizan para la clasificación.

En este trabajo, para reducir el volumen de información que a procesar, se seleccionó la región de la RTF cuyos valores resultaron ser mayores que cierto nivel umbral de comparación..La región así seleccionada depende de las características espectrales de la señal ECG que se analiza y de los ruidos que la afectan. En este caso, un factor a tener en cuenta es que los componentes espectrales de la señal ECG se ubican en el intervalo de frecuencias entre 0.05 y 100 Hz, y dentro de éste, los complejos QRS ocupan la zona alrededor de los 17 Hz, teniendo una distribución espectral de la energía que depende del tipo de latido,[23, 24].

El procedimiento de evaluación de la robustez del método de clasificación basado en el empleo de RTF frente al ruido consistió en los pasos siguientes:

a. Se contaminaron los seis patrones considerados con diferentes tipos de ruido y a diferentes valores de relación señal a ruido.

b. Se calcularon las RTF de todos los patrones contaminados y se redujo la información, tomando solo la región de la RTF cuyos valores están por encima del umbral.

c. Se compararon todos los patrones ruidosos con los originales y se estimó la probabilidad de aciertos en términos de la frecuencia relativa de éstos, expresada como un porcentaje. En este caso se define un acierto como la obtención de una distancia mínima entre un patrón ruidoso dado y el patrón no ruidoso del cual se obtuvo, con la consiguiente clasificación correcta. La probabilidad de acierto depende de la RTF empleada, el umbral considerado, los tipos de ruido y la relación señal a ruido. Para un conjunto de condiciones similares, los experimentos persiguieron determinar cuál es la RTF más favorable para realizar esta clasificación. Para los complejos QRS empleados en los experimentos, la zona del plano t-f utilizada en la comparación abarcó 160 ms, tomados desde 68 ms antes de la marca fiducial, y en frecuencias desde 0 hasta 16 Hz.

Entre los parámetros asociados a las RTF se escogieron los estimados de la energía en el plano t-f, para determinar las distancias entre los patrones contaminados y los de referencia. Los experimentos realizados considerando otras características tales como máximos locales y los marginales no arrojaron resultados relevantes.

Las diferencias entre las RTF de los patrones originales y los contaminados se determinaron utilizando las distancias de Chebyshev (D1) y Euclidiana (D2), dadas respectivamente por.

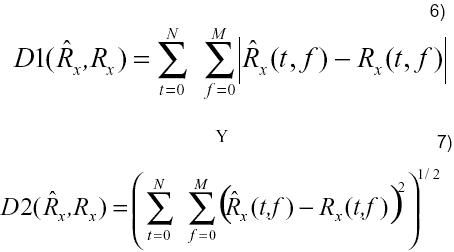
En (6) y (7) x(t,f) y x(t,f) contienen respectivamente los valores de los parámetros de las RTF de los patrones contaminados y de los originales que sirvieron como referencia.

Para determinar los estimados de efectividad en la clasificación se conformaron, a partir de los 6 patrones de complejos QRS escogidos, 37 alternativas contaminadas con igual número de variantes de ruido de tipo simple y combinado, siguiendo el método expuesto en [8]. Se obtuvieron las RTF de los patrones contaminados y se compararon con las correspondientes a los patrones originales. En la determinación de las distancias se emplearon umbrales para la discriminar los valores útiles de las RTF empleados en los cálculos. Como indicador de la efectividad en la clasificación se determinó la frecuencia relativa de aciertos.

2.2. Clasificación basada en los valores complejos de la STFT

Una de las causas fundamentales de la alteración morfológica de las ondas del ECG es la variación en la generación y/o conducción de los impulsos eléctricos en el corazón. Tales anomalías afectan la forma del complejo QRS debido a las perturbaciones de la amplitud y la fase de las señales que lo componen, por lo que se puede esperar que al utilizar simultáneamente la fase y la amplitud se disponga de mayor información para describir los latidos durante la clasificación. A partir de este razonamiento, se ha propuesto y analizado un método para la clasificación de latidos en la señal ECG en presencia de ruidos fisiológicos, utilizando como descriptores los valores complejos de la STFT.

De esta forma, para alcanzar el segundo objetivo de este trabajo se utilizó como RTF la STFT, tomando como criterio, a partir de los resultados anteriores, lograr altas probabilidades de acierto y simultáneamente una relativa independencia con respecto al nivel de umbral utilizado (Figuras 2 y 3). Se introdujo como nuevo elemento el empleo de los valores complejos de la STFT, como descriptores de los latidos en cada punto del plano t-f. Estos valores contienen información acerca de la magnitud y la fase de la componente espectral en un instante dado. El procedimiento general fue el mismo que se describe en la Figura 1, y en los experimentos se utilizó la ventana de Hamming, aplicada a segmentos de 17 muestras, equivalentes a intervalos de 34 ms de duración.

Los seis patrones de referencia utilizados, formados por vectores de 128 muestras, fueron centrados en la posición de la onda R del complejo QRS. Para cada tipo de ruido, se formaron versiones contaminadas hasta obtener 800 realizaciones por cada patrón de referencia, en condiciones similares a las descritas en [8]. Para analizar la clasificación con los valores complejos de la STFT, se emplearon tres tipos de ruido fisiológico: desplazamiento de los electrodos (ED), electromiográfico (EMG) y de respiración (RES). Para la simulación del ruido fueron utilizados los siguientes parámetros:

Desplazamiento en los electrodos (ED): señal sinusoidal de 0.07 Hz, con una amplitud 10 veces mayor que la señal de referencia (SNA = 0.1) y duración de 0.5 s.

Electromiográfico (EMG): ruido Gaussiano, con una relación señal-ruido (SNR) de –6dB.

De respiración (RES): combinación de modulación de amplitud, AM, y el desplazamiento de la línea de base (BLD), con SNR de 12 dB y 32 dB respectivamente.

Para realizar la clasificación, se utilizaron los valores contenidos en todas las columnas de las filas 1 a la 10 de las RTF, correspondientes a la duración del segmento, 255 ms, y a frecuencias en el intervalo de 0 a 37.1 Hz. Esto permitió incluir las componentes espectrales presentes en los complejos QRS [23]. La pertenencia de cada latido contaminado a una de las seis clases, se determinó utilizando el criterio de distancia mínima, comparando los valores calculados con cada uno de los patrones de referencia, sin emplear un umbral superior. Como métricas se probaron las distancias Euclidiana (6) y de Chebyshev (7), así como el Coeficiente de Correlación (CC),

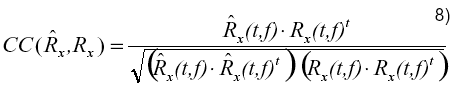
y la distancia de Manhattan (DM) o Taxi-Cab-Distance [25], en la que se hace uso explícito de los valores complejos de la STFT y que está dada por

3. Resultados

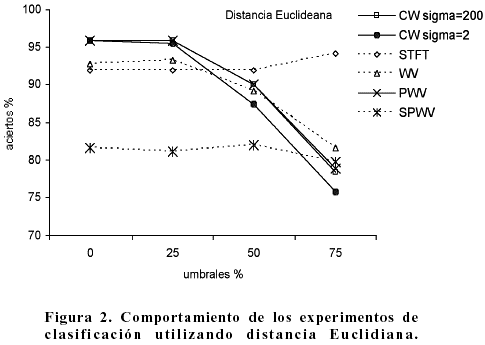
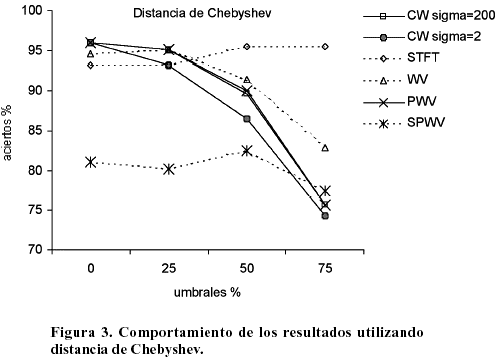
El comportamiento de los resultados de la clasificación en términos del porcentaje de clasificación correcta como función del nivel del umbral, se muestra para la distancia Euclideana en la Figura 2 y para la distancia de Chebyshev en la Figura 3. Se obtuvo en estos casos una familia de curvas, cada una de las cuales corresponde a una de las RTF consideradas en esta investigación: CW (s =2, s =200), WV, PWV, SWV, SPWV y STFT. En este caso se consideró que un patrón ruidoso fue clasificado correctamente, si la menor distancia se obtuvo con respecto al patrón no contaminado que le dio origen.

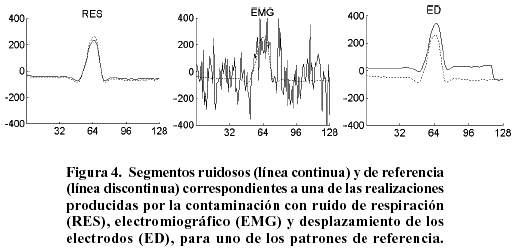
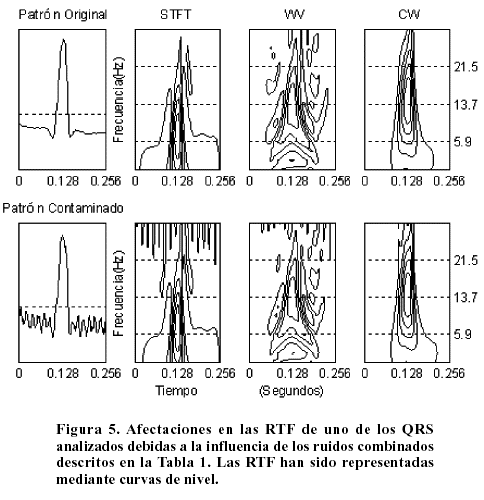
Los efectos de la contaminación con ruido de los diferentes patrones de la señal ECG se ilustran en la Figura 4 para un complejo QRS en particular, mientras que la Figura 5 ilustra las afectaciones en las RTF, representadas a partir de curvas de nivel, para uno de los complejos QRS analizados, debidas a la influencia de ruidos con la combinación descrita en la Tabla II. Nótese la diferencia entre las RTF para los patrones original y contaminado, y también cómo se reducen los términos cruzados en el caso de la CW. Estos términos se manifiestan en los gráficos como curvas de nivel espurias en zonas del plano t-f donde no debería aparecer energía. Obsérvese que los términos cruzados, que aparecen aún en ausencia de ruido, se modifican en amplitud y forma para el caso de las señales contaminadas.

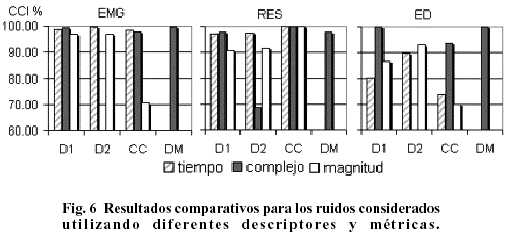
Finalmente, a partir de los resultados mostrados en las Figuras 2 y 3 se seleccionó la STFT para introducir un nuevo enfoque en el cálculo de las distancias, que utiliza explícitamente los valores complejos de la STFT según aparece en la ecuación (9). En este caso, para los tres tipos de ruido empleados en estos experimentos, se calcularon las distancias D1, D2 y CC en los experimentos con todos los descriptores y la distancia DM sólo para el caso en que se utilizaron los valores complejos. Se comparó el efecto de medir las distancias entre los patrones temporales, los valores complejos de la STFT y su magnitud. Los resultados obtenidos se muestran en la Tabla III. La Figura 6 muestra estos resultados:

3.1. Discusión de resultados

En las Figuras 2 y 3 puede apreciarse que los mejores resultados se obtuvieron para las distribuciones de CW, sin umbral y con umbral de 25 %, con 213 patrones correctamente clasificados de los 222 totales, lo que significa un 96 % de acierto. Se obtuvo un resultado similar para la PWV sin umbral.

Las distribuciones CW y PWV mostraron una relativamente alta estabilidad en los resultados con respecto a la variación de los umbrales y al tipo de distancia utilizada. La CW presenta una favorable reducción de los términos cruzados, a partir de una apropiada selección del parámetro s. La STFT, con resultados ligeramente inferiores en cuanto al porcentaje de clasificación correcta, mostró la mayor independencia con respecto a los umbrales. Este es un factor importante, pues el uso de umbrales más elevados puede implicar una mayor reducción de los datos utilizados en la comparación, con el consiguiente efecto positivo sobre la disminución del costo computacional del método, que es en general elevado. Este elemento determinó la selección de la STFT para la propuesta del nuevo método para elevar la efectividad en la clasificación, mediante el uso de los valores complejos de la STFT.

Las diferencias en los resultados que aparecen al utilizar las distancias Euclidiana y de Chebyshev indicaron una dependencia ligeramente menor de la efectividad en la clasificación que utiliza la primera, con respecto al valor de los umbrales que se utilizaron para realizar las comparaciones.

Aunque el empleo de umbrales en la comparación puede ser indispensable para incrementar la efectividad de la clasificación en presencia de ruido, sus valores más adecuados dependen de las características de las RTF que se utilizan y de la aplicación particular, pues las magnitudes de los estimados de la energía no tienen necesariamente una relación directa con su importancia para la discriminación de las clases en el proceso de clasificación. Se observó que el suavizamiento, utilizado para reducir el efecto de los términos cruzados, empeora en alguna medida la resolución que se logra con las RTF en el plano t-f. El suavizamiento en la frecuencia se logra utilizando la función de ponderación h(u) y en el tiempo mediante la función g(u), con los parámetros que aparecen en la Tabla I.

En la efectividad de los métodos empleados influyó significativamente la selección de los parámetros utilizados para caracterizar las RTF, que fue realizada aquí de forma experimental. Se deben reconocer las ventajas que podrían derivarse del empleo de métodos adaptativos, que tengan en cuenta la variabilidad de las características de las RTF de los patrones utilizados como referencia. La extracción de las características apropiadas permitió además reducir la dimensionalidad de la información a manipular, lo que incrementa las opciones de realización práctica de los procedimientos que utilicen este método.

El efecto del ruido pudiera reducirse aún más utilizando RTF de interferencia reducida, en las que se adapte la función de parametrización a las características de la señal ECG y de los ruidos que más la afectan.

En la Tabla III (Figura 6) puede apreciarse que en los experimentos realizados con los valores complejos de la STFT se logró el índice de clasificación correcta más elevado.

Utilizando una zona apropiada de la RTF, obtenida al aplicar el umbral correspondiente, se determinó la magnitud de la contribución al proceso de clasificación de cada descriptor analizado. En la Figura 6 se puede apreciar cómo el empleo conjunto de la información de la magnitud y la fase, obtenidos a partir de los valores complejos de la STFT, mejora el índice de clasificación correcta (CCI). Los índices alcanzados con este descriptor fueron superiores a los que se lograron empleando la información de la magnitud o la fase por separado y también a los que se logran con experimentos realizados totalmente en el dominio del tiempo.

El uso de la distancia DM en la clasificación produjo resultados similares a los obtenidos con la distancia D1, con la ventaja para la primera en la menor cantidad de operaciones aritméticas necesarias al procesar valores complejos. Este es un aspecto de peso a considerar en aplicaciones en tiempo real, debido a la alta dimensionalidad del conjunto de descriptores.

III. CONCLUSIONES

1. En los experimentos de clasificación, las RTF que mostraron una relativamente alta estabilidad en los resultados, con respecto a la variación de los umbrales y al tipo de distancia utilizada, fueron CW y PWV. La STFT obtuvo resultados ligeramente inferiores en el porcentaje de clasificación correcta, pero mostró ser más independiente de los umbrales.

2. La distancia Euclidiana se comportó algo menos dependiente del valor de los umbrales, en cuanto a la efectividad en la clasificación, en comparación con las demás distancias.

3. Se observó que el empleo del suavizamiento empeora en alguna medida el resultado de la clasificación, al reducirse la resolución que se logra en el plano conjunto t-f con las RTF.

4. En la efectividad de los métodos empleados influyeron significativamente la selección de los parámetros utilizados para caracterizar las RTF y el proceso de reducción de la dimensionalidad.

5. El índice de clasificación más elevado se logró con el método basado en el uso de los valores complejos de la STFT.

6. La distancia DM produjo resultados similares a los obtenidos con la distancia D1, pero con menor cantidad de operaciones aritméticas al procesar valores complejos.

IV. REFERENCIAS

1) Moraes J. et al.,“A Real Time QRS Complex Classification Method Using Mahalanobis Distance”, IEEE Computers in Cardiology 2002, 201-204.        [ Links ]

2) Nabney I. et al., “Benchmarking Beat Classification Algorithms”, IEEE Computers in Cardiology 2001, 529-532.        [ Links ]

3) Rasiah A. y Attikiouzel Y., “Syntactic Recognition of Common Cardiac Arrhythmias”, en 16th Annual International Conference of IEEE Engineering, Biology and Medicine Society, Baltimore, USA, Nov. 3-6, Vol. 1, 1994, 155-156.        [ Links ]

4) Barro, S., Presedo, J., Vila, J., “Patient Management in CCUs: Need for an Intelligent Interpretation of Signals”, Experts Systems with Applications, Vol. 6, 1998, 421-432.        [ Links ]

5) Pedryez, W., Bortolan, G., Degani, R., “Classification of Electrocardiographic Signals: a Fuzzy Pattern Matching Approach”, Artificial Intelligence in Medicine, Vol. 3, No. 4, 1999, 211-226.        [ Links ]

6) Barro, S., Ruiz, R., Mira, J. “Multiprocessor System for Online Monitoring in a CCU”, Computing and Data Processing, Vol. 28, 1993, 339-349.        [ Links ]

7) del Toro A., Santos, G., Cano, A., “Automatic Detection and Classification of Cardiac Arrhythmias using Finite State Automata”, en Proc. TELEC 2002 International Conference, Universidad de Oriente, Santiago de Cuba, 2002, CD-ROM de Actas del TELEC’2002. ISBN 84-8138-506-9.        [ Links ]

8) Orozco R., et al, “Evaluation of QRS Morphological Classifiers in the Presence of Noise”, Computers and Biomedical Research, Vol. 30, 1997, 200-210.        [ Links ]

9) Palreddy, S., “ECG Beat Classification”, Ph. D. Dissertation, Univ. of Wisconsin-Madison, 1996.        [ Links ]

10) Mendoza, M. y Lorenzo, J., “Clasificación de complejos QRS electrocardiográficos utilizando distribuciones tiempofrecuencia”, Revista Ingeniería Electrónica, Automática y Comunicaciones, Vol. XX, No. 2, 1999, 56-61.        [ Links ]

11) Durka P., Ircha D. y Blinowska K., “Stochastic Time-Frequency Dictionaries for Matching Pursuit”, IEEE Transactions on Signal Processing, Vol. 49, No. 3, 2001, 507-510.        [ Links ]

12) Chouvarda I., Maglaveras N., Pappas C., “Adaptive Time-Frequency ECG Analysis”, IEEE Computers in Cardiology, 2001, 265- 268.        [ Links ]

13) Miklos S., “Event Recognition, Separation and Classification from ECG Recordings”, en IEEE 20th Annual International Conference on Engineering in Medicine & Biology, 1998, 236 – 239.        [ Links ]

14) Williams, J.W., “Recent Advantages in Time-Frequency Representations: Some Theoretical Foundations”, en Time Frequency and Wavelets in Biomedical Signal Processing, M. Akay (Ed), Piscataway, NJ, IEEE Press, 1998 , 3-43.        [ Links ]

15) Boashash, B., Reilly, A., “Algorithms for Time-Frequency Signal Analysis”, en Time-Frequency Signal Analysis, B. Boashash (Ed.), London, Longman Cheshire, 1992, 163-181.        [ Links ]

16) Harris, F. “Techniques and Limitations of Spectrum Analysis, with the DFT”, en Time-Frequency Signal Analysis, B. Boashash (Ed.), London, Longman Cheshire, 1992, 184-207.        [ Links ]

17) Auger, F., Flandrin, P., Goncalves, P., Lemoine, O., “Time Frequency Toolbox, for Use with MATLAB”, Tutorial, Centre National de la Recherche Scientifique and Rice University, 1996, http://gdr-isis.org/Applications/tftb/iutsn.univnantes.fr/auger/tftb.html. Consultada en enero, 2000.        [ Links ]

18) Boudreaux-Bartels, G. F. y otros: “Time-Frequency Signal Representations of Biomedical Signals”, en The Biomedical Engineering Handbook, J. D. Bronzino (Ed.), CRC Press, Boca Raton, Fl., 1995, 866-885.        [ Links ]

19) Cohen, L.: “Time Frequency Distributions – A Review”, Proceedings of the IEEE, Vol. 77, No. 7, 1989, 941-981.        [ Links ]

20) Auger, F. y Flandrin, P.: “The Why and How of Time-Frequency Reassignment” en IEEE International Symposium of Time-Frequency and Time-Scale Analysis, 1994, 197-200.        [ Links ]

21) Williams, W. y Jeong, J.: “Reduced Interference Time-Frequency Distributions”, en Time-Frequency Signal Analysis, B. Boashash (Ed.), London, Longman Cheshire, 1992, 74-97.        [ Links ]

22) MIT-BIH Arrhythmia Database. Harvard University/Massachusetts Institute of Technology, Division of Health Sciences and Technology, Cambridge, MA, 1992.        [ Links ]

23) Cohen, A.: “Biomedical Signals: Origin and Dynamic Characteristics ; Frequency Domain Analysis” en The Biomedical Engineering Handbook, J. D. Bronzino (Ed.), CRC Press, Boca Raton, Fl., 1995, 805-827.        [ Links ]

24) Thakor, N. V. y otros: “Estimation of QRS Complex Power Spectra for design of a QRS Filter”, IEEE Transactions on Biomedical Engineering, Vol. 31, 1984, 702-705.        [ Links ]

25) Skiena, S., Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, London, Addison-Wesley, 1990, 172-227.        [ Links ]