PROGRAMACIÓN DE OPERACIONES CON TIEMPOS DE PREPARACIÓN MEDIANTE ALGORITMOS DE OPTIMIZACIÓN LOCAL

Companys, Ramón;  D' Armas, Mayra

Dr. Ramón Companys Pascual: Catedrático de Universidad en el Dpto. de Organización de Empresas, Escuela Técnica Superior de Ingeniería Industrial, Universidad Politécnica de Cataluña, Av. Diagonal 647, 7º, 08028 Barcelona, España. Telef. 34 934010769, fax 34 934016054, correo electrónico ramon.companys@upc.es.

MSc. Mayra D’ Armas Regnault: Profesor Ordinario con categoría Agregado en el Dpto. de Ingeniería Industrial de la Universidad Nacional Experimental Politécnica “Antonio José de Sucre” (UNEXPO) Vicerrectorado Puerto Ordaz, Final Calle China, Villa Asia, Puerto Ordaz. Edo. Bolívar, Venezuela, Telfax 58 286 9623066, correos electrónicos mdarmas@poz.unexpo.edu.ve. y mayra.darmas@upc.es

Resumen: El objetivo del presente trabajo es evaluar, mediante pruebas computacionales, el comportamiento de los algoritmos heurísticos directos y de optimización local para resolver el problema de programación de operaciones. Este artículo está dirigido al problema de secuenciación de operaciones en una máquina con familia de productos, en la que los tiempos de preparación están separados de los tiempos de procesamiento, y son dependientes de la secuencia, con el objetivo de minimizar la suma de los retrasos. Los algoritmos se codificaron en Visual Basic y se probaron en 1000 ejemplares con un número de familias entre 4-6 y con un número total de piezas entre 15–25. Los resultados computacionales mostraron que: (a) la heurística Índice Crítico es la que proporciona mejores soluciones iniciales; (b) a pesar de que con la heurística Earliest Due Date se obtuvo el mayor número de peores soluciones iniciales, con la aplicación de la heurística de mejora se logran alcanzar buenos resultados; (c) el uso de una solución inicial mejor no garantiza un mejor resultado después de la fase de mejora local (d) la capacidad de mejora de los algoritmos heurísticos de optimización local es dependiente de la heurística inicial aplicada.

Palabras clave: Algoritmos de Operaciones/ Algoritmos heurísticos directos/ Programación de Operaciones/ Tiempos de preparación dependientes de la secuencia.

OPERATION SCHEDULING WITH SETUP TIMES BY LOCAL OPTIMIZATION ALGORITHMS

Summary: The objective of this work is to evaluate, by means of computer tests, the behavior of the direct heuristics algorithms and local optimization to solve the operation scheduling problem. This article refers to the operation sequence problem on a machine with families of products, where setup times are separated from the processing times, and are dependent on the sequence, with the objective of minimizing the sum of delays. The algorithms were codified in Visual Basic and 1000 samples were tested with a number of families between 4-6 and with a total number of pieces between 15-25. Computer results showed that: (a) Critical Index heuristic is the one that provides better initial solutions; (b) although with Earliest Due Date heuristic a greater number of worse initial solutions was obtained, with the application of the improvement heuristic, good results are achieved; (c) the use of a better initial solution does not guarantee a better result after the phase of local improvement (d) the capacity of improvement of the heuristic algorithms of local optimization is dependent on the initial heuristic used.

Keywords: Direct Heuristics Algorithms / Operation Algorithms / Operation Scheduling / Sequence-Dependent Setup Times.

Finalizado el 2004/09/08   Recibido el 2004/08/09   Aceptado el 2005/03/05.

I. INTRODUCCIÓN

El prototipo de problema de secuenciación se encuentra en el denominado Problema del Taller Mecánico (Job-Shop Problem) cuyo enunciado básico es de la forma: n piezas (lotes, trabajos u órdenes) deben realizarse en m máquinas (secciones o puestos de trabajo). La realización de cada pieza está asignada a una máquina concreta y tiene una duración determinada conocida. Debe establecerse un programa, es decir, la secuencia de operaciones en cada máquina, que optimice un cierto índice de eficacia. [1]

De acuerdo con Allahverdi et al [2], los problemas de secuenciación con preparación se agrupan en aquellos que tienen y no tienen familias, donde la preparación puede ser dependiente o independiente de la secuencia.

Se considera que la preparación es dependiente de la secuencia, si su duración depende tanto de la operación actual como de la inmediatamente precedente, y la preparación es independiente de la secuencia, si su duración depende solamente de la operación actual a ser procesada. El problema de preparación con familia ocurre cuando se agrupan en familias (o familias de productos) tipos de piezas y se incurre en un tiempo de preparación (significativo) cuando se cambia entre los tipos de piezas de las diferentes familias, y, en algunas aplicaciones, se incurre en una preparación (menor) por el cambio entre los tipos de piezas dentro de la misma familia de productos. Es decir, el tiempo de preparación principal depende solamente de la familia que está siendo cambiada, y el tiempo de preparación menor depende solamente del tipo de pieza que está siendo cambiada.

En los ambientes industriales, es común que se lleven a cabo diversos tipos de operaciones que requieren la preparación de las máquinas y los procesos, que incluye actividades como la obtención de herramientas, la colocación del material en proceso, la limpieza, la colocación de plantillas y los accesorios requeridos, el ajuste de las herramientas, y la inspección de material. Sin embargo, muchas de las investigaciones en el área de la secuenciación de operaciones, consideran que cuando una máquina cambia de un trabajo a otro no hay tiempos de preparación, y si los hay, éstos se consideran independientes de la secuencia. [3] No obstante, la suposición de que los tiempos de preparación son insignificantes o forman parte del tiempo de procesamiento, no es válido para el caso de tiempos de preparación dependientes de la secuencia, y en el caso de tiempos de preparación independientes de la secuencia puede conducir a un incremento de los tiempos muertos en algunas de las máquinas. [4]

Las aplicaciones prácticas que apoyan la consideración de separar las tareas de preparación de las tareas de procesamiento se encuentran con frecuencia en los ambientes industriales, tales como la industria química, textil, del plástico, farmacéutica, de semiconductores, del metal y de procesamiento de productos, donde normalmente se realizan diversos tipos de operaciones en las instalaciones.

Varios autores han presentado ejemplos de aplicación: Conway et al [5] refieren la industria de la impresión; Pinedo[6] describe una fábrica de bolsa de papel donde se necesita preparación cuando la máquina cambia entre tipos de bolsas de papel; Das y Gupta [7] hacen referencia al requerimiento de tiempos de preparación dependientes de la secuencia, en la industria del plástico; França et al [8], y Ríos Mercado y Bard [9] presentan ejemplos de la industria química; Ng et al [10] y Aldowaisan [11], estudiaron la secuenciación con tiempos de preparación en la industria de la producción de acero.

Debido a que diversas industrias de Ciudad Guayana se caracterizan por una situación casi prototípica reducible a un problema de una máquina con fechas de vencimiento, en este trabajo se planteó encontrar una secuencia de n piezas, en un ambiente de una máquina, con familia de productos y tiempos de preparación dependientes de la secuencia, que minimice la suma de los retrasos. Para resolver el problema se aplicaron tres heurísticas directas y dos heurísticas de optimización local, y mediante una investigación no experimental se evaluó el comportamiento de dichos algoritmos heurísticos. La experiencia computacional se realizó en 1000 ejemplares con capacidad para procesar un número total de piezas entre 15–25, y un número de familias entre 4–6.

II. DESARROLLO

1. Formulación del problema

Esta investigación se enmarca dentro de la problemática de la programación de la producción. El problema de la programación de la producción consiste en asignar las órdenes de producción y/o las operaciones en que se descomponen a centros de trabajo específicos dentro de intervalos temporales concretos; en otras palabras un programa es una asignación más un calendario. [1] Siguiendo a Companys y Corominas [1], la nomenclatura utilizada es la siguiente: A/B/C/D, donde A corresponde al número de piezas (n indica un número de piezas arbitrario). B describe el número de máquinas en el taller (m indica un número arbitrario).

C se refiere al tipo de flujo de las piezas por el taller, y generalmente toma uno de los valores F, P, R o G:

F: indica flujo regular (flow shop), todas las piezas tienen la misma ruta.

P: indica un caso particular del anterior, donde todas las máquinas tienen la misma secuencia de piezas.

R: indica rutas aleatorias (randomly routed job shop)

G: indica flujo general.

D se refiere al índice de eficiencia elegido para evaluar los programas, por ejemplo: C_max (instante de salida de la última pieza del taller), F_max (tiempo de permanencia de la pieza que permanece más tiempo), F_med (tiempo medio de permanencia en el taller), T_max (retraso de la pieza que se retrasa más), T_med (retraso medio).

La nomenclatura n/1//ST que asume que no hay tiempos de preparación o que forman parte del tiempo de procesamiento, se transformó en n/1/STsd,b /ST para el caso de tiempos de preparación dependientes de la secuencia y familias de productos (STsd,b = sequence-dependent batch setup times). La notación usada es la siguiente:

Se tiene un conjunto de piezas que deben ser secuenciadas en una máquina. Se asume que la máquina puede procesar una sola pieza a la vez y que está disponible en el instante cero. Las piezas están disponibles al inicio del proceso (tiempo cero) y tienen un tiempo di límite de finalización o entrega. Se asume también que las piezas están clasificadas en g familias y que el tiempo de preparación ST se produce cuando se pasa de una familia a otra.

El tiempo de preparación de la máquina ST depende del orden de la secuencia, de tal manera que hay un tiempo de preparación que debe preceder al inicio del procesamiento de la pieza dada, que depende de la familia de la pieza a ser procesada y la familia de la pieza que la precede. La matriz de tiempos de preparación no tiene por que ser simétrica.

Para cada pieza i se conoce el tiempo de operación pi; el tiempo de entrega comprometida di y la familia a la que pertenece dicha pieza gi. Además, se conocen los tiempos de preparación de la máquina ST al pasar de una familia a otra. Según la secuencia escogida, para cada pieza i el instante en que la pieza sale del taller ci, viene dado por: ci = ri + wi +pi+SThi y su retraso Ti viene dado por: Ti = max{0, ci–di}

El objetivo es encontrar una secuencia de las piezas que minimice la suma del retraso de las piezas:

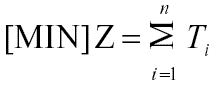
2. Metodología

El presente trabajo se realizó mediante una investigación no experimental del tipo exploratoria y evaluativa que permitió evaluar, mediante pruebas computacionales, el comportamiento de los algoritmos heurísticos directos y de optimización local para resolver el problema de secuenciación de operaciones.

Los algoritmos se codificaron en Visual Basic y las pruebas se realizaron en un computador personal. En la experiencia computacional se probaron 1000 ejemplares con un número de familias entre 4-6 y con un número de piezas entre 15–25. Los ejemplares se clasificaron en problemas de: (a)15 piezas de 4 familias, Nº de ejemplares: 200; (b) 20 piezas de 4 familias, Nº de ejemplares: 200; (c) 25 piezas de 4 familias, Nº de ejemplares: 200; (d) 20 piezas de 5 familias, Nº de ejemplares: 100; (e) 25 piezas de 5 familias, Nº de ejemplares: 100; y (f) 25 piezas de 6 familias, Nº de ejemplares: 200. Cada ejemplar se resolvió usando cada una de las tres heurísticas directas; y además a cada ejemplar se le aplicaron dos heurísticas de optimización local, con y sin tratamiento de empates.

Los datos dados para cada uno de los ejemplares son: número de piezas, número de familias, tiempo de preparación para pasar de una familia a otra, tiempo de operación de cada pieza, tiempo de entrega de cada pieza, familia a la que pertenece cada pieza y la familia procesada anteriormente (para la cual la máquina está preparada inicialmente).

3. Heurísticas

Una heurística o algoritmo heurístico es un método eficiente con respecto al tiempo de cómputo y al espacio de memoria, y con cierta verosimilitud de obtener una solución más o menos satisfactoria, es decir, relativamente cercana a la óptima mediante el examen de sólo un pequeño subconjunto de soluciones del número total.

Según Miller y Schmidt [12] en los algoritmos heurísticos no se puede probar rigurosamente que siempre el algoritmo convergerá a un óptimo global. El punto de terminación de un procedimiento heurístico puede ser un óptimo global, pero no se puede garantizar más adelante en el tiempo.

Por lo tanto, se aplicaron heurísticas que proporcionaron soluciones iniciales en un tiempo mínimo. Posteriormente, se aplicaron unos algoritmos que permitieran mejorar estas soluciones aproximándolas hacia el óptimo.

3.1 Heurísticas directas

Para resolver el problema se aplicaron tres heurísticas directas distintas, que permitieron generar soluciones iniciales en un tiempo de cálculo reducido. Las reglas de asignación de la secuencia de prioridades, para cada una de las heurísticas directas, se describen a continuación:

Heurística 1 (TSP-EDD): Asigna las piezas por familias y, además, ordena las piezas entre familia por fechas de vencimiento para favorecer un tiempo mínimo de cambios entre familias.

Heurística 2 (EDD): Secuencia conforme a la fecha de vencimiento. Esta regla favorece las piezas más prioritarias, sin embargo no aprovecha la ventaja de reducir los tiempos de preparación al procesar, sucesivamente, piezas de la misma familia.

Heurística 3 (CR): Asigna las piezas tomando en cuenta un índice crítico para cada pieza, el cual considera el tiempo de entrega d_i, el tiempo de preparación ST_h,i (dependiente de la familia de la pieza anterior h) y el tiempo de procesamiento pi

CR = a d_i + (1 - a) (p_i + ST_h,i)

Si a=0, CR equivale a aplicar la regla SPT (dinámico).

Si a=1, CR equivale a aplicar la regla EDD.

En el siguiente ejemplo se aplican las heurísticas TSP-EDD y EDD, para un ejemplar de 12/1/STsd,b/ST con cuatro familias, asumiendo que la familia anteriormente procesada es la número uno.

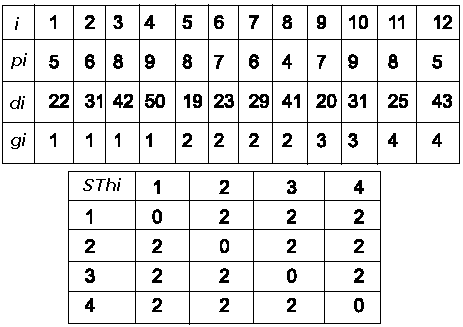
Si se ordena conforme a la fecha de vencimiento EDD, la secuencia es 5-9-1-6-11-7-2-10-8-3-12-4, y los resultados son los siguientes:

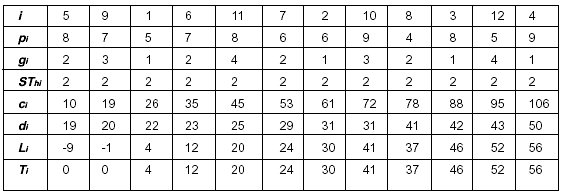
Si se ordenan por TSP-EDD la secuencia es 1-2-3-4-5-6-7-8-9-10-11-12, obteniéndose los resultados siguientes:

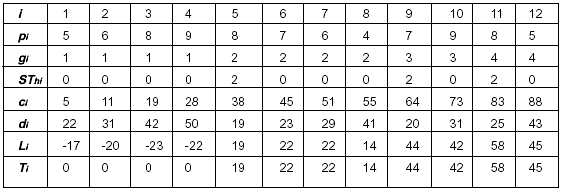
Si se comparan los resultados de las dos heurísticas, se puede observar que la secuencia TPS-EDD ofrece una suma de los retrasos menor; esta disminución puede ser debido a que se aprovecha la ventaja de reducir los tiempos de preparación al agrupar las piezas de la misma familia.

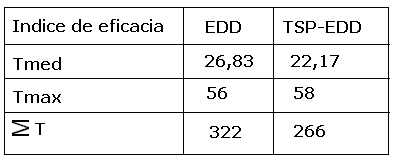
3.2 Heurísticas de mejora

A partir de las soluciones iniciales, se establecieron algoritmos de optimización local que permitieron mejorar estas soluciones. Los algoritmos de optimización local son algoritmos de mejora, de tipo determinista que tienen como objetivo alcanzar un óptimo local. En este estudio se aplicaron dos variantes de estos algoritmos, que exploran todo el entorno de la solución en curso con la que se esté operando, es decir el vecindario de una solución dada está compuesto por todos los cambios posibles entre dos piezas de una misma máquina, sean o no contiguas:

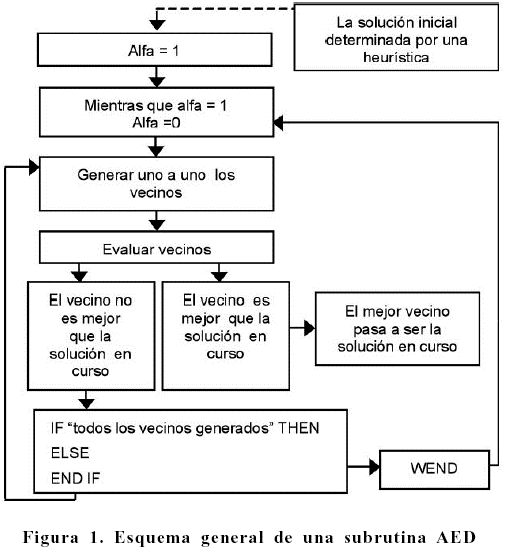
(1) Algoritmo Exhaustivo de Descenso (AED): partiendo de una solución inicial, se generan y evalúan todas sus vecinas. Si la mejor de las vecinas es mejor que la solución inicial, entonces la sustituye y se procede del mismo modo; en caso contrario finaliza el algoritmo. Ver Figura 1.

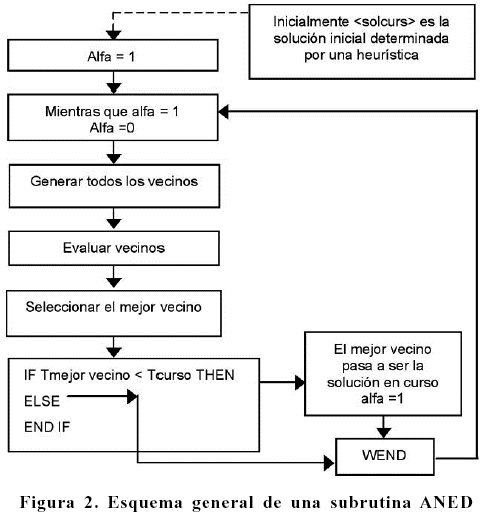
(2) Algoritmo no Exhaustivo de Descenso (ANED): partiendo de una solución inicial, se van generando y evaluando vecinas. En el momento que se encuentre una vecina cuya función objetivo es mejor que la función objetivo de la solución inicial, la sustituye y se vuelve a reiterar. El algoritmo finaliza si no hay ninguna mejor. Ver Figura 2

4. Resultados

En esta sección se describen las pruebas computacionales que se usaron para evaluar la eficiencia de los distintos métodos heurísticos.

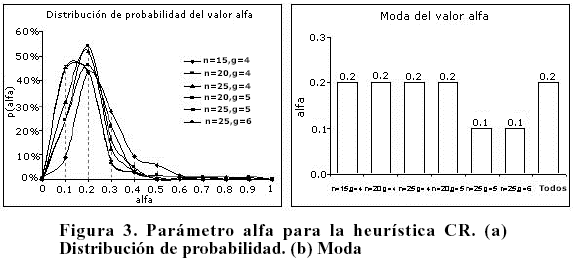
Valor del parámetro alfa que minimiza ST. Se inició con el estudio del valor a para la heurística directa Índice Crítico. Cada uno de los ejemplares se resolvió variando a en el intervalo [0,1], con incrementos de una décima, y seleccionando el menor retraso y su correspondiente valor a. La Figura 3 muestra los resultados de los valores del parámetro a que minimizan la función objetivo: (a) la distribución de probabilidad, y (b) la moda. En el gráfico se puede observar que la mayoría de las mejores soluciones para los ejemplares estudiados, se lograron con un alfa de 0,2.

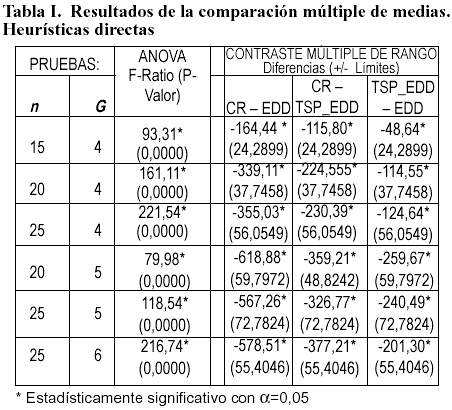
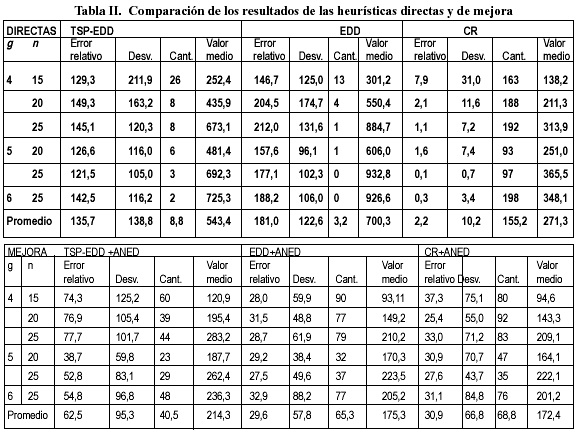
Comparación de los algoritmos heurísticos directos. Con el propósito de probar los efectos de los algoritmos heurísticos directos en la solución final, se realizó un análisis de varianza (ANOVA) de una vía a un nivel del 5%. Se determinó que existen diferencias significativas entre las medias de las tres heurísticas directas a un nivel de confianza del 95%. Además, se aplicó el procedimiento de las menores diferencias significativas de Fisher (LSD) para determinar las medias que son significativamente diferentes de otras. Los resultados indican que los tres pares muestran diferencias estadísticamente significativas a un nivel de confianza del 95%. (Ver Tabla I).

El rendimiento de las heurísticas se comparó en términos del porcentaje de error relativo, la desviación estándar, la cantidad de mejores soluciones y el valor medio del retraso total. Para el caso de la regla de secuenciación CR se tomó un valor alfa de 0,2. El porcentaje de error relativo se definió según Allahverdi y Aldowaisan [13] mediante la expresión:

Una vez obtenida las soluciones iniciales se le aplicó la heurística de optimización local ANED, sin tratamiento de empates. En la Tabla II se comparan para cada grupo de problemas, los resultados de la aplicación de las heurísticas directas (TSPEDD, EDD, CR) y de la heurística de mejora ANED (TSPEDD+ANED, EDD+ANED, CR+ANED).

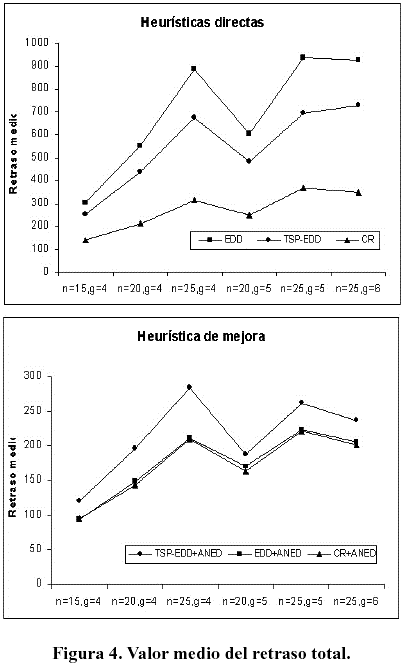
En la Figura 4 se muestra el valor medio del retraso total para (a) las heurísticas directas; y (b) la heurística de mejora ANED. Puede observarse que para todos los tipos de problemas, los mejores resultados de la solución inicial se obtienen con CR. En el caso de la aplicación de la heurística de mejora, el retraso medio es menor para EDD+AED y CR+AED con valores bastantes similares.

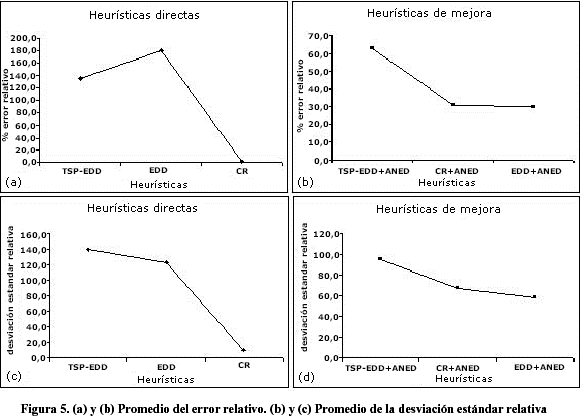
En la Figura 5 se presenta gráficamente el porcentaje de error relativo y la desviación estándar relativa de los retrasos, tanto para las heurísticas de mejora como para la heurística directa. En la Figura 5(a) se observa que la heurística directa CR tiene un porcentaje de error relativo muy bajo, lo que indica que la mayoría de las mejores soluciones iniciales se obtuvieron con esta heurística, y también se observa que el mayor % de error relativo lo arrojó la heurística EDD. En la Figura 5(b) se observa que son muy pequeñas las diferencias entre los porcentajes de error relativo de las soluciones obtenidas con EDD+ANED y CR+ANED. La heurística EDD, la cual presentó lo peores resultados iniciales, con la aplicación de la heurística de mejora logra alcanzar buenos resultados. La heurística directa CR y la de mejora EDD+ANED presentan la menor la desviación estándar relativa (Figura 5 (c)-(d)).

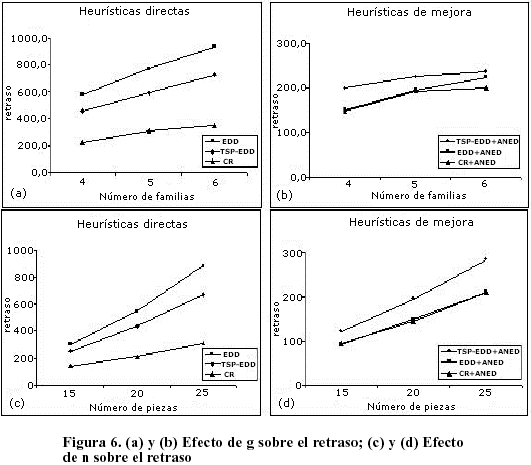
La Figura 6 muestra el efecto del número de familias y del número de piezas sobre el retraso total. En la Figura 6 (a)-(b) se observa que, tanto para las heurísticas directas como para la de mejora, el valor medio del retraso total aumenta a medida que aumenta el número de familias; sin embargo, en CR no sólo es menor el valor sino que el número de familias no influye tanto en el crecimiento del retraso. Un comportamiento similar se observa en la Figura 6 (c)-(d), donde el valor medio del retraso total aumenta a medida que aumenta el número de piezas.

Comparación de los algoritmos heurísticos de mejora.

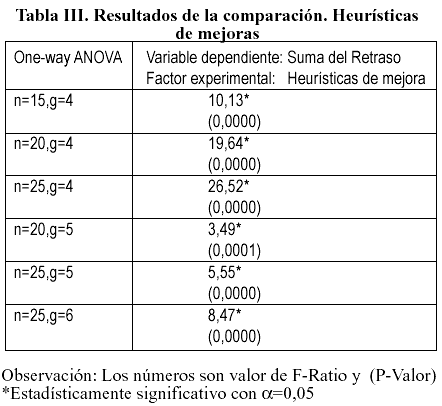
Adicionalmente, se compararon los resultados de las heurísticas de optimización local ANED y AED, con tratamiento de empates (CTE) y sin tratamiento de empates (STE). Se realizó un análisis de varianza de una vía para probar los efectos de las heurísticas de mejora en la solución final. Se determinó que hay diferencia estadísticamente significativa entre las medias de las 12 variables a un nivel de confianza del 95,0%. (Ver Tabla III).

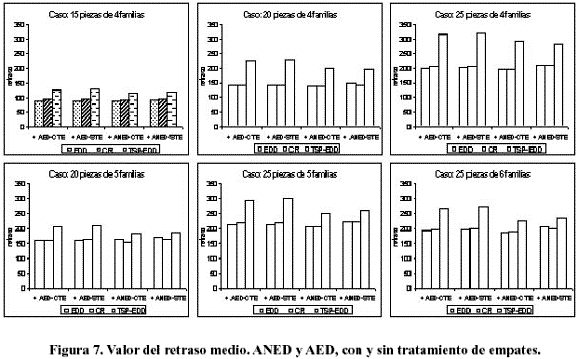
En la Figura 7 se presenta, para cada grupo de problemas, el valor del retraso de las heurísticas de mejora. De acuerdo con este gráfico, el comportamiento de las heurísticas de mejora depende de la heurística directa aplicada inicialmente, es decir proporcionan resultados distintos según la solución inicial de partida (EDD, CR o TSP-EDD). Para la solución inicial obtenida mediante CR, la heurística ANED con tratamiento de empates (CR+ANED-CTE) es la que arroja los mejores resultados. Para TSP-EDD, los mejores resultados se obtuvieron con ANED con tratamiento de empates (ANED-CTE) y con ANED sin tratamiento de empates (ANED-STE). Para la heurística EDD, los mejores resultados se lograron con la aplicación de ANED con tratamiento de empates.

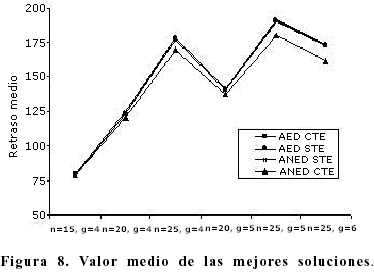
En la Figura 8 se presenta el valor medio del retraso de las mejores soluciones para las heurísticas de mejora. Se observa que en la mayoría de los problemas estudiados la heurística ANED con tratamiento de empates arroja el menor valor medio del retraso, y que las soluciones son similares cuando el número de piezas es menor, haciéndose notoria la diferencia en los casos donde el número de piezas es mayor.

5. Discusión de Resultados

Los resultados obtenidos mediante la variación del parámetro alfa para la heurística directa Índice Crítico (CR), muestran que las mejores soluciones se obtienen para valores alfa de: 0,1; 0,2 y 0,3; y que la mayoría de las mejores soluciones se logran con un alfa de 0,2. Este resultado es relevante para la investigación, ya que demuestra que el valor de alfa logra disminuir significativamente la función objetivo, es decir la suma de los retrasos de las diferentes órdenes de fabricación.

El análisis de varianza permitió demostrar que existen diferencias significativas en el retraso total de las heurísticas aplicadas. Sin embargo, la variación para los algoritmos heurísticos de mejora no fue tan significativa como la de las heurísticas directas. Los resultados experimentales obtenidos mediante la aplicación de las heurísticas directas EDD, TSP-EDD y CR, sugieren que heurística directa CR es una técnica viable que puede proporcionar buenas soluciones cuando se considera la función objetivo: ST con tiempos de preparación dependientes de la secuencia. Para todos los problemas estudiados CR es la mejor, ya que arrojó el menor valor medio del retraso, con el menor porcentaje de error relativo y de desviación estándar. Además, CR alcanzó las mejores soluciones en el 82% de los problemas de 15 piezas-4 familias, el 94% de los problemas de 20 piezas-4 familias, el 96% de los problemas de 25 piezas-4 familias, el 93% de los problemas de 20 piezas-5 familias, el 97% de los problemas de 25 piezas-5 familias y el 99% de los problemas de 25 piezas-6 familias.

La segunda mejor heurística directa es la que secuencia por familias y fechas de vencimiento (TSP-EDD), pero con un valor medio del retraso que duplica al obtenido con CR. Por otra parte, en todas las pruebas realizadas, los peores resultados se obtuvieron con la heurística EDD.

En el análisis del efecto del número de familias y del número de piezas sobre el retraso total, los resultados indican que el retraso total parece ser una función creciente del número de familias. Además, se observa una tendencia creciente del retraso en función del número de piezas. Estos efectos pueden ser debido a que la preparación depende tanto de la operación actual como de la inmediatamente precedente, y se incurre en un tiempo de preparación cuando se cambia de una familia a otra.

En cuanto a los algoritmos de mejora, a pesar de que la heurística EDD ofrece los peores resultados en la solución inicial, alcanza buenas soluciones con el algoritmo de optimización local, logrando en algunos casos, un retraso menor que el obtenido mediante la solución inicial CR. La heurística TSP-EDD no presenta un comportamiento muy positivo en la etapa de mejora, a pesar de que inicialmente mostró los segundos mejores resultados, con el algoritmo de optimización local arroja los mayores valores del retraso, con el mayor porcentaje de error relativo y de desviación estándar.

De la comparación de los resultados de la heurística ANED con la heurística AED, considerando el criterio de tratamiento de empates (CTE: con tratamiento de empates y STE: sin tratamiento de empates), se concluye que el comportamiento de las heurísticas de mejora varía dependiendo de la heurística directa aplicada inicialmente. Además, se encontró que tanto para la heurística ANED como para AED, en la mayoría de los casos, la aplicación del tratamiento de empates se tradujo en una reducción del valor medio de los retrasos. Sin embargo, las diferencias no son muy significativas.

III. CONCLUSIONES

1. Los valores de alfa que minimizan el retraso en la heurística CR se concentran en 0,1; 0,2 y 0,3. siendo a = 0,2 en la mayoría de las mejores soluciones.

2. Con la heurística CR se obtuvo el mayor número de mejores soluciones iniciales, mientras que con EDD se obtuvo el mayor número de peores soluciones iniciales.

3. A pesar de que la heurística EDD arrojó los peores resultados iniciales, con la aplicación de la heurística de mejora se logra alcanzar buenos resultados.

4. La heurística TSP-EDD, que inicialmente mostró los segundos mejores resultados, con la heurística de mejora arroja los peores resultados.

5. La aplicación de una solución inicial mejor no garantiza un mejor resultado después de la fase de mejora local.

6. La capacidad de mejora de los algoritmos heurísticos de optimización local ANED y AED, es dependiente de la heurística inicial aplicada. Aunque, la heurística ANED con tratamiento de empates alcanzó los mejores resultados en gran parte de los ejemplares, no se puede afirmar que sea la más ventajosa.

7. El tratamiento de empates, tanto para la heurística ANED como para AED, redujo el valor medio de los retrasos. Sin embargo, las disminuciones producidas fueron pequeñas.

IV. REFERENCIAS

1). Companys R y Corominas A. Organización de la Producción II: Dirección de Operaciones 4. Ediciones UPC, Barcelona, España. 1996. p.9-34.        [ Links ]

2). Allahverdi et al. A review of scheduling research involving setup considerations. Omega, International Journal of Management Science. Vol. 27, Nº 2, abril 2000, p. 219-239.        [ Links ]

3). D’Armas M y Companys R. Secuenciación de operaciones en una máquina con tiempos de preparación dependientes de la secuencia. Documento Interno de Trabajo. Universidad Politécnica de Cataluña. Departamento de Organización de Empresas. 2003. p.1-4.        [ Links ]

4). Allahverdi A. Minimizing mean flowtime in a two-machine flowshop with sequence-independent setup times. Computers & Operations Research. Vol. 27, Nº 2, febrero 2000, p.111-127.        [ Links ]

5). Conway RW, Maxwell WL y Miller LW. Theory of Scheduling. Dover Publications. Minneola, New York, 1967. p.57-67.        [ Links ]

6). Pinedo M. Scheduling: theory, algorithms and systems. Prentice Hall, Englewood Cliffs, 1995. p.15-22.        [ Links ]

7). Das S y Gupta J. A savings index heuristic algorithm for flowshop scheduling with sequence dependent set-up times. Journal of the Operational Research Society. Vol. 46. 1996. p. 1364-1372.        [ Links ]

8). França P, Gendreau M, Laporte G y Müller F. A tabu search heuristic for the multiprocessor scheduling problem with sequence dependent setup times. International Journal of Production Economics. Vol. 43, Nº 2-3, junio 1996. p. 79-89.        [ Links ]

9). Ríos-Mercado R y Bard J. Secuenciando óptimamente líneas de flujo en sistemas de manufactura. Ingenierías. Vol. 4, Nº 1, enero 2001. p. 39-45.        [ Links ]

10). Ng C-T-D, Cheng E y Kovalyov M. Single machine batch scheduling with jointly compressible setup and processing times. European Journal of Operational Research. Vol. 153, Nº 1, febrero 2004. p.211–219.        [ Links ]

11). Aldowaisan T y Allahverdi A. Total flowtime in no-wait flowshops with separated setup times. Computers Operation Research. Vol. 25, Nº 9, septiembre 1998. p. 757-765.        [ Links ]

12). Miller D y Schmidt J. Ingeniería Industrial e Investigación de Operaciones. México: Editorial Limusa. 1992. p. 245-264.        [ Links ]

13) Allahverdi A y Aldowaisan T. No-wait and separate setup threemachine flowshop with total completion time criterion. International Transactions in Operational Research. Vol. 7, Nº 3, mayo 2000. p. 245-264        [ Links ]