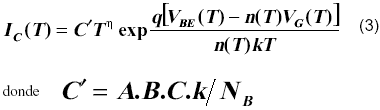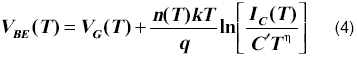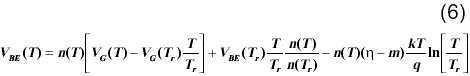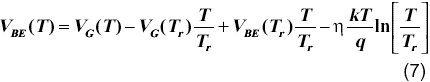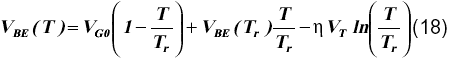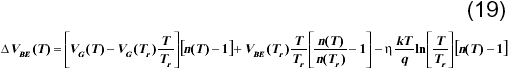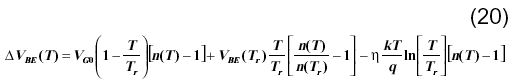LA INFLUENCIA DEL COEFICIENTE DE EMISIÓN N EN EL MODELO DE V_BE(T) DEL TRANSISTOR BIPOLAR

Nagy, Agnes;  Polanco, Alicia;  Álvarez, Manuel

Dra. Agnes Nagy Szomjas: Profesora Auxiliar en el Instituto Superior Politécnico José Antonio Echeverría (ISPJAE), P.O. Box 8016, Habana 10800, Cuba, Teléfono 53-7-452935, Fax 53-7-558939, correo electrónico agnes.nagy@electrica.cujae.edu.cu.

Dra. Alicia Polanco Risquet: Investigador Auxiliar en el mismo Instituto, mismos teléfono y fax, correo electrónico Alicia.polanco@electrica.cujae.edu.cu

Dr. Manuel Álvarez Blanco: Profesor Titular en el mismo Instituto, mismos teléfono y fax, correo electrónico Manuel@ind.cujae.edu.cu respectivamente.

Resumen: La necesidad de aumentar la exactitud y estabilidad en el diseño de los sensores de temperatura y referencias de banda prohibida bipolares, ha llevado recientemente a estudios experimentales sobre la variación del coeficiente de emisión n del transistor bipolar con la temperatura. El aumento de n con la disminución de la temperatura, observado en estos experimentos, aun no ha sido explicado. En el trabajo presente se explica la causa física de esta variación y se simula el comportamiento de n de un transistor bipolar a bajas temperaturas para diferentes condiciones de polarización. Se obtiene también una nueva expresión del potencial base-emisor VBE(T) que incluye el coeficiente de emisión. A partir de las expresiones teóricas se obtuvo un error en VBE(T ) superior a 2oC en el intervalo de 300 K a 240 K, al despreciar el coeficiente de emisión.

Palabras clave: Capacidad del emisor/ Coeficiente de emisión/ Modelo de VBE(T)/ Potencial baseemisor/ Transistor Bipolar.

INFLUENCE OF EMISSION COEFFICIENT N ON BIPOLAR TRANSISTOR V_BE(T) MODEL

Abstract: The need to increase accuracy and stability in the design of temperature sensors and bandgap references has led to recent experimental studies on the variation with temperature of the emission coefficient n. The increase of n with the decrease of temperature, observed in these experiments, has been not explained yet. In this paper the physical cause of this increase is explained and the behaviour of n as a function of temperature is simulated. A new expression of base-emitter voltage VBE(T) including the emission coefficient is also obtained. The error in VBE(T), calculated from theoretical expressions, caused by neglecting the emission coefficient is greater than 2oC.

Key words: Base-Emitter Voltage / Bipolar Transistor / Emission Coefficient / Emitter Capacitance / VBE(T) Model

Finalizado el 2005/01/13   Recibido el 2005/02/08   Aceptado el 2005/04/22.

I. INTRODUCCIÓN

A pesar de ser el transistor bipolar el primer dispositivo semiconductor activo, fabricado y comercializado hace más de 50 años, se mantiene vigente en muchos campos de aplicación. Sus excelentes propiedades en el rango de altas y muy altas frecuencias hacen que sea el elemento básico de los circuitos electrónicos para la tecnología de las comunicaciones [1]. La extensión del uso del transistor en nuevos campos de aplicación plantea cada vez mayores exigencias a la modelación del dispositivo, destacando la importancia de aspectos que años atrás habían sido considerados secundarios en importancia. Entre ellos se encuentra el coeficiente de emisión del emisor n, que hasta el momento ha sido considerado como un parámetro de valor constante próximo a 1, por lo que generalmente su efecto es despreciado.

El coeficiente de emisión n es el inverso de la pendiente de Gummel-plot o sea del gráfico In lc vs. qV_BE/KT y se utiliza para explicar las no idealidades en el comportamiento de la corriente del colector con el potencial base-emisor del transistor bipolar.

Sin embargo, en estudios recientes, reportados en la literatura [2,3] se ha detectado un aumento no explicado del coeficiente de emisión para bajas temperaturas en los transistores bipolares caracterizados.

La situación descrita sugiere la búsqueda de la respuesta a dos inquietudes:

• Como incluir el efecto de la variación del coeficiente de emisión en el modelo del potencial base-emisor V_BE(T)

• Como explicar el comportamiento descrito del coeficiente de emisión y obtener una expresión analítica que pueda reflejar este comportamiento

En el trabajo presente se explica la causa física de este aumento inesperado de n con la disminución de la temperatura a través de la variación de la capacidad del emisor y se demuestra la importancia del coeficiente de emisión del emisor en el diseño de sensores de temperatura y referencias de bandgap bipolares, mediante una nueva expresión del potencial base-emisor V_BE(T) que incluye sus efectos. La simulación del comportamiento del coeficiente de emisión n se basa en la expresión de Gummel-Poon [4], utilizando la expresión de C_e(T) del modelo compacto HICUM [5].

II DESARROLLO

1. Expresión de V_BE(T) incluyendo los efectos de n(T)

A partir de los años 80 la tecnología CMOS ha ido desplazando la tecnología bipolar.

Sin embargo los elementos sensores siguen siendo los transistores bipolares aun en los sensores de temperatura CMOS, que en este caso son los transistores parásitos PNP de substrato del proceso CMOS [6].

Los sensores de temperatura se basan en la altamente repetible y exacta dependencia del potencial base-emisor V_BE del transistor bipolar con la temperatura.

La modelación del potencial base-emisor del transistor bipolar es utilizada desde hace varias décadas en el análisis y diseño de sensores de temperatura y en la obtención de referencias de potencial compensadas en temperatura. Para lograr buena exactitud y estabilidad térmica en estos circuitos se requiere mejorar la modelación del potencial base-emisor en función de la temperatura, V_BE(T).

Teniendo en cuenta la variación del coeficiente de emisión del emisor n(T) en la dependencia de I_C(V_BE,T) [7],

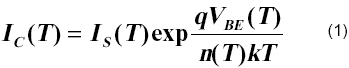
donde T es la temperatura absoluta, V_BE el potencial base-emisor, q la carga del electrón, k la constante de Boltzmann (8.617x10-5 eV/K) y n(T) el coeficiente de emisión.

La expresión de la corriente de saturación I_S viene dada por [8]

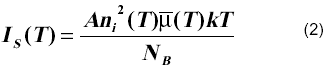
siendo A el área de la unión base-emisor, n_i(T) la concentración intrínseca, la movilidad efectiva de los portadores minoritarios en la base y N_B el número de Gummel en la base.

Considerando la dependencia de la concentración intrínseca n_i y de la movilidad de los portadores con la temperatura [8],

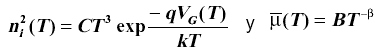
donde C, B y b son constantes y V_G(T) es el potencial de la banda prohibida en función de la temperatura absoluta, resulta

h - parámetro relacionado con la movilidad de los portadores minoritarios en la base del transistor - definido [8,9] como, h º 4 - b.

De la ecuación (3) se obtiene la expresión de V_BE(T) como,

En los sensores de temperatura, por razones prácticas, se utilizan corrientes de colector proporcionales a una potencia m de la temperatura,

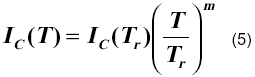
donde m = 0 para corriente constante y m = 1 para corriente PTA (proporcional a la temperatura absoluta).

Combinando las ecuaciones (5) y (4) se obtiene la siguiente expresión del potencial base-emisor en función de la temperatura,

La ecuación (6) refleja la influencia no sólo del valor del coeficiente de emisión del emisor sino de su variación con la temperatura.

Para el análisis del efecto del coeficiente de emisión n se distinguen tres casos:

a.) n = 1 para todas las temperaturas: Este es el caso típicamente reportado y empleado en la literatura [9,10]. Si se considera además que la corriente de colector utilizada es constante (m=0), la ecuación (6) se reduce a la ecuación siguiente,

b.) n >1 y constante para todas las temperaturas: En este caso, como n(T)=n(Tr), el único termino no afectado sería el término lineal.

c.) n >1 y dependiente de la temperatura: En este caso todos los términos se verían afectados.

Tanto los resultados experimentales reportados [2,3] como los resultados de la simulación del coeficiente de emisión (epígrafe 3.2 de este artículo) muestran que n puede ser diferente de 1 y su valor dependiente de la temperatura. Por esta razón su efecto, reflejado en la nueva expresión de V_BE(T) (ecuación (6)), se debe tener en cuenta en el diseño de sensores de temperatura exactos, ya que el error que se comete en el diseño al utilizar la ecuación de V_BE(T) reportada en la literatura hasta el momento (ecuación (7)), aumenta a medida que disminuye la temperatura.

2. Enfoque físico de la variación de n con la temperatura

Según la definición del coeficiente de emisión n es el inverso de la pendiente del Gummel-plot o sea del gráfico I_C vs qV_BE/kT, dada por la siguiente expresión analítica [4]:

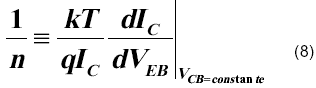
Para una temperatura dada, a cierto nivel de I_C su valor es constante para el dispositivo en cuestión. Sin embargo varía de dispositivo a dispositivo, así como también al variar el nivel de corriente del colector. Por esta razón en el modelo original de Gummel-Poon [4] n no es considerada como un parámetro de valor constante. (En oposición a modelos simplificados, como aquel que se utiliza en el simulador PSPICE [7] y se conoce como modelo de SPICE Gummel-Poon.)

Del modelo original de Gummel-Poon [4] para bajo nivel de inyección y V_CB=0 se puede demostrar que

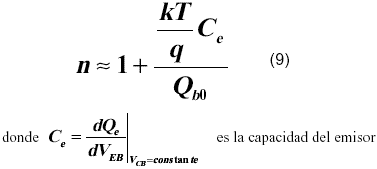
Esta expresión del coeficiente de emisión permite enfocar y simular el comportamiento del coeficiente de emisión n desde un punto de vista físico a través de la capacidad del emisor Ce. Existen diferentes modelos reportados en la literatura para el cálculo de Ce y para describir su comportamiento con la temperatura [4,5,7,11,12].

Uno de los modelos compactos mas recomendados a utilizar por el CCM [13] (Concilium of Compact Models) es el modelo compacto HICUM [5] y será precisamente éste, cuyo modelo de capacidad de emisor Ce se utilizara aquí en la simulación del coeficiente de emisión n(T).

2.1. Descripción del modelo Ce de HICUM

En el modelo compacto HICUM [5] la capacidad de emisor en polarización directa está dada por,

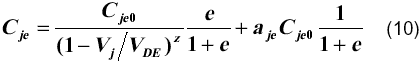
donde e, V_j, V_f y a_je están dadas por las expresiones,

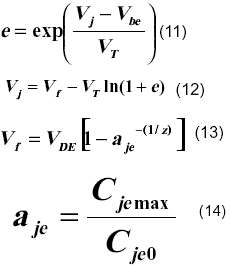
C_je0 es la capacidad de emisor sin polarización. La dependencia de este modelo con la temperatura se representa a través de las expresiones,

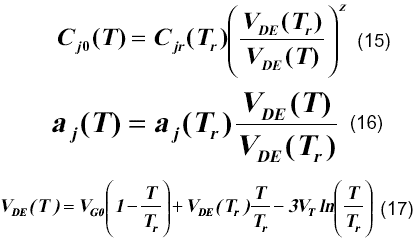
En este trabajo se utilizó la aproximación lineal del voltaje de banda prohibida para modelar la dependencia de la potencial base-emisor con la temperatura (ecuación (18)), debido a la exactitud que se obtiene cuando se utilizan los parámetros h y V_G0 medidos experimentalmente [3,9],

No se utiliza el modelo Gummel-Poon [4], por no ser adecuado para T≠Tr, mientras el modelo de V_BE que utiliza HICUM [5] no considera los parámetros h y V_G0 que dependen de la concentración de impurezas en la base [8, 14].

3. Simulación de n(T)

La simulación de n(T) se realizó en el intervalo de 240 K a 300 K utilizando las expresiones desde (10) hasta (18). Los valores de los parámetros del modelo Ce de HICUM fueron C_jeo(Tr) = 1.51 pF, a_je(Tr)= 5.735, z = 0.48, V_DE(Tr)= 0.700535 V. El valor de Q_b0 calculado es 6.0 pC y su dependencia con la temperatura se considera despreciable [5]. Los valores de h y V_G0 fueron tomadas de las mediciones experimentales de transistores bipolares verticales de substrato en tecnología CMOS [2,3]. Se consideraron dos niveles de corriente de polarización: 100 mA y 200mA.

4. Resultados de la simulación

Para el cálculo del coeficiente de emisión en el intervalo de 240 a 300 K se utilizaron los parámetros h= 5.1 y V_G0= 1.12046 V de los transistores bipolares verticales pnp en un proceso CMOS [2,3].

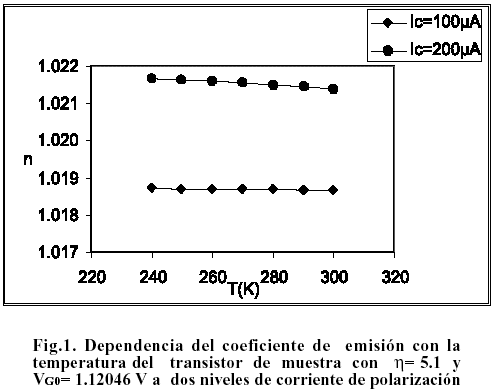
La simulación se realizó a I_C= 100 mA e I_C= 200 mA con los valores de V_BE(Tr)=0.612265 V y V_BE(Tr)=0.630702 V correspondientes al transistor de muestra a la temperatura Tr . Los resultados de simulación se muestran en la Figura 1.

En la Figura 1 se observa un aumento ligero del coeficiente de emisión n(T) con la disminución de la temperatura que se hace mas pronunciado a mayores corrientes de polarización.

5. Discusión de los resultados

El aumento ligero del coeficiente de emisión con la temperatura sugiere la idea que sus efectos pueden ser despreciados. Para valorar estos efectos se realizó el cálculo del error DV_BE(T) que se introduce al no tener en cuenta el coeficiente de emisión en el modelo del potencial base-emisor, restando las ecuaciones (6) y (7) para corrientes constantes (m=0),

Utilizando la aproximación lineal del potencial de la banda prohibida V_G(T)=V_G0-aT, de la ecuación (19) resulta,

Utilizando la ecuación (20) se realizó el calculo de DV_BE(T) para la temperatura T=240 K, siendo la temperatura de referencia Tr=300 K. La Tabla I. muestra los datos utilizados, así como los valores de DV_BE(T) y la temperatura equivalente calculados.

En el cálculo de la temperatura equivalente se tuvo en cuenta que la variación típica del potencial base-emisor a corriente constante es 2 mV para una disminución de 1ºC de la temperatura. Los resultados obtenidos indican que considerar el valor del coeficiente de emisión y su dependencia con la temperatura puede ser importante, sobre todo si se trata del diseño de sensores de temperatura muy exactos.

III CONCLUSIONES

1. Se obtuvo una expresión de V_BE(T) que incluye el coeficiente de emisión del emisor y su variación con la temperatura.

2. Se explica la causa de la variación del coeficiente de emisión n(T) desde un punto de vista físico, a través de la capacidad del emisor Ce.

3. Se observa un ligero aumento del coeficiente de emisión con la disminución de la temperatura, dependiente del nivel de polarización.

4. Se calcula el error que se comete en el calculo de V_BE(T) al despreciar el efecto del coeficiente de emisión que corresponde, en el intervalo entre 300 K y 240 K, a un error mayor de 2ºC en temperatura

5. El coeficiente de emisión y su variación con la temperatura se tienen en cuenta en el diseño de los sensores de temperatura exactos.

IV. REFERENCIAS

1. Mijalkovic, S., de Graaff, H. C., “Mextram 504 for SiGe HBT Applications”, in Proc. 4th Workshop on Semiconductor Advances for Future Electronics, Veldhoven, Netherlands, November 2001 pp. 115-122 Ian E.        [ Links ]

2. Wang, G.,. Meijer, G. C. M., “The Temperature Characteristics of Bipolar Transistors Fabricated in CMOS Temperature Sensors”, 13 th European Conference on Solid-State Transducers, The Hague, Netherlands, September 1999, pp. 553-556.        [ Links ]

3. Wang, G., Meijer, G. C. M., “The Temperature Characteristics of Bipolar Transistors Fabricated in CMOS Technology”, Sensors and Actuators, 87, 2000, pp. 81-89.        [ Links ]

4. Gummel, H. K., Poon, H. C., “An Integral Charge Control Model of Bipolar Transistors”, BSTJ, May-June. 1970, pp. 827-852.        [ Links ]

5. Schroter, M., HICUM, “A Scalable Physics-Based Compact Bipolar Transistor Model”, Available on the web: http://www.iee.et.tu-dresden.de/iee/eb/comp_mod.html, consulta 25/10/2004.        [ Links ]

6. Bakker, A., “High-Accuracy CMOS Smart Temperature Sensor” Ph.D Thesis, Delft University of Technology, The Netherlands, 2000, pp 37-45.        [ Links ]

7. Getreu, Modeling the Bipolar Transistor, New York, Elsevier, 1978, pp 92-95.        [ Links ]

8. Slotboom, J.W., de Graaff, H.C., Measurements of Bandgap Narrowing in Si Bipolar Transistors, Solid-State Electronics, Vol.19, 1976, pp. 857-862,.        [ Links ]

9. Meijer,G.C.M., Integrated Circuits and Components for Bandgap References and Temperature Transducers, Ph.D. Thesis, Delft University of Technology, The Netherlands, 1982, pp. 61-62.        [ Links ]

10. Tsividis, Y. P., IEEE J. Solid-State Circuits, Vol. Sc 5, No.6, 1980, 1076.        [ Links ]

11. Paasschens, J. C. J., Kloosterman, W. J., "The Mextram Bipolar Transistor Model – Level 504," Nat. Lab. Unclassified Report, NL –UR 2000/811, Koninklijke Philips Electronics N.V. 2000/2001, pp 7-10.        [ Links ]

12. McAndrew, C.C. et al, VBIC95, The Vertical Bipolar Inter-Company Model, IEEE Journal of Solid-State Circuits, Vol. 31, No. 10, October 1996, pp 1476-1483.        [ Links ]

13. CMC meeting June 5, 2000, Los Angeles, http://www.eigroup.org/cmc/minutes/m060500.htm, consulta 05/06/2000.        [ Links ]

14. Amador, R., Polanco, A., Nagy, A., “The Spread of h and VG0 and its Influence on the Sensitivity of a Bipolar IC Celsius Sensor” , Sensors and Actuators, Vol. 77, 1999, pp. 9-13.        [ Links ]