PROPUESTA DE RESOLUCIÓN DEL SISTEMA MATRICIAL EN EL SEGUNDO MÉTODO DE ESTABILIDAD DE LYAPUNOV

Marcano, Cosme

MSc. Cosme Rafael Marcano Gamero: Profesor Agregado en el Dpto. de Ingeniería Electrónica, Universidad Nacional Experimental Politécnica “Antonio José de Sucre” UNEXPO, Vicerrectorado Puerto Ordaz, Final Calle China, Villa Asia, Puerto Ordaz, Edo. Bolívar, Venezuela, Telf. 58-286-9619965, correo electrónico cmarcano@poz.unexpo.edu.ve..

Resumen: El Segundo Método de Estabilidad de Lyapunov consiste en la selección de una, así llamada, Función Candidata de Lyapunov, que satisfaga ciertas condiciones que permitan su utilización en el análisis de la estabilidad de un modelo matemático sintetizado a partir de un proceso que se desee someter a la acción de una Ley de Control determinada. En el caso de los sistemas lineales es siempre posible encontrar una función cuadrática, x^T Ax, que satisfaga las condiciones requeridas. Al aplicar el Segundo Método de Lyapunov a esta función candidata, aparece un sistema matricial de ecuaciones lineales ordinarias del tipo A^T P + PA = -Q, en donde P y Q son matrices nxn, definidas positivas. En este trabajo se propone la solución numérica de este sistema algebraico mediante la resolución de un sistema lineal de n² incógnitas e igual número de ecuaciones, lo cual puede ser realizado, después de algunas manipulaciones de las ecuaciones, con algún método tradicional como la Eliminación Inversa de Gauss o cualquiera de sus variantes. Se presentan aquí dos sencillos algoritmos que permiten reacomodar la ecuación matricial original en la forma convencional de un sistema de ecuaciones algebraicas, lineales y ordinarias.

Palabras clave: Eliminación Gaussiana / Segundo Método de Estabilidad de Lyapunov / Sistema Matricial

PROPOSAL OF RESOLUTION OF THE MATRICIAL SYSTEM IN THE SECOND METHOD OF STABILITY OF LYAPUNOV

Summary. The Second Method of Stability of Lyapunov consists of selecting a so-called Lyapunov’s Candidate Function, which satisfies certain conditions that allows its use in the stability analysis of a mathematical model synthesized from a process which it want to put under the action of a given Control Law. In the case of linear systems, it is always possible to find a quadratic function, x^TAx, that satisfies the desired conditions. When applying the Second Stability Method of Lyapunov to this candidate function, it appears a matricial system of ordinary linear equations of the type A^TP + PA = —Q, where P and Q are nxn definite positive matrixes. In this work, the numeric solution of this algebraic system is proposed by solving a linear system of n2 unknown data and the same number of equations, which can be achieved, after some manipulation to the equations, with some traditional method, such as the Inverse Elimination of Gauss or any of its variants. This work shows two easy algorithms that allows re-accommodating the original matrix equation into the conventional form of a system of algebraic linear and ordinary equations.

Keywords: Gaussian Elimination / Matrix System / Second Stability Method of Lyapunov

Finalizado el 2004/05/18   Recibido el 2004/06/17   Aceptado el 2005/03/09.

I INTRODUCCIÓN.

En el análisis de los sistemas de control en el dominio del tiempo, se presentan dos opciones de particular relevancia para la determinación de su estabilidad. La primera consiste en la determinación de los polos de la ecuación característica de la matriz del sistema [1], descrito por:

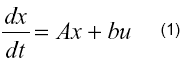
en donde A es una matriz nxn, denominada Matriz de Sistema, b es un vector fila de n elementos y x es un vector columna, denominado Vector de Estado; por su parte, u es una función escalar conocida como Función de Control, y que está determinada por las variables de estado, i.e., las componentes del Vector de Estado, x.

La ecuación característica del sistema (1) viene dada por  det(sI - A) , en donde s es la variable de Laplace. Los polos de la función de transferencia se obtienen calculando los ceros de la respectiva ecuación característica igualada a cero, i.e.,

det(sI - A) = 0             (2)

Según el Primer Método de Estabilidad de Lyapunov, también llamado Método Indirecto de Estabilidad de Lyapunov, los polos de esta ecuación deben estar en el semiplano negativo para poder garantizar la estabilidad del sistema dado por (1).

II DESARROLLO

1.- Fundamentación teórica del segundo método de lyapunov.

La segunda opción que se nos presenta es el Segundo Método de Estabilidad de Lyapunov, también conocido como Método Directo de Estabilidad de Lyapunov [1], el cual se fundamenta en la aplicación del siguiente Teorema.

Teorema

Sea x = 0 un punto de equilibrio de un sistema, en general, no lineal

Sea V : D ® R una función continuamente diferenciable en la vecindad D de x = 0, tal que V(0) = 0 y V(x) > 0 en D – {0}. Si V es siempre decreciente en D, i.e.,

entonces, se puede asegurar que el sistema es estable en x = 0.

Además, si en D – {0} entonces x = 0 es asintóticamente estable

La tarea es encontrar una V(x), llamada función candidata de Lyapunov, la cual debe satisfacer los siguientes requerimientos:

• V es continua

• V(x) tiene un único mínimo en xeq con respecto a todos los otros puntos en D

• A lo largo de cualquier trayectoria del sistema contenida en D el valor de V nunca se incrementa

El primer método de Lyapunov determina la estabilidad en la vecindad inmediata de un punto de equilibrio, mientras que el Segundo Método de Lyapunov permite determinar cuán lejos puede estar la trayectoria de un sistema de un punto de equilibrio y seguir acercándose a éste cuando t tiende a ¥

Región de Estabilidad asintótica (región de atracción)

Sea f(t;x) la solución del sistema de ecuaciones que parte del estado inicial x en el instante de tiempo t = 0. Entonces, la región de atracción está definida como el conjunto de todos los puntos x tales que limt®¥ f(t;x) = 0

Si Wc = { x Î Rⁿ | V(x) £ c } está limitado y contenido en D, entonces cada trayectoria que parte en Wc permanece en Wc y se aproxima al punto de equilibrio cuando t ® ¥. Así, Wc es un estimado de la región de atracción.

Tipos de estabilidad en relación a la región de atracción:

Lyapunov define tres tipos de estabilidad en relación a la Región de Atracción, a saber:

• Estabilidad local (estabilidad en la cercanía) – cuando un sistema permanece dentro de un región infinitesimal alrededor de un punto de equilibrio, cuando es sujeto a pequeñas perturbaciones

• Estabilidad Finita – cuando un sistema retorna al punto de equilibrio desde cualquier punto dentro de una región R de dimensiones finitas que lo rodean

• Estabilidad global (Estabilidad en la distancia) – si la región R incluye el espacio de estado entero

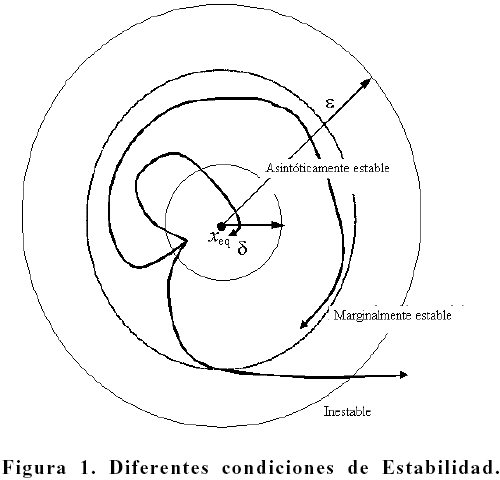
La Figura 1 describe gráficamente los distintos tipos de estabilidad que propone Lyapunov. Es oportuno destacar que siempre es posible encontrar una función de Lyapunov para un sistema lineal de la forma descrita por (1), sin perturbación externa, esto es, con u=0. En este caso, se puede escoger una función de Lyapunov de la forma cuadrática:

V = x^T Px         (3)

donde P es una matriz simétrica definida positiva. Entonces, se tiene

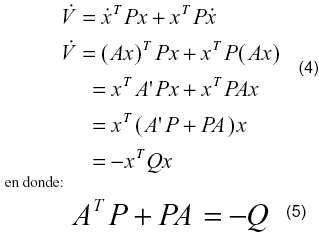
Nótese que el sistema matricial de ecuaciones (5), que se requiere resolver durante la aplicación del Segundo Método de Estabilidad de Lyapunov, tiene la forma general de un sistema del tipo AX + XB = C. Este sistema general debe ser adecuado para el sistema particular de Lyapunov, haciendo B = A^T y C = -Q. Chequeando la consistencia del sistema, comprobamos que todas las matrices deben ser cuadradas.

Si la matriz Q es definida positiva, entonces el sistema es asintóticamente estable. Por ejemplo, se puede escoger Q = I, la matriz identidad que es obviamente definida positiva, y resolver

A^T P + PA = -I

para P, y ver si ésta es también definida positiva (para lo cual se pueden examinar, por ejemplo, los n menores principales de P, según el criterio de Sylvester).

Aunque es cierto que podemos chequear la estabilidad de un sistema lineal, verificando las partes reales de los autovalores de A, la solución de la ecuación matricial de Lyapunov puede proveer un estimado para una función candidata de Lyapunov para sistemas no lineales en casos en que esto se realice computacionalmente.

Resolución del sistema de ecuaciones de lyapunov. A continuación, se abordará la solución del sistema matricial planteado por la aplicación del Segundo Método de Lyapunov, dado por

A^T P + PA = -Q

Para afrontar esta tarea, se resolverá primeramente un sistema genérico, de la forma

AX + XB = C

donde

B = A^T   

y

C = -Q    (6)

Expandiendo el sistema matricial de ecuaciones planteado en (6), se obtiene:

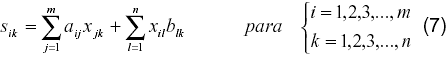
Nótese que, dada la naturaleza matricial de X, la solución de este sistema implica la resolución de un sistema de ecuaciones algebraicas lineales de mxn ecuaciones e igual número de incógnitas.

Una técnica para abordar la solución de este problema algebraico es reacomodar el sistema dado por (6) en la forma tradicional de un sistema de ecuaciones del tipo Sz=t, donde z es un vector de mxn componentes, cuya apariencia se muestra a continuación:

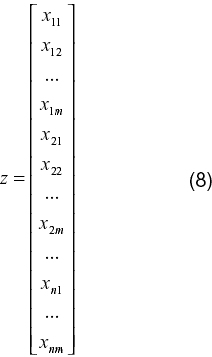
Como se puede observar en (8), las componentes del vector z son las mismas de la matriz X, del sistema (6), dispuestas en forma de una única columna, conformada por las componentes de cada una de las columnas de la matriz X colocadas en forma vertical. De igual manera, el vector t del sistema modificado se obtiene colocando en forma vertical, seguidas una tras otra, las columnas de la matriz C del sistema original. Más adelante, se explicará cómo preparar la matriz S.

El sistema matricial de ecuaciones que resulta de la aplicación del Segundo Método de Estabilidad de Lyapunov, tiene la característica particular de que todas las matrices son cuadradas, por lo que m = n, aparte de lo ya establecido en (6), relativo a que la matriz B es la transpuesta de la matriz A.

La matriz A es definida positiva y, naturalmente, no singular. La matriz C puede ser escogida arbitraria y convenientemente. Esta suele ser la matriz identidad, nxn, que es definida positiva.

La expansión de la expresión (7) para el caso particular de n=3, resulta en la formación de dos matrices auxiliares, U y V, las cuales se muestran a continuación

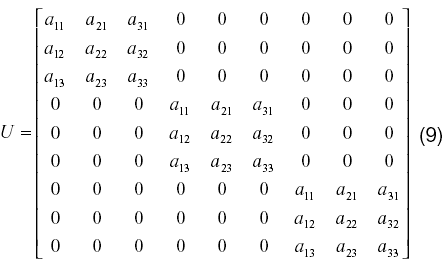
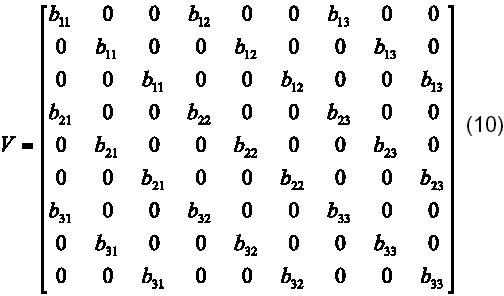
Obsérvese que los n bloques que aparecen sobre la diagonal principal de la matriz U son iguales entre sí y que, además, están conformados por la transpuesta de la matriz A del sistema matricial original, dado en (6). Por otra parte, la matriz V está conformada por los elementos de la matriz B, dispuestos en bandas diagonales. Nótese igualmente, que las matrices así obtenidas presentan un gran número de ceros. De la suma de U y V se obtiene la matriz S:

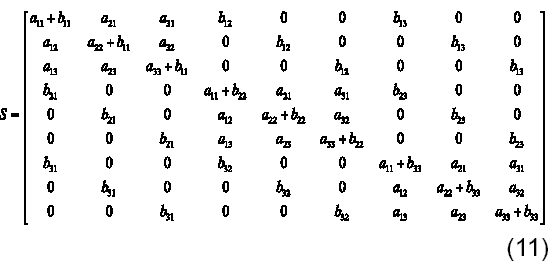
Seguidamente, se procede a sintetizar los algoritmos de preparación de las matrices U, V y S. Los algoritmos para la obtención de U y V se muestran a continuación:

Finalmente, la suma de U y V da por resultado la matriz S, como se muestra a continuación.

Una vez preparadas las matrices U, V y S, y el vector t, el sistema matricial original

AX + XB = -C

donde                       (12)

B = A^T

queda expresado en forma de un sistema algebraico, lineal, de primer orden, de nxn ecuaciones e igual número de incógnitas, dado por

Sz = t                 (13)

cuya solución consistirá de nxn valores para los elementos el vector z, los cuales, de acuerdo a (8), corresponden con las componentes de la matriz X, y constituyen la solución del sistema matricial dado por (6). Es por ello que, después de resolver el sistema modificado dado por (13), utilizando algún método de resolución de sistemas de ecuaciones algebraicas lineales, como Eliminación Inversa de Gauss [2], o cualquiera de sus variantes (Gauss-Jordan o Gauss-Seidel) sólo restaría reacomodar los elementos del vector z, en la forma matricial de X, como se muestra a continuación.

La matriz dada por (14) constituye la solución del sistema matricial dado por (6) y que representa la matriz requerida por el Segundo Método de Estabilidad de Lyapunov, también llamado Método Directo, debido a que puede ser aplicado en el estudio de la estabilidad de sistemas de control no lineales, sin necesidad de linealizar su comportamiento alrededor de algún punto de equilibrio, como es requerido por el Primer Método de Estabilidad de Lyapunov o Método Indirecto.

Sin la intención de extenderse en un estudio más exhaustivo de los sistemas de control, lo cual va más allá del tratamiento meramente computacional del presente trabajo, es importante hacer notar la posibilidad de aplicar el Segundo Método de Estabilidad de Lyapunov a los sistemas no lineales en donde radica la gran utilidad del mismo, ya que en los sistemas lineales resulta mucho más sencillo y expedito comprobar la estabilidad de tales sistemas verificando simplemente que las partes reales de las raíces de sus respectivas ecuaciones características estén en el semiplano negativo. Esa sencilla comprobación, no aplicable a los sistemas de control no lineales, evita la necesidad de obtener una función candidata adecuada y el planteamiento y resolución de un sistema matricial de ecuaciones, como plantea el Segundo Método de Estabilidad de Lyapunov.

La importancia del Segundo Método de Estabilidad de Lyapunov, se hace más evidente en los recientes enfoques para la síntesis y diseño de controladores para procesos industriales, particularmente los llamados Sistemas de Estructura Variable [1] y [3], en los cuales se utiliza la teoría subyacente al Segundo Método para sintetizar sistemas de control muy robustos, que confieren a las plantas controladas una estabilidad asintótica, atenuación de sobredisparos y disminución ostensible de los tiempos de respuesta y de establecimiento.

III. CONCLUSIONES.

1. A través de simples manipulaciones de filas y columnas, se puede reacomodar un sistema matricial de ecuaciones algebraicas para obtener un sistema convencional de ecuaciones lineales, ordinarias, que puede ser resuelto fácilmente mediante la utilización de algún método convencional de resolución de sistemas de ecuaciones ordinarias, lineal algebraicas, como Eliminación Gaussiana, o cualquiera de sus variantes, i.e., Gauss-Jordan o Gauss-Seidel..

2. Aprovechando la característica dispersa de los elementos de las matrices obtenidas después de la manipulación, pudiera utilizarse algún método que resulte más eficiente en cuanto al número de operaciones a realizar para alcanzar la solución definitiva.

3. Los algoritmos están presentados de manera que puedan ser fácilmente traducidos a algún lenguaje de programación comercial como Visual Basic o Visual C, ambos productos de Microsoft Corporation, o en cualquier otro lenguaje disponible.

IV REFERENCIAS

1) Marcano G., Cosme R. Síntesis y Diseño de Controladotes de Estructura Variable, Trabajo de Maestría, Universidad Nacional Experimental Politécnica “Antonio José de Sucre”, Mayo 2.004.        [ Links ]

2) Fadeeva, V.N., Métodos de Cálculo del Álgebra Lineal, Madrid, Editorial Paraninfo, 1973.        [ Links ]

3) Marcano G., Cosme R. Sistemas de Estructura Variable, Trabajo de Grado, Universidad de los Andes, Mérida – Venezuela, Mayo 1986.        [ Links ]

4) Kailath, Thomas. Linear Systems, Prentice Hall, Englewood Cliffs, New Jersey, 1980.        [ Links ]