ESTRUCTURAS DE MONTE CARLO PARA EL ANÁLISIS DEL DESEMPEÑO DE OOK Y L-PPM EN CANALES ÓPTICOS INALÁMBRICOS INFRARROJOS EN INTERIORES.

Biosca Rojas, Dioén; López Presmanes, Jorge Luis

Dres Dioén Biosca Rojas y Jorge Luis López Presmanes: Profesor Auxiliar y Profesor Titular respectivamente del Dpto. De Telecomunicaciones de la Facultad de Ingeniería Eléctrica del Instituto Superior Politécnico “José Antonio Echeverría” (ISPJAE), Calle 114 Nº 11901 e/119 y 127, Marianao, CP19390, Ciudad Habana, Cuba, Teléfono (537) 8303674, correos electrónicos dioen_biosca@yahoo.com y pres@reduniv.edu.cu.

Resumen: En el presente trabajo se propone un nuevo entorno de simulación, basado en las técnicas de análisis de Monte Carlo, para la evaluación del desempeño de OOK (On Off Reying) y L-PPM (Level –Pulse Position Modulation) en el canal infrarrojo en interiores. Se parte del conocimiento previo de la función respuesta al impulso del canal, obtenida mediante simulación. En el caso de OOK, junto con la estructura de modelación de Monte Carlo se desarrolla además una expresión teórica que permite la evaluación directa de la probabilidad de error, teniendo en cuenta los efectos del ruido y la interferencia entre símbolos inducida por la propagación multitrayecto propia de estos canales de comunicación. Los resultados de simulación obtenidos con las estructuras propuestas para OOK y L-PPM son validados en ambos casos por comparación contra los resultados teóricos arrojados por las expresiones para la probabilidad de error en el canal AWGN ideal, libre de interferencia entre símbolos.

Palabras clave: Análisis de desempeño/ Canal Infrarrojo Inalámbrico/ L-PPM/ Monte Carlo/ OOK.

MONTE CARLO STRUCTURES FOR PERFORMANCE ANALYSIS OF OOK AND L-PPM IN OPTICAL WIRELESS INDOOR INFRARED CHANNELS

Abstract: In this paper a new simulation framework, based on Monte Carlo analysis, is proposed to allow performance studies of OOK and L-PPM in the wireless indoor infrared channel. It is assumed that the impulse response of the channel is known and that it is obtained previously by simulation using a ray-tracing algorithm. In the case of OOK, along with the Monte Carlo simulation structure, an analytic expression is developed additionally to provide direct performance evaluation of OOK in the wireless channel, which takes into account the effects of noise and inter symbol interference induced by multipath propagation, proper phenomena of this kind of communication channels. The simulation results obtained with the proposed simulation structures for OOK and LPPM are validated in both cases by comparison against theoretical results given by the evaluation of the expressions for probability of error in the AWGN ideal channel, free of inter symbol interference.

Keywords: L-PPM/ Monte Carlo/ OOK/ Performance Analysis/ Wireless Infrared Channel

Finalizado el 2004/10/14   Recibido el 2004/11/15   Aceptado el 2005/07/06.

I. INTRODUCCIÓN.

Los enlaces ópticos inalámbricos infrarrojos (IR), tanto para accesos locales en interiores como para la interconexión de segmentos de redes a altas velocidades, proporcionan cada día con más fuerza, una alternativa viable a los sistemas de radiofrecuencia. El espectro de las señales ópticas comúnmente empleadas en estos sistemas se caracteriza por la abundancia de ancho de banda no regulado y por la posibilidad de reutilización que brinda en sistemas de acceso inalámbrico multicelulares. El desarrollo de modelos de propagación para la estimación de parámetros de los enlaces como la respuesta al impulso, la dispersión de retardo, las pérdidas de propagación, entre otros, ha sido objeto de intensas investigaciones en los últimos tiempos [1-3].

A partir de estos modelos puede estimarse también el desempeño de diferentes esquemas de transmisión, ya sean banda base o de subportadora. La utilización de esquemas de simulación de Monte Carlo en estos casos posibilita la incorporación de elementos para el análisis de los efectos que producen el ruido y la interferencia entre símbolos (IIS) para distintas configuraciones de canal preestablecidas.

La propuesta de estructuras de modelación novedosas, empleando técnicas de Monte Carlo, para el análisis del desempeño de los métodos de transmisión más comúnmente empleados en los sistemas ópticos inalámbricos: OOK y L-PPM, es el elemento fundamental tratado en el presente trabajo.

II. DESARROLLO

1. Entorno de Evaluación General.

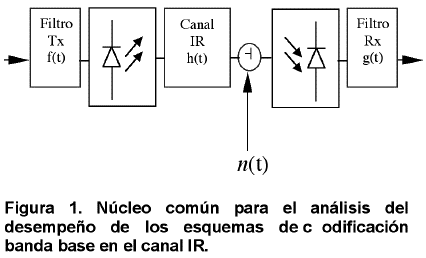
Como núcleo común para el análisis del desempeño de cualquier esquema de codificación banda base en el canal IR, puede emplearse el esquema mostrado en la Figura 1.

En cada caso particular se le puede añadir a este diagrama los bloques transmisores y receptores correspondientes a las técnicas de transmisión y detección empleadas, según sea el caso. Dada la naturaleza discreta de la mayoría de los algoritmos de los modelos de cálculo de la respuesta al impulso del canal IR, usualmente esta función se expresa en forma equivalente como [4]:

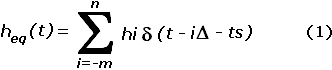
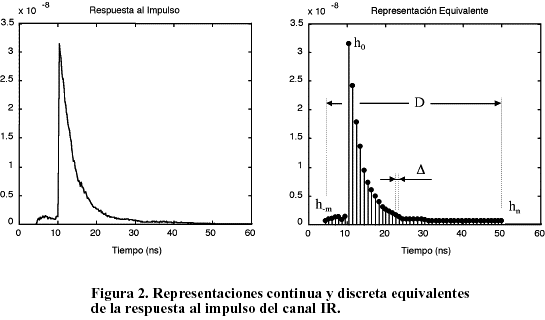
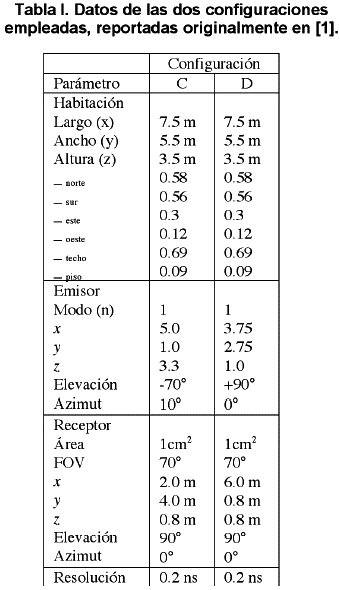
En esta expresión se presenta heq(t) como la suma de m+n+1 impulsos de amplitud igual al valor de la respuesta al impulso calculada para el intervalo de tiempo D correspondiente. El valor de D equivale a la resolución temporal escogida para la estimación, D=D/(m+n) donde D es la dispersión de retardo del canal. En la Figura 2 se aprecian las representaciones continua y discreta equivalentes para la respuesta al impulso de la configuración D reportada en [1] utilizada como ejemplo. Los datos correspondientes a esta configuración pueden encontrarse en la Tabla I.

Se considerará, como en [4], que la sincronización en el receptor es perfecta, o sea, que el origen de tiempo es desplazado de manera que h0 corresponda con el valor máximo de h_eq(t). De esta forma habrá m componentes que preceden a h₀ y n que la suceden, causantes de la IIS sobre el símbolo o bit detectado, que dependerá de la velocidad de transmisión.

La convolución de h_eq(t) con los equivalentes discretos de las respuestas al impulso de los filtros transmisor y receptor, (Figura 1), dan lugar a una respuesta al impulso extremo a extremo del canal, útil para la obtención del desempeño de los diferentes esquemas de transmisión mediante simulación de Monte Carlo.

2. Esquema de Transmisión OOK en el Canal Óptico Inalámbrico.

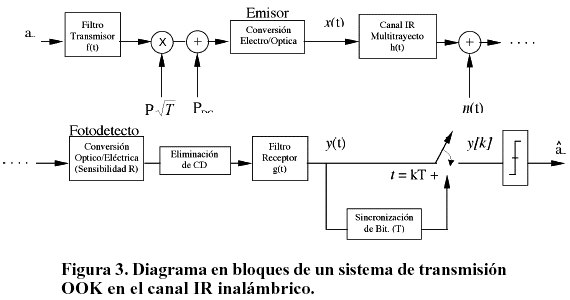
El diagrama en bloques de un sistema de comunicación utilizando OOK en el canal IR inalámbrico puede apreciarse en la Figura 3.

El canal se asume con respuesta al impulso h_eq(t) según (1), y ruido aditivo blanco gaussiano n(t). Los filtros transmisor y receptor son idénticos de tipo raíz de coseno alzado, cada uno llevando a cabo la mitad de la conformación de los pulsos. Como la densidad espectral de ruido es plana y el canal de transmisión es real, los filtros transmisor y receptor que eliminan la IIS y maximizan la relación señal a ruido (SNR) en el instante de muestreo son, siguiendo [5]:

F(f)G(f) = X_RC(f)               (2)

donde X_RC(f) es una respuesta de frecuencia de tipo coseno alzado. F(f) y G(f) son los filtros transmisor y receptor respectivamente. Las respuestas de amplitud de los filtros vienen dadas por:

por lo tanto, las respuestas al impulso de los filtros f(t) y g(t), se representan según:

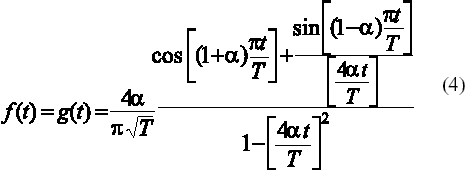
donde a es el factor de caída del filtro y T es el tiempo de bit.

La secuencia de datos de entrada puede considerarse como un tren de impulsos a la velocidad de bit ponderados por los coeficientes a_n Î{0, 1} que constituyen los bits de datos a transmitir:

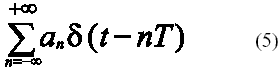
Después de pasar por el filtro conformador f(t) la señal se multiplica por un factor P que determina el nivel de potencia óptica de los pulsos transmitidos y se le añade un nivel de polarización PCD para cumplir con las dos condiciones impuestas para x(t) en el canal óptico por difusión: la de ser no negativa, x(t) ³ 0, y la de tener potencia promedio restringida <x(t)> £ Pm, por razones de seguridad para la visión humana. La forma de onda de la señal modulada x(t) será entonces [5]:

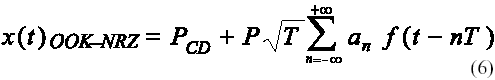
En [5] se obtiene la relación que deben mantener P y PCD para cumplir con las dos condiciones anteriormente comentadas. Por ejemplo, para el caso en que se fije una potencia promedio no superior a los Pm=20mW y utilizando filtros de factor de caída a=0.45, se obtienen valores de P=25.65mW, PCD=5.77mW. En la Figura 4. puede apreciarse la x(t) obtenida y como ésta, se mantiene siempre positiva y su potencia promedio <x(t)>=18.6mW por debajo del valor Pm prefijado. Estos resultados fueron obtenidos mediante simulación en MATLAB del esquema de la Figura 3 con los datos suministrados.

3. Esquema de Transmisión L-PPM.

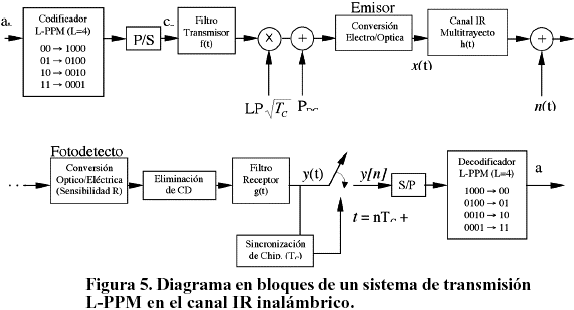
El diagrama en bloques de un sistema de comunicación utilizando L-PPM en el canal IR inalámbrico puede apreciarse en la Figura 5.

Como se sabe en L-PPM los bits, de duración T, son agrupados en bloques de longitud k=log₂L que se hacen corresponder con una de las L posibles formas de onda s_i(t) o símbolos del esquema, que formando un conjunto de señales ortogonales entre sí. El intervalo de duración de un símbolo es T_S = kT. Normalmente se divide el tiempo de símbolo en L intervalos llamados chips de duración T_C=T_S/L y se asigna una forma de onda a cada chip para conformar el conjunto. Los filtros en la Figura 1 deben ser diseñados para el tiempo de chip siguiendo (4) para T=T_C. La señal L-PPM que cumple con las dos condiciones impuestas para x(t) en el canal óptico por difusión es [5]:

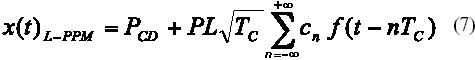
donde c_n Î [0, 1] representa la secuencia de chips a la entrada del filtro conformador f(t), cada secuencia de L chips conforman una palabra de código L-PPM. El factor P y P_CD=lP para x(t) limitada en potencia a Pm deben cumplir [5]:

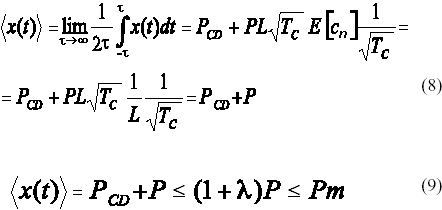
El coeficiente l es función del factor de caída del filtro, a, y de L. Por ejemplo para a=0.45 con L=4 se obtiene l=0.86.

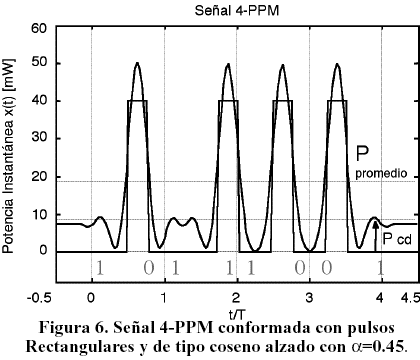
Fijando para x(t) un valor de potencia promedio máxima de Pm=20mW, se obtiene <x(t)>=18.6mW, P=10mW y P_CD=8.6mW. La potencia óptica instantánea x(t) simulada en MATLAB para una señal 4-PPM, conformada con pulsos rectangulares y de tipo coseno alzado con a=0.45, se puede apreciar en la Figura 6.

Obsérvese como x(t) se mantiene siempre positiva y su potencia promedio permanece por debajo de los 20mW prefijados. La señal recibida L-PPM puede escribirse como:

y(t) = RPLc_n x_ca(t) Ä h_eq(t)         (10)

Los c_n representan los valores de los chips de la secuencia L-PPM transmitida, h_eq(t) es igualmente (1) y se define la respuesta al impulso extremo a extremo del canal en este caso como:

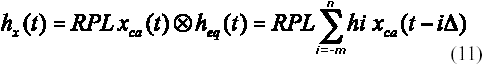
con la cual, utilizando (10), la secuencia de salida del comparador y[n], (Figura 5), se puede expresar como:

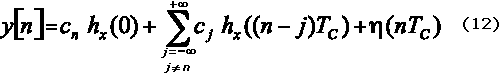
La secuencia y[n] se obtiene muestreando y(t) a la razón de chip t=nT_C, no a la de bit. Es tarea del receptor esperar la llegada de L chips que puedan ser considerados como un vector recibido para ser procesado. La sumatoria en (12) puede restringirse, teniendo en cuenta la naturaleza decreciente de h_x(t), a ± N_IIS términos adyacentes a h_x(0) para el calculo de la IIS sobre el chip c_n que esta siendo detectado.

4. Entorno Teórico de Evaluación de la Probabilidad de Error para OOK.

Para el desarrollo de una expresión teórica del desempeño de los sistemas OOK, considerando canales dispersivos caracterizados por su respuesta al impulso, se parte inicialmente de las ideas planteadas en [4], que se generalizan posteriormente. A partir de la Figura 3, la señal a la salida del receptor para un solo símbolo a_k transmitido es, siguiendo [4]:

y(t) = RPa_k f(t) Ä h_eq(t) Ä g(t)     (13)

donde R es la sensibilidad del fotodetector.

Como f(t) y g(t) obedecen las relaciones (4) y (3) respectivamente, la expresión anterior puede escribirse como:

y(t) = RPa_k x_ca(t) Ä h_eq(t)          (14)

donde x_ca(t) = f(t)Äg(t) es la respuesta al impulso correspondiente al filtro coseno alzado formado por la combinación de los filtros transmisor y receptor.

La combinación de x_ca(t) y h_eq(t) da lugar a la respuesta al impulso extremo a extremo a la que se hizo referencia en el apartado II, en este caso se define como:

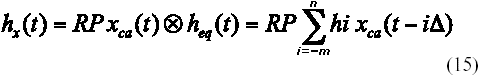
Expresando y(t) como la convolución de a_k con h_x(t) y muestreando el resultado en t = kT, se obtiene la secuencia y[k] a la entrada del dispositivo de decisión, (Figura 3), para infinitos símbolos transmitidos. Su expresión es [4]:

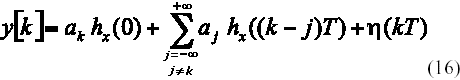
En (16) pueden apreciarse el término asociado a la detección del símbolo a_k , así como los relacionados con la IIS aportada por los símbolos vecinos a_j (segundo término) y el ruido. En [4] se demuestra que, al ser h_x(t) una función decreciente, la IIS aportada por los símbolos vecinos es despreciable más allá de seis intervalos de bit a ambos lados del bit a_k que esta siendo detectado. Obviando el término de ruido, (16) se reduce a:

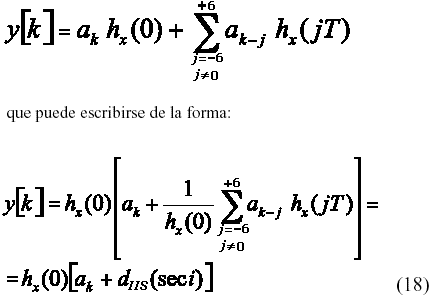
El término d_IIS(sec i) en (18) es la contribución a la IIS de la i-ésima secuencia de 2x6 bits que se forma con los 12 bits vecinos a ambos lados de a_k. Se tienen entonces 4096 posibles secuencias a del tipo sec i = [a-₆, a-₅, a-₄, ..., a-₁, a+₁, a+₂, ..., a+₅, a+₆].

A partir de las expresiones anteriores se desarrolla el entorno teórico de evaluación de la probabilidad de error para OOK. En este caso, con a_kÎ[0, 1], se establece el umbral de decisión óptimo en V_T = h_x(0)/2.

Cuando se transmite a_k=0, la probabilidad de que ocurra un error es, ver (18):

P(error a_k = 0) = P(h_x(0)d_IIS + n(kT) > V_T)   (19)

de manera equivalente para la transmisión de a_k=1 este valor es:

P(error a_k = 1) = P(h_x(0)d_IIS + n(kT) < -V_T)   (20)

El ruido n(t) corresponde a un proceso gaussiano muestreado de media cero y varianza s². Las expresiones anteriores pueden acomodarse y utilizando las propiedades de simetría de la función densidad de probabilidad gaussiana, escribirse de la forma:

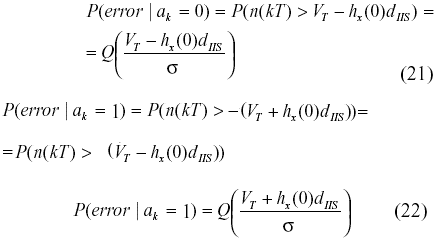
La probabilidad de error, suponiendo símbolos equiprobables, se obtiene según:

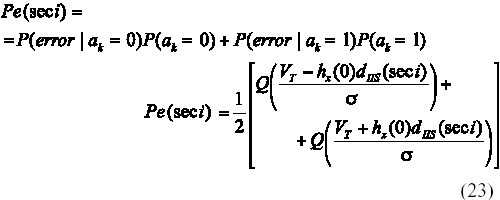
Promediando (23) para todas las secuencias interferentes posibles, que son también equiprobables, se tiene:

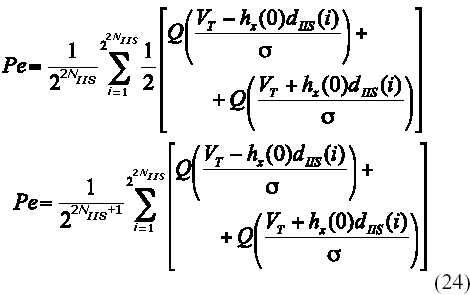
donde se ha incorporado N_IIS para generalizar la expresión para cualquier cantidad de símbolos vecinos, tomados en el cálculo de la contribución a la IIS sobre el símbolo en detección. Definiendo la relación señal a ruido como el cociente:

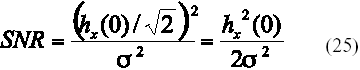
se tiene que la expresión (24) se transforma en:

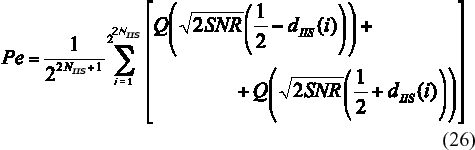
La expresión (26) brinda el marco teórico requerido para la evaluación del desempeño del esquema de codificación OOK en el canal IR inalámbrico, caracterizado por su respuesta al impulso, teniendo en cuenta el ruido y la IIS inducida por el efecto de la propagación multitrayecto.

La validez de (26) puede verificarse fácilmente haciendo d_IIS = 0, situación para la cual se obtiene la probabilidad de error teórica para OOK en el canal AWGN según:

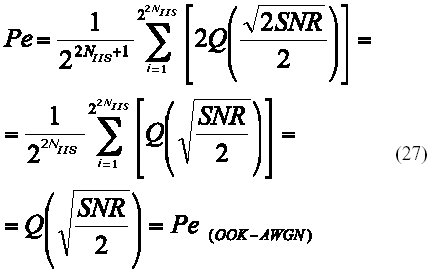
4. Entorno Teórico de Evaluación de la Probabilidad de Error para L-PPM.

La expresión teórica para la evaluación de la probabilidad de error de esquemas L-PPM en el canal AWGN ideal puede encontrarse por varios autores [6]. La probabilidad de error de símbolo en este caso es:

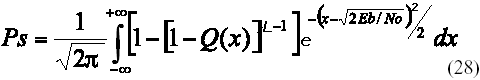
a partir de (28) la expresión de la probabilidad de error de bit se obtiene según [6]:

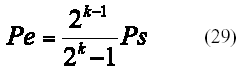
Una expresión analítica para la estimación del desempeño de LPPM en presencia de IIS inducida por la propagación multitrayecto en el canal IR, es mucho más compleja de obtener y para su estimación se han reportado expresiones aproximadas en [7-9]. Normalmente los resultados presentados en los trabajos referidos son obtenidos por simulación. La expresión (28) para el canal AWGN, dada su complejidad, se evalúa de forma numérica.

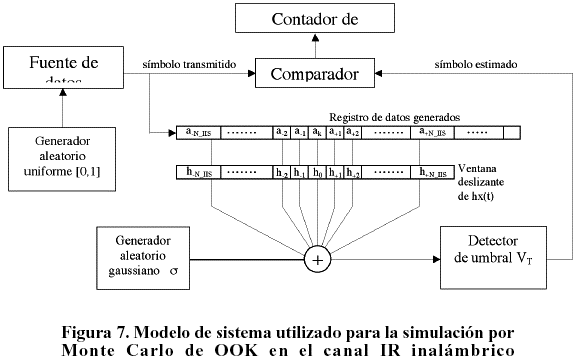
5. Estructura de Modelación de Monte Carlo para la Estimación de la Probabilidad de Error en OOK.

El modelo propuesto para la simulación de Monte Carlo de OOK según (16) puede apreciarse en la Figura 7. La contribución a la IIS se realiza con las dos estructuras centrales de la figura que implementan los dos primeros términos de (16). A medida que se van generando nuevos bits, se van incorporando al registro de datos por su parte izquierda, desestimando el último bit de la derecha y se va realizando la multiplicación término a término con la ventana de hx(t). Posteriormente estos valores se suman junto con la muestra de ruido n(kT) proporcionada por el generador gaussiano y se introducen al detector de umbral VT para obtener un estimado del bit transmitido. El bit transmitido original y su estimado se comparan para contabilizar los errores que ocurren. La probabilidad de error se estima según:

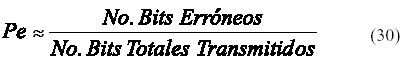
La estimación de la probabilidad de error es mejor mientras mayor es el número de bits transmitidos. La generación de los bits de la fuente de datos binarios se hace a partir de un generador uniforme en el intervalo [0, 1], disponible en prácticamente todos los entornos de programación. Si se identifica la salida del generador como S, los a_k se generan según: a_k=0 " S<0.5, a_k=1 " S>0.5.

A partir de la definición dada para la SNR en (25), las muestras de ruido se obtienen con un generador gaussiano al que se le suministra la desviación estándar s según:

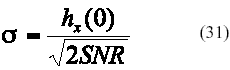
6. Resultados Obtenidos para OOK.

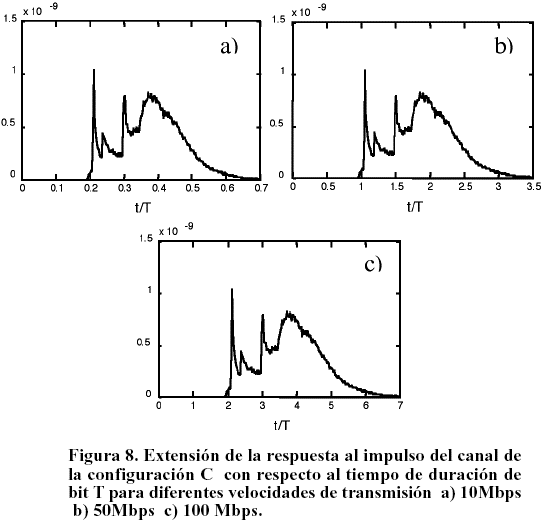
La h_x(t) se obtiene mediante la convolución de la h_eq(t) del canal IR, obtenida por simulación, con una versión discreta de x_ca(t) evaluada analíticamente en función de la velocidad de bit y muestreada a la razón que impone la h_eq(t). El resultado se multiplica por R.P para reproducir la definición en (15). La Figura 8 muestra como la cola de la respuesta al impulso del canal, a medida que aumenta la velocidad de transmisión, invade los tiempos de duración correspondientes a los símbolos vecinos. Se ha tomado para ejemplificar la respuesta al impulso simulada de la configuración C (Tabla I).

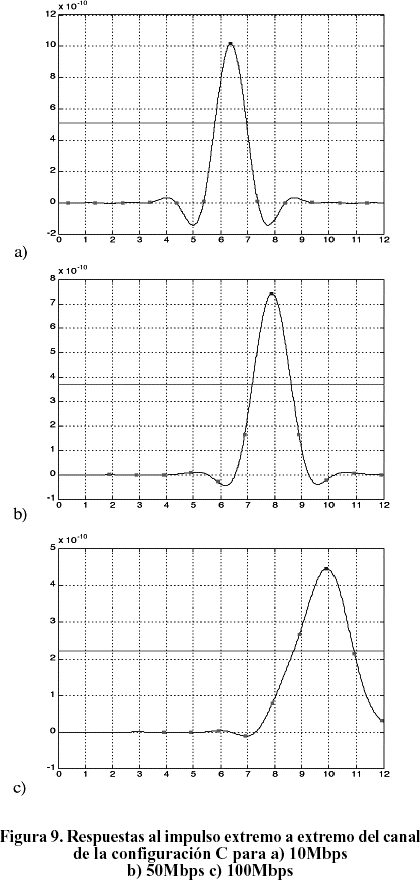
La h_x(t) obtenida para la misma configuración a velocidades de 10, 50 y 100Mbps puede apreciarse en la Figura 9.

En cada respuesta aparecen señalados los instantes de muestreo tomados a la razón t=kT así como el umbral V_T= h_x(0)/2. Puede constatarse como a medida que aumenta la velocidad se modifica la forma inicial prácticamente ideal de h_x(t), produciendo valores no nulos en los instantes de muestreo adyacentes a h_x(0) y por tanto la IIS.

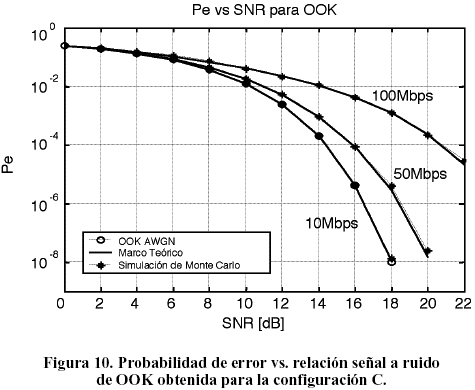
La comparación entre los resultados obtenidos por la evaluación del entorno teórico (26) con N_IIS=6 y la simulación de Monte Carlo con 10⁶ bits generados para la estimación del desempeño de OOK en la configuración C se pueden apreciar en la Figura 10. Las velocidades de transmisión son las mismas vistas anteriormente.

Los resultados obtenidos por ambas vías concuerdan de manera apropiada, demostrando la viabilidad del empleo de la simulación de Monte Carlo para la estimación de la probabilidad de error en estos sistemas.

Es notable también como en el caso de la transmisión a 10Mbps, (Figura 9a), para la cual el canal se comporta como un canal ideal libre de IIS, existe una gran correspondencia entre los resultados obtenidos por simulación y por evaluación del entorno teórico desarrollado y los que se obtienen por la evaluación directa de la probabilidad de error de OOK para el canal AWGN ideal dados por la última parte de la igualdad (27). En la Figura 10 puede apreciarse también la degradación en la probabilidad de error, a medida que aumenta la velocidad de transmisión, producida por la IIS inducida por la propagación multitrayecto en el canal.

Otra lectura de los efectos de la IIS la constituye la penalidad de potencia que impone el aumento de la velocidad, si se desea mantener la misma probabilidad de error.

7. Estructura de Modelación de Monte Carlo para la Estimación de la Probabilidad de Error en L-PPM.

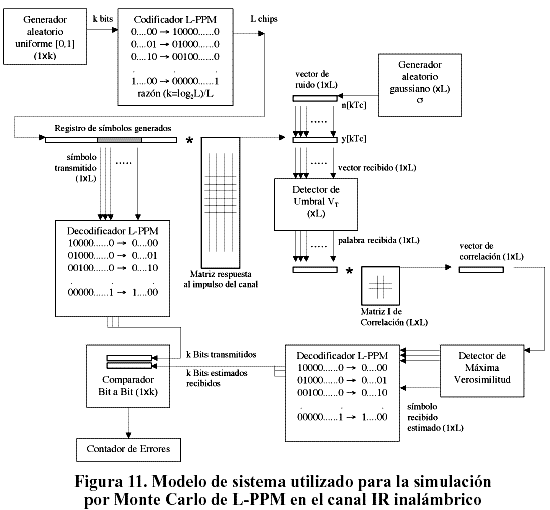
El modelo propuesto para la simulación de Monte Carlo de L-PPM siguiendo el diagrama de la Figura 5 puede apreciarse en la Figura 11.

De forma similar al caso de OOK se generan grupos de k bits, a partir de un generador uniforme en el intervalo [0, 1], que son convertidos en símbolos por el codificador L-PPM, la razón del codificador es k/L = (log₂L)/L.

Los símbolos, compuestos por L chips, van siendo almacenados secuencialmente en el registro de símbolos generados cuya estructura se muestra en la Figura 12.

Consta de un registro central RC de longitud 1xL que almacena el símbolo que emite la fuente a ser procesado y dos registros auxiliares laterales capaces de almacenar la cantidad de chips necesarios (N_IIS) para el cálculo de la IIS sobre cada uno de los chips en R_C. Los desplazamientos dentro del registro ocurren de izquierda a derecha en saltos de L chips, considerando el receptor perfectamente sincronizado, capaz de determinar con exactitud los instantes de comienzo y final de cada símbolo. Por comodidad, en la implementación del algoritmo se toma N_IIS = 8, divisor común para todos los valores de L excepto para L=4. Cuando L toma este valor, el registro acomoda espacio para dos símbolos siguientes en vez de uno, garantizándose la existencia de al menos N_IIS=8 chips a la derecha de RC para el cálculo de la IIS sobre c1.

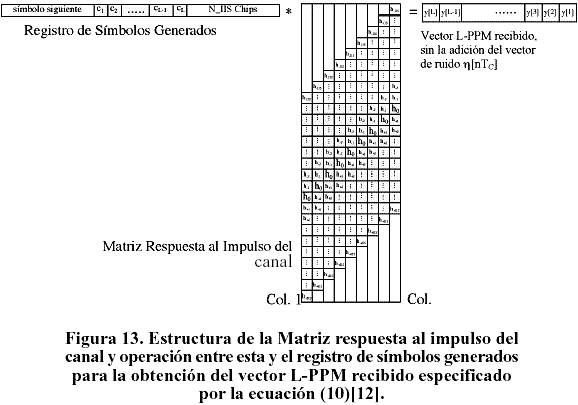
Para contabilizar los efectos de hx(t) sobre todos los chips del símbolo en RC a procesar se emplea una matriz, que se identifica en la Figura 11 como “Matriz respuesta al impulso del canal” cuya estructura se brinda en la Figura 13. Dicha matriz contiene tantas filas

como elementos tenga el registro de símbolos generados y L columnas, correspondientes a los L chips del símbolo en detección. En cada columna almacena, distribuidas convenientemente, las 2N_IIS+1 muestras de h_x(t) para el cálculo de la IIS sobre cada chip del símbolo transmitido.

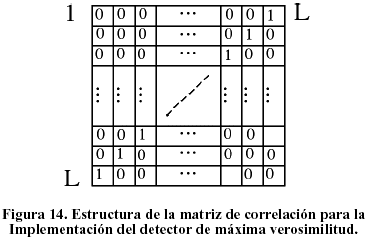
En la Figura 13 aparece representada la operación matricial que se lleva a cabo entre el registro y la matriz, cuyo resultado es el vector L-PPM recibido de componentes y[nTC] correspondientes al símbolo transmitido, que siguen (12) sin tener en cuenta aún el término de ruido añadido h(nTC). Una vez añadido el vector ruido, el vector recibido se pasa por el comparador de umbral V_T = h_x(0)/2, convirtiéndose en una palabra digital recibida que se correlaciona entonces con los L posibles símbolos transmitidos del esquema L-PPM, almacenados en las L columnas de una matriz I a la que se ha llamado Matriz de correlación, de (LxL) elementos y cuya estructura puede apreciarse en la Figura 14.

El resultado de la operación matricial [y[nTC] + h[nTC]]*I es un vector de correlación de dimensión (1xL), que en ausencia de ruido e IIS, tiene un único elemento en ‘1’, indicando correlación máxima de la palabra digital recibida con uno de los L símbolos posibles del esquema L-PPM. En presencia de ruido e IIS el vector de correlación alimenta al detector de máxima verosimilitud que debe decidir, sobre la base de las correlaciones calculadas, cuál es el símbolo recibido más probable. El vector de correlación obtenido puede tener tres formas posibles: la primera que tenga un solo elemento en ‘1’ y los demás en ‘0’, indicando correlación con un solo símbolo de los L posibles (operación normal); la segunda, que tenga Ep elementos en ‘1’, indicando correlación con más de uno de los L símbolos posibles y la tercera, que todos sus elementos sean ‘0’, indicando que la palabra digital recibida no correlaciona con ninguno de los L elementos del esquema. Las dos últimas situaciones corresponden a la operación del sistema bajo niveles de ruido e IIS elevados, en cuyo caso la respuesta del detector de máxima verosimilitud será escoger al azar uno de los E_p elementos que dan correlación, para un vector de correlación múltiple, o uno de los L elementos posibles si el vector de correlación es nulo. Después de realizada la estimación del símbolo recibido, el mismo se decodifica y se compara su secuencia de k bits con la del símbolo real transmitido. Las diferencias entre ambas alimentan el contador de errores de bit. En este caso la probabilidad de error de bit se estima a partir de la expresión:

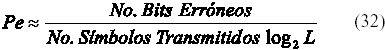
Considerando el transmisor L-PPM como un codificador de bloque (k bits – L chips) con razón de código R=k/L = log₂L/L, de manera similar a como se hace en [7,8], la SNR para L-PPM puede definirse como:

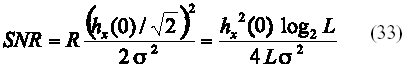
donde las muestras de ruido que se generan en el generador aleatorio gaussiano lo hacen con una desviación estándar:

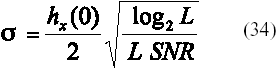
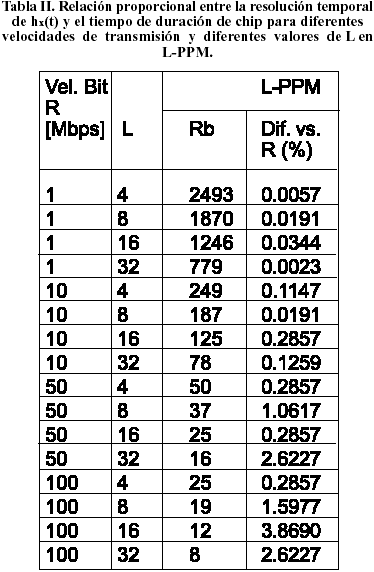
Debe existir una relación proporcional entre la resolución temporal de la respuesta al impulso del canal (D) y el tiempo de chip (T_C) del esquema L-PPM a simular en dependencia de la velocidad de bit y el número de niveles L. A partir de establecer la relación:

T_C = Rb D             (35)

Donde Rb es la constante de proporcionalidad, como T_S = L.T_C = L.kT, con R=1/T la velocidad de bit, queda que:

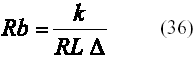
La Tabla II muestra los valores de la constante Rb para diferentes velocidades de transmisión y diferentes valores de L; en caso de ser fraccionaria se ajusta al valor entero más cercano, provocando una ligera variación en la velocidad de bit, cuya diferencia porcentual con respecto al valor indicado también se incluye en la tabla.

8. Resultados Obtenidos para L-PPM.

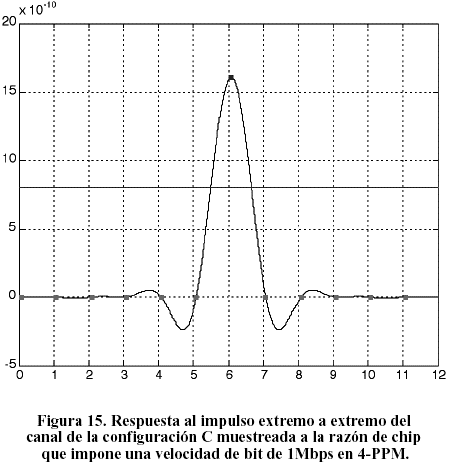
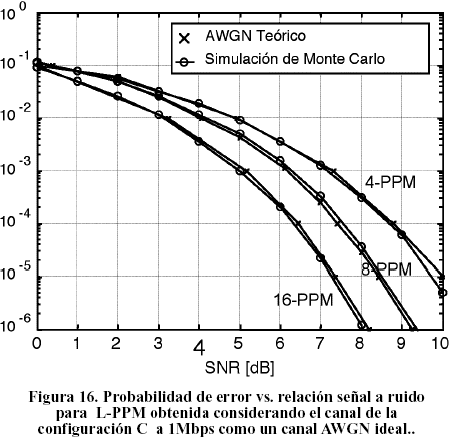
En la Figura 15 se aprecia la h_x(t) para la configuración C Tabla I) muestreada a la razón que impone una velocidad, de 1Mbps para 4-PPM. Como puede observarse a esta velocidad el canal se comporta como un canal libre de IIS equivalente al canal ideal AWGN. En la Figura 16 se presentan los resultados obtenidos de la evaluación del desempeño teórico de un esquema 4, 8 y 16-PPM sobre el canal AWGN [6] y la modelación por Monte Carlo de este mismo esquema sobre el canal de la configuración C, a 1Mbps, considerado como AWGN libre de IIS. La correspondencia entre ambos resultados puede ser fácilmente verificada.

III. CONCLUSIONES.

1. La expresión teórica que permite la evaluación directa de la probabilidad de error de la OOK, tiene en cuenta la IIS inducida por la propagación multitrayecto en el canal.

2. La expresión propuesta prueba su validez al ser reducible a la expresión de la probabilidad de error teórica de OOK para el canal AWGN ideal cuando se hace nulo el término relacionado con la IIS.

3. La incorporación en el esquema de Monte Carlo propuesto para el análisis de la OOK de dos estructuras, el registro de datos generados y la ventana de la respuesta al impulso del canal, posibilitan incluir en la estimación de la probabilidad de error, además del ruido modelado como blanco gaussiano, los efectos de la interferencia entre símbolos inducida por la propagación multitrayecto en el canal.

4. Las estructuras equivalentes para el caso de L-PPM son el registro de símbolos generados y la matriz respuesta al impulso de canal.

5. Los resultados de modelación obtenidos de la evaluación del desempeño de la OOK a partir del esquema propuesto concuerdan adecuadamente con los resultados ofrecidos tanto por el entorno teórico desarrollado como con los que se obtienen por la evaluación directa de la expresión teórica de la probabilidad de error para OOK en el canal ideal AWGN para una velocidad de transmisión en la que puede considerarse nula la interferencia entre símbolos.

6. En el caso de L-PPM los resultados de modelación obtenidos de la evaluación del desempeño, para varios valores de L (ej. 4, 8 y 16) a partir del esquema propuesto, para una velocidad de transmisión a la que puede considerarse el canal tomado como AWGN ideal, concuerdan igualmente de forma adecuada con los resultados ofrecidos por el entorno de teórico de evaluación de la probabilidad de error para L-PPM reportado por varios autores.

7. Estos resultados representan una especie de “puesta a cero” o “calibración” de los esquemas de modelación de Monte Carlo desarrollados, lo cual evidencia la viabilidad de los mismos para el estudio de la IIS que se presenta en el canal producto de la propagación multitrayecto para velocidades de transmisión superiores.

8. Los principios básicos utilizados en las estructuras desarrolladas pueden extrapolarse y ser aplicados exitosamente en el desarrollo de otros esquemas similares para el estudio del desempeño de nuevos esquemas de transmisión, tanto de codificación banda base como de modulación de subportadora eléctrica en el canal IR inalámbrico.

IV. REFERENCIAS.

1) KAHN J. M. AND J. R. BARRY: “Wireless Infrared Communications,” Proceedings of the IEEE, vol. 85, Feb. 1997 no. 2, pp. 265-298.        [ Links ]

2) CARRUTHERS J. B. AND J. M. KAHN: “Modeling of Nondirected Wireless Infrared Channels," IEEE Trans. on Commun., Vol. 45, Oct. 1997 No. 10, pp. 1260-1267.        [ Links ]

3) CARRUTHERS J. B. AND P. KANNAN: “Iterative Site-Based Modeling for Wireless Infrared Channels," IEEE Transactions on Antennas and Propagation, vol. 50, May 2002 pp. 759-765.        [ Links ]

4) ALQUDAH Y. A., M. KAVEHRAD: "On Optimum Order of Angle Diversity with Equal-Gain Combining Receivers for Broadband Indoor Wireless Infrared Communications," IEEE Transactions On Vehicular Technology, Vol. 53, Jan. 2004 pp. 94-105, No. 1.        [ Links ]

5) AKHAVAN K., M. KAVEHRAD AND S. JIVKOVA: "High-Speed Power-Efficient Indoor Wireless Infrared Communication Using Code Combining, Part I" Communications, IEEE Transactions on , Vol. 50, July 2002 No.7 , pp.1098 -1109,.        [ Links ]

6) PROAKIS, JOHN G. AND MASOUD SALEHI: “Contemporary Communications Systems Using MATLAB”,. PWS Publishing Company, ISBN 0-534-37173-6, 2000, pp 88-121.        [ Links ]

7) AUDEH M.D., J.M. KAHN AND J.R. BARRY: “Performance of Pulse-Position Modulation on Measured Non-Directed Indoor Infrared Channels”, IEEE Trans. on Comm., vol. 44, June 1996 pp. 654-659.        [ Links ]

8) PARK H. AND J. R. BARRY: “Performance of Multiple Pulse Position Modulation on Multipath Channels”, IEE Proceedings: Optoelectronics, vol. 143, no. 6, 1996 pp. 360-364.        [ Links ]