SÍNTESIS Y DISEÑO DE SISTEMAS DE ESTRUCTURA VARIABLE.

Marcano Gamero, Cosme Rafael

MSc. Cosme Marcano Gamero: Profesor Agregado en el Dpto. de Ingeniería Electrónica de la Universidad Nacional Experimental Politécnica “Antonio José de Sucre”, (UNEXPO) Vicerrectorado Puerto Ordaz, Final Calle China, Urbanización Villa Asia, Puerto Ordaz, Edo. Bolívar, Venezuela, Teléfono 9619965, correos electrónicos cmarcano@poz.unexpo.edu.ve y cosmemarcano@yahoo.com.

Resumen.- El objetivo principal de este trabajo consiste en comparar el comportamiento de una planta física bajo control de un Sistema de Estructura Variable (SEV) con el exhibido por la misma planta pero operando bajo control de un controlador convencional de tipo proporcional, retroalimentando, en ambos casos, la integral del error de la variable de referencia. La comparación es realizada a través de simulaciones digitales en MATLAB, en el dominio del tiempo. Los resultados obtenidos corroboran la disminución de tiempos de respuesta y de establecimiento; así como del máximo sobredisparo, el cual es prácticamente cancelado debido a la alternancia propia de los SEV, que obliga al sistema a entrar en los llamados Modos Deslizantes, hasta alcanzar un nuevo punto de operación. En la síntesis y diseño de los SEV utilizados en este trabajo, se utilizaron los conceptos básicos expuestos por V. Utkin et al., además de otras consideraciones como la optimización según algún Índice de Funcionamiento, propuesta por Krassowsky, y aquellas relacionadas con la estabilidad asintótica, usando el Segundo Método de Estabilidad de Lyapunov, propuesto por H. Sira-Ramírez, con el fin de mejorar el comportamiento general del sistema.

Palabra clave: Sistemas de Estructura Variable/ Modos Deslizantes/ Optimización.

SYNTHESIS AND DESIGN OF VARIABLE STRUCTURE SYSTEMS

Summary: The main objective of this work is to compare the behavior of a physical plant under the control of a Variable Structure System (VSS), with that showed by the same plant but operating under the control of a conventional controller of proportional kind, feeding back, in both cases, the error integral of the reference variable. The comparison is made through digital simulations with the MATLAB in the control of time. The results obtained confirm the decrease of response and settling times, as well as of the maximum overshoot, which is practically cancelled due to the alternation that is a characteristic of the VSS, and which forces the system to enter the so called Sliding Modes until it reaches a new operating point. In the synthesis and design process of the VSS used in this work, the basic concepts introduced by V. Utkin et al. were used, besides other considerations such as optimization according to the Performance Criterion proposed by Krassowsky, and those related to the asynthotic stability using the Second Stability Method of Lyapunov, proposed by H. Sira-Ramírez, in order to improve the overall system performance.

Keywords: Optimization/ Sliding Modes/ Variable Structure Systems.

Finalizado el 2005/03/17   Recibido el 2005/04/10   Aceptado el 2005/06/03.

I. INTRODUCCIÓN.

Existen muchas estrategias de control diseñadas para mejorar el comportamiento de los sistemas físicos desde diversos puntos de vista. Así, existen estrategias destinadas a disminuir los tiempos de respuestas y de establecimiento de los sistemas cuando son someetidos a la acción de ciertas señales de referencia. Por otro lado, existen aquellos dedicados a atenuar sobredisparo, i.e., la máxima diferencia entre el valor deseado y el valor medido de la variable controlada, asumiendo la estabilidad asintótica del modelo utilizado; también se pueden encontrar estrategias dirigidas fundamentalmente a lograr que el sistema sea estable. Los Sistemas de Estructura Variable (SEV) introducidos por Vadim Utkin et al., en la extinta Unión Soviética, a principios de los años setenta del siglo XX, tratan (y en buena medida, logran) mejorar todas estas características del sistema controlado simultáneamente, como se pretende demostrar en este trabajo de investigación.

En este trabajo, se diseña un sistema de control basado en la filosofía de Sistemas de Estructura Variable (SEV), [1] y [2], la cual consiste básicamente de la selección de ciertas ganancias de realimentación, que determinan el comportamiento de un sistema físico cuando es sometido a la acción de dicho sistema de control.

La planta física considerada consiste de un motor DC, acoplado directamente a una carga, a la cual se le desea controlar la velocidad de giro. La metodología utilizada consiste en la realización y comparación de una serie de simulaciones digitales utilizando el paquete de análisis numérico conocido como MATLAB de MathWorks, Inc, ejecutándose sobre una plataforma computacional basada en un procesador Intel Pentium IV, 2.4 GHz.

El análisis del sistema, partiendo desde la formulación del modelo matemático hasta la obtención de los resultados de las simulaciones, se realiza en el dominio del tiempo, i.e., en términos de ecuaciones diferenciales, que son resueltas por medio de métodos numéricos, como los de cuarto orden de Runge-Kutta, y son presentados en forma gráfica, utilizando las herramientas que ofrece MATLAB.

Este trabajo consiste en la comparación del comportamiento del sistema controlado sometido a la acción de un SEV, por un lado, y a la acción de un controlador del tipo proporcional, por la otra. En ambos casos se realimenta la integral del error de velocidad angular (la variable controlada), con lo cual se ha demostrado, [3], que se atenúan los efectos de perturbaciones externas. Los resultados muestran mejoras importantes en el comportamiento del sistema controlado por el SEV, en términos de disminución de los tiempos de respuesta y establecimiento, atenuación de sobredisparos, fidelidad en el seguimiento de cambios en la señal de referencia, imperturbabilidad ante variaciones en los valores de los parámetros, entre otras. Además, los SEV ofrecen una mayor versatilidad en la selección de los valores de las ganancias de realimentación de los controladores, lo cual les confiere una mayor robustez en ambientes industriales hostiles.

II. DESARROLLO

1. Descripción del sistema a controlar.

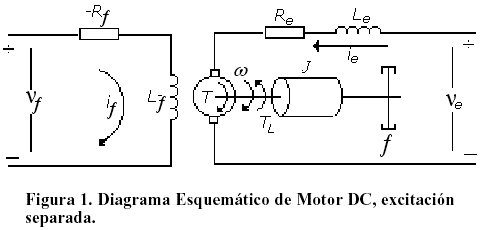
En el presente trabajo, se utiliza un sistema conformado por un motor de corriente continua (motor DC), a excitación separada: por campo y por armadura, con carga asociada, cuyo esquema se muestra en la Figura 1, para el que se diseñará un sistema de control de estructura variable destinado a controlar la velocidad angular del sistema motor-carga, [4].

La Tabla I, que aparece a continuación, contiene la definición de las abreviaturas así como los valores de estos parámetros que serán utilizados posteriormente en la simulación. Asimismo, en esta tabla se muestran las condiciones iniciales del sistema, en términos de la velocidad angular y las intensidades de corriente de campo y de armadura. Estos valores son tomados como el punto de equilibrio alrededor del cual se linealizará el modelo matemático del sistema motor-carga.

2. Deducción del modelo matemático.

Las ecuaciones de estado que describen el comportamiento del sistema son las siguientes:

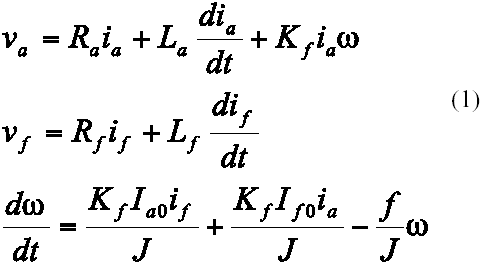
donde K_f es una constante. Nótese que el término K_f i_aw representa la fuerza contraelectromotriz (back emf), debida a la rotación de la armadura dentro de un campo magnético. Linealizando las ecuaciones en torno a un punto de operación, incluyendo un controlador integral, queda:

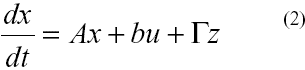
en donde x = [x₁ x₂ x₃ x₄]^T representa el vector de estado. Definiendo x_i,  i = 1,2,...4, como variables de desviación respecto de un punto de equilibrio, se obtiene así las siguientes definiciones:

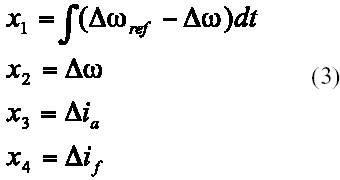
y la variable manipulada viene a ser:

Por último, la señal de comando viene dada por z = Dw_ref, i.e. la variación de la velocidad angular.

3. Síntesis del sistema de control de estructura variable (sev) para control por corriente de armadura.

Las ecuaciones de estado que describen el comportamiento del sistema se pueden expresar en forma matricial presentada en (2), tomando:

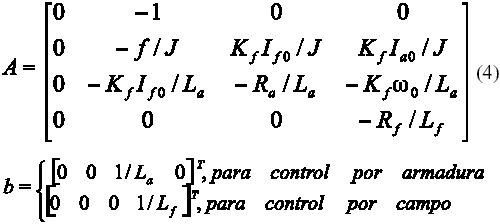
y, como x₁, es decir, la integral de la desviación del error de velocidad, es la variable de control, entonces G = [1 0 0 0].

Siguiendo el procedimiento de diseño de Krassowsky, se define una matriz de transformación, M, tal que  = MAM^-1, en donde  representa la matriz A del sistema transformada por la matriz M. Esta transformación consiste típicamente en permutaciones de filas y columnas de la matriz identidad, I, con lo cual se logra un cambio de base en el espacio de estados; de acuerdo a las características propias del sistema que se desea controlar. También se puede aprovechar esta matriz de transformación para incorporar algún factor de ganancia que resultare conveniente para mejorar el desempeño del sistema controlado. Si se toma:

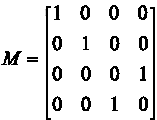
la matriz transformada del sistema, Â , viene a ser:

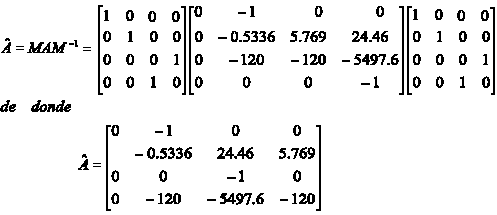
Nótese la permutación de las terceras y cuartas filas y columnas de la matriz original. Nótese además que tanto M como su inversa son iguales.

Por otro lado, se define la matriz Q, como:

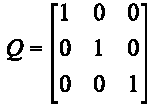
la cual es de tres dimensiones, por cuanto se trabaja sobre la síntesis de un SEV conformado por una sola dimensión de conmutación, i.e., m=1, en tanto que la dimensión del sistema original es n=4; de la teoría, se desprende el hecho de que la dimensión del controlador resultante es de n-m=3.

Seguidamente, se particionan convenientemente las matrices:

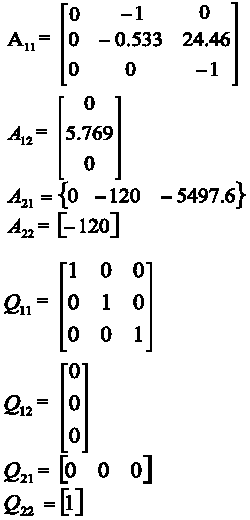
Nótese que Q₂₂^-1 = Q₂₂ = [1]. Seguidamente, se obtienen las matrices transformadas de acuerdo a las siguientes expresiones, derivadas por Krassowsky:

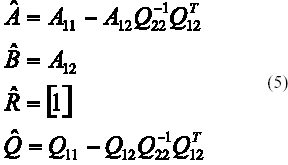
Siguiendo el procedimiento propuesto por Krassowsky, se requiere obtener la solución algebraica de la ecuación de Ricatti, para el cálculo de las ganancias del controlador. La ecuación de Ricatti correspondiente, se muestra a continuación:

cuya solución algebraica se obtiene fácilmente en MATLAB utilizando la función ARE (Algebraic Ricatti Equation), como se muestra a continuación.

Seguidamente, se procede a calcular el vector de conmutación, i.e., los valores de los gradientes de la Superficie de Deslizamiento, las cuales se definen como sigue:

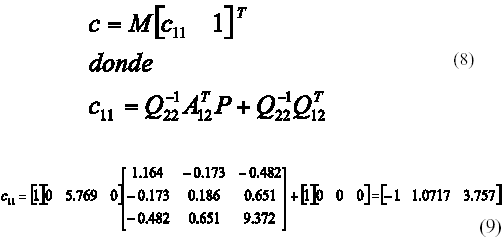
4. Simulaciones y resultados.

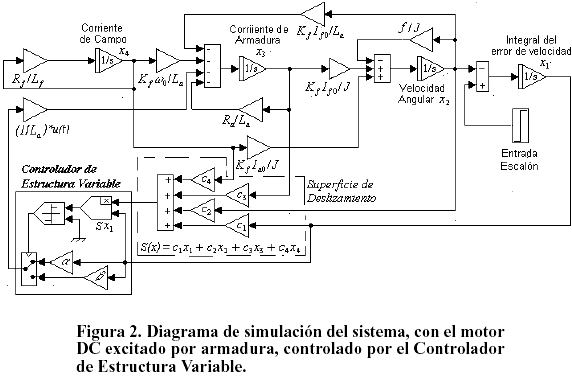
Una vez obtenidas las expresiones algebraicas del modelo del sistema a controlar y del controlador de estructura variable respectivo, se procede a elaborar el diagrama de simulación adecuado para simulink, la caja de herramientas propia de MATLAB y que permite obtener las gráficas que muestran el comportamiento del sistema bajo acción del controlador diseñado. Un diagrama de simulación adecuado se muestra en la Figura 2.

A continuación se muestra un programa en Matlab que permite obtener los valores de los coeficientes de la Superficie de Deslizamiento c_i, i = 1,2...,n-1, para el caso del motor gobernado por armadura. Nótese que c_n = 1, por convención. Asimismo, se obtienen los valores de las ganancias de realimentación.

Programa en MATLAB

% Motor DC, excitado separadamente, controlado por armadura (Vf = constante)

%Matrices del Sistema

A=[0 -1 0 0;0 -.5336 5.769 24.46;0 -120 -120 -5497.6; 0 0 0 -1];

B=[0 0 100 0]

C=[1 0 0 0]

D=[0 0 0 0]

% Definición de la Matriz M.

M = [1 0 0 0;0 1 0 0;0 0 0 1;0 0 1 0]

% Cálculo de la inversa IM = M^-1

IM = inv(M)

Definición de la Matriz Q como la matriz identidad. Nótese que más adelante se completa la definición de Q, con Q22, y que AT representa la matriz del sistema, A, transformada por M, que se aparece en el texto como .

Q=eye(3)

AT = M*A*IM

Obsérvese que, en este caso, M es igual a su inversa y AT = MAM^-1 es igual a la matriz A pero con la tercera fila intercambiada con la cuarta, así como la tercera columna intercambiada con la cuarta, esto es:

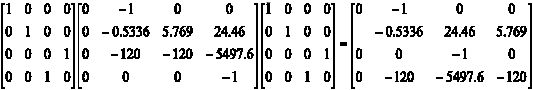
Seguidamente, se particionan las matrices:

A11 = [AT(1,1) AT(1,2) AT(1,3);AT(2,1) AT(2,2) AT(2,3); AT(3,1) AT(3,2) AT(3,3)]

A12 = [AT(1,4); AT(2,4); AT(3,4)]

A21 = [AT(4,1) AT(4,2) AT(4,3)]

A22 = AT(4,4)

Q11 = [1 0 0; 0 1 0; 0 0 1]

Q12 = [0; 0 ; 0]

Q21 = [0 0 0]

Q22 = 1

Nótese que, para dar generalidad a este programa, se calcula a continuación , que, dada la escogencia de Q, será igual a uno..

Las expresiones restantes que aparecen a continuación corresponden con las expresiones (5), salvando algunas diferencias en la nomenclatura, debidas a las limitaciones de MATLAB de utilizar superíndices y subíndices..

AA = A11 - A12*InvQ22*Q12'

BB = A12

RR = [1]

QQ = Q11 - Q12*InvQ22*Q12'

% Cálculo de la solución algebraica de la ecuación de Ricatti, para obtener las

% ganancias de realimentación

P=ARE(AA,BB*(inv(RR))*BB',QQ)

% Cálculo del vector de conmutación, i.e., los valores de las constantes de la

% Superficie de Deslizamiento (cfr. (8)) como sigue:

c11 = InvQ22*A12'*P + InvQ22*Q12'

Nótese que c es un vector de n componentes y c₁₁ que representa un vector conformado por las primeras (n-1) componentes de c, y se designa como c₁₁ para evitar confusiones con el primer componente de dichos vectores, i.e., c₁. Finalmente, las ganancias de realimentación del controlador de estructura variable se calculan utilizando la expresión c^Ta¹, en donde a¹ representa la primera columna de la matriz A del sistema. Nótese que la razón de muchas de las manipulaciones que se realizan a lo largo del procedimiento de diseño sobre las matrices del sistema, apuntan, entre otra razones, a obtener un c^Ta¹ igual a cero, para facilitar la implementación de los controladores de estructura variable, dando mucha mayor libertad para la escogencia de los valores de las ganancias de realimentación, a y b, permitiendo, por ejemplo, escoger ganancias de igual magnitud pero diferente signo. Nótese igualmente que, en el programa en MATLAB, CTA1 = c^Ta¹.

c = [c11,1]

CTA1 = c*[A(1,1) A(2,1) A(3,1) A(4,1)]'

En muchos casos, como el que se utilizó en este trabajo, se puede anticipar que este resultado será igual a cero, notando que los elementos de la primera columna de la matriz A original son iguales a cero. No obstante, es necesario realizar todo el procedimiento de diseño del controlador, debido a que siempre será necesario obtener los coeficientes del vector de conmutación para establecer el criterio de conmutación entre una ganancia y otra, la cual no es otra que S*x₁ > 0, según la siguiente ley de conmutación:

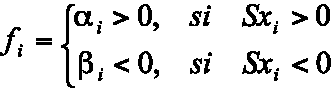
en donde f representa la ganancia de realimentación.

5. Análisis de resultados.

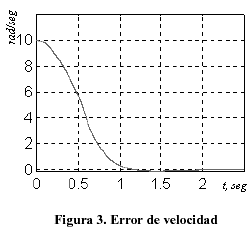
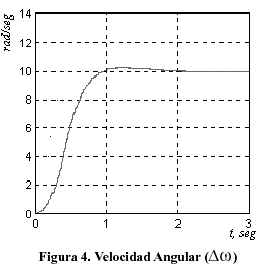
Las Figuras 3 a 6, que aparecen a continuación, muestran el comportamiento de las variables del sistema. Como se puede apreciar, el error de velocidad angular, i.e., la diferencia entre el valor nominal deseado y el valor final alcanzado por el sistema controlado, tiende a cero en poco más de un segundo (Figura 3), lo cual es consistente con el tiempo que demora en alcanzar la velocidad deseada (Figura 4).

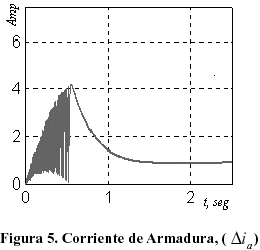
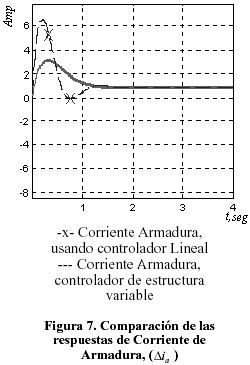
Por otra parte, la variación de la corriente de armadura presenta rápidas conmutaciones en su régimen transitorio, pero rápidamente se establece alrededor de 1A de incremento por encima del valor en el punto de equilibrio, alrededor del cual se linealizó el modelo matemático. En términos absolutos, para que el sistema experimente un incremento de 10 rad/seg en su velocidad angular, y comience a girar a 78.62 rad/seg (véase Tabla 1), la corriente de armadura debe experimentar un aumento de 1 A, aproximadamente, debiendo operar entonces con una corriente de armadura de 7.36 A. Finalmente, se aprecia, como era de esperarse, una variación nula en la corriente de campo, por cuanto el motor DC está siendo excitado por armadura, por lo que, en estas condiciones, actúa como un motor DC de imán permanente.

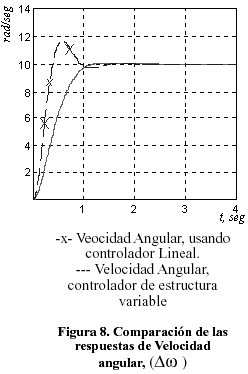
Para propósitos de comparación, las gráficas correspondientes a la variable controlada, i.e., la velocidad angular, como a la variable manipulada, o sea, la corriente de armadura, cuando el sistema está bajo control de un controlador proporcional, con realimentación de la integral del error de velocidad, se muestra en las Figuras 7 y 8:

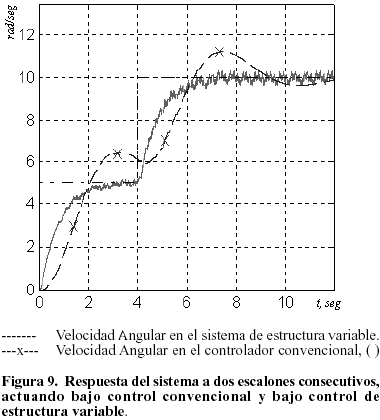
Nótese que, en ambos casos, las gráficas obtenidas a partir del sistema controlado por el controlador proporcional muestran un máximo sobredisparo de magnitud mayor a los presentados por el sistema sometido a la acción del SEV, aunque los tiempos de establecimiento no son sensiblemente diferentes. No obstante la fortaleza de los SEV frente a los controladores convencionales también se evidencia que éstos últimos permiten que el sistema pueda seguir con mayor fidelidad las variaciones en la entrada de referencia que los controladores convencionales como se puede apreciar en la Figura 9, en donde el sistema es sometido a dos entradas tipo escalón, que representan variaciones de 5 rad/seg cada uno, separadas en tiempo por 4 seg. Se puede observar que la fidelidad del controlador convencional es significativamente menor al SEV.

III. CONCLUSIONES.

De la teoría subyacente a los Sistemas de Estructura Variable y de los resultados obtenidos en las simulaciones digitales que se llevaron a cabo se desprenden las siguientes conclusiones:

1. Los Sistemas de Estructura Variable están conformados por subsistemas o estructuras continuas que son conmutadas en forma alternativa.

2. La Ley de Control resultante es, en realidad, una función continua a trozos.

3. Las trayectorias de estado del sistema sometido a la acción de este tipo de sistemas de control presentan modos particulares de funcionamiento conocidos como Modos de Deslizamiento.

4. El diseño de estos controladores se reduce entonces a escoger los parámetros de dichos subsistemas y la lógica de conmutación adecuada, de tal manera que se satisfagan las condiciones de existencia de los modos de deslizamiento.

5. Los sobredisparos son notablemente atenuados por efecto de la rápida conmutación de las estructuras que conforman al sistema de Estructura Variable. En consecuencia, la salida de  sistema controlado muestra un comportamiento críticamente amortiguado.

6. El seguimiento de la señal de entrada es mucho más fidedigna cunado el sistema está sometido a ala acción de los SEV.

IV. REFERENCIAS

1) Marcano G., Cosme R. Síntesis y Diseño de Controladotes de Estructura Variable, Trabajo de Maestría, Universidad Nacional Experimental Politécnica “Antonio José de Sucre”, Puerto Ordaz - Venezuela, Mayo 2.004.        [ Links ]

2) Marcano G., Cosme R. Sistemas de Estructura Variable, Trabajo de Grado, Universidad de los Andes, Mérida–Venezuela, Mayo 1986.        [ Links ]

3) Kailath, Thomas. Linear Systems, Prentice may, Englewood Cliffs, New Jersey EE.UU.1980.        [ Links ]

4) Yuan Yih Hsu y Wah-Chun Chan Optimal Variable Structure Controller for DC Motor Speed Control, IEE Proceedings, Vol. 131, November 1984.        [ Links ]

5) Utkin, Vadim. Variable Structure Control, Automation and Remote Control, 44, pp. 1105-1119, september 1983.        [ Links ]

6) Sira-Ramírez, Hebert. Nonlinear Sliding Manifolds for Linear and Bilinear Systems. Conférence Internationale Francophone d'Automatique, CIFA' 2000. París, 2000.        [ Links ]